Abstract
Transition-metal dipnictide PtBi2 exhibits rich structural and physical properties with topological semimetallic behavior and extremely large magnetoresistance (XMR) at low temperatures. We have investigated the electrical and magnetic properties of trigonal-phase PtBi2-x single crystals with x ~ 0.4. Profound de Haas–van Alphen (dHvA) and Shubnikov-de Haas (SdH) oscillations are observed. Through fast Fourier transformation (FFT) analyses, four oscillation frequencies are extracted, which result from α, β, γ, and δ bands. By constructing the Landau fan diagram for each band, the Berry phase is extracted demonstrating the non-trivial nature of the α, β, and δ bands. Despite Bi deficiency, we observe the Zeeman splitting in dHvA and SdH oscillations under moderate magnetic field and the moderate Landé g factor (4.97–6.48) for the α band. Quantitative analysis of the non-monotonic field dependence including the sign change of the Hall resistivity suggests that electrons and holes in our system are not perfectly compensated thus not responsible for the XMR effect.
Similar content being viewed by others
Introduction
Transition-metal dipnictide PtBi2 can crystalize in multiple structures, including the cubic, hexagonal (or trigonal), and two orthorhombic phases.1 While it has been considered as an excellent electrocatalyst,2 attention is recently paid to its exotic electronic properties. For the cubic phase, the electronic structure calculations predict a three-dimensional (3D) Dirac point along the Γ–R direction.3 Experimental investigation has indeed shown that the cubic PtBi2 exhibits Shubnikov–de Haas (SdH) oscillations with the non-trivial Berry phase.4 It was also proposed that the extremely large magnetoresistance (XMR) is due to the nearly compensated electron and hole concentration.4 Under hydrostatic pressure, the cubic PtBi2 also exhibits superconductivity.5 These rich phenomena seen in the cubic phase give rise to an important question: what is the role of the crystal structure in PtBi2? In other words, would properties be observed as in the cubic phase present in PtBi2 crystalized in different structures?
For the trigonal PtBi2, both band calculations and angle-resolved photoemission spectroscopy indicate the existence of linear dispersive Dirac bands located at Γ and M points,6,7 which may be responsible for the linear field dependence of the magnetoresistance.8 However, these Dirac bands are identified to be trivial without topological protection.6 While quantum oscillations are also observed,9 the topologies of individual bands are yet to be investigated. In addition, it was proposed that the XMR effect is caused by disorder due to Bi deficiency in the trigonal-phase PtBi2−x.6,8 In view of reported results summarized in Table 1, the XMR effect tends to be weaker in the trigonal phase than that in the cubic structure. Further study is thus necessary in order to understand the structure–property relationship in this unique system.
In this article, we report the experimental investigation on the trigonal PtBi2–x with Bi deficiency (x ~ 0.4). Both the XMR effect and profound SdH and de Haas–van Alphen (dHvA) oscillations are observed. Four oscillation frequencies are identified, corresponding to the α, β, γ, and δ bands. Quantitative data analysis allows to extract their effective masses and Berry phases. We also observe the Zeeman splitting in both the dHvA and SdH oscillations. This work sheds light on several unsolved issues: (1) despite Bi deficiency, PtBi1.6 exhibits long quantum relaxation time with small scattering; (2) there is clear evidence for non-trivial Berry phase for α, β, and δ bands; and (3) the XMR effect might not be attributed to either electron–hole compensation nor disorder but intrinsic to clean samples.
Results and discussion
Crystal structure and magnetotransport
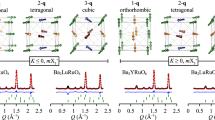
According to energy dispersive X-ray spectroscopy (EDS) measurements on several as-grown single crystals, the actual ratio of Pt:Bi ~ 1:1.6, indicating Bi deficiency compared with the targeted stoichiometry. Nevertheless, the powder and single crystal X-ray diffraction (XRD) pattern of PtBi1.6, shown in Fig. 1a, reveals peaks that are consistent with the trigonal structure with the space group of P31m (No. 157). The lattice parameters are a = b ~ 6.58 Å and c ~ 6.17 Å, consistent with previous reports.10 Theoretical calculations9 also suggest the same structure.
a Powder (black curve) and single crystal (red curve) XRD pattern of PtBi1.6 compared with the standard pattern for P31m (blue column).10 Inset: Picture of PtBi1.6 single crystals. b Temperature dependence of the ab-plane resistivity ρab. The solid line is the fit of data to the BG formula. Inset: ρab(T) below 20 K and fitting curve (solid line). c Temperature dependence of ρab(T) under different fields with H // c. The dashed line represents 3.5ρab(T, H = 0). Inset: field dependence of n and A. d Kohler plot: MR versus H/ρab(T, H = 0). The solid line is the fit to MR = 50(H/ρab(0))1.4. e dρab/dT as a function of temperature in the indicated fields. Two characteristic temperatures Tm (at which dρab/dT = 0) and Ti (at which dρab/dT is the minimum) are marked by arrows. f Field dependence of temperatures Tm and Ti (the error bars are estimated based on the nearest Tm or Ti intervals). The dashed line is the fit of Tm to Tm = 13.8(H−Hc)0.23.
Figure 1b shows the temperature dependence of the in-plane resistivity (ρab) between 2 and 300 K. Upon increasing temperature, ρab increases with ρ(2 K) = 0.82 μΩ cm and ρ(300 K) = 133 μΩ cm. This gives the residual resistivity ratio RRR = ρ(300 K)/ρ(2 K) ~ 162. Compared to another trigonal P31m-phase PtBi2,9 our sample exhibits smaller RRR, but larger than that in P\(\bar 3\)-phase PtBi28,11 (see Table 1). The small residual resistivity (~ρ(2 K)) and large RRR indicate high quality of our single crystals, despite Bi deficiency. Quantitatively, the high-temperature ρab(T) can be fitted by the Bloch–Grüneisen (BG) formula \(\displaystyle\rho _{ab}(T) = \rho _{ab}(0) + A_{\mathrm {el - ph}}\left( {\frac{T}{{\theta _D}}} \right)^5\mathop {\int }\nolimits_0^{\theta _{\mathrm{D}}/T} \frac{{x^5}}{({e^x - 1})({1 - e^{ - x}})}{\mathrm{d}}x\), where ρab(0) is the residual resistivity, Ael–ph is an electron–phonon interaction constant, and θD is the Debye temperature.12 With ρab(0) ~ 0.8 μΩ cm, Ael–ph ~ 257 μΩ cm, and θD ~ 143 K, the BG formula describes ρab(T) well between 20 and 300 K, as illustrated in Fig. 1b with the solid line. The θD value is almost identical to that obtained from the specific heat of P\(\bar 3\)-phase PtBi2.11 The low-temperature ρab(T) follows the power law ρab = ρab(0) + ATn with ρab(0) = 0.8 μΩ cm and n ~ 2.9, as shown in the inset of Fig. 1b. This implies dominant electron–phonon scattering in our system rather than electron–electron scattering reported in ref. 11
Figure 1c exhibits the temperature dependence of ρab under different magnetic field (H) applied along the c direction. Note that the application of H gradually increases ρab(T), especially at low temperatures. At H < ~2 T, ρab(T) remains metallic character (i.e., dρab/dT > 0), which can still be described by ρab = ρab(0) + ATn at low temperatures. However, the n value apparently increases with increasing field, as shown in the inset of Fig. 1c. On the other hand, the A value deceases with increasing field. These indicate that the application of magnetic field modifies the electron scattering with the trend of increasing electron–phonon interaction (e.g. increasing n) but reducing the electron–electron interaction (e.g. decreasing A). Above ~2 T, an upturn in ρab(T) gradually develops at low temperatures (i.e., dρab/dT < 0), which eventually saturates at even lower temperatures. The saturation valve and upturn range increase with increasing H, revealing the XMR effect. For example, MR = \(\frac{{\rho _{{{ab}}}\left( H \right) - \rho _{{{ab}}}\left( 0 \right)}}{{\rho _{{{ab}}}\left( 0 \right)}}\) ~ 1500% for H = 9 T and T = 2 K, and MR (H = 14 T, T = 2 K) ~ 2200%. Compared to the reported results, our sample shows smaller MR than that reported in ref., 9 but larger than the P\(\bar 3\)-phase PtBi28,11 (see Table 1). On the other hand, our MR is less than that observed in P\(a\bar 3\) phase.4,13 We note that the latter phases have even higher RRR values as shown in Table 1. This strongly suggests that the XMR effect is intrinsic: higher RRR larger MR. Similar trend is also observed in Weyl semimetal WTe2.14
Following data analysis in ref. 14 for WTe2, we plot our MR data in the Kohler formula, MR versus H/ρab(0), as shown in Fig. 1d. Note that all data taken at different field collapses into a single line, implying scaling behavior for PtBi1.6. Quantitatively, all data can be described by MR = 50(H/ρab(0))1.4, represented by the solid line in Fig. 1d. The power m = 1.4 is less than 2 (the standard Kohler’s rule), however. Ideally, the Kohler’s rule only applies to systems with either single band or multiple bands in perfect electron–hole compensation.15 As discussed below, PtBi1.6 does not meet either of these criteria.
According to Wang et al.14 the minimum resistivity \(\rho _{{{ab}}}^{\mathrm {min}}(T_{\mathrm{m}},H)\) can be described by \(\rho _{{{ab}}}^{\mathrm {min}}\left( {T_{\mathrm{m}},H} \right) = \left[ {m/\left( {m - 1} \right)} \right]\rho _{{{ab}}}\left( {T = T_{\mathrm{m}},\,H = 0} \right)\) derived from the scaling relationship. In Fig. 1c, we plot \(\rho _{{\mathrm{ab}}}^{\mathrm {min}}\left( {T_{\mathrm{m}},H} \right) = 3.5\rho _{{{ab}}}\left( {H = 0} \right)\) for m = 1.4 in a dashed line, which indeed passes through the \(\left( {T_{\mathrm{m}},\rho _{{{ab}}}^{\mathrm {min}}} \right)\) points in different field. To clearly see the field and temperature dependence of ρab, the temperature derivative of ρab for different field is plotted in Fig. 1e. In addition to a characteristic temperature Tm corresponding to dρab/dT = 0, we define Ti at which dρab/dT reaches the minimum. The field dependence of Tm and Ti is plotted in Fig. 1f: both increasing with increasing H. Quantitatively, the field dependence of Tm can be fit by the power law Tm = 13.8(H−Hc)0.23 with Hc ~ 3 T. Similar behavior has been observed in a number of other non-magnetic materials particularly in Dirac or Weyl semimetals with power close to 1/2.14,16,17,18,19 In the latter case, several mechanisms have been proposed to explain the resistivity upturn and the XMR effect at T < Tm, including the unique band structure involving Dirac bands,20 electron–hole compensation,21,22 a quantum phase transition,16 gap opening at the band-touching points,18,23 change of carrier concentration or mobility,24 or normal scattering.14
dHvA oscillations
To understand the origin of the XMR effect in the P31m-phase PtBi1.6, other low-temperature physical properties are investigated. Figure 2a displays the temperature dependence of the magnetic susceptibility along both the ab plane (χab) and c direction (χc). The negative sign of χab and χc, and positive slopes at high temperatures indicate that the atomic contribution (negative), is greater than that from itinerant electrons (positive). Previous report shows the negative χab but the positive χc in P\(\bar 3\)-phase PtBi2.11 While it is yet to be confirmed, the discrepancy in the sign of χc may be related to the Bi content and/or subtle structure difference, which varies the density of states near the Fermi level. Figure 2b shows the field dependence of the magnetization along the c direction (Mc) between 1.85 and 6 K. The diamagnetic background is more or less linear field dependent between 0 and 7 T, unlike the \(H^{\frac{1}{2}}\) dependence predicted for T < Tm.23,25 After subtracting the background, ΔMc is obtained and plotted as a function of H in Fig. 2c. There are clearly dHvA oscillations. If replotting data as ΔMc versus 1/H in Fig. 2d, the periodicity is more clearly seen. From the fast Fourier transformation (FFT) analysis, two principal frequencies Fδ = 4 T and Fα = 39 T are identified as shown in Fig. 2e. According to the Onsager relation F = (ħ/2πe)AF, the cross-section area of Fermi surface AF is determined to be 3.81 × 10−4 and 3.71 × 10−3 Å−2 for the δ and α bands, respectively. The corresponding Fermi wave vectors are kδ ~ 0.011 Å−1 and kα ~ 0.034 Å−1. The latter is almost identical to that reported in ref. 9
a Temperature dependence of the magnetic susceptibilities (χab, χc) measured at H = 1 T. b Isothermal out-of-plane (H//c) magnetization (Mc) at indicated temperatures. c Field dependence of oscillatory ΔMc after background subtraction. d Data replotted as ΔMc versus 1/H at indicated temperatures. e FFT spectra of the dHvA oscillations at indicated temperatures. f FFT amplitudes of Fδ and Fα as a function of temperature. The solid lines are the fits to the temperature damping factor RT of the LK formula (Eq. 1).
The amplitude of dHvA oscillations is usually described by the Lifshitz–Kosevich (LK) formula26,27
Here, the thermal damping factor RT = XT/sinh(XT) and the Dingle damping factor RD = exp(–XTD) (TD is the Dingle temperature) with X = 2π2kBm*/(ħe\(H^{-}\)) (kB is the Boltzmann constant and m* is the effective mass). The spin reduction factor RS = cos(πgm*/2m0) (g is Landé factor and m0 is the free electron mass). The phase factor ϕB is the Berry phase, and δ′ dpends on the dimensionality of the Fermi surface (FS) with 0 for 2D, −1/8 for the maxima (minima) of a 3D electron (hole) type FS, and +1/8 for the minima (maxima) of a 3D electron (hole) type FS.28 The exponent λ is 0 (2D) or 1/2 (3D). By fitting the temperature dependence of the FFT amplitude for the relevant frequency to RT (the inverse field 1/\(\bar H\) used in RT is the average inverse field used for FFT analysis, 1/\(\bar H\) = (1/Hmin + 1/Hmax)/2) with Hmin and Hmax being the field range), we obtain the effective masses \(m_\delta ^ \ast\) = 0.092m0 and \(m_\alpha ^ \ast\) = 0.189m0 for the δ and α bands, respectively. These values are considerably lower than that reported in ref. 9
To extract the topological phase for each band, two oscillatory components are separated via filtering process. Figure 3a, b shows ΔMc(1/H) at T = 1.85 K for Fδ and Fα, respectively. Given that dM/dH (i.e., the magnetic susceptibility) is proportional to the density of states (DOS) at the Fermi level,29 we can then assign the minimum of ΔMc to N−1/4,30 with N being the Landau level (LL) index. Figure 3d, e show the Landau level indices N as a function of 1/H for δ and α bands, respectively. The peaks (red) and valleys (blue) of ΔMc are denoted as N + 1/4 and N − 1/4 Landau level indices, respectively. The solid lines are the linear fit of the data using the Lifshitz–Onsager quantization criterion N = F/H + ϕB/2π + δ′.27,30 From fitting, we obtain Fδ = 4.17 T and \(\phi _{\mathrm{B}}^\delta\)/2π = 0.40−δ′ for the δ band, and Fα = 39.37 T and \(\phi _{\mathrm{B}}^\alpha\)/2π = 0.43−δ′ for the α band. These frequencies are in excellent agreement with that obtained from FFT analysis (Fδ = 4 T and Fα = 39 T). According to band calculations, both the δ and α bands are 3D hole type pockets.9 We thus set δ′ = −1/8 corresponding to the FS minima at the Fermi level, leading to Berry phase \(\phi _{\mathrm{B}}^\delta\) ~ 1.05π and \(\phi _{\mathrm{B}}^\alpha\) ~ 1.11π. These indicate that both the δ and α bands exhibit non-trivial Berry phase. According to calculations for P31m-PtBi2,9 the α band disperses linearly across the Fermi level, and connected with the triply degenerate point along the H–K direction. However, the δ band is different with the result in ref. 9
In view of the FFT spectra of the dHvA oscillations (see Fig. 2e), there is the second harmonic oscillation (2Fα) from the α band. To identify its origin, we inspect the field and temperature dependence of the α band oscillation by filtering the contribution from the δ band in ΔMc. As can be seen in Fig. 3c, three are three remarkable features. First, for T = 1.85 K, the oscillation peaks clearly split at high field. The splitting becomes more profound with the enlarged amplitude of the difference between two peaks with increasing magnetic field. Second, the splitting only occurs at peaks instead of both peaks and valleys. Third, the splitting gradually smears out with increasing temperature, because of the thermal broadening of Landau levels. Based on these characteristics, the 2Fα peak in Fig. 2e should result from the Zeeman splitting. Thus, in Fig. 3c, we mark a pair of peaks using red and blue arrows representing the contributions from spin-up and spin-down electrons at each Landau level, respectively.
For PtBi2, the Zeeman splitting effect has not been reported prior to our study. A low threshold field, where the discernible peak splitting starts to appear (~5 T for our sample), is usually ascribed to the large Landé g factor.31,32,33,34 By lifting the spin degeneracy, the LL index plot should be revised to N = F/H + ϕB/2π + δ′ + \(\frac{1}{2}\)φ and N = F/H + ϕB/2π + δ′−\(\frac{1}{2}\)φ for spin-up and spin-down Landau levels, respectively.27,33 Here, φ = \(\frac{{{\mathrm{g}}m_\alpha ^ \ast }}{{2m_0}}\). Figure 3f shows the Landau fan diagram for both spin-up (red) and spin-down (blue) cases. By fitting these two sets of data, we obtain g ~ 4.97. Compared to that for free electrons (g0 = 2), the g factor for PtBi1.6 is enhanced. However, the enhancement is moderate compared to many topological materials such as ZrSiS,32 ZrTe5,33 and Cd3As2.34 With moderate Zeeman energy, the strong Zeeman splitting in our system must be attributed to the narrow LL width. The latter decreases with decreasing temperature and scattering. According to Eq. (1), one can estimate TD ~ 0.45 K by calculating the slope of ln(ΔMc/H0.5RT) versus 1/H (λ = 0.5 for the α band9), which is about one order less than that obtained in the cubic-phase PtBi2,4 ZrSiS,32 and Cd3As2.34 This implies that the quantum relaxation time τq = ħ/2πkBTD ~ 2.7 × 10−12 s is considerably longer for the trigonal-phase PtBi1.6, despite Bi deficiency.
Shubnikov-de Haas oscillations
With the long quantum relaxation time, the quantum effect should be seen in other properties. Figure 4a shows the field dependence of the in-plane resistivity ρab with H//c at 1.8 K. There are SdH oscillations under high field (see the inset of Fig. 4a). In order to construct a reliable LL fan diagram, we convert ρab to the electrical conductivity σxx via the following formula:30
where ρxy is the Hall resistivity (shown in Fig. 5a). Figure 4b presents the field dependence of the oscillatory Δσxx after subtracting the smooth background, which clearly shows multiple oscillations. By FFT shown in Fig. 4c, four peaks are revealed, corresponding to Fα, 2Fα, Fβ ~ 515 T, and Fγ ~ 1245 T. Contribution from each band is separated and presented in Fig. 4d–f for the α, β, and γ bands, respectively. Note that, in Fig. 4d, there is obvious Zeeman splitting, similar to that seen in ΔMc (Fig. 3c). Assigning the Landau fan diagram for both spin-up (red) and spin-down (blue), we obtain g ~ 6.48, which is greater than that from ΔMc splitting, likely due to sample composition variation. For the β band, data fitting to the Lifshitz-Onsager quantization relation yield \(\phi _{{\mathrm B}}^\upbeta\)/2π = 0.83 − δ′. For the 3D hole type β band with the maxima at the Fermi level as derived from calculations,9 δ′ = 1/8 leading to \(\phi _{\mathrm{B}}^\upbeta\) ~ 1.4π, again a non-trivial Berry phase. According to band structure calculations,9 the β band also exhibits linear dispersion at the Fermi level and is connected with the doubly degenerate points along the H–Γ and H–D directions. Similarly, for the γ band shown in Fig. 4i, we obtain the intercept of N(1/H) ~ 0.23, which leads to \(\phi _{\mathrm{B}}^\gamma\)/2π = 0.23 − δ′. Given δ′ = 1/8 for the 3D hole type γ band with the maxima at the Fermi level,9 \(\phi _{\mathrm{B}}^\gamma\)→ 0, representing a trivial Berry phase, which is consistent with the claim in ref. 9 It should be noted that the Berry phase for both the β and γ bands are extracted from high Landau levels, which may not provide precise Berry phase. In addition, the calculation of σxx involves the in-plane resistivity and Hall resistivity: both were measured on different samples. Discrepancy due to sample difference may result in a phase shift between two quantities. In order to more accurately determine the Berry phase for high-frequency bands, measurements under higher field is necessary so to reach lower Landau levels.
a Field dependence of ρab at 1.8 K. Inset: ρab at high field. b Field dependence of the oscillatory Δσxx plotted as a function of 1/H. c FFT spectra of the SdH oscillation of Δσxx. d–f Δσxx versus 1/H for the α band with Zeeman splitting at 1.8 and 5 K (d), β band (e), and γ band (f); g–i Landau fan diagram for the α band with Zeeman splitting (g), β band (h), and γ band (i).
a Field dependence of the Hall resistivity ρxy at the indicated temperatures. b Field dependence of Hall conductivity σxy at the indicated temperatures. The solid lines are the fit to Eq. (4). c Temperature dependence of the carrier concentrations ne and nh,e. Inset: ratio of nh/ne as a function of temperature. d Temperature dependence of the mobilities μh,e. The error bars in c and d are errors obtained from the fitting of Eq. (4) to the experimental data.
In previous reports, the SdH oscillation has not been observed in the Hall effect of PtBi2. Figure 5a shows the field dependence of the Hall resistivity ρxy at the indicated temperatures for PtBi1.6. Several features can be seen: (1) at each temperature, ρxy exhibits non-monotonic H dependence; (2) ρxy is positive at high temperatures, but gradually pushes down toward the negative direction with decreasing temperature; (3) there is sign change below ~ 50 K (see the inset of Fig. 5a); and (4) there are clear oscillations below ~15 K, again indicating the high quality of our samples. For further analysis, we calculate the Hall conductivity σxy via the following formula:30
Figure 5b displays σxy versus H, showing the sign change in all indicated temperatures. For a system involving both electrons (concentration ne) and holes (concentration nh), the Hall conductivity (σxy) can be described by the following equation:35,36
where μe(h) is the mobility of electron (hole). By fitting our experimental σxy (Fig. 5b) to Eq. (4) for different temperatures, we obtain the temperature dependence of carrier concentration nh,e and mobility μh,e which are shown in Fig. 5c, d, respectively. Note both nh and ne are in the order of 1019 cm−3, while they are temperature dependent. This is consistent with the semimetal picture with the Fermi level close to the edge of the electron and hole bands. What is remarkable is that the ratio nh/ne ~ 2.5 below ~30 K for PtBi1.6 as shown in the inset of Fig. 5c, which is not compensated. This implies that nh/ne would be even larger for stoichiometric PtBi2. From this point of view, the XMR effect in trigonal-phase PtBi2 may not be attributed to the electron–hole compensation. On the other hand, both μh and μe increase with decreasing temperature with μe > μh. At 2 K, μh ~ 0.7 × 104 cm2 V−1 s−1 and μe ~ 2.1 × 104 cm2 V−1 s−1. These values are higher than that obtained for the P\(\bar 3\)-phase PtBi28 and YSb,37 but lower than that obtained in the cubic-phase PtBi2.4
It should be pointed out that, strictly speaking, Eq. (4) cannot precisely describe the Hall conductivity of PtBi1.6, as it consists of more than two bands. On the other hand, if all bands are considered, it would be impossible to obtain meaningful information through the fitting due to a large number of fitting parameters. Nevertheless, there are many other XMR semimetals in which electrons and holes are not compensated, such as MoTe2 (hole dominated),38 LaBi (hole dominated),39 YSb (hole dominated),40 PtSn4 (electron dominated),41,42 and Cd3As2 (electron dominated).43 In Cd3As2,44 high mobility is considered as the possible origin of the XMR effect. The diminishing of the Hall factor κH = (\(\rho _{{{xy}}}\)/\(\rho _{{{xx}}}\))2 has also been proposed to be a key factor to describe the unsaturated MR in NbP semimetal.45 We find that κH has non-monotonic field dependence, thus difficult to explain the monotonic field dependence of MR in our PtBi1.6.
In conclusion, we have successfully grown and investigated the physical properties of the trigonal-structured PtBi2−x single crystals. In spite of Bi deficiency with x ~ 0.4, both the dHvA and SdH oscillations have been observed in the magnetization, electrical resistivity, and Hall resistivity. Through FFT analysis, four oscillation frequencies are identified with Fα = 39 T, Fβ = 515 T, Fγ = 1245 T, and Fδ = 4 T, corresponding to the α, β, γ, and δ bands. By fitting the temperature dependence of the FFT amplitude to the LK formula, we obtain nearly-zero effective mass for electrons residing in the α and δ bands. By constructing the Landau fan diagram, the Berry phase for four bands is extracted: non-trivial for the α, β, and δ bands but trivial for the γ band. As Fβ and Fγ are considerably high, our observed oscillations correspond to high Landau levels, further measurements under high magnetic field are necessary to exam the Berry phase at low Landau levels. Nevertheless, we also observe the Zeeman splitting effect in the α band under moderate field and moderate Landé g factor (4.97 from the magnetization and 6.48 from the electrical conductivity). The only explanation is its extremely narrow Landau level breadth with little scattering, which is reflected in the long quantum relaxation time (i.e., small Dingle temperature).
The XMR effect is also observed in our Bi-deficient crystals. This together with evidence accumulated from previous reports strongly suggest that the XMR effect is the property of clean samples reflected by the large residual resistivity ratio. The resistivity under various fields actually collapses into a single line when plotted in Kohler formula. Although the exponent for PtBi1.6 deviates from the standard Kohler’s rule, it is worth to investigate underlying physics in such a multiband system. Quantitative analysis of the Hall conductivity indicates that electrons and holes in our system are not perfectly compensated, thus might not be responsible for the XMR effect. Since the δ band has reached the first Landau level at 5 T, the XMR effect, which can only be observed in clean materials, is likely the consequence of the quantum limit under high magnetic field.
Methods
PtBi2−x single crystals were grown using the self-flux (Bi) method. Pt (99.99%, Alfa Aesar) and Bi (99.5%, Alfa Aesar) powder was mixed with the molar ratio Pt: Bi = 1: 5. The mixture was loaded into an alumina crucible and sealed in a quartz tube after evacuation. The quartz tube was then placed in a box furnace, then heated up to 600 °C. After staying at this temperature for 50 h, the furnace was cooling down to 450 °C with a rate −2 °C h−1. Finally, the quartz tube was taken out and centrifuged to remove excess Bi flux. Single crystals with shiny surfaces were obtained, as shown in the inset of Fig. 1a.
The phase of as-grown single crystals was characterized by XRD. The chemical composition of single crystals was determined by EDS. The magnetization was measured using a magnetic property measurement system (MPMS, Quantum Design) with magnetic field up to 7 T. The electrical resistivity and Hall effect measurements were performed using the standard four-probe technique in a physical property measurement system (PPMS, Quantum Design) with a magnetic field up to 14 T.
Data availability
All data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Okamoto, H. The Bi-Pt (bismuth-platinum) system. J. Phase Equilibria 12, 207–210 (1991).
Xia, D. et al. Synthesis of ordered intermetallic PtBi2 nanoparticles for methanol-tolerant catalyst in oxygen electroreduction. Chem. Mater. 18, 5746–5749 (2006).
Gibson, Q. D. et al. Three-dimensional Dirac semimetals: design principles and predictions of new materials. Phys. Rev. B 91, 205128 (2015).
Gao, W. et al. Extremely large magnetoresistance in a topological semimetal candidate pyrite PtBi2. Phys. Rev. Lett. 118, 256601 (2017).
Chen, X. et al. Pressure-induced multiband superconductivity in pyrite PtBi2 with perfect electron-hole compensation. Phys. Rev. Mater. 2, 054203 (2018).
Yao, Q. et al. Bulk and surface electronic structure of hexagonal structured PtBi2 studied by angle-resolved photoemission spectroscopy. Phys. Rev. B 94, 235140 (2016).
Thirupathaiah, S. et al. Possible origin of linear magnetoresistance: observation of Dirac surface states in layered PtBi2. Phys. Rev. B 97, 035133 (2018).
Yang, X. et al. Giant linear magneto-resistance in nonmagnetic PtBi2. Appl. Phys. Lett. 108, 252401 (2016).
Gao, W. et al. A possible candidate for triply degenerate point fermions in trigonal layered PtBi2. Nat. Commun. 9, 3249 (2018).
Kaiser, M., Baranov, A. I. & Ruck, M. Bi2Pt(hP9) by low-temperature reduction of Bi13Pt3I7: reinvestigation of the crystal structure and chemical bonding analysis. Z. Anorg. Allg. Chem. 640, 2742–2746 (2014).
Xu, C. Q. et al. Synthesis, physical properties, and band structure of the layered bismuthide PtBi2. Phys. Rev. B 94, 165119 (2016).
Bid, A., Bora, A. & Raychaudhuri, A. K. Temperature dependence of the resistance of metallic nanowires of diameter ≥15nm: applicability of Bloch-Grüneisen theorem. Phys. Rev. B 74, 035426 (2006).
Zhao, L. et al. Fermi surface and carrier compensation of pyrite-type PtBi2 revealed by quantum oscillations. Phys. Rev. B 98, 085137 (2018).
Wang, Y. L. et al. Origin of the turn-on temperature behavior in WTe2. Phys. Rev. B 92, 180402(R) (2015).
Feng, D. & Jin, G. Introduction to Condensed Matter Physics. Vol. 1 (World Scientific, 2005).
Kopelevich, Y., Pantoja, J. C. M., da Silva, R. R. & Moehlecke, S. Universal magnetic-field-driven metal-insulator-metal transformations in graphite and bismuth. Phys. Rev. B 73, 165128 (2006).
Du, X., Tsai, S.-W., Maslov, D. L. & Hebard, A. F. Metal-insulator-like behavior in semimetallic bismuth and graphite. Phys. Rev. Lett. 94, 166601 (2005).
Singha, R., Pariari, A. K., Satpati, B. & Mandal, P. Large nonsaturating magnetoresistance and signature of nondegenerate Dirac nodes in ZrSiS. Proc. Natl Acad. Sci. USA 114, 2468–2473 (2017).
Singha, R., Satpati, B. & Mandal, P. Fermi surface topology and signature of surface Dirac nodes in LaBi. Sci. Rep. 7, 6321 (2017).
Wang, Y.-Y., Yu, Q.-H., Guo, P.-J., Liu, K. & Xia, T.-L. Resistivity plateau and extremely large magnetoresistance in NbAs2 and TaAs2. Phys. Rev. B 94, 041103(R) (2016).
Pletikosic, I., Ali, M. N., Fedorov, A. V., Cava, R. J. & Valla, T. Electronic structure basis for the extraordinary magnetoresistance in WTe2. Phys. Rev. Lett. 113, 216601 (2014).
Kumar, N. et al. Observation of pseudo-two-dimensional electron transport in the rock salt-type topological semimetal LaBi. Phys. Rev. B 93, 241106(R) (2016).
Khveshchenko, D. V. Magnetic-field-induced insulating behavior in highly oriented pyrolitic graphite. Phys. Rev. Lett. 87, 206401 (2001).
Lv, Y.-Y. et al. Mobility-controlled extremely large magnetoresistance in perfect electron-hole compensated α-WP2 crystals. Phys. Rev. B 97, 245151 (2018).
Sercheli, M. S., Kopelevich, Y., Ricardo da Silva, R., Torres, J. H. S. & Rettori, C. Evidence for internal field in graphite: a conduction electron spin-resonance study. Solid State Commun. 121, 579–583 (2002).
Lifshitz, I. M. & Kosevich, A. M. Theory of magnetic susceptibility in metals at low temperatures. JETP 2, 636–645 (1956).
Shoenberg, D. Magnetic Oscillations in Metals (Cambridge University Press, Cambridge, 1984).
Li, C. et al. Rules for phase shifts of quantum oscillations in topological nodal-line semimetals. Phys. Rev. Lett. 120, 146602 (2018).
Hu, J. et al. Evidence of topological nodal-line fermions in ZrSiSe and ZrSiTe. Phys. Rev. Lett. 117, 016602 (2016).
Ando, Y. Topological insulator materials. J. Phys. Soc. Jpn. 82, 102001 (2013).
Ando, T., Fowler, A. B. & Stern, F. Electronic properties of two-dimensional systems. Rev. Mod. Phys. 54, 437–672 (1982).
Hu, J. et al. Nearly massless Dirac fermions and strong Zeeman splitting in the nodal-line semimetal ZrSiS probed by de Haas–van Alphen quantum oscillations. Phys. Rev. B 96, 045127 (2017).
Liu, Y. et al. Zeeman splitting and dynamical mass generation in Dirac semimetal ZrTe5. Nat. Commun. 7, 12516 (2016).
Cao, J. et al. Landau level splitting in Cd3As2 under high magnetic fields. Nat. Commun. 6, 7779 (2015).
Wang, J. et al. Magnetoresistance and robust resistivity plateau in MoAs2. Sci. Rep. 7, 15669 (2017).
Ziman, J. M. Electrons and Phonons (Oxford University Press, New York, 2001).
Pavlosiuk, O., Swatek, P. & Wiśniewski, P. Giant magnetoresistance, three-dimensional Fermi surface and origin of resistivity plateau in YSb semimetal. Sci. Rep. 6, 38691 (2016).
Thirupathaiah, S. et al. MoTe2: an uncompensated semimetal with extremely large magnetoresistance. Phys. Rev. B 95, 241105 (2017).
Jiang, J. et al. Observation of topological surface states and strong electron/hole imbalance in extreme magnetoresistance compound LaBi. Phys. Rev. Mater. 2, 024201 (2018).
He, J. et al. Distinct electronic structure for the extreme magnetoresistance in YSb. Phys. Rev. Lett. 117, 267201 (2016).
Mun, E. et al. Magnetic field effects on transport properties of PtSn4. Phys. Rev. B 85, 035135 (2012).
Jo, N. H. et al. Extremely large magnetoresistance and Kohler’s rule in PdSn4: a complete study of thermodynamic, transport, and band-structure properties. Phys. Rev. B 96, 165145 (2017).
Liang, T. et al. Ultrahigh mobility and giant magnetoresistance in the Dirac semimetal Cd3As2. Nat. Mater. 14, 280–284 (2014).
Narayanan, A. et al. Linear magnetoresistance caused by mobility fluctuations in n-doped Cd3As2. Phys. Rev. Lett. 114, 117201 (2015).
Xu, J. et al. Reentrant metallic behavior in the Weyl semimetal NbP. Phys. Rev. B 96, 115152 (2017).
Acknowledgements
This material is based upon work supported by the U.S. Department of Energy under EPSCoR Grant No. DE-SC0016315.
Author information
Authors and Affiliations
Contributions
R.J. designed research; L.X. synthesized the sample and conducted physical property measurements with assistance from R.C. and R.N.; L.X. and R.J. wrote the manuscript with the contributions from all the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xing, L., Chapai, R., Nepal, R. et al. Topological behavior and Zeeman splitting in trigonal PtBi2-x single crystals. npj Quantum Mater. 5, 10 (2020). https://doi.org/10.1038/s41535-020-0213-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-020-0213-9
This article is cited by
-
Evidence for topological semimetallicity in a chain-compound TaSe3
npj Quantum Materials (2020)