Abstract
We use neutron scattering to study Vanadium (hole)-doped LiFe1−xVxAs. In the undoped state, LiFeAs exhibits superconductivity at Tc = 18 K and transverse incommensurate spin excitations similar to electron overdoped iron pnictides. Upon Vanadium doping to form LiFe0.955V0.045, the transverse incommensurate spin excitations in LiFeAs transform into longitudinally elongated ones in a similar fashion to that of potassium (hole)-doped Ba0.7K0.3Fe2As2 but with dramatically enhanced magnetic scattering and elimination of superconductivity. This is different from the suppression of the overall magnetic excitations in hole-doped BaFe2As2 and the enhancement of superconductivity near optimal hole doping. These results are consistent with density function theory plus dynamic mean field theory calculations, suggesting that Vanadium doping in LiFeAs may induce an enlarged effective magnetic moment Seff with a spin crossover ground state arising from the inter-orbital scattering of itinerant electrons.
Similar content being viewed by others
Introduction
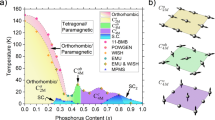
The flexible spin states of Fe2+ ions are interesting due to its extensive distribution, from the lowermost mantle in the earth1 to the innermost hemoglobin in our human body2 and from the most common ferrite magnet to the most recent iron-based superconductors.3,4,5 Ignoring the orbital angular momentum, each Fe2+ ion with six electrons distributed in five d orbitals has three possible spin states, S = 0, 1, or 2 [Fig. 1a]. In iron-based superconductors, where Fe2+ ion is surrounded by crystal electric field of As atoms, the fivefold degeneracy of the d orbitals is split into a twofold degenerate eg and a threefold degenerate t2g states nearby the Fermi level [Fig. 1a].3 Although it is widely believed that Hund’s rule plays a critical role in determining the electronic configuration of iron,6 the S = 2 spin state has never been observed in metallic iron pnictides.5,7
a Possible spin states of Fe2+ in t2g and eg states within a localized moment picture. b Fermi surfaces of LiFe0.955V0.045As. Red and blue colors represent dxy and dxz/yz orbital characters, respectively. c Summary of the doping dependence of low-energy spin excitations in BaFe2As2 (Top) and LiFeAs (bottom). The shapes of the magnetic scattering are marked by blue (BaFe2As2) and red (LiFeAs) colored points. It is worth noting that spin excitations in LiFe0.955V0.045As are considerably diffusive in reciprocal space. d Theoretical and experimental local dynamical spin susceptibility in LiFeAs (x = 0), LiFe0.88Co0.12As (xe = 0.12), LiFe0.955V0.045As (xh = 0.135), and BaFe2As2.
The total moment sum rule within a Heisenberg model for system with spin S requires \(\left\langle {m}^{2}\right\rangle ={(g{\mu }_{{\mathrm{B}}})}^{2}S(S+1)\), where g ≈ 2 is the Landé g-factor, when magnetic scattering is integrated over all energy and momentum space within the Brillouin zone (BZ).8 Since neutron scattering directly measures the energy (E) and momentum (Q) dependence of the dynamic structure factor S(Q, E), it is therefore possible to estimate the effective spin-fluctuating moment Seff by integrating the magnetic spectral weight over all energies and wave vectors within the BZ. In previous inelastic neutron scattering on electron-doped BaFe2As2 compounds, it is established that electron doping via Ni substitution in BaFe2−xNixAs2 reduces slightly the total spin-fluctuating moment, changing from \(\left\langle {m}^{2}\right\rangle \approx 3.5\)\({\mu }_{{\mathrm{B}}}^{2}\)/Fe at x = 0 to \(\left\langle {m}^{2}\right\rangle \approx 2.7\)\({\mu }_{{\mathrm{B}}}^{2}\)/Fe at x = 0.3.9,10,12 These values approximately correspond to Seff ≈ 1/2.9,11 For hole-doped Ba1−xKxFe2As2, the total spin-fluctuating moment decreases rapidly with increasing x,9 and Seff reduces to 0.14 at x = 1.13 For electron-doped NaFe1−xCoxAs,5 the total spin-fluctuating moment also decreases slightly with increasing x but has almost identical value as that of BaFe2−xNixAs2,14 thus suggesting universal nature of the Seff ≈ 1/2 for two different families of iron pnictides. This is different from the superconducting LiFeAs, where the low-energy spin fluctuations coupled to superconductivity are about a factor 4 smaller than that of the Co-underdoped superconducting BaFe2As2.15,16 The total fluctuating moment of LiFeAs is \(\left\langle {m}^{2}\right\rangle \approx 1.5\pm 0.3\)\({\mu }_{{\mathrm{B}}}^{2}\)/Fe, more than a factor of 2 smaller than that of BaFe2As2.17,18 On the other hand, the total spin-fluctuating moment for iron chalcogenide compounds FeSe and FeTe are significantly larger. In the case of FeSe, the total spin-fluctuating moment of \(\left\langle {m}^{2}\right\rangle \approx 5.2\)\({\mu }_{{\mathrm{B}}}^{2}\)/Fe arises entirely from dynamic magnetic excitations as the system has no static ordered moment.19 For FeTe, the effective moment of Fe may change from Seff ≈ 1 at 10 K to Seff ≈ 3/2 at 300 K, suggesting entangled local magnetic moments with the itinerant electrons on warming.20
The total moment sum rule strictly speaking is only valid for insulating local moment systems, where quantum effect and itinerant electron-induced magnetism are not important.8 In iron-based superconductors, itinerant electrons and hole–electron Fermi surface nesting are known to be important for magnetism and superconductivity [Fig. 1b].21 Theoretically, many physical properties of iron-based superconductors can be understood within the orbital-selective Mott phase picture, where electrons in Fe2+ ion with different orbitals can behave differently.22,23,24 In this model, hole-doped compounds are believed to be more correlated and therefore should have large effective local moments.22,23,24 From combined density functional theory (DFT) and dynamic mean field theory (DMFT) calculations,6 the total fluctuating moments in the paramagnetic state are nearly invariant around 2.2 μB/Fe in a wide variety of iron pnictide/chalcogenide families. In X-ray emission spectroscopy (XES) experiments, values of magnetic spin moments in the paramagnetic phase are about 1.3 μB/Fe for iron pnictides, including BaFe2As2 and Ba(Fe,Co)2As2.7 These values are considerably smaller than the predictions from DFT+DMFT calculation but larger than those from neutron-scattering experiments,9,10,12 possibly due to the fast time scale of the XES measurements.7 Therefore, to fully understand the key ingredients of magnetism in iron-based superconductors, it is important to study the evolution of Seff in different families of hole-doped iron-based superconductors in a controlled and systematic way.
While it is easy to dope holes in BaFe2As2 family of iron pnictides by substituting Ba2+ cation with K1+, replacing Fe with Cr/Mn introduces impurities and/or disorders instead of holes.25,26,27 For NaFeAs family, systematic neutron scattering and angle-resolved photoemission spectroscopy (ARPES) experiments reveal that replacing Fe with Cu dopes holes into the system and induces large ordered magnetic moment for x > 0.1 in NaFe1−xCuxAs.28,29 However, there are no inelastic neutron-scattering experiments to determine the total fluctuating moment for this family of compounds. In the case of LiFeAs family, ARPES experiments indicate that doping V into Fe sites actually introduces hole carriers with a rate of 0.3 hole per V dopant and selectively enlarges the inner hole Fermi surface [Fig. 1b],30 even though the doping-induced impurity and disorder effects might still play a role in the transport and susceptibility measurements with higher V doping ratio. Although hole doping via K substitution in Ba1−xKxFe2As2 induces superconductivity, <2% V doping in LiFe1−xVxAs quickly suppresses the superconductivity in pure LiFeAs, even with a perfect nesting condition established between the inner hole and electron Fermi pockets at x = 0.084 [see arrows in Fig. 1b].30 The rapid suppression of superconductivity in LiFe1−xVxAs has been suggested as due to magnetic impurity effect of V dopant, but there are no neutron-scattering experiments to establish the effect of V doping to spin excitations of pure LiFeAs .15,16,17
Results
We report the magnetic excitations in hole-doped nonsuperconducting LiFe0.955V0.045As, which has nearly nested hole–electron Fermi surfaces with dxz/yz and dxy orbital characters, respectively, and exhibits non-Fermi-liquid behavior.30 We observe enhanced commensurate magnetic fluctuations at antiferromagnetic (AF) wave vectors, suggesting that the non-Fermi-liquid behavior is intimately associated with magnetic fluctuations. The broadness and diffuseness of the spin excitations are also distinct from the sharp commensurate spin fluctuations in electron-doped LiFe0.88Co0.12As,18 probably reflecting the local nature of quantum spin fluctuations.31 More importantly, we find that the intensities of spin fluctuations are strongly enhanced in the energy range of our measurements with a larger Seff, in sharp contrast to the reduced effective moment in hole-doped Ba1−xKxFe2As2.9,13 Considering the different superconducting behavior in Ba1−xKxFe2As2 and LiFe1−xVxAs, we argue that the inter-orbital scattering processes between dxz/yz and dxy orbitals increase the fluctuating moment but are detrimental to superconductivity.32 These results are consistent with the notion that intra-orbital scattering processes between hole and electron pockets, particularly those involving dyz–dyz orbital characters, are good for superconductivity in different classes of iron-based superconductors.33,34,35,36,37
We first plot in Fig. 2 the two-dimensional images of spin excitations in LiFe0.955V0.045As at different energies and their comparison with the DFT+DMFT calculations for 10% hole doping (about LiFe0.967V0.033As). At energy transfer E = 3 ± 1 meV, spin excitations occur at commensurate QAF = (1,0) and (0,1) positions [Figs. 1c and 2a], different from the transverse incommensurate spin fluctuations in LiFeAs.15,16,17 Instead, spin excitations display a small elongation along the longitudinal direction, mimicking the low-energy spin excitations of hole-doped Ba1−xKxFe2As2.38 As the energy transfer increases from E = 3 to E = 18 meV, the elongation of the elliptical spin fluctuations changes from the longitudinal to transverse direction, similar to that in Ba0.67K0.33Fe2As2,9 reflecting the hole–electron Fermi surface nesting contribution from itinerant electrons.32,38 The wave vector-dependent spectra at the corresponding energies are confirmed by the DFT+DMFT calculations in the 10% hole-doped LiFeAs [Fig. 2e–h]. These results are significantly different from Mn-substituted BaFe2As2, where Mn doping induces diffusive magnetic scattering at the checkerboard wave vector (1,1).27 The broad and diffusive magnetic scattering at (1,0)/(0,1) may be attributed to the short-range spin fluctuations from localized moment and/or not perfect nesting condition between hole and electron Fermi surfaces.
a–d 2D images of measured dynamic spin susceptibility of LiFe0.955V0.045As in the [H, K] plane at E = 3 ± 1, 10 ± 2, 18 ± 2, and 28 ± 2 meV, respectively. The elongation of spin excitations along [H,0,0] can be observed in both experimental (dashed circle) and theoretical (green and red area) results. The data were collected at T = 5 K and folded to improve statistics with radially symmetric backgrounds subtracted. e–h The corresponding results from DFT+DMFT calculations. The color bars indicate scattering intensity in absolute units from experiments and theory.
To compare the magnitude of spin fluctuations in LiFeAs, LiFe0.88Co0.12As, and LiFe0.955V0.045As, we calculate in Fig. 1d the energy dependence of the local dynamic spin susceptibility χ″(E) for these materials obtained by integrating wave vector-dependent dynamic spin susceptibility χ″(Q, E) over the entire BZ.5 Compared with those of LiFeAs and LiFe0.88Co0.12As,18 χ″(E) in LiFe0.955V0.045As is clearly enhanced about <80 meV, although we do not have data >80 meV. Such an enhancement is also captured in the DFT+DMFT calculations as shown in red and blue solid lines of Fig. 1d. The local dynamic spin susceptibility of LiFe0.955V0.045As in the measured energy range is somewhat larger than that of BaFe2As2.39,40 For comparison, magnetic scattering of LiFeAs is considerably smaller than that of the Co-doped superconducting Ba(Fe0.92Co0.08)2As2.15,16
The differences between LiFeAs, LiFe0.88Co0.12As, and LiFe0.955V0.045As can be further confirmed in Fig. 3a in which we plot constant-energy cuts of spin excitations along the transverse and longitudinal directions. In all cases, we obtain the magnitude of magnetic scattering by normalizing it to phonon intensities,14 making it possible to compare magnetic scattering of different materials measured on different instruments. It is clear that the magnetic scattering in LiFe0.955V0.045As is both wider and higher than those in LiFeAs and LiFe0.88Co0.12As at E = 5 meV, resulting in a large increase in χ″(E) [Fig. 1d]. This cannot be explained by the extra Vanadium magnetic impurities since the 3d3 electronic configuration of V2+ ions only has S = 3/2, which is smaller than the expected S = 2 for 3d6 of Fe2+ in iron-based superconductors. Therefore, the enhanced magnetic scattering has to be associated with the introduction of hole carriers, which effectively modifies the spin configuration of Fe2+ ions.
a Constant-energy cuts of spin excitations along the transverse [1,K] (left) and longitudinal [H,0] (right) directions for LiFeAs, LiFe0.88Co0.12As, and LiFe0.955V0.045As at E = 5 ± 1 meV, respectively. The solid lines are corresponding single- or two-Gaussian fits. The intensity is normalized by relative phonon intensity to account for spectrometer differences.14 b Line width and correlation length of the low energy spin fluctuations along the longitudinal [H,0] direction in LiFeAs and hole/electron-doped compounds. The doping ratio is a theoretical value assuming that each V dopant contributes three holes. c Energy dependence of the line widths of the low energy spin fluctuations in LiFe0.955V0.045As along the transverse and longitudinal directions, respectively.
In Fig. 3b, we show the line width of spin excitations and the corresponding dynamic spin-spin correlation length for LiFeAs, LiFe0.88Co0.12As, and LiFe0.955V0.045As. The sudden drop of spin correlation length in LiFe0.955V0.045As suggests that short-range spin correlations of local moments may become important. Figure 3c shows the line widths of spin excitations along both the transverse and longitudinal directions at different energies in LiFe0.955V0.045As. The crossing around 10 meV is consistent with the isotropic spin excitations in Fig. 2b. Therefore, LiFe1−xVxAs is distinct from Cr/Mn-doped BaFe2As2 in which magnetic impurities induce Néel-type diffusive AF spin fluctuations at low concentrations.25,26,27
Figure 4a, b compare the DFT+DMFT calculated wave vector and energy dependence of χ″(Q, E) for LiFeAs and LiFe0.967V0.033As, respectively. Consistent with Fig. 1d, we find that LiFe0.967V0.033As has larger magnetic spectral weight, especially at low energies. In Fig. 4c, we show the estimated effective spin Seff for different iron-based superconductors. It is clear that all values are distributed between S = 0 and S = 1 with most of them around Seff = 1/2. The discrepancy of hole-doping dependence of the magnetic excitations between BaFe2As2 and LiFeAs families may arise mostly from the fact that we have only integrated the energy range of χ″(E) from 0 to about 60 meV where we have solid data for V-doped and pure LiFeAs. Although these numbers cannot be compared with absolute values of Seff determined for BaFe2As2 and FeSe, the trend of increasing total magnetic susceptibility with hole doping in V-doped LiFeAs is unmistakable. Therefore, it is interesting to understand the microscopic origin of magnetic excitations in V-doped LiFeAs.
a, b The calculated S(Q, E), obtained by using computed dynamical spin susceptibility χ″(Q, E) and \({\chi }{^{\prime\prime} }({\bf{Q}},E)={g}^{2}{\mu }_{{\mathrm{B}}}^{2}\frac{\pi }{\hslash }(1-\exp (-\hslash \omega /{k}_{{\mathrm{B}}}T))S({\bf{Q}},E)\) of LiFeAs and 10% hole-doped LiFe0.967V0.033As by DFT+DMFT.5 They are plotted in the same color scale for direct comparison. The factor 2 in the units comes from a factor of 2 in the formula that we did not multiply when we wrote the code to compute χ″. The color bar indicates scattering intensity in absolute units from the DFT+DMFT calculation. c The effective spin Seff in various iron pnictide/chalcogenides superconductors obtained from neutron-scattering experiments.12,13,14,18,19,54 NFA, BFA, and LFA represent NaFeAs, BaFe2As2, and LiFeAs families, respectively. The energy integration range of χ″(E) for LiFeAs family of materials is from 0 to about 60 meV and thus does not represent the total local dynamic susceptibility. d Schematics of dynamic mixing of spin states with S = 0 and 1.
Discussion
Theoretically, the reduction of effective spins in iron pnictides/chalcogenides can be understood in either an itinerant or a localized moment picture. The former considers Fe2+ ions embedded in a Fermi sea of conduction electrons,41,42 and the lower spin states can be achieved through a multiple-stage Kondo screening process,31,43 where the system is in a quantum critical incoherent metallic state down to 0 K. In the local moment scenario, due to the sensitivity of spin states of Fe2+ to the ionic radius, the effective magnetic moment in iron-based material can be tuned by controlling the strength of crystal electric field in the local FeAs4 tetrahedral structure.44,45 This picture can successfully explain some phenomena such as temperature-dependent magnetic moments46,47 and coherent–incoherent crossover.31,48,49,50,51 However, it is still difficult to understand the large variety of the fluctuated moments in iron-based superconductor by assuming a reduced spin state with S = 1 or 0. To achieve an intermediate crossover between spin state S = 1 and S = 0, a dynamic “spin mixing” process was proposed44,45 as schematically shown in Fig. 4d. When two Fe2+ ions exchange their electrons, their spin states would effectively change from S = 0 to S = 1 and vice versa. This results in a continuous evolution of the effective spin state with 0 < Seff < 1. In this scenario, the probability of each S = 0 or 1 state is closely related to both the local structure and conduction electrons.44 We note that this spin crossover scenario is a localized model and may not completely reflect the itinerant nature of iron-based superconductors. Further theoretical and experimental evidences are needed to clarify the situation.
In insulating copper oxides, local moments are locked into the S = 1/2 state by the elimination of doubly occupied states with a large charge gap.52 Doping charge carriers introduce doubly occupied states and lead to the destruction of local moments, resulting in the suppression of the neutron-scattering spectral weight in the energy range of typical neutron-scattering experiments.8 Similarly, in iron pnictides, the effective moment on each Fe2+ ion is also affected by the population of doubly occupied states or spin singlets due to Kondo screening. However, this cannot be simply attributed to the introduction of charge carriers since the doping dependence of Seff in Ba1−xKxFe2As2 and LiFe1−xVxAs is rather different. Such a difference may be rooted in the different sites of the dopants. Since Vanadium is directly introduced into the FeAs layer while K+ is not, the Fe–As bond length is affected by V doping30 and a high spin state is favored in V-doped LiFeAs. With increasing V- doping, the nesting condition improves between the inner hole Fermi surface with dxz∕yz orbital character and the inner electron pocket mainly derived from dxy orbital character.30 Therefore, the enhanced inter-orbital scattering between dxz∕yz and dxy orbitals, which suppresses superconductivity,32 favors the “spin mixing” process [Fig. 4d] and enhances fluctuated moments. This is different from the intra-orbital dyz–dyz hole–electron Fermi surface nesting scattering, which favors superconductivity and induces a neutron spin resonance only at the AF wave vector in detwinned FeSe33 and underdoped iron pnictides.37,53
To conclude, we performed time-of-flight neutron-scattering measurements on LiFe0.955V0.045As and did DFT+DMFT calculation on the corresponding 10% hole-doped LiFeAs system. We found that the low-energy spin fluctuations are influenced by itinerant electrons following the same doping dependence of spin excitations in BaFe2As2. More importantly, both the experimental and theoretical results suggest that magnetic excitations are dramatically enhanced by doping holes with Vanadium. We discuss the possible origin of such enhancement and argue that the inter-orbital scattering between dxz/yz and dxy orbitals are bad for superconductivity and may dynamically mix the spin states of Fe2+ ions.
Methods
Sample preparation
We grew single crystals of LiFe0.955V0.045As by self-flux method.55 In all, 7.2 g of single crystals were used in our time-of-flight neutron-scattering experiments, of which 1.8 g were synthesized by using isotope 7Li to reduce neutron absorption. Samples were wrapped by Aluminum foil with Hydrogen-free glue in the glove box filled with Argon gas since the samples are air and humidity sensitive. All samples were co-aligned and glued on five 40 × 40 mm2 Aluminum plates as shown in Fig. S1b. The [1, 0, 0] direction is along the horizontal direction and [1, 1, 0] along the diagonal [Fig. S1a].
Neutron-scattering experiments
Our inelastic neutron-scattering measurements on LiFe0.955V0.045As were carried out on the time-of-flight 4D-Space Access Neutron Spectrometer (4SEASONS) at Materials and Life Science Experimental Facility (MLF), Japan Proton Accelerator Research Complex (J-PARC).56 We define the momentum transfer Q in three-dimensional reciprocal space in Å−1 as Q = Ha* + Kb* + Lc*, where H, K, and L are Miller indices and \({{\bf{a}}}^{* }=\hat{{\bf{a}}}2\pi /a\), \({{\bf{b}}}^{* }=\hat{{\bf{b}}}2\pi /b\), and \({{\bf{c}}}^{* }=\hat{{\bf{c}}}2\pi /c\) with a = b ≈ 5.316 Å, and c = 6.315 Å.17,18 Samples are co-aligned in the [H, 0, L] scattering plane with mosaic <5° and incident beam (Ei = 16, 39, 75, and 200 meV) parallel to the c-axis of the crystals. In principle, absolute magnetic neutron-scattering intensity from LiFe0.955V0.045As can be normalized by comparing the scattering with a Vanadium standard.5 However, LiFe0.955V0.045As has considerable unknown amount of Vanadium-containing flux from the growth, rendering this method unreliable. To obtain the absolute intensity, we therefore use phonon normalization method as discussed below.
Background subtraction and data analysis
The background subtraction processes are shown in Fig. S2.14 The raw magnetic scattering appears in a fourfold symmetry at wave vectors [1, 0], [0, 1], [−1, 0], and [0, −1] [Fig. S2a] due to the tetragonal symmetry of the lattice structure. We symmetrized the scattering spectra in order to enhance the magnetic signal and then remove the background [Fig. S2b]. Background was obtained by masking the signal within the white squares [Fig. S2c] and assumed to be radially symmetric. A polynomial function of \(\left|{\bf{Q}}\right|\) was used to fit the background intensity [Fig. S2e] and then was subtracted from the raw data. The results were shown in Fig. S2d. Figure S2f, g are cuts along the [H, 0] and [1, K] directions, respectively. We note that there are still residual background intensities, which likely come from phonon scattering and affect the calculation of local dynamical spin susceptibility. Different treatments to these intensities might result in the differences of the final estimated local dynamical spin susceptibility. Therefore, we recalculate the local dynamical spin susceptibility of pure LiFeAs and LiFe0.88Co0.12As from the previous data with the same method we used for V-doped LiFeAs. In this way, we can have a better comparison between different compounds. The recalculated local dynamical spin susceptibilities are shown in Fig. 1d.
Absolute neutron-scattering intensity normalization
We performed our inelastic neutron scattering on LiFeAs and LiFe0.88Co0.12As at the wide Angular-Range Chopper Spectrometer and Cold Neutron Chopper Spectrometer at Spallation Neutron Source, Oak Ridge National Laboratory and on LiFe0.955V0.045As at 4SEASONS, MLF, J-PARC. The neutron-scattering intensity of the LiFeAs and LiFe0.88Co0.12As have already been normalized by standard Vanadium sample. The neutron-scattering intensity of LiFe0.955V0.045As is normalized by phonon intensities since a standard Vanadium is unavailable during the experiment. As discussed in the main text, V normalization is actually less reliable in V-doped LeFeAs because of the unknown amount of V-containing flux in the sample. Therefore, phonon normalization using the same phonon for LiFeAs, which we re-analyzed from using previous data, and V-doped LiFeAs should be more reliable than the standard Vanadium scan when comparing the results from different spectrometers.14
We identified two phonons, one is around (1, 1) and the other originates from (2, 0). The incident neutron energy is almost the same, about 39 meV for LiFe0.955V0.045As and 35 meV for LiFeAs and LiFe0.88Co0.12As. The one-dimensional cuts of these phonons are shown in Fig. S3, and the integrated intensity of each phonon can then be calculated. By comparing the phonon intensities of different materials, we estimated the scale factor, which is defined as the ratio of phonon intensity between LiFeAs/LiFe0.88Co0.12As and LiFe0.955V0.045As. Since the intensity of LiFeAs and LiFe0.88Co0.12As has been normalized already by the standard Vanadium scan, we could calculate the absolute value of the intensities in LiFe0.955V0.045As. The data of LiFeAs and LiFe0.88Co0.12As can be used as a cross-check and the absolute value we obtained for LiFe0.955V0.045As is consistent with these two references.
Figures S3a, b show the acoustic phonon near (1,1) at 4.5 and 5.5 meV [Fig. S3e], and Figs. S3c, d display another phonon around (2,0) [Fig. S3f] at 12.5 and 13.5 meV. In Fig. S3g, we plot the estimated factor from Fig. S3a–d. An average scale factor about 200 is obtained.
Alternatively, the incoherent nuclear scattering can be used as another reference to normalize the data. In Fig. S4, we show the incoherent peak for LiFe0.955V0.045As, LiFeAs, and LiFe0.88Co0.12As. The incident energy Ei is 39 and 75 meV for LiFe0.955V0.045As and 35 and 80 meV for LiFeAs and LiFe0.88Co0.12As. The estimated scale factor is about 70, significantly smaller than the value from phonon normalization. We note here that the residual flux trapped in the single crystal samples is an issue that may affect the estimation of the absolute value. This has been observed in our previous paper on Co-doped NaFeAs in which a difference of 30% was observed.14 This situation would be even more serious since the LiFe0.955V0.045As actually was grown out of a nominal composition of LiFe0.9V0.1As. In particular, the neutron incoherent scattering cross-section of V is huge compared with that of Fe, Li, and As. The trapped flux with rich V having a large neutron incoherent cross-section would lead to a serious underestimation of the scale factor. Therefore, we argue that the phonon normalization is more accurate than the normalization by incoherent peaks.
More importantly, we emphasize that, even with this smaller scale ratio, we can still observe the enhancement of magnetic scattering in LiFe0.955V0.045As [Fig. S5], demonstrating the robustness of our conclusion that the low-energy magnetic excitations in V-doped LiFeAs is greatly enhanced. In the main text, we used the scale factor 200 to normalize all the data. In Fig. S5, we display the local dynamical spin susceptibility of LiFe0.955V0.045As from both normalization methods, as well as others for comparison.
Transport results
Figure S6 shows the magnetic susceptibility and electric resistivity in a series of V-doped LiFeAs. The effective magnetic moments were obtained from the fits with a Curie–Weiss form \(\frac{1}{\chi -{\chi }_{0}}=(T-\theta )/C\), in which θ is the Curie temperature and χ0 is the temperature-independent constant. It is clear that the effective magnetic moment increases with the concentration of Vanadium, as shown in inset of Fig. S6a. Figure S6b shows that the temperature dependence of resistivity of LiFe1−xVxAs varies from x = 0 to x = 0.15, showing the evolution from metallic to insulating behavior. A non-Fermi liquid region was identified with x between 0.05 and 0.15, suggesting enhanced electronic correlation [Fig. S6b inset]. We note that, although the susceptibility and resistivity probe the energy scales different from neutron scattering, the increase of moments and resistivity is qualitatively consistent with the enhancement of low-energy magnetic excitations.
DFT+DMFT calculations
We use DFT+DMFT57 to compute the electronic structure and spin dynamics of V-doped LiFeAs in the paramagnetic state. The DFT part is based on the full-potential linear augmented plane wave method implemented in Wien2K58 in conjunction with Perdew–Burke–Ernzerhof generalized gradient approximation59 of the exchange correlation functional. DFT+DMFT is implemented on top of Wien2K and documented in ref. 60. In the DFT+DMFT calculations, the electronic charge was computed self-consistently on DFT+DMFT density matrix. The quantum impurity problem was solved by the continuous time quantum Monte Carlo (CTQMC) method61,62 with a Hubbard U = 5.0 eV and Hund’s rule coupling J = 0.8 eV in the paramagnetic state.6,63,64 Bethe–Salpeter equation is used to compute the dynamic spin susceptibility where the bare susceptibility is computed using the converged DFT+DMFT Green’s function while the two-particle vertex is directly sampled using CTQMC method after achieving full self-consistency of DFT+DMFT density matrix. The detailed method of computing the dynamic spin susceptibility is documented in ref. 6 and was shown to be able to compute accurately the spin dynamics of many iron pnictide superconductors. The experimental crystal structure (space group I4/mmm, #139) of V-doped LiFeAs with lattice constants a = b = 3.7914 Å and c = 6.3639 Å65 is used in the calculations. Virtual crystal approximation is employed to approximate the V-doping effect. In Fig. S7, we plot the calculated dynamic spin susceptibility from two inter-orbital scattering channels, which are dxy–dxz and dxy–dyz in LiFeAs and LiFe0.967V0.033As. The enhancement of electron scattering in both channels in LiFe0.967V0.033As is closely associated with the Fermi surface nesting between the inner hole pockets (dxz/dyz) and the inner electron pocket (dxy). Such an enhanced electron scattering between different orbitals is consistent with the “spin mixing” process as shown in Fig. 4c in the manuscript and drives the system into the S = 1/2 state. Furthermore, such spin-state fluctuations might be responsible for the biquadratic exchange coupling, which is essential for the nematic instability existing extensively in iron pnictide/chalcogenide superconductors.
Data availability
The neutron-scattering and numerical data used in this work, and in the figures of this manuscript, are available upon request from the corresponding authors.
Code availability
The computer codes used to carry out the DFT+DMFT calculations used in this work are available upon request from the corresponding author.
References
Lin, J. F. et al. Intermediate-spin ferrous iron in lowermost mantle post-perovskite and perovskite. Nat. Geosci. 1, 688–691 (2008).
Bren, K. L., Eisenberg, R. & Gray, H. B. Discovery of the magnetic behavior of hemoglobin: a beginning of bioinorganic chemistry. Proc. Natl Acad. Sci. USA 112, 13123–13127 (2015).
Stewart, G. R. Superconductivity in iron compounds. Rev. Mod. Phys. 83, 1589–1652 (2011).
Krüger, F., Kumar, S., Zaanen, J. & van den Brink, J. Spin-orbital frustrations and anomalous metallic state in iron-pnictide superconductors. Phys. Rev. B 79, 054504 (2009).
Dai, P. C. Antiferromagnetic order and spin dynamics in iron-based superconductors. Rev. Mod. Phys. 87, 855 (2015).
Yin, Z. P., Haule, K. & Kotliar, G. Kinetic frustration and the nature of the magnetic and paramagnetic states in iron pnictides and iron chalcogenides. Nat. Mater. 10, 932 (2011).
Mannella, N. The magnetic moment enigma in Fe-based high temperature superconductors. J. Phys. Condens. Matter 26, 473202 (2014).
Lorenzana, J., Seibold, G. & Coldea, R. Sum rules and missing spectral weight in magnetic neutron scattering in the cuprates. Phys. Rev. B 72, 224511 (2005).
Wang, M. et al. Doping dependence of spin excitations and its correlations with high-temperature superconductivity in iron pnictides. Nat. Commun. 4, 2874 (2013).
Luo, H. Q. et al. Electron doping evolution of the anisotropic spin excitations in BaFe2−xNixAs2. Phys. Rev. B 86, 024508 (2012).
Liu, M. S. et al. Nature of magnetic excitations in superconducting BaFe1.9Ni0.1As2. Nat. Phys. 8, 376–381 (2012).
Luo, H. Q. et al. Electron doping evolution of the magnetic excitations in BaFe2−xNixAs2. Phys. Rev. B 88, 144516 (2013).
Horigane, K. et al. Spin excitations in hole-overdoped iron-based superconductors. Sci. Rep. 6, 33303 (2016).
Carr, S. V. et al. Electron doping evolution of the magnetic excitations in NaFe1−xCoxAs. Phys. Rev. B 93, 214506 (2016).
Qureshi, N. et al. Inelastic neutron-scattering measurements of incommensurate magnetic excitations on superconducting LiFeAs single crystals. Phys. Rev. Lett. 108, 117001 (2012).
Qureshi, N. et al. Fine structure of the incommensurate antiferromagnetic fluctuations in single-crystalline LiFeAs studied by inelastic neutron scattering. Phys. Rev. B 90, 144503 (2014).
Wang, M. et al. Effect of Li-deficiency impurities on the electron-overdoped LiFeAs superconductor. Phys. Rev. B 86, 144511 (2012).
Li, Y. et al. Orbital selective spin excitations and their impact on superconductivity of LiFe1−xCoxAs. Phys. Rev. Lett. 116, 247001 (2016).
Wang, Q. S. et al. Magnetic ground state of FeSe. Nat. Commun. 7, 12182 (2016).
Zaliznyak, I. A. et al. Unconventional temperature enhanced magnetism in Fe1.1Te. Phys. Rev. Lett. 107, 216403 (2011).
Hirschfeld, P. J., Korshunov, M. M. & Mazin, I. I. Gap symmetry and structure of Fe-based superconductors. Rep. Prog. Phys. 74, 124508 (2011).
de’Medici, L., Giovannetti, G. & Capone, M. Selective Mott physics as a key to iron superconductors. Phys. Rev. Lett. 112, 177001 (2014).
Yu, R. & Si, Q. Orbital-selective Mott phase in multiorbital models for iron pnictides and chalcogenides. Phys. Rev. B 96, 125110 (2017).
Komijani, Y. & Kotliar, G. Analytical slave-spin mean-field approach to orbital selective Mott insulators. Phys. Rev. B 96, 125111 (2017).
Gastiasora, M. N. & Anderson, B. M. Enhancement of magnetic stripe order in iron-pnictide superconductors from the interaction between conduction electrons and magnetic impurities. Phys. Rev. Lett. 113, 067002 (2014).
Inosov, D. S. et al. Possible realization of an antiferromagnetic Griffiths phase in Ba(Fe1−xMnx)2As2. Phys. Rev. B 87, 224425 (2013).
Tucker, G. S. et al. Competition between stripe and checkerboard magnetic instabilities in Mn-doped BaFe2As2. Phys. Rev. B 86, 020503 (2012).
Song, Y. et al. A Mott insulator continuously connected to iron pnictide superconductors. Nat. Comm. 7, 13879 (2016).
Matt, C. E. et al. NaFe0.56Cu0.44As: a pnictide insulating phase induced by on-site Coulomb interaction. Phys. Rev. Lett. 117, 097001 (2016).
Xing, L. Y. et al. Observation of non-Fermi liquid behavior in hole-doped LiFe1−xVxAs. Phys. Rev. B 94, 094524 (2016).
Ong, T. T. & Coleman, P. Local quantum criticality of an iron-pnictide tetrahedron. Phys. Rev. Lett. 108, 107201 (2012).
Zhang, J. H., Sknepnek, R. & Schmalian, J. Spectral analysis for the iron-based superconductors: anisotropic spin fluctuations and fully gapped s±-wave superconductivity. Phys. Rev. B 82, 134527 (2010).
Chen, T. et al. Anisotropic spin fluctuations in detwinned FeSe. Nature Materials 18, 709 (2019).
Pfau, H. et al. Momentum dependence of the nematic order parameter in iron-based superconductors. Phys. Rev. Lett. 123, 066402 (2019).
Pfau, H. et al. Detailed band structure of twinned and detwinned BaFe2As2 studied with angle-resolved photoemission spectroscopy. Phys. Rev. B 99, 035118 (2019).
Watson, M. D. et al. Probing the reconstructed Fermi surface of antiferromagnetic BaFe2As2 in one domain. npj Quant. Mater. 4, 36 (2019).
Tian, L. et al. Spin fluctuation anisotropy as a probe of orbital-selective hole-electron quasiparticle excitations in detwinned Ba(Fe1−xCox)As2. Phys. Rev. B 100, 134509 (2019).
Zhang, C. L. et al. Neutron scattering studies of spin excitations in hole-doped Ba0.67K0.33Fe2As2 superconductor. Sci. Rep. 1, 115 (2011).
Harriger, L. W. et al. Nematic spin fluid in the tetragonal phase of BaFe2As2. Phys. Rev. B 84, 054544 (2011).
Lu, X. Y. et al. Spin waves in detwinned BaFe2As2. Phys. Rev. Lett. 121, 067002 (2018).
Georges, A., de’Medici, L. & Mravlje, J. Strong electronic correlations from Hund’s coupling. Annu. Rev. Condens. Matter Phys. 4, 137–178 (2013).
Aron, C. & Kotliar, G. Analytic theory of Hund’s metals: a renormalization group perspective. Phys. Rev. B 91, 041110 (2015).
Stadler, K. M., Yin, Z. P., von Delft, J., Kotliar, G. & Weichselbaum, A. Dynamical mean-field theory plus numerical renormalization-group study of spin-orbital separation in a three-band hund metal. Phys. Rev. Lett. 115, 136401 (2015).
Chaloupka, J. & Khaliullin, G. Spin-state crossover model for the magnetism of iron pnictides. Phys. Rev. Lett. 110, 207205 (2013).
Gütlich, P. & Goodwin, H. A. (eds) Spin Crossover in Transition Metal Compounds I (Springer, Berlin, 2004).
Gretarsson, H. et al. Spin-state transition in the Fe pnictides. Phys. Rev. Lett. 110, 047003 (2013).
Klingeler, R. et al. Local antiferromagnetic correlations in the iron pnictide superconductors LaFeAsO1−xFx and Ca(Fe1−xCox)2As2 as seen via normal-state susceptibility. Phys. Rev. B 81, 024506 (2010).
Yang, R. et al. Observation of an emergent coherent state in the iron-based superconductor KFe2As2. Phys. Rev. B 96, 201108 (2017).
Wiecki, P. et al. Pressure dependence of coherence-incoherence crossover behavior in KFe2As2 observed by resistivity and 75As-NMR/NQR. Phys. Rev. B 97, 064509 (2018).
Hardy, F. et al. Evidence of strong correlations and coherence-incoherence crossover in the iron pnictide superconductor KFe2As2. Phys. Rev. Lett. 111, 027002 (2013).
Miao, H. et al. Orbital-differentiated coherence-incoherence crossover identified by photoemission spectroscopy in LiFeAs. Phys. Rev. B 94, 201109 (2016).
Lee, P. A., Nagaosa, N. & Wen, X. G. Doping a Mott insulator: physics of high-temperature superconductivity. Rev. Mod. Phys. 78, 17 (2006).
Wang, W. Y. et al. Orbital selective neutron spin resonance in underdoped superconducting NaFe0.985As0.015. Phys. Rev. B 95, 094519 (2017).
Wang, M. et al. Antiferromagnetic spin excitations in single crystals of nonsuperconducting Li1−xFeAs. Phys. Rev. B 83, 220515 (2011).
Xing, L. Y. et al. The anomaly Cu doping effects on LiFeAs superconductors. J. Phys. Condens. Matter 26, 435703 (2014).
Kajimoto, R. et al. The Fermi chopper spectrometer 4SEASONS at J-PARC. J. Phys. Soc. Jpn. 80, SB025 (2011).
Kotliar, G. et al. Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 78, 865 (2006).
Blaha, P., Schwarz, K., Madsen, G., Kvasnicka, D. & Luitz, J. WIEN2K, An Augmented Plane Wave+Local Orbitals Program for Calculating Crystal Properties (Karlheinz Schwarz, Techn. Universität Wien, Wien, 2001).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Haule, K., Yee, C.-H. & Kim, K. Dynamical mean-field theory within the full-potential methods: electronic structure of CeIrIn4, CeCoIn5, and CeRhIn5. Phys. Rev. B 81, 195107 (2010).
Haule, K. Quantum Monte Carlo impurity solver for cluster dynamical mean-field theory and electronic structure calculations with adjustable cluster base. Phys. Rev. B 75, 155113 (2007).
Werner, P., Comanac, A., de’Medici, L., Troyer, M. & Millis, A. J. Continuous-time solver for quantum impurity models. Phys. Rev. Lett. 97, 076405 (2006).
Yin, Z. P., Haule, K. & Kotliar, G. Magnetism and charge dynamics in iron pnictides. Nat. Phys. 7, 294 (2011).
Yin, Z. P., Haule, K. & Kotliar, G. Spin dynamics and orbital-antiphase pairing symmetry in iron-based superconductors. Nat. Phys. 10, 845 (2014).
Tapp, J. H. et al. LiFeAs: an intrinsic FeAs-based superconductor with Tc = 18 K. Phys. Rev. B 78, 060505(R) (2008).
Acknowledgements
The neutron-scattering work at Beijing Normal University is supported by the Fundamental Research Funds for the Central Universities (Grant Nos. 310432101 and 2014JJCB27) and the National Natural Science Foundation of China (Grant No. 11734002) (to X.L.). Z.Y. was supported by the NSFC (Grant No. 11674030), the Fundamental Research Funds for the Central Universities (Grant No. 310421113), and the National Key Research and Development Program of China grant 2016YFA0302300. The calculations used high-performance computing clusters at BNU in Zhuhai and the National Supercomputer Center in Guangzhou. The neutron-scattering work at Rice is supported by the U.S. DOE BES under contract no. DE-SC0012311 (to P.D.). The neutron experiment at the Materials and Life Science Experimental Facility of the J-PARC was performed under a user program 2017B0216.
Author information
Authors and Affiliations
Contributions
P.D., G.T., X.L., and C.J. designed the research. Single crystals were grown by G.D. and L.X. under the instructions of X.W. and C.J. Neutron-scattering experiments were carried out by Z.X., G.T., Y.R., L.T., Y.L., P.L., H.W., Y.W., R.K., K.I., and D.L.A. Theoretical calculations were carried out by Z.Y. The paper was written by P.D., Y.L., Z.X., and Z.Y. All authors made comments on the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xu, Z., Dai, G., Li, Y. et al. Strong local moment antiferromagnetic spin fluctuations in V-doped LiFeAs. npj Quantum Mater. 5, 11 (2020). https://doi.org/10.1038/s41535-020-0212-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-020-0212-x