Abstract
The interplay of orbital and spin degrees of freedom is the fundamental characteristic in numerous condensed matter phenomena, including high-temperature superconductivity, quantum spin liquids, and topological semimetals. In iron-based superconductors (FeSCs), this causes superconductivity to emerge in the vicinity of two other instabilities: nematic and magnetic. Unveiling the mutual relationship among nematic order, spin fluctuations, and superconductivity has been a major challenge for research in FeSCs, but it is still controversial. Here, by carrying out 77Se nuclear magnetic resonance (NMR) measurements on FeSe single crystals, doped by cobalt and sulfur that serve as control parameters, we demonstrate that the superconducting transition temperature Tc increases in proportion to the strength of spin fluctuations, while it is independent of the nematic transition temperature Tnem. Our observation therefore directly implies that superconductivity in FeSe is essentially driven by spin fluctuations in the intermediate coupling regime, while nematic fluctuations have a marginal impact on Tc.
Similar content being viewed by others
Introduction
In correlated Fermi fluids, nematicity refers to the state in which rotational symmetry is spontaneously broken, while time-reversal invariance is preserved, and consequently, the symmetry of the crystal changes from tetragonal to orthorhombic.1 An important aspect in iron-based superconductors (FeSCs) is the propensity for nematic ordering, which is usually followed by a spin-density-wave (SDW) transition, near a superconducting (SC) dome.2,3,4 Regardless of the origin of nematicity that is still under debate,5,6 this raises the fundamental issue of whether superconductivity in FeSCs is closely related to nematicity7,8 or magnetism9,10 or both.11 To address this issue, it is much desirable to separate nematic order from the magnetic one. In this respect, FeSe has been a key platform for studying the origin of nematicity and its role in superconductivity,12 as it exhibits nematic and SC orders at well-separated temperatures, Tnem ~ 90 K and Tc ~ 9 K, respectively, without involving magnetic order. Numerous recent studies in FeSe show that nematicity causes the strongly anisotropic SC gap symmetry,13,14,15,16 and further discuss that nematic fluctuations might play an important role for the superconducting pairing mechanism.17,18 On the other hand, the leading role of spin fluctuations (SFs) in the SC mechanism of FeSe, as in other FeSCs whose parent materials magnetical orders, has been also proposed in the literature.19,20,21,22 In this spin fluctuation-mediated pairing scenario, the subsequent question arises whether weak or strong coupling approach is appropriate to establish theory of superconductivity in FeSCs. It is quite interesting to note that recent NMR studies of FeSe under high pressure reveal the persistence of local nematicity at temperatures far above Tnem, which suggests a correlation between local nematicity and magnetism.23,24 Another interesting observation by NMR is the unusual suppression of \({({T}_{1}T)}^{-1}\) at optimal pressure,25 suggesting that the interplay of SFs and superconductivity may undergo a critical change with high pressure.
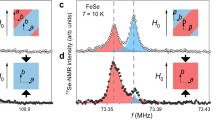
As a system undergoes a nematic transition (C4 → C2), two nematic domains are naturally formed below Tnem, still preserving the C4 symmetry on average. Accordingly, it is usually required to detwin nematic domains, for example, by an external strain to study nematicity. As a local probe in real space, on the other hand, NMR is uniquely capable of observing the two nematic domains at the same time. Indeed, it has been established that the splitting of the NMR line in FeSCs at an external field H applied along the crystallographic a axis represents the nematic order parameter and its onset temperature corresponds to the nematic transition temperature Tnem (refs., 26,27,28 see Fig. 1c). In order to investigate whether and how nematicity is related to superconductivity, we measured the 77Se line splitting for H∥a in FeSe1−ySy and Fe1−xCoxSe single crystals. In general, it is considered that substituting isovalent S for Se is equivalent to the application of (negative) chemical pressure, and Co substituted for Fe supplies an additional electron and also plays as a paramagnetic impurity. Therefore, a systematic NMR study on the two different doped systems may enable a full understanding of the relationship between nematicity, magnetism, and superconductivity.
a, b Temperature dependence of 77Se spectrum of Fe1−xCoxSe. For x = 0.018 (b), the 77Se spectrum shows a very similar behavior as the undoped one, except a moderate line broadening. For a slightly larger doping, x = 0.025 (a), the 77Se line undergoes a considerable line broadening. While the splitting of the two 77Se lines was clearly identified at low temperatures (vertical bars), the onset of the splitting is not well defined, being ascribed to local disorder. c Temperature dependence of 77Se spectrum for undoped FeSe. d, e Temperature dependence of 77Se spectrum of FeSe1−ySy for y = 0.05 and 0.1, respectively. Tnem is progressively suppressed with increasing S doping.
Results and discussion
Figure 1 shows how the temperature dependence of the 77Se NMR spectrum in FeSe is modified as a function of x in Fe1−xCoxSe (Fig. 1a, b) and as a function of y in FeSe1−ySy (Fig. 1d, e). For FeSe1−ySy, we find that the onset temperature of the line splitting or Tnem is gradually suppressed, consistent with previous studies.17,21 For Fe1−xCoxSe, however, Tnem hardly changes for x = 0.018. Upon further doping to slightly higher x = 0.025, the 77Se line becomes significantly broad, making it difficult to identify the onset of the line splitting. The much larger 77Se line broadening for Co doping than for S doping is well understood because Co has a strong influence on Fe moments as a nonmagnetic impurity. We notice, however, that the 77Se line broadening is not simply proportional to the concentration of Co dopants, but rather it appears to increase drastically above x ~ 0.025. In fact, for x = 0.036, it is not possible to observe the line splitting anymore, because the linewidth is much larger than the nematic splitting (see Supplementary Fig. 1). On the other hand, the 77Se linewidth is proportional to both S and Co dopants similarly, as long as Co doping is less than 2.5%, as shown in Supplementary Fig. 2. This suggests that doped Co impurities beyond ~2.5% of Fe sites cause a strong disorder effect on the correlation between Fe spins, indicating the existence of a critical doping level above which the magnetic correlation length becomes sufficiently long to induce a short-range exchange.
Although Tnem cannot be accurately determined for x = 0.025 due to the large line broadening in the nematic state, we clearly observed the line splitting below 80 K, as shown in Fig. 1a. While this puts a lower limit of Tnem, the fitting analysis of 77Se spectra in Fig. 1a also suggests that the line splitting seems to persist even up to 100 K (see vertical bars). (The detailed Knight shift data as a function of temperature and doping are shown in Supplementary Fig. 3). This suggests that Co impurities may induce a spatial distribution of Tnem in the temperature range, 80 ≤ Tnem ≤ 100 K. Regardless of the details, Tnem is marginally suppressed by Co doping within the doping range investigated, as shown in Fig. 2a. Note that the Co-doping range investigated is very narrow, and thus we are unable to argue whether Tnem remains a constant at higher Co doping. In any case, Fig. 2a, b reveals that Tnem and Tc are clearly decoupled.
a, b, The phase diagrams of Fe1−xCoxSe and FeSe1−ySy, respectively. For Co doping, Tnem is hardly influenced, but Tc is strongly suppressed. In contrast, for S doping, Tnem is suppressed with increasing y, and Tc remains nearly the same. The asterisk (*) and cross (×) symbols are the Tnem and Tc data, respectively, extracted from ref. 17. c, The spin-lattice relaxation rate divided by temperature, \({({T}_{1}T)}^{-1}\) which measures spin fluctuations, as a function of temperature and Co-doping x in Fe1−xCoxSe. The enhancement of \({({T}_{1}T)}^{-1}\) at low temperatures is progressively suppressed with increasing x (see Fig. 3). The solid lines are guides to the eyes. d, \({({T}_{1}T)}^{-1}\) as a function of temperature and S-doping y in FeSe1−ySy. Spin fluctuations are unchanged with increasing S-doping y, being consistent with Tc that is nearly independent of y.
Interestingly, the split 77Se lines below 80 K for x = 0.025 are notably anisotropic, i.e., the peak for the lower frequency side is broader than that for the higher frequency. The origin of the anisotropic line shape is unclear, but we note that the similar anisotropic 77Se line shape is also observed at T < 20 K for x = 0.018 (see Fig. 1b). This implies that magnetic inhomogeneity, which otherwise appears at low temperatures, prevails at higher temperatures with higher Co doping.
Contrasting sharply with the weak dependence of nematicity on both S and Co dopants, our susceptibility measurements reveal that superconductivity is strongly dependent only on Co dopants. That is, Tc is rapidly suppressed by small Co doping, whereas it is robust with regard to S doping, as shown in Fig. 2a, b, being consistent with previous studies.29,30 The very different behavior of Tnem and Tc with doping indicates that nematic and superconducting orders are not directly coupled (Coldea, A. I. et al., Evolution of the Fermi surface of the nematic superconductors FeSe1−xSx. arXiv:1611.07424, unpublished),31 raising a strong question as to whether nematicity and superconductivity are closely related.7,8,17,32
Having established the lack of a coupling of the nematic and superconducting transition temperatures, we now discuss the role of SFs for superconductivity. For probing low-energy SFs, we measured the spin-lattice relaxation rate, \({T}_{1}^{-1}\), as the quantity \({({T}_{1}T)}^{-1}\) is a measure of SFs at very low energy
where χ″(k, ω) is the imaginary part of the dynamic susceptibility at momentum k and frequency ω, γn is the nuclear gyromagnetic ratio, and A(k) is the structure factor of the hyperfine interaction. Figure 2c, d shows \({({T}_{1}T)}^{-1}\) as a function of Co and S doping, respectively, at H∥a = 9 T. The data for the undoped FeSe crystal were taken from ref. 26 With increasing Co-doping x in Fe1−xCoxSe, \({({T}_{1}T)}^{-1}\) or SFs above Tc is rapidly suppressed, which is exactly parallel with the suppression of Tc, as shown in Fig. 2a. Note that for x = 0.035, superconductivity is completely absent, and correspondingly SFs are not enhanced at all at low temperatures. On the other hand, \({({T}_{1}T)}^{-1}\) above Tc is unchanged with increasing S-doping y in FeSe1−ySy up to y = 0.1, as precisely as Tc does (see Fig. 2b). From the data presented in Fig. 2, therefore, one sees that Tc depends only on the strength of spin fluctuations, but not on Tnem. (At larger S doping near y = 0.2, it was reported that both \({({T}_{1}T)}^{-1}\) and Tc are strongly suppressed in such a way that the correlation between SFs and Tc persists,21 somewhat similar to the behavior in Co-doped samples).
For further quantitative information on how SFs are related to Tc, we adopt a spin fluctuation model in the Eliashberg formalism,33 or Millis–Monien–Pines (MMP) model.34 For this, we separate out the enhancement of \({({T}_{1}T)}^{-1}\) that is solely associated with SFs from the data shown in Fig. 2c. Noting that \({({T}_{1}T)}^{-1}\) for the non-superconducting sample (x = 0.035) approaches a constant, \({({T}_{1}T)}_{0}^{-1}\equiv {\Gamma }_{0}\), without any enhancement at zero temperature, one may define the strength of SFs Γ for H∥a from the \({({T}_{1}T)}^{-1}(x)\) values just above Tc:
While the MMP model indicates that Γ is proportional to the square of the correlation length,34 ξ2 (T), the estimation of the low- energy part of the Eliashberg bosonic spectral function suggests that the coupling constant λ is proportional to ξ, i.e., \(\sqrt{\Gamma }\). As it was analyzed by Radtke et al.35 and Popovich et al.,36 the direct use of the MMP spectrum gives overestimation of Tc and the gap function due to a long tail at high energies of the bosonic spectral functions ~1∕ω. To cure the problem, it was proposed to introduce a cutoff or calculate the bosonic self-energy at high energies.37 For simplicity, we use the approach of cutoff proposed in ref. 36 A detailed procedure of the calculation is described in Supplementary Note 1.
The plot of Tc vs. \(\sqrt{\Gamma }\) is shown in Fig. 3. The solid curve is a theoretical calculation (Tc vs. \(\lambda \propto \sqrt{\Gamma }\)) based on the Eliashberg theory in which electron correlation effects are substantial. The good agreement of our theory with the experimental data evidences that the magnetic scenario for superconductivity in which Cooper pairing is mediated by spin fluctuations applies to FeSe, and it is likely a universal superconducting mechanism among FeSCs.
Based on our NMR finding that Tc relies only on SFs, the seeming relevance of nematicity with superconductivity may be simply due to the closeness with magnetism, rather than to superconductivity itself. It should be noted that the strongly anisotropic gap structure13,14,15,16,22 observed in FeSe may be a natural consequence of the presence of nematicity within the superconducting state. It is because nematicity involves the splitting of dxz and dyz orbitals that should have an inevitable influence on the gap symmetry. However, Tc itself is not necessarily affected by nematicity.38 Nevertheless, nematicity may be considered as an important barometer for superconductivity in FeSCs, as it is strongly coupled to magnetism,18 which in turn directly correlates with superconductivity.
Methods
Crystal growth and characterization
The growth of Fe1−xCoxSe and FeSe1−ySy single crystals was performed by using the KCl–AlCl3 flux technique in permanent T gradient in accordance with refs. 39,40 All preliminary operations for the preparation of the reaction mixture were carried out in a dry box with a residual pressure of O2 and H2O not higher than 0.1 ppm. At the first stage, polycrystalline samples of the composition Fe1−xCoxSe and FeSe1−ySy were obtained. For this, Fe, Co, S, and Se powders were carefully ground in a mortar in the appropriate ratio, and then annealed in evacuated quartz ampoules at 420 °C for a few days. In the second stage, 0.5 g of the prepared sample was placed on the bottom of a thick-walled ampoule, and then the mixture of AlCl3 and KCl in a molar ratio of AlCl3:KCl = 2:1 is added to the ampule, after that the ampule was evacuated and sealed. The sealed ampoule with polycrystalline sample of Fe–Co–Se–S loads was placed in a horizontal two-zone furnace and heated for 5 weeks in such a way that the hot-zone temperature was set to 420 °C and the cold-zone temperature was set to 370 °C. After 5 weeks, the furnace was turned off, and the ampoule was removed from the furnace. Next, the ampoule was cut, and the single crystals from the cold zone were separated from the flux by dissolving it in water. The single crystals obtained were thin square plates with metallic luster. The single crystals were grown with platelet-like morphology, and were characterized by SEM/EDX for compositional analysis.
Nuclear magnetic resonance
77Se (nuclear spin I = 1∕2) NMR was carried out in undoped and doped FeSe single crystals at an external magnetic field, and in the range of temperature 4.2–160 K. The samples were oriented using a goniometer for the accurate alignment along the external field. The 77Se NMR spectra were acquired by a standard spin-echo technique with a typical π∕2 pulse length 2–3 μs. The nuclear spin–lattice relaxation rate \({T}_{1}^{-1}\) was obtained by fitting the recovery of the nuclear magnetization M(t) after a saturating pulse to the following fitting function:
where A is a fitting parameter that is ideally unity.
Determination of T c and T nem
The superconducting transition temperature Tc was determined from magnetic susceptibility (χ) measurements by comparing field-cooled and zero-field-cooled data, while we obtained the nematic transition temperature Tnem by measuring the temperature at which the 77Se NMR line splits (see Fig. 1). Due to the weakness of the signal intensity, we were unable to determine Tc by \({({T}_{1}T)}^{-1}\) measurements, except the undoped FeSe sample. This could give an error in extracting spin fluctuations just above Tc and Γ, which was reflected in an experimental error indicated in Fig. 3.
Data availability
The data that support the findings of this study are available from the corresponding author (S-H.B.).
References
Fradkin, E., Kivelson, S. A., Lawler, M. J., Eisenstein, J. P. & Mackenzie, A. P. Nematic fermi fluids in condensed matter physics. Ann. Rev. Cond. Mat. Phys. 1, 153–178 (2010).
Fernandes, R. M., Chubukov, A. V. & Schmalian, J. What drives nematic order in iron-based superconductors? Nature Phys. 10, 97–104 (2014).
Böhmer, A. E. & Meingast, C. Electronic nematic susceptibility of iron-based superconductors. C. R. Physique 17, 90–112 (2016).
Si, Q., Yu, R. & Abrahams, E. High-temperature superconductivity in iron pnictides and chalcogenides. Nat. Rev. Mater. 1, 16017 (2016).
Yamakawa, Y., Onari, S. & Kontani, H. Nematicity and magnetism in FeSe and other families of Fe-based superconductors. Phys. Rev. X 6, 021032 (2016).
Chubukov, A. V., Khodas, M. & Fernandes, R. M. Magnetism, superconductivity, and spontaneous orbital order in iron-based superconductors: which comes first and why? Phys. Rev. X 6, 041045 (2016).
Kuo, H.-H., Chu, J.-H., Palmstrom, J. C., Kivelson, S. A. & Fisher, I. R. Ubiquitous signatures of nematic quantum criticality in optimally doped Fe-based superconductors. Science 352, 958–962 (2016).
Wang, C. G. et al. Electron mass enhancement near a nematic quantum critical point in NaFe1−x Cox As. Phys. Rev. Lett. 121, 167004 (2018).
Wang, F. & Lee, D.-H. The electron-pairing mechanism of iron-based superconductors. Science 332, 200–204 (2011).
Dai, P. Antiferromagnetic order and spin dynamics in iron-based superconductors. Rev. Mod. Phys. 87, 855–896 (2015).
She, J.-H., Lawler, M. J. & Kim, E.-A. Quantum spin liquid intertwining nematic and superconducting order in FeSe. Phys. Rev. Lett. 121, 237002 (2018).
Böhmer, A. E. & Kreisel, A. Nematicity, magnetism and superconductivity in FeSe. J. Phys.: Condens. Matter 30, 023001 (2018).
Xu, H. C. et al. Highly anisotropic and twofold symmetric superconducting gap in nematically ordered FeSe0.93S0.07. Phys. Rev. Lett. 117, 157003 (2016).
Hashimoto, T. et al. Superconducting gap anisotropy sensitive to nematic domains in FeSe. Nat. Commun. 9, 282 (2018).
Liu, D. et al. Orbital origin of extremely anisotropic superconducting gap in nematic phase of FeSe superconductor. Phys. Rev. X 8, 031033 (2018).
Kushnirenko, Y. S. et al. Three-dimensional superconducting gap in FeSe from angle-resolved photoemission spectroscopy. Phys. Rev. B 97, 180501 (2018).
Hosoi, S. et al. Nematic quantum critical point without magnetism in FeSe1−xSx superconductors. Proc. Natl. Acad. Sci. USA 113, 8139–8143 (2016).
Matsuura, K. et al. Maximizing Tc by tuning nematicity and magnetism in FeSe1−x Sx superconductors. Nat. Commun. 8, 1143 (2017).
Imai, T., Ahilan, K., Ning, F. L., McQueen, T. M. & Cava, R. J. Why does undoped FeSe become a high-Tc superconductor under pressure? Phys. Rev. Lett. 102, 177005 (2009).
Sun, J. P. et al. High-Tc superconductivity in FeSe at high pressure: dominant hole carriers and enhanced spin fluctuations. Phys. Rev. Lett. 118, 147004 (2017).
Wiecki, P. et al. Persistent correlation between superconductivity and antiferromagnetic fluctuations near a nematic quantum critical point in FeSe1−xSx. Phys. Rev. B 98, 020507 (2018).
Rhodes, L. C. et al. Scaling of the superconducting gap with orbital character in FeSe. Phys. Rev. B 98, 180503 (2018).
Wang, P. S. et al. Robust short-range-ordered nematicity in FeSe evidenced by high-pressure NMR. Phys. Rev. B 96, 094528 (2017).
Wiecki, P. et al. NMR evidence for static local nematicity and its cooperative interplay with low-energy magnetic fluctuations in FeSe under pressure. Phys. Rev. B 96, 180502 (2017).
Kuwayama, T. et al. 77Se-NMR study under pressure on 12%-S doped FeSe. J. Phys. Soc. Jpn. 88, 033703 (2019).
Baek, S.-H. et al. Orbital-driven nematicity in FeSe. Nature Mater. 14, 210–214 (2015).
Baek, S.-H. et al. Nematicity and in-plane anisotropy of superconductivity in β -FeSe detected by 77Se nuclear magnetic resonance. Phys. Rev. B 93, 180502 (2016).
Ok, J. M. et al. Nematicity and magnetism in LaFeAsO single crystals probed by 75As nuclear magnetic resonance. Phys. Rev. B. 97, 180405 (2018).
Urata, T. et al. Superconductivity pairing mechanism from cobalt impurity doping in FeSe: Spin (s±) or orbital (s++) fluctuation. Phys. Rev. B 93, 014507 (2016).
Abdel-Hafiez, M. et al. Impurity scattering effects on the superconducting properties and the tetragonal-to-orthorhombic phase transition in FeSe. Phys. Rev. B 93, 224508 (2016).
Massat, P. et al. Collapse of critical nematic fluctuations in FeSe under pressure. Phys. Rev. Lett. 121, 077001 (2018).
Lederer, S., Schattner, Y., Berg, E. & Kivelson, S. A. Enhancement of superconductivity near a nematic quantum critical point. Phys. Rev. Lett. 114, 097001 (2015).
Allen, P. B. & Mitrović, B. Theory of superconducting Tc. Solid State Physics 37, 1–92 (1983).
Millis, A. J., Monien, H. & Pines, D. Phenomenological model of nuclear relaxation in the normal state of YBa2Cu3O7. Phys. Rev. B 42, 167–178 (1990).
Radtke, R. J., Ullah, S., Levin, K. & Norman, M. R. Constraints on superconducting transition temperatures in the cuprates: antiferromagnetic spin fluctuations. Phys. Rev. B 46, 11975–11985 (1992).
Popovich, P. et al. Specific heat measurements of Ba0.68K0.32Fe2As2 single crystals: evidence for a multiband strong-coupling superconducting state. Phys. Rev. Lett. 105, 027003 (2010).
Abanov, A., Chubukov, A. V. & Schmalian, J. Quantum-critical theory of the spin-fermion model and its application to cuprates: normal state analysis. Adv. Phys. 52, 119–218 (2003).
Kang, J., Fernandes, R. M. & Chubukov, A. Superconductivity in FeSe: the role of nematic order. Phys. Rev. Lett. 120, 267001 (2018).
Chareev, D. et al. Single crystal growth and characterization of tetragonal FeSe1−x superconductors. CrystEngComm 15, 1989–1993 (2013).
Chareev, D. et al. Single crystal growth, transport and scanning tunneling microscopy and spectroscopy of FeSe1−xSx. CrystEngComm 20, 2449–2454 (2018).
Acknowledgements
We acknowledge A. Chubukov for useful discussions. S.H.B. has been supported by the Deutsche Forschungsgemeinschaft (Germany) via DFG Research Grants BA 4927/2-1 and by the National Research Foundation of Korea (NRF-2019R1F1A1057463). D.V.E., B.B., I.M., and S.A. were supported by RSF-DFG project (no. 19-43-04129, BU887/25-1, EF86/7-1). D.V.E. and I.M. were also supported by VW foundation in the frame of the VW Trilateral Initiative. S.A. acknowledges financial support from Deutsche Forschungsgemeinschaft (DFG) via Grant No. DFG AS 523/4-1. The work at POSTECH was supported by Institute for Basic Science (no. IBS-R014-D1) and also by the National Research Foundation (NRF) of Korea through the SRC (no. 2018R1A5A6075964) and the Max Planck-POSTECH Center for Complex Phase Materials in Korea (MPK) (no. 2016K1A4A4A01922028). The work of DACh was supported by the program 211 of the Russian Federation Government, agreement No. 02.A03.21.0006, by the Russian Government Program of Competitive Growth of Kazan Federal University.
Author information
Authors and Affiliations
Contributions
S-H.B. and B.B. have proposed and initiated the project. J.M.O., J.S.K., S.A., I.M., D.C., T.U., K.T. and Y.T. have grown single crystals and characterized transport and superconducting properties. S-H.B. and J.M.O. performed NMR measurements and analyzed data; S-H.B., D.V.E. and B.B. participated in writing of the paper. All authors discussed the results and commented on the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Baek, SH., Ok, J.M., Kim, J.S. et al. Separate tuning of nematicity and spin fluctuations to unravel the origin of superconductivity in FeSe. npj Quantum Mater. 5, 8 (2020). https://doi.org/10.1038/s41535-020-0211-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-020-0211-y
This article is cited by
-
Peculiarities of the Nematic Transition in FeSe\(_{0.675}\)Te\(_{0.3}\)S\(_{0.025}\) and Its Proximity to the Quantum Critical Point
Journal of Superconductivity and Novel Magnetism (2024)