Abstract
Three-dimensional topological insulators (TIs) in proximity with superconductors are expected to exhibit exotic phenomena, such as topological superconductivity (TSC) and Majorana-bound states (MBS), which may have applications in topological quantum computation. In superconductor–TI–superconductor Josephson junctions, the supercurrent versus the phase difference between the superconductors, referred to as the current–phase relation (CPR), reveals important information including the nature of the superconducting transport. Here, we study the induced superconductivity in gate-tunable Josephson junctions (JJs) made from topological insulator BiSbTeSe2 with superconducting Nb electrodes. We observe highly skewed (non-sinusoidal) CPR in these junctions. The critical current, or the magnitude of the CPR, increases with decreasing temperature down to the lowest accessible temperature (T ~ 20 mK), revealing the existence of low-energy modes in our junctions. The gate dependence shows that close to the Dirac point the CPR becomes less skewed, indicating the transport is more diffusive, most likely due to the presence of electron/hole puddles and charge inhomogeneity. Our experiments provide strong evidence that superconductivity is induced in the highly ballistic topological surface states (TSS) in our gate-tunable TI-based JJs. Furthermore, the measured CPR is in good agreement with the prediction of a model which calculates the phase-dependent eigenstate energies in our system, considering the finite width of the electrodes, as well as the TSS wave functions extending over the entire circumference of the TI.
Similar content being viewed by others
Introduction
Three-dimensional (3D) topological insulators (TIs) are a new class of quantum matters and are characterized by an insulating bulk and conducting topological surface states (TSS). These TSS are spin-helical with linear Dirac fermion-like energy-momentum dispersion.1,2 The TSS of 3D TIs in proximity to s-wave superconductors are among the top candidates proposed to realize topological superconductors,3 capable to support Majorana-bound states (MBS) and promising for future applications in topological quantum computing.4,5
A Josephson junction (JJ) made of a TI with two superconducting contacts is one of the most common platforms to study the nature of the induced superconductivity in TIs and possible topological superconductivity. One of the fundamental properties of a JJ is its supercurrent (I) as a function of the phase (φ) difference between the two superconducting contacts, referred to as the current–phase relation (CPR), where the maximum of I(φ) is the critical current (IC) of the JJ. Given the topological protection or the prohibited backscattering from non-magnetic impurities in the TSS of 3D TIs,1,2 superconductor–TI–superconductor (S–TI–S) junctions are expected to demonstrate novel features in their CPR.6,7,8,9 While for conventional junctions the CPR is 2π-periodic, for TI-based JJs the CPR is predicted to have an additional 4π-periodic component.3,10 This 4π-periodicity originates from the zero-energy crossing (at φ = π) of the Andreev bound states (ABS) and is protected by the fermion parity conservation. However, if the temporal variation of φ is slower than the quasiparticle poisoning time, the 2π-periodicity of the CPR is restored, which can mask the unique topological nature of the JJs.10,11,12 Nonetheless, in this case the topologically protected modes can give rise to a highly non-sinusoidal (“skewed”) 2π-periodic CPR similar to a perfectly ballistic (scattering free) JJ.11,13,14
JJs have been experimentally studied in 3D TIs15,16,17,18,19,20,21,22,23,24,25,26 including TI nanoribbons (TINRs).27,28 These earlier studies of TI-based JJs have reported indirect signatures of skewed CPR using a variety of techniques, such as temperature-dependent IC and Fraunhofer patterns.17,20,25 However, it has been challenging to observe significant skewness in direct phase-sensitive measurements of CPR.18,28 In this work, we fabricate S–TI–S junctions based on the topological insulator BiSbTeSe2 flakes, which have an insulating bulk and demonstrate TSS-dominated electrical properties at low temperatures.29,30 We measure the CPR in the S–TI–S junctions using an asymmetric superconducting quantum interference device (SQUID).31 Remarkably, the measured CPR in our S–TI–S junctions are highly skewed, revealing that the superconducting transport is carried by the ballistic TSS in our TI JJs. Furthermore, we observe that the skewness depends on the back-gate voltage (Vg) and is the smallest close to the charge neutrality point (CNP). We present a theoretical model based on the induced superconductivity in the ballistic TSS of the TI. This model takes into account the finite-size (of both Nb and TI) and proximity effects, and relates the induced supercurrent to the TSS that extend over the entire circumference of the TI. The calculated energy spectrum (energy vs. phase φ) of the junction reveals the existence of extremely low-energy modes that exist over the entire range of phases, i.e. 0 ≤ φ < 2π. The computed CPR from the theory is in good agreement with the experimental results.
Results and discussion
We adapt an asymmetric SQUID technique31 to measure the CPR in our TI (BiSbTeSe2)-based JJ. Our BiSbTeSe2 crystals are among the most bulk-insulating 3D TIs, where the Fermi energy lies within the bulk bandgap and inside the TSS, as verified by the angle-resolved photoemission spectroscopy (ARPES) and transport measurements.29 Exfoliated thin films of this material exhibit ambipolar field effect, as well as several signatures of topological transport through the spin-helical Dirac fermion TSS, including the half-integer quantum Hall effect and π Berry phase.29,30 Furthermore, we have recently observed an anomalous enhancement of the critical current in JJs based on BiSbTeSe2 nanoribbons, demonstrating the induced superconductivity in the TSS.28 Figure 1a shows a scanning electron microscope (SEM) image of an asymmetric SQUID with a BiSbTeSe2 flake (sample A). The asymmetric SQUID consists of two JJs in parallel. The first JJ is the S–TI–S junction with an unknown CPR, I(φ), and is highlighted by the dashed white rectangle in Fig. 1a. The second JJ is a conventional S–S′–S junction (REF junction), where S and S′ are 300 and 80 nm wide Nb lines, respectively. The data presented here comes from two devices, sample A (width W ~ 2 μm and thickness t ~ 40 nm) and sample B (W ~ 4 μm and t ~ 13 nm). All our measurements are performed in a dilution refrigerator with a base temperature (T) of ~20 mK.
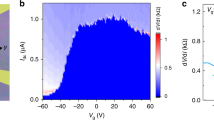
a A scanning electron microscope (SEM) image of an asymmetric superconducting quantum interference device (SQUID) used to measure the current–phase relation (CPR), the supercurrent I vs. φ (the phase difference between the superconductors), in the topological insulator (TI)-based Josephson junction (JJ). The asymmetric SQUID is formed between a TI-based JJ with superconducting Nb contacts and a reference (REF) junction in parallel. The REF junction is a conventional S–S′–S Josephson junction with the supercurrent IREF(φR) = ICREF sin(φR), where ICREF and φR are the critical current and the phase difference across the REF junction, respectively. Scale bar is 1 μm. b Schematic of the CPR measurement setup. We use a low-frequency (~17 Hz) square-wave pulsed current (ISQUID) with 50% duty cycle to bias the SQUID. The voltage VS across the SQUID is monitored with a lock-in amplifier. A perpendicular magnetic field B is applied to control the phase difference inside the SQUID loop (with area S). i.e. φ − φR = 2πΦB/Φ0, where ΦB = B·S is the magnetic flux and Φ0 = h/2e is the superconducting flux quantum. c Color map of VS as functions of ISQUID and B. The solid white curve marks the critical current ICSQUID of the SQUID and the dashed red line is the critical current ICREF of the REF junction. d The current–phase relation (symbols) represented by the normalized current (I/IC) of the TI-based JJ vs. the phase φ measured in sample A at temperature T = 20 mK. Dashed blue curve depicts sin(φ). Since the absolute value of the flux inside the SQUID is unknown, we shift the experimental curve in the horizontal axis so that φ = 2πΦB/Φ0.
Supercurrent (IREF) in the REF junction follows a sinusoidal behavior vs. the phase difference (φR) across the junction, hence IREF(φR) = ICREF sin(φR), where ICREF is the critical current of the REF junction. The total current (ISQUID) of the SQUID device is ISQUID = IREF(φR) + I(φ). Furthermore, the phase differences across the two JJs and the external magnetic flux ΦB = B·S, where S is the area of the SQUID, are related by φ − φR = 2π(ΦB − LsI)/Φ0, where Φ0 = h/2e is the superconducting magnetic flux quantum, and Ls is the self-inductance of the SQUID loop. We can estimate Ls ~ 5 pH32 for our SQUID assuming a constant current density, Nb London penetration depth λ ~ 39 nm33 and Nb film thickness t ~ 40 nm. Although penetration depth may not be applied easily in our system, the calculated Ls is acceptable within a factor of 2. Since LsI/Φ0 ~ 0.04 ≪ 1, we can ignore the contribution of the self-inductance Ls in the phase difference, thus φ − φR = 2πΦB/Φ0 and ISQUID = IREF(φR) + I(2πΦB/Φ0 + φR). In general, we can reconstruct the CPR of the TI-based junction using an analytical approach presented in ref. 34 However, in our asymmetric SQUID, the REF junction is designed such that ICREF ≫ IC, where IC is the critical current of the S–TI–S junction. Thus φR ≈ π/2 when the SQUID reaches its critical current with ICSQUID ~ ICREF + I(2πΦB/Φ0 + π/2). Therefore, the modulation of the ICSQUID vs. B = ΦB/S (in period of B0 = Φ0/S) will provide a very good approximation of the CPR, particularly the skewness of I(φ) in the TI-based JJ.
Figure 1b depicts the set-up for the measurement of the CPR in our TI-based JJs. In order to reduce the uncertainty of the measured ICSQUID due to thermal and quantum fluctuations, we use a square wave pulsed current (frequency f ~ 17 Hz) with 50% duty cycle to bias the SQUID. The voltage (VS) across the SQUID is measured by a lock-in amplifier and the magnetic flux in the SQUID is varied by an external magnet. We also performed dc measurements, which resulted in qualitatively similar behavior to the pulsed measurements. However, the dc mode is more sensitive to thermal fluctuations and the Joule heating effect. Therefore, the CPR is noisier and its amplitude (i.e., the critical current IC) is smaller compared with the pulsed measurement.
For a fixed ΦB, once the amplitude of the pulsed current is increased above ICSQUID, a non-zero voltage appears across the SQUID. Figure 1c depicts a color map of VS as functions of ISQUID and the external magnetic field (B) applied out of the plane of the SQUID. The solid white curve highlights ICSQUID vs B. We estimate ICREF ~ 18 μA (the dashed red line in Fig. 1c) by taking average of ICSQUID vs. B. Then I(φ) ~ ICSQUID(2πΦB/Φ0) −ICREF. Figure 1d shows the supercurrent I(φ) normalized by its amplitude (IC) vs. φ measured in sample A for Vg = 0 V at T = 20 mK (red symbols). The measured CPR does not exhibit any hysteresis vs. magnetic flux. However, since the absolute value of the flux in the SQUID is unknown (for instance, due to a remnant field), we shift the experimental curve in the horizontal direction such that φ = 2πΦB/Φ0. The measured CPR is contrasted with a reference sin(φ) shown by the dashed blue curve in Fig.1d. The measured CPR in sample A is forward skewed, i.e. its maximum occurs at φ = 0.75π (instead of π/2 for sin(φ)).
It is also noted that the measured CPR in Fig. 1d (at T = 20 mK) is non-anti-symmetric (NAS) around zero, i.e., not symmetric under simultaneous sign changes in ΦB and I (note for a 2π periodic function such as the CPR, being antisymmetric around zero is equivalent to also being antisymmetric around π). A similar NAS current vs. flux curve can also be seen in the theoretical and experimental results of ref. 31 for atomic contacts. Although those authors do not explicitly discuss this NAS, they do discuss the difference between the observed current–flux relation (which is taken as a measure of the CPR) and a theoretically predicted CPR (based on conventional models which ignores stochastic switching processes) with an explanation that we find plausible in our case as well. In particular, like ref., 31 we observe NAS only for the highly skewed CPR and not for the more sinusoidal ones. This NAS is an artifact of the assumption that switching to the normal state occurs when the phase φR across the REF junction is exactly π/2, used in reconstructing the CPR from experimental data. In practice, the superconducting to normal transition of the SQUID is governed by the stochastic switching processes, as well as thermal fluctuations, and the tilted washboard potential used to take these processes into account31 is not symmetric under a sign change of the applied flux. As a result, even if the underlying CPR of the TI junction in our case is anti-symmetric (AS) around zero, i.e. symmetric under simultaneous sign change in φ and I, the one reconstructed from the experiment may be NAS. We further note that while the stochastic processes could smear the “real CPR” and introduce artifacts, such as NAS (not present in the real CPR) in the measured CPR, such NAS observed in the experimental CPR does not mask the qualitative fact that the underlying real CPR of the junction is skewed. In other words, as found in ref. 31 for junctions with the sinusoidal CPR, the current vs. flux curves are AS. However, for junctions with non-sinusoidal CPR, the current vs. flux curve becomes NAS. The above argument is further supported by the observation that when we use different TI flakes or use gate tuning (in either case the reference junction and SQUID arm are not affected), we can obtain less skewed or non-skewed (sinusoidal) CPR and at the same time the NAS goes away. Moreover, a similar measurement (on a TI nanoribbon JJ) using an asymmetric SQUID with the same geometry as the one used here resulted in a sinusoidal CPR.28 Therefore, we conclude the skewness of the CPR observed in sample A originates from the TI flake and not the REF junction or the stochastic switching process.
Figure 2a depicts the normalized supercurrent I/IC vs. φ measured at a few different temperatures in sample A. The amplitude of the CPR (i.e. IC) as a function of T is plotted in Fig. 2b. We observe that the CPR remains highly non-sinusoidal up to T ~ 400 mK, but becomes nearly sinusoidal at higher T = 1.3 K. Furthermore, IC exhibits a strong T dependence and increases as we decrease the temperature down to the lowest accessible T = 20 mK. Such a temperature dependence is in contrast to that of conventional junctions, where IC is expected to saturate at low temperatures.35 Figure 2c depicts the amplitude of the fast Fourier transform (FFT) normalized by the amplitude of the first harmonic as a function of 2π/φ = B0/B, where B0 = Φ0/S ~ 1.1 G and S ~ 16 μm2 is the area of the SQUID. The FFT is calculated for the data taken at T = 20 mK in the range −10π ≤ φ ≤ 10π and reveals that the CPR can be described by a Fourier series with up to six harmonics. The blue and black curves are predictions of a general model for ballistic junction and our model for TI junction, respectively, and will be discussed later. In order to describe the shape of the CPR in our samples, we define the total harmonic distortion (THD) as
where Aj is the amplitude of the jth harmonic. Figure 2d depicts THD, A2/A1, and A3/A1 vs. T in sample A at Vg = 0 V. We observe that THD, A2/A1, and A3/A1 are nearly temperature independent up to T ~ 400 mK. Moreover, at T = 1.3 K, A3/A1 ~ 0 and THD ~ A2/A1, indicating that at this temperature, only the first and second harmonics are present in the CPR. Thus, the CPR of the TI junction is less skewed compared to that at the base temperature.
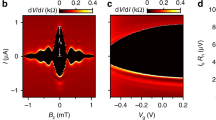
a The CPR measured at different temperatures. Symbols are experimental data and solid curves are theoretical calculations. All curves are shifted vertically for clarity. b Temperature dependence of the critical current (IC, the amplitude of the CPR). Solid blue curve is the theoretical calculation. c The amplitude of the fast Fourier transform (FFT, red curve) of the CPR measured over −10π ≤ φ ≤ 10π at 20 mK, normalized to the amplitude (A1) of the first harmonic vs. 2π/φ = B0/B, where B0 = Φ0/S ~ 1.1 G and S = 16 μm2. Black and blue curves are FFTs of the calculated CPR using our theoretical model and the perfectly ballistic model (Eq. (4)), respectively. d Total harmonic distortion (THD) and the normalized amplitude of the second (A2/A1) and third (A3/A1) harmonics vs. T, where Aj is the amplitude of the jth harmonic. All data in this figure are measured in Sample A at the gate voltage Vg = 0 V. Theoretical calculations are performed for L = 100 nm, b = 300 nm, Cx = 6 μm, Δ0 = 0.3 meV, μ′ = 50 meV, and ħvF = 1 eV Å.
Figure 3a demonstrates the CPR measured at different Vg’s for sample B at T = 30 mK. The inset of Fig. 3b depicts the two-terminal resistance R of the SQUID vs. Vg measured at T = 8 K, above the critical temperature (TCNb ~ 7 K) of the Nb electrodes. Sample B exhibits a strong gate dependence and an ambipolar field-effect in its normal-state resistance with the CNP at VCNP ~ −15 V. We also observe that in sample B the skewness changes as a function of Vg. Figure 3b plots the THD vs. Vg for both sample A (red) and sample B (blue). We note that the CPR is most skewed in sample B at Vg = 30 V, where the chemical potential is inside the bulk bandgap yet away from the CNP (see the inset of Fig. 3b). The reduced skewness at Vg ~ 0 V may be a result of the charge inhomogeneity and electron/hole puddles near the CNP.
a The CPR measured in sample B at T = 20 mK for different Vg’s. Curves are shifted vertically for clarity. Dashed red and black curves are theoretically calculated CPR with chemical potential μ‘ = 0 and 50 meV, respectively. b The total harmonic distortion THD of the CPR as a function of Vg for samples A (red) and B (blue) at T = 20 mK. Inset: two-terminal resistance R of the SQUID in sample B (containing the parallel contribution of the TI JJ resistance and the REF JJ resistance) vs. Vg at T ~ 8 K above the critical temperature of Nb electrodes (T > TCNb ~ 7 K).
Theoretical modeling
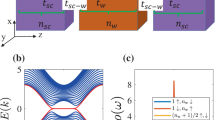
In this section, we introduce a theoretical model based on the induced superconductivity in the spin-helical surface states of TIs. Our model builds upon the existing model proposed by Fu and Kane3 and adapts it to systems of the type studied in the present experiment. Specifically, it considers the finite size of the superconducting contacts as well as the TI flakes. Since the superconducting (Nb) contacts in our case are only 300 nm wide (a value comparable to the expected coherence length ξ = ħvF/Δ0 ~ 330 nm of the junction), we cannot assume existence of the ABS (confined inside the junction) but should suppose instead that the surface state wavefunction extends over the entire circumference of the sample (see Fig. 4a). We denote the circumference Cx and define the longitudinal coordinate x to be in the range −Cx/2 ≤ x ≤ Cx/2. We adopt the Hamiltonian of Fu and Kane3 and take the pairing amplitude to be a piecewise constant function of x as follows: Δ(x) = Δ0 exp(iφ/2) for L/2 < x < L/2 + b, Δ0 exp(−iφ/2) for −L/2−b < x < −L/2, and zero otherwise. Here L and b are the separation and width of the contacts, respectively. The wavefunction is subject to antiperiodic boundary conditions in x.36 In this simple model, we assume that the system is translationally invariant in the y direction, so the wavefunction depends on y as exp(ikyy) for some ky. This renders the problem effectively one-dimensional.
a Schematic representation of the TI-based Josephson junction in our theoretical model. We assume the TSS wavefunctions extend over the entire circumference of the TI as shown by the black circle in this figure. The pairing amplitude Δ is a piecewise constant function of x, as follows: Δ(x) = Δ0 exp(iφ/2) for L/2 < x < L/2 + b, Δ0exp(−iφ/2) for −L/2−b < x < −L/2, and zero otherwise. b Energy spectrum (energy E vs. phase φ) of the modes with ky = 0 and energies within the superconducting gap Δ0 (the lowest energy ones are highlighted with red) and parameters (L = 100 nm, b = 300 nm, Cx = 6 μm, Δ0 = 0.3 meV, μ′ = 50 meV, and ħvF = 1 eV Å) of sample A.
Our explanation of the CPR and temperature dependence of the critical current is based on an interplay between the finite-size and proximity effects. To compute the CPR, we first rewrite, following ref., 3 the Hamiltonian of the surface fermions as \(H = \left( {\frac{1}{2}} \right){\mathrm{\Psi }}^\dagger \{ {\cal{H}}\} {\mathrm{\Psi }}\), where Ψ is an extended (four component) fermion multiplet and \(\{ {\cal{H}}\}\) is a 4 by 4 matrix in the component space. For given values of ky and chemical potential μ, the x component of the wavenumber, kx, at the Fermi surface is kx = ±k′, where \(\hbar v_{\mathrm{F}}k^\prime = \sqrt {\mu ^2 - \hbar ^2v_{\mathrm{F}}^2k_y^2}\), and vF is the Fermi velocity of the TSS. We choose two ranges of kx, each consisting of j = 60–200 values, one range around k′ and the other symmetrically to it around −k′ and look for Ψ as a Fourier expansion in the corresponding set of plane waves. Components of Ψ with different values of kx are connected by the Fourier transform of the pairing amplitude Δ(x). This converts the eigenvalue problem for \(\{ {\cal{H}}\}\) into a matrix problem, which we diagonalize numerically for various values of the phase difference φ. \(\{ {\cal{H}}\}\) has a particle–hole symmetry, which stems from using four fermionic components in place of two: at each φ, the energy levels come in ±E pairs. In terms of the nonnegative levels En ≥ 0 (one from each pair), the total free energy at finite temperature T is37,38
and the current is obtained as \(I(\varphi) = \left( {\frac{{2{e}}}{\hbar }} \right)\frac{{{\mathrm {d}}F}}{{{\mathrm {d}}\varphi }}\). As we increase the number of kx (or j) participating in the expansion, F(φ) suffers from an ultraviolet divergence, but the current does not. To calculate finite temperature properties, we replace Δ0 above with the T-dependent superconducting gap Δ(T) modeled using the BCS self-consistent equation.39
The energy spectrum (±En vs. φ) for sample A for the modes with ky = 0 and energies within the gap, |En| ≤ Δ0 is shown in Fig. 4b. Interestingly, we observe modes with energies much smaller than Δ0 that extend over the entire range of φ, see red curves in Fig. 4b. These low-energy states lead to the non-saturation of the junction’s critical current down to our lowest accessible temperature (T ~ 20 mK) as seen in Fig. 2b in the theoretical (blue) curve, consistent with the experimental data (symbols).
Because the wavefunction extends over the entire circumference Cx, while the Nb contacts occupy only a small part of it, the energy scale of the low-energy modes is only a fraction of the full Δ0. Our results can be understood qualitatively using the perturbation theory. For Δ0 = 0, the energies are \(E = \pm \left| {\hbar v_{\mathrm{F}}\sqrt {k_x^2 + k_y^2} \pm \mu}\right|\),3 so there is a strictly zero energy state whenever k′, defined above, equals one of the quantized free-fermion momenta
where n ≥ 0 is an integer. When Δ0 > 0, these states are gapped roughly by 2bΔ0/Cx. For sample A with Cx ~ 6 μm and the contact width b ~ 300 nm, this is about 0.1Δ0. Crucially, these low-energy states exist for the entire range of phases, 0 ≤ φ ≤ 2π, in contrast for instance to the case of a conventional ballistic junction (the Kulik–Omelyanchuk theory40), where the minimal excitation energy remains on the order Δ0 except for a narrow vicinity of φ = π.
For a given μ, the condition (3) will be satisfied better for some ky than for others. In practice, the translational invariance in the y direction is not precise, so ky is not an exact quantum number. Nevertheless, because of the large size of the TI flake in the transverse (y) direction, the quantization interval for ky is small, so unless μ is exceptionally close to zero, we expect there will be a significant number of modes for which Eq. (3) is satisfied to a good accuracy. We therefore adopt the simple model in which we calculate the supercurrent for ky = 0 only and multiply the result by an effective number of transverse channels Nch to account for the contribution of all the modes. We determine Nch by matching the overall magnitudes of the experimental and computed critical currents. We find Nch ~ 19 and Nch ~ 46 for sample A at Vg = 0 V and sample B at Vg = 30 V, respectively. The role of the chemical potential in this effectively one-dimensional model is played by μ‘ = ħvFk’, which is now considered as a parameter. It is distinct from the true chemical potential μ, obtained from the gate voltage using \(\mu = \hbar v_{\mathrm{F}}\sqrt {\frac{{4{\uppi}C_{\mathrm{g}}}}{{e}}\left( {V_{\mathrm{g}} - V_{{\mathrm{CNP}}}} \right)}\), where e is the electron charge and Cg = 12 nF cm−2 is the parallel plate capacitance per unit area of a 300-nm SiO2.
We plot the computed CPR for sample A as solid curves in Fig. 2a, where an excellent agreement with the measured data is observed. The blue curve in Fig. 2c is the FFT calculated for the theoretical CPR (in the range −10π < φ < 10π and at T = 20 mK) of a perfectly ballistic short junction:35,41
where Δ(T) is the temperature-dependent superconducting gap of the junction obtained from the BCS theory.39 Notably, the experimentally observed A2/A1 in Fig. 2c is within 3% of that predicted for the fully ballistic junction (blue curve) and the THD = 0.46 extracted from our measured CPR at T = 20 mK is within 20% of the theoretical ballistic limit (THD = 0.55), indicating sample A is nearly ballistic. The black curve in Fig. 2c plots the FFT of the CPR calculated using our theoretical model (Fig. 4). We observe that the FFT of the CPR, calculated using our model, is in reasonable agreement with the FFT of the measured CPR. In contrast, the perfectly ballistic model (blue curve) notably overestimates the higher harmonics (A3 and above). The computed CPR for sample B is plotted with dashed curves in Fig. 3a at two different Vg’s. Theoretical calculations were done with μ′ = 0 and 50 meV, respectively. While the theoretical CPR agrees well with the experiment for Vg = 30 V, we see a deviation between the theory and experiment for Vg = 0 V. Sample B is much thinner (t ~ 13 nm) than sample A (t ~ 40 nm). When a TI becomes sufficiently thin, there may be a gap opening in the TSS close to the Dirac point due to hybridization of the top and bottom surface states. This gap causes the TI to transition into a trivial insulator. Moreover, there are electron–hole puddles and charge inhomogeneity near the CNP. Therefore, the transport may be more diffusive, i.e. the CPR is more sinusoidal, close to the CNP due to effects of disorder and hybridization. Such effects are not included in our theory and may be responsible for the discrepancies between the calculated and measured CPR at Vg = 0 V in sample B. Lastly, we note that even though both samples are exfoliated from the same crystal and undergone similar fabrication processes, sample to sample variations may still be present and play a role for the observed differences between the CPR’s of samples A and B.
In our previous experiments on S–TINR–S JJs,28 even though we have also observed evidence that the superconductivity is induced in the TSS, we only observe a sinusoidal CPR. A possible reason for this is a much smaller transverse size (Cy) of the TINR compared to the flakes used in the current work. As a consequence, ky is quantized in larger units (i.e. 2π/Cy), and the condition (3) is less readily satisfied. Effectively, the small transverse size generates a gap in the TSS spectrum, preventing the occurrence of low-energy states and rendering the CPR more sinusoidal at our experimental temperatures.28 A similar explanation may be relevant also for sample B of the present paper near the CNP.
We lastly note that the non-sinusoidal CPR was previously reported in ref. 18 However, the observed CPR in our TI flakes are more skewed. Moreover, our TI flakes are more disordered compared to HgTe quantum wells of ref. 18 For instance, the normal-state transport in HgTe samples shows mobilities as large as 10,000–40,000 cm2 V−1 s−1,17 while our TI flakes have normal-state mobility of ~1000 cm2 V−1 s−1.29 Therefore, the observed skewed CPR and the underlying ballistic superconducting transport in our disordered TI flakes provide strong evidence for the topological protection of the modes with ky near zero. This is further corroborated by the fact that in our previously studied junctions based on TINRs,28 where such “topology” is changed (since Dirac point becomes gapped, removing the ky ~ 0 modes and backscattering is now allowed for the remaining modes with finite ky), the observed CPR becomes sinusoidal (skewness disappears).
In conclusion, we have measured the CPR, one of the fundamental properties of a JJ, in a topological insulator BiSbTeSe2-based JJ using an asymmetric SQUID technique. We observed highly forward-skewed CPR, indicating that the transport through the TSS of the TI junction was close to ballistic. Temperature and gate dependence of the CPR were also studied, where we observed that CPR became more sinusoidal at high temperatures (T ~ 1.3 K) and close to the CNP. The reduced skewness near CNP was an indication of diffusive transport and was associated with the existence of electron–hole puddles and charge inhomogeneity in the very thin TI. Moreover, we developed a theoretical model that considered induced superconductivity in the spin-helical TSS of TIs. Our model assumed that the surface states can extend over the entire circumference of the TI. The predicted skewness of the CPR and the dependence on the temperature were consistent with our experimental observations. Overall, the experiment and the theory pointed toward robust features that make our TI system an excellent candidate to observe topological superconductivity and MBS.
Methods
Sample preparation
High-quality single crystals of BiSbTeSe2 were grown using the Bridgman technique as described elsewhere.29 We obtain BiSbTeSe2 flakes using the standard scotch-tape exfoliation technique and transfer them onto a 300-nm-thick SiO2/500-μm-thick highly doped Si substrates, which are used as back gates. We then locate the BiSbTeSe2 flakes with different width and thickness using an optical microscope. Subsequently, electron beam lithography is performed to define a SQUID consisting of the TI-based JJ and the REF junction (based on a narrower Nb line). The electrode separation, L, in the TI-based JJ is ~100 nm. Finally, a thin layer (t ~ 40 nm) of superconducting Nb is deposited in a DC sputtering system. Prior to the Nb deposition, a brief (~3 s) in situ Ar ion milling is used to clean the interface between Nb and the TI flake.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Fu, L. & Kane, C. L. Superconducting proximity effect and Majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 100, 096407 (2008).
Kitaev, A. Y. Unpaired Majorana fermions in quantum wires. Phys.-Uspekhi 44, 131–136 (2001).
Kitaev, A. Y. Fault-tolerant quantum computation by anyons. Ann. Phys. 303, 2–30 (2003).
Akhmerov, A. R., Nilsson, J. & Beenakker, C. W. J. Electrically detected interferometry of Majorana fermions in a topological insulator. Phys. Rev. Lett. 102, 216404 (2009).
Tanaka, Y., Yokoyama, T. & Nagaosa, N. Manipulation of the Majorana fermion, Andreev reflection, and Josephson current on topological insulators. Phys. Rev. Lett. 103, 107002 (2009).
Potter, A. C. & Fu, L. Anomalous supercurrent from Majorana states in topological insulator Josephson junctions. Phys. Rev. B 88, 121109(R) (2013).
Vasenko, A. S., Golubov, A. A., Silkin, V. M. & Chulkov, E. V. Unconventional pairing in three-dimensional topological insulators with a warped surface state. JETP Lett. 105, 497–501 (2017).
Fu, L. & Kane, C. L. Josephson current and noise at a superconductor/quantum-spin-Hall-insulator/superconductor junction. Phys. Rev. B 79, 161408 (2009).
Peng, Y., Pientka, F., Berg, E., Oreg, Y. & von Oppen, F. Signatures of topological Josephson junctions. Phys. Rev. B 94, 085409 (2016).
Badiane, D. M., Houzet, M. & Meyer, J. S. Nonequilibrium Josephson effect through helical edge states. Phys. Rev. Lett. 107, 177002 (2011).
Tkachov, G. & Hankiewicz, E. M. Helical Andreev bound states and superconducting Klein tunneling in topological insulator Josephson junctions. Phys. Rev. B 88, 075401 (2013).
Spanton, E. M. et al. Current-phase relations of few-mode InAs nanowire Josephson junctions. Nat. Phys. 13, 1177–1181 (2017).
Zhang, D. et al. Superconducting proximity effect and possible evidence for Pearl vortices in a candidate topological insulator. Phys. Rev. B 84, 165129 (2011).
Sacépé, B. et al. Gate-tuned normal and superconducting transport at the surface of a topological insulator. Nat. Commun. 2, 575 (2011).
Wiedenmann, J. et al. 4π-periodic Josephson supercurrent in HgTe-based topological Josephson junctions. Nat. Commun. 7, 10303 (2015).
Sochnikov, I. et al. Nonsinusoidal current–phase relationship in josephson junctions from the 3D topological insulator HgTe. Phys. Rev. Lett. 114, 066801 (2015).
Williams, J. R. et al. Unconventional Josephson effect in hybrid superconductor–topological insulator devices. Phys. Rev. Lett. 109, 056803 (2012).
Veldhorst, M. et al. Josephson supercurrent through a topological insulator surface state. Nat. Mater. 11, 417–421 (2012).
Qu, F. et al. Strong superconducting proximity effect in Pb–Bi2Te3 hybrid structures. Sci. Rep. 2, 339 (2012).
Sochnikov, I. et al. Direct measurement of current–phase relations in superconductor/topological insulator/superconductor junctions. Nano Lett. 13, 3086–3092 (2013).
Cho, S. et al. Symmetry protected Josephson supercurrents in three-dimensional topological insulators. Nat. Commun. 4, 1689 (2013).
Oostinga, J. B. et al. Josephson supercurrent through the topological surface states of strained bulk HgTe. Phys. Rev. X 3, 021007 (2013).
Kurter, C., Finck, A. D. K., Hor, Y. S. & Van Harlingen, D. J. Evidence for an anomalous current–phase relation in topological insulator Josephson junctions. Nat. Commun. 6, 7130 (2015).
Lee, J. H. et al. Local and nonlocal Fraunhofer-like pattern from an edge-stepped topological surface Josephson current distribution. Nano Lett. 14, 5029–5034 (2014).
Jauregui, L. A. Gate-tunable supercurrent and multiple Andreev reflections in a superconductor-topological insulator nanoribbon-superconductor hybrid device. Appl. Phys. Lett. 112, 093105 (2018).
Kayyalha, M. et al. Anomalous low-temperature enhancement of supercurrent in topological-insulator nanoribbon Josephson junctions: evidence for low-energy Andreev bound states. Phys. Rev. Lett. 122, 047003 (2019).
Xu, Y. et al. Observation of topological surface state quantum Hall effect in an intrinsic three-dimensional topological insulator. Nat. Phys. 10, 956–963 (2014).
Xu, Y., Miotkowski, I. & Chen, Y. P. Quantum transport of two-species Dirac fermions in dual-gated three-dimensional topological insulators. Nat. Commun. 7, 11434 (2016).
Della Rocca, M. L. et al. Measurement of the current-phase relation of superconducting atomic contacts. Phys. Rev. Lett. 99, 127005 (2007).
Clem, J. R. & Brandt, E. H. Response of thin-film SQUIDs to applied fields and vortex fields: linear SQUIDs. Phys. Rev. B 72, 174511 (2005).
Maxfield, B. W. & Mclean, W. L. Superconducting penetration depth of niobium. Phys. Rev. 139, A1515 (1965).
Ginzburg, L. V. et al. Determination of the current–phase relation in Josephson junctions by means of an asymmetric two-junction SQUID. JETP Lett. 107, 48–54 (2018).
Golubov, A. A., Kupriyanov, M. Y. & Il’ichev, E. The current–phase relation in Josephson junctions. Rev. Mod. Phys. 76, 411–469 (2004).
Zhang, Y., Ran, Y. & Vishwanath, A. Topological insulators in three dimensions from spontaneous symmetry breaking. Phys. Rev. B 79, 245331 (2009).
Furusaki, A. & Tsukada, M. Dc Josephson effect and Andreev reflection. Solid State Commun. 78, 299–302 (1991).
Beenakker, C. W. J. Universal limit of critical-current fluctuations in mesoscopic Josephson junctions. Phys. Rev. Lett. 67, 3836 (1991).
Tinkham, M. Introduction to Superconductivity (McGraw-Hill, New York, 1996).
Kulik, I. O. & Omel’yanchuk, A. N. Properties of superconducting microbridges in the pure limit. Sov. J. Low Temp. Phys. 3, 459–461 (1977).
Likharev, K. K. Superconducting weak links. Rev. Mod. Phys. 51, 101–159 (1979).
Acknowledgements
M.K. and Y.P.C. acknowledge support from National Science Foundation (NSF) under Award DMR-1410942. M.K. and Y.P.C. acknowledge partial support from NSF under Award EFMA-1641101. L.P.R. and A.K. acknowledge support from the U.S. Department of Energy (DOE), Office of Basic Energy Sciences (BES) under Award DE-SC0008630.
Author information
Authors and Affiliations
Contributions
Y.P.C. supervised the research. I.M. synthesized the crystals. M.K. fabricated the devices. M.K. and A.K. performed the low-temperature measurements. M.K. analyzed the data with the help from Y.P.C. and L.P.R. S.K. performed the theoretical calculations. M.K., S.K., and Y.P.C. wrote the paper with contributions from all the co-authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kayyalha, M., Kazakov, A., Miotkowski, I. et al. Highly skewed current–phase relation in superconductor–topological insulator–superconductor Josephson junctions. npj Quantum Mater. 5, 7 (2020). https://doi.org/10.1038/s41535-020-0209-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-020-0209-5
This article is cited by
-
The superconducting diode effect
Nature Reviews Physics (2023)
-
Circulator function in a Josephson junction circuit and braiding of Majorana zero modes
Scientific Reports (2021)