Abstract
Complex electron interactions underlie the electronic structure of several families of quantum materials. In particular, the strong electron Coulomb repulsion is considered the key ingredient to describing the emergence of exotic and/or ordered phases of quantum matter, from high-temperature superconductivity to charge- and magnetic-order. However, a comprehensive understanding of fundamental electronic properties of quantum materials is often complicated by the appearance of an enigmatic partial suppression of low-energy electronic states, known as the pseudogap. Here we take advantage of ultrafast angle-resolved photoemission spectroscopy to unveil the temperature evolution of the low-energy density of states in the electron-doped cuprate Nd2-xCexCuO4, an emblematic system where the pseudogap intertwines with magnetic degrees of freedom. Using an optical excitation we drive the electronic system across the pseudogap onset temperature T*, and we report the direct relation between the momentum-resolved pseudogap spectral features and the spin-correlation length with a remarkable sensitivity. This transient approach, corroborated by mean-field model calculations, allows us to establish the pseudogap in electron-doped cuprates as a precursor to the incipient antiferromagnetic order even when long-range antiferromagnetic correlations are not established, as in the case of optimal doping.
Similar content being viewed by others
Introduction
In the presence of strong correlations, the interactions within and among various degrees of freedom often obfuscate the microscopic origin of exotic electronic phenomena.1,2,3 As an example, the interplay between intertwined orders4 continues to preclude a thorough understanding of the pseudogap (PG) phenomenon, a mysterious state of correlated matter ubiquitous to systems as diverse as unconventional superconductors,5,6,7 dichalcogenides,8,9 and ultracold atoms.10,11,12 Broadly speaking, the PG in condensed matter is associated with a partial suppression of the electronic spectral weight in the vicinity of the Fermi level (ω = 0), and evidence for the PG has been widely reported.13 This behavior may be anticipated in the presence of long-range (or mesoscopic) order, e.g. spin- or charge-order, which breaks the translational symmetry of the crystal: the loss of spectral weight in particular momentum-energy regions would be simply a consequence of the avoided crossings in the symmetry-reduced bandstructure.8,9,14,15 However, this argument may be unsatisfactory in the presence of strong electronic correlations and short-range orders with correlation length of few unit cells. Copper-oxide high-temperature superconductors are a paradigmatic example where the origin of the PG—which presents different phenomenology for hole and electron doping—is still debated, and a universal understanding has yet to emerge.1,5,6,7,14,15,16,17,18
In the specific case of electron-doped cuprates, the PG is stable above the entire antiferromagnetic (AF) and superconducting (SC) domes, with its onset temperature indicated by T* as measured by spectroscopic and transport probes,18,19,20,21,22 as illustrated in Fig. 1a (orange shadow). Scattering experiments on electron-doped cuprates have shown that the long-range AF order disappears when entering the narrow SC dome,23,24 and that the commonly reported charge-order in cuprates does not exhibit a clear connection to the AF order,25,26 although a coupling to dynamic magnetic correlations has been recently shown.27 In addition, 3D collective charge modes, which may play a substantial role in mediating high-temperature superconductivity, have been reported.28
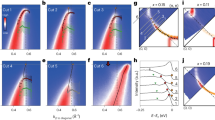
a Phase-diagram of the electron-doped cuprate Nd2−xCexCuO4 showing the onset temperature of the pseudogap T*.19,20,21,22 The doping measured in this study is highlighted by the yellow arrow. b Experimental Fermi surface of optimally-doped NCCO measured with 6.2-eV probe pulse, 10 K base temperature. The integration window in energy is 20 meV at the Fermi level. The solid blue line is a tight-binding constant energy contour at ω = 0,41 the red dashed line the AF zone boundary (AFZB). The violet dotted circle encloses the hot-spot (HS). The black dashed line represents the nodal direction, and the green and the black solid lines the two momentum directions explored in this work, φ ~ 39° and φ ~ 26.5°, respectively, where φ is the angle between (0, π)–(π, π) and the nodal direction. c Simulated Fermi surface using Eq. (1), ΔPG = η = Γ = 85 meV (details in Supplementary Discussion C, D, E, F). d Momentum-integrated energy distribution curves (EDCs) at the HS for 50 K (black) and 130 K (red). Panel d1: EDCs simulated using Eq. (1), and Γ = 85 and 160 meV for low and high temperature conditions, respectively. d2 Experimental background-subtracted EDCs in the HF regime (the background is estimated from the integrated ARPES intensity in regions where no dispersive spectral features are detected; solid lines, smoothed data). e Simulated (e1) and experimental (e2) symmetrized EDCs (SEDCs). For Te = 130 K the shortening of ξspin leads to a filling-up of the PG (red curves). f Simulated (f1) and experimental (f2) differential EDCs (dEDCs), as defined in Eq. (2), where we demonstrate that a filling of the PG manifests as an increase of the photoemission intensity at ω ~ −50 meV (blue arrows).
The PG in electron-doped cuprates is believed to be related to the AF order:18,19,20,21,22,24,29,30,31,32 in the presence of long-range AF order, i.e. when the instantaneous spin-correlation length (ξspin) diverges at low temperature and a Néel temperature is defined, T* has been proposed to be a temperature crossover for which the quasiparticle de Broglie wavelength (λB ~ vF∕πT, where vF is the Fermi velocity) becomes comparable to ξspin.24,33 However, these considerations seem to fail at optimal doping, where only short-range spin-fluctuations (ξspin ≃ 20–25 a, where a is the unit cell size) are detected by inelastic neutron scattering.24 Indeed, for dopings where the long-range AF order disappears, i.e. when the short-range ξspin does not diverge at low temperature, an unambiguous identification of a temperature crossover with λB is prevented. In addition, the underlying SC phase has been proposed to limit the development of ξspin.24 Finally, and most importantly, a momentum-resolved study connecting explicitly the PG spectral features and short-range AF correlations in electron-doped cuprates is still missing.
In order to tie together the observations of the PG and short-range AF correlations via a unique experimental approach, we performed a time- and angle-resolved photoemission (TR-ARPES) study of optimally doped Nd2-xCexCuO4 (NCCO, Tc ~ 24 K, yellow arrow in Fig. 1a), which is characterized by ξspin ~ 20 a at low temperatures (T ~ Tc).24 TR-ARPES provides an alternative, more effective and controlled experimental approach to measure a detailed temperature-dependence than the standard equilibrium ARPES, which is often complicated by surface degradation as well as coarse and uncorrelated sampling. As in standard pump-probe spectroscopy, a near-infrared pump pulse is used to perturb the system, whose subsequent relaxation is studied by varying the temporal delay of a UV probe pulse. Photoexcited quasiparticles in cuprates—and in general in strongly correlated electron systems—release the energy deposited by the pump pulse through electron–electron and electron–boson scattering, thermalizing and reaching a state of quasi-equilibrium on an ultrafast time scale of about 100 fs.34,35,36,37,38,39 After this initial relaxation, an effective electronic temperature Te is defined at each point in time, allowing a temperature-dependent scan to be performed continuously and with remarkable accuracy and efficiency.40 Since the acquisition of TR-ARPES data is performed by cycling continuously the pump-probe delays, each time delay—and consequently each electronic temperature—is acquired in the same experimental conditions (details in the Methods section). By applying this transient approach (which minimizes aging and sample drift) and computing differential curves (which remove any extrinsic background contribution, see Eq. (2)), we demonstrate the direct relation between the subtle momentum-resolved spectroscopic features of the PG and short-range ξspin(Te), as extracted from inelastic neutron scattering.24 In particular, we identify T* as the crossover temperature above which the spectral broadening due to the reduction of ξspin exceeds the PG amplitude, establishing the PG as a precursor of the underlying AF order.
Results
Fermi surface mapping and modeling
Figure 1b displays the equilibrium Fermi surface mapping of NCCO acquired with 6.2 eV probe pulsed-light. A tight-binding constant energy contour at ω = 041 (blue solid line), and the AF zone boundary (AFZB, red dashed line), are superimposed over the experimental Fermi surface. The intersection point between the tight-binding at ω = 0 and AFZB is commonly referred to as the hot-spot (HS), and coincides with the location where an AF-driven PG is expected to be particle-hole symmetric.18 In a mean field description, the commensurate q = (π,π) folding of the Fermi surface is driven by a strong quasi-2D AF order in the copper-oxygen plane.18 The Green’s function can then be written as:15,22,33
where ϵk is the bare energy dispersion, ΔPG the AF-driven pseudogap spectroscopic amplitude determined by the local Coulomb interaction and spin susceptibility,33 η the single-particle scattering rate, and Γ a broadening term that leads to a filling of the pseudogap via the reduction of ξspin.32,33 Using Eq. (1) we can calculate the spectral function \(A({\bf{k}},\omega )\ =\ -\frac{1}{\pi }{\rm{Im}}[G({\bf{k}},\omega )]\)42 and compute the Fermi surface (Fig. 1c), which agrees well with our and previous ARPES data.29,30 We used ΔPG = η = Γ = 85 meV for simulation purposes, as suggested by our experimental results (see Fig. 1d–f and Supplementary Discussion C, D, E), and in agreement with previous optical and ARPES studies.19,20,21,29,30,43
Tracking the pseudogap spectral weight in an ultrafast fashion
Before moving to a detailed discussion of the temperature evolution of the PG in NCCO, we illustrate our experimental strategy for tracking the PG via TR-ARPES. The simulated and experimental energy distribution curves (EDCs) integrated along the momentum direction through HS for two (transient) electronic temperatures are presented in Fig. 1d1–d2, respectively; however, the PG is best visualized by the symmetrized EDCs (SEDCs, Fig. 1e1–e2). The symmetrization procedure removes the dependence of the photoemission signal on the Fermi-Dirac distribution function, providing direct access to underlying modifications of the density of states (DOS) along that particular momentum cut.44 Note that this procedure is strictly valid only at the HS where particle-hole symmetry is satisfied, as indicated by model calculations.15,22,32,33 Experimental SEDCs highlight the filling of the PG at high temperature and allow to extract a PG amplitude ΔPG ~ 85 meV. The filling of the PG can be well modeled by increasing the spin-fluctuation spectral broadening term Γ from 85 meV (50 K, black curves) to 160 meV (130 K, red curves), while ΔPG = η = 85 meV are kept fixed (details in Supplementary Discussion D, E, F). However, we remark that any experimental estimate of the temperature dependence of the PG spectral weight by fitting of SEDCs may be affected by intrinsic and uncorrelated noise, as well as extrinsic electron background (arising from irregular cleaves, secondary electrons, and electrons scattered in the detection process). We overcome this limitation by computing the difference between the photoemission intensity for high temperature (130 K) and its counterpart for low temperature (50 K), as shown in Fig. 1f1–f2. As discussed later in more detail in Eq. (2), this quantity is proportional to the differential momentum-integrated EDCs (dEDCs) and, by removing spurious contributions, highlights the temperature evolution of the PG spectral features and Fermi-Dirac distribution. While the latter would lead to a symmetrical suppression (increase) of the photoemission intensity for all ω < 0 (ω > 0), independently of the explored momentum region, it is evident that a filling of the PG may lead to an increase of the photoemission intensity at ω ~ −50 meV (blue arrows in Fig. 1f1–f2). Since thermal contributions are negligible at ω ~ −50 meV within the range of electronic temperatures explored in this work (4kBT ~ 50 meV for T = 150 K), this approach allows to track the evolution of the PG with high sensitivity. We note that a similar approach was recently used to track the electron–boson interaction in hole-doped cuprates via a transient analysis/modeling of the band renormalization (kink);45 in the specific case of NCCO, only a very weak kink was reported (see ref. 43 and Supplementary Discussion A), which does not affect the following analysis and conclusions.
Direct relation of the pseudogap to the spin-correlation length
Having defined the framework for our investigation, we now track the temperature-dependent modification of the low-energy DOS at the HS in optimally-doped NCCO by introducing thermal excitations via optical pumping. To estimate an effective electronic temperature Te,40 we fit the Fermi edge of the momentum-integrated EDCs along the near-nodal direction (φ ~ 39o, green solid line in Fig. 1b), as shown in Fig. 2a for various pump-probe delays; the resulting Te is then plotted versus time delay in Fig. 2b for the two pump fluences employed in this work, here labeled as low fluence (LF) and high fluence (HF). The transient Te can be phenomenologically fit by a double exponential function (solid lines in Fig. 2b), reminiscent of the two-temperature-model framework.34,35,36,37,40 Note that near-nodal momentum-integrated EDCs are well described by a thermal Fermi-Dirac distribution for time delays τ ≥ 0.3 ps, a timescale comparable to the temporal resolution of our TR-ARPES system (~250 fs). Non-thermal features are instead detected for τ ~ 0 ps, i.e. when pump and probe pulses are overlapped in time, and data corresponding to those time delays are highlighted in gray in Fig. 2b, c (and omitted in Fig. 2d, see also Supplementary Discussion G).
a Momentum-integrated energy distribution curves (EDCs) along the near-nodal direction (green line in Fig. 1b) for different pump-probe delays. Fermi-Dirac distribution fits are shown as solid black lines. The inset displays three delays (−0.5 ps LF, +0.33 ps HF, +2 ps HF) in logarithmic scale. b Transient electronic temperature extracted by fitting the Fermi edge broadening along the near-nodal direction (a), for both LF and HF. The solid lines are phenomenological double exponential-decay fits (decay times are: 0.6 ± 0.1 ps and 7.5 ± 1.3 ps for LF, 0.45 ± 0.15 ps and 8.3 ± 2 ps for HF). Grey points indicate time delays for which a pure thermal-fitting is not accurate (see Supplementary Discussion G). Error bars represent the confidence interval in the fitting procedure corresponding to ±3σ (σ is the standard deviation). c Temporal evolution of the photoemission intensity at the HS for ω = −50 ± 10 meV (see black line and violet dotted circle in Fig. 1b), for both the employed pump fluences LF and HF. The solid black line is a phenomenological single exponential-decay fit for the LF curve while the HF curve saturates in the first 2 ps after the pump excitation. Error bars represent ±σ. d Photoemission intensity at the HS, ω = −50 ± 10 meV, as a function of the electronic temperature (black and red circles for LF and HF, respectively; data points are plotted vs. the electronic temperature determined from the phenomenological fits in (b)). Non-thermal time delays, grey points in (b, c), have been omitted. The green line and transparent shadow represent the inverse of the spin-correlation length ξspin from neutron scattering studies for optimal doping Tc ~ 24 K,24 appropriately scaled and offset. We identify T* as the temperature at which the PG is completely filled (in agreement with the saturation of the photoemission intensity at the HS for ω = −50 ± 10 meV for HF). Error bars are defined in (b, c). Data have been replicated for three different cleaves.
Figure 2c displays the transient enhancement of the photoemission intensity at the HS in a 20 meV energy window about ω = −50 meV (\({I}_{\omega \ =\ -50}^{PG}\), given by the momentum-integrated EDC along φ ~ 26.5°, direction indicated by the black solid line in Fig. 1b). This particular choice of energy window was motivated by the dEDCs at the HS shown in Fig. 1f1–f2 and Fig. 3b. We note that the temporal response of \({I}_{\omega \ =\ -50}^{PG}\) is dependent on the pump fluence: while the enhancement of \({I}_{\omega \ =\ -50}^{PG}\) recovers exponentially within 2 ps for the LF regime, in the HF regime \({I}_{\omega \ =\ -50}^{PG}\) saturates for ~2 ps and does not fully recover within the domain of pump-probe delays studied here. This saturation of \({I}_{\omega \ =\ -50}^{PG}\) in the HF regime suggests a vanishing of the PG. To further investigate the origin of the suppression of the PG spectral weight, we plot \({I}_{\omega \ =\ -50}^{PG}\) directly as a function of Te in Fig. 2d (the non-thermal points—grey circles in Fig. 2b, c—are omitted). One can see a close resemblance between the temperature dependence of \({I}_{\omega \ =\ -50}^{PG}\) and \({\xi }_{spin}^{-1}\) reported in ref. 24 for optimal doping, shown as a green line and shadow in Fig. 2c (with appropriate offset and scaling). However, for temperatures Te > 110 K, \({I}_{\omega \ =\ -50}^{PG}\)(Te) is found to saturate, departing from \({\xi }_{spin}^{-1}\); this onset of saturation is in good agreement with T* reported by other experimental probes.19,20,21,22 Note that the deviation of \({I}_{\omega \ =\ -50}^{PG}\)(Te > T*) from \({\xi }_{spin}^{-1}\) is not associated with a phase transition, but is rather a crossover stemming from the filling—not the closure—of the PG.
a Momentum-integrated differential energy distribution curves (dEDCs), experimental (a1) and simulated (a2), at HS (HF regime). Simulated traces in a2 have been generated using the fit of the experimental transient Te shown in Fig. 2b, and assuming \(\Gamma ({{\rm{T}}}_{{\rm{e}}})\ =\ C\cdot {\xi }_{spin}^{-1}({{\rm{T}}}_{{\rm{e}}})\) as in ref. 33 (C ~ 1.9 a eV, where a is the unit cell size, details in Supplementary Discussion E, F). b Experimental (b1) and simulated (b2) dEDCs along the near-nodal direction (green line, LF), and at HS (black and red lines for LF and HF, respectively), at τ = +0.6 ps. c Simulated dEDCs at HS assuming as initial values before the arrival of the pump ΔPG = η = Γ0 = 85 meV and T = 50 K, and as final values after the arrival of the pump T = 130 K, ΔPG → 0 (gap closure, black line), or Γ = 2.5 ⋅ Γ0 (gap filling, red line), respectively (with the other parameters left unchanged, in each of these two cases). d Simulated photoemission intensity at the HS, ω = −50 ± 10 meV, as a function of the electronic temperature (black dashed line). The green line is the inverse of ξspin, obtained from ref. 24 as discussed in Fig. 2d.
Discussion
To further clarify the origin of T*, we now present a comprehensive analysis and modeling of the photoinduced thermal modification of the PG for both LF and HF pump regimes. The spectral features of NCCO are inherently broad and their intensity is comparable to the underlying background level, precluding the sort of detailed quantitative modeling of the transient spectral function which has been achieved for hole-doped cuprates.46 Alternately, here we focus our analysis on the temporal evolution of dEDCs, defined as:
where DOS0(ω) and the Fermi-Dirac electronic distribution f0(ω) are the unperturbed quantities (see refs 45,47 and Supplementary Discussion B). Note that the photoemission matrix-elements, not included in Eq. (2), represent a constant multiplicative factor and can be neglected to the first approximation. Figure 3a1 displays experimental dEDCs as a function of pump-probe delay (τ) and binding energy (ω), at HS (HF regime). The TR-ARPES data reported here can be simulated remarkably well using the simple model of Eq. (1) (see Fig. 3a2). The experimental dEDCs are reproduced through a substantial increase of the broadening term Γ alone, which phenomenologically describes the filling of the PG due to the reduction of the spin-correlation length.32,48 Note that \(\Gamma ({{\rm{T}}}_{{\rm{e}}})\propto {\xi }_{spin}^{-1}({{\rm{T}}}_{{\rm{e}}})\) in Eq. (1) is assumed for simulation purposes, in agreement with theoretical predictions of Vilk and Tremblay.33
In further support of our interpretation of the HS data, in Fig. 3b1, b2 we compare single experimental and simulated dEDCs along the near-nodal direction and HS, for τ = +0.6 ps. Along the near-nodal direction we find an approximately symmetric transient population/depletion (increase/decrease of the photoemission intensity for ω >/< 0), characteristic of a mere thermal broadening effect (along the near-nodal region the PG is located well above the Fermi level, thus only mildly affecting the symmetry of the near-nodal dEDCs; see also Supplementary Discussion B, G). In contrast, at the HS we observe the increment of the intensity for ω ~ −50 meV and a modest (null) depletion signal for ω ~ −20 meV for LF (HF), in good agreement with the model and data of Fig. 1d–f and Fig. 2. We also emphasize that a full closure of the gap fails to reproduce our TR-ARPES data. Figure 3c compares simulated dEDCs at the HS for a complete gap closure (ΔPG → 0, black line) and gap filling (Γ = 2.5 ⋅ Γ0, red line, where Γ0 = 85 meV), and only the latter matches the experimental curve shown in Fig. 3b1 (red line, HF).
Finally, we plot in Fig. 3d the simulated analog to Fig. 2d, noting a clear correspondence between the two figures. In particular, assuming the direct relationship between the filling of the PG and ξspin (as predicted for 2D spin-fluctuations33), we find that the simulated filling of the PG saturates for temperatures T ~ T*, when Γ(T*) ~ 2ΔPG ~ 170 meV. This empirical observation agrees well with recent theoretical investigations of the vanishing of the PG in the electron-doped cuprate Pr1.3-xLa0.7CexCuO4.49
In conclusion, we have reported the direct relation between the partial suppression of the electronic spectral weight, a.k.a pseudogap, and short-range magnetic correlations in electron-doped cuprates. In particular, by performing a detailed ultrafast ARPES study at the hot-spot of the optimally-doped NCCO electron-doped cuprate, we have demonstrated that the temperature dependence of the low-energy DOS is closely related to the spin-correlation length ξspin. We identified two different temperature regimes for the PG, moving from low to high temperature: (i) T < T*, in which the PG begins to fill alongside with the reduction of ξspin; (ii) T > T*, where ξspin ~ 10–15 a and the PG is completely filled-up. Our results show that the PG phenomenology in optimally-doped NCCO originates from short-range AF correlations, parametrized by ξspin(T), and T* is a crossover temperature above which the spectral broadening driven by the reduction of ξspin overcomes the PG amplitude ΔPG. This suggests that the frequently reported onset temperature T* does not represent a thermodynamic phase transition, i.e. a sharp quenching of a well-defined order parameter; rather, T* is associated with the weakening of the short-range AF correlations and incipient (π,π)-folding.32,48 In addition, the observation of the filling—not closure—of the PG suggests that the energy scale associated with the PG survives to temperatures well above T*, possibly reminiscent of scattering results23,24 which show that the spectral weight associated with magnetic excitations remains finite up to much higher temperatures than the spin-correlation length itself. This phenomenology may bear a relation to the underlying Mott physics,33 or to the recent proposal of a crossover of the SU(2) gauge theory for fluctuating spin-density-waves near optimal-doping.50 Finally, we note that our transient momentum-resolved study demonstrates that even underlying orders with correlation lengths of about ten unit cells may play a significant role in shaping the Fermi surface topology and associated transport properties of complex materials.18,19,20,21,29,30,31,32,43,51,52
Methods
Experimental design
Our TR-ARPES setup exploits the classic pump-probe scheme. A 6.2 eV probe beam is generated by fourth-harmonic generation of the fundamental wavelength (800 nm, 1.55 eV) of a Ti:sapphire laser (Vitesse Duo and RegA 9000 by Coherent, 250 kHz repetition rate). The 1.55 eV pump beam is split from the source before harmonic generation. The pump and probe beam diameters on the sample are 300 μm and 150 μm, respectively. The angle of incidence on the sample is approximately normal for both beams. The two pump incident fluences were 28 ± 5 μJ/cm2 for LF and 50 ± 10 μJ/cm2 for HF. The pump and probe beams were s-polarized. The sample was cleaved and measured at <5 × 10−11 torr base pressure and 10 K temperature. Overall thermal effects have been taken into account and we estimate a temperature of approximately 40 K and 60 K for negative pump-probe delays for LF and HF excitations, respectively. Photoemitted electrons were detected by an hemispherical analyzer (Specs Phoibos 150). Energy and temporal resolutions were 17 meV and 250 fs, respectively. The acquisition time of a full delay/temperature cycles is about 5 min and this is repeated for a total of 100–150 cycles for each momentum-direction/fluence, corresponding to a total acquisition time of 8–13 h.
Sample
High quality electron-doped single crystals Nd2-xCexCuO4+δ were grown by the container-free traveling solvent floating zone (TSFZ) technique. The optimally doped Nd2-xCexCuO4+δ crystals (x ~ 0.15) exhibit an oxygen surplus directly after growth which has to be removed by an additional post-growth annealing treatment. Such annealed crystals exhibit a transition temperature Tc of 23.5 K with transition widths of 1 K.53,54 The very high crystal quality of Nd2-xCexCuO4+δ is manifest particularly well in magnetic quantum oscillations observed on several samples at different doping levels.51
Data availability
Data shown in the main text are available at the Harvard Dataverse.55 Additional data may be requested from the authors.
References
Fradkin, E., Kivelson, S. A. & Tranquada, J. M. Colloquium: Theory of intertwined orders in high temperature superconductors. Rev. Mod. Phys. 87, 457–482 (2015).
Keimer, B. & Moore, J. E. The physics of quantum materials. Nature Physics 13, 1045–1055 (2017).
Basov, D. N., Averitt, R. D. & Hsieh, D. Towards properties on demand in quantum materials. Nat. Mater. 16, 1077–1088 (2017).
Davis, J. C. S. & Lee, D.-H. Concepts relating magnetic interactions, intertwined electronic orders, and strongly correlated superconductivity. Proc. Natl Acad. Sci. USA 110, 17623–17630 (2013).
Timusk, T. & Statt, B. The pseudogap in high-temperature superconductors: an experimental survey. Reports on Progress in Physics 62, 61–122 (1999).
Hüfner, S., Hossain, M. A., Damascelli, A. & Sawatzky, G. A. Two gaps make a high-temperature superconductor? Rep. Prog. Phys. 71, 062501 (2008).
Vishik, I. M. Photoemission perspective on pseudogap, superconducting fluctuations, and charge order in cuprates: a review of recent progress. Rep. Progr. Phys. 81, 062501 (2018).
Borisenko, S. V. et al. Pseudogap and charge density waves in two dimensions. Phys. Rev. Lett. 100, 196402 (2008).
Rossnagel, K. On the origin of charge-density waves in select layered transition-metal dichalcogenides. J. Phys. Condens. Matter 23, 213001 (2011).
Stajic, J. et al. Nature of superfluidity in ultracold Fermi gases near Feshbach resonances. Phys. Rev. A 69, 063610 (2004).
Randeria, M. Pre-pairing for condensation. Nat. Phys. 6, 561–562 (2010).
Chen, Q. & Wang, J. Pseudogap phenomena in ultracold atomic Fermi gases. Front. Phys. 9, 539–570 (2014).
Mott, N. F. Metal-insulator transition. Rev. Mod. Phys. 40, 677–683 (1968).
Kordyuk, A. A. Pseudogap from ARPES experiment: Three gaps in cuprates and topological superconductivity (review article). Low Temp. Phys. 41, 319–341 (2015).
Norman, M. R., Kanigel, A., Randeria, M., Chatterjee, U. & Campuzano, J. C. Modeling the Fermi arc in underdoped cuprates. Phys. Rev. B 76, 174501 (2007).
Keimer, B., Kivelson, S. A., Norman, M. R., Uchida, S. & Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015).
Sato, Y. et al. Thermodynamic evidence for a nematic phase transition at the onset of the pseudogap in YBa2Cu3Oy. Nat. Phys. 13, 1074–1078 (2017).
Armitage, N. P., Fournier, P. & Greene, R. L. Progress and perspectives on electron-doped cuprates. Rev. Mod. Phys. 82, 2421–2487 (2010).
Onose, Y., Taguchi, Y., Ishizaka, K. & Tokura, Y. Doping dependence of pseudogap and related charge dynamics in Nd2−xCexCuO4. Phys. Rev. Lett. 87, 217001 (2001).
Matsui, H. et al. Evolution of the pseudogap across the magnet-superconductor phase boundary of Nd2−xCexCuO4. Phys. Rev. B 75, 224514 (2007).
Onose, Y., Taguchi, Y., Ishizaka, K. & Tokura, Y. Charge dynamics in underdoped Nd2−xCexCuO4: pseudogap and related phenomena. Phys. Rev. B 69, 024504 (2004).
Zimmers, A. et al. Infrared properties of electron-doped cuprates: Tracking normal-state gaps and quantum critical behavior in Pr2−xCexCuO4. EPL. Europhys. Lett. 70, 225–231 (2005).
Lee, W. S. et al. Asymmetry of collective excitations in electron- and hole-doped cuprate superconductors. Nat. Phys. 10, 883–889 (2014).
Motoyama, E. M. et al. Spin correlations in the electron-doped high-transition-temperature superconductor Nd2−xCexCuO4±δ. Nature 445, 186–189 (2007).
da Silva Neto, E. H. et al. Charge ordering in the electron-doped superconductor Nd2−xCexCuO4. Science 347, 282–285 (2015).
da Silva Neto, E. H. et al. Doping-dependent charge order correlations in electron-doped cuprates. Science Advances 2, e1600782 (2016).
da Silva Neto, E. H. et al. Coupling between dynamic magnetic and charge-order correlations in the cuprate superconductor Nd2−xCexCuO4. Phys. Rev. B 98, 161114 (2018).
Hepting, M. et al. Three-dimensional collective charge excitations in electron-doped copper oxide superconductors. Nature 563, 374–378 (2018).
Armitage, N. P. et al. Anomalous electronic structure and pseudogap effects in Nd1.85Ce0.15CuO4. Phys. Rev. Lett. 87, 147003 (2001).
Armitage, N. P. et al. Doping dependence of an n-type cuprate superconductor investigated by angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 88, 257001 (2002).
Matsui, H. et al. Angle-resolved photoemission spectroscopy of the antiferromagnetic superconductor Nd1.87Ce0.13CuO4: Anisotropic spin-correlation gap, pseudogap, and the induced quasiparticle mass enhancement. Phys. Rev. Lett. 94, 047005 (2005).
Park, S. R. et al. Interaction of itinerant electrons and spin fluctuations in electron-doped cuprates. Phys. Rev. B 87, 174527 (2013).
Vilk, Y. & Tremblay, A.-M. Non-perturbative many-body approach to the Hubbard model and single-particle pseudogap. J. Phys. I France 7, 1309–1368 (1997).
Perfetti, L. et al. Ultrafast electron relaxation in superconducting Bi2Sr2CaCu2O8+δ by time-resolved photoelectron spectroscopy. Phys. Rev. Lett. 99, 197001 (2007).
Dal Conte, S. et al. Disentangling the electronic and phononic glue in a high-Tc superconductor. Science 335, 1600–1603 (2012).
Dal Conte, S. et al. Snapshots of the retarded interaction of charge carriers with ultrafast fluctuations in cuprates. Nat. Phys. 11, 421–426 (2015).
Giannetti, C. et al. Ultrafast optical spectroscopy of strongly correlated materials and high-temperature superconductors: a non-equilibrium approach. Adv. Phys. 65, 58–238 (2016).
Hinton, J. P. et al. Time-resolved optical reflectivity of the electron-doped Nd2−xCexCuO4+δ cuprate superconductor: Evidence for an interplay between competing orders. Phys. Rev. Lett. 110, 217002 (2013).
Vishik, I. M. et al. Ultrafast dynamics in the presence of antiferromagnetic correlations in electron-doped cuprate La2−xCexCuO4±δ. Phys. Rev. B 95, 115125 (2017).
Graf, J. et al. Nodal quasiparticle meltdown in ultrahigh-resolution pump-probe angle-resolved photoemission. Nat. Phys. 7, 805–809 (2011).
Markiewicz, R. S., Sahrakorpi, S., Lindroos, M., Lin, H. & Bansil, A. One-band tight-binding model parametrization of the high-Tc cuprates including the effect of kz dispersion. Phys. Rev. B 72, 054519 (2005).
Damascelli, A., Hussain, Z. & Shen, Z.-X. Angle-resolved photoemission studies of the cuprate superconductors. Rev. Mod. Phys. 75, 473–541 (2003).
He, J. et al. Fermi surface reconstruction in electron-doped cuprates without antiferromagnetic long-range order. Proc. Natl Acad. Sci. USA 116, 3449–3453 (2019).
Norman, M. R. et al. Destruction of the Fermi surface in underdoped high-Tc superconductors. Nature 392, 157–160 (1998).
Miller, T. L. et al. Interplay of superconductivity and bosonic coupling in the peak-dip-hump structure of Bi2Sr2CaCu2O8+δ. Phys. Rev. B 97, 134517 (2018).
Boschini, F. et al. Collapse of superconductivity in cuprates via ultrafast quenching of phase coherence. Nat. Mater. 17, 416–420 (2018).
Parham, S. et al. Ultrafast gap dynamics and electronic interactions in a photoexcited cuprate superconductor. Phys. Rev. X 7, 041013 (2017).
Kyung, B., Hankevych, V., Daré, A.-M. & Tremblay, A.-M. S. Pseudogap and spin fluctuations in the normal state of the electron-doped cuprates. Phys. Rev. Lett. 93, 147004 (2004).
Li, T. & Yao, D.-W. Why is the antinodal quasiparticle in the electron-doped cuprate Pr1.3−xLa0.7CexCuO4 immune to the antiferromagnetic band-folding effect? EPL (Europhys. Lett.) 124, 47001 (2018).
Sachdev, S., Scammell, H. D., Scheurer, M. S. & Tarnopolsky, G. Gauge theory for the cuprates near optimal doping. Phys. Rev. B 99, 054516 (2019).
Helm, T. et al. Evolution of the Fermi surface of the electron-doped high-temperature superconductor Nd2−xCexCuO4 revealed by Shubnikov-de Haas oscillations. Phys. Rev. Lett. 103, 157002 (2009).
Cyr-Choinière, O. et al. Anisotropy of the Seebeck coefficient in the cuprate superconductor YBa2Cu3Oy: Fermi-surface reconstruction by bidirectional charge order. Phys. Rev. X 7, 031042 (2017).
Lambacher, M., Helm, T., Kartsovnik, M. & Erb, A. Advances in single crystal growth and annealing treatment of electron-doped HTSC. The European Physical Journal Special Topics 188, 61–72 (2010).
Werfel, F. N. et al. Technology, Preparation, and Characterization, ch. 3, 193–402 (Wiley-Blackwell, 2015).
Boschini, Fabio Replication Data for: Emergence of pseudogap from short-range spin-correlations in electron doped cuprates. Harvard Dataverse, (2019). https://doi.org/10.7910/DVN/IPK86O.
Acknowledgements
We gratefully acknowledge M. Greven, A.-M. Tremblay, L. Taillefer, N. P. Armitage and G. A. Sawatzky for useful discussions. This research was undertaken thanks in part to funding from the Max Planck-UBC-UTokyo Centre for Quantum Materials and the Canada First Research Excellence Fund, Quantum Materials and Future Technologies Program. This project is funded in part by the Gordon and Betty Moore Foundation’s EPiQS Initiative, Grant GBMF4779 to A.D. and D.J.J.; the Killam, Alfred P. Sloan, and Natural Sciences and Engineering Research Council of Canada’s (NSERC’s) Steacie Memorial Fellowships (A.D.); the Alexander von Humboldt Fellowship (A.D.); the Canada Research Chairs Program (A.D.); NSERC, Canada Foundation for Innovation (CFI); British Columbia Knowledge Development Fund (BCKDF); and CIFAR Quantum Materials Program. E.R. acknowledges support from the Swiss National Science Foundation (SNSF) grant no. P300P2_164649. C.G. acknowledges financial support from MIUR through the PRIN 2015 Programme (Prot. 2015C5SEJJ001) and from Università Cattolica del Sacro Cuore through D.1, D.2.2, and D.3.1 grants.
Author information
Authors and Affiliations
Contributions
F.B. and M.Z. equally contributed to this work. F.B., M.Z., E.R. and A.D. conceived the investigation. F.B. and M.Z. performed TR-ARPES measurements with the assistance of E.R. and M.M., and F.B., M.Z., E.R., R.P.D., M.M., B.Z., P.N., M.S., S.Z., A.K.M., G.L. were responsible for operation and maintenance of the experimental system. F.B., M.Z., E.R., E.H.d.S.N., C.G., D.J.J., and A.D. were responsible for data analysis and interpretation. A.E. provided NCCO samples. All of the authors discussed the underlying physics and contributed to the paper. F.B., M.Z., R.P.D., and A.D. wrote the paper. A.D. was responsible for the overall direction, planning, and management of the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Boschini, F., Zonno, M., Razzoli, E. et al. Emergence of pseudogap from short-range spin-correlations in electron-doped cuprates. npj Quantum Mater. 5, 6 (2020). https://doi.org/10.1038/s41535-020-0208-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-020-0208-6
This article is cited by
-
Critical charge fluctuations and emergent coherence in a strongly correlated excitonic insulator
npj Quantum Materials (2021)