Abstract
Complete theoretical understanding of the most complex superconductors requires a detailed knowledge of the symmetry of the superconducting energy-gap \({\mathrm{{\Delta}}}_{\mathbf{k}}^\alpha\), for all momenta k on the Fermi surface of every band α. While there are a variety of techniques for determining \(|{\mathrm{{\Delta}}}_{\mathbf{k}}^\alpha |\), no general method existed to measure the signed values of \({\mathrm{{\Delta}}}_{\mathbf{k}}^\alpha\). Recently, however, a technique based on phase-resolved visualization of superconducting quasiparticle interference (QPI) patterns, centered on a single non-magnetic impurity atom, was introduced. In principle, energy-resolved and phase-resolved Fourier analysis of these images identifies wavevectors connecting all k-space regions where \({\mathrm{{\Delta}}}_{\mathbf{k}}^\alpha\) has the same or opposite sign. But use of a single isolated impurity atom, from whose precise location the spatial phase of the scattering interference pattern must be measured, is technically difficult. Here we introduce a generalization of this approach for use with multiple impurity atoms, and demonstrate its validity by comparing the \({\mathrm{{\Delta}}}_{\mathbf{k}}^\alpha\) it generates to the \({\mathrm{{\Delta}}}_{\mathbf{k}}^\alpha\) determined from single-atom scattering in FeSe where s± energy-gap symmetry is established. Finally, to exemplify utility, we use the multi-atom technique on LiFeAs and find scattering interference between the hole-like and electron-like pockets as predicted for \({\mathrm{{\Delta}}}_{\mathbf{k}}^\alpha\) of opposite sign.
Similar content being viewed by others
Introduction
The macroscopic quantum condensate of electron pairs in a superconductor is represented by its order-parameter \({\Delta}_{\mathbf{k}}^\alpha \propto \langle c_{\mathbf{k}}^{\alpha \dagger }c_{ - {\mathbf{k}}}^{\alpha \dagger }\rangle\), where \(c_{\mathbf{k}}^{\alpha \dagger }\) is the creation operator for an electron with momentum k on band α. But electron pair formation can occur through a wide variety of different mechanisms and in states with many possible symmetries1. Thus, it is the symmetry properties of \({\Delta}_{\mathbf{k}}^\alpha\) that are critical for identification of the Cooper pairing mechanism1 and, moreover, for understanding the macroscopic phenomenology1. While macroscopic techniques can reveal energy-gap symmetry for single-band systems2,3, no general technique existed to determine the relative signs of \({\Delta}_{\mathbf{k}}^\alpha\) and \({\Delta}_{{\mathbf{k}}^\prime }^\beta\) between kα and kβ for all Fermi surface (FS) momenta in an arbitrary superconductor.
In 2015, a conceptually simple and powerful technique for determining \({\Delta}_{\mathbf{k}}^\alpha\) symmetry was introduced4, by Hirschfeld, Eremin, Altenfeld, and Mazin (HAEM). It is based on interference of weakly scattered quasiparticles at a single, non-magnetic, impurity atom. Given a superconductor Hamiltonian
where Hk is the normal-state Hamiltonian and Δk the superconducting energy gap, a non-magnetic impurity atom is modeled as a weak point-like potential scatterer, with Hamiltonian \(H_{{\mathrm{imp}}} = V_0c_{\mathbf{r}}^\dagger c_{\mathbf{r}}\) centered at the origin of coordinates r = 0. Effects of scattering are then represented by a T-matrix derived from the local Green’s function \(G_0\left( E \right) = \mathop {\sum}\nolimits_{\mathbf{k}} {G_{\mathbf{k}}^0} (E)\), where \(G_{\mathbf{k}}^0(E) = \left( {E + i0^ + - {\cal{H}}_{\mathbf{k}}} \right)^{ - 1}\). When the impurity potential is constant in k-space, the Green’s function becomes \(G_{{\mathbf{k}},{\mathbf{k}}^{\prime} }\left( E \right) = G_{{\mathbf{k}},{\mathbf{k}}^{\prime} }^0\left( E \right) + G_{\mathbf{k}}^0\left( E \right)T\left( E \right)G_{{\mathbf{k}}^{\prime} }^0\left( E \right)\), with the T-matrix given by \(T\left( E \right) = \left[ {1 - V_{{\mathrm{imp}}}G_0\left( E \right)} \right]^{ - 1}V_{{\mathrm{imp}}}\), where Vimp is the impurity matrix. From \(G_{{\mathbf{k}},{\mathbf{k}}^\prime }\left( E \right)\), the perturbations to the local density-of-states δN(r, E) are predicted surrounding the impurity atom, and its Fourier transform can be determined directly from Δk as
which is a purely real quantity because, in the theoretical calculation, the single impurity is exactly at the origin of coordinates. The authors of ref. 4 realized that the particle-hole symmetry of Eq. (2) for scattering interference wavevector \({\mathbf{q}} = {\mathbf{k}}_{\mathrm{f}}^\beta - {\mathbf{k}}_{\mathrm{i}}^\alpha\), depends on the relative sign of the energy-gaps \({\Delta}_{{\mathbf{k}}_{\mathbf{i}}}^\alpha\) and \({\Delta}_{{\mathbf{k}}_{\mathbf{f}}}^\beta\) at these two momenta. Consequently, the experimentally accessible energy-antisymmetrized function ρ−(q, E) of phase-resolved Bogoliubov scattering interference amplitudes
can be used to determine the relative sign of the superconducting energy-gaps connected by \({\mathbf{q}} = {\mathbf{k}}_{\mathrm{f}}^\beta - {\mathbf{k}}_{\mathrm{i}}^\alpha\). In the simplest case with two isotropic gaps Δα and Δβ on distinct bands, it was demonstrated that
where \(E_ + = E + i0^ +\), so that the functional form of \(\rho ^ - \left( {{\mathbf{q}},E} \right)\) is very different when the product ΔαΔβ is positive or negative. An elementary implication of Eq. (4) is that, when the order parameter has opposite signs on the two bands so that ΔαΔβ < 0, ρ−(q, E) does not change sign and exhibits pronounced maxima or minima near E ≈ Δα,β whereas if the order parameter has the same sign so that ΔαΔβ > 0, ρ−(q, E) exhibits weak maxima or minima near E ≈ Δα,β with a sign of change in between. More generally, especially with multiple bands and anisotropic gaps, HAEM requires that ρ−(q, E) be predicted in detail for a specific Hk and Δk in Eq. (1) and then compared with quasiparticle interference imaging5 in which the scanning tunneling microscope (STM) differential electron tunneling conductance, \(g\left( {{\mathbf{r}},E} \right) \propto \delta N\left( {{\mathbf{r}},E} \right)\) is visualized.
This single-atom phase-resolved HAEM method has been established experimentally6,7. For example, in the case of the multiband s± superconductor FeSe, the complete energy and wavevector dependence of ρ−(q, E) was used to determine that the k-space structure including relative sign of \({\Delta}_{\mathbf{k}}^\alpha\) and \({\Delta}_{\mathbf{k}}^\beta\), for all kα and all kβ on two different bands. But this result required that the impurity atom be highly isolated from other impurities and centered precisely at the origin of coordinates, with respect to which the ReδN(q, E) of Eq. (3) is then properly defined. This was critical because, an error of on the order of ~1% of a crystal unit cell in the coordinate of the origin (at the impurity atom) produces significant errors in ReδN(q, E) and ImδN(q, E) (Supplementary Note 1 and Fig. S1). Moreover, single impurity atom-based measurements limit the k-space resolution because the field of view (FOV) is typically restricted in size, making them unsuitable for superconductors with large impurity-atom densities. This provides the motivation for a variety of approaches to \({\Delta}_{\mathbf{k}}^\alpha\) determination beyond single-atom HAEM. One is to study Bogoliubov bound-states at individual impurity atoms8,9,10, although this has proven problematic because the elementary HAEM concept (Eq. (3)) is only valid in the weak scattering range, i.e. well below the scattering strength sufficient to generate Bogoliubov bound states11. Another approach is to use sparse blind deconvolution12 to analyze images of scattering interference at multiple atoms, yielding the phase-resolved real space structure of δN(r, E) although not the ρ−(q, E) of Eq. (3). Overall, therefore, widespread application of the HAEM technique (Eq. (3)) as a general tool for \({\Delta}_{\mathbf{k}}^\alpha\) determination remains a challenge.
Here, we introduce a practical technique for determining ρ−(q, E) of Eq. (3) from multiple impurity atoms in a large FOV. To understand this approach, consider the key issue of phase analysis as depicted in Fig. 1, a schematic simulation of Friedel oscillations \(\delta N\left( {\mathbf{r}} \right) = I_0\mathop {\sum}\nolimits_{{\mathbf{R}}_i} {\cos } \left( {2{\mathbf{k}}_{\mathrm{F}} \cdot ({\mathbf{r}} - {\mathbf{R}}_i) + \vartheta } \right)/\left| {{\mathbf{r}} - {\mathbf{R}}_i} \right|^2\) from multiple atoms at random locations Ri. The Fourier transform components of this δN(r) are shown in the top two panels of Fig. 1b. Obviously, the ReδN(q) required for the HAEM technique in Eq. (3), is weak, does not have a clear sign, and is indistinguishable from ImδN(q). Such effects occur because the spatial phases of all the individual Friedel oscillations at Ri are being added at random. The consequence is most obvious in the azimuthally integrated ReδN(q) shown in Fig. 1f where the phase information of single-atom Friedel oscillation is completely scrambled and the HAEM technique of Eq. (3) thereby rendered inoperable.
a Simulation of density of states perturbation δN(r) in amplitude units I0 due to two-dimensional Friedel oscillations surrounding 100 impurity atoms at random locations Ri. b Real part of Fourier transform ReδN(q) from δN(r) in a. We use an integer grid, hence the units of Fourier transform are also I0. c Imaginary part of Fourier transform ReδN(q) from δN(r) in a. d Real part of Fourier transform ReδNMA(q) calculated using multi-atom technique of Eq. (7). e Imaginary part of Fourier transform ReδNMA(q) calculated using multi-atom technique of Eq. (7). f ReδN(q) from δN(r) in a for \(\vartheta = 0\) and \(\vartheta = \pi\), integrated azimuthally from b. Its strong random fluctuations versus |q| are due to summing the Friedel oscillations in δN(r) of a with random phases due to the random locations Ri. g ReδNMA(q) from δN(r) in a integrated azimuthally from d. ReδNMA(q) is now orders of magnitude more intense than in f, and the phase of the Friedel oscillations in δN(r) of a is now very well defined because the effects of random locations Ri are removed by using Eq. (7). Note that, now, changing the oscillation phase \(\vartheta = 0\) to \(\vartheta = \pi\) surrounding all Ri in δN(r) produces the correct evolution of ReδNMA(q).
This problem could be mitigated if the Fourier transform of the scattering interference pattern surrounding each Ri were evaluated as if it were at the zero of coordinates. In this regard, consider the Fourier transform of a scattering interference surrounding a single impurity atom at Ri = (xi, yi),
This “shift theorem” shows how the correctly phase-resolved Fourier transform of a δNi(r) oscillation centered on an atom located at Ri = (xi, yi), can be determined using
where δN(q) is the Fourier transform using the same arbitrary origin as determines the Ri. Thus we may define a multi-atom phase-preserving algorithm for QPI
The consequences of Eq. (7) are illustrated in Fig. 1d, e (Supplementary Note 3 and Supplementary Fig. S4). The real part ReδNMA(q) now becomes well-defined and the overall magnitude is also strongly enhanced compared to ReδN(q). Moreover, the azimuthally integrated ReδNMA(q) plotted in Fig. 1g shows that the sign of ReδNMA(q) changes for \(\vartheta = 0\) and \(\vartheta = \pi\) as expected. Here it is essential that the impurity atom coordinates Ri be determined accurately so that the phase is well-defined. We therefore employ a picometer-scale transformation13,14,15 which renders topographic images T(r) perfectly periodic with the lattice, and then use the same transformation on the simultaneously recorded g(r,E) to register all the scattering interference oscillations precisely to the crystal lattice (Supplementary Note 2).
Equation 7 then allows to correctly define the quantities in Eq. (3) for arbitrarily large numbers of scattering atoms. By using the analog of Eq. (6) for \(g\left( {{\mathbf{r}},E} \right) \propto \delta N({\mathbf{r}},E)\), ρ−(q, E) for each impurity atom is determined from
while from Eq. (7) the sum over these \(\rho _i^ - \left( {{\mathbf{q}},E} \right)\) yields
This procedure adds all the individual \(\rho _i^ - \left( {{\mathbf{q}},E} \right)\) signals from every impurity atom at Ri in-phase, while effectively averaging out the random phase variations due to both locating the origin and the contributions of all other scatterers (Supplementary Fig. S5). We designate this procedure multi-atom HAEM (MAHAEM).
Results and discussions
Multi-atom quasiparticle interference for \({\Delta}_{\mathbf{k}}^\alpha\) determination
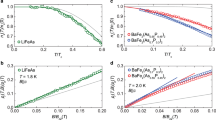
Determination of the magnitude of superconducting energy gaps \(|{\Delta}_{\mathbf{k}}^\alpha |\) has long been achieved16,17,18,19,20,21,22,23 using quasiparticle scattering interference (QPI). MAHAEM is the most recent advance of the QPI technique, and to test it we consider FeSe where the single impurity atom HAEM technique for determining \({\Delta}_{\mathbf{k}}^\alpha\) was established experimentally6. We measure the differential tunneling conductance \(g({\mathbf{r}},E) \equiv {\mathrm{d}}I/{\mathrm{d}}V({\mathbf{r}},E)\) in a 30 nm FOV at T = 280 mK, followed by determination of Ri = (xi, yi) for 17 scattering sites (Supplementary Note 3), some of which are shown in the FOV in Fig. 2a (Supplementary Fig. S2 shows all the sites). These sites are well-known Fe-atom vacancies identified by their crystal locations, and are non-magnetic6; their empirical identicality is confirmed by high-resolution electronic structure imaging. We then use Eq. (9) to calculate \(\rho _{{\mathrm{MA}}}^ - ({\mathbf{q}},E)\). Figure 2b shows the FeSe FS with the hole-pocket α around Γ-point and electron pockets ε(δ) around X(Y) points. Scattering between α and ε at wavevector p1 was studied. A representative layer \(\rho _{{\mathrm{MA}}}^ - ({\mathbf{q}},E = 1.05{\,\mathrm{meV}})\) is shown in Fig. 2c, where the scattering feature at vector p1 is marked with a circle. We then sum over the encircled q-region to get \(\rho _{{\mathrm{MA}}}^ - (E)\) for this scattering feature which is shown as black dots in Fig. 2d. Results from our MAHAEM measurements agree very well with the experimental results using a single impurity atom \(\rho _{{\mathrm{Single}}}^{ - {\mathrm{Exp}}}\) (black crosses) and the theoretically predicted curve for \(\rho _{{\mathrm{s}}_ \pm }^{ - {\mathrm{Th}}}\) (solid, black) in FeSe. This demonstrates the validity and utility of the multi-atom HAEM technique.
a Topography of FeSe showing the type of defects (Fe-atom vacancies) used for analysis. The x- and y-axes are along top Se–Se atoms. Inset shows the differential conductance spectrum recorded at a point on superconducting FeSe. The dashed rectangle represents the energy limits of the high-resolution dI/dV maps used herein for ρ−(q, E) analysis. b Fermi surface of FeSe showing the scattering between hole-pocket α and electron-pocket ε with scattering vector p1, which is the subject of study. The delta pocket is predicted in LDA calculations, hence it is shown dim in the image, but is now reported not to exist in reality6,38. Due to the orbital content, the scattering between quasi-parallel Fermi surfaces would be strongly suppressed in this orbitally selective material6. c \(\rho _{{\mathrm{MA}}}^ - ({\mathbf{q}},E = 1.05\,{\mathrm{meV}})\) calculated using Eq. (9) for a FOV containing 17 Fe-vacancies. The circle denotes the region where the \(\alpha \to {\it{\varepsilon }}\) scattering occurs and we integrate the \(\rho _{{\mathrm{MA}}}^ - ({\mathbf{q}},E)\) over the q in this region. Black crosses denote the Bragg peaks. d The integrated \(\rho _{{\mathrm{MA}}}^ - (E)\) (dots, black) from our MAHAEM analysis of FeSe compare to the theoretical predictions from an accurate band- and gap-structure model of FeSe for s++ (solid, pink) and s± (solid, black) superconducting energy gap symmetry, and to measured \(\rho _{{\mathrm{single}}}^{ - {\mathrm{Exp}}}(E)\) (crosses, black) from single impurity analysis as reported in ref. 6. Clearly, the single atom \(\rho _{{\mathrm{single}}}^{ - {\mathrm{Exp}}}(E)\) and the MAHAEM \(\rho _{{\mathrm{MA}}}^ - (E)\) are in good agreement. Note that the 2D plots may show both red and blue colors due to non-ideal nature of real experimental data. However, subsequent to the integration over relevant q-space region, the \(\rho _{{\mathrm{MA}}}^ - (E)\) is well defined as demonstrated here.
Next we consider LiFeAs, a complex iron-based superconductor that is a focus of contemporary physics interest24,25,26, particularly the relative sign of \({\Delta}_{\mathbf{k}}^\alpha\) between all five bands. Figure 3b shows the FS of LiFeAs calculated using a tight-binding fit27,28 to the experimental data. It consists of three hole pockets h1, h2, and h3 around Γ-point and two electron pockets e1 and e2 around X-point. The hole pockets around Γ−point on the FS revealed by spectroscopic imaging STM (SI-STM)18 and confirmed by angle resolved photoemission spectroscopy (ARPES)29,30, are much smaller as compared to most other Fe-based superconductors. Local density approximation (LDA) and dynamical mean field theory (DMFT) calculations have attributed the small size of hole pocket to stronger electron–electron correlation in this material. The superconducting energy-gaps \({\Delta}_{\mathbf{k}}^\alpha\) are substantially anisotropic18. Theoretically, in the case of \({\Delta}_{\mathbf{k}}^\alpha\) with s± symmetry, if both electron-like and hole-like pockets are present31,32, the pairing arises from spin-fluctuations which are enhanced by nesting between the electron-like and hole-like pockets. But the presence of three hole pockets, combined with relatively weak spin fluctuations33, allow for several possible competing ground states in the presence of repulsive interactions. In ref. 34, it was pointed out that, under these conditions, several s-wave channels are nearly degenerate. These channels include the s± state where the signs on all hole pockets are the same35,36 and opposite to the signs on the electron bands, so-called “orbital antiphase state” that occurs when the interaction is diagonal in orbital space24, and a distinct sign structure obtained when vertex corrections were included36. Reference 37 considered the question of whether these various proposed phases could be distinguished using HAEM based on Eq. (3) and concluded that it would be challenging.
a Topograph recorded at a LiFeAs surface showing Fe-atom vacancies. The x-axis and the y-axis directions are along As–As directions. The orange circle denotes the type of weak scatterer we chose for our MAHAEM analysis. Inset shows the g(E) spectrum measured at a point for superconducting LiFeAs. The dashed rectangle represents the energy limits of the high-resolution dI/dV maps used herein for ρ−(q, E) analysis. b The Fermi surface model for LiFeAs showing three hole pockets h1, h2, and h3 around Γ-point and two electron pockets e1 and e2 around X-point in a 2-Fe zone. The scattering from hole-like to electron-like pockets takes place as indicated by a dashed vector qeh. c Theoretical prediction for single atom |\(\delta N({\mathbf{q}},E = 3.25\,{\mathrm{meV}})\)| using band- and gap-structure values fitted from experiments18. The electron-hole scattering near qeh appears as a “horn”-shaped feature which is enclosed by a circle. d Theoretical prediction for single atom ρ−(E) integrated over the circular region shown in Fig. 3c for both s± (black) and s++ (pink) symmetry.
Here we examine the relative signs of \({\Delta}_{\mathbf{k}}^\alpha\) in LiFeAs by using MAHAEM. Figure 3a shows the typical cleaved surface of LiFeAs. The scattering sites used in our analysis are Fe-atom vacancies which are non-magnetic (Supplementary Fig. S3). The theoretical simulations for LiFeAs were performed from the experimentally fitted tight binding model27 and anisotropic gap magnitude structure18,30. At wavevectors corresponding to electron-hole scattering in q-space, a “horn-shaped” feature in g(q, E) appears within which we focus on an exemplary scattering vector qeh indicated by a dashed arrow in Fig. 3b. Figure 3d then shows the theoretical, single-atom ρ−Th(q, E) integrated for the q in the brown oval in Fig. 3c for s± and s++ gaps, where sign of the gap was imposed by hand. The sign of \(\rho _{{\mathrm{s}} \pm }^{ - {\mathrm{Th}}}\) does not change for the energy values within the superconducting gap and its amplitude peaks at the energy \(E \approx {\Delta}^{{\mathrm{e}}_1}{\Delta}^{{\mathrm{h}}_1}\), both characteristics of a sign changing gap37; contrariwise \({\uprho}_{{\mathrm{s}}_{ + + }}^{ - {\mathrm{Th}}}\) changes sign indicative of same sign energy gaps throughout.
For comparison, differential conductance g(r, E) imaging of LiFeAs is performed at T = 1.2 K. The typical g(E) spectrum consists of two gaps corresponding to Δ1 = 5.3 meV and Δ2 = 2.6 meV. The measured g(q, E) are shown in Fig. 4a and the feature at qeh expected from the theoretical model in Fig. 3c is indicated by a circle. We evaluate \(\rho _{{\mathrm{MA}}}^ - ({\mathbf{q}},E)\) from Eq. (9) for N = 100 atomic scale Fe-atom vacancy sites (Supplementary Note 4). The resulting image \(\rho _{{\mathrm{MA}}}^ - ({\mathbf{q}},E)\) at a representative subgap energy E = 3.3 meV is shown in Fig. 4b.
a The measured |g(q)| pattern recorded in the FOV with multiple atomic scattering sites. The hole-like to electron-like scattering as predicted in Fig. 3c is detected clearly and indicated by a brown circle at the same location as 3c. The features inside the circle do not appear identical because the intensity in real experimental data falls off at higher |q|, while the theoretical simulation is replicated about the q-space Brillouin zone boundary with the same intensity, creating a non-physical equal intensity reflected feature. A Gaussian mask of σ = 0.68 Å−1 = 0.8π/a is used to suppress the |g(q)| data in the |q| ≈ 0 core region, to allow clearer presentation of the high-|q|- under study. Much of this |q| ≈ 0 signal intensity is believed to emanate from long-range disorder and is, moreover, unrelated to the scientific objectives of this paper. b The measured \(\rho _{{\mathrm{MA}}}^ - ({\mathbf{q}},E = 3.33\,{\mathrm{meV}})\) using Eq. (9); it is typical of all \(\rho _{{\mathrm{MA}}}^ - ({\mathbf{q}},E)\) between 1 and 6 meV. The circle indicates the hole-like to electron-like scattering in a. We integrate the \(\rho _{{\mathrm{MA}}}^ - ({\mathbf{q}},E)\) over the range of q within this region. The dashed lines are guide to eye to a feature which is consistent with intra h3 scattering. Again, a Gaussian mask of \(\sigma = 0.68\,{{\mathrm{\AA}}}^{ - 1} = 0.8\pi /a\) is used to suppress the intense core emanating from long range disorder, to allow clearer presentation of the \(\rho _{{\mathrm{MA}}}^ - \left( {{\mathbf{q}},E} \right)\) information at high-|q|. This suppressed area corresponds to ~18% of the total area of the first q-space Brillouin zone, and the unprocessed \(\rho _{{\mathrm{MA}}}^ - ({\mathbf{q}},E)\) data for this figure are provided in its entirety at Supplementary Fig. S6a. c The resulting \(\rho _{{\mathrm{MA}}}^ - (E)\) calculated by summing over the oval enclosed region in b (black dots), and the theory curves (solid) for s± (black) and s++ (pink) overlaid. Clearly, this demonstrates using MAHAEM that the superconducting energy gap symmetry of LiFeAs is s± (black).
Of note in Fig. 4b is the variety of structures at \(\left| {\mathbf{q}} \right| \ll |{\mathbf{q}}_{{\mathrm{eh}}}|\), which are challenging to understand. The thin outer blue ring (indicated by dashed light blue curve as guide-to-eye) is located at a radius in q-space that corresponds well to the expected intraband scattering within pocket h3. Furthermore, much of the q-space within this ring is blue and of rather high intensity for 1 meV < |E| < 6 meV (Supplementary Fig. S6a shows dashed contours for various possible inter-hole-band scatterings overlaid on the unprocessed ρ−(q, E)). The blue color, indicating sign-preserving scattering, is consistent with the conventional s± picture within a HAEM scenario, but the high intensity is not. As discussed in Supplementary Note 5 there are several possible explanations of these low |q| phenomena, including strong scattering, quasiparticle bound states, and antiphase hole-pocket gaps.
Nevertheless, when the high |q| scattering between hole-like and electron-like pockets (Fig. 3b, c) is integrated within the q-space region shown by a brown circle on the \(\rho _{{\mathrm{MA}}}^ - ({\mathbf{q}},E)\) of Fig. 4a, it yields \(\rho _{{\mathrm{MA}}}^ - (E)\) as plotted in Fig. 4c. The theoretically predicted \(\rho _{\,}^ - (E)\) curves are overlaid for comparison. It is clear that the experimental \(\rho _{{\mathrm{MA}}}^ - (E)\) is consistent with the \(\rho _ \pm ^{ - {\mathrm{Th}}}(E)\) theory because it does not change sign and exhibits a peak at \(E \approx 3.7\,{\mathrm{meV}} \approx \sqrt {{\Delta}_1{\Delta}_2}\). In this way, the MAHAEM technique efficiently demonstrates that \({\Delta}_{\mathbf{k}}^\alpha\) changes sign between electron-like and hole-like bands of LiFeAs.
Conclusions
We report development and demonstration of an improved approach for signed \({\Delta}_{\mathbf{k}}^\alpha\) determination (Eq. (9)), but now for use with multiple impurity atoms or scattering centers. This MAHAEM technique for measuring ρ−(q, E) is based on a combination of the Fourier shift theorem and high-precision registry of scatterer locations. It extends the original HAEM approach4 to more disordered superconductors (Figs. 2a, 3a), enables its application to far larger fields of view thereby enhancing q-space resolution (Fig. 4b), and greatly increases signal-to-noise ratios (Figs. 1d, 4b) by suppressing phase randomization in multi-atom scattering interference. Overall, MAHAEM now represents a powerful and general technique for \({\Delta}_{\mathbf{k}}^\alpha\) determination in complex superconductors.
Methods
Sample growth and preparation
FeSe samples with Tc ≈ 8.7 K were prepared using KCl3/AlCl3 chemical-vapor transport and LiFeAs samples with Tc ≈ 15 K were grown using LiAs flux method. The highly reactive LiFeAs samples are prepared in a dry nitrogen atmosphere in a glove box.
SI-STM measurements and analysis
All samples are cleaved in situ in our ultra-high cryogenic vacuum STM at low temperature. The g(r, E) data were acquired with a 3He-refrigerator-equipped STM. The picometer level atomic registration was performed before applying the HAEM technique as described in full detail in the Supplementary Note 2. Full details of the multi-atom HAEM analysis are presented in detail in Supplementary Note 3. Theoretical predictions for ρ−(E) curves were performed using the T-matrix formalism with energy gap on each band and normal state tight binding parameters fitted to experiments.
Data availability
The datasets generated and/or analyzed during this study are available to qualified requestors from the corresponding author.
Code availability
The simulation code for Fig. 1 is provided as Supplemental material. All the other codes used during the current study are available to qualified requestors from the corresponding author.
References
Norman, M. R. The challenge of unconventional superconductivity. Science 332, 196–200 (2011).
Van Harlingen, D. J. Phase-sensitive tests of the symmetry of the pairing state in the high-temperature superconductors—evidence for \(d_{x^2 - y^2}\) symmetry. Rev. Mod. Phys. 67, 515 (1995).
Tsuei, C. C. & Kirtley, J. R. Pairing symmetry in cuprate superconductors. Rev. Mod. Phys. 72, 969 (2000).
Hirschfeld, P. J., Altenfeld, D., Eremin, I. & Mazin, I. I. Robust determination of the superconducting gap sign structure via quasiparticle interference. Phys. Rev. B 92, 184513 (2015).
Wang, Q. H. & Lee, D. H. Quasiparticle scattering interference in high-temperature superconductors. Phys. Rev. B 67, 020511(R) (2003).
Sprau, P. O. et al. Discovery of orbital-selective Cooper pairing in FeSe. Science 357, 75–80 (2017).
Du, Z. et al. Sign reversal of the order parameter in (Li1−xFex)OHFe1−yZnySe. Nat. Phys. 14, 134–139 (2017).
Chi, S. et al. Determination of the superconducting order parameter from defect bound state quasiparticle interference. Preprint at https://arxiv.org/abs/1710.09089 (2017).
Chen, M. et al. Direct visualization of sign-reversal s±-superconducting gaps in FeTe0.55Se0.45. Phys. Rev. B 99, 014507 (2019).
Gu, Q. et al. Directly visualizing the sign change of d-wave superconducting gap in Bi2Sr2CaCu2O8+δ by phase-referenced quasiparticle interference. Nat. Commun. 10, 1603 (2019).
Böker, J. et al. Phase-sensitive determination of nodal d-wave order parameter in single-band and multiband superconductors. Phys. Rev. B 101, 214505 (2020).
Cheung, S. C. et al. Dictionary learning in Fourier-transform scanning tunneling spectroscopy. Nat. Commun. 11, 1081 (2020).
Lawler, M. J. et al. Intra-unit-cell electronic nematicity of the high-Tc copper-oxide pseudogap states. Nature 466, 347–351 (2010).
Fujita, K. et al. Direct phase-sensitive identification of a d-form factor density wave in underdoped cuprates. Proc. Natl Acad. Sci. USA 111, E3026–E3032 (2014).
Hamidian, M. H. et al. Picometer registration of zinc impurity states in Bi2Sr2CaCu2O8+δ for phase determination in intra-unit-cell Fourier transform STM. New J. Phys. 14, 053017 (2012).
Hoffman, J. E. et al. Imaging Quasiparticle Interference in Bi2Sr2CaCu2O8+δ. Science 297, 1148–1151 (2002).
Hanaguri, T. et al. Quasiparticle interference and superconducting gap in Ca2−xNaxCuO2Cl2. Nat. Phys. 3, 865–871 (2007).
Allan, M. P. et al. Anisotropic energy gaps of iron-based superconductivity from intraband quasiparticle interference in LiFeAs. Science 336, 563–567 (2012).
Allan, M. P. et al. Imaging Cooper pairing of heavy fermions in CeCoIn5. Nat. Phys. 9, 468–473 (2013).
Zhou, B. B. et al. Visualizing nodal heavy fermion superconductivity in CeCoIn5. Nat. Phys. 9, 474–479 (2013).
Du, Z. et al. Scrutinizing the double superconducting gaps and strong coupling pairing in (Li1−xFex)OHFeSe. Nat. Commun. 7, 10565 (2016).
Hanaguri, T. et al. Two distinct superconducting pairing states divided by the nematic end point in FeSe1−xSx. Sci. Adv. 4, eaar6419 (2018).
Sharma, R. et al. Momentum resolved superconducting energy gaps of Sr2RuO4 using quasiparticle interference. Proc. Natl Acad. Sci. USA 117, 5222–5227 (2020).
Lu, X., Fang, C., Tsai, W.-F., Jiang, Y. & Hu, J. s-wave superconductivity with orbital-dependent sign change in checkerboard models of iron-based superconductors. Phys. Rev. B 85, 054505 (2012).
Yin, Z. P., Haule, K. & Kotliar, G. Spin dynamics and orbital-antiphase pairing symmetry in iron-based superconductors. Nat. Phys. 10, 845–850 (2014).
Hirschfeld, P. J. Using gap symmetry and structure to reveal the pairing mechanism in Fe-based superconductors. C. R. Phys. 17, 197–231 (2016).
Eschrig, H. & Koepernik, K. Tight-binding models for the iron-based superconductors. Phys. Rev. B 80, 104503 (2009).
Wang, Y. et al. Superconducting gap in LiFeAs from three-dimensional spin-fluctuation pairing calculations. Phys. Rev. B 88, 174516 (2013).
Borisenko, S. V. et al. One-sign order parameter in iron based superconductor. Symmetry 4, 251–264 (2012).
Umezawa, K. et al. Unconventional anisotropic s-wave superconducting gaps of the LiFeAs iron-pnictide superconductor. Phys. Rev. Lett. 108, 037002 (2012).
Chubukov, A. Pairing mechanism in Fe-based superconductors. Annu. Rev. Condens. Matter Phys. 3, 57–92 (2012).
Maiti, S., Korshunov, M. M., Maier, T. A., Hirschfeld, P. J. & Chubukov, A. V. Evolution of the superconducting state of Fe-based compounds with doping. Phys. Rev. Lett. 107, 147002 (2011).
Qureshi, N. et al. Fine structure of the incommensurate antiferromagnetic fluctuations in single-crystalline LiFeAs studied by inelastic neutron scattering. Phys. Rev. B 90, 144503 (2014).
Ahn, F. et al. Superconductivity from repulsion in LiFeAs: novel s-wave symmetry and potential time-reversal symmetry breaking. Phys. Rev. B 89, 144513 (2014).
Platt, C., Thomale, R. & Hanke, W. Superconducting state of the iron pnictide LiFeAs: a combined density-functional and functional-renormalization-group study. Phys. Rev. B 84, 235121 (2011).
Saito, T. et al. Reproduction of experimental gap structure in LiFeAs based on orbital-spin fluctuation theory: s++-wave, s±-wave, and hole-s±-wave states. Phys. Rev. B 90, 035104 (2014).
Altenfeld, D., Hirschfeld, P. J. H., Mazin, I. I. & Eremin, I. Detecting sign-changing superconducting gap in LiFeAs using quasiparticle interference. Phys. Rev. B 97, 054519 (2018).
Rhodes, L. C. et al. Revealing the single electron pocket of FeSe in a single orthorhombic domain. Phys. Rev. B 101, 235128 (2020).
Acknowledgements
Work done by P.C.C. and A.E.B. was supported by the U.S. Department of Energy, Office of Basic Energy Science, Division of Materials Sciences and Engineering and was performed at the Ames Laboratory. Ames Laboratory is operated for the U.S. Department of Energy by Iowa State University under Contract No. DE-AC02-07CH11358. R.S. acknowledges support from Cornell Center for Materials Research with funding from the NSF MRSEC program (DMR-1719875). The authors are thankful to M.A. Müller for the discussion of the QPI results in LiFeAs. P.J.H. and M.A.S. acknowledge support from NSF-DMR-1849751; H.E. acknowledges Grant-in-Aid for Scientific Research on Innovative Areas “Quantum Liquid Crystals” (KAKENHI Grant No. JP19H05823) from JSPS of Japan. J.C.S.D. acknowledges support from the Moore Foundation’s EPiQS Initiative through Grant GBMF9457, from the Royal Society through Award R64897, from Science Foundation Ireland under Award SFI 17/RP/5445, and from the European Research Council (ERC) under Award DLV-788932.
Author information
Authors and Affiliations
Contributions
R.S., A.Kr., and M.A.S. contributed to this project equally. P.O.S., R.S., P.J.H., and J.C.S.D. designed the project. P.O.S. and M.A.S. developed the phase-resolved multi-atom averaging method; M.P.A., A.Ko., and P.O.S. carried out the experiments; R.S. and P.O.S. carried out the data analysis; A.Kr., M.A.S., J.B., P.J.H., and I.E. carried out the theoretical analysis. P.C.C. and A.E.B. synthesized single-crystalline FeSe samples; H.E. synthesized single-crystalline LiFeAs samples. J.C.S.D. and P.J.H. supervised the investigation and wrote the paper with key contributions from P.O.S., R.S., M.A.S., and A.Kr. The manuscript reflects the contributions of all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sharma, R., Kreisel, A., Sulangi, M.A. et al. Multi-atom quasiparticle scattering interference for superconductor energy-gap symmetry determination. npj Quantum Mater. 6, 7 (2021). https://doi.org/10.1038/s41535-020-00303-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-020-00303-4
This article is cited by
-
Electronic stripe patterns near the fermi level of tetragonal Fe(Se,S)
npj Quantum Materials (2023)
-
Interplay of hidden orbital order and superconductivity in CeCoIn5
Nature Communications (2023)