Abstract
Nematic fluctuations occur in a wide range physical systems from biological molecules to cuprates and iron pnictide high-Tc superconductors. It is unclear whether nematicity in pnictides arises from electronic spin or orbital degrees of freedom. We studied the iron-based Mott insulators La2O2Fe2OM2M = (S, Se), which are structurally similar to pnictides. Nuclear magnetic resonance revealed a critical slowing down of nematic fluctuations and complementary Mössbauerr spectroscopy data showed a change of electrical field gradient. The neutron pair distribution function technique detected local C2 fluctuations while neutron diffraction indicates that global C4 symmetry is preserved. A geometrically frustrated Heisenberg model with biquadratic and single-ion anisotropic terms provides the interpretation of the low temperature magnetic fluctuations. The nematicity is not due to spontaneous orbital order, instead it is linked to geometrically frustrated magnetism based on orbital selectivity. This study highlights the interplay between orbital order and spin fluctuations in nematicity.
Similar content being viewed by others
Introduction
Nematic phases occur in a variety of very different physical systems throughout nature. A nematic phase is formed when a discrete rotational symmetry is broken or reduced, while the translational symmetry is preserved. Nematicity has been studied mostly in the structural organization of soft matter such as liquid crystals1,2,3. In these materials it is easy to visualize the nematic state’s defining characteristic: the presence of a preferred axis along which liquid crystal molecules are, on average, aligned. This spatial anisotropy is generally described by C2 rotational symmetry. In the context of cuprate high-temperature superconductivity (HTSC) bond-nematicity was introduced as a competing order with HTSC itself. In recent years, nematicity has become the central focus of efforts to illuminate mechanism(s) of HTSC in iron-based superconductors (FeBS). By now, a variety of iron pnictides have been shown to exhibit electronic nematic states4,5 and in numerous theoretical pictures, the nematic phase is thought to be intimately related to the superconducting mechanism in iron-based materials6
The origin of the nematic phase in iron superconductors is heavily debated. Two scenarios are proposed5: One proposal suggests that anisotropic spin fluctuations are necessary precursors of the nematic ordering that has been experimentally observed7; the other claims that ferro-orbital ordering involving dxz,yz orbitals is responsible for nematicity8. Complicating this debate is the fact that various Fe-based materials exhibit different magnetic order. Nematicity has been mainly studied in the 122 iron pnictides such as BaFe2As2, but recently nematic behavior was reported in the 1111 material LaAsFeO1−xFx9. An important question emerges. Is nematicity a general phase behavior that exists in other Fe-based materials across the HTSC electronic phase diagram? For example, do Fe-based parent materials that are Mott insulators also exhibit nematicity? What role does electron correlation in multiorbital systems play in the formation of the interlinked nematic and spin density wave (SDW) phase and the competing superconducting phase10. Increasing evidence points to an electronic mechanism of nematicity which would place the nematic order in the class of correlation-driven electronic instabilities, like superconductivity and density-wave transitions.
In this work, we report a combined experimental and theoretical investigation of magnetism intrinsic to the correlation-induced11 Mott insulators La2O2Fe2O(S, Se)2 (see Fig. 1). Neutron powder diffraction was employed to make a magneto-structural comparison of the materials. A short range nematic fluctuating behavior was revealed by pair distribution function methods. A critical slowing down of nematic fluctuations is observed in the nuclear magnetic resonance (NMR) spin relaxation rate; this result was complemented by Mössbauer spectroscopy data. In contrast to Fe-based superconductors, orbital nematicity does not play a role in the iron oxychalcogenides, since a dxz,yz orbital degeneracy is not present due to an alternating orientation of the FeM4O2 octahedra. Therefore, a different mechanism must be responsible for the nematicity we observe in La2O2Fe2O(S, Se)2. Since these are Mott insulators, a strong-coupling view should be relevant.
The intensity of an antiferrommagnetic peak (103) in La2O2Fe2O(S, Se)2 as a function of temperature. At room temperature La2O2Fe2O(S, Se)2 are in the paramagnetic phase. The development of magnetic ordering is observed for both materials as the temperature decreases. The Neel temperatures TN, indicated by the arrows, for M = S and Se are 107.2(6) ± 0.06 K and 90.1(9) ± 0.16 K, respectively. The inset shows the crystal structure of La2O2Fe2OSe2.
Our magnetic neutron diffraction data reveal the establishment of antiferromagnetic (AFM) ordering and the similarity of magnetic behavior in these materials. The theoretical modeling explains the low-temperature nematic fluctuations as being related to quadrupolar fluctuations in a strongly frustrated magnet. This agrees well with NMR 1/T1 data. The quadrupolar fluctuations are closely related to geometric frustration in the non-collinear spin structure, which itself arises as a consequence of strong orbital selectivity in the compounds. Thus, orbital-selective Mott correlations are important for understanding magnetism in the Mott-insulating states of the oxychalcogenides. Such selective-Mott correlations have recently been the focus of attention in the iron-selenides12,13,14,15, and the present study provides an example of the relevance of orbital-selective Mott physics in Fe-based materials.
The next section contains the results from different experimental techniques that were applied to La2O2Fe2O(S, Se)2. The experimental tools can be classified as either global or local structural and electronic probes. All work presented here was performed on powder samples. Neutron powder diffraction was performed in order to determine long-range magnetic ordering as well as structural ordering. The main text details the global magnetic ordering while Supplemental Material provides information about the global structural behavior. Nuclear pair distribution function (PDF), nuclear magentic resonance (NMR) and Mössbauer spectroscopy expose local structural details associated with short-lengths scale in proximity to specifically probed atoms. At the section’s end, we present theoretical modeling that is helpful in interpreting our findings.
Results and discussion
Neutron diffraction
Neutron powder diffraction experiments were performed on powder samples of La2O2Fe2O(S, Se)2 using the C2 high-resolution diffractometer at the Canadian Nuclear Laboratories in Chalk River, Ontario. The C2 diffractometer is equipped with an 800 wire position sensitive detector covering a range of 80 degrees. Data were collected in the 2θ angular range from 5° to 117° using a Si (5 3 1) monochromator at a wavelength λ of 1.337 Å (see Supplementary Fig. 1). The lattice parameters of La2O2Fe2O(S, Se)2 were determined by Rietveld analysis of the diffraction data: for La2O2Fe2OS2 [a = 4.0453(5) Å, c = 17.9036(3) Å] and La2O2Fe2OSe2 [a = 4.4087(5) Å, c = 18.6005(3) Å]. We did not observe nuclear Bragg peak splittings, that would be indicative of a structural phase transition, in the La2O2Fe2O(S, Se)2 diffraction data collected over the temperature range from 4 to 300 K. Thus, we did not detect a change of lattice symmetry over this temperature range.
We verified the consistency of the data with the non-collinear 2-k magnetic structure previously obtained for La2O2Fe2OSe216,17. The high-temperature paramagnetic (PM) phase is compared to the 2-k antiferromagnetic phase in Fig. 2. The Sarah suite of programs18 was used to analyze the representations and provide the magnetic basis vectors for refinement with Fullprof19,20. The magnetic cell is commensurate and is doubled, in both a and c, with respect to the structural cell. The ordering is associated with k1 = (1/2, 0, 1/2) and k2 = (0, 1/2, 1/2), and the single Fe site on (1/2, 0, 0) in the nuclear I4/mmm cell is described by two distinct orbits governing the two (1/2, 0, 0) and (0, 1/2, 0) Fe sites that are independent in the magnetically ordered state. However, we note that for powder samples the diffraction pattern is indistinguishable from the pattern assigned as the collinear AFM3 model in the literature16,21. Neutron diffraction shows that the magnetic structures of La2O2Fe2O(S, Se)2 are similar with a distinction in the AFM onset temperatures TN. The magnetic Bragg peak intensity measured over a temperature range from 4 to 300 K, shown in Fig. 1, is proportional to the square of the magnetic order parameter. The data reveal the onset of AFM ordering at 90.1(9) ± 0.16 K and 107.2(6) ± 0.06 K for La2O2Fe2OSe2 and La2O2Fe2OS2, respectively. The TN value for La2O2Fe2OSe2 is in excellent agreement with values in the literature11,16,21.
Nuclear pair distribution function
In order to gain insight on the short-scale geometrical atomic arrangment, PDF measurements on La2O2Fe2O(S, Se)2 were performed using the nanoscale ordered materials diffractometer (NOMAD)22 beamline at the spallation neutron source (SNS) at Oak Ridge National Laboratory (ORNL). PDF measurements are well-suited to provide details of the structural arrangement of atoms. Pair distribution function analysis involves obtaining the Fourier transform of the measured total scattering intensity S(Q) in order to obtain a real space representation of interatomic correlations. The pair distribution function is given as \(G(r)=\frac{2}{\pi }\mathop{\int}\nolimits_{0}^{{Q}_{{\rm{max}}}}Q[S(Q)-1]\sin (Qr){\rm{d}}Q\), where Q is the scattering vector and r is the interatomic distance. PDF is a total scattering method i.e., meaning that both Bragg and diffuse scattering intensity data is simultaneously collected. Therefore, the technique is sensitive to deviations from the average structure23. Our PDF data were generated from the total scattering experiments using neutrons of a wavelength band from 0.1 to 2.9 Å. The maximum momentum transfer used for the Fourier transform was 31.4 Å−1. The instrument parameters Qdamp = 0.017 Å−1 and Qbroad = 0.019 Å−1 were fixed for all of our fits and structural refinements of the data were performed using the PDFGUI24 program and DIFFPY-CMI25 suite.
We performed data refinements using an orthorhombic model of La2O2Fe2O(S, Se)2 with a sliding fit range from (1.5–21.5) Å to (29.5–49.5) Å in 1 Å steps to investigate the temperature dependent structure on these various length scales (see Supplementary Fig. 2). This resulted in 29 fits for each temperature at which PDF data were collected. We have extracted the orthorhombicity parameter δ = (a − b)/(a + b) for both length scale and temperature series sequential refinements, where a, b are lattice parameters. Figure 3 shows the refined orthorhombicity δ extracted from fits of neutron PDF data. Structural models obtained from refining PDF data are strictly valid within the refined length scale26; this specificity condition enables the probing of local structure on different length scales by varying the refinement range. By conducting such fittings, we observed higher orthorhombicity for short-range fitting (1.5–21.5) Å compared to long-range fitting (30.0–50.0) Å. This suggests that by tracking the orthorhombicity parameter we observe local scale distortions from tetragonal to orthorhombic structure. These spatially limited distortions represent fluctuating nematic order27,28 over a broad range of temperatures. It should be emphasized that neutron powder diffraction, from the same samples, provides clear evidence that the average, long-range structures of La2O2Fe2O(S, Se)2 remain tetragonal throughout the high and low temperature regimes29. However, the PDF results provide evidence of local symmetry breaking that results in nematic C2 regions of fluctuating order27,28,30,31.
Temperature dependence of orthorhombicity for short-fitting range (1.5–21.5) Å and long-fitting range (30.0–50.0) Å for a M = S and b M = Se. In both of these figure orthorhombicity is along y-axis and temperature is in x-axis. A solid circle symbol indicates the short-fitting range (1.5–21.5) Å and a solid triangle symbol indicates the long-fitting range.
Mössbauer spectroscopy
In order to investigate the magnitude and the orientation of the ordered static Fe magnetic moment with respect to the electric field gradient (EFG) principal axis within the distorted FeO2S4 octahedra, and to study the modification of the electronic surroundings via the electric quadrupole interaction, 57Fe Mössbauer spectroscopy was performed on La2O2Fe2OS2 and is discussed in comparison to similar work on La2O2Fe2OSe217. The 57Fe nucleus probes the onsite magnetism of the Fe ion, therefore any significant changes in orbital and spin degrees of freedom should be reflected in the 57Fe Mössbauer spectra.
Figure 4a shows the low temperature zero field 57Fe Mössbauer spectra for La2O2Fe2OSe2 and La2O2Fe2OS2. At high temperatures, in the paramagnetic (PM) state, we observe a single asymmetric doublet (spectra not shown here) with a quadrupole splitting of Δ = 1.95 mm/s corresponding to a principal EFG component of Vzz =117 V/Å2. The basic features of the spectra in the PM phase look similar to previously reported La2O2Fe2OSe2 results17,32,33. As the temperatures goes below 110 K a sextet develops thereby indicating the long range magnetic ordering of La2O2Fe2OS2. The Supplemental Material provides a full set of Mössbauer spectra in Supplementary Fig. 3.
a Low temperature 57Fe Mössbauer spectra of La2O2Fe2OSe217 and La2O2Fe2OS2 fitted with the full static Hamiltonian as described in the text. A single sextet indicates full long-range magnetic order rapidly arising below TN. b Magnetic hyperfine field Bhyp or the magnetic order parameter determined from 57Fe Mössbauer measurements. The lines denote the fit of sublattice magnetization by using the equation \(M(t)\propto {B}_{{\rm{hyp}}}(T)\propto {(1-T/{T}_{{\rm{N}}})}^{{\beta }_{{\rm{crit}}}}\). c The temperature dependence of the principal axis component Vzz of the EFG decreases above TN for La2O2Fe2OSe2 and La2O2Fe2OS2. Dotted lines are the guides to the eye.
The Mössbauer spectra were analyzed using the full static Hamiltonian
with nuclear spin operators Iz, I+ = Ix + iIy, and I− = Ix − iIy. Here B is the hyperfine field at the 57Fe site while Q, gI, and μN indicate the nuclear quadrupole moment, g factor, and nuclear magneton, respectively. The polar angle θ and the azimuthal angle ϕ describe the orientation of the Fe hyperfine field B with respect to the EFG z-axis. The azimuthal angle ϕ was set to zero to avoid cross correlations. This is justified, because the asymmetry parameter η is small and the polar angle θ is close to zero for both systems. For both samples, the whole temperature series was fitted simultaneously to determine η, then η was fixed, and then the spectra were fitted individually. Within error bars, both samples La2O2Fe2O(S, Se)2 have η ≈ 0.1.
In the magnetically ordered state a magnetic sextet is observed in La2O2Fe2O(S, Se)2 data, indicating the presence of a magnetically long range ordered (LRO) state. In terms of the magnitude of the ordered moment (magnetic hyperfine field B(T)) and its temperature dependence, the nature of this LRO state is the same for both systems. The lines in Fig. 4b) indicate fits of the sub-lattice magnetization M(t) by using the equation \(M(t)\propto B(T)\propto {(1-T/{T}_{{\rm{N}}})}^{{\beta }_{{\rm{crit}}}}\). The magnetic critical exponent βcrit is deduced from these fits (see Table 1).
The 57Fe Mössbauer spectroscopy provides clear evidence that in both systems the angle θ between the strongest EFG component (local z main axis), and the magnetic hyperfine field Bhyp is equal to zero in the magnetically ordered regime, i.e., the magnetic hyperfine field B is oriented parallel to the local z-axis of the EFG principal axis system. The strongest EFG component is aligned along the O–Fe–O chains in agreement with local spin density approximation + U (LSDA + U) calculations32. This indicates that the Fe moments are oriented parallel to O–Fe–O chains. Therefore, both La2O2Fe2OS2 and La2O2Fe2OSe2 exhibit non-collinear magnetic order with a 90° angle between two different magnetic sublattices. This is consistent with three different spin structures as discussed for La2O2Fe2OSe217. The 139La NMR experiments presented below decisively identify the 2-k structure shown in Fig. 2b as the actual magnetic structure in both systems.
The temperature dependence of the EFG is comparable in La2O2Fe2O(S, Se)2. Below ≈1.4 TN the principal component Vzz decreases significantly in a near-linear fashion (Fig. 4c). Previously reported thermal expansion data of La2O2Fe2OSe2 also showed an unusual change in this temperature range21. It is known34 that thermal behavior can influence the values of the EFG tensors; however, another relevant possibility is that any degree of orbital electronic anisotropy can significantly modify the orbital occupancy. This would lead to a change in the valence contribution reflected in the EFG tensors. This particular scenario is well supported by the NMR spin-lattice relaxation rate data presented below.
Nuclear magnetic resonance
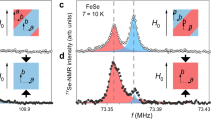
Figure 5 shows the representative 139La field sweep NMR spectra on La2O2Fe2OS2. Each spectrum consists of three pairs of satellites, and one split central transition. For lower symmetries, such as tetragonal systems, in the presence of finite EFG at the probed nucleus with nuclear spin I = 7/2, one would expect such NMR spectra. Upon lowering T, the spectral shape remains unchanged down to 109 K. At lower temperatures in the magnetically long-range ordered state the spectral shape changes considerably, because of the development of static internal magnetic hyperfine fields associated with the Fe ordering.
In general, for a nuclear spin (I = 7/2), in a lower symmetry system such as orthorhombic and tetragonal, for the presence of finite EFG at the La site, there are seven peaks due to the selective transitions between the levels (m, m−1, where m = 7/2, 5/2, ... and −5/2). For T > TN typical non-magnetic I = 7/2 powder spectra are observed. Arrows indicate the corresponding satellite transitions. Black solid lines are simulated spectra. Green and red solid lines at 100, 50, and 20 K represent calculated sub spectra due to magnetically nonequivalent sites. The vertical line indicates the field at which 139(1/T1) were measured.
The field swept NMR spectra can be well described by diagonalizing the full nuclear Hamiltonian
where B is the external magnetic field, z axis being the principle axis of EFG and \(\frac{\gamma }{2\pi }=\) 6.0146 \(\frac{MHz}{T}\). B⊥ (B∥) are the hyperfine fields (internal fields) at the La site due to the Fe ordered moment. At temperatures T > TN NMR field sweep spectra can be adequately described without any additional internal fields (B⊥ = 0 mT, B∥ = 0 mT). In the magnetically ordered state two different local fields B1 and B2 at magnetically nonequivalent 139La sites must be introduced in Eq. 2 to describe the observed spectra. The shape of the presented NMR spectra on La2O2Fe2OS2 look very similar to the Se variant La2O2Fe2OSe217. We ascertain a non-collinear magnetic structure for La2O2Fe2OS2 in agreement with the 57Fe Mössbauer results. The presence of two different sub-spectra of equal intensity with local hyperfine fields parallel and perpendicular to the c-axis unambiguously confirm the 2-k magnetic structure to be realized in both systems17. The applied external field does not change the magnetic structure of the sublattices due to anisotropy fields much larger than 7 T. This was checked by 57Fe Mössbauer spectroscopy, where a model based on pure superposition of internal and external field reproduces the measured spectra, similar to the NMR results.
There are no 139La NMR spectral anomalies near or below 150 K in La2O2Fe2OS2 nor near or below 125 K in La2O2Fe2OSe217. In contrast, the 57Fe Mössbauer reveals an almost linear decrease of the principal component Vzz of the EFG below 125 K and 150 K in La2O2Fe2OSe2 and La2O2Fe2OS2, respectively. That no effect is observed in the 139La NMR static parameters is not surprising because the local hyperfine interaction at the 139La nucleus is not necessarily sensitive to the Fe electronic structure.
Figure 6 shows the temperature dependence of La2O2Fe2OS2139(1/T1) data collected at 5.0 T. The data are qualitatively similar to La2O2Fe2OSe2 both in the paramagnetic and antiferromagnetic states17. Upon lowering T below approximately 150 K (\({T}_{{\rm{S}}}^{* }\)) the La2O2Fe2OS2139(1/T1) data starts to increase reaching a divergence around 108 K. Similarly, the 139(1/T1) signal in La2O2Fe2OSe2 is enhanced below approximately 125 K (\({T}_{{\rm{Se}}}^{* }\)) and approaches a divergence near 90 K. The divergences are associated with the critical slowing down of the Fe spin fluctuations. The enhancements of 1391/(TT1) below (\({T}_{{\rm{S}}}^{* }\)) and (\({T}_{{\rm{Se}}}^{* }\)) occur in the same temperature ranges where Mössbauer spectra exhibit a decrease of the principal component Vzz of the EFG for La2O2Fe2O(S, Se)2. The enhancements are related to short range correlations above TN which influence the spin-lattice relaxation rate. We emphasize that also the c-lattice constant of La2O2Fe2O(S, Se)2 have been reported to exhibit anomalous contractions near (\({T}_{{\rm{S}}}^{* }\)) and (\({T}_{{\rm{Se}}}^{* }\)). The c-lattice reductions manifest as a deviation from the Einstein temperature model21. The lattice change is concomitant with the decrease in Vzz which suggests that EFG is influenced by the change in the crystal field associated with octahedral height.
Temperature dependence of the 139La spin-lattice relaxation rate of La2O2Fe2OS2 (filled circle) and La2O2Fe2OSe2(filled square)17. Lines indicate the activation gap model \(\sim {T}^{2}\exp (-\Delta /T)\). Dotted vertical lines denote the AFM ordering temperature. Inset shows the 1/T1T versus temperature, while arrow marks the temperature regime where principal component Vzz of the EFG start to decrease.
Generally, the NMR spin-lattice relaxation rate is proportional to the imaginary part of the dynamic susceptibility at the Larmor frequency (1/T1T ~ ∑qχ″ (q, ω0)), where q is the wave vector and ω0 is the Larmor frequency35,36. Therefore the NMR 139(1/T1) is very sensitive to fluctuations related to the orbital and spin degrees of freedom at the Fe site. The NMR 139(1/T1) data in Fig. 6 provide a clear indication of a continuous slowing down of the Fe spin or orbital degrees of freedom above the AFM ordered phase. Similar observations were also reported for LaFeAsO9,37,38 where, just below the structural transition, 139(T1) starts to increase before it diverges at the antiferromagnetic ordering temperature. Both La2O2Fe2O(S, Se)2 fit well into this framework albeit they have not been observed to undergo structural phase transitions.
For T < TN, the spin-lattice relaxation rate 139(1/T1) is strongly reduced over a very short temperature interval. Below 87 K, for La2O2Fe2OS2139(1/T1) can be fitted by an activation gap-like behavior \(\sim {T}^{2}\exp (-\Delta /T)\), with a gap Δ = 70 K, where as for the Se variant it is Δ = 55 K. This observation is consistent with the opening of a spin excitation gap as reported in a neutron scattering study39. For T < 30 K, we find a smooth crossover from gap-like behavior to a gapless regime, where 1/T1 ≃ T3. Therefore, two distinct regimes are observed where 1/T1 ≃ T3 for T << Δ, while \(1/{T}_{1} \sim {T}^{2}\exp (-\Delta /T)\) for T > Δ.
The NMR 1/T1 behavior for T < 30 K follow an T3 power-law form which suggests the activation of an additional gapless spin fluctuation channel. We now address the origin of this behavior within the framework of an Heisenberg model with appreciable geometric frustration, an additional bi-quadratic term, and single-ion anisotropy as it is appropriate for Fe-based systems.
Theory
Motivated by earlier40 local density approximation + dynamical mean-field theory (LDA + DMFT) calculations in which we estimated an S = 1 on each Fe site, we begin with the spin S = 1 bilinear-bi-quadratic model of the square lattice. This model serves mainly illustrative purposes (The current calculation provides an illustrative example as S = 2 for the high spin state for Fe atoms in M = S and Se as reported in ref. 16), and has been widely employed in context of magnetism and nematicity in Fe-based SCs41,42 (While ref. 16 reported spin S = 2 to be consistent with inelastic neutron scattering data collected from La2O2Fe2OSe2, we employed S = 1 in order to include the well-established bilinear bi-quadratic model plus the effect of magnetic frustration). The Hamiltonian is
where Si is a spin-1 operator on site i. Jij = J1a, Jij = J1b such that J1a is ferromagnetic (FM) and J1b is AFM. Jij = J2 for [ij] along the square-diagonal, and K is the coefficient of the biquadratic interaction for S = 1 along with D being the single-ion anisotropy term that fixes the orientation of the spin. It is known that this model admits various ordered phases, depending upon the relative values of the Jij and K for a given D43: a q = (π, 0) collinear antiferromagnetic (CAF) phase, a q = (π/2, π) AFM* phase, a q = (π, π) Néel AFM phase, and a q = (π, 0) anti-ferro-quadrupolar (AFQ) phase. Additionally, the strong geometrical frustration (supported by small value of the ordered moment relative to density functional theory estimates) inherent in the model, along with sizable biquadratic and single-ion terms can yield a non-collinear AF phase as observed in our systems. The FM and AFM couplings, along with sizable D, also favor D = 2 Ising-like spin fluctuations (as extracted from the critical exponent for M(T)). With this in mind, we have estimated the temperature dependence of the NMR relaxation rate, \(1/{T}_{1}\simeq {\mathrm{lim}\,}_{\omega \to 0}{\sum }_{{\bf{q}}}\)Im\(\frac{\chi ({\bf{q}},\omega )}{\omega }\) by computing the local spin correlation function, \({\chi }_{{\rm{ii}}}(\omega )=\mathop{\int}\nolimits_{0}^{\infty }dt{e}^{{\rm{i}}\omega t}\langle T[{S}_{{\rm{i}}}^{+}(t){S}_{{\rm{i}}}^{-}(0)]\rangle\) using quantum-Monte Carlo (QMC) methods applied to the H [Eq. (3)] above44. The 1/T1 QMC results (green squares) are shown in Fig. 7.
A large-lattice size Quantum Monte Carlo technique was used by employing the Algorithms and Libraries for Physics Simulations (ALPS) to estimate (1/T1). By doing so, we computed the local transverse spin-spin correlation function for a S = 1 Heisenberg model with geometrical frustration, biquadratic exchange, and single-ion anisotropy as relevant for the Fe-based systems. The QMC results (green squares) were fitted with \({T}^{2}\exp (-\Delta /T)\) (magenta dashed line) and T3 (blue line) in the high-T and low-T regions, respectively. The main panel indicates that a \(1/{T}_{1}\simeq {T}^{2}\exp (-\Delta /T)\) form for T > 40 K, with an estimated spin gap of 98 K, smoothly evolves into 1/T1 ≃ T3 for T < 30 K. The low-T power law behavior emerges due to an additional two-magnon relaxation channel opening up at low T. Good accord between theory and experimental NMR data can be seen (see inset).
Within the temperature range 30 < T < TN( ~ 100 K), the experimental data for NMR 1/T1 fits AT2exp(−Δ/T) to a very good approximation, with Δ estimated to be approximately 100 K. Moreover, at low temperatures T < 30 K, we also find that the 1/T1 ≃ T3, indicating gapless spin excitations in the spin fluctuation spectrum. This is in line with earlier findings on the Se compound17. Our theoretical modeling is consistent with strong suppression of magnetic fluctuations below TN. The modeling also suggests, consistent with available inelastic neutron scattering data, a crossover to a gapped regime of spin fluctuations with a crossover scale O(50 K). Finally, at low T < 30 K, another spin relaxation channel opens up, indicating low-energy spin excitations below the gap.
These findings can be understood in by considering that a field-theoretic analysis for a collinear AF yields 1/T1 ≃ T3 for T << Δ, but 1/T1 ≃ T2Δexp(−Δ/T) for T >> Δ. For an AFQ ordered state the same analysis yields \({T}_{1}^{-1}\simeq {T}^{3}{e}^{-\Delta /T}\) for T << Δ, but \({T}_{1}^{-1}\simeq {T}^{7}\) for T >> Δ. Both of these outcomes are inconsistent with our experimental findings and, at first glance, would rule out both collinear AFM and AFQ phases at low T in the oxychalcogenides. However, our results are not in conflict with the previously proposed non-collinear AFM phase in the iron oxychalcogenides16,17. Three-magnon processes can be ruled out, since no T5-dependence is observed in our experimental data (nor in the calculations) at any studied temperature45. In considering all of the presented data and our theoretical results, the clear scenario emerges in which the La2O2Fe2O(S, Se)2 Mott insulators exhibit a non-collinear magnetic structure that might support the presence of AFQ phases. Furthermore, these materials each contain gapless excitations in the spin fluctuation spectrum. However, a detailed, full understanding of the low-temperature region T << Δ deviation of the NMR 1/T1 experimental data from a spin gapped regime needs to be developed. We mention that we are not able to rule out the possibility of impurities or defects causing 1/T1 signal deviation from gap-like behavior at low temperatures. The presence of slight impurities was suggested to be the source of the low-temperature upturn in magnetic susceptibility data of La2O2Fe2O(S, Se)229.
Were it possible to electron-dope the iron oxychalcogenides by chemical substitution or strain in order to modify their Mott insulating electronic structure, one would expect the small density of metallic carriers near the Mott transition to strongly scatter off these low-lying spin correlations. This would involve carriers propagating by emitting and absorbing two magnons in the usual view of a doped Mott antiferromagnet. The doped carriers would propagate by scattering off dynamical spin fluctuations that are encoded in the one-spin-flip fluctuation spectrum. We note that these processes might give rise to anomalous metallic features but they remain un-investigated. In addition, the orbital selectivity that arises from the multiorbital character of the iron oxychalcogenides will also generally lead to incoherent metallicity. How the interplay between these distinct electronic mechanisms might conspire to generate unconventional ordered state(s) in Mott systems remains a fascinating open issue. The current work should encourage efforts along these lines.
In summary, we have performed a combined theoretical and experimental study of the iron oxychalcogenides La2O2Fe2O(S, Se)2. A global structure analysis indicates the presence of a magnetic phase transition to a 2-k non-collinear AFM magnetic structure in both systems, while no average symmetry changes are detected. Striking signatures of local nematic fluctuations in the magnetic responses of these materials are observed as the AFM phase is approached from high temperatures. Nematic fluctuations are observed to occur by virtue of short lengthscale rotational symmetry breaking. The nematic fluctuation data is consistent with features observed with PDF and NMR exprimental techniques. Quadrupolar behavior is responsible for the critical slowing down of spin fluctuations was observed in the 139(T1) NMR data. These emergent quadrupolar fluctuations arise from sizable geometric frustration, which is itself a consequence of strong orbital selectivity of the compounds46. Our theoretical modeling shows that such orbital selectivity underpins numerous behaviors in the correlation-induced Mott-insulating states of the oxychalcogenides. Along with earlier DMFT work, the current results also establish the relevance of a strong correlation-based approach for iron oxychalcogenides. Finally, we note that nematicity has been invoked47 in both experimental and theoretical contexts to describe order that competes with high-Tc superconductivity in the cuprates and the iron pnictides. Therefore, the current work expands a current topic in iron-based high-temperature superconductivity while demonstrating the underlying relevance of structural nematicity to larger set of quantum materials.
Methods
Material preparation
Polycrystalline La2O2Fe2OM2M = (S, Se) samples were synthesized by a solid-state reaction method. The powders of La2O3 (99.99%), Fe (99.99%), and Se or S (99.99%) were mixed according to the stoichiometric ratio, ground fully, then pressed into several slices. These slices were placed in an alumina crucible, sealed in an evacuated quartz tube, heated at 1000 °C for 24 h, cooled to room temperature after the furnace was shut down. Then the sintered slices were fully ground, and the above process was repeated.
Neutron pair distribution function
The sample was contained in a standard 5.85 mm inner diameter vanadium can and mounted to vanadium tail liquid He cryostat. Data were taken between 2 and 300 K for a constant accelerator proton charge of 2.66 C, roughly equivalent to 40 min at full accelerator power. A diamond sample was measured for calibration and a vanadium sample was measured for normalization in the cryostat. Likewise, an empty container and empty cryostat measurement were used for background correction.
57Mössbauer spectroscopy
The 57Fe Mössbauer spectroscopy was performed in transmission geometry on samples with an area density of 2.6 mg Fe/cm2 prepared by evaporation of a methanol suspension of the powdered samples. The samples were mounted in a Cryovac He-4 bath cryostat. A commercial WissEl Mössbauerr spectrometer with a 57Co-in-Rh source was operated in sinusoidal velocity mode. The transmitted 14.4 keV photons were detected using a KeTek SDD detector.
NMR experiments
139La NMR experiments in a temperature range of 5.0 ≤ T ≤ 170 K were performed by conventional pulsed NMR techniques with an optimized Ï/2 pulse condition. The NMR data were recorded in an 8 T superconducting magnet system with a 4He variable temperature insert using a Tecmag LapNMR spectrometer. The polycrystalline powder sample was placed in a glass tube inside a Cu coil with a frequency of the resonant circuit 30 MHz. The spin-lattice relaxation rate was measured by using the saturation recovery method at the central transition in the fixed field. The data were well-fit to a single T1 value. Both 57Mössbauer spectroscopy and NMR experiments were performed on samples prepared from the same batch of crushed polycrystalline material.
Theoretical modeling
The quantum spin Hamiltonian was solved using the loop algorithm as implemented in ALPS. Convergence on the relevant observables were achieved by solving the quantum spin Hamiltonian on a 12 × 12 square lattice.
Data availability
The data sets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
References
de Gennes, P. The Physics of Liquid Crystals (Clarendon Press, Oxford, 1974).
de Gennes, P. An analogy between superconductors and smectics A. Solid State Commun. 10, 753–756 (1972).
de Vries, A. The use of x-ray diffraction in the study of thermotropic liquid crystals with rod-like molecules. Mol. Cryst. Liq. Cryst. 131, 125–145 (1985).
Fernandes, R. M. & Schmalian, J. Manifestations of nematic degrees of freedom in the magnetic, elastic, and superconducting properties of the iron pnictides. Supercond. Sci. Technol. 25, 084005 (2012).
R. M. Fernandes, A. V. C. & Schmalian, J. What drives nematic order in iron-based superconductors? Nat. Phys. 10, 97–104 (2014).
Kretzschmar, F. et al. Critical spin fluctuations and the origin of nematic order in Ba(Fe1 − xCo)2As2. Nat. Phys. 12, 560–563 (2016).
Kasahara, S. et al. Electronic nematicity above the structural and superconducting transition in BaFe2(As1−xPx)2. Nature 486, 382–385 (2012).
Baek, S.-Hea Orbital-driven nematicity in FeSe. Nat. Mater. 14, 210–214 (2015).
Hess, C. et al. Nematicity in LaFeAsO1−xFx. Phys. Status Solidi (b) 254, 1600214 (2017).
Matsuura, K. et al. Maximizing Tc by tuning nematicity and magnetism in FeSe1−xSx superconductors. Nat. Commun. 8, 1143 (2017).
Zhu, J.-X. et al. Band narrowing and mott localization in iron oxychalcogenides La2O2Fe2O(Se,S)2. Phys. Rev. Lett. 104, 216405 (2010).
Yi, M. et al. Observation of temperature-induced crossover to an orbital-selective mott phase in AxFe2−ySe2 (a=K, Rb) superconductors. Phys. Rev. Lett. 110, 067003 (2013).
Nica, E. M., Yu, R. & Si, Q. Orbital-selective pairing and superconductivity in iron selenides. npj Quantum Mater. 2, 24 (2017).
Si, Q., Yu, R. & Abrahams, E. High-temperature superconductivity in iron pnictides and chalcogenides. Nat. Rev. Mater. 1, 16017 (2016).
Stock, C. & McCabe, E. E. The magnetic and electronic properties of oxyselenides—influence of transition metal ions and lanthanides. J. Phys. Condens. Matter 28, 453001 (2016).
McCabe, E. E. et al. Weak spin interactions in mott insulating La2O2Fe2OSe2. Phys. Rev. B 89, 100402 (2014).
Günther, M. et al. Magnetic order and spin dynamics in La2O2Fe2OSe2 probed by 57Fe Mössbauer, 139La NMR, and muon-spin relaxation spectroscopy. Phys. Rev. B 90, 184408 (2014).
Wills, A. A new protocol for the determination of magnetic structures using simulated annealing and representational analysis (sarah). Phys. B 276-278, 680–681 (2000).
Rodriguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Phys. B 192, 55–69 (1993).
Rodríquez-Carvajal, J. & Roisnel, T. Winplotr: a windows tool for powder diffraction pattern analysis. Eur. Powder Diffr. 378, 118–123 (2001).
Free, D. G. & Evans, J. S. O. Low-temperature nuclear and magnetic structures of La2O2Fe2OSe2 from x-ray and neutron diffraction measurements. Phys. Rev. B 81, 214433 (2010).
Neuefeind, J., Feygenson, M., Carruth, J., Hoffmann, R. & Chipley, K. K. The nanoscale ordered materials diffractometer nomad at the spallation neutron source sns. Nucl. Instrum. Methods B 287, 68–75 (2012).
Egami, T. & Billinge, S. J. L. Underneath the Bragg Peaks. Mater. Today 6, 57 (2003).
Farrow, C. L. et al. PDFfit2 and PDFgui: computer programs for studying nanostructure in crystals. J. Phys. Condens. Matter 19, 335219 (2007).
Juhás, P., Louwen, J. N., van Eijck, L., Vogt, E. T. C. & Billinge, S. J. L. PDFgetN3: atomic pair distribution functions from neutron powder diffraction data using ad hoc corrections. J. Appl. Crystallogr. 51, 1492–1497 (2018).
Proffen, T. et al. Atomic pair distribution function analysis of materials containing crystalline and amorphous phases. Z. Kristallogr. 220, 1002–1008 (2005).
Frandsen, B. A. et al. Local orthorhombicity in the magnetic C4 phase of the hole-doped iron-arsenide superconductor Sr1−xNaxFe2As2. Phys. Rev. Lett. 119, 187001 (2017).
Frandsen, B. A. et al. Widespread orthorhombic fluctuations in the (Sr, Na)Fe2As2 family of superconductors. Phys. Rev. B 98, 180505 (2018).
Freelon, B. et al. Magnetic and structural properties of the iron oxychalcogenides La2O2Fe2OM2(M=S, Se). Phys. Rev. B 99, 024109 (2019).
Frandsen, B. A. et al. Real-space investigation of short-range magnetic correlations in fluoride pyrochlores NaCaCo2F7 and NaSrCo2F7 with magnetic pair distribution function analysis. Phys. Rev. Mater. 1, 074412 (2017).
Frandsen, B. A. et al. Local atomic and magnetic structure of dilute magnetic semiconductor (Ba,K)(Zn,Mn)2As2. Phys. Rev. B 94, 094102 (2016).
Fuwa, Y., Wakeshima, M. & Hinatsu, Y. Crystal structure, magnetic properties, and mössbauer spectroscopy of new layered iron oxyselenide Nd2Fe2O3Se2. J. Phys. Condens. Matter 22, 346003 (2010).
Kabbour, H. et al. Structure and magnetic properties of oxychalcogenides A2F2Fe2OQ2 (A=Sr, Ba; Q=S, Se) with Fe2O square planar layers representing an antiferromagnetic checkerboard spin lattice. J. Am. Chem. Soc. 130, 8261–8270 (2008).
Ingalls, R. Electric-field gradient tensor in ferrous compounds. Phys. Rev. 133, A787–A795 (1964).
Moriya, T. The effect of electron–electron interaction on the nuclear spin relaxation in metals. J. Phys. Soc. Jpn 18, 516–520 (1963).
Smerald, A. & Shannon, N. Angle-resolved NMR: quantitative theory of 75As T1 relaxation rate in BaFe2As2. Phys. Rev. B 84, 184437 (2011).
Fu, M. et al. NMR search for the spin nematic state in a LaFeAsO single crystal. Phys. Rev. Lett. 109, 247001 (2012).
Nakai, Y., Ishida, K., Kamihara, Y., Hirano, M. & Hosono, H. Evolution from itinerant antiferromagnet to unconventional superconductor with fluorine doping in LaFeAs(O1−xFx) revealed by 75As and 139La nuclear magnetic resonance. J. Phys. Soc. Jpn 77, 073701 (2008).
Lumsden, M. D. & Christianson, A. D. Magnetism in fe-based superconductors. J. Phys. Condens. Matter 22, 203203 (2010).
Freelon, Bea Mott-kondo insulator behavior in the iron oxychalcogenides. Phys. Rev. B 92, 155139 (2015).
Si, Q. & Abrahams, E. Strong correlations and magnetic frustration in the high Tc iron pnictides. Phys. Rev. Lett. 101, 076401 (2008).
Hu, W.-J. et al. Frustrated magnetism and quantum transitions of nematic phases in FeSe. Preprint at https://arxiv.org/abs/1606.01235 (2016).
Yu, R. & Si, Q. Antiferroquadrupolar and ising-nematic orders of a frustrated bilinear-biquadratic heisenberg model and implications for the magnetism of fese. Phys. Rev. Lett. 115, 116401 (2015).
Bauer, B. et al. The ALPS project release 2.0: open source software for strongly correlated systems. J. Stat. Mech. 2011, P05001 (2011).
Beeman, D. & Pincus, P. Nuclear spin-lattice relaxation in magnetic insulators. Phys. Rev. 166, 359–375 (1968).
Yu, R., Zhu, J.-X. & Si, Q. Orbital-selective superconductivity, gap anisotropy, and spin resonance excitations in a multiorbital t-J1-J2 model for iron pnictides. Phys. Rev. B 89, 024509 (2014).
Kivelson, S. A., Fradkin, E. & Emery, V. J. Electronic liquid-crystal phases of a doped mott insulator. Nature 393, 550–553 (1998).
Acknowledgements
R.S. and H.-H.K. are partially supported by the DFG through SFB 1143 for the project C02. V.G. was partially supported by the DFG through GR 4667. L.C.’s work is supported by CNPq (Grant No. 304035/2017-3). Acknowledgment (L.C.) is also made to CAPES. Zhejiang University research is supported by the National Key R&D Program of China under Grant No. 2016YFA0300402, and the National Natural Science Foundation of China (Grants No. NSFC-12074335 and 11974095) and the Fundamental Research Funds for the Central Universities. Work at Lawrence Berkeley National Laboratory was funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division under Contract No. DE-AC02-05-CH11231 within the Quantum Materials Program (KC2202). This work used resources of the Spallation Neutron Source, a DOE office of Science User Facility operated by the Oak Ridge National Laboratory. This manuscript has been authored by UT-Battelle, LLC, under contract DE-AC05-00OR22725 with the US Department of Energy (DOE). The US government retains and the publisher, by accepting the article for publication, acknowledges that the US government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for US government purposes. DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan).
Author information
Authors and Affiliations
Contributions
B.F., M.L., L.C., R.S., and H.H.K. wrote the paper. B.F., Z.Y., and R.F. performed the neutron experiments. B.F., Z.Y., R.F., B.K., Y.H., and I.S. analyzed neutron data. R.S., S.K., F.B., V.G., and H.H.K. conducted NMR and Mössbauer experiments. B.Fran advised B.K., A.A. and R.B. on performing and interpreting PDF refinement. M.L. and S.A. conceived and performed the theory work. M.F. grew the samples. B.F. conceived of the overall project. All authors edited and assessed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Freelon, B., Sarkar, R., Kamusella, S. et al. Nematic fluctuations in iron-oxychalcogenide Mott insulators. npj Quantum Mater. 6, 4 (2021). https://doi.org/10.1038/s41535-020-00302-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-020-00302-5
This article is cited by
-
Pressure-induced transition from a Mott insulator to a ferromagnetic Weyl metal in La2O3Fe2Se2
Nature Communications (2023)