Abstract
Log-periodic quantum oscillations discovered in transition-metal pentatelluride give a clear demonstration of discrete scale invariance (DSI) in solid-state materials. The peculiar phenomenon is convincingly interpreted as the presence of two-body quasi-bound states in a Coulomb potential. However, the modifications of the Coulomb interactions in many-body systems having a Dirac-like spectrum are not fully understood. Here, we report the observation of tunable log-periodic oscillations and DSI in ZrTe5 and HfTe5 flakes. By reducing the flakes thickness, the characteristic scale factor is tuned to a much smaller value due to the reduction of the vacuum polarization effect. The decreasing of the scale factor demonstrates the many-body effect on the DSI, which has rarely been discussed hitherto. Furthermore, the cut-offs of oscillations are quantitatively explained by considering the Thomas-Fermi screening effect. Our work clarifies the many-body effect on DSI and paves a way to tune the DSI in quantum materials.
Similar content being viewed by others
Introduction
One of the most important concepts in the area of phase transitions is scale invariance. A scale invariant system reproduces itself on different temporal and spatial scales. This is described by the relation \(f\left( {kx} \right) = k^\lambda f(x)\), where k is an arbitrary parameter, λ is the scaling dimension, and f is a physical field. Discrete scale invariance (DSI) is a weaker case of the scale invariance, where a system only obeys the scale invariance for specific choices of k1,2. With a fundamental scaling ratio λ and characteristic log-periodicity, DSI arises in various contexts, such as earthquakes, financial crashes, turbulence and so on1. After being introduced to bound-state problems of quantum systems by Vitaly Efimov in 1970 (ref. 3), the DSI had been observed only in cold atom systems for a long time4,5,6,7. It had not previously been observed in the solid state. The discovery of Dirac materials has changed that situation8,9,10,11,12,13,14. Especially in the topological transition-metal pentatelluride ZrTe5, the quantum oscillations with log-periodicity have revealed the existence of DSI in a solid-state system10. The origin is attributed to the quasi-bound states induced by the supercritical Coulomb interaction between the massless Dirac fermions and charged impurities10,12,13. Further studies reported the log-periodic oscillations in HfTe514 and elemental semiconductor tellurium15, confirming that the DSI feature can be a universal characteristic of Dirac materials with Coulomb impurities.
ZrTe5 and HfTe5 are predicted to be quantum spin Hall insulators in the two-dimensional (2D) limit and the three-dimensional (3D) crystals are located near the phase boundary between weak and strong topological insulators16. Later studies indicated that the topological natures of both ZrTe5 and HfTe5 are very sensitive to the crystal lattice constant and detailed composition17,18. Taking ZrTe5 as an example, some angle-resolved photoemission spectroscopy (ARPES)19,20 and magneto-infrared spectroscopy studies show that ZrTe5 is a Dirac semimetal21. The observed negative magnetoresistance (MR) that is related to the chiral anomaly and the anomalous Hall effect support the hypothesis of a massless Dirac band structure22,23,24. However, other ARPES and scanning tunneling microscopy (STM) results suggest that ZrTe5 is a topological insulator25,26,27,28. Thus, the transition-metal pentatelluride ZrTe5 and HfTe5 are ideal platforms to investigate different intriguing physical properties due to their high tunability29,30,31,32,33,34. In particular, the very small Fermi surface of the compounds has enabled some peculiar findings in the ultraquantum regime, such as log-periodic quantum oscillations and 3D quantum Hall effect10,14,35. As described above, the log-periodic oscillations revealing the DSI feature can be convincingly explained by a two-body quasi-bound state model. However, the solids ZrTe5 and HfTe5 are in fact many-body systems, and the Coulomb interactions are modified by screening effects that are not fully understood. The screening of the Coulomb interaction is closely related to the carrier density. In the experiments, we find that the carrier density in ZrTe5 flakes changes with thickness29. The interaction between the layers of ZrTe5 and HfTe5 is comparable to graphene, making it easy to get flakes from the bulk samples by exfoliation16. Thus, it is interesting to study the log-periodic quantum oscillations in the transition-metal pentatelluride flakes with different carrier density by thickness control, which may provide insights into many-body effects on DSI.
In this work, we carried out systematic magnetotransport measurements on ZrTe5 and HfTe5 flakes under magnetic fields (B) up to 53 Tesla (T). The logB-periodic oscillations can be detected in both ZrTe5 and HfTe5 flakes with thicknesses down to about 160 nm. In the thick ZrTe5 flake (~1200 nm), logB oscillations with a scale factor λ ~ 3.3 is observed. The consistent scale factors between the flake (λ ~ 3.3) and bulk crystals (λ ~ 3.2)10 show that the quality of the samples is not affected by the process of exfoliation and flake fabrication. More interestingly, a relatively smaller scale factor λ ~ 1.6 can be extracted in the MR and Hall traces of flakes with a thickness of about 160 nm. Theoretically, this index λ decreases with increasing the effective charge of impurities that compose quasi-bound states responsible for the DSI and the log-periodicity. Further analysis shows that the carrier density in the flakes increases as the thickness decreases. We believe that the high carrier density makes the vacuum polarization effect weaker and leads to a larger effective charge, which results in a smaller scale factor. Thus, this work reveals a thickness-tuned scale factor of logB quantum oscillations in ZrTe5 and HfTe5 flakes and provides a perspective on the DSI in solid-state systems.
Results
Temperature dependence of resistance
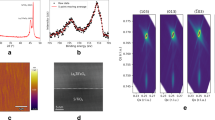
ZrTe5 and HfTe5 belong to the orthorhombic space group Cmcm (\(D_{2h}^{17}\))36. Figure 1a shows the crystal structure of ZrTe5 and HfTe5. Within the a–c plane, the trigonal prismatic chains of “ZrTe3” or “HfTe3” run along the a axis and are linked by parallel zigzag chains of “Te2” along the c axis. The layers of ZrTe5 and HfTe5 are stacked along the b axis. The false-color scanning electron microscopy (SEM) image of a fabricated ZrTe5 flake (gray color) with six electrodes (gold color) is displayed in Fig. 1b. A schematic measurement structure of standard six-electrode-method is illustrated in the inset of Fig. 1c. The current is applied along the a axis and the magnetic field is along the b axis for all measurements.
a Crystal structures of ZrTe5 and HfTe5. b Scanning electron microscope false color image of a typical ZrTe5 flake. Scale bar represents 10 μm. c Typical temperature-dependent longitudinal resistance of the transition-metal pentatelluride flakes. The peak anomaly appears at Tp ~ 65 K and 74 K for HfTe5 (300 nm thick) and ZrTe5 (190 nm thick) flakes, respectively. Inset shows a schematic structure for the electrical transport measurements.
Figure 1c represents typical resistance–temperature (R–T) curves of HfTe5 (~300 nm thick) and ZrTe5 (~190 nm thick) flakes. Resistance peaks at Tp ~ 65 K and 74 K can be detected for HfTe5 and ZrTe5 flakes, respectively. It is noted that the Tp of the flakes are definitely higher than that of the bulk10,14. The origin of the resistance peak in ZrTe5 and HfTe5 has been discussed for decades, and recently the view of the Lifshitz transition during the changing of temperatures explains some findings in the compounds28. However, in other reports, the Hall resistances of ZrTe5 and HfTe5 remain p type with increasing temperatures, which is not consistent with the picture of a Lifshitz transition29,37. An alternative two-band model has been presented to be responsible for the transport anomaly and the various Tp in different samples14,29. In this picture, at low temperatures, the metallic R–T curve mainly relies on a semi-metallic Dirac band, while a semiconducting band dominates at higher temperatures. The combination and competition between the two bands lead to the resistance peak at Tp. In exfoliated flakes, the carrier density of the Dirac holes commonly increases with decreasing thickness, indicating a shift of the Fermi level toward the valence band. Thus, the thickness decrease can alter the competition balance and result in a higher Tp.
Tunable log-periodic oscillations and DSI
A ZrTe5 flake labeled s1 with a thickness of about 1200 nm was measured under magnetic fields up to 53 T and the MR curves in a semilogarithmic scale are shown in Fig. 2a. By subtracting a smooth background, the logB-periodic oscillating components can be extracted and are shown in Fig. 2b. For clarity, data curves in Fig. 2a, b are shifted. Distinct log-periodic magneto-oscillations can be observed at low temperatures. With increasing temperature, thermal broadening eventually becomes comparable to the intrinsic width of the quasi-bound states that induce log-periodic oscillations10,14. Thus, the oscillations gradually attenuate with increasing temperature and finally disappear above 120 K (see Supplementary Fig. 1a, b), which agree with the observations in bulk crystals10. Consistent results were also acquired by using the second differential method to extract the oscillations, as shown in Supplementary Fig. 1d. The independence of the oscillations on the subtraction methods demonstrates that the log-periodic structures are intrinsic properties of the materials (see Supplementary Note 1 and Supplementary Figs. 1–5 for more details). The characteristic magnetic fields (Bn) of the observed oscillation peaks and dips can be indexed as n and (n−0.5), respectively. By plotting log (Bn) as a function of n, a linear dependence is revealed to confirm the log-periodic property (Fig. 2c). Based on the linear fitting in Fig. 2c, a dominant scale factor λ = Bn/Bn+1 ~3.34 can be obtained. Further, the Fast Fourier Transform (FFT) result of the log-periodic oscillations is shown in Fig. 2d. The sharp FFT frequency peak is located at F ~1.87, which indicates a period of log (Bn) ~0.53 and a main scale factor λ ~3.38. The FFT shows some broadening, with a full-width at half-maximum (FWHM) analysis giving a reasonable λ range of about [2.58, 5.98]. It is noted that the properties of the oscillations in the 1200-nm-thick ZrTe5 flake are very close to those observed in the bulk10, showing that the quality of the device is still reserved during the process of the thin flake fabrication.
The thinner flakes are further studied for comparison. Figure 3 shows the log-periodic oscillations in the MR and Hall traces of the ZrTe5 flake (s2) with a thickness of about 137 nm. The oscillatory part of MR at 4.2 K after subtracting a smooth background is displayed in Fig. 3a. The inset of Fig. 3a plots the MR of s2 at 4.2 K as a function of the magnetic field. The log-periodic oscillations can be observed and survive up to 120 K (Supplementary Fig. 6). The index plot and FFT result of the oscillations are shown in Fig. 3b. Both the linear fitting and the sharp FFT frequency peak confirm the log-periodicity and give a λ ~1.60. The FWHM of the frequency peak further indicates a range for λ of [1.45, 3.61]. The log-periodic oscillations are also observed in the Hall traces of the s2, as shown in Fig. 3c, d. We subtract the background of the Hall signal by using similar methods to the MR. ΔRyx as a function of log B is plotted in Fig. 3c. Figure 3d displays the linear fitting of the index and the FFT analysis of the data shown in Fig. 3c. A scale factor λ ~1.66 can be obtained for the oscillations in the Hall resistance, coinciding with λ ~1.60 for the MR. The near equality of λ in the MR and the Hall resistance is in agreement with the theoretical expectation14. Further measurements on a ZrTe5 flake with a thickness of about 50 nm show log-periodic quantum oscillations in Hall trace with λ ~1.52 (Supplementary Fig. 7). The decrease of the scale factor is also supported by the observations in the HfTe5 flake, which shows clearer oscillations. Figure 4 displays the magnetotransport results of the HfTe5 flake (s3) with a thickness of about 180 nm. By using the same background subtraction method, the log-periodic oscillations in MR and Hall traces can be extracted, as shown in Fig. 4a, c. The oscillations in MR at high magnetic fields can survive up to 78 K (Supplementary Fig. 8). Figure 4b, d plots the linear fitting and FFT analysis for the oscillations in the MR and the Hall trace, respectively. The scale factor λ in s3 is estimated to be around 1.6, smaller than λ ~3.5 in the bulk14.
a Extracted oscillatory part from MR of s2 at 4.2 K. Inset: MR of s2 at 4.2 K. b LogB-periodicity of the MR oscillations in s2. Inset: FFT result of the MR oscillations at 4.2 K in a. The scale factor λ of the oscillations in the MR is about 1.60. c, d Results for the Hall trace of s2 at 4.2 K. The scale factor λ of the oscillations in the Hall trace is about 1.66, coincided with that for the MR.
a Extracted oscillatory part from MR of s3 at 4.2 K. Inset: MR of s3 at 4.2 K. b LogB-periodicity of the MR oscillations in s3. Inset: FFT result of the MR oscillations at 4.2 K in a. c, d Results for the Hall traces of s3 at 4.2 K. The scale factor λ for the log-periodic oscillations in the Hall trace is about 1.59, consistent with that (~1.62) for the MR.
Discussion
As discussed in previous works, the log-periodic quantum oscillations can be attributed to the two-body quasi-bound states composed of a massless Dirac particle and a stationary attractive Coulomb impurity10,14. For DSI to occur, we need the supercritical condition α > 1 to occur in the system, where \(\alpha = Ze^2/\varepsilon \hbar v_{\mathrm{F}}\) is the effective fine-structure constant of the impurity. Here Z is the ionicity, ε is the background dielectric constant, and vF is the Fermi velocity. When the supercritical condition holds, the radius of the quasi-bound states of the impurity is discrete scale invariant according to the relation \(\frac{{R_{n + 1}}}{{R_n}} = \sqrt \lambda = e^{\frac{\pi }{{s_0}}}\) with \(s_0 = \sqrt {\alpha ^2 - 1}\). Rn is the characteristic radius of the quasi-bound state and when the magnetic length \(\ell _n = \sqrt {\frac{{\hbar c}}{{eB_n}}} = s_0R_n\) under an applied magnetic field, the energy of the n-th quasi-bound states rises rapidly and moves through the Fermi energy. Hence, the sequence of fields at which there is a peak in the density of states at the Fermi energy satisfies \(\frac{{B_{n + 1}}}{{B_n}} = e^{2\pi /s_0} = e^{2\pi /\sqrt {\alpha ^2 - 1} } = \lambda\)10. When B = Bn, the resonant scattering between the mobile carriers and the quasi-bound states influences the transport properties and results in a log-periodic correction to the MR and Hall traces.
The most interesting feature of our results is that compared to the bulk or thick flakes of ZrTe5 and HfTe5, the scale factor λ in the thinner flakes becomes quite small. As mentioned above, λ is a monotonically decreasing function of α and \(\alpha = Ze^2/\varepsilon \hbar v_{\mathrm{F}}\). The Fermi velocity vF is expected to be the same in bulk and thin flakes of a Dirac material. The background dielectric constant ε depends on the core electrons and so it is also unlikely to change. Thus, we must look for changes in Z to explain the change in λ.
Based on Figs. 2–4, we notice that the ratio of oscillation amplitude to MR, i.e., ΔRxx(B)/Rxx(B), for the n = 1 peak in thick and thin flakes are 1.3% and 0.5%, respectively. The larger surface-volume ratio but weaker oscillations in thinner flakes may exclude the possibility that the log-periodicity arises from a surface effect. By estimating from the Hall traces (Supplementary Figs. 1, 6), the Dirac hole carrier density of the 1200-nm-thick ZrTe5 flake is 2.6 × 1015 cm−3, very close to that of bulk ZrTe5 (ref. 10), whereas the Dirac carrier density of the 137-nm-thick ZrTe5 flake is 9.9 × 1016 cm−3. The greatly increased carrier density in the thinner flakes can have a profound effect on screening of the Coulomb interaction. There are three types of screening in the transition-metal pentatelluride compounds, including the usual effects arising from bound electrons and conduction carriers, as well as vacuum polarization. The screening from the bound core electrons is responsible for background dielectric constant ε. As mentioned above, this screening effect is unlikely to change between the bulk and flakes since it depends only on very local features of the atomic structure. The screening from conduction carriers occurs in ordinary metals and in Weyl metals. It is noticed that the screening effect does not change the effective charge (ionicity Z) and has little influence on λ. The vacuum polarization is a specific feature of Dirac and Weyl semimetals and comes from the fact that the joint density of states for particle-hole excitations is large at low energies38,39. The introduction of an impurity charge excites many virtual particle-hole pairs in Dirac and Weyl semimetals, much more than in a typical insulator with a hard gap. In ref. 38, it was found in two dimensions that this effect renormalizes Z downward: Z → Z* = Z / [1 + ZQ ln (1/κa)], where κ is proportional to the Fermi wavevector and thus to the square root of the carrier concentration ne; a is a short-distance cutoff at the atomic scale and Q is a numerical factor of order 1. A review of interaction effects in the Coulomb impurity problem in graphene concluded that this is the main effect40. There is no such complete theory in three dimensions to our knowledge, but the physics is expected to be similar. The renormalization of Z is substantial due to its large starting value and indeed if nea2 is of order 10−4, as in our thin flakes, then changes in λ by a factor of 2 are easily obtained. Essentially, in the thinner flakes the vacuum polarization effect decreases and the effective charge becomes larger, which gives an increase in s0 and a smaller λ. Therefore, we propose that vacuum polarization plays a crucial role in the decrease of λ in flakes. Further theoretical efforts are still needed to make this connection fully quantitative.
Although at 4.2 K there are more than three oscillating cycles detected in the thin flakes due to the smaller scale factor, the oscillation signal becomes clear only above 3–5 T for the thin flakes, much higher than that for thick flakes or bulk10. We explain that the critical field Bc over which the oscillations should be observed is closely related to the Thomas-Fermi screening length ξ. Though the screening from conduction carriers has little influence on λ, it can affect the visibility of the oscillations by converting the Coulomb potential Ze2/r to \(\frac{{Ze^2}}{r} \times e^{ - r/{\upxi}}\). When the distance from the impurity is greater than ξ, the Coulomb potential becomes exponential and DSI is lost. In the thinner flakes, the increased carrier density leads to decreased ξ accompanying with a larger Bc. For the thinner flakes, the calculated Bc ~3.5 T and the number of oscillations N ~5 are consistent with the experimental results (see Supplementary Note 2 for more details).
In summary, we carried out systematic transport measurements on the transition-metal pentatelluride ZrTe5 and HfTe5 flakes with different thicknesses. LogB-periodic oscillations and DSI feature are detected in both the MR and the Hall traces of these flakes. The scale factor is observed to decrease with decreasing thickness, which is attributed to the weaker vacuum polarization effect resulting from higher carrier density. This work offers a way to tune the DSI and log-periodic oscillations in quantum materials. It also provides deep insights into many-body effects with a Dirac-like spectrum.
Methods
Sample information
The high-quality ZrTe5 and HfTe5 single crystals were grown by the Te-flux method as described in previous reports10,14,37. The crystals were characterized by powder X-ray diffraction, SEM with energy dispersive X-ray spectroscopy, and transmission electron microscopy.
Device fabrication
The ZrTe5 and HfTe5 flakes were exfoliated by using the Scotch tape method onto 300-nm-thick SiO2/Si substrates. After spin coating of poly (methyl methacrylate) (PMMA), the standard electron beam lithography in a FEI Helios NanoLab 600i Dual Beam System was carried out to define electrodes. Metal electrodes (Pd/Au, 6.5/300 nm) were deposited in a LJUHV E-400L E-Beam Evaporator after Ar plasma cleaning.
Transport measurements
Electronic transport measurements in this work were mainly conducted in the pulsed high magnetic field facility (53 T) at Wuhan National High Magnetic Field Center. Standard six-electrode-method was used for the measurements. The current is applied along the a axis and the magnetic field is along the b axis for all measurements. Gold wires are attached to the electrodes by the silver epoxy and fixed on the substrate by GE varnish to avoid the vibration under pulsed field (see Supplementary Fig. 9).
Data availability
The data that support the findings of this study are available from the corresponding author on reasonable request.
Code availability
The code in this work is available from the corresponding author on reasonable request.
References
Sornette, D. Discrete-scale invariance and complex dimensions. Phys. Rep. 297, 239–270 (1998).
Braaten, E. & Hammer, H. W. Universality in few-body systems with large scattering length. Phys. Rep. 428, 259–390 (2006).
Efimov, V. Energy levels arising from resonant 2-body forces in a 3-body system. Phys. Lett. B 33, 563–564 (1970).
Kraemer, T. et al. Evidence for Efimov quantum states in an ultracold gas of caesium atoms. Nature 440, 315–318 (2006).
Huang, B., Sidorenkov, L. A., Grimm, R. & Hutson, J. M. Observation of the second triatomic resonance in Efimov’s scenario. Phys. Rev. Lett. 112, 190401 (2014).
Pires, R. et al. Observation of Efimov resonances in a mixture with extreme mass imbalance. Phys. Rev. Lett. 112, 250404 (2014).
Tung, S. K. et al. Geometric scaling of Efimov states in a 6Li-133Cs mixture. Phys. Rev. Lett. 113, 240402 (2014).
Shytov, A. V., Katsnelson, M. I. & Levitov, L. S. Atomic collapse and quasi–Rydberg states in graphene. Phys. Rev. Lett. 99, 246802 (2007).
Nishida, Y. Vacuum polarization of graphene with a supercritical Coulomb impurity: low-energy universality and discrete scale invariance. Phys. Rev. B 90, 165414 (2014).
Wang, H. C. et al. Discovery of log-periodic oscillations in ultraquantum topological materials. Sci. Adv. 4, eaau5096 (2018).
Ovdat, O. et al. Observing a scale anomaly and a universal quantum phase transition in graphene. Nat. Commun. 8, 507 (2017).
Liu, H. et al. Discrete scale invariance in topological semimetals. Preprint at https://arxiv.org/abs/1807.02459 (2018).
Zhang, P. & Zhai, H. Efimov effect in Dirac semi-metals. Front. Phys. 13, 137204 (2018).
Wang, H. et al. Log-periodic quantum magneto-oscillations and discrete-scale invariance in topological material HfTe5. Natl Sci. Rev. 6, 914 (2019).
Zhang, N. et al. Magnetotransport signatures of Weyl physics and discrete scale invariance in the elemental semiconductor tellurium. Proc. Natl Acad. Sci. USA 117, 11337 (2020).
Weng, H. M., Dai, X. & Fang, Z. Transition-metal pentatelluride ZrTe5 and HfTe5: a paradigm for large-gap quantum spin Hall insulators. Phys. Rev. X 4, 011002 (2014).
Fan, Z. J. et al. Transition between strong and weak topological insulator in ZrTe5 and HfTe5. Sci. Rep. 7, 45667 (2017).
Shahi, P. et al. Bipolar conduction is the origin of the electronic transition in pentatellurides: metallic vs. semiconducting behavior. Phys. Rev. X 8, 021055 (2018).
Li, Q. et al. Chiral magnetic effect in ZrTe5. Nat. Phys. 12, 550–554 (2016).
Shen, L. et al. Spectroscopic evidence for the gapless electronic structure in bulk ZrTe5. J. Electron Spectrosc. Relat. Phenom. 219, 45–52 (2017).
Chen, R. Y. et al. Magnetoinfrared spectroscopy of Landau levels and Zeeman splitting of three-dimensional massless Dirac fermions in ZrTe5. Phys. Rev. Lett. 115, 176404 (2015).
Zheng, G. L. et al. Transport evidence for the three-dimensional Dirac semimetal phase in ZrTe5. Phys. Rev. B 93, 115414 (2016).
Liang, T. et al. Anomalous Hall effect in ZrTe5. Nat. Phys. 14, 451–455 (2018).
Ge, J. et al. Unconventional Hall Effect induced by Berry Curvature. Natl. Sci. Rev. https://doi.org/10.1093/nsr/nwaa163 (2020).
Wu, R. et al. Evidence for topological edge states in a large energy gap near the step edges on the surface of ZrTe5. Phys. Rev. X 6, 021017 (2016).
Manzoni, G. et al. Evidence for a strong topological insulator phase in ZrTe5. Phys. Rev. Lett. 117, 237601 (2016).
Li, X.-B. et al. Experimental observation of topological edge states at the surface step edge of the topological insulator ZrTe5. Phys. Rev. Lett. 116, 176803 (2016).
Zhang, Y. et al. Electronic evidence of temperature-induced Lifshitz transition and topological nature in ZrTe5. Nat. Commun. 8, 15512 (2017).
Niu, J. J. et al. Electrical transport in nanothick ZrTe5 sheets: From three to two dimensions. Phys. Rev. B 95, 035420 (2017).
Zhou, Y. et al. Pressure-induced superconductivity in a three-dimensional topological material ZrTe5. Proc. Natl Acad. Sci. USA 113, 2904–2909 (2016).
Qi, Y. P. et al. Pressure-driven superconductivity in the transition-metal pentatelluride HfTe5. Phys. Rev. B 94, 054517 (2016).
Liu, Y. et al. Superconductivity in HfTe5 across weak to strong topological insulator transition induced via pressures. Sci. Rep. 7, 44367 (2017).
Zheng, G. L. et al. Field-induced topological phase transition from a three-dimensional Weyl semimetal to a two-dimensional massive Dirac metal in ZrTe5. Phys. Rev. B 96, 121401(R) (2017).
Liu, Y. et al. Zeeman splitting and dynamical mass generation in Dirac semimetal ZrTe5. Nat. Commun. 7, 12516 (2016).
Tang, F. et al. Three-dimensional quantum Hall effect and metal–insulator transition in ZrTe5. Nature 569, 537–541 (2019).
Okada, S., Sambongi, T. & Ido, M. Giant resistivity anomaly in ZrTe5. J. Phys. Soc. Jpn. 49, 839–840 (1980).
Wang, H. C. et al. Chiral anomaly and ultrahigh mobility in crystalline HfTe5. Phys. Rev. B 93, 165127 (2016).
Katsnelson, M. I. Nonlinear screening of charge impurities in graphene. Phys. Rev. B 74, 201401(R) (2006).
Shytov, A. V., Katsnelson, M. I. & Levitov, L. S. Vacuum polarization and screening of supercritical impurities in graphene. Phys. Rev. Lett. 99, 236801 (2007).
Kotov, V. N. et al. Electron-electron interactions in graphene: current status and perspectives. Rev. Mod. Phys. 84, 1067 (2012).
Acknowledgements
We thank Liqin Huang, Zihan Yan, Qingzheng Qiu, Haiwen Liu, and Yongjie Liu for discussions on the data. This work was financially supported by the National Key Research and Development Program of China (2018YFA0305604 and 2017YFA0303302), the National Natural Science Foundation of China (Grant Nos. 11888101, 11774008, 12004441), Beijing Natural Science Foundation (Z180010), and the Strategic Priority Research Program of Chinese Academy of Sciences (Grant No. XDB28000000). J.Y. and D.M. were supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division. H.W. acknowledges the support of the Hundreds of Talents program of Sun Yat-Sen University and the Fundamental Research Funds for the Central Universities (No. 20lgpy165).
Author information
Authors and Affiliations
Contributions
Jian Wang conceived and supervised the research. Y.Liu, H.W. performed the transport measurements. Y.Li and J.G. fabricated the devices. J.Y. and D.M. grew the ZrTe5 and HfTe5 bulk crystals. H.Z., Junfeng Wang, L.L., and J.-Y.D. helped in the transport measurements. R.J. carried out theoretical calculations. Y.Liu, H.W., and Jian Wang analyzed the data. Y.Liu, H.W., R.J., and Jian Wang wrote the manuscript with input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liu, Y., Wang, H., Zhu, H. et al. Tunable discrete scale invariance in transition-metal pentatelluride flakes. npj Quantum Mater. 5, 88 (2020). https://doi.org/10.1038/s41535-020-00290-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-020-00290-6