Abstract
The evidence for proximity-induced superconductivity in heterostructures of topological insulators and high-Tc cuprates has been intensely debated. We use molecular-beam epitaxy to grow thin films of topological insulator Bi2Te3 on a cuprate Bi2Sr2CaCu2O8+x, and study the surface of Bi2Te3 using low-temperature scanning tunneling microscopy and spectroscopy. In few unit-cell thick Bi2Te3 films, we find a V-shaped gap-like feature at the Fermi energy in dI/dV spectra. By reducing the coverage of Bi2Te3 films to create nanoscale islands, we discover that this spectral feature dramatically evolves into a much larger hard gap, which can be understood as a Coulomb blockade gap. This conclusion is supported by the evolution of dI/dV spectra with the lateral size of Bi2Te3 islands, as well as by topographic measurements that show an additional barrier separating Bi2Te3 and Bi2Sr2CaCu2O8+x. We conclude that the prominent gap-like feature in dI/dV spectra in Bi2Te3 films is not a proximity-induced superconducting gap. Instead, it can be explained by Coulomb blockade effects, which take into account additional resistive and capacitive coupling at the interface. Our experiments provide a fresh insight into the tunneling measurements of complex heterostructures with buried interfaces.
Similar content being viewed by others
Introduction
When a superconductor (SC) is interfaced with a normal, non-superconducting material, Cooper pairs are able to tunnel across the interface, and the normal material can become superconducting via the superconducting proximity effect (SPE). In the past decade, interest in the SPE has been brought to the forefront by the discovery of 2D materials predicted to harbor exotic electronic phenomena if interfaced with superconductors, such as Majorana modes in topological superconductors1 and superluminescence in proximitized p-n junctions2. A wide range of different SCs have been used as a scaffolding in these efforts, such as NbSe23,4,5,6,7, elemental SCs8,9, FeTe0.55Se0.4510,11, and copper-oxide (cuprate) high-Tc SC Bi2Sr2CaCu2O8+x (Bi-2212)12,13,14,15,16,17. While the majority of SCs used have led to well-established platforms for proximity studies, the experiments using cuprates, which exhibit significantly larger superconducting gap (ΔSC) and Tc18, have given unexpectedly conflicting results12,13,14,15,16,17. On one side, the majority of angle-resolved photoemission spectroscopy (ARPES) measurements reported the absence of an induced gap in the TI band structure, attributed to the very short coherence length of Bi-2212 along the c-axis12, and the mismatch between the Fermi surfaces of the TI and Bi-221212,13. On the other hand, tunneling measurements have observed a gap in dI/dV spectra in both Bi17 and Bi2Te316 grown on Bi-2212, interpreted to arise due to proximity-induced superconductivity in the topological material.
In this work, we provide strong evidence suggesting that Coulomb blockade effects, which arise due to strong electron–electron interactions19, not proximity-induced Cooper pairing, govern the formation of the observed gap at the Fermi level in Bi2Te3 grown on Bi-2212. This is largely unexpected, because Coulomb gaps have typically been associated with highly-localized quantum dot like structures20 and systems in high magnetic field21, not continuous, millimeter-scale heterostructures at zero field such as the ones studied here. However, our experiments reveal that despite continuity of our thicker films (up to ~4 nm thickness in Supplementary Fig. 7) over macroscopic length scales, inevitable domain formation in this system and an imperfect interface can lead to the same mesoscopic effect in tunneling measurements.
Results
Thin film growth of Bi2Te3 on Bi-2212
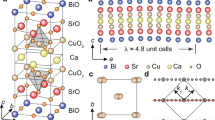
Bi2Te3 films are grown on UHV-cleaved, optimally doped Bi-2212 (Tc~91 K) using molecular-beam epitaxy (MBE), following a recipe similar to previous related work12,13 (Methods section). As the proximity-induced superconducting gap at the exposed bare surface of the normal material is expected to decrease with its thickness22, we explore a range of Bi2Te3 thicknesses, from ~10 quintuple layers (QLs) down to a partial coverage of a single QL film. There are two main challenges in growing Bi2Te3 on superconducting Bi-2212. The first one is incompatibility of the in-plane atomic structures of the two materials. Bi-2212 cleaves between two BiO planes to reveal a square lattice of Bi atoms observed in STM topographs (Fig. 1b), which is in contrast to Bi2Te3 that has a hexagonal lattice structure (Fig. 1c). This structural mismatch leads to the formation of two types of Bi2Te3 domains that are rotated 30 degrees with respect to each other (Fig. 1e and Supplementary Fig. 1)11. Despite the domain formation, we are still able to routinely locate large (at the order of ~50 nm squared) single-domain areas using STM in thicker films. Second crucial issue is that the electronic properties of the Bi-2212 surface can change upon heating23. At ideal Bi2Te3 growth temperatures of ~350 °C24, interstitial oxygen dopants escape from the topmost surface layers of Bi-2212, leading to an effective lowering of the hole density and degradation of superconducting properties23. To mitigate this issue, in this work we use much lower Bi2Te3 growth temperatures below 250 °C (Supplementary Note 1). Our ~0.1 QL film leads to the formation of nano-islands allowing us to verify the superconducting properties of our Bi-2212 substrate after it has been exposed to our growth conditions (Supplementary Fig. 2).
a Schematic of the Bi2Te3/Bi2Sr2CaCu2O8+x heterostructure. STM topograph showing b Bi2Sr2CaCu2O8+x (Bi-2212) substrate before deposition, c Bi2Te3 film after deposition. Scale bars in b, c represent 3 nm. Reflection high-energy electron diffraction (RHEED) images acquired d before and e after the Bi2Te3 growth, showing characteristic Bi-2212 and Bi2Te3 features, respectively. STM setup condition: b Iset = 10 pA, Vsample = 100 mV; c Iset = 50 pA, Vsample = −50 mV.
Electronic characterization of Bi2Te3 Films
To characterize the large-scale electronic structure of our Bi2Te3 films, we use quasiparticle interference (QPI) imaging25,26, rooted in elastic scattering and interference of electrons on the surface of a material, which can be seen as waves in STM dI/dV maps. We observe the characteristic scattering pattern and energy dispersion, which is qualitatively similar to that reported on cleaved bulk Bi2Te3 single crystals26,27, as well as Bi2Te3 films11,28 (Supplementary Figs. 3 and 4). Next, we look for any evidence of induced superconductivity at the surface of Bi2Te3 films, starting with thinner films. dI/dV spectra acquired on 1 QL and 2 QL Bi2Te3 films show a small suppression in the local density of states within ± ~5–10 meV around the Fermi level (Fig. 2b, e). To test if the surface state is gapped within the energy range of the gap-like feature, we acquire dI/dV maps at small bias near the Fermi level energy, well within the observed gap feature (Fig. 2a, d). Given that we observe a prominent 6-fold QPI signal due to hexagonal warping of the Dirac dispersion starting at ~200 meV below the Fermi level to several hundred meV above the Fermi level (Supplementary Fig. 3), if the surface state is indeed fully gapped within the narrow energy range across the Fermi level, we would expect to observe a strong suppression of the QPI signal. However, the FTs of the dI/dV maps in both films show a noticeable QPI signal (insets in Fig. 2b, e), which allows us to place an upper bound on the magnitude of the induced gap in the Bi2Te3 surface state, if any, to ~2–3 meV, set by the finite temperature thermal broadening and lock-in excitation used in our experiments. In comparison to the average dI/dV spectrum of optimally-doped Bi-2212 that shows ~40 meV magnitude and prominent coherence peaks (Supplementary Fig. 2c), the gap-like feature observed on Bi2Te3 is shallow, often asymmetric and does not show clear coherence peaks (Fig. 2c, f). Previous experiments have attributed a qualitatively similar gap-like feature to an induced superconducting gap in the normal material in proximity to cuprates16,17. We note that similarly to ref. 16, our dI/dV spectra occasionally show more prominent gap edge peaks (Supplementary Fig. 10), but as we discuss later, the peaks are notably asymmetric with respect to the Fermi level.
a, d dI/dV map taken on a 1 QL and d 2 QL thick Bi2Te3 films showing distinct QPI signature at a 1 mV bias. The scale bar in a is 5 nm and the scale bar in d is 3 nm. b, e Average dI/dV spectra obtained on b 1 QL and e 2 QL films showing a gap-like feature at the Fermi energy in the density of states denoted by dashed lines and arrows. Insets in b and e are the six-fold symmetrized Fourier transforms of a and d, respectively. Scale bars in insets of (b, e) denote 1 per Å. c, f 10 nm line cut of dI/dV spectra on c 1 QL and f 2 QL films offset for clarity showing the variation of the gap-like feature. Colored lines in a, d denote the positions of the linecuts in c, f. STM setup conditions: a Iset = 3 pA, Vsample = 1 mV, Vexc = 1 mV (zero-to-peak); b, c Iset = 40 pA, Vsample = 100 mV, Vexc = 4 mV; d–f Iset = 100 pA, Vsample = 50 mV, Vexc = 2 mV.
The films of reduced coverage below 1 QL enable us to investigate bonding of the two materials at the interface. We analyze STM topographs in more detail to extract their topographic height with respect to the substrate (Fig. 3a). Interestingly, we find the apparent height of all 1 QL Bi2Te3 islands to be ~1.2 nm with respect to Bi-2212 (Fig. 3d and Supplementary Fig. 9), ~20% taller than the expected ~1 nm height for a single QL of Bi2Te3. The same result is confirmed in a film with a nearly complete 1 QL coverage, where the island height is also found to be ~20% larger than expected (Fig. 3b, e). To demonstrate that our STM scanner has been properly calibrated, we plot the topographic height profile across a step in the 2 QL thick film with respect to the Bi2Te3 layer below, which shows the expected step height of ~1 nm (Fig. 3c, f). As STM topographs contain both electronic and structural information, to provide evidence that this height difference is of structural origin, and not purely due to the variation in electronic density of states, we point out the following. First, the same island height is extracted from topographs acquired at both positive and negative STM bias (Supplementary Fig. 5). Second, 1 QL Bi2Te3 nano-islands grown on a superconductor Fe(Te,Se) and on an insulator SrTiO3(001), two materials that are electronically very different, yield a ~1-nm step height in both cases (Supplementary Fig. 6). To explain the larger height of the first Bi2Te3 layer with respect to the Bi-2212 substrate, we postulate that there may be an intergrowth layer forming at the interface (Fig. 3g–i). This intergrowth layer could be composed of dilute amounts of excess Bi or Te, possibly the same as the small clusters that we see in topographs of exposed regions of Bi-2212, which are also approximately equal to the barrier height (Supplementary Fig. 2). This has occasionally been observed at the interface of other van der Waals heterostructures29.
a–c STM topographs showing a Bi2Te3 nano-islands on Bi-2212 with ~10% coverage (scale bar is 40 nm), b Bi2Te3 nano-islands on Bi-2212 with ~90% coverage (scale bar is 20 nm) and c ~2 QL Bi2Te3 film (scale bar is 80 nm). d–f Topographic profiles from a–c along the lines indicated by red dashed arrows in a–c. g–i Schematic depiction of the cross-section of the interface, consistent with the observed step heights in d–f. STM setup condition: a Iset = 10 pA, Vsample = −500 mV; b Iset = 20 pA, Vsample = 2 V; and c Iset = 10 pA, Vsample = 500 mV.
We examine the consequences of this imperfect interface in the context of TI/SC heterostructures. A crucial insight comes from investigating the electronic properties of Bi2Te3 nano-islands themselves (Fig. 4a, b). The average dI/dV spectrum acquired on a small island with ~10 nm diameter (Fig. 4a) shows a markedly different shape compared to that observed on a much larger flat terrace of 1 QL Bi2Te3 film (Fig. 2). We observe a hard gap spanning the Fermi level with ~150 meV magnitude, much larger than 2ΔSC of Bi-2212. Interestingly, the gap displays a pronounced asymmetry in energy, which as we will show can be attributed to a residual charge on the island (Supplementary Fig. 10). Due to this asymmetry, and the fact that a gap as large as several hundred meV can be seen on other islands, we rule out the superconducting origin of the gap.
a–c Average dI/dV spectra acquired over the regions denoted by the red dashed squares in the inset topographs. Inset scale bars are a 5 nm, b 20 nm, and c 30 nm. Average dI/dV measured on the surface of a ~90 nm2 island, b ~400 nm2 island, and c ~4500 nm2 region of Bi2Te3 nano-island. d Schematic of a double tunnel junction, where C1 and C2 are the capacitance of tip to film and film to substrate junctions, and R1 and R2 are their respective resistances. STM setup conditions: a Iset = 50 pA, Vsample = 200 mV, Vexc = 2 mV, Inset topography: Iset = 10 pA, Vsample = 1000 mV; b Iset = 50 pA, Vsample = 200 mV, Vexc = 2 mV, Inset topography: Iset = 10 pA, Vsample = −500 mV; c Iset = 40 pA, Vsample = 100 mV, Vexc = 4 mV, Inset topography: Iset = 5 pA, Vsample = 600 mV.
Coulomb blockade origins of the spectral gap
Given the additional barrier at the interface we have discovered and the finite size of the system, a natural explanation for the gap could be understood in terms of a Coulomb blockade (CB) gap30, which arises due to single electrons exchanging energy with the environment as they tunnel through a barrier31,32. The CB effect has been widely reported in tunneling measurements of finite-size heterostructures when there is an extra barrier at the interface of the two materials sandwiched together33,34,35,36. It can be modeled by a double tunnel junction, one being the tip-sample junction and the other one being the sample-substrate junction, each consisting of a capacitor and a resistor connected in parallel (Fig. 4d). The overall size of the CB gap (ΔCB) is roughly inversely proportional to the capacitance between the film and the substrate (C2)33,34. The shape of the gap will change depending on the resistive component at the film-substrate junction (R2), where large R2 would lead to a sharp-cutoff in conductance at the gap edge, while smaller R2 would lead to a gradual suppression of conductance approaching zero energy33,34.
In small Bi2Te3 islands, due to small C2 and large R2, we observe a sharp CB gap (Fig. 4a), with zero dI/dV conductance within the gap. As the size of the island increases (C2 should become larger and R2 smaller), ΔCB is expected to evolve into a smaller V-shaped gap33,34. This is exactly what we observe in our data (Fig. 4b). As the islands grow even larger and start to connect, the V-shape gap-feature becomes progressively more subdued (Fig. 4c), with finite conductance near the Fermi level where we are still able to observe a QPI signal. Similarly to refs. 33,34, we use the dynamical Coulomb blockade P(E) theory to fit the overall spectral shape, which show a good agreement for a reasonable set of C2 and R2 parameters (Supplementary Figs. 11 and 12 and Supplementary Note 2). We note that Bi2Te3 films inevitably contain domains due to structural mismatch between Bi2Te3 and Bi-2212, observed in reflection high-energy electron diffraction (RHEED) images (Supplementary Fig. 1b) and in real space (Supplementary Fig. 1a), which can lead to the finite size effects as seen in STM/S measurements, even as the islands merge together in one or more QL thick films. On our thicker films, the gap-like feature gets suppressed and the zero-bias conductance increases (Fig. 5). Specifically, while the gap-like feature is prominent in 1, 2, and 4 QL films, we only see a small suppression at zero energy in ~9–10 QL films, which nearly completely disappears in the thickest ~11 QL region (Fig. 5). This can be understood as a consequence of the decrease in resistivity. We also postulate that domains, on average, may become larger in thicker films due to strain relaxation as the films grow thicker. Therefore, the CB effect will still be present, but weaker in thicker films (Supplementary Fig. 12), and the gap-like feature observed in our measurements is most likely a simple consequence of this phenomenon, not proximity-induced Cooper pairing.
Average dI/dV spectra taken over Bi2Te3 of various thickness on four different samples: 1 QL, 2 QL, and 4 QL films were all different samples, while ~9, ~10, and ~11 QL data was acquired on consecutive terraces of the same sample with ~10 QL nominal thickness. All spectra were normalized by integral of dI/dV from 0 to −50 mV. The difference in the shape of the background conductance of the 4 QL spectrum is likely an artifact of the STM tip with slightly anisotropic density of states. STM setup conditions: (1 QL) Iset = 40 pA, Vsample = 100 mV, Vexc = 4 mV; (2 QL) Iset = 100 pA, Vsample = 50 mV, Vexc = 2 mV; (4 QL) Iset = 200 pA, Vsample = 200 mV, Vexc = 2 mV; (9, 10, 11 QL) Iset = 100 pA, Vsample = 50 mV, Vexc = 2 mV.
Discussion
Our measurements resolve the outstanding controversy between ARPES and STM measurements of MBE-grown heterostructures of topological materials and cuprates, by shedding light on an overlooked aspect of the underlying physics in these systems rooted in the CB effects. Although CB should in principle be negligible in continuous millimeter-scale heterostructures, we find that tunneling measurements of Bi2Te3 films can still exhibit a CB gap due to domain formation during growth and the additional barrier at the interface between Bi2Te3 and Bi-2212. The gap is as large as a few hundred meV in the smallest Bi2Te3 islands, but as the size of the islands increases, this leads to the mitigation of the CB effect, and a much smaller V-shaped gap in the nearly continuous (but with inevitable domains) Bi2Te3 films of one or more QL thickness. We note that the complex structure of additional peaks in dI/dV spectra outside the gap (Fig. 4a) may be due to quantized bound states within the islands (Supplementary Fig. 8), similarly to what had been observed in quantum dots37. Another explanation for these peaks may be due to the capacitive coupling between the tip and the island36, which could be explored in future experiments and analysis. However, a quantitative understanding of each peak position is beyond the scope of this paper. Our work cautions the interpretation of gap-like features in tunneling measurements of complex heterostructures with inaccessible, buried interfaces.
Methods
Synthesis of heterostructures
Bulk Bi-2212 single crystals were attached to our sample holder using H20E silver epoxy (EPO-TEK), and heated in ultra-high vacuum (UHV) prior to cleaving in order to minimize the surface contamination during outgassing. After cleaving in UHV, the substrates were brought back to the growth temperature ranging from ~170 to ~250 °C. To grow Bi2Te3 films, high purity Bismuth (99.999%) and Tellurium (99.99%) were co-evaporated from Knudsen cells (Sentys Inc) in a nominal flux ratio of ~1:10 Bi:Te determined by quartz crystal microbalance (QCM). Based on the Bismuth flux rate, the Bi2Te3 growth rate is calculated to be ~4 min per quintuple layer. RHEED (Sentys Inc) is used to monitor the quality of the surface before, during and after Bi2Te3 deposition. Our RHEED patterns show streaky lines (Fig. 1e), indicating a layer-by layer deposition. After the sample had been cooled to room-temperature, we transferred it to the STM using a vacuum suitcase held at 10−11 mbar base pressure. This step ensures that our samples are never exposed to air and that the surface remains pristine, from growth to preforming STM measurements.
STM/S characterization
STM/S data were acquired using a Unisoku USM1300 STM at the base temperature of ~4.5 K (Supplementary Note 1). Spectroscopic measurements were acquired using a standard lock-in technique at 915 Hz frequency, with bias excitation ranging from ~1 to 10 mV as detailed in figure captions. The STM tips used were homemade chemically-etched tungsten tips that are annealed in vacuum prior to STM imaging.
Data availability
The data supporting the findings of this study and the computer code used for data analysis are available upon request from the corresponding author.
References
Fu, L. & Kane, C. L. Superconducting proximity effect and Majorana Fermions at the surface of a topological insulator. Phys. Rev. Lett. 100, 096407 (2008).
Asano, Y., Suemune, I., Takayanagi, H. & Hanamura, E. Luminescence of a Cooper pair. Phys. Rev. Lett. 103, 187001 (2009).
Wang, M. et al. The coexistence of superconductivity and topological order in the Bi2Se3 thin films. Science 336, 52–55 (2012).
Xu, J. P. et al. Artificial topological superconductor by the proximity effect. Phys. Rev. Lett. 112, 217001 (2014).
Xu, S.-Y. et al. Momentum-space imaging of Cooper pairing in a half-Dirac-gas topological superconductor. Nat. Phys. 10, 943–950 (2014).
Xu, J.-P. et al. Experimental detection of a Majorana mode in the core of a magnetic vortex inside a topological insulator-superconductor Bi2Te3/NbSe2 heterostructure. Phys. Rev. Lett. 114, 017001 (2015).
Sun, H.-H. et al. Majorana zero mode detected with spin selective Andreev reflection in the vortex of a topological superconductor. Phys. Rev. Lett. 116, 257003 (2016).
Yang, F. et al. Proximity effect at superconducting Sn-Bi2Se3 interface. Phys. Rev. B 85, 104508 (2012).
Qu, F. et al. Strong superconducting proximity effect in Pb-Bi2Te3 hybrid structures. Sci. Rep. 2, 339 (2012).
Chen, M., Chen, X., Yang, H., Du, Z. & Wen, H.-H. Superconductivity with twofold symmetry in Bi2Te3/FeTe0.55Se0.45 heterostructures. Sci. Adv. 4, eaat1084 (2018).
Zhao, H. et al. Superconducting proximity effect in a topological insulator using Fe(Te, Se). Phys. Rev. B 97, 224504 (2018).
Yilmaz, T. et al. Absence of a proximity effect for a thin-films of a Bi2Se3 topological insulator grown on top of a Bi2Sr2CaCu2O8+δ cuprate superconductor. Phys. Rev. Lett. 113, 067003 (2014).
Xu, S.-Y. et al. Fermi-level electronic structure of a topological-insulator/cuprate-superconductor based heterostructure in the superconducting proximity effect regime. Phys. Rev. B 90, 085128 (2014).
Zareapour, P. et al. Proximity-induced high-temperature superconductivity in the topological insulators Bi2Se3 and Bi2Te3. Nat. Commun. 3, 1056 (2012).
Wang, E. et al. Fully gapped topological surface states in Bi2Se3 films induced by a d-wave high-temperature superconductor. Nat. Phys. 9, 621–625 (2013).
Wan, S. et al. Twofold symmetry of proximity-induced superconductivity on Bi2Te3/Bi2Sr2CaCu2O8+δ heterostructures revealed by scanning tunneling microscopy. Phys. Rev. B 101, 220503 (2020).
Shimamura, N. et al. Ultrathin bismuth film on high-temperature cuprate superconductor Bi2Sr2CaCu2O8+δ as a candidate of a topological superconductor. ACS Nano 12, 10977–10983 (2018).
Hüfner, S., Hossain, M. A., Damascelli, A. & Sawatzky, G. A. Two gaps make a high-temperature superconductor? Rep. Prog. Phys. 71, 062501 (2008).
Averin, D. V. & Likharev, K. K. Coulomb blockade of single-electron tunneling, and coherent oscillations in small tunnel junctions. J. Low Temp. Phys. 62, 345–373 (1986).
Shin, S. J. et al. Room-Temperature charge stability modulated by quantum effects in a nanoscale silicon island. Nano Lett. 11, 1591–1597 (2011).
Morgenstern, M., Haude, D., Klijn, J. & Wiesendanger, R. Coulomb pseudogap caused by partial localization of a three-dimensional electron system in the extreme quantum limit. Phys. Rev. B 66, 121102 (2002).
Lee, K., Vaezi, A., Fischer, M. H. & Kim, E.-A. Superconducting proximity effect in topological metals. Phys. Rev. B 90, 214510 (2014).
Zhao, H. et al. Charge-stripe crystal phase in an insulating cuprate. Nat. Mater. 18, 103–107 (2019).
Krumrain, J. et al. MBE growth optimization of topological insulator Bi2Te3 films. J. Cryst. Growth 324, 115–118 (2011).
Seo, J. et al. Transmission of topological surface states through surface barriers. Nature 466, 343–346 (2010).
Okada, Y. et al. Direct observation of broken time-reversal symmetry on the surface of a magnetically doped topological insulator. Phys. Rev. Lett. 106, 206805 (2011).
Sessi, P. et al. Signatures of Dirac Fermion-mediated magnetic order. Nat. Commun. 5, 5349 (2014).
Zhang, H. et al. Experimental demonstration of topological surface states protected by time-reversal symmetry. Phys. Rev. Lett. 103, 266803 (2009).
Altfeder, I. et al. Scanning tunneling microscopy observation of phonon condensate. Sci. Rep. 7, 43214 (2017).
Amman, M., Wilkins, R., Ben-Jacob, E., Maker, P. D. & Jaklevic, R. C. Analytic solution for the current-voltage characteristic of two mesoscopic tunnel junctions coupled in series. Phys. Rev. B 43, 1146–1149 (1991).
Delsing, P., Likharev, K. K., Kuzmin, L. S. & Claeson, T. Effect of high-frequency electrodynamic environment on the single-electron tunneling in ultrasmall junctions. Phys. Rev. Lett. 63, 1180–1183 (1989).
Devoret, M. H. et al. Effect of the electromagnetic environment on the Coulomb blockade in ultrasmall tunnel junctions. Phys. Rev. Lett. 64, 1824–1827 (1990).
Brun, C. et al. Dynamical Coulomb blockade observed in nanosized electrical contacts. Phys. Rev. Lett. 108, 126802 (2012).
Serrier-Garcia, L. et al. Scanning tunneling spectroscopy study of the proximity effect in a disordered two-dimensional metal. Phys. Rev. Lett. 110, 157003 (2013).
Hong, I.-P., Brun, C., Pivetta, M., Patthey, F. & Schneider, W.-D. Coulomb blockade phenomena observed in supported metallic nanoislands. Front. Phys. 1, 13 (2013).
Reiner, J. et al. Spectroscopic visualization of a robust electronic response of semiconducting nanowires to deposition of superconducting islands. Phys. Rev. X 10, 011002 (2020).
Subramaniam, D. et al. Wave-function mapping of graphene quantum dots with soft confinement. Phys. Rev. Lett. 108, 046801 (2012).
Acknowledgements
I.Z. gratefully acknowledges the support from Army Research Office Grant Number W911NF-17-1-0399. The work in Brookhaven was supported by the Office of Science, US Department of Energy under Contract No. DE-SC0012704. J.S. and R.Z. were supported by the Center for Emergent Superconductivity, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science. The work of C.F. was supported by the Academy of Finland (projects No. 308515 and 312299).
Author information
Authors and Affiliations
Contributions
MBE growth was performed by B.R. and Z.R. STM experiments were carried out by H.Z., H.L., and S.G.; B.R., H.Z. and H.L. analyzed the STM data with the guidance from I.Z.; J.S., R.Z., and G.G grew single crystals of Bi-2212. K.H.T. and C.F. provided theory and code for the P(E)-calculations of the differential conductance. B.R. and J.M. computed and compared theoretical fits with experimental data. I.Z. supervised the project. I.Z. and B.R. wrote the manuscript with input from all the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rachmilowitz, B., Zhao, H., Ren, Z. et al. Coulomb blockade effects in a topological insulator grown on a high-Tc cuprate superconductor. npj Quantum Mater. 5, 72 (2020). https://doi.org/10.1038/s41535-020-00274-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-020-00274-6