Abstract
The perovskite NaOsO3 has a metal–insulator transition at temperature 410 K, which is delicate, intriguing, and provokes a lot of debate on its nature. Our combined electrical resistance, Raman, and synchrotron x-ray diffraction experiments show that the insulating ground state in this osmate endures under high pressure up to at least 35 GPa. In this pressure range, compression reveals hidden hysteretic resistance properties with a transient metallic state near 200 K, manifested three electronic character anomalies (at 1.7, 9.0, and 25.5 GPa), and a structural transition to the singular polar phase (at ~18 GPa). We distinguish NaOsO3 from the regular crystallographic behavior of perovskites, though the electrical specificities resemble iridates and nickelates. The theoretical first-principle band structure and lattice dynamics calculations demonstrate that the magnetically itinerant Lifshitz-type mechanism with spin–orbit and spin–phonon interactions is responsible for these pressure-induced changes. Our findings provide another new playground for the emergence of new states in 5d materials by using high-pressure methods.
Similar content being viewed by others
Introduction
The composition of NaOsO3 in the primitive cubic form has been known since 19741. The orthorhombic perovskite NaOsO3 was only obtained in 20082,3. The new orthorhombic phase attracted a lot of attention, because of its rare metal–insulator transition (MIT) which coincides with a long-range commensurate three-dimensional antiferromagnetic (AFM) ordering at a rather high Néel temperature TN = TMIT = 410 K3,4,5,6. Initially, a Slater-like mechanism was proposed to explain this unusual MIT behavior4. Subsequent insights have revealed that this transition is better interpreted by a relativistic magnetic Lifshitz mechanism where MIT is driven by magnetic fluctuations and spin–orbit-induced renormalization of the electron correlation7,8.
At high temperatures (T > 410 K), NaOsO3 shows paramagnetic Fermi liquid behavior, but with decreasing temperature Fermi surface undergoes continuous reconstruction prompted by the changes in the amplitude and direction of the spins which eventually causes a narrow band gap of ~0.1 eV at ambient conditions. On the other hand, a huge interaction between spins and lattice vibrations was also observed in NaOsO3 where pressure or strain directly influences the OsO6 octahedra9. The anomalous spin-phonon behavior was linked to the extended 5d orbitals which relate to the magnetic structure through the Os–O–Os superexchange interactions. In this regard, pressure becomes a favorable tool to induce many new features to emerge, because it can substantially affect the Fermi surface reconstruction10,11 and, in turn, unpredictably vary the band gap. For this reason, we have initiated a combined experimental and theoretical study to reveal the electronic and structural properties of NaOsO3 under high pressure.
In general, for perovskites, the relative stability in different modifications can be estimated with a wide range of methods where the tendencies for plausible symmetry transformations can be predicted by considering possible octahedral distortions12,13,14,15. Hence, the orthorhombic distortion in NaOsO3 arises from the concerted rotation of the OsO6 octahedra in the a–c plane, coupled with a tilting about the b-axis. According to the mentioned theoretical sources, an orthorhombic configuration should be lowered to a monoclinic one if more distortion occurs. The sequence of structural transitions is predicted in theory as: cubic (\(Pm\bar 3m\)) → orthorhombic (\(Pnma\)) → monoclinic (\(P2_1{\mathrm{/c}}\)). Another indicator for possible high-pressure trends is the ratio of cation coordination polyhedra volume (VA/VB in ABO3) that combines both the the tilt angle and the deformation of the A and B-site polyhedra. An investigation on existing perovskite structures (~1300 perovskites) shows that the orthorhombic (\(Pnma\)) can reach a polyhedral volume ratio as low as 3.816. Among perovskites, there are very few materials reaching values of VA/VB < 4, which is a distortion factor and also an indicator for a perovskite to undergo the so-called ‘post-perovskite’ transition17.
In the orthorhombic \(Pnma\) arrangement NaOsO3 has a value of 4.6 for the VA/VB ratio15,16. Increasing pressure is known to stimulate the rotation of the BO6 octahedra in ABO3 perovskites, and therefore decreases the polyhedral volume ratio. Hence, the perovskite NaOsO3 at 16 GPa and 1135 K was found to stabilize in a post-perovskite form18. Strikingly, we discovered that, without increasing the temperature, the orthorhombic phase of NaOsO3 could transform into a polar perovskite phase with a space group of \(Pna2_1\), which violates the general trend of the perovskite oxides and has only been detected in PbRuO3 (\(Pbnm\) → \(Pbn2_1\))19 and LiOsO3 (\(R {\bar 3}c\) → \(R3c\))20 so far. The latter two materials are non-magnetic, while NaOsO3 has obvious magnetic properties2,3,4,5,6,7,8,9 and preserves the band gap during the transition with a slow reduction of the MIT towards lower temperatures (T < 410 K). In addition, compression of NaOsO3 manifests much more complicated emergent structural and electronic phenomena, which could be only characterized by using multiple techniques, such as electrical transport, Raman, synchrotron x-ray diffraction techniques (XRD), and first-principles calculations that are applied in this study.
Results
Electrical anomalies
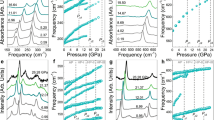
As already mentioned, the G-type long-range commensurate AFM order occurs at the same temperature as the continuous MIT. The neutron diffraction measurements confirmed that there is no symmetry change through the MIT at ambient pressure4,21. Hence, a purely electronic band gap opening mechanism was considered. The most fundamental property, resistivity, measured at ambient pressure indicated a very clear distinction between metallic behavior at T > 410 K and insulating behavior at T < 410 K3 (see the inset of Fig. 1b), while more detailed analysis indicates that there are actually three regions in the resistivity ρ(T) curve: metallic (T > 410 K), bad-metal (BM) (T = 30–410 K), and insulating (T < 30 K)7.
a Temperature dependence of the resistance at various pressures. The inset emphasizes the hysteresis evolution over pressure at T = 295 K. b TMIT vs. pressure. The inset for MIT observed at ambient pressure is taken from ref. 3. The inset demonstrating MIT at 32.5 GPa represents data from this work. The resistance at high pressure becomes low and TMIT is washed. The error bars represent the uncertainty in determining TMIT and P. c The electrical resistivity measurement during sample compression at fixed temperature of T = 295 K. The inset shows the actual set-up for the resistivity measurement between a pair of diamond anvils: four thin platinum probes attached to the sample, and the ruby sphere loaded for pressure determination.
The BM state was distinguished from the change of ρ taking place around 30 K, where the insulating indirect band gap closes and NaOsO3 starts to develop the Fermi surface characterized by several hole and electron pockets with a direct gap (pseudogap). The pseudogap continues to decrease with increasing temperature and eventually closes at TMIT. These changes are also observed in our high-pressure electrical transport measurements (see Fig. 1). Furthermore, the warming and cooling curves slightly deviate, forming a narrow thermal hysteresis loop below MIT (Fig. 1a). The hysteresis is progressively attenuated upon pressure but eventually disappears at about 18 GPa. Intriguingly, there is no hysteresis below 30 K, where the deep insulating state is developed. One more anomaly revealed under pressure emerges at around 200 K where the R(T) curve bends down. It is likely that this feature exists even at ambient pressure, because the resistivity in the BM regime does not show straight linear dependence on temperature (Supplementary Fig. 1) and, therefore, is naturally enhanced by pressure. As highlighted in the Arrhenius plot, this feature at 0.63 GPa manifests a kink which develops into the metallic state with increased pressure (see Fig. 2). The measurements at higher pressures clearly show that the metallic state unfolds most at 10.60 GPa and reenters the original electronic state at around 18.70 GPa, which is on the border of the structural transition. We refer to this anomaly as the BM–M–BM transition because of the following change: BM → M → BM. The origin of this transition is discussed in the theoretical modeling section.
In terms of the MIT, the pressure-dependent electrical transport measurements indicate that the metallic state extends to the lower temperatures very slowly (Fig. 1b). As one can observe, the TMIT scales almost linearly upon pressure. At around 32 GPa, the MIT becomes much broader, but can still be identified. Importantly, up to this pressure, NaOsO3 preserves the insulating ground state. It is known that nickelates such as PrNiO3 and NdNiO3 exhibit similar MITs from the paramagnetic metal to the AFM insulator that are electronically driven as well22. The suppression of the first-order MIT in PrNiO3 is very fast, within 0–1.3 GPa range, but ρ(T) curves manifest a highly broadened thermal hysteresis loop under pressure. In comparison, pressure-stimulated hysteretic properties in NaOsO3 are relatively small and likely to be hard to distinguish at ambient pressure. However, this questions if MIT is really the second-order type that was initially assigned3. On the other hand, this feature may emerge for various reasons such as the spin canting effect, inhomogeneity, or defects, and, therefore, could be addressed in detail in the future. Meanwhile, precise compression of NaOsO3 at a fixed temperature of T = 295 K revealed four anomalies of which none are attributable to the MIT (Fig. 1c). This underlines the uniqueness of this sample and discerns it from nickelates, which have a short track to the metallic state. The first anomaly in compression appears at a sufficiently low pressure ~1.7 GPa; the resistivity drops most sharply here. The second anomaly manifests at 9 GPa as deceleration in resistivity with increased pressure. The third, at 18.8 GPa, is related to the structural change, as explained in the next section. The last and fourth anomaly at 25.5 GPa indicates the limit where the resistivity value no longer decreases.
Structural transformation under high pressure
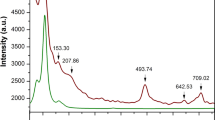
Although orthorhombic perovskite NaOsO3 (Space group Pnma, no. 62. Lattice parameters a = 5.38420(1) Å, b = 7.58038(1) Å, and c = 5.32817(1) Å) exhibits pronounced changes in its magnetic and electronic properties, the structure is reliably stable over the wide range of temperatures from 2 to 480 K2,3,4,5 and up to 16 GPa pressure investigated so far18. A clear transformation to the post-perovskite structure (Space group \(Cmcm\), no. 63. Lattice parameters a = 2.8321(3) Å, b = 10.6928(17) Å, and c = 7.3342(10) Å) was observed under very exceptional conditions of 16 GPa and 1135 K. The mentioned study on NaOsO3 also showed that pentavalent post-perovskite structure may be obtained even if all the criteria normally used to anticipate such transitions are not fulfilled18. Our pressure-dependent Raman measurements support the fact that the crystal symmetry does not change up to 16 GPa at room temperature and indicates that further pressure increase causes structural transformation to a different symmetry. Figure 3 shows the Raman spectra observed in the low-frequency range at different temperature and pressure conditions. Here, seven optical peaks are clearly visible at ambient conditions. The magnon excitations identified using resonant inelastic x-ray scattering (RIXS) can be observed in the Raman spectra in many cases as well. A peak at 400 cm−1 seen in Fig. 3a could represent a single-magnon excitation observed in the NaOsO3 RIXS experiments8,23. By reducing the temperature, we show that this peak exhibits three components α, β, and γ (see Fig. 3c). Here, β shows the most pronounced changes, but the intensity does not change much and, therefore, it can be assumed that these three components are regular Raman modes rather than the manifestation of a magnon. Overall, the optical data is in good agreement with the electrical transport measurements confirming four anomalies at similar pressures. Ambient crystal symmetry should be maintained up to 18 GPa, even though some of the weak modes disappear in the background during compression (see Fig. 3b, d). The phonons substantially rearrange and increase in number at 18 GPa, signaling the onset of a structural change. Then, at about 26 GPa, the continuous large-scale reduction in intensity is observed as the pressure increases. Finally, the Raman modes almost vanish at 35 GPa, indicating that sample is approaching a metallic state, that is the MIT. It should be noted that these observed changes are reversible when the sample is released to the ambient pressure.
a Raman spectrum at ambient pressure, and room temperature acquired for 120 s and five accumulations using a 488 nm wavelength. b Selected Raman spectra for the different high-pressure states of NaOsO3. The measuring time of 200 s were kept constant for all spectra. c Raman spectra at ambient pressure and different temperatures revealing three components α, β, and γ hidden within a broad peak at nearly 400 cm−1. Data acquired for 120 s and five accumulations using a 532 nm wavelength. d Pressure evolution of the phonon frequencies. Here the dashed lines indicate notable changes associated with the pressure-induced phenomena. The Raman mode marked as no. 8 is the weak mode, marked with an asterisk in b, and is possibly the reappearance of mode no. 3.
To determine the crystal symmetry in the new structure above 18 GPa, we performed synchrotron powder X-ray diffraction (see Fig. 4 and Supplementary Figs. 2–4). The new structure seems to fit well to the space group of \(Pna2_1\) (orthorhombic and non-centrosymmetric) which agrees with the Raman results. We notice the analogy of this rare transition with the one observed in PbRuO3 samples, whose high-pressure phase is claimed to have the most distorted octahedra in a perovskite structure19. The PbRuO3 demonstrated that applied pressure can substantially shorten A–B range and distort the octahedra thereby compacting ABO3 perovskite structure. The perovskite structure proves flexible through the A–B bonding and bypasses the collapse into the post-perovskite structure. Our discovered high-pressure structural transition for NaOsO3 also avoids a possible collapse into the post-perovskite structure and manifests more distorted octahedra in the polar perovskite phase. Besides, the polar phase exhibits bad metal characteristics for both PbRuO3 and NaOsO3. In addition, a non-polar to polar transition is also observed in metallic LiOsO320. The recent study shows that the transition temperature to the polar phase of metallic LiOsO3 can reach to room temperature at 16 GPa24. This structural transition is closely linked to the changes in the local bonding environment where Li ions form bonds with out-of-plane oxygen atoms forming the LiO6 octahedra. This reaffirms that pressure-induced octahedral deformations play a key role in the formation of the polar phase.
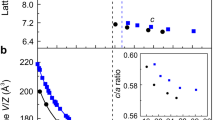
a Evolution of diffraction patterns over sample compression (strongest Bragg peaks are marked up to 18°). Here, the wavelength of the incident X-ray beam is 0.4133 Å. The shaded area around 18 GPa is the transition area where a change of the space group from centrosymmetric \(Pnma\) to non-centrosymmetric \(Pna2_1\) was observed. The detailed XRD profiles can be found in the Supplementary Figs. 2–4. b Pressure dependence of the unit-cell volume. Solid curves are the calculated third-order Birch–Murnaghan equation of states (EoS) fitted to the experimental data. The fitting was performed using EoSFit software45. c Pressure dependence of a/a0, b/b0, and c/c0 ratios. Here, a0 and c0 are the lattice constants at ambient pressure. Inset is the zoomed area for lattice parameter change at the smaller pressure.
A remark concerning the symmetry of the new structure above 18 GPa at room temperature is in place here. From our Raman results (Fig. 3), we are certain that NaOsO3 experiences a structural change above 18 GPa. When the pressure is increased, the Raman spectra in particular demonstrate the enhancement of the number of phonons and the pressure-induced-splitting of phonon mode (Fig. 3b). This is consistent with a shift in symmetry toward lower space groups. The reduction of the space group in the original orthorhombic crystal system is the most appropriate assertion, given that the changes in the diffraction patterns are only minor alterations from the new high-pressure phase. It should be noted that the space group change in the powder XRD measurements is subtle (Fig. 4a), because the patterns between \(Pnma\) and \(Pna2_1\) symmetries are in many cases not remarkably different19. The transition is very smooth giving a tiny volume contraction (<0.1%) as well as slight fracture in the lattice parameters (Fig. 4b, c). A Birch–Murnaghan third-order equation of state fitted to the volume versus pressure shows a bulk modulus increase from \(K_0 = 152.0\) GPa to \(K_0 = 200.0\) GPa for the \(Pnma\) and \(Pna2_1\) phases, respectively (see Fig. 4b). This increase is typical for such samples. For instance, the change of bulk modulus in PbRuO3 is similar: \(K_0 = 189.8\) GPa → \(K_0 = 205.1\) GPa19.
Discussion
Figure 5 shows the phonon dispersion curves for NaOsO3 in the \(Pnma\) phase at ambient pressure. No imaginary frequencies are obtained, which indicates the stability of the structure at the given condition. It is worth noting that the inclusion of the G-AFM ordering is needed to obtain stable phonon data, showing the importance of the spin ordering in stabilizing the structure. The phonon bands are clearly divided into two groups: the lower frequency (0–52 meV) and higher frequency (75–97 meV). The results of partial phonon density of states (DOS) indicate that all atoms contribute to the lattice vibrations at lower frequency range, while vibrations of O atoms are dominant at higher frequency range (Fig. 5). Symmetry-mode analysis of the atomic displacements predicts 24 Raman active modes in NaOsO3 at the Brillouin zone center25: 7Ag + 5B1g + 7B2g + 5B3g. All these modes were observed in our DFT calculations as well. Table 1 represents a comparison of the frequencies of the calculated and observed Raman-active modes, showing overall good agreement between experiment and simulation, in particular at low temperature.
The structural evolution under pressure is more problematic. The pressure evolution of the simulated XRD spectra agrees very well with the measured XRD spectra [compare Supplementary Fig. 2a, d], but, in contrast to the Raman results, our DFT calculations do not discern any marked symmetry change even up to high pressure (90 GPa) as evinced by the pressure–volume curves shown in Supplementary Fig. 5. The phase with initial \(Pna2_1\) symmetry is found to be unstable and finally reduces to the \(Pnma\) symmetry after structural relaxations (see Supplementary Fig. 5). The apparent disagreement might originate from thermal effects, not considered in our DFT analysis. Another possible reason for the experimentally observed structure change above 18 GPa could be the existence of a certain degree of anisotropy in the applied pressure. However, the nonpolar–polar phase transition is normally disfavored by temperature. On the other hand, the LiOsO3 case unambiguously demonstrates the enhanced stability of the polar phase under high-pressure20. Thus, in contrast to conventional ferroelectrics, pressure can give rise to a polar phase or enhance the existing transition temperature in these systems.
Moving to the electronic properties, Fig. 6 shows our DFT calculated band gap and magnetic moment evolution as a function of pressure. Upon pressure, the indirect gap is closed at around 20 GPa, while the direct gap survives even up to very high pressure, indicating the insulator to BM transition upon pressure. As expected, the magnetic moment is suppressed by the pressure, but the suppression rate is relatively slow and the system remains magnetically ordered even at ~40 GPa. The detailed evolution of the band structure as a function of pressure is shown in Fig. 7.
a Reduction of the indirect and direct band gaps with pressure increase. The indirect band gap closes at around 20 GPa, terminating the insulating state and giving rise to BM state while the direct band gap manifests nonlinear curvature against pressure and survives beyond 40 GPa, retaining the BM state. b The magnetic moment of the Os ion indicating its gradual suppression along with applied pressure.
Figure 8 is a combined temperature–pressure electronic and structural phase diagram of NaOsO3 based on our experimental and theoretical results, which shows the different types of transitions occurring in the system when pressure and temperature are applied: insulator-to-bad metal, BM-to-M, the anomalous metal island in the BM region, and the subtle non-polar to polar structural transition. At low temperature the system remains insulating up to a certain critical pressure (~20 GPa in DFT) and then transforms into a bad metal due to the closing of the indirect gap. In this pressure range the valence and conduction bands are still separated by a direct gap (Figs. 6 and 7). This direct gap closes at very large pressure (>90 GPa in DFT), indicating that the evolution of the electronic properties upon pressure share similarities with the temperature-induced band gap closing process through a magnetically itinerant Lifshitz mechanism7.
The squares with error bars indicate the experimental measurements. The error bars represent the s.d. estimated by taking into account instrumental resolution. Green squares denote the M–BM transition (formerly considered as a metal-to-insulator transition or MIT) while the blue squares refer to the BM–M–BM transition. The experimentally observed Pnma to \(Pna2_1\) phase transition at finite temperature is highlighted in white. The pattern-filled area at low temperatures represents the theoretically validated insulating state of the sample.
As the temperature increases, a metal island emerges in the BM region under increasing pressure. Considering that the pressure-enhanced structural distortion in NaOsO3 favors an insulating state26, we speculate that depending on the distortion track, re-entrance transitions are possible and we believe that the unique existence of the BM state enables such manifestations to take place. On the other hand, the resistance might contain specific anisotropic properties that are not considered in this work. Finally, above a critical temperature TMIT NaOsO3 becomes metallic. TMIT is less affected by pressure, and the experimentally traced rate of TMIT decrease is quite slow ~0.36 GPa/K. We note that such sluggish process of metallization during compression among 5d systems (especially iridates) is common with the presence of strong SOC, which usually sustains a rigid band gap27,28,29,30,31. In NaOsO3 with the t32g electronic configuration, the SOC formally should not play a dominant role because the resulting Leff = 0 state yields a vanishing orbital moment, yet it is found to be responsible for the weakening of the electron–electron correlation7, magnetic anisotropy, and large spin wave gap formation32. As the MIT is considered to be the SOC-driven for the most part, its evolution during compression is likely governed by the same source. In this aspect, NaOsO3 is akin to iridates. However, a high degree of spin-phonon-electronic coupling was proclaimed as a dominant force in this compound9, and, therefore, some features manifest differently. Our combined experimental–theoretical study proves a close spin-phonon-electronic interaction in that all anomalies, including the MIT, are captured in both the electronic and optical spectra and exhibit relatively good accuracy. We found that pressure and temperature both induce a MIT accompanied by the formation of an intermediate BM regime and by the progressive decrease of the local magnetic moment. This process can be assimilated to an itinerant Lifshitz MIT associated with magnetic fluctuations. This scenario is apparently different from the MIT induced by electron doping where NaOsO3 undergoes a straightforward transition to a metallic state even at a moderately low doping level33, hereby highlighting the complex nature of this compound.
In summary, a comprehensive temperature-dependent electrical transport, Raman scattering, synchrotron XRD, and DFT study has been carried out to understand the effect of external pressure on perovskite NaOsO3. A sluggish temperature-dependent MIT was followed up to 35 GPa where TMIT = 410 K was suppressed only to a near room temperature, reiterating the common behavior of iridium-based insulators that are known to have strong SOC and own narrow band gaps in Mott, Mott–Hubbard, or Slater paradigms. However, NaOsO3 manifests a magnetically itinerant Lifshitz-type transition regardless of external conditions and possesses a high degree of spin-phonon-electronic coupling. The optical and electrical spectra revealed clear anomalies at 1.7, 9, 18, and 25.5 GPa. Furthermore, during compression, the BM regime manifested hysteretic resistance anomalies and a BM–M–BM transition at ~200 K during compression. The later anomalies are canceled by the structural change that takes place at 18 GPa from a centrosymmetric \(Pnma\) to a non-centrosymmetric (polar) \(Pna2_1\) phase. The high-pressure phase has more distorted octahedra and is unexpected according to commonly used theoretical prediction models. Thus, NaOsO3 is in line with PbRuO3 and LiOsO3, where pressure favors the polar phase19,20,24. However, magnetism is absent in the latter examples and, therefore, NaOsO3 might be an example that can acquire the unique shape of a polar-magnetic metal.
Methods
Sample synthesis
The starting materials Na2O2 (97%, Sigma-Aldrich) and OsO2 (laboratory-made from 99.95% Os, Nanjing Dongrui Platinum Co., Ltd. by heating at 400 °C in a few % oxygen in Argon balance) were sealed in a platinum capsule at a molar ratio of Na:Os = 2:1 with 0.5 mol of NaCl (99.99%, Rare Metallic Co.) per f.u. The procedure was conducted in an Ar-filled glove box. The capsule was heated at 1500 °C for 60 min under a pressure of 6 GPa in a multi-anvil-type apparatus (CTF-MA1500P, C&T Factory Co., Ltd, Japan). Then, the pressure was gradually released. The product was rinsed with water in an ultrasonic bath for a few minutes several times, separated mechanically, and then tested to confirm there was no damage by single-crystal XRD and powder XRD. Small, ≤0.5 mm-sized NaOsO3 crystals with a silver-purple tint were obtained together with black crystals of the hexavalent Na2OsO42,34 in the same batch.
Optical Raman measurements
A Mao-type symmetric diamond anvil cell (DAC) with 400 μm culet-sized anvils was used for the Raman experiments. A stainless-steel gasket was precompressed to 35 μm thickness and a hole of 150 μm was drilled to load the sample, a ruby sphere for pressure determination35, and neon gas to serve as a pressure-transmitting medium36. Initially, we made several attempts to use a methanol–ethanol mixture as a pressure-transmitting medium, but the results were unreliable because the pressure medium reacted with the sample when pressure was applied. The high-pressure Raman spectra were measured on a Renishaw inVia spectrometer with a 488 nm laser wavelength, which gave the best signal. The data collection time was 200 s and a laser power of 8 mW was maintained for each spectrum. The sample was placed in the cryostat under vacuum conditions for the temperature-dependent data at ambient pressure. In this case, Raman spectra were measured on a MonoVista CRS+ system with a 532 nm laser.
Synchrotron x-ray diffraction measurements
The in situ high-pressure powder XRD measurements were carried out in an angle-dispersive mode at the beamline 16-BM-D of the Advanced Photon Source (APS), Argonne National Laboratory. The same type of DAC with the loaded ruby and neon pressure medium was used as the Raman experiments. The experiments were performed two times where the incident monochromatic x-ray beam had the wavelengths of λ = 0.4133 Å and λ = 0.3100 Å. Each time, the wavelength of the x-ray was calibrated using a CeO2 standard. Diffraction patterns were recorded on a MAR345 image plate and then integrated by using DIOPTAS software37. Indexing and Rietveld refinements were carried out in EXPO201438.
Electrical measurements
The electronic transport properties under high pressure and low temperature were investigated via the four-probe electrical conductivity method in a DAC made of CuBe alloy. Pressure was generated by a pair of diamonds with a 400 μm diameter culet. A gasket made of stainless steel was pressed and a hole in the center of the gasket was drilled to the diameter of the diamond culet. A cubic boron nitride (c-BN)-epoxy insulation layer was prepared to protect the electrode leads from the metallic gasket. Finally, a hole of 280 μm diameter was drilled in the center of the c-BN gasket. NaCl powder was used as the pressure-transmitting medium. Four platinum strips were arranged to contact the sample in the chamber. The pressure-dependent resistance measurements were performed using the laboratory designed electrical transport system where a Keithley 6221 current source, 2182A nanovoltmeter, and 7001 switch device were used as the current supply, voltmeter, and voltage/current switcher, respectively. The experiments at different pressure–temperature conditions were performed using the Quantum Design Physical Properties Measurement System. The pressure was measured via the ruby fluorescence method at room temperature, before and after cooling.
First-principles calculations
The computational study was based on the density functional theory (DFT) as implemented in the VASP software39. We used the projector-augmented wave method (PAW)40 and the revised Perdew–Burke–Ernzerhof (PBEsol) functional41, which is known to give a better description of densely packed structures than the standard PBE functional42. NaOsO3 with \(Pnma\) symmetry with a long b-axis was employed3. A comparison with \(Pna2_1\) symmetry with a long c-axis was made to inspect the structural transitions. A fully relativistic setup was used with the inclusion of spin–orbit coupling (SOC) in the framework of the DFT + U43 (Ueff = 1.0 eV) and G-type AFM order. For the energetics and electronic structure calculations, the plane-wave cutoff for the orbitals was set to 600 eV and Brillouin zone sampling of 10 × 6 × 10 (10 × 10 × 6) k-point grid according to Monkhorst–Pack scheme was used for the \(Pnma\) (\(Pna2_1\)) phase. For the phonon calculation, we used a 2 × 2 × 2 supercell with 5 × 3 × 5 k-point mesh considering AFM ordering (SOC not included) using PHONOPY software44.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Sleight, A. W. New ternary oxides of Re, Os, Ir and Pt with cubic crystal structures. Mater. Res. Bull. 9, 1177–1184 (1974).
Yamaura, K. Short review of high-pressure crystal growth and magnetic and electrical properties of solid-state osmium oxides. J. Solid State Chem. 236, 45–54 (2016).
Shi, Y. G. et al. Continuous metal–insulator transition of the antiferromagnetic perovskite NaOsO3. Phys. Rev. B 80, 161104(R) (2009).
Calder, S. et al. Magnetically driven metal–insulator transition in NaOsO3. Phys. Rev. Lett. 108, 257209 (2012).
Vecchio, I. L. et al. Infrared evidence of a Slater metal–insulator transition in NaOsO3. Sci. Rep. 3, 2990 (2013).
Middey, S., Debnath, S., Mahadevan, P. & Sarma, D. D. NaOsO3: a high Neel temperature 5d oxide. Phys. Rev. B 89, 134416 (2014).
Kim, B. et al. Lifshitz transition driven by spin fluctuations and spin–orbit renormalization in NaOsO3. Phys. Rev. B 94, 241113(R) (2016).
Vale, J. G. et al. Evolution of the magnetic excitations in NaOsO3 through its metal-Insulator transition. Phys. Rev. Lett. 120, 227203 (2018).
Calder, S. et al. Enhanced spin-phonon-electronic coupling in a 5d oxide. Nat. Commun. 6, 8916 (2015).
Stillwell, R. L. et al. Pressure-driven Fermi surface reconstruction of chromium. Phys. Rev. B 88, 125119 (2013).
Terashima, T. et al. Fermi surface reconstruction in FeSe under high pressure. Phys. Rev. B 93, 094505 (2016).
Howard, C. J. & Stokes, H. T. Group-theoretical analysis of octahedral tilting in perovskites. Acta Crystallogr. B54, 782–789 (1998).
Lufaso, M. W. & Woodward, P. M. Prediction of the crystal structures of perovskites using the software program SPuDS. Acta Crystallogr. B57, 725–738 (2001).
Balachandran, P. V. & Rondinelli, J. M. Interplay of octahedral rotations and breathing distortions in charge-ordering perovskite oxides. Phys. Rev. B 88, 054101 (2013).
Avdeev, M., Caspi, E. N. & Yakovlev, S. On the polyhedral volume ratios VA/VB in perovskites ABX3. Acta Crystallogr. B63, 363–372 (2007).
Martin, C. D. & Parise, J. B. Structure constraints and instability leading to the post-perovskite phase transition of MgSiO3. Earth Planet. Sci. Lett. 265, 630–640 (2008).
Murakami, M., Hirose, K., Kawamura, K., Sata, N. & Ohishi, Y. Post-perovskite phase transition in MgSiO3. Science 304, 855–858 (2004).
Crichton, W. A., Yusenko, K. V., Riva, S., Mazzali, F. & Margadonna, S. An alternative route to pentavalent postperovskite. Inorg. Chem. 55, 5738–5740 (2016).
Cheng, J.-G. et al. Anomalous perovskite PbRuO3 stabilized under high pressure. PNAS 110, 20003–20007 (2013).
Paredes Aulestia, E. I. et al. Pressure-induced enhancement of non-polar to polar transition temperature in metallic LiOsO3. Appl. Phys. Lett. 113, 012902 (2018).
Gurung, N. et al. Direct observation of electron density reconstruction at the metal–insulator transition in NaOsO3. Phys. Rev. B 98, 115116 (2018).
Zhou, J.-S., Goodenough, J. B. & Dabrowski, B. Pressure-induced non-Fermi-liquid behavior of PrNiO3. Phys. Rev. Lett. 94, 226602 (2005).
Vale, J. G. et al. Crossover from itinerant to localized magnetic excitations through the metal–insulator transition in NaOsO3. Phys. Rev. B 97, 184429 (2018).
Gao, J.-J., Fu, S.-Y., Yamaura, K., Lin, J. F. & Zhou, J.-S. Room-temperature polar metal stabilized under high pressure. Phys. Rev. B 101, 220101(R) (2020).
Kroumova, E. et al. Bilbao crystallographic server: useful databases and tools for phase-transition studies. Phase Trans. 76, 155–170 (2003).
Mohapatra, S., Bhandari, C., Satpathy, S. & Singh, A. Effect of structural distortion on the electronic band structure of NaOsO3 studied within density functional theory and a three-orbital model. Phys. Rev. B 97, 155154 (2018).
Chen, C. et al. Persistent insulating state at megabar pressures in strongly spin–orbit coupled Sr2IrO4. Phys. Rev. B 101, 144102 (2020).
Zhang, J. et al. Lattice frustration in spin–orbit Mott insulator Sr3Ir2O7 at high pressure. npj Quantum Mater. 4, 23 (2019).
Cao, G. & Schlottmann, P. The challenge of spin–orbit-tuned ground states in iridates: a key issues review. Rep. Prog. Phys. 81, 042502 (2018).
Samanta, K., Ardito, F. M., Souza-Neto, N. M. & Granado, E. First-order structural transition and pressure-induced lattice/phonon anomalies in Sr2IrO4. Phys. Rev. B 98, 094101 (2018).
Kim, S.-W. et al. Nature of the insulating ground state of the 5d postperovskite CaIrO3. Phys. Rev. Lett. 115, 096401 (2015).
Singh, A., Mohapatra, S., Bhandari, C. & Satpathy, S. Spin–orbit coupling induced magnetic anisotropy and large spin wave gap in NaOsO3. J. Phys. Commun. 2, 115016 (2018).
Dobrovits, S. et al. Doping-induced insulator–metal transition in the Lifshitz magnetic insulator NaOsO3. J. Phys.: Condens. Matter 31, 244002 (2019).
Sereika, R. et al. Anomalous behavior of the quasi-one-dimensional quantum material Na2OsO4 at high pressure. Mater. Today Phys. 8, 18–24 (2019).
Mao, H. K., Xu, J. & Bell, P. M. Calibration of the ruby pressure gauge to 800 kbar under quasi-hydrostatic conditions. J. Geophys. Res. 91, 4673–4676 (1986).
Rivers, M. et al. The COMPRES/GSECARS gas-loading system for diamond anvil cells at the Advanced Photon Source. High Press. Res. 28, 273–292 (2008).
Prescher, C. & Prakapenka, V. B. DIOPTAS: a program for reduction of twodimensional X-ray diffraction data and data exploration. High. Press. Res. 35, 223–230 (2015).
Altomare, A. et al. EXPO software for solving crystal structures by powder diffraction data: methods and application. Appl. Crystallogr. 46, 1231–1235 (2013).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Perdew, J. et al. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 100, 136406 (2008).
Hinuma, Y., Hayashi, H., Kumagai, Y., Tanaka, I. & Oba, F. Comparison of approximations in density functional theory calculations: energetics and structure of binary oxides. Phys. Rev. B 96, 094102 (2017).
Dudarev, S. L., Botton, G. A., Savrasov, S. Y., Humphreys, C. J. & Sutton, A. P. Electron-energy-loss spectra and the structural stability of nickel oxide: an LSDA+U study. Phys. Rev. B 57, 1505–1509 (1998).
Togo, A., Oba, F. & Tanaka, I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 78, 134106 (2008).
Angel, R. J., Gonzalez-Platas, J. & Alvaro, M. EosFit7c and a Fortran module (library) for equation of state calculations. Z. Kristallogr. - Crystallogr. Mater. 209, 405–419 (2014).
Acknowledgements
Portions of this work were performed at HPCAT (Sector 16) of Advanced Photon Source (APS), Argonne National Laboratory. HPCAT operations are supported by DOE-NNSA’s Office of Experimental Sciences. The APS is a DOE Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. Y.D and H.-k.M. acknowledges the support from National Key Research and Development Program of China 2018YFA0305703, Science Challenge Project No. TZ2016001 and The National Natural Science Foundation of China (NSFC): U1930401, 11874075. S.K. acknowledges support from the National Research Foundation of Korea (NRFK) (No. 2019R1F1A1052026). B.K. acknowledges support from the NRFK (No. 2018R1D1A1A02086051) and KISTI supercomputing center (Project No. KSC-2019-CRE-0231). P.L. and C.F. acknowledge support from the Austrian Science Fund (FWF). The computational results presented have been achieved in part using the Vienna Scientific Cluster (VSC). The work in Japan was supported in part by a research grant (#40-37) from Nippon Sheet Glass Foundation for Materials Science and Engineering, and research funding from Innovative Science and Technology Initiative for Security (Grant Number JPJ004596), ATLA, Japan.
Author information
Authors and Affiliations
Contributions
R.S. measured the XRD, Raman spectra, and electrical transport, analyzed the data, and wrote the article. K.Y. synthesized the samples and assured their quality by measuring laboratory XRD at ambient conditions. C.P. contributed technically during high-pressure synchrotron XRD experiments at Sector 16-BM-D, APS, USA. J.Z. and B.C. assisted for the XRD measurements. P.L., B.K, and C.F. computed the electronic and magnetic properties. S.K. performed the phonon calculations. Y.D. and H-k.M. supervised the project. All the authors discussed the data and commented on the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sereika, R., Liu, P., Kim, B. et al. Aberrant electronic and structural alterations in pressure tuned perovskite NaOsO3. npj Quantum Mater. 5, 66 (2020). https://doi.org/10.1038/s41535-020-00269-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-020-00269-3