Abstract
Quantum Monte Carlo (QMC) simulations of correlated electron systems provide unbiased information about system behavior at a quantum critical point (QCP) and can verify or disprove the existing theories of non-Fermi liquid (NFL) behavior at a QCP. However, simulations are carried out at a finite temperature, where quantum critical features are masked by finite-temperature effects. Here, we present a theoretical framework within which it is possible to separate thermal and quantum effects and extract the information about NFL physics at T = 0. We demonstrate our method for a specific example of 2D fermions near an Ising ferromagnetic QCP. We show that one can extract from QMC data the zero-temperature form of fermionic self-energy Σ(ω) even though the leading contribution to the self-energy comes from thermal effects. We find that the frequency dependence of Σ(ω) agrees well with the analytic form obtained within the Eliashberg theory of dynamical quantum criticality, and obeys ω2/3 scaling at low frequencies. Our results open up an avenue for QMC studies of quantum critical metals.
Similar content being viewed by others
Introduction
Understanding non-Fermi liquid (NFL) behavior near a metallic quantum critical point (QCP) remains one of the most ambitious goals of the studies of interacting electrons. Examples of systems evincing metallic quantum criticality include fermions in spatial dimensions D ≤ 3 at the verge of either spin density-wave, charge density-wave, or nematic-order, 2D fermions at a half-filled Landau level, quarks at the verge of an instability to color superconductivity, and several Sachdev–Ye–Kitaev (SYK)-type models with either electron–electron or electron–phonon interaction1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43. At a QCP, fluctuations of the corresponding bosonic order parameter become soft. The fermion–fermion interaction, mediated by these soft fluctuations, yields a fermionic self-energy Σ(ω) ∝ ∣ω∣a with a < 1. The real and imaginary parts of this self-energy are comparable in magnitude and both are larger than ω at low frequencies. This implies that the damping of quasiparticles remains comparable to their energy even infinitesimally close to the Fermi surface, in variance with the central paradigm of Landau’s theory of a Fermi liquid (FL). Studies of NFL became the mainstream of research on correlated electrons after a series of discoveries of high-temperature superconductors, which display unconventional metallic properties in the normal state15,24,44,45. In most of these materials, superconductivity borders other ordered phases with either spin or charge order. There are also multiple overlaps between the behavior of fermions at a QCP and high-energy physics and string theory44,46.
In recent years, several analytical approaches have been developed to study NFL behavior at a QCP. These approaches are based on effective fermion–boson models, in which soft fluctuations of a specific order parameter serve as the source of NFL behavior. The long-standing goal of these studies is to find the functional form of Σ(ω) at a QCP and extract the exponent a < 1 from its small ω behavior. One-loop calculations show that Σ(ω) does become singular at a QCP, for example, in 2D at a transition to nematic or Ising ferromagnetic (FM) order with momentum Q = 0, it scales at the lowest frequencies as ω2/3 (a = 2/3). Whether this behavior extends beyond one loop is a more tricky issue. Power counting arguments indicate that higher-order terms in the loop expansion for the self-energy reproduce the ω2/3 scaling form7. However, detailed calculations reveal that additional \({(\mathrm{log}\,\omega )}^{n}\) factors appear, and that n increases with the loop order25,27,29,31,32,35. Such logarithms imply that at low enough frequencies, \(\omega \ll {\omega }_{{\rm{mod}}}\), Σ(ω) gets modified from its one-loop form. As a further complication, the same interaction that gives rise to NFL behavior also gives rise to superconductivity at a non-zero Tc, so normal state self-energy holds only at ω > Tc. It is difficult to extract from analytical studies whether \({\omega }_{{\rm{mod}}}\) is larger or smaller than Tc, that is, whether the modification of Σ(ω) from higher-order processes is relevant for a metal, which displays superconductivity near a QCP, or only for a putative normal state at T = 0. This uncertainty has triggered an interest in independent numerical studies of the behavior of fermions at a metallic QCP.
Numerical methods for itinerant fermions near a QCP have witnessed great progress in recent years, and at present one can analyze quantum criticality via reliable large-scale numerical simulations47,48. In particular, it has been found that designer models of fermion–boson models offer a pathway to access fermionic QCPs while avoiding the notorious sign problem in large-scale quantum Monte Carlo (QMC) simulations. Such models have been implemented in several simulations, studying nematic49,50, ferromagnetic51, antiferromagnetic52,53,54,55,56, gauge field57,58,59,60,61,62, and Yukawa-SYK-type41 QCPs. The focusing on a particular soft boson offers an unbiased numerical test for either a Q = 0 or a finite Q analytical theory of metallic quantum criticality. The mutual inspiration and dialog between numerical and theoretical communities, arising from these studies, has also stimulated progress along the numerical front (SLMC63 and EMUS64 are successful examples of this).
Sign-problem-free QMC has its own limitations as well. To avoid superconductivity and finite size effects, simulations are done at a finite T, which is not the smallest energy scale in the system, such that on a Matsubara axis the fermionic self-energy Σ(ωn) is a function of a discrete Matsubara frequency ωn = (2n + 1)πT. (The self-energy also has a momentum dependence Σ = Σ(ωn, k), but here and henceforth we suppress this notation for clarity, except where needed.) At non-zero T, it can generally be expressed as Σ(ωn) = ΣT(ωn) + ΣQ(ωn), where the “thermal” part ΣT(ωn) is the contribution from static thermal fluctuations and the “quantum” part ΣQ(ωn) is the contribution from dynamical bosonic fluctuations. At T = 0, ωn is a continuous variable, ΣT = 0, and Σ = ΣQ(ωn) is an NFL self-energy at a QCP. However, at a finite T, the self-energy differs from its T = 0 form, and the presence of ΣT(ωn) can mask the behavior associated with ΣQ(ωn). Besides, at a finite T, ΣQ(ωn) also generally differs from its T = 0 form. We note that in the Yukawa-SYK model these finite-temperature effects have recently been analyzed using an emergent conformal (reparametrization) symmetry of the low-energy theory, which automatically incorporates thermal and quantum effects41. However, the treatment of the present critial FS model without conformal symmetry requires separate analyses of ΣQ and ΣT.
The main purpose of this paper is to provide the method to disentangle ΣT and ΣQ from QMC data for the self-energy. Our approach is based on three observations:
-
First, to study QC behavior one should avoid the effect of fluctuations from fermions with energies of order of the bandwidth, such as would lead to, or example, Mott physics. For this, the effective femion–boson coupling (labeled \(\bar{g}\) in the text) should be much smaller than the bandwidth W. In systems with a large Fermi surface, W is comparable to the Fermi energy, so the necessary condition is \(\bar{g}\ll {E}_{{\rm{F}}}\).
-
Second, at small \(\bar{g}\), there is a wide range of frequencies ωn ≪ EF, for which ωn is much larger than Σ(ωn). In this range, the thermal self-energy has a simple form, valid for finite temperatures and frequencies ωn ≫ Σ, ΣT(ωn) ≈ α(T)/ωn up to logarithmic corrections, that is, ωnΣT(ωn) = α(T) is approximately independent of ωn.
-
Third, in the same range, ΣQ(ωn) still has NFL form and is well approximated by the one-loop, T = 0, expression, modulo that ωn is discrete.
By considering the above points, one arrives at the following conclusion: if a QMC study is performed at \(\bar{g}\ll {E}_{{\rm{F}}}\) and provides data for Σ(ωn) for a substantial number of Matsubara points in the range ωn ≫ Σ(ωn), it is possible to extract ΣQ from the data by the following simple procedure. First, extract (the approximately constant) α(T) from the data by fitting ωnΣ(ωn) by a continuous function of frequency and extrapolating to zero frequency, where it is equal to α(T) because ωnΣQ(ωn) extrapolates to zero. Once αT is known, subtract ΣT(ωn) = α(T)/ωn from the full Σ(ωn) and obtain ΣQ(ωn), which, as we said, should have the same form as T = 0 self-energy. For a more accurate separation of ΣQ from ΣT include the slow frequency dependence of α(T) in the fitting procedure, which is still quite straightforward to do, as we will show later.
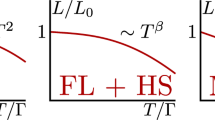
We apply our strategy to a metal near an Ising FM-QCP. We show the schematic phase diagram in Fig. 1a. It contains regions of a paramagnetic metal (PM) and an ordered Ising FM, separated by a QCP. Right above the QCP, there is a region of small T, where the system displays truly NFL behavior, that is, Σ(ωn) is non-analytic and larger than ωn. At higher T, Σ(ωn) becomes smaller than ωn, yet the self-energy still has non-FL form, and, by our reasoning, its quantum part, ΣQ(ωn) should be almost the same as at T = 0. In Fig. 1b we show the full self-energy, obtained in QMC simulation, and in Fig. 1c we show ΣQ(ωn), extracted using the approximate procedure outlined above. The black line in Fig. 1c is the analytical one-loop result for the self-energy at a QCP at T = 0. We see that the data for all ωn nicely fall onto this curve. At small ωn, the analytic one-loop self-energy behaves as \({\omega }_{n}^{2/3}\), and the fact that QMC data fall onto the T = 0 curve implies that the QMC data are consistent with \({\omega }_{n}^{2/3}\) scaling at the lowest ωn at a QCP. The deviation from \({\omega }_{n}^{2/3}\) scaling in the analytical formula (Eq. (16) in the text) is due to two reasons. First, for the model used for QMC simulations, the bosonic propagator D(q, Ω) contains a regular Ω2 term along with the Landau damping term, Ω/q. When this term becomes relevant, ΣQ(ωn) tends to saturate. Second, even when the Landau damping term dominates, the ω2/3 form is the low-frequency limit of a more complicated function \({\Sigma }_{{\rm{Q}}}({\omega }_{n})\propto {\omega }_{n}^{2/3}{\mathcal{U}}\left({\omega }_{n}/{\omega }_{b}\right)\), and ω2/3 behavior holds only when ωn ≪ ωb, that is, \({\mathcal{U}}(z)\approx {\mathcal{U}}(0)\). The crossover frequency \({\omega }_{{b}} \sim {(\bar{g}{E}_{{\rm{F}}})}^{1/2}\) (see Eq. (12) below). In our simulations, this ωb is much larger than the upper boundary of NFL behavior, \({\omega }_{{\rm{F}}} \sim {\bar{g}}^{2}/{E}_{{\rm{F}}}\), but is still much smaller than EF. Accordingly, most of our ωn fall into ωn > ωb, where ΣQ(ωn) differs from \({\omega }_{n}^{2/3}\). We emphasize that ΣQ(ωn) has an NFL form regardless of the ratio ωn/ωb. Figure 2 presents a summary of the relevant energy scales in our QMC study.
a Schematic phase diagram of an FM (2 + 1)D QCP, adapted from ref. 51. b Fermionic self-energy at an FM (2 + 1)D QCP, calculated by QMC simulation, adapted from ref. 51. Here, we focus on the point on the Fermi surface with Fermi wavevector along the x-direction. The QMC self-energy appears to have a leading term of the form 1/ωn. c Quantum part of fermionic self-energy at an FM (2 + 1)D QCP. The black dashed line shows the theoretical prediction of the zero-temperature Fermi self-energy, while the red dashed line marks the low-frequency asymptotic form. We emphasize that the theory is parameter free, and all system parameters, for example, Fermi velocities, are determined separately from the model or QMC measurement.
It is instructive to compare our results with recent analysis of QMC data for similar models. Reference65 demonstrated that a rather flat dispersion of Σ(ωn), obtained in QMC simulations, is reasonably well reproduced by Σ(ωn) = ΣT(ωn) + ΣQ(ωn), where both are computed analytically within a metallic QC theory. For that study, a larger coupling \(\bar{g} \sim {E}_{{\rm{F}}}\) was used to increase the magnitude of the self-energy. The discrepancy between the analytic and QMC self-energies in ref. 65 was ~20%. This was small enough to see that analytic and QMC self-energies have similar dispersion, but still too high to reliably extract ΣQ(ωn) from the QMC data. For the current study, \(\bar{g}\) is smaller, and typical Σ(ωn)/ωn is roughly five times smaller than in that work. In this situation, we argue that the QC form of ΣQ(ωn) can be extracted from the data.
The structure of the paper is the following. In section “The lattice model, phase diagram and QMC self-energy”, we describe the lattice model for which the QMC simulations have been performed, and present the numerical results for the self-energy. In section “Analytic self-energy at Ising FM-QCP”, we present the analytical results for the self-energy within the self-consistent one-loop analysis. In section “Analysis of QMC data”, we extract ΣQ(ωn) from QMC data and show that for all n > 0 it falls onto the analytic, T = 0 form of ΣQ(ωn). In section “Discussion”, we summarize the results and discuss the implication of this work to other QC cases studied in QMC simulations. We argue that the computational scheme that we proposed can be used as a generic method to extract NFL self-energy at a QCP and can be further extended to study more subtle effects, for example, the flow of the dynamical exponent z.
Results
The lattice model, phase diagram, and QMC self-energy
As shown in Fig. 3, we consider a model describing Ising FM fluctuations coupled to a Fermi surface51. The model is implemented on a square lattice with Hamiltonian \(\hat{H}={\hat{H}}_{{\rm{f}}}+{\hat{H}}_{{\rm{s}}}+{\hat{H}}_{{\rm{sf}}}\) and each part reads
where \({\hat{H}}_{{\rm{f}}}\) describes two layers (or orbitals, λ = 1, 2) of spinful (σ = ↑, ↓) fermions with nearest-neighbor hopping on a square lattice, and the chemical potential μ tunes the size of bare Fermi surface. The bare fermion dispersion dictated by \({\hat{H}}_{{\rm{f}}}\) is \(\epsilon ({\bf{k}})=-2t(\cos ({k}_{x})+\cos ({k}_{y}))-\mu\) and the bandwidth is W = 8t. \({\hat{H}}_{{\rm{s}}}\) represents a transverse field Ising model on the same lattice, where by tuning T and h/J an Ising FM to PM transition can be obtained. The onsite coupling term \({\hat{H}}_{{\rm{sf}}}\) between the fermions and Ising spins mediates a fermion–fermion interaction, establishing a metallic system with ferromagnetic fluctuations. We present the schematic phase diagram in Fig. 1a. In the analysis that follows, we focus on the model parameters {t = 1, μ = − 0.5t, J = 1, ξ/t = 1}, for which we find an FM-QCP at hc/J ≈ 3.270(6). The parameters associated with the fermiology for these parameters are listed in Table 1.
Adapted from ref. 51.
As shown in ref. 51, our model gives rise to an FM-QCP. However, the bare numerical fermionic self-energy data from QCP, as shown in Fig. 1b, shows a behavior distinctively different from the expected NFL, \(\Sigma ({\omega }_{n})\propto {\omega }_{n}^{2/3}\). At low frequency, the self-energy shows an unusual upturn instead of going to zero. Such a upturn in the imaginary part of fermionic self-energy, in the usual numeric setting, implies a gap opening on the Fermi surface. However, our data of the fermionic Green’s function does not show a well-formed gap on the FS. Similar behavior of the numerical NFL self-energies has also been observed in other cases, including nematic and AFM-QCPs49,53. As discussed in the “Introduction”, the rest of this paper is devoted to an analysis of the self-energy data in Fig. 1b, and to understand how to disentangle the thermal and quantum parts of the self-energy, as shown in Fig. 1c.
Analytic self-energy at Ising FM-QCP
We begin with a brief review of the diagrammatic theory for interacting fermions near the ferromagnetic QCP. As the derivations of the electron–boson models and their relationship to itinerant QCP and NFL physics, as well as superconductivity, are scattered over numerous research papers and reviews encompassing decades of work, assiduous readers are suggested to directly consult these refs 2,3,5,6,7,12,14,16,17,19,21,22,24,25,27,28,29,33,34,35,43,66,67,68,69,70,71,72. Here, we will keep our derivation concise and try to be self-contained.
To understand the situation described in Eq. (1) of itinerant electrons coupled to critical bosonic fluctuations, we can encode the dynamics of bosons and fermions in their propagators,
and
where k = (ωn, k), q = (Ωm, q) are three-vectors with ωn = (2n + 1)πT and Ωm = 2mπT, the fermionic and bosonic Matsubara frequencies, respectively, ϵ(k) is the dispersion from section “The lattice model, phase diagram and QMC self-energy”, \({M}_{0}^{2}\) represents the bare distance to the QCP before the interaction is turned on (in the QMC it is controlled by the transverse magnetic field, M0 = M0(h)), and Σ, Π are, respectively, the fermionic and bosonic self-energies. Both self-energies are represented by a diagrammatic series in \(\bar{g}={(\frac{\xi }{2})}^{2}{D}_{0}\). The series is depicted pictorially in Fig. 4, where solid and wiggly lines are the full propagators G(k), D(q) and the triangles are fully dressed vertices. In general, it is not justified to neglect the vertex corrections. However, it is customary to split the corrections into two types: those coming from fermions away from the Fermi surface (“high-energy” fermions on the scale of the bandwidth W), and those coming from near the Fermi surface. The high-energy contributions just give some static corrections to an effective low-energy theory, which can be absorbed into an effective renormalized coupling \(\bar{g}\). The condition for the smallness of these corrections is weak coupling,
This condition is valid away from the QCP, that is, when \({M}_{0}^{2} \sim {k}_{{\rm{F}}}^{2}\). In the low-energy theory, at low enough temperatures and frequencies, it is not justified to neglect vertex corrections. However, those vertex corrections that contribute to Σ(k) can be neglected if we are in a regime where ∣Σ(ωn)∣ ≪ ωn. As shown in Fig. 1b, the lowest fermionic frequency in our QMC simulation is ω0 = πT = 0.157 with T = t/20 and the corresponding fermionic self-energy ∣Σ(kF, ω0)∣ = 0.058, so this condition is satisfied. A longer discussion on this is presented in another work by some of us65.
In our QMC study, we are always in the regime ∣Σ(ωn)∣ ≪ ωn, and Eq. (4) is obeyed, so without further discussion we will assume that vertex corrections are negligible. Then, Π, Σ are described by the coupled self-consistent equations,
Here Nf is the number of fermion flavors (Nf = 2 in the model of section “The lattice model, phase diagram and QMC self-energy”) and the factor 2 in Π comes from spin summation.
In principle, Eqs. (5) and (6) have momentum integrals over the entire Brillouin zone, which means that they still include contributions to the self-energies that come from high energies. One of these is a static contribution to Π. This contribution just renormalizes the mass towards the QCP, that is, \({M}_{0}^{2}\) in Eq. (3) is replaced by
Thus, M2 can be tuned to a QCP by varying \(\bar{g}\), or alternatively by varying \({M}_{0}^{2}\) (this is what is done in the QMC simulations). An additional static contribution renormalizes D0 and we absorb it into \(\bar{g}\). There are also static contributions to Σ, but they do not change the critical dynamics so we absorb them into the fermionic dispersion. Then, there are dynamical contributions that we will now compute.
Beyond neglecting vertex corrections, we further assume that the fermionic dispersion can be linearized near the FS, which means that the theory describes a low-energy effective theory near the FS. Then, integrating over linearized fermionic dispersion we obtain,
where Θ(x) is the step function, the density of states \({{\mathcal{V}}}_{{\rm{F}}}(\theta )={k}_{{\rm{F}}}(\theta )/{\upsilon }_{{\rm{F}}}(\theta )\) and kF, \({\upsilon}_{\mathrm{F}}\) are the Fermi vector and velocity at an angle θ on the FS, as given in Table 1. In Eq. (8), as ∣Σ(ωn)∣ ≪ ωn, we neglected contributions from self-energy and assumed that the kF and υF vector are approximately parallel. For the fermionic self-energy we get,
where σ(x) is the sign function and \(\hat{n}({\theta }_{k})={\left.\frac{(-{{\mathbf{\upsilon}}}_{{{\rm{F}}}_{y}},{{\mathbf{\upsilon}}}_{{{\rm{F}}}_{x}})}{{\upsilon }_{{\rm{F}}}}\right|}_{\theta = {\theta }_{k}}\) is an unit vector pointing parallel to the FS at the angle θk. In a C4 symmetric system, we can replace \(\hat{n}\) by \({\boldsymbol{\upsilon}}_{\mathrm{F}}/{\upsilon}_{\mathrm{F}}\), since the unit vector only determines the value of \(\upsilon_{\mathrm{F}}\)(θ) in Eq. (8).
We first evaluate the bosonic self-energy which to leading order is,
where the C4 symmetry of the lattice is used to replace \(\upsilon_{\mathrm{F}}\)(θ ± π/2) = \(\upsilon_{\mathrm{F}}\)(θ) and similarly for \({{\mathcal{V}}}_{{\rm{F}}}\). Next, we turn to the fermionic self-energy. Plugging Eq. (10) into Eq. (9) yields,
In Eq. (11) we rescaled momentum to frequency ω = υFp, and hid the explicit angular dependence υF = υF(θk) for conciseness. The frequency scale introduced by Π is
From Eq. (11) we can read the relevant frequency scales for Σ(ωn). The typical scale of the ωl sum is ωl ~ ωn due to the sign function, that is, typical internal frequencies are constrained to be on order of the external frequency.
We now show that at finite-temperature, but as long as ∣Σ(ωn)∣ ≪ ωn the fermionic self-energy in Eq. (5) splits into two parts: thermal and quantum (for detailed derivations and discussions see, e.g., refs 16,21,34,43,65). The quantum part recovers the zero-temperature fermionic self-energy, while the thermal part takes on a very simple form and scales as 1/ωn. Thus, after simply deducting this 1/ωn term, the finite-temperature self-energy directly provides the zero-temperature behavior of fermions, although the measurement is done at finite temperature, at which thermal fluctuations has a significant contribution. This is one of the key conclusions of this work. We separate the summation in Eq. (11) into two parts
where ΣT is the ωl = ωn piece of the sum in Eq. (11), namely
where
As \({\mathcal{S}}(x)\) vanishes rapidly at large x, it predicts that ΣT only contributes significantly at finite temperature and close enough to the QCP (πT ≳ \(\upsilon_{\mathrm{F}}\)υFM). In that regime, as noted in the introduction, α(T, ωn) = ωnΣT(ωn) depends at most logarithmically on frequency at the smallest ωn, α(T, ωn) ≈ α(T).
The quantum part includes all other terms in the Matsubara sum. This sum can be approximately replaced by an integral, which immediately recovers the T = 0 form of the fermionic self-energy, that is,
with
The scaling function \({\mathcal{U}}(z)\) has the following asymptotics,
where \({z}_{c}^{-1}={({\upsilon }_{{\rm{F}}}/c)}^{3/2}\) and u0 is a constant which depends on \(\upsilon_{\mathrm{F}}/c\). For \(\upsilon_{\mathrm{F}}/c\) ≪ 1, u0 ≈ 1/8; while for parameters of section “The lattice model, phase diagram and QMC self-energy” (\(\upsilon_{\mathrm{F}}/c\) ≈ 0.42), u0 ≈ 0.1. Note in the case of our QMC study zc ≈ 3.7, so that the intermediate regime cannot really be seen. Equation (17) is exactly the formula we used to generate the black line in the Fig. 1c, and is the quantum NFL self-energy ΣQ of an FM-QCP. It saturates in the large frequency region as shown in the figure, as predicted by Eq. (18) in the zc ≪ z limit. Combining Eqs. (14) and (16), we indeed see that the self-energy has a thermal 1/ωn term plus the zero-temperature quantum self-energy.
Let us briefly elaborate on the physics behind the scaling function \({\mathcal{U}}(z)\). In Eq. (17), the part in the square brackets correspond to the fermionic propagator and the other part in the integral corresponds to the bosonic propagator. Consider the limit ω ≪ ωb corresponding to z ≪ 1. Expanding for z ≪ 1 we find that to leading order the terms in the square brackets are a constant, and the dx integral is limited to 0 < x < 1. Physically this is the statement that the momentum integration (∫dy) is only on bosonic momentum parallel to the FS. In addition, the \({({\upsilon }_{{\rm{F}}}/c)}^{2}{x}^{2}y\) term in the boson propagator is also negligible, which corresponds to the fact that the bare Ω2 part of the boson dynamics is irrelevant at low frequency. Evaluating Eq. (16) for ωn ≪ ωb we find,
where
Equation (19) is the formula used to generate the red dashed line in Fig. 1c, as an asymptotic line of the quantum part of the self-energy predicted by Eq. (17). The analysis of Σ leading to Eqs. (19) and (20), as well as analogous analysis for superconducting self-energy, is conventionally termed “Eliashberg theory” (ET), due to its similarity to ET of superconductivity from electron–phonon interactions73.
Now consider the opposite limit, ω ≫ ωb, corresponding to z ≫ 1. For simplicity let us assume υF/c ≪ 1. In that case the term in the square brackets, corresponding to the fermionic propagator, is not constant, and the bulk of the contribution to u0 is given by the range 1 < x < ∞. Physically this means that scattering is not confined to be parallel to the FS and is two dimensional, although it is still confined to be near the FS. It is instructive to compute the subleading term for small z. After some algebra, one finds that this contribution is also given by 2D scattering, and gives \((2\pi /\sqrt{3}){\mathcal{U}}(z)\approx 1-0.73{z}^{1/3}\). This means that for z ~ 1, Σ0 is reduced by a factor of almost 4 from the expected value if one considers only the leading contribution. This is the reason that the deviation from the asymptotic red line in Fig. 1c is so large. At even larger z, the Ω2 term in the bosonic propagator begins to contribute, which just modifies the high-frequency behavior of the self-energy. However, the deviations from ω2/3 scaling occur already at z ~ 1. We term the theory which accounts for both high-frequency modifications and the finite-temperature corrections of Eq. (14) a modified Eliashberg theory (MET).
Analysis of QMC data
Now we turn to the QMC data analysis. We study the fermionic self-energy from the FM-QCP model described in section “The lattice model, phase diagram and QMC self-energy” and compare the QMC data with the MET in section “Analytic self-energy at Ising FM-QCP”.
Let us begin by going through the relevant physical parameters in the QMC data. We normalize all quantities by the hopping energy t = 1, see section “The lattice model, phase diagram and QMC self-energy” for details. By tuning the transverse field h, ref. 51 was able to extract QMC data for different T above the QCP, and also deep in the disordered phase, where the self-energy should have an FL form Σ(ωn) ∝ ωn at low frequencies. We concentrate on the data at the QCP. The parameters from section “The lattice model, phase diagram and QMC self-energy” imply a bare \(\bar{g}=1/4\), which is much smaller than EF ≈ 1.6, implying the QMC is in the weak coupling regime (we remind that all energies are quoted in units of the hopping). The bosonic propagator in QMC was found to agree well (as shown in ref. 51, it turns out the bosonic propagator is dominated by the bosonic self-energy part, with a small finite anomalous dimension in q2 and Ω2 terms, it will not change the main results of this paper) with Eqs. (3), (7), and (10), that is,
with D0 = 1, M2(T) = 0.13T1.48, c = 3.16, that is, the measured D0 agrees with the bare one, all obtained from the bosonic propagator data in ref. 51. In addition, it was found that Σ(ωn) ≪ ωn for all temperatures and Matsubara frequencies that were obtained. Thus, we may expect that corrections to the bare \(\bar{g}\) are small, and the renormalized \(\bar{g}\), which is an input to MET is at the order of the bare one. Under this condition, the relevant scales for Σ are
The temperatures we analyze are T = 0.05, …, 0.1, which implies the first Matsubara frequency is πT = 0.16, …, 0.31, see the schematics of energy scale in Fig. 2. Thus, ωF is completely irrelevant as is verified by the fact that the self-energy is always small. As we discussed in section “Introduction”, the QMC self-energy appears to have a leading term of the form
as shown in Fig. 1b. This is consistent with the prediction of MET, see Eqs. (14) and (15).
We analyze the data in two ways. First, we extract the quantum self-energy and compare it to the T = 0 prediction. To do this, we need to remove the thermal part. This is most conveniently done simply by studying the product ωnΣ(ωn). As discussed in the “Introduction” and the previous section, according to Eqs. (13) and (16) we have,
providing we treat α(T) as constant, neglecting its slow frequency dependence, see Eq. (15). In Eq. (24), α(T) includes both the contribution from ΣT(ωn, T), and corrections from finite size effect (such as a possible small gap due to the mismatch of finite size hc and the thermodynamic hc). The second part, that is, ωnΣQ(ωn), comes from the MET prediction for ΣQ(ωn), Eq. (16), which recovers ET prediction Eq. (19) in the low-frequency limit (ωn ≪ ωb).
We fit Eq. (24) to the data for all T simultaneously. Importantly, in Eq. (24), the fitting parameters are only the constants α(T) and \(\bar{g}\). This is because ΣQ is a function only of \(\bar{g}\) and system parameters, see Eq. (17). Figure 1c from the beginning of our paper depicts the result of our fit. We obtain a fitting of \(\bar{g}=0.245\pm 0.023\) for 95% confidence intervals, in excellent agreement with the theory. Regarding α(T), we find that α(T) ≈ 8 × 10−3 is almost a constant, in disagreement with the expected ∝ T behavior of ωnΣT(ωn, T). Clearly, part of this discrepancy is due to our neglecting the frequency dependence of α. We therefore repeat the analysis using the following fitting procedure,
which takes the full frequency behavior of ΣT into account. Guided by the previous fit, we set \(\bar{g}=0.25\) to be the bare one to reduce the number of fitting parameters. We show the result of this fit in Fig. 5 and the extracted \(\alpha ^{\prime} (T)\) in Fig. 6. The agreement is very good, and we checked that the data collapse can be made even better by allowing \(\bar{g}\) to vary somewhat (equivalent to about 13% change in the bare vertex ξ). The extracted \(\alpha ^{\prime} (T)\) indicates the formation of a small gap forming at around T = 0.1, which is expected to yield a self-energy contribution of the form α'(T)/ωn = Δ2(T)/ωn. The gap size Δ corresponding to \(\alpha ^{\prime} (T)\) is much less than the numerical inverse reciprocal lattice spacing, so the appearance of this gap is actually an expected effect, which however is beyond the resolution of the standard methods for verifying the appearance of long-range order. Thus, our analysis of the self-energy yields a method for more accurately finding the QCP in our system.
The solid dots correspond to the QMC ωnΣ(ωn) for different T, while for each T dataset, the thermal part and a constant α'(T) has been deducted (see Fig. 6). The dashed line corresponds to ωnΣQ(ωn), computed at T = 0, for the bare \(\bar{g}\) from the parameters of section “The lattice model, phase diagram and QMC self-energy”. The gray shaded area is the 95% confidence interval.
See Eq. (25) for details.
Here we add a word of caution. Previous work has shown33,38,74 that the first Matsubara frequency does not obey the quantum critical scaling ΣQ(πT) ∝ (πT)2/3, and therefore should not be included in the fitting procedure. We verified that dropping the first Matsubara point does not change our results. Also, note that within the error range in Fig. 5, it is possible that ΣQ(πT) < 0. In fact, it can be verified that ΣQ(πT) is always negative21,65.
To avoid this issue, we also numerically computed ΣT(ωn) and ΣQ(ωn) by performing the Matsubara sum in Eq. (9), using \(\bar{g}=0.25\). This procedure takes into account the full frequency dependence of ΣT(ωn) as well as finite mass effects and the first Matsubara frequency issues. Figure 7 depicts a comparison of the QMC self-energy with the numerical summation. There is an excellent agreement between the two, except for a T-dependent constant offset between the MET and QMC results. The result is consistent with the first analysis we performed above. For completeness, we also performed a comparison between the MET and QMC data for the data in the disordered phase (the FL regime). Figure 8 shows this comparison, again with very good agreement.
The solid dots correspond to the QMC data, and the hollow dots correspond to a numerical summation of the Matsubara sums in Eq. (11).
The solid dots correspond to the QMC data, and the hollow dots correspond to a numerical summation of the Matsubara sums in Eq. (11).
We therefore conclude that we have extracted the quantum self-energy from the QMC data, and that it shows excellent agreement with the expected QC behavior.
Discussion
NFLs play a crucial role in a wide range of quantum many-body phenomena, such as quantum criticality, high-temperature superconductivity in correlated materials, unconventional transport in strange metals, and have been a key focus in the study of modern condensed matter physics1,2,3,5,6,7,12,14,15,16,17,18,19,22,24,25,27,28,29,33,35,36,44,45,47,48,53,66,67,68,69,70,71,72,75. Despite of the intensive research efforts, key questions remained open and the problem of NFLs is still one of the most challenging topics in many-body physics, even with the most sophisticated field theoretical treatments16,25,27,29,35, powerful numerical many-body algorithms and high-performance supercomputers47,48,63,64.
Our work provides a pathway to address a key challenge in the study of NFLs, that is, the fact that the smoking-gun signature of NFLs (the predicted unconventional low-temperature fermion self-energy), has never been directly observed or verified in large-scale unbiased numerical methods. Through combined numerical and theoretical efforts, we proved that this key signature of NFLs can be accessed through QMC simulations, by simply deducting a ∝ 1/ωn thermal-fluctuation background. This technique enabled us to directly compare numerical results with theoretical predictions, providing a bridge between theoretical, numerical, and experimental studies.
Although this paper mainly focuses on the itinerant ferromagnetism QCP as an example to demonstrate the physics, the technique is universal and can be easily generalized to other itinerant QCPs, such as nematic and AFM-QCPs49,52,53,56. Furthermore, this technique can also be used to explore the predicted non-trivial effects from higher-order corrections16,25,27,29,35,76, and thus open up a pathway towards a full understanding about this challenging subject of NFLs.
Methods
Numerical calculations
The numerical results for fermionic and bosonic self-energies have been obtained using state-of-art determinantal QMC simulations as reported in ref. 51.
Analytical calculations
Analytical calculations have been carried out diagrammatically within ET and MET, by solving the set of self-consistent equations for fermionic and bosonic self-energies.
Data availability
The data that support the findings of this study are available from the first author upon reasonable request.
References
Sachdev, S. Quantum Phase Transitions 2nd edn (Cambridge Univ. Press, 2011).
Hertz, J. A. Quantum critical phenomena. Phys. Rev. B 14, 1165–1184 (1976).
Moriya, T. Spin Fluctuations in Itinerant Electron Magnetism (Springer, Berlin, Heidelberg, 1985).
Lee, P. A. Gauge field, Aharonov-Bohm flux, and high-Tc superconductivity. Phys. Rev. Lett. 63, 680–683 (1989).
Millis, A. J. Nearly antiferromagnetic Fermi liquids: an analytic Eliashberg approach. Phys. Rev. B 45, 13047–13054 (1992).
Millis, A. J. Effect of a nonzero temperature on quantum critical points in itinerant fermion systems. Phys. Rev. B 48, 7183–7196 (1993).
Altshuler, B. L., Ioffe, L. B. & Millis, A. J. Low-energy properties of fermions with singular interactions. Phys. Rev. B 50, 14048–14064 (1994).
Polchinski, J. Low-energy dynamics of the spinon-gauge system. Nucl. Phys. B 422, 617–633 (1994).
Nayak, C. & Wilczek, F. Non-Fermi liquid fixed point in 2+1 dimensions. Nucl. Phys. B 417, 359–373 (1994).
Son, D. T. Superconductivity by long-range color magnetic interaction in high-density quark matter. Phys. Rev. D. 59, 094019 (1999).
Chubukov, A. V. & Schmalian, J. Superconductivity due to massless boson exchange in the strong-coupling limit. Phys. Rev. B 72, 174520 (2005).
Abanov, A. & Chubukov, A. V. Spin-fermion model near the quantum critical point: one-loop renormalization group results. Phys. Rev. Lett. 84, 5608–5611 (2000).
Oganesyan, V., Kivelson, S. A. & Fradkin, E. Quantum theory of a nematic Fermi fluid. Phys. Rev. B 64, 195109 (2001).
Abanov, A., Chubukov, A. V. & Finkel’stein, A. M. Coherent vs. incoherent pairing in 2d systems near magnetic instability. Europhys. Lett. 54, 488 (2001).
Stewart, G. R. Non-Fermi-liquid behavior in d- and f-electron metals. Rev. Mod. Phys. 73, 797–855 (2001).
Abanov, A., Chubukov, A. V. & Schmalian, J. Quantum-critical theory of the spin-fermion model and its application to cuprates: normal state analysis. Adv. Phys. 52, 119–218 (2003).
Metzner, W., Rohe, D. & Andergassen, S. Soft Fermi surfaces and breakdown of Fermi-liquid behavior. Phys. Rev. Lett. 91, 066402 (2003).
Custers, J. et al. The break-up of heavy electrons at a quantum critical point. Nature 424, 524–527 (2003).
Abanov, A. & Chubukov, A. Anomalous scaling at the quantum critical point in itinerant antiferromagnets. Phys. Rev. Lett. 93, 255702 (2004).
Chubukov, A. V. Self-generated locality near a ferromagnetic quantum critical point. Phys. Rev. B 71, 245123 (2005).
Dell’Anna, L. & Metzner, W. Fermi surface fluctuations and single electron excitations near Pomeranchuk instability in two dimensions. Phys. Rev. B 73, 045127 (2006).
Rech, J., Pépin, C. & Chubukov, A. V. Quantum critical behavior in itinerant electron systems: Eliashberg theory and instability of a ferromagnetic quantum critical point. Phys. Rev. B 74, 195126 (2006).
Maslov, D. L., Chubukov, A. V. & Saha, R. Nonanalytic magnetic response of Fermi and non-Fermi liquids. Phys. Rev. B 74, 220402 (2006).
Löhneysen, Hv., Rosch, A., Vojta, M. & Wölfle, P. Fermi-liquid instabilities at magnetic quantum phase transitions. Rev. Mod. Phys. 79, 1015–1075 (2007).
Lee, S.-S. Low-energy effective theory of Fermi surface coupled with U(1) gauge field in 2 + 1 dimensions. Phys. Rev. B 80, 165102 (2009).
Maslov, D. L. & Chubukov, A. V. Nonanalytic paramagnetic response of itinerant fermions away and near a ferromagnetic quantum phase transition. Phys. Rev. B 79, 075112 (2009).
Metlitski, M. A. & Sachdev, S. Quantum phase transitions of metals in two spatial dimensions. I. Ising-nematic order. Phys. Rev. B 82, 075127 (2010).
Metlitski, M. A. & Sachdev, S. Instabilities near the onset of spin density wave order in metals. N. J. Phys. 12, 105007 (2010).
Metlitski, M. A. & Sachdev, S. Quantum phase transitions of metals in two spatial dimensions. II. Spin density wave order. Phys. Rev. B 82, 075128 (2010).
Mross, D. F., McGreevy, J., Liu, H. & Senthil, T. Controlled expansion for certain non-fermi-liquid metals. Phys. Rev. B 82, 045121 (2010).
Holder, T. & Metzner, W. Fermion loops and improved power-counting in two-dimensional critical metals with singular forward scattering. Phys. Rev. B 92, 245128 (2015).
Holder, T. & Metzner, W. Anomalous dynamical scaling from nematic and U(1) gauge field fluctuations in two-dimensional metals. Phys. Rev. B 92, 041112 (2015).
Wang, Y., Abanov, A., Altshuler, B. L., Yuzbashyan, E. A. & Chubukov, A. V. Superconductivity near a quantum-critical point: the special role of the first Matsubara frequency. Phys. Rev. Lett. 117, 157001 (2016).
Wang, H. & Torroba, G. Non-Fermi liquids at finite temperature: normal-state and infrared singularities. Phys. Rev. B 96, 144508 (2017).
Lee, S.-S. Recent developments in non-Fermi liquid theory. Annu. Rev. Condens. Matter Phys. 9, 227–244 (2018).
Shen, B. et al. Strange-metal behaviour in a pure ferromagnetic Kondo lattice. Nature 579, 51–55 (2020).
Damia, J. A., Kachru, S., Raghu, S. & Torroba, G. Two-dimensional non-Fermi-liquid metals: a solvable large-N limit. Phys. Rev. Lett. 123, 096402 (2019).
Wu, Y.-M., Abanov, A., Wang, Y. & Chubukov, A. V. Special role of the first Matsubara frequency for superconductivity near a quantum critical point: nonlinear gap equation below Tc and spectral properties in real frequencies. Phys. Rev. B 99, 144512 (2019).
Esterlis, I. & Schmalian, J. Cooper pairing of incoherent electrons: an electron–phonon version of the Sachdev–Ye–Kitaev model. Phys. Rev. B 100, 115132 (2019).
Wang, Y. Solvable strong-coupling quantum-dot model with a non-Fermi-liquid pairing transition. Phys. Rev. Lett. 124, 017002 (2020).
Pan, G., Wang, Y. & Meng, Z. Y.Self-tuned quantum criticality and non-Fermi-liquid in a Yukawa-SYK model: a quantum Monte Carlo study. Preprint at https://arxiv.org/abs/2001.06586 (2020).
Xu, Y., Geng, H., Wu, X.-C., Jian, C.-M. & Xu, C. Non-Landau quantum phase transitions and nearly-marginal non-Fermi liquid. J. Stat. Mech. Theory Exp. 2020, 073102 (2020).
Aguilera Damia, J., Solis, M. & Torroba, G. How non-Fermi liquids cure their infrared divergences. Phys. Rev. B 102, 045147 (2020).
Hartnoll, S. A., Lucas, A. & Sachdev, S. Holographic quantum matter. Preprint at https://arxiv.org/abs/1612.07324 (2016).
Keimer, B., Kivelson, S. A., Norman, M. R., Uchida, S. & Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015).
Maldacena, J. & Stanford, D. Remarks on the Sachdev–Ye–Kitaev model. Phys. Rev. D. 94, 106002 (2016).
Berg, E., Lederer, S., Schattner, Y. & Trebst, S. Monte Carlo studies of quantum critical metals. Annu. Rev. Condens. Matter Phys. 10, 63–84 (2019).
Xu, X. Y. et al. Revealing fermionic quantum criticality from new Monte Carlo techniques. J. Condens. Matter Phys. 31, 463001 (2019).
Schattner, Y., Lederer, S., Kivelson, S. A. & Berg, E. Ising nematic quantum critical point in a metal: a Monte Carlo study. Phys. Rev. X 6, 031028 (2016).
Xu, X. Y., Beach, K. S. D., Sun, K., Assaad, F. F. & Meng, Z. Y. Topological phase transitions with SO(4) symmetry in (2+1)d interacting Dirac fermions. Phys. Rev. B 95, 085110 (2017).
Xu, X. Y., Sun, K., Schattner, Y., Berg, E. & Meng, Z. Y. Non-Fermi liquid at (2+1)d ferromagnetic quantum critical point. Phys. Rev. X 7, 031058 (2017).
Liu, Z. H., Xu, X. Y., Qi, Y., Sun, K. & Meng, Z. Y. Itinerant quantum critical point with frustration and a non-Fermi liquid. Phys. Rev. B 98, 045116 (2018).
Liu, Z. H., Pan, G., Xu, X. Y., Sun, K. & Meng, Z. Y. Itinerant quantum critical point with fermion pockets and hotspots. Proc. Natl Acad. Sci. USA 116, 16760–16767 (2019).
Schattner, Y., Gerlach, M. H., Trebst, S. & Berg, E. Competing orders in a nearly antiferromagnetic metal. Phys. Rev. Lett. 117, 097002 (2016).
Gerlach, M. H., Schattner, Y., Berg, E. & Trebst, S. Quantum critical properties of a metallic spin-density-wave transition. Phys. Rev. B 95, 035124 (2017).
Bauer, C., Schattner, Y., Trebst, S. & Berg, E. Hierarchy of energy scales in an O(3) symmetric antiferromagnetic quantum critical metal: a Monte Carlo study. Phys. Rev. Res. 2, 023008 (2020).
Xu, X. Y. et al. Monte Carlo study of lattice compact quantum electrodynamics with fermionic matter: the parent state of quantum phases. Phys. Rev. X 9, 021022 (2019).
Chen, C., Xu, X. Y., Qi, Y. & Meng, Z. Y. Metal to orthogonal metal transition. Chin. Phys. Lett. 37, 047103 (2020).
Assaad, F. F. & Grover, T. Simple fermionic model of deconfined phases and phase transitions. Phys. Rev. X 6, 041049 (2016).
Gazit, S., Randeria, M. & Vishwanath, A. Emergent Dirac fermions and broken symmetries in confined and deconfined phases of Z2 gauge theories. Nat. Phys. 13, 484–490 (2017).
Gazit, S., Assaad, F. F. & Sachdev, S. Fermi-surface reconstruction without symmetry breaking. Preprint at https://arxiv.org/abs/1906.11250 (2019).
Chen, C., Yuan, T., Qi, Y. & Meng, Z. Y. Doped orthogonal metals become Fermi arcs. Preprint at https://arxiv.org/abs/2007.05543 (2020).
Xu, X. Y., Qi, Y., Liu, J., Fu, L. & Meng, Z. Y. Self-learning quantum Monte Carlo method in interacting fermion systems. Phys. Rev. B 96, 041119 (2017).
Liu, Z. H., Xu, X. Y., Qi, Y., Sun, K. & Meng, Z. Y. Elective-momentum ultrasize quantum monte carlo method. Phys. Rev. B 99, 085114 (2019).
Avraham Klein, E. B., Yoni, S. & Chubukov, A.V. Normal state properties of quantum critical metals at finite temperature. Preprint at https://arxiv.org/abs/2003.09431 (2020).
Bonesteel, N. E., McDonald, I. A. & Nayak, C. Gauge fields and pairing in double-layer composite fermion metals. Phys. Rev. Lett. 77, 3009–3012 (1996).
Lederer, S., Schattner, Y., Berg, E. & Kivelson, S. A. Superconductivity and non-Fermi liquid behavior near a nematic quantum critical point. Proc. Natl Acad. Sci. USA 114, 4905–4910 (2017).
Maslov, D. L. & Chubukov, A. V. Fermi liquid near Pomeranchuk quantum criticality. Phys. Rev. B 81, 045110 (2010).
Fradkin, E., Kivelson, S. A., Lawler, M. J., Eisenstein, J. P. & Mackenzie, A. P. Nematic Fermi fluids in condensed matter physics. Annu. Rev. Condens. Matter Phys. 1, 153–178 (2010).
Raghu, S., Torroba, G. & Wang, H. Metallic quantum critical points with finite BCS couplings. Phys. Rev. B 92, 205104 (2015).
Metlitski, M. A., Mross, D. F., Sachdev, S. & Senthil, T. Cooper pairing in non-Fermi liquids. Phys. Rev. B 91, 115111 (2015).
Lederer, S., Schattner, Y., Berg, E. & Kivelson, S. A. Enhancement of superconductivity near a nematic quantum critical point. Phys. Rev. Lett. 114, 097001 (2015).
Abrikosov, A., Gorkov, L. & Dzyaloshinski, I. Methods of Quantum Field Theory in Statistical Physics. Dover Books on Physics Series (Dover Publications, 1975).
Chubukov, A. V. & Maslov, D. L. First-Matsubara-frequency rule in a Fermi liquid. I. Fermionic self-energy. Phys. Rev. B 86, 155136 (2012).
Chubukov, A. V. Ward identities for strongly coupled Eliashberg theories. Phys. Rev. B 72, 085113 (2005).
Schlief, A., Lunts, P. & Lee, S.-S. Exact critical exponents for the antiferromagnetic quantum critical metal in two dimensions. Phys. Rev. X 7, 021010 (2017).
Acknowledgements
We thank Subir Sachdev, Max Metlitski, Yuxuan Wang, Yoni Schattner, Erez Berg, and Dmitrii Maslov for insightful discussions on fermionic QCPs and NFL. X.Y.X. also thank Tarun Grover for helpful discussion on related projects. We acknowledge the support from RGC of Hong Kong SAR China through 17303019 and 17301420, MOST through the National Key Research and Development Program (2016YFA0300502). The work by A.K. and A.V.C. was supported by the Office of Basic Energy Sciences, U.S. Department of Energy, under award DE-SC0014402. We also thank the Center for Quantum Simulation Sciences in the Institute of Physics, Chinese Academy of Sciences, the Computational Initiative at the Faculty of Science at the University of Hong Kong and the Tianhe platforms at the National Supercomputer Centers in Tianjin and Guangzhou for their technical support and generous allocation of CPU time. This research was initiated at the Aspen Center for Physics, supported by NSF PHY-1066293.
Author information
Authors and Affiliations
Contributions
All authors discussed and designed the study together. X.Y.X. and A.K. analyzed the data. All authors together discussed the theory and drafted the article.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xu, X.Y., Klein, A., Sun, K. et al. Identification of non-Fermi liquid fermionic self-energy from quantum Monte Carlo data. npj Quantum Mater. 5, 65 (2020). https://doi.org/10.1038/s41535-020-00266-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-020-00266-6
This article is cited by
-
Non-Hertz-Millis scaling of the antiferromagnetic quantum critical metal via scalable Hybrid Monte Carlo
Nature Communications (2023)
-
Monte Carlo study of the pseudogap and superconductivity emerging from quantum magnetic fluctuations
Nature Communications (2022)
-
Measuring Rényi entanglement entropy with high efficiency and precision in quantum Monte Carlo simulations
npj Quantum Materials (2022)