Introduction

Topologically protected electronic states at material interfaces are attractive because they cannot be destroyed by many types of perturbations1,2. An especially fruitful host of such exotic states is MoTe2, which has had both its bulk orthorhombic Td phase, and hole-doped monolayer specimens identified as possible topological superconductors3,4,5. In addition, a topological superconducting phase was recently discovered in sulfur-substituted samples, with S+−-wave pairing6. MoTe2 also features topologically nontrivial normal states: the Td phase has been identified as a type II Weyl semimetal7,8,9,10, whereas the monoclinic T’ phase is predicted to be a higher-order topological material11; the latter is also found to describe the Td phase in some calculations11. In this work, we demonstrate via quantum oscillations and neutron scattering measurements, and first-principles calculations, how pressure drives MoTe2 between the Td and T’ phases, through an intermediate mixed-phase region. The mixed-phase region gives rise to a network of topological interface states that yield quantum oscillations that survive despite the strong structural disorder.

Results

Orthorhombic Td–MoTe2

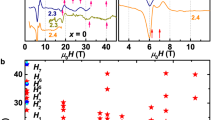
The first-order structural transition separating the T’ and Td phases in MoTe2 has a distinct pressure dependence (Fig. 1a). At ambient pressure, the inversion-symmetric T’ phase is stable at room temperature, only transforming into the noncentrosymmetric Td phase when cooled below roughly 250 K3,12. Neutron diffraction allows the determination of the relative volume fraction of these phases under different conditions12. As pressure increases, the transition temperature decreases. At pressures higher than 0.8 GPa, a completely different phenomenon emerges, where a roughly balanced mixture of the T’ and Td phases stabilizes over an appreciable temperature range, and crucially, extends to the lowest measured temperatures. The existence of this frozen mixed-phase region is stabilized by the lack of sufficient entropy at these suppressed temperatures for atoms to move to their lowest-energy configuration, implying that there is a dominant extrinsic transformation energy barrier between two energetically nearly degenerate structures12.

Fig. 1: Pressure–temperature phase diagram of MoTe2.
figure 1

a Pressure–temperature phase diagram of MoTe2. The green and blue symbols delineate the extent of 100% volume fraction of T' and Td phases, respectively, determined through neutron scattering. The onset of full volume superconductivity coincides with the end of the Td phase at 0.8 GPa 12, where a topological interface network (TIN) is observed. b Pressure dependence of the quantum oscillation frequency, with different branches labeled by Greek letters. The numbers correspond to the effective mass, which changes slightly with pressure. The quantum oscillations with the strongest pressure dependence, α and β in the Td phase, and η in the T' phase, correspond to extremal orbits on the large electron pockets. In the TIN region, these disappear and are replaced by a completely distinct set of oscillations arising from topological interface states. Representative quantum oscillations (c) at ambient pressure (Weyl semimetal in Td), d 0.9 GPa (TIN), and e 1.8 GPa (higher-order topology in T'). Clear changes in the quantum oscillations reflect significant changes in the electronic structure.

Full size image

The basic components underlying the Weyl semimetallic state of the low-pressure, low-temperature Td phase are a large hole pocket centered on the Brillouin zone and two neighboring electron pockets along the Γ –X direction8,9,10,13. The hole pocket is observed in angle-resolved photoemission spectroscopy (ARPES)8,9,10, but is not apparent in SdH measurements14. Prominent quantum oscillations observed in the Td phase arise from orbits associated with the electron pocket14. Figure 2a, b shows magnetoresistance and SdH oscillations at ambient pressure, in which these are clearly seen. As the fast Fourier transform (FFT) explicitly shows (Fig. 2c), the beating seen in Fig. 2b is due to two similar frequencies, Fα = 240.5 T and Fβ = 258 T, the result of symmetry-allowed spin–dorbit splitting. First-principles calculations identify these frequencies with the larger extremal kz = 0 cross sections of the electron pocket.

Fig. 2: Quantum oscillations in the magnetoresistance in MoTe2 at ambient pressure.
figure 2

a The longitudinal MR of the bulk Td-MoTe2 measured at ambient pressure with a magnetic field parallel to the c axis. b The corresponding SdH oscillations after subtraction of a second-order polynomial background. c The fast Fourier transform (FFT) spectra show three Fermi surfaces with oscillation frequencies at Fγ = 32.5 T, Fα = 240.5 T, and Fβ = 258 T. The inset shows the α and β orbits on the calculated electron pocket. d Fit to the SdH oscillation at 1.8 K yield nontrivial Berry’s phases ϕγ = π, ϕα = 0.88π, and ϕβ = 0.88π. Details of the fit are discussed in the Supplementary Information. e The effective masses of the carriers are obtained through temperature-dependent Lifshitz–Kosevich fits.

Full size image

Modeling of the SdH oscillations yields a remarkably good fit (Fig. 2d) to the experimental SdH by the Bumps program15 (Supplementary Figs. 15–23, Supplementary Table 5, Supplementary Notes 9 and 10). Notably, all of the oscillations feature a π Berry’s phase16, consistent with a Weyl topology (Supplementary Figs. 3–7, 14, and Supplementary Note 2). The effective band masses are light and slightly less than previously reported14,17, as shown in Fig. 2e. As a function of pressure, the electron pockets increase modestly in size due to lattice compression, but the nontrivial phase shift is maintained throughout the Td phase (Supplementary Tables 1–4). This trend is consistent with first-principles calculations as shown in Fig. 3a and b, which indicates the persistence of Weyl nodes up to 1.4 GPa (Supplementary Fig. 6 and Supplementary Note 2).

Fig. 3: Comparison between the calculated and experimental quantum oscillation frequencies for Td and T’ phases.
figure 3

a, b Calculated in-plane quantum oscillation frequencies for the Td and T' phases. The SdH oscillation frequencies arising from the electron pockets increase with the same pressure dependence in both phases. c A comparison between calculated and measured frequencies shows excellent quantitative agreement. The discontinuity in measured values is due to the jump in c axis dilation between phases. d, e Calculated bulk Fermi surfaces of the Td and T' phases.

Full size image

Monoclinic T’– MoTe2

In the T’ phase at pressures of 1.2 GPa and greater, one main frequency Fη replaces the two frequencies Fα and Fβ. The Fermi surface in the T’ phase closely resembles that of the Td phase, with the exception that the centrosymmetry of the T’ phase nullifies the spin–orbit splitting of the bands that contribute to this electron pocket (Fig. 3d, e). This similarity leads to a common pressure dependence of the measured electron pocket frequency in both phases, consistent with the pressure evolution of the calculated Fermi surface (Fig. 3c, Supplementary Fig. 8, and Supplementary Tables 1–4). The main feature not captured by the calculations is a pronounced discontinuity in band structure between Td and T’ phases due to the discontinuous c axis dilation at the structural transition, which is not modeled (Fig. 3c). Unexpectedly, our SdH oscillations analysis shows that a π Berry’s phase also exists in the centrosymmetric T’ phase (Supplementary Table S6). After an ARPES study identified surface states in this phase13, it was identified theoretically with an unusual type of nontrivial topological state11. Our results are consistent with this prediction, and further have the exciting implication that the high-pressure superconductivity in the T’ phase may be inherently topologically nontrivial, as suggested by μSR measurements at these pressures18.

Natural topological interface network (TIN)

A structural mixed region exists over a range of pressures and temperatures in between the bulk Td and T’ phases (Fig. 1a). It consists of an approximately balanced partial volume fraction of Td and T’. We emphasize that no other structural phases or ordered superstructures are apparent from neutron diffraction measurements (Supplementary Figs. 1 and 2). It would, therefore, be expected that any measured SdH oscillations in the mixed region would consist of a superposition of Td and T’ signals, but we do not observe oscillations from either phase. We conclude that the mixed region is sufficiently disordered that SdH oscillations from both the Td and T’ phases are suppressed due to increased electron scattering.

In light of this, it is completely unexpected that a distinct set of SdH oscillations appears (Fig. 1b, d). This is a robust effect; the oscillations in the mixed phase always appear on both increasing and decreasing applied pressures through the critical range, over multiple cycles, confirming their intrinsic nature. A different band structure in the mixed region is inferred from the presence of frequencies corresponding to changed Fermi surfaces, and a change in effective mass and much weaker oscillation amplitude relative to bulk Td and T’, as shown in Fig. 4a–f. These quantum oscillations reflect features typical of topologically protected states, namely, persistence in the presence of strong disorder, as well as π Berry’s phases (Supplementary Tables 5 and 6). Because there are no additional structural phases in the mixed region, only Td and T’, these topological states must be surface states of the bulk phases, which in this case, exist at their interfaces. Thus, the multiple natural interfaces stabilized in MoTe2 by the first-order nature of the structural transition serve as the foundation for a completely different type of electronic system in MoTe2: a natural topological interface network (TIN).

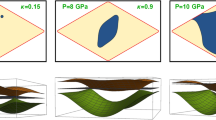
Fig. 4: Quantum oscillations in the magnetoresistance in MoTe2 under pressure.
figure 4

Temperature dependence of the SdH oscillations of MoTe2 measured at (a) 0.6 GPa in the Td phase, (c) 0.9 GPa in the topological interface network (TIN), and (e) 1.8 GPa in the T' phase. Note the large changes in oscillation amplitude at different pressures. Corresponding fast Fourier transform (FFT) spectra of (b) Td, (d) TIN, and (f) T' emphasize the dramatic changes in quantum oscillation frequency, due to changes in the dominant electronic orbits, as pressure tunes through the different phases. g Schematic of the topological interface network (TIN) showing the 3D mixed Td–T' microstructure. The relatively weak but coherent signals are robust against pressure-induced disorder and only come from the connected interfaces between grains of Td and T'. This TIN heterostructure can parametrically increase the number of surface channels and is a promising approach to increasing the surface-to-volume ratio of mixed-phase topological materials. The SdH signal is only related to cyclotron motion in the ab plane since electric current (I) and magnetic field (B) are along a and c crystallographic axis.

Full size image

In the TIN, due to the layered structure of both Td and T’ phases, the ab plane is preserved, and the largest grain boundaries fall along the ab plane, which is the orientation probed by the SdH measurements (Fig. 4g). In MoTe2, a naturally generated heterostructure provides an interesting demonstration of topological transport protection. The lateral dimensions of the interfaces are the same as those of the bulk grains, based upon which one naively expects similar damping of the SdH oscillations from the interfaces. The absence of quantum oscillations from bulk Td and T’ phases illustrates that the scattering from the TIN microstructure is significant for the bulk bands. Yet the clear SdH oscillations from the interfaces prove that the interfacial states have lower scattering than the bulk, and are a sign of their topologically nontrivial nature. In other words, the interfacial signal has been amplified by suppressing the bulk SdH oscillations through grain boundary scattering, and increasing the interface volume.

Density-functional theory (DFT) calculation of Td–T’ slab model

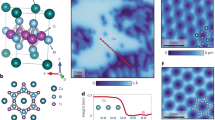
First-principles calculations offer additional insight into the electronic structure of the TIN and its stability. We investigated a variety of possible mixed phases that might describe the mixed region, including Td-like phases with different MoTe2 stacking orders, periodic superstructures, and finite slabs of Td and T’ phases and their interfaces as shown in Fig. 5a and b (detailed calculations are discussed in the Supplementary Figs. 9–13 and Supplementary Notes 4–6). Calculations demonstrate that the only model consistent with the experimentally determined high-frequency oscillations of ~1 kT (Fig. 4d) is a system consisting of only Td–T’ interfaces, the TIN (Fig. 5d).

Fig. 5: The topological interface network Td–T’ superstructure model.
figure 5

a Six layers of Td–T' periodic superstructure, consisting of three layers of Td and T' phases with L–L interface. b Three layers of Td and T' slabs, separated (top) and joined (bottom). c Fermi surface obtained from separated (top) and joined slabs (bottom). d—top: The difference in the Fermi surfaces of the separated (c—top) and joined slabs (c—bottom), directly indicating the states due to the Td–T' interface. Similarly, (d—bottom) shows the interface Fermi pockets from the periodic superstructure shown in (a). The middle panel in (d) shows the quantum oscillations from the Td–T' joint slab calculations (b—bottom) compared with the experimental frequencies, which are represented as Gaussian curves with equal but arbitrary intensities.

Full size image

The Fermi-surface pockets associated with the interface are identified in two different but complementary calculations. Consider a periodic superstructure of Td and T’ phases, as shown in Fig. 5a. Surprisingly, the Td–T’ interface has lower energy if the MoTe2 layers at the interface have the same type of Te distortion, labeled as L or R, compared to the L–R–L–R-type stacking order found in bulk Td and T’ phases. Since L- or R-type planes cannot be converted to each other by simply sliding the planes, this sort of interface presents a large energy barrier to the removal of stacking faults. The fact that this LL-type interface has lower energy than the interface with L–R stacking explains the stability of the mixed intermediate phase. Comparing the Fermi surfaces of the pure Td and T’ phases with the Td–T’ superstructure yields distinct Fermi-surface pockets with quantum oscillation orbits of 0.16 kT and 1.0 kT (bottom panel of Fig. 5d) in excellent agreement with our measurements.

Even though the periodic superstructure calculations of the Td–T’ interface are consistent with the TIN model, the interface pockets have some dispersion due to interactions between the periodic images of the interface. To eliminate this effect, consider two slabs of Td and T’ initially separated by about 9.5 Å (Fig.5b). These two slabs are brought together to form the Td–T’ interface in a supercell where the combined Td–T’ slab is separated by ~16.3 Å, large enough to avoid any image interactions (Fig. 5b, bottom). Comparing the Fermi surfaces of the isolated slabs (Fig. 5b) and combined slabs with the interface (shown in Fig. 5c), yields Fermi-surface pockets associated with the interface (Fig. 5d, top).

The agreement is excellent between the surface states from the periodic and finite slab calculations. These 2D quantum oscillation orbits are in impressive agreement with the experimental results (middle panel of Fig. 5d). Thus, the slab calculations directly link the observed high-frequency oscillation in the mixed region to interface states, as a TIN would produce.

Discussion

Essential to any topological surface state is the meeting of two bulk phases with different topological invariants. A typical example is that of a Weyl semimetal interfaced with a topologically trivial vacuum, on whose boundary Fermi arcs are observed, as in Td–MoTe28. In contrast, the second phase of the TIN is the topologically nontrivial T’ phase, which forms a large number of Td/T’ interfaces due to the structural disorder. Then, for surface states to exist at these interfaces, there must be a change in topology between Td and T’ phase, as expected for phases of Weyl and higher-order topological states. Although such interfaces have until now not received much theoretical attention, recent scanning tunneling microscopy measurements on MoTe2 have suggested the existence of conducting hinge states in the T’/Td domain wall at ambient pressure19. Our results did not directly observe 1D-hinge state, but cannot completely exclude the possibility of 1D paths. Our measurements and calculations show that 2D topological interfaces are also possible. Our discovery suggests that topological interfaces in 3D materials are a rich area for future exploration and exploitation.

Finally, we briefly discuss the relationship between the TIN and superconductivity in MoTe2. Both the superconducting volume fraction and Tc increase dramatically at the same pressure at which the TIN is stabilized (Fig. 1a). Taking into further consideration the 2D nature of superconductivity, based on our previous calculations12 and recent upper critical field measurements under pressure20, a strong case is made that superconductivity is topologically nontrivial, consistent with previous claims from μSR measurements18. The combination of pressure-sensitive structure and topology in MoTe2 makes this an exciting playground for the use of topological interfaces, with potential applications in a variety of quantum devices.

Methods

First-principles calculations

The total energy, structure optimization under pressure, and band structure and Fermi-surface calculations were performed by Quantum Espresso21, which is based on DFT, using a plane-wave basis set and fully relativistic all-electron projected augmented wave (PAW) potentials22. The 4s, 4p, 4d, and 5s electrons of Mo and the 4d, 5s, and 5p electrons of Te were treated as valence. We used 0.02 Ry Methfessel–Paxton smearing with wavefunction and charge density cut-off energies of 100 Ry and 800 Ry, respectively. The exchange-correlation interactions were described by the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof exchange-correlation functional23. The Brillouin-zone integration was performed using Monkhorst-Pack grids of special points with 16 × 8 × 4 for total energy and structure optimizations and 32 × 16 × 8 with tetrahedra method for electronic density of states and Fermi-surface calculations. The spin–orbit (SO) interactions and the weak inter-layer van der Waals (vdW) interactions were all included in our calculations. We used grimme-d224 vdW correction with parameter london—s6 = 0.6. The effect of electron correlations is included within DFT+U method with U = 3.0 eV for the Mo 4d-states. Including electron correlation brings the calculated band structure and Fermi surface into an excellent agreement with quantum oscillation and ARPES measurements, as discussed in Supplementary Information and also found in other very recent studies25,26. Fermi-surface sheets and SdH orbits are visualized by our custom python code using Mayavi27. The quantum oscillation frequencies/orbits and their angle dependence were calculated using the skeaf code28.

Crystal synthesis

Large single crystals were grown using the Te self flux method described elsewhere12 using high purity Mo powder (5N metals basis excluding W, Alpha Aesar), and Te shot (6N, Alpha Aesar). High sample quality has been confirmed by X-ray and neutron diffraction, stoichiometry has been confirmed by wavelength dispersive spectroscopy, and the samples measured have residual resistivity ratios >1000.

Structural measurements

Determinations of the temperature and pressure-dependent crystal structure were made using elastic neutron scattering measurements at 14.7 meV on the BT-4 triple-axis spectrometer at the NIST Center for Neutron Research using a collimation and filter setup of open-pg-40’-pg-s-pg-40’-120’, where pg refers to pyrolytic graphite. Single crystals were mounted in a steel measurement cell aligned in the H0LM zone, and He was supplied as a pressure medium to maintain hydrostatic pressure conditions as described elsewhere12. The Td and T’ phases and their volume fractions were identified from the position and intensity of (201)M reflections, which both split in 2θ and shift in ω in the T’ phase. Rocking curves and ω–2θ scans were taken at each pressure and temperature. Scans along (00L) from (2 0 0.5) to (2 0 4.5) were also obtained at 0.8 GPa in all Td or T’ condition, as well as in the mixed region at both 0.8 and 1 GPa to look for possible superstructure reflections. None were observed.

Transport measurements

A nonmagnetic piston-cylinder pressure cell was used for transport measurements under pressure up to 1.8 GPa, using a 1:1 ratio of n-Pentane to 1-methyl-3-butanol as the pressure medium and superconducting temperature of lead as pressure gauge at base temperature.

All transport measurements were performed on the same MoTe2 crystal with 110-μm thickness using four-point contacts made with silver epoxy. The pressure dependence of the superconducting transition and structural transition12 were determined in a Quantum Design PPMS and dilution refrigerator in the first pressure run (1 atm to 1.8 Gpa and back to 1 atm). The SdH oscillations were measured in a PPMS and dilution refrigerator (only 0.6 Gpa) in the second pressure run (1 atm to 1.8 Gpa and back to 1 atm) and in an Oxford Instruments Heliox at 0.3 K and 6–18 T in a third pressure run (pressure range below 1.8 Gpa). The identification of commercial equipment does not imply endorsement by NIST.