Abstract
Here we investigate antiferromagnetic Eu5In2Sb6, a nonsymmorphic Zintl phase. Our electrical transport data show that Eu5In2Sb6 is remarkably insulating and exhibits an exceptionally large negative magnetoresistance, which is consistent with the presence of magnetic polarons. From ab initio calculations, the paramagnetic state of Eu5In2Sb6 is a topologically nontrivial semimetal within the generalized gradient approximation (GGA), whereas an insulating state with trivial topological indices is obtained using a modified Becke−Johnson potential. Notably, GGA + U calculations suggest that the antiferromagnetic phase of Eu5In2Sb6 may host an axion insulating state. Our results provide important feedback for theories of topological classification and highlight the potential of realizing clean magnetic narrow-gap semiconductors in Zintl materials.
Similar content being viewed by others
Introduction
Narrow-gap semiconductors exhibit a breadth of striking functionalities ranging from thermoelectricity to dark matter detection1,2. More recently, the concept of topological insulating phases in bulk materials has renewed the interest in this class of materials3,4,5. Independent of the target application, a primary goal from the experimental point of view is the synthesis of genuine insulators free of self doping. Materials design is usually guided by simple electron count (e.g. tetradymite Bi2Te36), correlated gaps (e.g. Kondo insulators SmB67 and YbB128) or the Zintl concept (e.g. Sr2Pb9 and BaCaPb10). Zintl phases are valence precise intermetallic phases formed by cations (alkaline, alkaline-earth and rare-earth elements) and covalently bonded (poly)anionic structures containing post-transition metals. The electron transfer between these two entities gives rise to an insulating state, whereas the inclusion of rare-earth elements allows for magnetism, which breaks time-reversal symmetry and may promote new quantum ground states11,12,13.
The myriad of crystal structures within the Zintl concept provides a promising avenue to search for clean semiconductors. Here we experimentally investigate Zintl Eu5In2Sb6 in single crystalline form. Low-carrier density magnetic materials containing Europium are prone to exhibiting colossal magnetoresistance (CMR)14,15,16,17,18. The strong exchange coupling between the spin of the carriers and the spins of the Eu2+ background causes free carriers at low densities to self-trap in ferromagnetic clusters around the Eu sites, which gives rise to a quasiparticle called magnetic polaron19. This quasiparticle has been identified in several Zintl materials ranging from simple cubic EuB617,20 to monoclinic Eu11Zn4Sn2As1218. Most CMR compounds have a ferromagnetic ground state, including doped magnanites RE1 − xAxMnO3 (RE = rare-earth, A = divalent cation) in which CMR was first observed21,22. EuTe and Eu14MnBi11, however, revealed the possibility of realizing CMR in antiferromagnets14,16,23, which also brings promise for applications due to their small stray fields24.
Additionally, nonsymmorphic symmetries are expected to be particularly powerful in creating protected band crossings and surface states, which provide an additional organizing principle within the Zintl concept25,26. For instance, Wieder et al. predicted that Zintl Ba5In2Sb6, the non-f analog of Eu5In2Sb6, hosts fourfold Dirac fermions at \(\bar{M}\) connected to an hourglass fermion along \(\bar{\Gamma }\bar{X}\)27. Recent attempts to theoretically catalog all known uncorrelated materials indicate that Ba5In2Sb6 may be classified as a topological insulator28,29 or trivial insulator30,31. This discrepancy begs for an experimental investigation.
Eu5In2Sb6, just like its Ba analog, crystallizes in space group Pbam. As expected from the 4f localized moments in multiple sites, Eu5In2Sb6 orders antiferromagnetically at TN1 = 14 K in a complex magnetic structure. Remarkably, CMR sets in at 15TN1 and is accompanied by an anomalous Hall component. Our data collectively point to the presence of magnetic polarons. To shed light on the topology of the band structure of Eu5In2Sb6, we have performed first-principles calculations using different functionals and magnetic phases. Though an insulating state with trivial topological indices is obtained using modified Becke−Johnson (mBJ) functional in the paramagnetic state, topological nontrivial states with strong indices emerge in the generalized gradient approximation (GGA) + U calculations within putative antiferromagnetic states.
Results
Magnetic susceptibility measurements
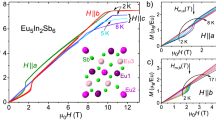
We first discuss the thermodynamic properties of Eu5In2Sb6 single crystals. Figure 1a highlights the complex anisotropy in the low-temperature magnetic susceptibility of Eu5In2Sb6. Two magnetic transitions can be identified at TN1 = 14 K and TN2 = 7 K, in agreement with previous measurements on polycrystalline samples32. One can also infer that the c-axis is the magnetization hard-axis and that the moments lie in the ab-plane. No hysteresis is observed between zero-field-cooled and field-cooled measurements at 0.1 T, which rules out hard ferromagnetic order or spin-glass behavior; however, a small in-plane ferromagnetic component (0.06 μB) is observed at very low fields (B ≤ 0.1 T), indicative of a complex magnetic structure with canted moments (see Supplementary Fig. 1).
a Magnetic susceptibility, χ(T), in both zero-field-cooled (ZFC) and field-cooled (FC) sweeps. Inset shows χT. Black solid line shows the high-temperature CW fit. b Magnetization vs applied field at 2 K. Inset shows high-field magnetization data at 4 K. c Zero-field specific heat as a function of temperature. Inset shows C/T at different applied fields.
The inset of Fig. 1a shows the product of magnetic susceptibility and temperature as a function of temperature. At high temperatures (T > 225 K), a Curie–Weiss (CW) fit yields a ferromagnetic (FM) Weiss temperature of θ = 30 K despite the antiferromagnetic (AFM) order at low temperatures, which further corroborates the presence of a complex magnetic configuration with multiple exchange interactions. The inverse of the magnetic susceptibility is shown in Supplementary Fig. 3. The CW fit also yields an effective moment of 8 μBEu−1, in good agreement with the Hund’s rule moment of 7.94 μBEu−1 for Eu2+. In fact, our X-ray absorption spectra at the Eu L edges33 confirm that all three Eu sites are divalent (see Supplementary Fig. 5). Previous X-ray absorption studies observed a finite Eu3+ component, which could be due to an impurity phase present in polycrystalline samples32. The fully divalent character of europium in Eu5In2Sb6 has been recently confirmed by Mossbauer measurements34.
Notably, our magnetic susceptibility data deviate from the CW fit at temperatures well above the ordering temperature (inset of Fig. 1a). In purely divalent compounds such as Eu5In2Sb6, Eu2+ is a localized S-only ion (J = S = 7/2), which implies crystal-field and Kondo effects to be negligible to first order. As a result, the deviation from a CW fit indicates the presence of short-range magnetic interactions as observed previously in the manganites RE1 − xAxMnO3 (RE = rare-earth, A = divalent cation). Based on small-angle neutron scattering measurements, this deviation was argued to be due to the formation of magnetic polarons35. As temperature decreases, magnetic polarons are expected to grow in size and eventually overlap when nξ3 ≈ 1, where n is the carrier density and ξ is the magnetic correlation length36. The inset of Fig. 1a shows a sharp decrease in χ(T)T at T* ~ 40 K, which reflects the onset of strong antiferromagnetic correlations between polarons. Figure 1b shows the low-temperature anisotropic magnetization of Eu5In2Sb6. The hard c-axis magnetization increases linearly with field, whereas a field-induced transition is observed within the basal plane before saturation is reached at about 10 T (inset of Fig. 1b). Figure 1c shows the temperature dependence of the specific heat, C, at zero field. In agreement with magnetic susceptibility data, C/T exhibits two phase transitions at TN1 and TN2 as well as a magnon contribution below TN2, typical of Eu2+ compounds. The entropy recovered at TN1 is about 90% of Rln8 (not shown), the expected entropy from the Eu2+ (J = 7/2) ground state. The extrapolation of the zero-field C/T to T = 0 gives a Sommerfeld coefficient of zero within the experimental error, indicating that Eu5In2Sb6 is an insulator with very small amounts of impurities. A Schottky-like anomaly at about 35 K indicates the presence of short-range correlations, in agreement with magnetic susceptibility data at T*. The inset of Fig. 1c displays the field dependence of the low-temperature transitions when field is applied along the b-axis. The transitions are mostly suppressed by 9 T, in agreement with the saturation in magnetization.
Electrical transport measurements
We now turn our attention to electrical transport data. Figure 2a shows the temperature-dependent electrical resistivity, ρ(T), of Eu5In2Sb6 measured with current along the c-axis. Remarkably, ρ(T) rises by almost six orders of magnitude in the paramagnetic state, in agreement with the clean insulating response observed in C/T but in stark contrast to ρ(T) measurements in polycrystals37. Below TN1, ρ(T) decreases by three orders of magnitude, pointing to the overlap of magnetic polarons within the antiferromagnetic state. Finally, at lower temperatures ρ(T) rises again, and a small kink is observed at TN2.
a Temperature-dependent electrical resistivity, ρ(T), at zero field. Electrical current was applied along the c-axis. Inset shows an activated log ρ vs 1/T plot. b ρ(T) in a log plot. Inset shows a zoom in the low-temperature region. c ρ(T) at various magnetic fields applied long the b-axis. Inset shows MR vs reduced magnetization (M/Ms) squared. d MR vs applied field at various temperatures.
The high-temperature electrical resistivity can be fit to an activated behavior given by \({\rho }_{0}{\tilde{T}}^{n}\exp ({E}_{{\rm{a}}}/{k}_{{\rm{B}}}T)\) (inset of Fig. 2a), where \(\tilde{T}\) is the reduced temperature. For n = 0, the Arrhenius plot yields a narrow gap of 40 meV whereas a slightly larger energy is extracted when n = 1 for adiabatic small-polaron hopping conduction38. From these data alone, it is not possible to differentiate between the two mechanisms. Nevertheless, the activated behavior breaks down at about T* ~ 40 K, indicating that another mechanism is present. This energy scale is more pronounced in a log plot shown in Fig. 2b.
The evolution of the CMR in Eu5In2Sb6 is summarized in Fig. 2d. Though the negative magnetoresistance is small at room temperature, it rapidly increases below about 15TN1. At liquid nitrogen temperatures (T ~ 75 K), for instance, the MR reaches −50% at only 3 T and −94% at 9 T. Ultimately, the MR peaks at −99.999% at 9 T and 15 K. This is, to our knowledge, the largest CMR observed in a stoichiometric antiferromagnetic compound.
Hall measurements provide valuable information on the type of carriers and the scattering mechanisms in a material. Figure 3 shows the Hall resistivity, RH ≡ ρxz, for fields applied along the b-axis of Eu5In2Sb6. At room temperature, RH is linear, as expected from a nonmagnetic single-band material (inset of Fig. 3a). The positive slope, R0, implies positive (hole) carriers and a carrier density of nh = 1/R0e = 1017/cm3, typical of narrow-gap semiconductors.
As the temperature is lowered, however, a nonlinear RH component sets in at about 15TN1, the same temperature at which CMR emerges. As the band structure of this band insulator is not expected to change dramatically in this temperature range, our result may indicate that the formation of magnetic polarons is responsible for the anomalous Hall effect (AHE). We note, however, that the presence of multiple carriers cannot be ruled out at this time. Though the ferromagnetic nature of the magnetic polaron cluster is a natural explanation for the anomalous contribution, a quantitative analysis of the various intrinsic and extrinsic contributions to the AHE will require determining the anisotropic conductivity tensor using micro-fabricated devices, including the region below 50 K.
Electron spin resonance measurements
We complete our experimental investigation with microscopic electron spin resonance (ESR) measurements. Electron spin resonance is a site-specific spectroscopic technique, and Eu2+ ions are particularly suitable paramagnetic probes because of their S-only state39,40. The Eu2+ ESR spectra of Eu5In2Sb6 in the paramagnetic state, shown in Fig. 4, consists of a single unresolved resonance (i.e., no fine or hyperfine structure). The ESR linewidth, ΔH, provides information on the interactions of the spins with their environment and their motion. In the case of semimetallic EuB6, the Eu2+ΔH was claimed to be dominated by spin-flip scattering due to the exchange between 4f and conduction electrons39. As a result, ΔH narrows at higher fields due to a reduction in the spin-flip scattering, consistent with the presence of magnetic polarons. The linewidth of Eu5In2Sb6 also narrows at higher fields (Q-band) when compared to low fields (X-band), though not as strongly as in EuB639. This narrowing further indicates that the resonance is homogeneous in the paramagnetic state. In the case of a small-gap insulator as Eu5In2Sb6, the Eu2+ ESR linewidth is dominated by spin−spin interactions39,41,42. The resulting relaxation mechanism is set by T2, the spin−spin relaxation time, which in turn is affected by the distribution of Eu−Eu exchange interactions and internal fields. An applied magnetic field causes an increase in T2 as the size of the ferromagnetic polaron grows, which results in the observed ESR line narrowing. At the same time, the g-value decreases as a function of magnetic field, which indicates an antiferromagnetic inter-polaron coupling. Therefore, our ESR results are also consistent with the presence of magnetic polarons in Eu5In2Sb6. More detailed ESR measurements will be the focus of a separate study.
Band structure calculations
To shed light on the possible topological nature of the band structure of Eu5In2Sb6, we perform band structure calculations in the paramagnetic state by taking the 4f orbitals of Eu as core states, as shown in Fig. 5. Both barium and europium are divalent in the 526 structure, and our experimental results imply that europium has a well-localized f-electron contribution. One would therefore naively expect that the band structure and topology of Eu5In2Sb6 are similar to that of Ba5In2Sb6, whose topology is not indicated by any symmetry indicators but can be characterized by nontrivial connecting pattern in the Wilson bands27.
Calculations in the paramagnetic state using the GGA + SOC method are shown in the left panel with the band representations near Γ point indicated in the inset. Calculations in the paramagnetic state using the mBJ method with cMBJ = 1.18 are shown in the right panel. The band inversion disappears and a trivial band gap of about 10 meV opens along the Y−Γ direction.
Remarkably, GGA + SOC calculations in the paramagnetic state of Eu5In2Sb6 indicate a semimetal state with one extra band inversion compared to Ba5In2Sb6 at the Γ point. Because there are no symmetry-protected band crossings between the valence and conduction bands at any k-point, a k-dependent chemical potential can be defined, which yields a fully gapped state. By calculating the topological indices of the bands below the k-dependent chemical potential, we find that the extra band inversion at Γ point yields a strong topological insulator with (z2; z2w,1z2w2z2w,3) = (1; 000), where z2 is strong index and z2w,i is weak index43, as shown in Fig. 5a. Compared with our experimental results, however, the ab initio calculation with the GGA functional incorrectly predicts Eu5In2Sb6 to be semimetallic. Considering the possible underestimation of the band gap in semiconductors by the GGA functional, we have also performed band structure calculations using the mBJ potential with a coefficient cMBJ = 1.18, which was obtained self-consistently. As shown in Fig. 5b, the band inversion near the Γ point disappears, and a small gap opens along the Γ−Y path. The topological indices (z2; z2w,1z2w2z2w,3) are computed to be (0;000). In fact, surface states are not detected by our electrical transport measurements. Scanning tunneling microscopy and angle-resolved photoemission measurements will be valuable to confirm the absence of in-gap states.
We now investigate the topology of Eu5In2Sb6 in the magnetically ordered state. Because the magnetic structure of Eu5In2Sb6 has not been solved yet, we investigate theoretically, using the GGA + U + SOC approach, three A-type AFM phases with the easy axis along different directions. All of the antiferromagnetic phases are theoretically characterized by the so-called Type-IV magnetic space groups (MSGs) with inversion symmetry. The magnetic topological quantum chemistry theory therefore describes the topology of these MSGs by an index group (\({Z}_{4}\times {Z}_{2}^{3}\)), as proposed recently44. From the calculations detailed in Supplementary Fig. 5, the magnetic moment is about 7 μB/Eu, and the energy difference between the different phases is within 3 meV per unit cell. From the results tabulated in Supplementary Table 1, all three AFM phases are axion insulators with strong indices \(({z}_{4},{z}_{{2}_{1}},{z}_{{2}_{2}},{z}_{{2}_{3}})=(2,0,0,0)\). By comparing the band structures for three different AFM phases, the polarized 4f states do not change the band inversion characteristics of the paramagnetic state but induce a small exchange splitting near the Fermi level. Though the AFM structure at low temperatures has yet to be determined experimentally, we proposed that this phase is an axion insulator candidate that preserves inversion symmetry.
Discussion
The magnetic polaron picture is fully consistent with our data. At high temperatures (~15TN1 = 210 K), the formation of isolated magnetic polarons is manifested in magnetic susceptibility measurements via a deviation from the Curie−Weiss law (inset of Fig. 1a) and in electrical resistivity measurements via the onset of negative magnetoresistance (Fig. 2c). As the temperature is further lowered, these polarons increase in size until they start to interact at T* giving rise to a sharp decrease in the χT plot, a Schottky anomaly in the specific heat data (Fig. 1c), and an anomaly in electrical resistivity measurements (Fig. 2b). At TN1, the polarons coalesce and become delocalized, which gives way to a drastic increase in conductivity. Though the delocalization temperature virtually coincides with TN1 at zero field, delocalization is expected to occur at higher temperatures as the size of the polarons increase in field. Antiferromagnetic-driven T*, however, is suppressed in field. This opposite field dependence causes the delocalization temperature and T* to merge into one at about 3 T, which gives rise to a resistivity maximum above TN1 that moves to higher temperatures in field (see Supplementary Fig. 7). Importantly, the increase in size of magnetic polarons in applied fields also promotes large negative (termed colossal) magnetoresistance in the paramagnetic state. In fact, CMR sets in at about 200 K and peaks just above TN1, as shown in Fig. 2c.
Another characteristic of CMR materials is the scaling of the low-field MR with the square of the reduced magnetization, \(\Delta \rho /{\rho }_{0}=C{(M/{M}_{{\mathrm {sat}}})}^{2}\), where Msat is the saturation magnetization36,45. Just above TN1, this scaling is valid and yields C = 50 (inset of Fig. 2c). When electron scattering is dominated by magnetic fluctuations, the scaling constant C is proportional to n−2/3, n being the carrier density36. The scaling constant calculated this way (n ~ 1012/cm3 at 15 K) is four orders of magnitude higher than the experimentally determined constant, which is an indication of a distinct mechanism. Another notable exception is EuB6, for which the field-dependent resistivity was argued to be dominated by the increase in polaron size with field rather than by the suppression of critical scattering17,46. In fact, recent scanning tunneling microscopy measurements have directly imaged the formation of magnetic polarons in EuB620.
In summary, we investigate the thermodynamic and electrical transport properties of single crystalline Eu5In2Sb6, a nonsymmorphic Zintl antiferromagnetic insulator. Colossal magnetoresistance sets in at temperatures one order of magnitude higher than the magnetic ordering temperature, TN1 = 14 K, and peaks just above TN1 reaching −99.7% at 3 T and −99.999% at 9 T. This is, to our knowledge, the largest CMR observed in a stoichiometric antiferromagnetic compound. Our combined electrical transport and microscopic ESR measurements point to the presence of magnetic polarons that generate an anomalous Hall component. Our first-principles band structure calculations yield an insulating state with trivial topological indices in the paramagnetic state, whereas an axion insulating state emerges within putative antiferromagnetic states. Our results highlight that Zintl phases could provide truly insulating states in the search for topological insulators, and rare-earth elements provide a route for the discovery of topological interacting phenomena. In fact, Zintl EuX2As2 (X = In, Sn) have been recently proposed to be antiferromagnetic topological insulators47,48. The metallic-like behavior observed in electrical resistivity, however, suggests that these materials have a semimetallic ground state akin to EuB649.
Methods
Experimental details
Single crystalline samples of Eu5In2Sb6 were grown using a combined In-Sb self-flux technique. The crystallographic structure was verified at room temperature by both single-crystal diffraction using Mo radiation in a commercial diffractometer (see Supplementary Fig. 6) and powder diffraction using Cu radiation in a commercial diffractometer. Eu5In2Sb6 crystallizes in an orthorhombic structure (space group 55) with lattice parameters a = 12.553(5) Å, b = 14.603(2) Å and c = 4.635(1) Å. As shown in Supplementary Fig. 6, the observed mosaicity of the Bragg reflections is limited by the resolution of the diffractometer. The crystals have a rod-like shape, the c-axis is the long axis, and typical sizes are 0.5 mm × 0.5 mm × 3 mm. In addition, the stoichiometry of crystals was checked by energy dispersive X-ray spectroscopy (EDX). Magnetization measurements were performed in a commercial SQUID-based magnetometer. Specific heat measurements were made using the thermal relaxation technique in a commercial measurement system. Because of the difficulties in the synthesis of phase pure Ba5In2Sb6, no phonon background was subtracted from the data. A four-probe configuration was used in the electrical resistivity experiments performed using a low-frequency AC bridge. High-field magnetization measurements were performed in the 65 T pulse field magnet at 4 K at the National High Magnetic Field Laboratory at Los Alamos National Laboratory. Details of the magnetometer design are described in ref. 50. The sample was mounted in a plastic cup oriented with b-axis parallel to the magnetic field. The data were normalized by the low-field data obtained from a commercial SQUID magnetometer.
ESR measurements were performed on single crystals in X-band (f = 9.5 GHz) and Q-band (f = 34 GHz) spectrometers equipped with a goniometer and a He-flow cryostat in the temperature range of 4 K < T < 300 K.
Theoretical details
First-principle calculations were performed using the Vienna ab initio simulation package (VASP), and the GGA with the Perdew−Burke−Ernzerhof (PBE) type exchange correlation potential was adopted. The Brillouin zone (BZ) sampling was performed by using k grids with an 7 × 7 × 9 mesh in self-consistent calculations. In the paramagnetic state, we employed a europium pseudopotential with seven f electrons treated as core electrons. In the antiferromagnetic states, we performed the LSDA + U calculations with U = 5 eV for the three distinct magnetic structures.
Data availability
Data presented in this study are available from authors upon request.
References
Tomczak, J. M. Thermoelectricity in correlated narrow-gap semiconductors. J. Phys. Condens. Matter 30, 183001 (2018).
Hochberg, Y. et al. Detection of sub-MeV dark matter with three-dimensional Dirac materials. Phys. Rev. D 97, 015004 (2018).
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Moore, J. E. The birth of topological insulators. Nature 464, 194–198 (2010).
Hasan, M. Z. & Moore, J. E. Three-dimensional topological insulators. Annu. Rev. Condens. Matter Phys. 2, 55–78 (2011).
Cava, R. J., Ji, H., Fuccillo, M. K., Gibson, Q. D. & Hor, Y. S. Crystal structure and chemistry of topological insulators. J. Mater. Chem. C 1, 3176–3189 (2013).
Eo, Y. S. et al. Transport gap in SmB6 protected against disorder. Proc. Natl. Acad. Sci. USA 116, 12638–12641 (2019).
Sato, Y. et al. Unconventional thermal metallic state of charge-neutral fermions in an insulator. Nat. Phys. 15, 954–959 (2019).
Sun, Y. et al. Strain-driven onset of nontrivial topological insulating states in Zintl Sr2X compounds (X = Pb, Sn). Phys. Rev. B 84, 165127 (2011).
Wang, L.-L., Kaminski, A., Canfield, P. C. & Johnson, D. D. Different topological quantum states in ternary Zintl compounds: BaCaX (X = Si, Ge, Sn and Pb). J. Phys. Chem. C 122, 705–713 (2018).
Chang, C.-Z. Marriage of topology and magnetism. Nat. Mater. 19, 484–485 (2020).
Yu, R. et al. Quantized anomalous Hall effect in magnetic topological insulators. Science 329, 61–64 (2010).
Zhang, D. et al. Topological axion states in the magnetic insulator MnBi2Te4 with the quantized magnetoelectric effect. Phys. Rev. Lett. 122, 206401 (2019).
Shapira, Y., Foner, S., Oliveira, N. F. & Reed, T. B. EuTe. II. Resistivity and Hall effect. Phys. Rev. B 5, 2647–2657 (1972).
Chan, J. Y., Kauzlarich, S. M., Klavins, P., Shelton, R. N. & Webb, D. J. Colossal magnetoresistance in the transition-metal Zintl compound Eu14MnSb11. Chem. Mater. 9, 3132–3135 (1997).
Chan, J. Y., Kauzlarich, S. M., Klavins, P., Shelton, R. N. & Webb, D. J. Colossal negative magnetoresistance in an antiferromagnet. Phys. Rev. B 57, R8103–R8106 (1998).
Süllow, S. et al. Magnetotransport in the low carrier density ferromagnet EuB6. J. Appl. Phys. 87, 5591–5593 (2000).
Devlin, K. P. et al. Eu11Zn4Sn2As12: a ferromagnetic Zintl semiconductor with a layered structure featuring extended Zn4As6 Sheets and ethane-like Sn2As6 units. Chem. Mater. 30, 7067–7076 (2018).
Kasuya, T. & Yanase, A. Anomalous transport phenomena in Eu-chalcogenide alloys. Rev. Mod. Phys. 40, 684–696 (1968).
Pohlit, M. et al. Evidence for ferromagnetic clusters in the colossal-magnetoresistance material EuB6. Phys. Rev. Lett. 120, 257201 (2018).
Jin, S. et al. Thousandfold change in resistivity in magnetoresistive La-Ca-Mn-O films. Science 264, 413–415 (1994).
Salamon, M. B. & Jaime, M. The physics of manganites: structure and transport. Rev. Mod. Phys. 73, 583–628 (2001).
Sakurai, H. Novel colossal magnetoresistance in NaCr2O4. J. Kor. Phys. Soc. 63, 583–586 (2013).
Baltz, V. et al. Antiferromagnetic spintronics. Rev. Mod. Phys. 90, 015005 (2018).
Young, S. M. & Kane, C. L. Dirac semimetals in two dimensions. Phys. Rev. Lett. 115, 126803 (2015).
Parameswaran, S. A., Turner, A. M., Arovas, D. P. & Vishwanath, A. Topological order and absence of band insulators at integer filling in non-symmorphic crystals. Nat. Phys. 9, 299–303 (2013).
Wieder, B. J. et al. Wallpaper fermions and the nonsymmorphic Dirac insulator. Science 361, 246–251 (2018).
Bradlyn, B. et al. Topological quantum chemistry. Nature 547, 198–305 (2017).
Vergniory, M. G. et al. A complete catalogue of high-quality topological materials. Nature 566, 480–485 (2019).
Zhang, T. et al. Catalogue of topological electronic materials. Nature 566, 475–479 (2019).
Tang, F., Po, H. C., Vishwanath, A. & Wan, X. Comprehensive search for topological materials using symmetry indicators. Nature 566, 486–489 (2019).
Subbarao, U., Sarkar, S., Joseph, B. & Peter, S. C. Magnetic and X-ray absorption studies on the RE5X2Sb6 (RE = Eu, Yb; X = Al, Ga, In) compounds. J. Alloy. Compd. 658, 395–401 (2016).
Ruck, B. J. et al. Magnetic state of EuN: X-ray magnetic circular dichroism at the Eu M4,5 and L2,3 absorption edges. Phys. Rev. B 83, 174404 (2011).
Radzieowski, M. et al. On the divalent character of the Eu atoms in the ternary Zintl phases Eu5In2Pn6 and Eu3MAs3 (Pn = As-Bi; M = Al, Ga). Mater. Chem. Front. 4, 1231–1248 (2020).
Teresa, J. M. D. et al. Evidence for magnetic polarons in the magnetoresistive perovskites. Nature 386, 256–259 (1997).
Majumdar, P. & Littlewood, P. Magnetoresistance in Mn pyrochlore: electrical transport in a low carrier density ferromagnet. Phys. Rev. Lett. 81, 1314–1317 (1998).
Cordier, G. & Stelter, M. Sr5Al2Sb6 and Ba5In2Sb6: two new Zintl phases with different chain anions. Z. Naturforsch. B 43, 463–466 (1988).
Emin, D. & Holstein, T. Studies of small-polaron motion IV. Adiabatic theory of the Hall effect. Ann. Phys. 53, 439–520 (1969).
Urbano, R. R. et al. Magnetic polaron and Fermi surface effects in the spin-flip scattering of EuB6. Phys. Rev. B 70, 140401 (2004).
Rosa, P. F. S. et al. Electron spin resonance of the intermetallic antiferromagnet EuIn2As2. Phys. Rev. B 86, 094408 (2012).
Huber, D. L. Analysis of electron paramagnetic resonance experiments in colossal magnetoresistance materials. J. Appl. Phys. 83, 6949–6951 (1998).
Yang, Z., Bao, X., Tan, S. & Zhang, Y. Magnetic polaron conduction in the colossal magnetoresistance material Fe1−xCdxCr2S4. Phys. Rev. B 69, 144407 (2004).
Fu, L. & Kane, C. L. Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302 (2007).
Xu, Y. et al. High-throughput calculations of antiferromagnetic topological materials from magnetic topological quantum chemistry. Preprint at https://arxiv.org/abs/2003.00012 (2020).
Furukawa, N. Transport properties of the Kondo lattice model in the limit S = ∞ and D = ∞. J. Phys. Soc. Jpn. 63, 3214–3217 (1994).
Süllow, S. et al. Metallization and magnetic order in EuB6. Phys. Rev. B 62, 11626–11632 (2000).
Xu, Y., Song, Z., Wang, Z., Weng, H. & Dai, X. Higher-order topology of the axion insulator EuIn2As2. Phys. Rev. Lett. 122, 256402 (2019).
Li, H. et al. Dirac surface states in intrinsic magnetic topological insulators EuSn2As2 and MnBi2nTe3n+1. Phys. Rev. X 9, 041039 (2019).
Nie, S. et al. Magnetic semimetals and quantized anomalous Hall effect in EuB6. Phys. Rev. Lett. 124, 076403 (2020).
Detwiler, J. A. et al. Magnetization of UBe13 to 60 T. Phys. Rev. B 61, 402–404 (2000).
Acknowledgements
We acknowledge constructive discussions with Z. Fisk, S. Wirth, J. Muller, O. Erten and C. Kurdak. Synthesis and macroscopic measurements at low fields were supported by the U.S. Department of Energy (DOE) BES “Quantum Fluctuations in Narrow-Band Systems” project. High-field magnetization measurements were supported by the DOE BES “Science of 100 Tesla” project. S.K. acknowledges support from the LANL Director’s Postdoctoral LDRD program. The National High Magnetic Field Laboratory is supported by the National Science Foundation through NSF/DMR-1644779 and the State of Florida. Scanning electron microscope and energy dispersive X-ray measurements were performed at the Center for Integrated Nanotechnologies, an Office of Science User Facility operated for the DOE Office of Science. Electron spin resonance measurements were supported by FAPESP (SP-Brazil) grants no. 2018/11364-7, 2017/10581-1, 2012/04870-7, CNPq Grant no. 141026/2017-0, CAPES and FINEP-Brazil. We thank Diamond Light Source for the provision of beamtime under proposal MT18991. Work at UCL is supported by the UK Engineering and Physical Sciences Research Council (Grants No. EP/N027671/1 and No. EP/N034694/1) Theory efforts were supported by DOE de-sc0016239, NSF EAGER 1004957, Simons Investigator Grants, ARO MURI W911NF- 12-1-0461, the Packard Foundation, and the Schmidt Fund for Innovative Research. Y.X. and A. Bernevig were supported by Max Planck society. Z.W. received support from the National Natural Science Foundation of China (No. 11974395), the Chinese Academy of Sciences (CAS) (Grant No. XDB33000000), and the CAS Pioneer Hundred Talents Program.
Author information
Authors and Affiliations
Contributions
P.R. and F.R. conceived the project. P.R. and E.B. synthesized single crystals for the measurement. P.R. and S.T. performed electrical transport and specific heat measurements. J.T. performed magnetization measurements to 6 T. S.K., M.C., and N.H. performed magnetization measurements to 60 T. J.S. and P.P. performed electron spin resonance measurements. M.R., L.V., M.J., and A. Bombardi performed X-ray absorption measurements measurements. Y.X., Z.W., and A. Bernevig performed band structure calculations. P.R. wrote the manuscript with input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rosa, P., Xu, Y., Rahn, M. et al. Colossal magnetoresistance in a nonsymmorphic antiferromagnetic insulator. npj Quantum Mater. 5, 52 (2020). https://doi.org/10.1038/s41535-020-00256-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-020-00256-8
This article is cited by
-
Two-Stage Cryogenic HEMT-Based Amplifier for Low-Temperature Detectors
Journal of Low Temperature Physics (2024)
-
Magnetic and electronic properties unveil polaron formation in Eu\(_5\)In\(_2\)Sb\(_6\)
Scientific Reports (2023)
-
Intrinsic magnetic topological materials
Frontiers of Physics (2023)
-
Control of chiral orbital currents in a colossal magnetoresistance material
Nature (2022)
-
Field-induced metal-to-insulator transition and colossal anisotropic magnetoresistance in a nearly Dirac material EuMnSb2
npj Quantum Materials (2021)