Abstract
In magnetic Weyl semimetals, where magnetism breaks time-reversal symmetry, large magnetically sensitive anomalous transport responses are anticipated that could be useful for topological spintronics. The identification of new magnetic Weyl semimetals is therefore in high demand, particularly since in these systems Weyl node configurations may be easily modified using magnetic fields. Here we explore experimentally the magnetic semimetal PrAlGe, and unveil a direct correspondence between easy-axis Pr ferromagnetism and anomalous Hall and Nernst effects. With sizes of both the anomalous Hall conductivity and Nernst effect in good quantitative agreement with first principles calculations, we identify PrAlGe as a system where magnetic fields can connect directly to Weyl nodes via the Pr magnetisation. Furthermore, we find the predominantly easy-axis ferromagnetic ground state co-exists with a low density of nanoscale textured magnetic domain walls. We describe how such nanoscale magnetic textures could serve as a local platform for tunable axial gauge fields of Weyl fermions.
Similar content being viewed by others
Introduction
In Dirac and Weyl semimetals, the emergence of large Berry curvatures due to electron band degeneracies, or singular band touching points (Weyl nodes), leads to striking topological effects on conduction electrons1,2 that can be detected by measurements of negative magnetoresistance,3 and the anomalous Hall effect (AHE).4,5 In magnetic semimetals, it is known that both the size and direction of the magnetisation can generate Weyl nodes and shift their positions, which provides the possibility for magnetic field control of the Weyl node positions and the emergence of the AHE, a critical aspect of the nascent field of topological electronics.6
Experimentally, recent studies connecting the size of the AHE to Weyl-node induced Berry curvature in magnetic systems include antiferromagnetic (AFM) Mn3Sn,7,8 kagome ferromagnetic (FM) semimetal Co3Sn2S2,5 and the topological nodal line ferromagnetic semimetal Fe3GeTe2.9 Similarly, other works have connected the anomalous Nernst effect to the Berry curvature.10,11 In these studies, a theoretical description of the observations provides the direct link between topological properties of the band structure and magnetically sensitive observables. This motivates both experiments and computational material science aimed at the rational engineering of band structures and the prediction of new systems with magnetically sensitive topological properties.
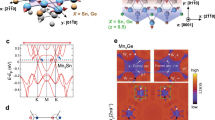
The rare-earth compounds RAlGe (R = Ce, Pr, La) with polar tetragonal I41md crystal structure were proposed recently to host either type-I and/or type-II Weyl fermions depending on the rare-earth ion.12 With CeAlGe13 and LaAlGe14 respectively proposed to be magnetic and nonmagnetic type-II Weyl semimetals, PrAlGe is expected to be a magnetic type-I Weyl semimetal with space-inversion symmetry broken by the polar lattice symmetry, and time-reversal symmetry broken at the onset of an easy-axis ferromagnetic ordering along c (Fig. 1a).12 As illustrated schematically in Fig. 1b, c, the momentum space locations of Weyl nodes are expected to vary with the size of the magnetisation, and display a time-reversal symmetry breaking configuration. An observable consequence is the emergence of anomalous Hall conductivity (AHC) in the plane normal to the direction of the magnetisation, which is due to the associated Berry curvature that remains finite when evaluated over the Brillouin zone below the Fermi energy.
a Polar tetragonal PrAlGe crystal structure (space group I41md, Nr. 109).66 Arrows indicate localised magnetic Pr moments aligned with the c-axis. Image made using VESTA.67 b, c Schematic of Weyl node locations in momentum space b with no magnetisation, and c in the presence of a spontaneous magnetisation Mz. The magnetisation shifts the Weyl nodes along directions determined by their chirality, contributing to an observable anomalous Hall effect (indicated by green arrows). d Phase diagram for PrAlGe in magnetic fields applied along the c-axis constructed from the present study. For magnetic fields below the saturation field Bs ~ 0.4 T, and temperatures below Tc ~ 16 K, a predominantly easy-axis ferromagnetic state is found by neutron scattering. This regime also hosts a large field-derivative of the Hall resistivity found in transport measurements, as shown by the colormap. The thick red solid line guides the eye for the boundary of the ferromagnetic phase. The thin red dashed line indicates a spin-freezing transition identified from magnetisation measurements. The white dashed line denotes a crossover between paramagnetic and field polarised regimes.
Here we apply a range of experimental techniques combined with first principle calculations to determine the relationship between magnetism and anomalous transport in PrAlGe summarised in Fig. 1d. Neutron scattering experiments reveal that below the critical temperature Tc, PrAlGe orders predominantly as an easy-c-axis ferromagnet. Notably we obtain further evidence that in part of the sample Pr moments tilt away from c over a characteristic nanometric length scale, which we interpret to be due to large FM domain walls. From electrical transport, we find the ground state displays no spontaneous anomalous Hall or Nernst signals in zero magnetic field. Both responses emerge sharply as small magnetic fields polarise the Pr moments along c. As seen in Fig. 1d, the magnetic field derivative of the Hall resistivity dρxy/dB is large and positive for T < Tc and magnetic fields B < Bs, where Bs is the saturation field. This observation signifies a contribution to the Hall resistivity beyond the usual Hall effect due to the anomalous Hall effect (AHE). We discuss the origin of the observed AHE and furthermore an anomalous Nernst effect (ANE), and provide theoretical support that the origin of both is due to the Weyl node-induced Berry curvature. PrAlGe is thus a magnetic Weyl semimetal that displays easily controllable transverse electronic responses using low applied magnetic fields that couple to the Pr magnetisation.
Results
Neutron scattering
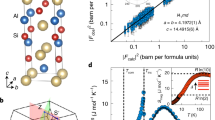
To determine the magnetic order in PrAlGe, we obtained powder neutron diffraction (PND) data at DMC, Paul Scherrer Institute (PSI) shown in Fig. 2a. Upon cooling below Tc, extra scattered intensity due to magnetism appears at scattering angles commensurate with the tetragonal point symmetry of the PrAlGe lattice, and can be described by a propagation vector Q = 0. Within a standard magnetic symmetry analysis, the Q = 0 propagation vector and spacegroup symmetry lead to three symmetry-allowed magnetic structure models that can be tested against the data. Figure 2b shows a successful refinement of the PND profile obtained at 1.6 K, which includes both the nuclear and magnetic scattering. The model for magnetic order is the standard irreducible representation Γ1 that describes a ferromagnetic (FM) order with moments aligned with the c-axis (Fig. 1a). Magnetic structure refinements according to the other allowed irreducible representations do not describe the observed magnetic scattering and are disregarded. This result shows that below Tc PrAlGe displays ferromagnetic correlations along the easy c-axis. The size of the ferromagnetic moment refined from the data is 2.29(3) µB/Pr.
a PND profiles obtained at DMC from PrAlGe at base T = 1.6 K below Tc, and at 20 K above Tc. Blue ticks denote the expected positions for nuclear peaks in the I41md space group. The inset shows a zoom of the {101} peak. b Refinement of the profile measured at T = 1.6 K (black line). The dark grey line shows the difference between the refined model profile and the data. The blue ticks denote the expected positions for nuclear peaks, and the green ticks denote possible positions for magnetic peaks according to the magnetic structure model. In both a and b, positions due to certain scattering planes are labelled. In b, * denotes scattering planes only allowed according to magnetic symmetry, the absence of intensity at the labelled peaks implies directly that the magnetic moments are aligned along c. The good profile refinement using fixed diffraction peak profile and shape parameters (see Methods) indicates the main scattering peak profiles are close to resolution-limited. SANS patterns obtained from PrAlGe at 1.9 K in c µ0H = 0, and d µ0H = 0.3 T, each after ZFC. A square beamstop is placed at the centre of the reciprocal space q = 0 to protect the detector from saturation due to the unscattered beam. The [001] axis is out of the page, and the [100] axis horizontal. Contour lines are plotted in steps of 0.5 on the logarithmic intensity scale, with the highest intensity contour drawn for Log Intensity = 4.5 counts per standard monitor (Cts./per Std. Monitor). e The log-log plot of the azimuthal-averaged SANS intensity versus |q| as a function of T in µ0H = 0. The solid lines are fits of the data according to the model described in the text and the Supplementary Note 3. f The total magnetic scattering contribution to the SANS profiles shown in e as a function of T in µ0H = 0. The solid line is a power law fit. g A µ0H -increasing scan of the magnetic SANS intensity at 1.9 K. In panels a, b, e, f, g, error bars indicating the statistical error are smaller than the symbol size.
To investigate the magnetic correlations further, small-angle neutron scattering (SANS) measurements were performed on a PrAlGe single crystal using the SANS-I instrument, PSI. SANS probes variations in the magnetisation density on the meso- to nanoscale, covering a typical range of real-space length scales from 5 to 500 nm. Therefore, the observation of magnetic SANS at low momentum transfers near |q| = 0 (which is the FM zone centre) can signify the existence of short-range spin correlations and/or magnetic spins correlated over nanometric length scales. From PrAlGe we indeed observe significant magnetic SANS to emerge for T < Tc and for B < Bs as shown in Fig. 2c–g. This observation suggests that in addition to dominant easy-c-axis ferromagnetic correlations, a co-existing nanoscale magnetic texture also exists in the sample below Tc.
Figure 2c shows the typical SANS pattern obtained at 1.9 K and µ0H = 0. The intensity is distributed uniformly in azimuth around the origin, and falls monotonically over an extended range of |q|. Figure 2e shows the azimuth-averaged one-dimensional profiles of SANS intensity versus |q| at various temperatures during a T-warming scan. Profiles obtained at T > Tc overlap and show no T-dependence, thus representing background scattering. Subtracting the high-T background from the data obtained for T < Tc leaves the magnetic scattering, the profile integral of which is shown at each T in Fig. 2f. The extracted intensity clearly disappears at Tc confirming its magnetic origin. A power law fit of the data near to Tc according to I∝(1-T/Tc)2β yields Tc = 15.1(1) K and β = 0.30(1). The latter is reasonably close to the value of 0.325 expected for the 3D Ising model.15 Finally, Fig. 2d, g show SANS data obtained after applying a magnetic field along the easy c-axis (µ0H || c) after a ZFC to 1.9 K. The magnetic SANS intensity is largely suppressed by ~ 0.3 T as the system is driven field-polarised.
Thermodynamic and transport measurements
Zero-field resistivity data shown in Fig. 3a reveal the ground state of PrAlGe is metallic. The flux-grown single crystal displays a residual resistivity of ρ0 = 102 µΩ cm and a modest residual resistivity ratio ρ(300 K)/ρ0 ~ 2. These values are comparable with those determined previously from resistivity measurements on a floating-zone grown sample,16 where it is found that ρ0 = 228 µΩ cm and ρ(300 K)/ρ0 ~ 1.7. Below Tc, Fig. 3a shows that the resistivity scales as T3. This scaling has a remarkably sharp cut-off at Tc and above this temperature the resistivity is well described by the standard Bloch-Grüneisen formula (minus a T3 correction term).
a Low T resistivity showing a clear cusp at Tc due to magnetic order. The red line shows a T3 scaling of the resistivity up to Tc. The inset show the T-dependent resistivity over a wider T range and a fit to the Bloch-Grüneisen formula minus a T3 correction term. b The magnetic moment as a function of temperature for magnetic fields as indicated. Saturation magnetisation is reached at 0.35 T. Each curve was measured zero-field-cooled (ZFC) and field-cooled (FC). Below the saturation field, the two curves bifurcate at Tg ~ 10 K (indicated by arrows), and the ZFC branch has a lower moment than the FC branch. c Hall resistivity as a function of T and magnetic field, showing clear resemblance to the magnetisation in panel b.
Figure 3b shows the dc magnetisation obtained on a floating-zone grown PrAlGe crystal for magnetic fields applied along the c-axis. At low fields, we observe a steep rise of the magnetisation upon cooling below Tc, followed by a further rise around 12 K suggested previously to be due to a spin-reorientation transition,16 and finally a weaker T-dependent plateau down to base T. With increasing field strength, the sharp features broaden, and the plateau saturates at 2.3 µB/Pr.
For fields above 0.1T until saturation Bs ~ 0.35 T, the magnetisation data display a characteristic temperature scale Tg ~ 10 K, below which the magnetisation is history dependent and field-cooled and zero-field-cooled (FC and ZFC) curves bifurcate. This feature is consistent with Tg corresponding to a spin-freezing transition temperature. In Supplementary Note 1, we characterise the regime below Tg further, presenting evidence in Supplementary Fig. 1 for the so-called thermoremnant magnetisation effect characteristic of slow spin glass-like dynamics.17,18
For fields of 0.1 T and higher, Fig. 3b shows Tg < Tc, consistent with reentrant spin glass behaviour.17,18 Previous work shows that at fields below 0.1 T Tg increases, and tends towards Tc in mT fields.16 In the reentrant spin-glass picture, the magnetic ground state displays a co-existence of spin components described as longitudinal and transverse with respect to an applied field. Here the longitudinal spin component is aligned with the Ising anisotropy axis, and leads to both the bulk magnetisation and the ferromagnetic Bragg peaks observed by PND. The spin-glass properties are expected to arise from a freezing at Tg of transverse spin components tilted randomly from the longitudinal axis. In principle, the tilted components can display short-range magnetic correlations observable as diffuse magnetic neutron scattering near to the ferromagnetic Bragg peaks.19,20 From PrAlGe, we find agreement between the size of the refined longitudinal Pr moment from the PND data and that determined from the bulk magnetisation, and there is no clear signature of diffuse scattering in the range of momentum transfer explored by PND. Therefore, we conclude that the transverse spin components are small enough such that any associated correlations lie below our detection limit. In turn, this observation supports the allocation for the origin of the magnetic SANS signal at low momentum transfer as less likely due to short-range correlations, and instead more likely due to a nanoscale magnetic texture, as we discuss later.
In Fig. 3c we show the thermal dependence of the Hall resistivity ρxy from a flux-grown crystal at various magnetic fields along the c-axis to display a strong resemblance to the magnetisation curves. In the low-field regime, both Hall resistivity and magnetisation display a sharp upturn across Tc and history-dependence below Tg - see also Supplementary Fig. 1. This, combined with the observation of a pronounced kink in the resistivity at Tc, confirms the direct coupling between the conduction electrons and the microscopic magnetism.
Anomalous Hall and Nernst effect in PrAlGe
Next we explore the coupling between itinerant and localised electrons from both Hall and Nernst effect measurements. Above Tc, both Hall and Nernst isotherms vary linearly for magnetic fields applied along the c-axis (Fig. 4a, b). The Hall coefficient RH = ρxy/µ0H is positive and increases mildly on cooling from 100 K down to Tc. Since RH > 0 hole-like carriers most likely dominate the charge transport. While the observed Hall coefficient is likely the result of compensated electron- and hole-like transport, it is interesting to apply a single band model RH = 1/ep where p is the hole carrier concentration. At T = 100 K, we obtain p = 7.8 × 1020 cm−3 (EF = 310 meV), placing PrAlGe in the semi-metallic regime. In a similar fashion, we obtain the Nernst coefficient ν = N/B = 20 nV/(K T) at T = 21 K, where the Nernst signal N is the ratio of the transverse electrical field and the longitudinal temperature gradient N = −Ey/(∇xT). With a Hall mobility µ = 8 × 10−3 T−1, this corresponds to ν/T = (4.6 × 10−4 V K−1) µ/TF, falling close to the universality curve [ν/T = (2.83 × 10−4 V K−1) µ/TF] for the quasiparticle Nernst effect.21,22 Above Tc, PrAlGe thus behaves as a standard ‘dirty’ semimetal.
a The Hall resistivity ρxy(µ0H) for various T. Below Tc, a kink at magnetic saturation is observed that gets more pronounced at lower T. Grey lines indicate extrapolations to zero magnetic field. b Nernst isotherms for temperatures as indicated, resembling the behaviour of the Hall isotherms. c The T-dependence of the anomalous Hall conductivity σxyA and Nernst effect NA extrapolated to zero magnetic field from data measured above magnetic saturation. Error bars are obtained by varying the fitting window to account for slight curvature. The red line is a fit of σxyA to a power law.
Below Tc, both the Hall and Nernst isotherms display a non-linear dependence on magnetic field. Compared with the regime above Tc, both the Hall and Nernst coefficients display a five-fold increase in the µ0H → 0 limit. In the field-polarised regime, the slope of the Hall resistivity and Nernst signal each fall back to values comparable to those found high above Tc, where no influence of the anomalous contribution persists. For the Hall effect this is also illustrated by plotting dρxy/dB in Fig. 1d. Whereas we observe no spontaneous Hall and Nernst signals in zero magnetic field, their non-linearity with magnetic field and their correlation to the magnetic properties strongly suggest magnetism to drive the emergence of anomalous transport signals.
To quantify the sizes of the observed anomalous Hall and Nernst effects in zero field, one way is by extrapolation from above the saturation field to the µ0H → 0 limit. In this fashion, an anomalous Hall conductivity -σAxy = ρxy/(ρ2xy + ρ2xx) ≈ ρxy/ρ2xx = 367 Ω−1 cm−1 is found at 2 K. An extrapolated anomalous Nernst response NA ≈ 28 nV/K is found at T = 11 K. As shown in Fig. 4c, both the onset of anomalous Hall and Nernst effects coincide with the onset of magnetism. The solid line corresponds to a power law fit of the anomalous Hall conductivity to the same equation as used for fitting the T-dependent SANS intensity (Fig. 2f). The fitted exponent β = 0.28(4) is in good agreement with the value obtained from the SANS data, reinforcing the conclusion that the anomalous transport is sensitive to local moments. In Supplementary Note 3 and Supplementary Fig. 3, we compare the sizes of σAxy and NA in PrAlGe with those observed in other semimetals, and find them to lie within the ranges typical of known relevant systems.
For comparison with theory, it is useful to connect the anomalous Nernst response NA with the off-diagonal Peltier coefficient αxyA = σxxNA + σxxS(σxyA/σxx + κxyA/κxx).23,24 Generally, insights into αxyA require measurements of the Seebeck coefficient S and thermal conductivity κ. In the present case of PrAlGe, Supplementary Fig. 2 shows S ≈ 0 at T ≈ 14 K. Thus in this temperature range, it is reasonable to assume αxyA ≈ σxxNA. At T = 14 K, we therefore estimate αxyA/T ≈14 µV/(K2 Ω cm). We note that due to the poor mobility, the normal state quasiparticle Nernst response is at a level where this relatively modest anomalous Nernst signal is accessible in our experiment.
Discussion
Based on our experimental results, we find that below Tc PrAlGe displays easy-c-axis ferromagnetism, with a refined ferromagnetic moment close to that measured from the bulk magnetisation. From SANS in particular, we evidence that a low volume of regions (estimated to be <1%) where the magnetisation tilts away from c over a nanometric length scale that enriches the magnetism. A minimal model for the |q|-dependence of the SANS intensity is one that describes a cycloidal-like tilting of neighbouring moments away from the c-axis and toward in-plane directions25,26 (see Supplementary Note 4 and Supplementary Figs. 4–6 for more details). Physically this description is compatible with being due to nanoscale ferromagnetic domain walls. Figure 2e shows a global fit of the model to all SANS profiles that provides a successful description of both the |q|-dependence of the intensity and a quantification of the nanometric magnetic length scale that varies from 14 nm at 2 K to ~ 25 nm close to Tc (see Supplementary Fig. 5).
In addition to a cycloidal-like tilting of moments, the SANS data at hand may also have contributions from the afore-mentioned short-ranged transverse spin correlations that form either within ferromagnetic domains or around crystallographic defects. Further studies by microscopy and polarised SANS techniques can lead to a more precise description of the nanoscale magnetisation texture. Nonetheless, an important common feature among all candidate models is the existence of magnetisation components tilted from the c-axis. While this could be considered surprising due to the clear easy-axis anisotropy of the system, non-collinear moment arrangements may arise due to either symmetry-allowed Dzyaloshinskii-Moriya interactions in the I41md spacegroup, and/or competing interactions between in-plane AFM or out-of-plane FM interactions.16 The latter can also be responsible for the observed spin glass-like behaviour below Tg similarly as for other Pr magnets.27,28,29,30
Next we turn to the origin of anomalous transport, focusing firstly on the anomalous Hall effect (AHE). In general, an AHE arises in any FM in the presence of spin-orbit coupling and includes both intrinsic (due to Berry curvature) and extrinsic (due to scattering) contributions. In FM Weyl semimetals, the origin of the intrinsic AHE is particularly transparent: it originates from the Weyl node-induced Berry curvature monopoles.2 Here we present first principles calculations to estimate the intrinsic σxyA in PrAlGe for a uniform magnetisation along c, and the limit T → 0. In accordance with ref. 31 extrinsic effects are not expected for our observed magnitude of σxx. Other scenarios that can also lead to a large Berry curvature (and hence AHE) include a presence of massive Dirac fermions32 or magnetic nodal lines.33,34 Due to the symmetry of the present crystal structure however, such effects are not expected for PrAlGe.
Following ref. 12 we calculated the band structure of PrAlGe finding multiple Weyl nodes existing close to the Fermi energy that do not lie on high symmetry points in the Brillouin zone (see Fig. 5a, Supplementary Note 5 and Supplementary Fig. 7 for more details). The anomalous hall conductivity is evaluated as
where \(A_{kn} = i\left\langle {u_{kn} | \partial _ku_{kn}} \right\rangle\) is the Berry connection, Ωkn is the Berry curvature, Ekn is the band energy, θ is the Heaviside step function, and the integral is over the Brillouin zone with [dk] ≡ d3k/(2π).3 When the magnetisation is along the z-axis, σxy is determined by the component Ωz of the Berry curvature. Figures 5a, b show how the distribution of Weyl nodes affects the Berry curvature (and σxyA), by plotting the calculated momentum space (k-)resolved Ωz obtained by summing over states below the Fermi level. Figure 5b shows the kz-resolved Berry curvature that is integrated in the xy-plane. We see sharp steps near kz = 0 and kz ~ 2π/c, indicating the presence of Berry curvature dipoles. These dipoles are formed by pairs of Weyl nodes of opposite chirality, separated in momentum space along the z direction. Note that if all the Weyl nodes would be exactly at the Fermi level, this curve would have sharp integer-valued steps at the kz coordinates of the Weyl points. However, since the Fermi surface has finite size, these steps are smooth. Figure 5a shows a colormap of the Berry curvature in the kx–ky plane together with the projection of the positions of the Weyl points. The large intensity around the Weyl nodes that are located close to the Fermi level demonstrate that they are indeed an important source for the observed anomalous Hall conductivity. Our calculations further reveal that large Berry curvature can also exist near avoided crossings that arise generally in the band structure, see Supplementary Note 5 and Supplementary Fig. 7 for further details.
a The negative Berry curvature integrated along kz as a function of kx, ky. Due to the C4 rotational symmetry of PrAlGe, we show only a quarter of the kx−ky plane. The circles indicate the projections of the Weyl nodes. Green indicates positive chirality and magenta negative chirality. The numbers correspond to the distance to the Fermi level in meV. Only one circle of each symmetric pair is indicated with a number. b The negative Berry curvature (summed over states below the Fermi level) integrated in the kx−ky plane in the range –π/a ≤ kx, ky ≤ π/a, as a function of kz. c Dependence of the calculated σxyA at T = 0 (blue line, left axis) and αxy/T at T = 14 K (green line, right axis) on the position of the chemical potential relative to the calculated Fermi level. The diamonds denote the experimentally determined values of σxyA at 2 K (red diamond) and αxy/T at 14 K (magenta diamond).
Figure 5c shows the calculated σxyA as the chemical potential is varied over a range of ± 0.1 eV around the calculated Fermi level. By varying the chemical potential, we take into account possible effects due to doping of the sample, or inaccuracies in the calculated band structure. We observe that the experimental estimate for σxyA at 2 K (red diamond in Fig. 5c) lies in broad agreement with those expected for the explored range of chemical potential, in particular for µ = EF, where the theoretical estimate is σxyA = 330 Ω−1 cm−1. The agreement between the experimental and the calculated values for σxyA supports the conclusion that the dominant origin for the observed anomalous Hall effect is the large Berry curvature induced by the Weyl nodes.
To consider a theoretical estimate of the Nernst coefficient, we computed αxy as35
which relates the Hall conductivity to the off-diagonal Peltier coefficient αxy and is valid also for the anomalous components. One can see in Fig. 5c that in contrast to the AHC which depends weakly on the chemical potential, the coefficient αxy fluctuates rapidly between positive and negative values. At µ = EF we find αxyA/T ≈ 20 µV/(K2 Ω cm), which is a factor 1.4 greater than the experimental value marked by a magenta diamond in Fig. 5c. Taking into account the complexity of both experiment and numerical calculation, this can be considered as good level of agreement. However, one should bear in mind that the strong dependence of αxyA on the chemical potential suggests that this quantity is also very sensitive to tiny details of the band structure, which probably lie beyond the accuracy of any modern ab initio method. On the other hand, the order of magnitude estimate |αxyA/T| < 100 µV/(K2 Ω cm) may be considered as a reliable estimation.
Finally, we discuss an important implication of our results, namely that in magnetic Weyl semimetals, spatially inhomogeneous magnetism such as that implied from the SANS data here in PrAlGe, may serve as a platform for tunable axial gauge fields of Weyl fermions. When coupled to electromagnetic gauge fields, Weyl semimetals display phenomena distinct to trivial metals due to the strong Berry field in momentum space near the Weyl nodes.2 When considered as relativistic fermions, different external perturbations on a Weyl semimetal find a unified description in terms of additional gauge fields coupled to the Weyl fermions. In particular, inhomogeneities can act as an axial gauge field which, unlike the real electromagnetic field, distinguishes the node chirality.36
The effects of axial magnetic fields have been realised in synthetic systems; two-dimensional arrays of CO molecules on copper,37 and three-dimensional acoustic metamaterials and photonic systems.38,39 In hard condensed matter systems, however, axial fields have been observed in two-dimensional graphene sheets,40 but never in three-dimensional systems. The spatially varying magnetisation observed by SANS here in PrAlGe potentially makes PrAlGe a natural host of tunable axial gauge fields at low temperatures and low magnetic fields.41 Since a spatially varying magnetisation profile in a Weyl semimetal is tantamount to a position-space-dependent Weyl node separation in momentum space, the variation of the Weyl node positions defines axial gauge fields in time-reversal breaking Weyl semimetals.41,42,43 Our measurements indicate that the proliferation of spatial inhomogeneities (i.e., domain walls) is tunable by changing the temperature and the external magnetic field. This suggests that PrAlGe is not only a magnetic Weyl system, but also a platform to tune axial gauge fields in a solid-state system. As discussed further in ref. 36 unique experimental signatures due to axial gauge fields are expected in quantum oscillation and transport measurements. Since domain averaging precludes the observation of the effects of axial gauge fields in the present bulk measurements, the future challenge is to probe the system on the local scale of a single domain, or equivalently a single nanometric domain wall, such that the signatures of axial gauge fields may be observed, and potentially exploited.
In summary, we applied neutron scattering, magnetisation, resistive and thermoelectric transport techniques to elucidate the direct link between magnetism and the anomalous Hall and Nernst effects in the magnetic Weyl semimetal PrAlGe. From transport data obtained in an easy c-axis magnetic field, we determined the size of the anomalous Hall conductivity -σxyA = 367 Ω−1 cm−1 at 2 K, and the anomalous Nernst signal NA ≈ 28 nV / K at 11 K. The sizes of -σxyA and NA are in good agreement with those obtained from first-principle calculations of the electronic structure in the presence of uniform c-axis magnetisation, and allows us to allocate their origin as due to the Berry curvature distribution. From SANS measurements in particular, we obtain further evidence in the ferromagnetic ground state for a small fraction of a co-existing nanoscale-sized magnetisation texture involving moments tilted away from c, which is likely due to nanoscale ferromagnetic domain walls. The existence of such nanoscale domain walls in a Weyl semimetal could make PrAlGe a hitherto unique local platform for tunable axial gauge fields of Weyl fermions in a three-dimensional solid. This makes the RAlGe system particularly promising to explore this physics, since the electronic structure, magnetism and nature of Weyl nodes is expected to depend strongly on the magnetic rare earth ion R.12,44,45 Therefore chemical substitution promises a straightforward route towards an easy low magnetic field control of both Weyl node types and possible axial gauge fields of Weyl fermions, complementing other control methods such as rotation of a uniform magnetisation,46 photo-induction,47,48 or external pressure-induction,49 and thus adding to the catalogue of functional responses that may be useful for applications.
During completion of this work we became aware of another study investigating the anomalous Hall effect in PrAlGe.50
Methods
Sample synthesis and characterisation
PrAlGe single crystals were obtained by both flux-growth and floating-zone growth techniques.16 As discussed in Ref. 16 crystals grown by the two different approaches exhibit similar physical properties, with small differences in characteristic transition fields and temperatures arising due to slight variations in stoichiometry. For the present study, energy dispersive x-ray spectra (EDS) analysis shows flux-grown crystals are typically Pr1.0(1)Al1.14(1)Ge0.86(1) with an Al excess and Ge deficiency with respect to the intended 1:1:1 stoichiometry. Floating zone-grown crystals are closer to the 1:1:1 stoichiometry within uncertainty, with typical composition Pr1.08(24)Al0.97(7)Ge0.95(17).
In the present study, the flux-grown crystals display Tc ~ 16 K and Bs (T = 2 K) ~0.4 T, while floating-zone crystals display Tc ~ 15 K and Bs (T = 2 K) ~0.3 T. Neutron and transport data have been obtained on samples prepared by both methods and are found to be in good general agreement.
Powder neutron diffraction
PND was performed using the DMC instrument at the Paul Scherrer Institute (PSI). The neutron wavelength was 2.457 Å. Diffraction profiles were collected from a 2 g powder sample grown from flux, and loaded into a standard cylindrical vanadium container. The sample temperature was controlled using a standard Orange cryostat with a base sample temperature 1.6 K. No magnetic field was applied. The refinement of the PND profile in Fig. 2b was performed using the FullProf software.51 In the software, the instrumental contributions to the diffraction peak shape are taken into account by using fixed peak profile and shape parameters determined from standard sample measurements done in the same instrument setup.
Small-angle neutron scattering
SANS measurements were performed using the SANS-I instrument at PSI. Most of the SANS data presented here were obtained on a 25-mg floating zone grown single crystal. For the experiment the crystal was mounted with a horizontal plane defined by orthogonal [001]−[100] tetragonal axes and [010] vertical. The [001] axis was aligned approximately with the incoming neutron wavevector ki, and loaded into a horizontal field cryomagnet installed at the SANS beamline such that µ0H || c || ki. The base sample T was 1.9 K.
SANS measurements made use of two instrument configurations to measure magnetic scattering over an extended range of momentum transfer. (1) an incident beam with neutron wavelength λn = 8 Å (Δλ/λ = 10 %) collimated over a distance of 18 m before the sample, with the scattered neutrons detected by a two-dimensional multi-detector placed 18 m behind the sample, and 2) an incident beam with λn = 8 Å (Δλ/λ = 10 %) collimated over 8 m before the sample, and scattered neutrons collected by the multi-detector placed 8 m behind the sample. Data measured in each configuration were normalised with respect to the incident beam intensity to cover a q-range 0.007 Å−1 < q < 0.055 Å−1. Exploratory measurements done upon rotating the sample and magnet together (‘rocking’ measurements) showed no angle-dependence of the scattered magnetic intensity on the detector over a range of ±5°. Therefore, we collected data at fixed sample angle, with a data collection time at each stabilised T, µ0H typically of 5–20 min. To obtain the one-dimensional profiles in Fig. 2c, the scattered intensity at constant magnitude in |q| on the two-dimensional multidetector was integrated over 360° around the beam axis (so-called azimuthal averaging). The SANS data reduction and analysis was performed using the GRASP52 and SASfit53 softwares, respectively.
Bulk magnetic and electrical measurements
Bulk magnetisation, electronic, and thermoelectric transport properties have been explored using commercial Quantum Design Magnetic and Physical Property Measurement Systems (MPMS and PPMS). For the resistivity experiments a Hall-bar electrical contact geometry was created. Good electrical contacts (~1 Ω) were established using DuPont 6838 silver paste cured at 500 °C for 10 min and subsequent application of short high voltage pulses. For the thermoelectric transport a home-built insert for the PPMS was used. The temperature gradient in the sample was held at ≈3% of the sample temperature and was measured with Cernox thermometers,54 while the voltage was measured using nanovoltmeters. For all measurements magnetic fields were applied along the easy-c-axis.
First-principles calculations
Electronic structure calculations were performed using the VASP code,55,56 within the GGA-PBE approximation57 for the exchange-correlation functional and employing the projector augmented-wave method.58,59 The Hubbard on-site energy U = 4 eV was used to push the f-electrons of Pr away from the Fermi level. In order to perform integration in (1a) over a fine grid of k-points, we construct the maximally localised Wannier functions (MLWF)60 by means of the Wannier90 code.61,62,63 The MLWF are chosen to reproduce the d and f electrons of Pr, as well as sp3 states of Al and Ge, and the upper edge of the frozen window for the band-disentanglement procedure64 is fixed at 1 eV above the Fermi level. Finally Eq. (1) is evaluated by means of the Wannier interpolation procedure,65 that we implemented in our Wannier19 code68. Wannier19 is a new Python code for evaluation of Brillouin-zone integrals of Berry curvature-related properties, that closely follows the postw90.x module of Wannier90 Fortran code, but with important improvements, that significantly speed-up the calculations and improve the result quality. Among the advances are usage of fast Fourier transform, explicit account of symmetries, and a recursive-adaptive refinement procedure, which recursively increases the density of k-points sampling around the points which give the major contribution. Technical details of the implementation of Wannier19 will be published elsewhere, and the code is freely available on github. The evaluation of Eq. (3) is much more susceptible to computational inaccuracies than the AHE in Eq. (1), in particular in terms of the BZ sampling at which the AHC is calculated. We find that to get a converged value of αxyA/T, we need a hyperfine grid of 432 × 432 × 432 k-points with a subsequent recursive refinement of 3% of the k-points.
Data availability
All experimental data presented in the figures that support the findings of this study are available at the Zenodo online repository with identifier https://doi.org/10.5281/zenodo.3568739.
Code availability
The Wannier19 code used for the first principle calculations of the anomalous transport is freely available without restriction online at: https://github.com/stepan-tsirkin/wannier19.
References
Bansil, A., Lin, H. & Das, T. Topological band theory. Rev. Mod. Phys. 88, 021004 (2016).
Armitage, N. P., Mele, E. J. & Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 90, 015001 (2018).
Huang, X. et al. Observation of the chiral-anomaly-induced negative magnetoresistance in 3D Weyl semimetal TaAs. Phys. Rev. X 5, 031023 (2015).
Suzuki, T. et al. Large anomalous Hall effect in a half-Heusler antiferromagnet. Nat. Phys. 12, 1119–1123 (2016).
Liu, E. et al. Giant anomalous Hall effect in a ferromagnetic kagome-lattice semimetal. Nat. Phys. 14, 1125–1131 (2018).
Tokura, Y., Kawasaki, M. & Nagaosa, N. Emergent functions of quantum materials. Nat. Phys. 13, 1056–1058 (2017).
Kuroda, K. et al. Evidence for magnetic Weyl fermions in a correlated metal. Nat. Mater. 16, 1090–1095 (2017).
Nakatsuji, S., Kiyohara, N. & Higo, T. Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature. Nature 527, 212–215 (2015).
Kim, K. et al. Large anomalous Hall current induced by topological nodal lines in a ferromagnetic van der Waals semimetal. Nat. Mater. 17, 794–799 (2018).
Sakai, A. et al. Giant anomalous Nernst effect and quantum-critical scaling in a ferromagnetic semimetal. Nat. Phys. 14, 1119–1124 (2018).
Guin, S. N. et al. Anomalous Nernst effect beyond the magnetization scaling relation in the ferromagnetic Heusler compound Co2MnGa. NPG Asia Mater. 11, 16 (2019).
Chang, G. et al. Magnetic and noncentrosymmetric Weyl fermion semimetals in the RAlGe family of compounds (R = rare earth). Phys. Rev. B 97, 041104 (2018).
Hodovanets, H. et al. Single-crystal investigation of the proposed type-II Weyl semimetal CeAlGe. Phys. Rev. B 98, 245132 (2018).
Xu, S.-Y. et al. Discovery of Lorentz-violating type II Weyl fermions in LaAlGe. Sci. Adv. 3, e1603266 (2017).
Gebhardt, W. & Krey, G. Phasenübergänge Und Kritische Phänomene (Vieweg, Braunschweig, 1980).
Puphal, P. et al. Bulk single-crystal growth of the theoretically predicted magnetic Weyl semimetals RAlGe (R = Pr, Ce). Phys. Rev. Phys. Rev. Mater. 3, 024204 (2019).
Mydosh, J. A. Spin glasses: redux: an updated experimental/materials survey. Rep. Prog. Phys. 78, 052501 (2015).
Mydosh, J. A. Spin Glasses An Experimental Introduction (Taylor & Francis, London, 1993).
Ryan, D. H. Recent Progress in Random Magnets (World Scientific, 1992).
Hennion, M., Mirebeau, I., Hennion, B., Lequien, S. & Hippert, F. Magnetic structure observed in an applied field in two kinds of re-entrant spin glasses. Europhys. Lett. 2, 393–399 (1986).
Behnia, K. The Nernst effect and the boundaries of the Fermi liquid picture. J. Phys. Condens. Matter 21, 113101 (2009).
Behnia, K. & Aubin, H. Nernst effect in metals and superconductors: a review of concepts and experiments. Rep. Prog. Phys. 79, 046502 (2016).
Onose, Y., Li, L., Petrovic, C. & Ong, N. P. Anomalous thermopower and Nernst effect in CeColn5: loss of entropy current in precursor state. Europhys. Lett. 79, 17006 (2007).
Shiomi, Y., Kanazawa, N., Shibata, K., Onose, Y. & Tokura, Y. Topological Nernst effect in a three-dimensional skyrmion-lattice phase. Phys. Rev. B 88, 064409 (2013).
Boucher, B., Chieux, P., Convert, P. & Tournarie, M. Small-angle neutron scattering determination of medium and long range order in the amorphous metallic alloy TbCu3.54. J. Phys. F Met. Phys. 13, 1339–1357 (1983).
Schmidt, P. W. Modern Aspects of Small-Angle Scattering (Kluwer Academic, 1995)
Krimmel, A. et al. Spin-glass behavior in PrAu2Si2. Phys. Rev. B 59, R6604–R6607 (1999).
Goremychkin, E. A. et al. Spin-glass order induced by dynamic frustration. Nat. Phys. 4, 766–770 (2008).
Anand, V. K., Adroja, D. T. & Hillier, A. D. Ferromagnetic cluster spin-glass behavior in PrRhSn3. Phys. Rev. B 85, 014418 (2012).
Anand, V. K. et al. Magnetic and transport properties of Pr2Pt3Si5. J. Magn. Magn. Mater. 324, 2483–2487 (2012).
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539–1592 (2010).
Ye, L. et al. Massive Dirac fermions in a ferromagnetic kagome metal. Nature 555, 638–642 (2018).
Chang, G. et al. Topological Hopf and chain link semimetal states and their application to Co2MnGa. Phys. Rev. Lett. 119, 156401 (2017).
Belopolski, I. et al. Discovery of topological Weyl fermion lines and drumhead surface states in a room temperature magnet. Science 365, 1278–1281 (2019).
Xiao, D., Yao, Y., Fang, Z. & Niu, Q. Berry-phase effect in anomalous thermoelectric transport. Phys. Rev. Lett. 97, 026603 (2006).
Ilan, R., Grushin, A. G. & Pikulin, D. I. Pseudo-electromagnetic fields in topological semimetals. Nat. Rev. Phys. https://www.nature.com/articles/s42254-019-0121-8 (2019).
Gomes, K. K., Mar, W., Ko, W., Guinea, F. & Manoharan, H. C. Designer Dirac fermions and topological phases in molecular graphene. Nature 483, 306–310 (2012).
Peri, V., Serra-Garcia, M., Ilan, R. & Huber, S. D. Axial-field-induced chiral channels in an acoustic Weyl system. Nat. Phys. 15, 357–361 (2019).
Jia, H. et al. Observation of chiral zero mode in inhomogeneous three-dimensional Weyl metamaterials. Science 363, 148–151 (2019).
Levy, N. et al. Strain-induced pseudo–magnetic fields greater than 300 tesla in graphene nanobubbles. Science 329, 544–547 (2010).
Grushin, A. G., Venderbos, J. W., Vishwanath, A. & Ilan, R. Inhomogeneous Weyl and Dirac semimetals: transport in axial magnetic fields and Fermi arc surface states from pseudo-Landau levels. Phys. Rev. X 6, 041046 (2016).
Cortijo, A., Ferreirós, Y., Landsteiner, K. & Vozmediano, M. A. Elastic gauge fields in Weyl semimetals. Phys. Rev. Lett. 115, 177202 (2015).
Pikulin, D., Chen, A. & Franz, M. Chiral anomaly from strain-induced gauge fields in Dirac and Weyl semimetals. Phys. Rev. X 6, 041021 (2016).
Soluyanov, A. A. et al. Type-II Weyl semimetals. Nature 527, 495–498 (2015).
Zyuzin, A. A. & Tiwari, R. P. Intrinsic anomalous Hall effect in type-II Weyl semimetals. JETP Lett. 103, 717–722 (2016).
Ghimire, M. P. et al. Creating Weyl nodes and controlling their energy by magnetization rotation. Phy. Rev. Res. 1, 032044 (2019).
Hübener, H., Sentef, M. A., De Giovannini, U., Kemper, A. F. & Rubio, A. Creating stable Floquet-Weyl semimetals by laser-driving of 3D Dirac materials. Nat. Commun. 8, 13940 (2017).
Menon, A., Chowdhury, D. & Basu, B. Photoinduced tunable anomalous Hall and Nernst effects in tilted Weyl semimetals using Floquet theory. Phys. Rev. B 98, 205109 (2018).
Zhou, Y. et al. Pressure-induced new topological Weyl semimetal phase in TaAs. Phys. Rev. Lett. 117, 146402 (2016).
Meng, B. et al. Large anomalous Hall effect in ferromagnetic Weyl semimetal candidate PrAlGe. APL. Materials 7, 051110 (2019).
Rodríguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Phys. B 192, 55–69 (1993).
Dewhurst, C. D., GRASP User Manual. Technical Report No. ILL03DE01T, Institut Laue- Langevin, Grenoble (2003), available at: www.ill.fr/lss/grasp.
Breßler, I., Kohlbrecher, J. & Thünemann, A. F. SASfit: a tool for small-angle scattering data analysis using a library of analytical expressions. J. Appl. Cryst. 48, 1587–1598 (2015).
Cyr-Choinière, O. et al. Enhancement of the Nernst effect by stripe order in a high-Tc superconductor. Nature 458, 743–745 (2009).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 48, 13115–13118 (1993).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Marzari, N., Mostofi, A. A., Yates, J. R., Souza, I. & Vanderbilt, D. Maximally localized Wannier functions: theory and applications. Rev. Mod. Phys. 84, 1419–1475 (2012).
Mostofi, A. A. et al. wannier90: A tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 178, 685–699 (2008).
Mostofi, A. A. et al. An updated version of wannier90: a tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 185, 2309–2310 (2014).
Pizzi, G. et al. Wannier90 as a community code: new features and applications. J. Phys. Condens. Matter. https://iopscience.iop.org/article/10.1088/1361-648×/ab51ff/meta (2019)
Souza, I., Marzari, N. & Vanderbilt, D. Maximally localized Wannier functions for entangled energy bands. Phys. Rev. B 65, 035109 (2001).
Wang, X., Yates, J. R., Souza, I. & Vanderbilt, D. Ab initio calculation of the anomalous Hall conductivity by Wannier interpolation. Phys. Rev. B 74, 195118 (2006).
Gladyshevskii, E. I., Nakonechna, N. Z., Cenzual, K., Gladyshevskii, R. E. & Jorda, J.-L. Crystal structures of PrAlxGe2−x compounds. J. Alloy. Compd. 296, 265–271 (2000).
Momma, K. & Izumi, F. VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272–1276 (2011).
Acknowledgements
We thank B. Fauqué for fruitful discussions. D.D., L.D. and J.K. acknowledge support by the Swiss National Science Foundation (SNF). D.D. acknowledges further support by the Forschungskredit of the University of Zurich, grant no. FK-18–088. L.D. is partially funded by the Swiss Government through Excellence scholarship. J.S.W. acknowledges funding from the SNF Sinergia Network “NanoSkyrmionics” Grant No. CRSII5_171003, and the SNF project 200021_188707. S.S.T. and T.N. acknowledge funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (ERC-StG-Neupert-757867-PARATOP). A.G.G. acknowledges financial support from the ANR under the grant ANR-18-CE30-0001-01 and the European Union’s Horizon 2020 research and innovation programme under grant agreement No 829044.
Author information
Authors and Affiliations
Contributions
The project was conceived and led by J.S.W., J.C., and T.N. Bulk magnetic and transport measurements were performed and analysed by D.D., L.D., Y.X., J.C. and A.S. Neutron experiments and data analysis were performed by J.S.W., L.K. and J.K.; J.K. developed the models for interpreting the SANS data. Theoretical calculations were done by S.S.T., T.N. and A.G.G. Samples were prepared by P.P. and E.P. The paper was prepared by D.D., S.S.T., J.C., T.N. and J.S.W. All authors reviewed the manuscript and agree with the results and conclusions.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Destraz, D., Das, L., Tsirkin, S.S. et al. Magnetism and anomalous transport in the Weyl semimetal PrAlGe: possible route to axial gauge fields. npj Quantum Mater. 5, 5 (2020). https://doi.org/10.1038/s41535-019-0207-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-019-0207-7
This article is cited by
-
Spin-orbit-splitting-driven nonlinear Hall effect in NbIrTe4
Nature Communications (2024)
-
Tunable positions of Weyl nodes via magnetism and pressure in the ferromagnetic Weyl semimetal CeAlSi
Nature Communications (2024)
-
Spin order and dynamics in the topological rare-earth germanide semimetals
Science China Physics, Mechanics & Astronomy (2024)
-
Weyl metallic state induced by helical magnetic order
npj Quantum Materials (2024)
-
Emergence of Weyl fermions by ferrimagnetism in a noncentrosymmetric magnetic Weyl semimetal
Nature Communications (2023)