Abstract
Despite its potential for device application, the nonmagnetic Zeeman effect has only been predicted and observed in two-dimensional compounds. We demonstrate that noncentrosymmetric three-dimensional compounds can also exhibit a Zeeman-type spin splitting, allowing the splitting control by changing the growth direction of slabs formed by these compounds. We determine the required conditions for this effect: (i) noncentrosymmetric including polar and nonpolar point groups, (ii) valence band maximum or conduction band minimum in a generic k-point, i.e., non-time-reversal-invariant momentum, and (iii) zero magnetic moment. Using these conditions as filters, we perform a material screening to systematically search for these systems in the AFLOW-ICSD database. We find 20 candidates featuring the Zeeman-type effect. We also find that the spin splitting in confined systems can be controlled by an external electric field, which in turns can induce a metal–insulator transition. We believe that this work will open the way for the discovery of novel fundamental effects related to the spin polarization control.
Similar content being viewed by others
Introduction
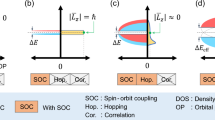
The manipulation of inversion and time-reversal (TR) symmetries have been the cornerstone of novel phenomena allowing the generation and control of spin-polarized states in crystalline materials, the principal goal of spintronics.1,2,3,4 The TR-symmetry breaking, which is usually induced by external magnetic fields or the intrinsic magnetic order, can lead to a separation in energy of bands with opposite spin, i.e., Zeeman spin splitting.5,6,7 In nonmagnetic compounds, the combination of the atomic-site polarity and bulk point group results in all possible structural configurations leading to intrinsic spin-polarized states.8,9,10 For instance, in bulk inversion asymmetry (IA) materials, the spin polarization is always accompanied by a spin splitting typically referred to as either Dresselhaus11 or Rashba effect12,13 according to the spin-texture orientation (see Fig. 1a). The split bands have the opposite helical in-plane spin-texture in Rashba semiconductors and the same helicity in band inverted Rashba semiconductors.14 In the Dresselhaus effect, the spin polarization is parallel to k (\(\langle \vec S\rangle \parallel \vec k\)) for kx = 0 and ky = 0. The band dispersion curves related to these effects, which are represented in Fig. 1b, have been characterized by spectroscopic measurements for many surfaces and interfaces,15,16,17,18 and can be described by a simplified Hamiltonian model,
where \({\cal{H}}_0 = \frac{{\hbar ^2k_\parallel ^2}}{{2m^ \ast }}1\), Ω(k) is the spin–orbit coupling (SOC) field, and σi are the Pauli matrices. Here, \(k_\parallel = k_x^2 + k_y^2\), m* is the effective mass of electrons, and 1 is the 2 × 2 unitary matrix. The specific form of Ω(k) depends on the material symmetry.19,20 For instance, in a two-dimensional system with \({\cal{C}}_3\) point group, the Rashba and Dresselhaus fields are written as ΩR = λR(−ky, kx, 0) and ΩD = λD(kx, ky, 0), respectively. The strength of the Rashba (Dresselhaus) field is given by the parameter λR (λD). The parameter λR is different from zero in systems featuring a nonzero electric dipole,21 which can be intrinsic or, as originally proposed by Rashba, induced by interfacing semiconductors or external electric fields.12,13 The Rashba effect is typically used for the electrical control of the spin polarization.22 For these reasons, IA materials have historically been the most promissory candidates for spintronic devices.2,3,4
Spin polarized states preserving the TR-symmetry. a Schematic representation of the band structure and spin-texture of systems featuring the Rashba, Dresselhaus, and nonmagnetic Zeeman effects. The arrows stand for the spin polarization orientation. In the Rashba and Dresselhaus effects, the bands (green and purple) cross each other at the origin of the BZ (Γ is a TR-invariant point). b Filters used in the materials prediction for each spin polarization phenomenon. The band structure without SOC is represented in black. After considering the SOC, for IA compounds, the bands split. The up and down spins are represented in blue and red, respectively. For compounds with IS, we have also represented each band separately to make evident the different spin components
Besides the Rashba and Dresselhaus effects, another kind of spin splitting in nonmagnetic IA compounds, whose spin texture is similar to the one observed in the magnetic Zeeman effect, is the so-called Zeeman-type spin splitting (See Fig. 1a). Despite its potential for device application, this nonmagnetic effect has only been predicted and observed in the two-dimensional WSe2 and MoS2.23,24,25 Unlike the Rashba and Dresselhaus splitting, the Zeeman-type splitting does not have a band crossing (see Fig. 1a) and has been related to the effect of an electric dipole or an external electric field.23 This suggests that this effect can only be induced in two-dimensional systems. Indeed, it has not been explored in three-dimensional compounds.
Here, we demonstrate that IA three-dimensional compounds can also exhibit a Zeeman-type spin splitting, allowing the splitting control by changing the growth direction of slabs formed by these compounds. For this purpose, we first establish the conditions for nonmagnetic spin-split bands. Using these conditions as filters, we perform a material screening in the AFLOW-ICSD database,26,27 i.e., a systematic search of fabricated materials. We find 20 binary three-dimensional compounds featuring the Zeeman-type effect. Aside from the prediction of large Zeeman splitting in the three-dimensional version of layered systems exhibiting this effect (the VBM in MoS2 and WS2 have a spin splitting of 187 and 510 meV, respectively), we also find large spin splitting in compounds that are not formed by van der Waals layered materials, such as, OsC, WN2, and SnTe, with splittings between 330 and 490 meV. A representative example of these non-magnetic Zeeman materials is the SnTe compound stabilizing the Zinc-Blende (ZB) structure.28 We confirm that in the SnTe slab, the Zeeman-type splitting depends on the growth direction, suggesting that the total electric dipole is modified by the surface induced dipole. Based on this, we then propose the electrical control of the Zeeman-type effect.
Results
Design principles and materials screening
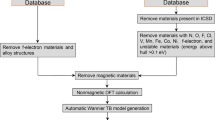
Based on the space group and chemical composition analyses, we determine the conditions that a material should meet to exhibit the Zeeman-type effect. Design principles are typically used as filters to predict or select compounds from the materials databases,29,30 e.g., AFLOW26,27 and materials project.31,32 By combining the materials screening with high-throughput density functional theory (DFT) calculations (see section “Methods”), we have an efficient approach to predict novel Zeeman-type semiconductors.
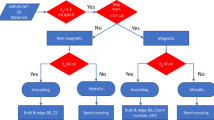
The Zeeman-type effect is the spin discrimination as a consequence of the inversion symmetry (IS) breaking at non-TR invariant k-points, rather than the effect of an intrinsic electric dipole, as we discuss below. We then define the conditions that a material should satisfy to exhibit the Zeeman-type effect: (i) IA and TR-symmetry (noncentrosymmetric bulk and nonmagnetic moment) and (ii) the VBM and CBM must take place at a non-TR-invariant k-point. In addition, a total electric dipole is not needed, allowing the presence of the Zeeman-type effect in compounds with polar and nonpolar point groups. These conditions are summarized in Fig. 1b. Specifically, the Zeeman-type splitting is related to noncentrosymmetric nonmagnetic materials, i.e., only compounds with bulk point groups Cn, Cnv, Dn (with n = 1, 2, 3, 4, and 6), S4, D2h, C3h, D3h, T, Td, and O could feature the nonmagnetic Zeeman effect. When the VBM or CBM take place at a TR-invariant k-point, the compounds with this bulk point groups are classified as Rashba or Dresselhaus semiconductors (see Fig. 1b). In addition, materials in other symmetries could feature the hidden-spin-polarization, which is characterized by spin-degenerated bands, as represented in Fig. 1b.
We use the previously established conditions as filters for a systematic search of nonmagnetic Zeeman materials. We perform a materials screening in the AFLOW-ICSD database,26,27 which contains information of ~59,000 fabricated materials. After eliminating compounds with the same formula, space group, and the number of atoms in the unit cell, we obtain 32,553 entries. In this work we will focus on binary compounds, what leads to a total of 8360 materials, which in turn can be divided into 1326 IA and 7034 IS materials. Among the IA compounds, we find 587 nonmagnetic gaped and 739 gapless magnetic materials. Finally, only 20 nonmagnetic IA compounds exhibit either the CBM or the VBM at non-TR-invariant k-points. Detailed information of the predicted Zeeman-type materials is presented in Table 1.
Some materials in the ICSD database have been fabricated under specific conditions of pressure and temperature; therefore, these compounds could be above the boundary of the convex Hull, i.e., the phase diagram representing the set of the lowest possible potential energy states obtained from both single materials and mixtures of those materials. Remarkably, in the selected compounds, we find systems forming the boundary of the convex Hull (EAH = 0), suggesting that they are in the most stable structural configuration, such as, WN2 and RuSi, FeSi, Ir4Ge5, In2Te5, and Cs2Te3 in the space groups P\(\bar 6\)m2, P213, P213, P\(\bar 4\)c2, Cc, and Cmc21, respectively. We find that for RuGe, OsSi, MoS2, WS2, and Tl2Te3 the energy above the convex Hull is less than 30 meV/atom, which means that these materials could be easily synthesized.
For WS2 and MoS2 (space group P63/mmc), the bulk is centrosymmetric and the site point group D3h and C3v of the Mo and S atoms are noncentrosymmetric, which results in a hidden Dresselhaus spin polarization.23,25 However, in the noncentrosymmetric space group R3m, the VBM of these materials has a giant Zeeman-type splitting about 510 and 187 meV, as shown in Table 1. We also find that compounds with the same formula but with different structure could exhibit different splitting values. For instance, Bi2O3 (space group R3m) has a splitting of 81 meV in the CBM, whereas the VBM of this compound in the \(P\bar 4m2\) space group has a splitting of 15 meV. This is expected since the on-site SOC is not the unique property related to the spin splitting.21 Indeed, systems formed by atoms with a relatively weak SOC could also have large splitting values, e.g., ΔZ,V = 192 meV in Mn2Ge.
Surfaces and electrical control
Since surfaces and two-dimensional confinement affect the symmetry and the total electric dipole, we here explore the spin splitting in the surfaces of Zeeman-type semiconductors and its possible electrical control. For illustrative purposes, we will present here the results for SnTe (one of the materials with the largest splitting). We consider three growth directions corresponding to planes parallel, oblique, and perpendicular to the Sn–Te bonding along the axis normal to the surface (111) (see Fig. 2a), i.e., planes at the crystallographic directions (10\(\bar 1\)), (110), and (111), respectively. We find that the spin splitting change according to the growth direction of the slab. Specifically, the splitting is near zero for the plane (10\(\bar 1\)) and increases as the angle between the plane and the bonding increases. Thus, the (110) and (111) planes exhibit a splitting of 50 and 491 meV (see Fig. 2c–e). Consequently, the slab (10\(\bar 1\)) is an insulator, whereas the (110) and (111) surfaces are metallic. This insulator–metal transition is a remarkable effect arising from large spin splittings in nonmagnetic Zeeman semiconductors. If the spin splitting in the VBM is greater than the band gap, the highest energy band can cross the Fermi energy, leading to majority spin channels for given non-TR-invariant k-point, as shown for SnTe in Fig. 2c–e. The TR-symmetry imposes that a given k-point and its respective TR-partner—k have opposite spin polarization, which in turn implies that the spin filtering requires the breaking of the valley symmetry. However, we find that the metal–insulator transition can be induced and controlled in a specific slab by manipulating the Zeeman splitting, which can be used for application in spintronics. For instance, a perpendicular external electric field E = Ez could modify the electric dipole induced by the surface. For SnTe slab along the (111) surface, an applied electric field E = Ez decreases the spin splitting, leading to a metal–insulator transition for Ez = 0.12 eV/Å. By increasing the electric field, the band gap opens again due to the change on the electric dipole orientation, resulting in an insulator–metal transition for Ez = 0.145 eV/Å.
Surface states in Zeeman-type semiconductors. a Crystal structure and b BZ of SnTe in the ZB structure. In a and b, the crystallographic planes corresponding to slabs growth directions (10\(\bar 1\)), (110), and (111) are presented by the green, blue, and purple planes, respectively. The top view and side view of the real space and band structure for the (10\(\bar 1\)), (110), and (111) surfaces are shown in c–e, respectively. For illustrative purposes, we only show slabs formed by eight atomic layers. The red arrows stand for the spin splitting, which is zero for the (10\(\bar 1\)) surface
Discussion
The Zeeman-type splitting in the so far proposed layered materials has been interpreted in terms of a nonzero intrinsic dipole.23 This interpretation, based on the common understanding of the Rashba effect, implies that compounds in which the atomic dipoles add up to zero, e.g., ZB GaAs, cannot exhibit this splitting, which is not necessarily correct, as we discuss below. GaAs (space group F\(\bar 4\)3m) is a historical example of Dresselhaus semiconductors. In this IA compound, the dipoles add up to zero due to the tetrahedral chemical environment imposed by the crystal symmetry, as represented in Fig. 3a. Thus, although the Rashba terms do not contribute to the Hamiltonian describing the GaAs band structure, the spin splitting reaches high values (≈120 meV) at the high symmetry point W (see Fig. 3b), as early reported in ref. 33 On the other hand, for ZB binary semiconductors, the position of the CBM and VBM can change according to the chemical composition (AB):34 GaAs has a direct band gap at Γ, but in Silicon and GaP, the CBM is at the X point. Here, we find that the VBM can take place at the W point (highest spin splitting in GaAs) for A = Sn and B = Te, as represented in Fig. 3c. Naturally, SnTe has also a zero total dipole, but a giant spin Zeeman-type splitting of 491 meV (see Table 1). States exhibiting large spin splitting can be brought up to the Fermi energy by changing the atomic composition, as evident from the predicted compounds. This can be a different route to find this kind of materials, which typically exhibit splittings larger than the observed in the Rashba and Dresselhaus effects, as we demonstrate below.
Spin texture at non-TR invariant k-points for GaAs and SnTe. a Schematic representation of the local electric dipoles formed by the Ga–As atomic interaction. Since the Ga–As bonding has the same length, the atomic-sites are nonpolar (Td point symmetry) and the dipoles add up to zero. b GaAs band structure with SOC. The inset corresponds to the spin splitting at the W point. c Band structure without and with SOC for SnTe in the ZB structure (space group F\(\bar 4\)3m). The color code stands for the orientation of the spin components. The detailed description of the spin texture for all these materials is presented in the supplementary information
In ZB semiconductors, the spin-polarized states near the Γ point are described by the Eq. (1) with \({\cal{H}}_0({\boldsymbol{k}}) = \frac{{\hbar ^2k^2}}{{2m^ \ast }}1\) and the effective Rashba and Dresselhaus fields given by ΩR(k) = λR(n × k) and \({\mathbf{\Omega }}_D({\boldsymbol{k}}) = \lambda _D\left( {k_x(k_y^2 - k_z^2),k_y(k_z^2 - k_x^2),k_z(k_x^2 - k_y^2)} \right)\), respectively. Here, n is a unitary vector along the direction of the electric dipole. Accordingly, the spin splitting generated by these odd-in-k effective magnetic fields is:
where ε↑(k) and ε↓(k) are the eigenvalues of the Hamiltonian \({\cal{H}}\). In order to show that the Zeeman splitting is typically larger than the Rashba and Dresselhaus splitting, we consider an illustrative case: λD = 0 and \({\boldsymbol{n}} = \hat z\). Thus, the spin splitting becomes \(\Delta ({\boldsymbol{k}}) = \lambda _R\left| {k_\parallel } \right|\). In the Rashba effect, the momentum offset kR usually reaches small values between 10−2 and 10−1 Å−1 (see Fig. 1b).3 Therefore, although the parameter may be large (λR ≈ 1 eVÅ), the splitting values are always limited to some meV.3,15,16,17,18 This is also valid in compounds in which the atomic dipoles add up to zero, where λR = 0 and Δ(k) = ΩD(k). Since the non-TR-invariant high symmetry k-points are at the boundary of the BZ, Zeeman-type splitting are always larger than Rashba and Dresselhaus splitting. In addition, due to the spin splitting position in the BZ, the Zeeman-type effect offers alternative mechanisms for spin polarization control.
In the WSe2 monolayer, an in-plane electric dipole generates an out-of-plane effective magnetic field, which can be locally described in terms of the Hamiltonian in Eq. (1). The effective magnetic field Ωk comes from the SOC interaction and forbids spin degenerated states at non-TR-symmetry k-points. Thus, the spin splitting and the spin-texture are consequence of the intrinsic effective magnetic field, but not the origin. Specifically, the spin direction depends on the direction of the effective magnetic field. For example, in MoS2 case, the effective magnetic field is along the z-axis and hence, only the expected value of the spin operator Sz is different from zero. The same analysis can be applied to the SnTe compound. For instance, in this compound, the total electric dipole is zero, and hence, only the Dresselhaus term contributes to the effective magnetic field. Therefore, at the kxy plane, by imposing λR = 0, the effective magnetic field along the X–W symmetry line is written as \({{\mathbf{\Omega}} _D}({\mathbf{k}}) \approx ({k_x}k_y^2,0,0)\), since in this direction kz = 0 and \({k_{x}^{2}} \approx 0\). In our density functional calculations, we obtain that the spin texture of the SnTe band structure is dominated by Sx spin components at this plane, as shown in Fig. 2c. Since the Dresselhaus effective magnetic field can also lead to the Zeeman-type spin texture, electric dipoles are a sufficient condition but not necessary for this effect, as we initially proposed in the design principles.
The proposed design principles for the Zeeman-type effect are also applicable to the two-dimensional compounds with external electric fields in which the VBM or CBM take place at a non-TR-symmetry k-point. The external electric field is the key ingredient to break the IS, generating a perpendicular effective magnetic field and consequently, a Sz spin component. For instance, this specific behavior has been found for k-points near the high symmetry point K in the graphene band structure with a perpendicular electric field,35,36 but it was not related with the Zeeman-type effect. For k-points far form the K point, the spin texture is the observed in the common Rahsba effect.37
The spin splitting can be controlled by changing the growth direction of slabs. For instance, when the systems are confined along the (10\(\bar 1\)) direction, we can write 〈ky〉 = 0. Consequently, the Zeeman spin splitting at the W point (S-point in the equivalent two-dimensional BZ, as shown in Fig. 2b) vanishes. Different from the Rashba and Dresselhaus splitting at TR-invariant k-points, the non-magnetic Zeeman effect does not allow the spin polarization electrical control, but the metal–insulator transition mediated by the electrical control of the splitting size. Specifically, an external electric field does not change the spin polarization, but the splitting size. Thus, the electric field can bring states to the Fermi energy. This control mechanism is different from the recently reported in the magnetic Zeeman splitting.38 As previously discussed, the electrical control of the spin splitting can also be achieved in these materials according to the growth direction of the slab.
In conclusion, we demonstrate that IA three-dimensional non-magnetic compounds can exhibit a Zeeman-type spin splitting, providing the possibility to grow slabs in which the electrical dipole is perpendicular to the surface and hence, allowing the electrical control of the spin splitting. The required conditions for this effect are: valence band maximum or conduction band minimum in a non-TR-invariant k-point, IA, and zero magnetic moment. Using these conditions as filters, we perform a material screening and high-throughput ab initio calculations to systematically search for these materials in the AFLOW-ICSD database. We find 20 candidates featuring this splitting. Our calculated spin splittings can be as large as 433, 510, and 491 meV for the compounds WN2 (P6m1), WS2 (R3m), and SnTe (F43m), respectively. We also demonstrate that the spin splitting in slabs of these compounds depends on the growth direction and can be controlled by an external electric field. We believe that this work will open the way for the discovery of novel fundamental effect related to the spin-polarization control.
Methods
The ab initio calculations were performed within the DFT using Perdew–Burke–Ernzenhof generalized gradient approximation39 exchange-correlation functional and the Hubbard on-site term40,41 as implemented in the Vienna Ab initio Simulation Package.42,43 All the specific settings of the calculations without SOC (e.g., cutoff energies, k-point sampling, effective U parameters, atomic configurations) were the same as to those used on the AFLOW database.26,27 We have then included the spin–orbit interaction keeping the zero magnetic moment.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Jansen, R. Silicon spintronics. Nat. Mater. 11, 400–408 (2012).
Maekawa, S., Valenzuela, S. O., Saitoh, E. & Kimura, T. Spin Current, Series on Semiconductor Science and Technology, Vol 17 (Oxford University Press, Oxford, 2012).
Manchon, A., Koo, H. C., Nitta, J., Frolov, S. M. & Duine, R. A. New perspectives for rashba spin-orbit coupling. Nat. Mater. 14, 871–882 (2015).
Bercioux, D. & Lucignano, P. Quantum transport in rashba spin-orbit materials: a review. Rep. Prog. Phys. 78, 106001 (2015).
Zeeman, P. The effect of magnetisation on the nature of light emitted by a substance. Nature 55, 347 EP (1897).
Preston, T. Radiation phenomena in the magnetic field. Nature 59, 224 EP (1899).
Li, Y. et al. Valley splitting and polarization by the Zeeman effect in monolayer MoSe2. Phys. Rev. Lett. 113, 266804 (2014).
Zhang, X., Liu, Q., Luo, J.-W., Freeman, A. J. & Zunger, A. Hidden spin polarization in inversion-symmetric bulk crystals. Nat. Phys. 10, 387 EP (2014).
Ryoo, J. H. & Park, C.-H. Hidden orbital polarization in diamond, silicon, germanium, gallium arsenide and layered materials. NPG Asia Mater. 9, e382 EP – (2017).
Ramrez-Ruiz, J., Boutin, S. & Garate, I. NMR in an electric field: a bulk probe of the hidden spin and orbital polarizations. Phys. Rev. B 96, 235201 (2017).
Dresselhaus, G. Spin-orbit coupling effects in zinc blende structures. Phys. Rev. 100, 580–586 (1955).
Rashba, E. I. Properties of semiconductors with an extremum loop. 1. Cyclotron and combinational resonance in a magnetic field perpendicular to the plane of the loop. Sov. Phys. Solid State 2, 1224–1238 (1960).
Bychkov, Y. A. & Rashba, E. I. Properties of a 2D electron gas with lifted spectral degeneracy. JETP Lett. 39, 78 (1984).
Mera Acosta, C., Babilonia, O., Abdalla, L. & Fazzio, A. Unconventional spin texture in a noncentrosymmetric quantum spin hall insulator. Phys. Rev. B 94, 041302 (2016).
LaShell, S., McDougall, B. A. & Jensen, E. Spin splitting of an Au(111) surface state band observed with angle resolved photoelectron spectroscopy. Phys. Rev. Lett. 77, 3419–3422 (1996).
Ast, C. R. et al. Giant spin splitting through surface alloying. Phys. Rev. Lett. 98, 186807 (2007).
Koroteev, Y. M. et al. Strong spin-orbit splitting on Bi surfaces. Phys. Rev. Lett. 93, 046403 (2004).
Nitta, J., Akazaki, T., Takayanagi, H. & Enoki, T. Gate control of spin-orbit interaction in an inverted In0.53Ga0.47As/In0.52Al0.48As heterostructure. Phys. Rev. Lett. 78, 1335–1338 (1997).
Vajna, S. et al. Higher-order contributions to the Rashba-Bychkov effect with application to the Bi/Ag(111) surface alloy. Phys. Rev. B 85, 075404 (2012).
Tao, L. L. & Tsymbal, E. Y. Persistent spin texture enforced by symmetry. Nat. Commun. 9, 2763 (2018).
Park, S. R., Kim, C. H., Yu, J., Han, J. H. & Kim, C. Orbital-angular-momentum based origin of Rashba-type surface band splitting. Phys. Rev. Lett. 107, 156803 (2011).
Acosta, C. M. & Fazzio, A. Spin-polarization control driven by a Rashba-type effect breaking the mirror symmetry in two-dimensional dual topological insulators. Phys. Rev. Lett. 122, 036401 (2019).
Yuan, H. et al. Zeeman-type spin splitting controlled by an electric field. Nat. Phys. 9, 563 (2013).
Xiao, D., Liu, G.-B., Feng, W., Xu, X. & Yao, W. Coupled spin and valley physics in monolayers of MoS2 and other group-VI dichalcogenides. Phys. Rev. Lett. 108, 196802 (2012).
Liu, Q. et al. Search and design of nonmagnetic centrosymmetric layered crystals with large local spin polarization. Phys. Rev. B 91, 235204 (2015).
Curtarolo, S. et al. Aflowlib.org: a distributed materials properties repository from high-throughput ab initio calculations. Comput. Mater. Sci. 58, 227–235 (2012).
Taylor, R. H. et al. A RESTful API for exchanging materials data in the aflowlib.org consortium. Comput. Mater. Sci. 93, 178–192 (2014).
Goldschmidt, V. Geochemische verteilungsgesetze viii. bau und eigenschaften von krystallen. Skrifter utgitt av det Norske Videnskaps-Akademi i Oslo 1: Matematisk-Naturvidenskapelig Klasse, 1927, 1–156 (Norwegian Academy of Sciences, Oslo, 1927).
Zunger, A. Inverse design in search of materials with target functionalities. Nat. Rev. Chem. 2, 0121 EP – (2018).
Schleder, G. R., Padilha, A. C. M., Acosta, C. M., Costa, M. & Fazzio, A. From DFT to machine learning: recent approaches to materials science—a review. J. Phys. Mater. 2, 032001 (2019).
Jain, A. et al. The Materials Project: a materials genome approach to accelerating materials innovation. APL Materials 1, 011002 (2013).
Jain, A. et al. Formation enthalpies by mixing GGA and GGA + U calculations. Phys. Rev. B 84, 045115 (2011).
Luo, J.-W., Bester, G. & Zunger, A. Full-zone spin splitting for electrons and holes in bulk GaAs and GaSb. Phys. Rev. Lett. 102, 056405 (2009).
Yeh, C.-Y., Wei, S.-H. & Zunger, A. Relationships between the band gaps of the zinc-blende and wurtzite modifications of semiconductors. Phys. Rev. B 50, 2715–2718 (1994).
Garcia, J. H., Vila, M., Cummings, A. W. & Roche, S. Spin transport in graphene/transition metal dichalcogenide heterostructures. Chem. Soc. Rev. 47, 3359–3379 (2018).
Cummings, A. W., Garcia, J. H., Fabian, J. & Roche, S. Giant spin lifetime anisotropy in graphene induced by proximity effects. Phys. Rev. Lett. 119, 206601 (2017).
Zhang, H., Ma, Z. & Liu, J.-F. Equilibrium spin current in graphene with Rashba spin-orbit coupling. Sci. Rep. 4, 6464 EP – (2014).
Marcellina, E. et al. Electrical control of the Zeeman spin splitting in two-dimensional hole systems. Phys. Rev. Lett. 121, 077701 (2018).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Liechtenstein, A. I., Anisimov, V. I. & Zaanen, J. Density-functional theory and strong interactions: orbital ordering in Mott-Hubbard insulators. Phys. Rev. B 52, R5467–R5470 (1995).
Dudarev, S. L., Botton, G. A., Savrasov, S. Y., Humphreys, C. J. & Sutton, A. P. Electron-energy-loss spectra and the structural stability of nickel oxide: an LSDA + U study. Phys. Rev. B 57, 1505–1509 (1998).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Charifi, Z., Baaziz, H. & Hamad, B. Theoretical prediction of the structural and electronic properties of pseudocubic X3As4 (X = C, Si, Ge, and Sn) compounds. Phys. B Condens. Matter 404, 1632–1637 (2009).
Badachhape, S. & Goswami, A. Structure of evaporated tin sulphide. J. Phys. Soc. Jpn. 17, 251–253 (1962).
Po, D. X. & Xu, W. Y. Investigation of osmium carbides with various stoichiometries: first-principles calculations. J. Appl. Phys. 107, 053506–1–053506–6 (2010).
Luo, H. et al. Origin of the Z-28 rule in Mn2Cu-based heusler alloys: a comparing study. J. Magn. Magn. Mater. 324, 2127–2130 (2012).
Raub, E. & Fritzsche, W. Germanium-ruthenium legierungen. Zeitschrift fuer Metallkund 53, 779–781 (1962).
Goeransson, K., Engstroem, I. & Nolaeng, B. Structure refinements for some platinum metal monosilicides. J. Alloy. Compd. 219, 107–110 (1995).
Vocadlo, L., Knight, K., Price, G. & Wood, I. Thermal expansion and crystal structure of FeSi between 4 and 1173 K. Phys. Chem. Miner. 29, 132–139 (2002).
Wood, I., David, W., Hull, S. & Price, G. A high-pressure study of ε-FeSi, between 0 and 8.5 GPa, by time-of-flight neutron powder diffraction. J. Appl. Crystallogr. 29, 215–218 (1996).
Pauling, L. & Soldate, A. The nature of the bonds in the iron silicide, FeSi, and related crystals. Acta Crystallogr. 1, 212–216 (1948).
Weitzer, F., Rogl, P. & Schuster, J. X-ray investigations in the systems ruthenium-silicon and ruthenium-silicon-nitrogen. Zeitschrift fuer Metallkund 79, 154–156 (1988).
Weitzer, F., Perring, L., Gachon, J., Feschotte, P. & Schuster, J. Structure refinements of some compounds of the RuSi, RuGe and RuSn systems. Electrochem. Soc. Proc. 39, 241–249 (1997).
Finnie, L. Structures and compositions of the silicides of ruthenium, osmium, rhodium, and iridium. J. Less-Common Met. 4, 24–34 (1962).
Mattheiss, L. Calculated structural properties of CrSi2, MoSi2 and WSi2. Phys. Rev. 45, 3252–3259 (1992).
d’Heurle, F., Petersson, C. & Tsai, M. Observations on the hexagonal form of MoSi2 and WSi2 films produced by ion implantation and on related snowplow effects. J. Appl. Phys. 51, 5976–5980 (1980).
Soto, G. Computational study of Hf, Ta, W, Re, Ir, Os and Pt pernitrides. Comput. Mater. Sci. 61, 1–5 (2012).
Matsumoto, A., Koyama, Y. & Tanaka, I. Structures and energetics of Bi2O3 polymorphs in a defective fluorite family derived by systematic first-principles lattice dynamics calculations. Phys. Rev. 81, 094117–1–094117–11 (2010).
Jellinek, F., Brauer, G. & Mueller, H. Molybdenum and niobium sulphides. Nature 185, 376–377 (1960).
Traill, R. A rhombohedral polytype of molybdenite. Can. Mineral. 7, 524–526 (1962).
Takeuchi, Y. & Nowacki, W. Detailed crystal structure of rhombohedral MoS2 and systematic deduction of possible polytypes of molybdenite. Schweizerische Mineralogische und Petrographische Mitteilunge. 44, 105–120 (ETH Zurich, Ramistrasse 101, 8092 Zurich, Switzerland, 1964).
Schutte, W., de Boer, J. & Jellinek, F. Crystal structures of tungsten disulfide and diselenide. J. Solid State Chem. 70, 207–209 (1987).
Wildervanck, J. & Jellinek, F. Preparation and crystallinity of molybdenum and tungsten sulfides. Zeitschrift für Anorganische und Allgemeine Chemie 328, 309–318 (1964).
Flieher, G., Voellenkle, H. & Nowotny, H. Die kristallstruktur von Ir4Ge5. Monatshefte für Chemie 99, 877–883 (1968).
Bhan, S. & Schubert, K. Zum aufbau der systeme kobalt - germanium, rhodium - silizium sowie einiger verwandter legierungen. Z. fuer Metallkd. 51, 327–339 (1960).
Panday, P., Singh, G. & Schubert, K. Kristallstruktur von Ir4Ge5. Zeitschrift für Metallkunde 125, 274–285 (1967).
Bhan, S. & Schubert, K. Kristallstruktur von Tl5Te3 und Tl2Te3. J. Less-Common Met. 20, 229–235 (1970).
Uno, R. et al. Powder diffractometry at the tsukuba photon factory. Aust. J. Phys. 41, 133–144 (1988).
Verkelis, J. Single crystals of In2Te5. Mater. Res. Bull. 9, 1063–1065 (1974).
Sutherland, H., Hogg, J. & Walton, P. Indium polytelluride In2Te5. Acta Crystallogr. B 32, 2539–2541 (1976).
Boettcher, P. Synthesis and crystal structure of Rb2Te3 and Cs2Te3. J. Less-Common Met. 70, 263–271 (1980).
Chuntonov, K., Orlov, A., Yatsenko, S., Grin’, Y. & Miroshnikova, L. Synthesis of chalcogenides with the composition A2(I)B3(VI) and crystal structure of Rb2Te3 and Cs2Te3. Izvestiya Akademii Nauk SSSR, Neorganicheskie Materialy 18, 1113–1116 (1982).
Acknowledgements
This work was financed by FAPESP (grants 18/11856-7 and 17/02317-2), and CNPq. This work was performed using the computational infrastructure of the LNCC supercomputer center (Santos Dumont).
Author information
Authors and Affiliations
Contributions
C.M.A. performed the materials screening and the band structure calculations. All authors participated on the conceptual development of the project, analysis of the results and shaping the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
41535_2019_182_MOESM1_ESM.pdf
Supplemental Material - Zeeman-type spin splitting in non-magnetic three-dimensional compounds: Material prediction and electrical control
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mera Acosta, C., Fazzio, A. & Dalpian, G.M. Zeeman-type spin splitting in nonmagnetic three-dimensional compounds. npj Quantum Mater. 4, 41 (2019). https://doi.org/10.1038/s41535-019-0182-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-019-0182-z
This article is cited by
-
Unconventional spin textures emerging from a universal symmetry theory of spin-momentum locking
npj Quantum Materials (2024)
-
High-throughput inverse design and Bayesian optimization of functionalities: spin splitting in two-dimensional compounds
Scientific Data (2022)
-
Progress of hidden spin polarization in inversion-symmetric crystals
Science China Physics, Mechanics & Astronomy (2022)