Abstract
The MPX3 family of magnetic van-der-Waals materials (M denotes a first row transition metal and X either S or Se) are currently the subject of broad and intense attention for low-dimensional magnetism and transport and also for novel device and technological applications, but the vanadium compounds have until this point not been studied beyond their basic properties. We present the observation of an isostructural Mott insulator–metal transition in van-der-Waals honeycomb antiferromagnet V0.9PS3 through high-pressure x-ray diffraction and transport measurements. We observe insulating variable-range-hopping type resistivity in V0.9PS3, with a gradual increase in effective dimensionality with increasing pressure, followed by a transition to a metallic resistivity temperature dependence between 112 and 124 kbar. The metallic state additionally shows a low-temperature upturn we tentatively attribute to the Kondo effect. A gradual structural distortion is seen between 26 and 80 kbar, but no structural change at higher pressures corresponding to the insulator–metal transition. We conclude that the insulator–metal transition occurs in the absence of any distortions to the lattice—an isostructural Mott transition in a new class of two-dimensional material, and in strong contrast to the behavior of the other MPX3 compounds.
Similar content being viewed by others
Introduction
Layered two-dimensional van-der-Waals materials are currently the subject of broad and detailed research.1 In particular, the addition of magnetism into such systems leads to many interesting fundamental questions and opportunities for device applications,2,3,4,5 and the ability to select or tune electronic and transport properties in these materials would be a powerful tool indeed for the fabricators of a new generation of nanoscale devices. One particular family of materials enjoying a sudden surge of interest is that of MPX3, where M denotes a first row transition metal and X either S or Se. First synthesized by Klingen in 1969,6,7,8 initial interest in these materials beyond their basic characterization was for application as battery materials, see Grasso and Silipigni9 for a review. In more recent years they have been studied in detail as excellent examples of two-dimensional magnetic systems—these materials all share very similar structures, but spin states, magnetic ordering, magnetic anisotropy, and critical behavior change with the transition metal.10,11,12,13,14,15,16,17,18,19 MPX3 form a layered honeycomb lattice of the metal ions20,21,22,23 with monoclinic space group C2/m and interplanar forces solely through a van-der-Waals interaction between the surrounding P2S6 clusters. They can be easily mechanically exfoliated as with graphene and have been shown to maintain their magnetic ordering down to monolayer thickness.24,25 These materials are all insulating—they exhibit an exponentially increasing resistivity with decreasing temperature—and can be understood as p-type semiconductors9 and as Mott insulators.26 Recent works have demonstrated Mott insulator–metal transitions in MnPS3 and FePS326,27,28 and additionally superconductivity in FePSe3.29 A large focus in 2D materials research is and has been into the transition metal dichalcogenide systems,30,31,32,33 leading to the discovery of many new states—MPX3 are a new family in the same vein, with rich magnetic and correlated-electron properties to explore. Being magnetic, they naturally introduce the physics of Coulomb U interactions, i.e., Mott physics, in the true 2D limit. The tuning of clean and controllable materials like these from an antiferromagnetic Mott insulating state into a metallic, or indeed superconducting, state is of great interest for fundamental magnetism and Mott physics. Moreover, this same physics forms the foundation for our understanding of the underlying phase diagram and mechanisms for systems like the cuprate superconductors.
VPS3, or more generally V1−xPS3 with x the level of vanadium deficiency, is a member of the family that has received very little attention, despite hosting great potential for interesting study. It has the smallest band gap of these insulating materials at around 0.25 eV,22,34,35 and by far the lowest resistivity (on the order of Ωcm) at room temperature. This can additionally be tuned over an order of magnitude by altering the level of vanadium deficiency.35 Theoretical band structure calculations for the whole material family, including VPS3 are given in Chittari et al.36 showing a band gap and insulating/semiconducting behavior, but such calculations on these materials are challenging and historically often contradict with experiment. More theoretical work, informed by experimental results, is essential for fully understanding the electronic properties of the MPX3 materials, but a near-universal result is that band structure calculations will suggest a metallic system (unlike the reality), until an on-site repulsion term is included, splitting the metal d bands. This and the ability to induce a metallic state through pressure are strong evidence for VPS3 being a Mott insulator, as has been previously argued for FePS3.26 V1−xPS3 is antiferromagnetic,22 with a Néel temperature of around 62 K but little is known about its magnetic structure and behavior. As the metal ion in MPX3 must take the charge M2+, the vanadium deficiency in V1−xPS3 can be explained as due to valence mixing on the vanadium site between V2+ and V3+ states. It is this valence mixing that Ichimura and Sano35 argue to be responsible for the comparatively high conductivity in this material, but the resulting high degrees of local electronic disorder and vacancies can be expected to have a large effect on the transport and scattering properties.
Results
Crystal structure
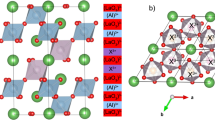
High-pressure powder x-ray diffraction patterns were taken at room temperature up to 177 kbar. Besides an expected decreasing unit cell volume as the sample is pressurized, no changes in the diffraction patterns from the ambient pressure patterns, and hence the structure described by Ouvrard et al.22 were observed up to 26 kbar. From 26 to 80 kbar however, a gradual transition to an alternative high-pressure structure was observed (see Fig. 1). This new phase (we will denote the ambient and low-pressure structural phase LP and this high-pressure phase HP-I) can be attributed to the same structure seen in FePS3 at intermediate pressures and designated HP-I by Haines et al.26 The layers of V0.9PS3 shift relative to each other in a sliding motion of ~a/3 along the a-axis such that the S atoms become arranged in a hexagonal close packing layout between the layers, resulting in the monoclinic unit cell’s β angle shifting from a value of 107° in the LP to a value close to 90° (90.13° at 177 kbar) in the HP-I structure. In this structure the P atoms are slightly distorted along the a-axis (x coordinate value of 0.0074 at 177 kbar) of the unit cell, and this distortion results in the same C2/m symmetry in the HP-I structure. In the absence of the distortion of P atoms, HP-I would have a trigonal symmetry, but certain peak shapes cannot be adequately fitted in refinements made with this space group so we conclude that it remains monoclinic. As there is no symmetry or even volume change associated with this LP–HP-I phase transition, it is consistent to observe it to occur so gradually over a large pressure range, in both FePS3 and now V0.9PS3. Integrated x-ray diffraction patterns, Rietveld refinements and relevant parameters are shown in the Supplementary Material, SM, along with appropriate ref. 37
Crystal structures and parameters of the high and low pressure phases. a Crystal structure of V0.9PS3 at 11 kbar—the LP phase and b at 177 kbar—the HP-I phase. The HP-I structure has β close to 90° so atoms in each plane are aligned with their equivalents in neighboring planes. c, d Projections of the same structures along the b axis. e Phase fractions of the LP (blue circles) and HP-I (red crosses) phases as a function of pressure. f Refined unit cell volumes for each phase. The LP phase volume is plotted as blue circles and the HP-I as red crosses. The two phases coexist over a wide pressure range, rather than an abrupt transition between the two, and the unit cell volume shows no jumps or sudden transitions
There are no sudden or discontinuous changes in the cell volume accompanying this shift; the c lattice spacing changes as its orientation is altered, but this does not reflect a change in the inter-layer spacing. The HP-I to HP-II first-order structural transition observed in FePS326 and linked there with the metallization was not observed in V0.9PS3. In fact, no transitions or distortions of the HP-I phase were observed up to the maximum pressure measured, 177 kbar.
Resistivity and insulator–metal transition
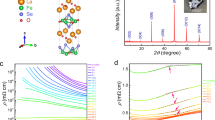
The temperature dependence of the resistivity ρ of a single crystal of V0.9PS3 is shown in Fig. 2a for pressures p ranging from ambient up to 140 kbar. The ambient pressure resistivity (8 × 105 μΩcm) and an energy gap fitted from an Arrhenius \(e^{E_a/k_bT}\) form (0.2 eV) are consistent with values previously reported35 for V0.78PS3 and VPS3—these are substantially lower than all other members of the MPS3 family. As pressure is increased, the overall magnitude of the resistivity is dramatically and continuously reduced, and the curves become shallower, suggesting a reduction of the effective band gap. Between 112 and 124 kbar the resistivity switches from an increasing trend with decreasing temperature to a decreasing trend— the insulator–metal transition. An order-of-magnitude estimate of the Mott–Ioffe–Regel limit,38 following the treatment of Kurosaki et al.39 is superimposed and falls between the insulating and metallic resistivity curves as expected. Besides the crossover from insulating to metallic behavior, there appear to be no sudden changes or transitions in the temperature dependence of the resistivity as pressure is increased—the evolution of the curves is smooth and continuous. As discussed in the previous section, there is a structural distortion from the LP to HP-I structure over the range 26–80 kbar, but no structural changes at pressures above this—the insulator–metal transition observed in the resistivity is not accompanied by any structural changes. An isostructural Mott transition such as this is a very rare phenomenon, particularly in van-der-Waals materials. Previous examples include specific transition metal dichalcogenide systems,31,40 but an equivalent kink in lattice parameter pressure dependence to that seen in these cases was not observed here in V0.9PS3—there is no signature of the transition in the structure at all.
Resistivity data showing the insulator–metal transition. a Resistivity plotted against temperature for V0.9PS3, for pressures ranging from ambient (blue, topmost) to 140 kbar (red, bottom). Above 112 kbar the resistivity transitions from an insulating temperature dependence to a metallic, decreasing with decreasing temperature. An estimate of the Mott–Ioffe–Regel limit, as discussed in the text, is shown as a dotted line, and clearly separates the insulating and metallic regimes. b Resistivity of V0.9PS3 at 140 kbar in the metallic state. Data at 124 kbar, close to the transition, are shown in the left inset. Right inset shows the low-temperature detail of the data at 124 kbar with a fit to a Kondo effect expression as a black dashed line
The resistivity in the high-pressure metallic state is replotted in detail in Fig. 2b. The resistivity shows a linear temperature dependence down to around 70 K, and then exhibits a flattening off and upturn below 40 K. The residual resistance ratio R300K/R2K is very low at around 1.2, as one would expect for a highly disordered system like V0.9PS3. As the lower inset shows, the upturn in the low-temperature data can be described by the Kondo effect,41 but alternative forms of localization could also be responsible for this feature.
Interestingly, and in contrast to the case of other MPX3 materials such as FePS3,26 the resistivity cannot be well described by a simple Arrhenius-type insulating temperature dependence, see Supplementary Material. The data were found to be best described by a generalized variable-range-hopping (VRH)38,42,43 expression for highly locally disordered systems \(\rho = \rho _0Te^{(T_0/T)^\alpha }\). The inclusion of a Tn prefactor in the exponential resistivity of an insulator is a common method to describe the thermal dependence of scatterers in the system—we find a T-linear prefactor44 to best fit the data. The exponent α is given by α = 1/(d + 1) with d the effective dimensionality of the system; T0 is a characteristic temperature or energy scale of the electron-hopping process.
Figure 3 plots the resistivity against pressure and temperature, showing the full phase diagram of V0.9PS3. The insulator–metal transition is clearly visible as the point where resistivity no longer increases with decreasing temperature. The end point of the LP–HP-I mixed structural phase where the LP phase fraction goes to zero is accompanied by a visible kink in the resistivity curves at 80 kbar. The upper panel gives the pressure dependence of the VRH exponent α, with dotted lines showing the values expected for 1D, 2D, and 3D systems of 1/2, 1/3, and 1/4. A strong pressure dependence of this exponent is observed, with α continuously decreasing in value as pressure is increased and the insulator–metal transition approached—the fits lose validity at pressures close to the transition. The T0 characteristic temperature is also continuously suppressed (see Supplementary Material) as electron overlap is increased. As the application of pressure narrows the van-der-Waals gap between the crystal planes and increases hopping and tunneling between them, we can reasonably expect a gradual crossover from 2D to 3D conduction mechanisms. The greater overlap and correlation of vanadium sites across the crystal planes in HP-I, as well as the important P2S6-cluster9 conduction pathways will also bear a role. However the apparent one-dimensional hopping at low pressures is less easily explained. One explanation could be one-dimensional ‘chains’ of conduction percolating through the lattice, with the continuous planes seen in other MPX3 materials broken up by the vanadium vacancies and valence mixing. This would in fact resemble the case of Haldane chain system AgVP2S6,45 where the differently valanced metal ions form ordered chains within the ab plane. Dimerization of the vanadium–vanadium bonds due to the vacancies could again contribute to this picture. Another possibility is that the system is exhibiting so-called Efros-Shklovskii variable-range-hopping (ES–VRH)46,47,48 which takes the same form as the standard Mott VRH but with an exponent α of 0.5, independent of dimensionality. ES–VRH results from the inclusion of electron–electron interactions and the development of a Coulomb gap at the Fermi level below a temperature characteristic of this gap.
Resistivity plotted against temperature and pressure on a logarithmic color scale for V0.9PS3. The pressures corresponding to the beginning and end of the gradual LP–HP-I structural transition and the insulator–metal transition are marked with arrows. Upper panel shows pressure-dependent values of the exponent α extracted from the variable-range-hopping fits described in the text, with dotted lines to show the gradual increase in effective transport dimensionality these represent
Discussion
We have demonstrated a continuous transition from insulating to metallic states in 2D antiferromagnet V0.9PS3. No change in the crystal lattice was observed in the vicinity of the transition, in contrast to previous results on FePS3 and MnPS3 where the insulator–metal transition is accompanied by a dramatic first-order structural phase transition: a collapse of the interplanar spacing. Mott’s original and simplest explanation of the Mott transition38 involves the gradual closing of the split metallic bands as the strength of electron hopping is increased, an eventual touching of the bands causing the metallization. This mechanism, rather than a structural change, appears to match the observed behavior in V0.9PS3.
V0.9PS3 does, however, undergo a structural transition or distortion—over the wide pressure range 26–80 kbar a new structural phase emerges attributed to a sliding motion of the crystal planes. This brings the c axis to approximately perpendicular to the planes, and hence the honeycombs of vanadium ions are no longer offset between planes. This is then consistent with an increase in hopping dimensionality. The sulfur atoms enter a hexagonal close packed configuration, and this HP-I structure is very close to possessing a trigonal symmetry—a slight distortion in the phosphorus positions results in it belonging to the same monoclinic space group as the LP structure. This transition, common to all MPX3 so far measured, occurs well below the metallization pressure. Accompanying this distortion is a continuous increase in the effective dimensionality in the VRH expression found to fit the transport data. V0.9PS3 forms a unique case—unlike other MPX3 materials its resistivity follows a VRH rather than an Arrhenius form, and unlike archetypal 3D VRH-metal transitions,49 such as in doped silicon, the metallization process cannot be mapped onto a simple scaling relation. In such cases, the data follow the same functional form, but T0 is continuously suppressed to zero—this is not the case here as the functional form of the resistivity is constantly and smoothly altered, in addition to T0, as the effective dimensionality of the electronic transport increases. The evolution of the VRH exponent from 1D to 2D-like can be potentially understood as originating from ES–VRH hopping, due to the formation of a Coulomb gap, or from a 1D character of the ambient phase. The data and results of the fits are clear—a VRH expression fits the data, its exponent lowers consistently with an increase in dimensionality, and the exponent and scaling are not attributable to any previously seen standard—but without more sound theoretical understanding at this point, interpretation is limited to speculation. In the ES–VRH case, as pressure and hence inter-site hopping is increased, the Coulomb gap is suppressed and Mott VRH hopping discovered. This is then subsequently tuned to fully 3D hopping and metallization. The lattice remains 2D throughout, whereas the transport properties are continuously tuned between regimes, resulting in eventual metallization. This is a novel mechanism fundamentally in contrast to previous results, particularly in other members of this material’s family, and the resistivity behavior close to metallization does not fit any conventional forms and is yet to be explained.
A metallic temperature dependence of the resistivity was observed at pressures above 112 kbar, with a low-temperature upturn potentially due to the Kondo effect. The dilute magnetic impurities of which the Kondo effect is a signature we can tentatively attribute to the vanadium deficiency and disordered valence mixing on the vanadium sites. As the system is known to be highly locally disordered however, alternative, more exotic, forms of localization could be responsible for this effect.
As the Mott transition is isostructural, it is likely to be second order and could potentially be tuned to a quantum critical point. We can also suspect from magnetotransport data that the metallization also involves a transition from antiferromagnetic order to paramagnetism, as is the case in vanadium oxides.50 If this is found to be the case via further experiments, it would open the interesting possibility of a spin liquid phase of exotic nature near the critical point due to the honeycomb lattice, perhaps through a Kitaev interaction. And, of course, an extremely challenging but exciting experiment would be to examine the insulator–metal transition in monolayer, truly two-dimensional, VPS3. There additionally exists potential for the formation of a dimerized valence-bond-solid state51 at high pressure. The spin 3/2 V2+ positioned on a honeycomb lattice with antiferromagnetic order is a candidate for such a state, and our observations, paired with the changes in magnetic moment seen in the iron compounds at metallization,29 consistent with its formation.
VPS3 has, until now, not been studied beyond its basic properties, while many other members of the MPX3 family are enjoying wide attention for their potential in two-dimensional physics and technological applications. We have demonstrated that this material has many intriguing opportunities and puzzles for further work, and have demonstrated an isostructural Mott transition in a new class of 2D van-der-Waals material for the first time. The insulator–metal transition and the overall transport mechanisms contrast strongly to the behavior observed in other members of this family—more work is required to ascertain exactly why. The lack of an accompanying structural change suggests that the transport properties of V0.9PS3 can be much more easily and responsively switched than in other van-der-Waals materials, whether by chemical doping, thin film strain or electrostatic gating. This and the material’s small and highly tunable band gap show great promise for future device applications based on van-der-Waals materials.
Methods
Single crystals of V0.9PS3 were grown via a chemical vapor transport method in a two-zone tube furnace at temperatures of 600 and 350 °C for 1 month using 0.1 g of TeCl4 flux for 1 g of reactants. Prior to the reaction, the quartz tubes used were cleaned and dried, loaded with V (99.5%), P (99.99%), and S (99.98%) powders under an argon atmosphere, then evacuated to 5 × 10−3 mbar with an oil diffusion pump before sealing. The crystals form with a vanadium deficiency, due to its natural tendency to V3+ valence (the transition metal in MPX3 is M2+), so a 20% excess of vanadium powder was added to the reactant mixture to attempt to mitigate this. In addition, it is worth noting that these reactions will form V2S3 or VS2 at higher temperatures so it is desirable to keep the hot zone temperature as low as possible for the reaction (Klingen gives the solid-state reaction temperatures for MPX38) while allowing sufficient heat for the flux to function. Crystals were characterized by powder and single-crystal diffraction for phase purity and by EDX for stoichiometry. The samples used in this study had stoichiometry of V0.9PS3, with an uncertainty of ±0.05 on the 0.9 vanadium fraction.
The pressure evolution of the crystal structure was found from powder x-ray diffraction carried out at room temperature on the I15 beamline at the Diamond Light Source. The powder sample used was ground under an argon atmosphere (to prevent water uptake) and in liquid nitrogen to attempt to mitigate the effects of preferred orientation. Helium was used as the pressure-transmitting medium and the shift in fluorescence wavelength of ruby spheres placed inside the high-pressure region was used as the pressure calibrant.52 An x-ray energy of 29.2 KeV (λ = 0.4246 Å) was used to collect the diffraction patterns. A MAR345 2D detector with pixel size 100 × 100 μm was used to record the diffraction patterns with 120 s exposure times and a 24° rocking of the sample. The data were initially processed using Dawn53 (with a LaB6 calibration), the subsequent Rietveld refinements were calculated using the GSAS-II software package54 and the structures visualized in VESTA.55 For the structural refinements, a spherical harmonics model for the observed peak heights was used to take into account the strong (and pressure-dependent) effects of preferred orientation.
Resistivity measurements were performed on single crystals using a Keithley 2410 Source Meter with a fixed supplied current of 0.01 μA at an ambient pressure, and for high pressures using the internal resistance bridge of the PPMS (Quantum Design) cryostat used for temperature control. To prepare the samples for these measurements, they were first mechanically cleaved to expose clean surfaces in the ab plane and a 50 nm layer of gold was then sputtered onto the surface to form contact pads in the standard 4-wire geometry via a foil mask. As can be seen in the sample photograph presented in the Supplementary Material, in this particular case the paired voltage and current wires were attached to only two contact pads, for a quasi-4-point setup—but the resistance of the gold pads was verified to be orders of magnitude below the sample resistance at all points and so the measurement indistinguishable from 4-wire. Gold wires were then bonded to these using Dupont 6838 silver epoxy, cured at 180 °C for 1 h.
A diamond anvil cell56,57 with 1 mm anvil culets and heat-treated Be-Cu gasket was used for the high-pressure resistivity measurements. Glycerol was used as the hydrostatic pressure medium and ruby was used to determine the pressure as with the x-ray study. Estimated pressure uncertainties are ±1 kbar and the environment can be expected to be close to hydrostatic over the range considered, as with the structural experiments. No effect was seen on the sample properties at the freezing pressure of the helium used in the x-ray study.
Data availability
All relevant data are available from the authors upon reasonable request.
References
Ajayan, P., Kim, P. & Banerjee, K. Two-dimensional van der Waals materials. Phys. Today 69, 38–44 (2016).
Park, J.-G. Opportunities and challenges of 2D magnetic van der Waals materials: magnetic graphene? J. Phys. Condens. Matter 28, 301001 (2016).
Samarth, N. Condensed-matter physics: magnetism in flatland. Nature 546, 216–218 (2017).
Zhou, Y., Lu, H., Zu, X. & Gao, F. Evidencing the existence of exciting half-metallicity in two-dimensional TiCl3 and VCl3 sheets. Sci. Rep. 6, 19407 (2017).
Burch, K. S., Mandrus, D. & Park, J.-G. Magnetism in two-dimensional van der Waals materials. Nature 563, 47–52 (2018).
Klingen, W., Eulenberger, G. & Hahn, H. Über Hexathio- und Hexaselenohypodiphosphate vom Typ \({\mathrm{M}}_2^{II}\) P2X6. Naturwissenschaften 5, 229–230 (1968).
Klingen, W., Eulenberger, G. & Hahn, H. Über Hexachalkogeno-hypodiphosphate vom Typ M2P2X6. Naturwissenschaften 57, 88 (1970).
Klingen, W., Ott, R. & Hahn, H. Uber die Darstellung und Eigenschaften von Hexathio- und Hexaselenohypodiphosphaten. Z. fur Anorg. und Allg. Chem. 396, 271–278 (1973).
Grasso, V. & Silipigni, L. Low-dimensional materials: the MPX3 family, physical features and potential future applications. Riv. Del. Nuovo Cim. 25, 6 (2002).
Kurosawa, K., Saito, S. & Yamaguchi, Y. Neutron diffraction study on MnPS3 and FePS3. J. Phys. Soc. Jpn 52, 3919–3926 (1983).
Okuda, K. et al. Magnetic properties of layered compound MnPS3. J. Phys. Soc. Jpn 55, 4456–4463 (1986).
Wildes, A. R., Kennedy, S. J. & Hicks, T. J. True two-dimensional magnetic ordering in MnPS3. J. Phys. Condens. Matter 6, L335–L341 (1994).
Wildes, A. R., Roessli, B., Lebech, B. & Godfrey, K. W. Spin waves and the critical behaviour of the magnetization in MnPS3. J. Phys. Condens. Matter 10, 6417–6428 (1998).
Rule, K. C., McIntyre, G. J., Kennedy, S. J. & Hicks, T. J. Single-crystal and powder neutron diffraction experiments on FePS3: search for the magnetic structure. Phys. Rev. B 76, 134402 (2007).
Wildes, A. R., Rønnow, H. M., Roessli, B., Harris, M. J. & Godfrey, K. W. Anisotropy and the critical behaviour of the quasi-2D antiferromagnet, MnPS3. J. Magn. Magn. Mater. 310, 1221–1223 (2007).
Wildes, A. R., Rule, K. C., Bewley, R. I., Enderle, M. & Hicks, T. J. The magnon dynamics and spin exchange parameters of FePS3. J. Phys. Condens. Matter 24, 416004 (2012).
Wildes, A. R. et al. Magnetic structure of the quasi-two-dimensional antiferromagnet NiPS3. Phys. Rev. B 92, 224408 (2015).
Wildes, A. R., Simonet, V., Ressouche, E., Ballou, R. & McIntyre, G. J. The magnetic properties and structure of the quasi-two-dimensional antiferromagnet CoPS3. J. Phys. Condens. Matter 29, 455801 (2017).
Lançon, D. et al. Magnetic structure and magnon dynamics of the quasi-two-dimensional antiferromagnet FePS3. Phys. Rev. B 94, 214407 (2017).
Brec, R., Schleich, D. M., Ouvrard, G., Louisy, A. & Rouxel, J. Physical properties of lithium intercalation compounds of the layered transition-metal chalcogenophosphites. Inorg. Chem. 18, 1814–1818 (1979).
Ouvrard, G., Brec, R. & Rouxel, J. Structural determination of some MPS3 layered phases (M = Mn, Fe, Co, Ni and Cd). Mater. Res. Bull. 20, 1181–1189 (1985).
Ouvrard, G., Fréour, R., Brec, R. & Rouxel, J. A mixed valence compound in the two dimensional MPS3 family: V0.78PS3 structure and physical properties. Mater. Res. Bull. 20, 1053–1062 (1985).
Brec, R. Review on structural and chemical properties of transition metal phosphorous trisulfides MPS3. Solid State Ion. 22, 3–30 (1986).
Lee, J. U. et al. Ising-type magnetic ordering in atomically thin FePS3. Nano Lett. 16, 7433–7438 (2016).
Kuo, C. T. et al. Exfoliation and Raman spectroscopic fingerprint of few-layer NiPS3 van der Waals crystals. Sci. Rep. 6, 20904 (2016).
Haines, C. R. S. et al. Pressure-induced electronic and structural phase evolution in the van der Waals compound FePS3. Phys. Rev. Lett. 121, 266801 (2018).
Wang, Y. et al. Pressure-driven cooperative spin-crossover, large-volume collapse, and semiconductor-to-metal transition in manganese(II) honeycomb lattices. JACS 138, 15751–15757 (2016).
Tsurubayashi, M. et al. Metal–insulator transition in Mott-insulator FePS3. AIP Adv. 8, 101307 (2018).
Wang, Y. et al. Emergent superconductivity in an iron-based honeycomb lattice initiated by pressure-driven spin-crossover. Nat. Commun 9, 1914 (2018).
Stojchevska, L. et al. Ultrafast switching to a stable hidden quantum state in an electronic crystal. Science 344, 177–180 (2014).
Nayak, A. P. et al. Pressure-modulated conductivity, carrier density, and mobility of multilayered tungsten disulfide. ACS Nano 9, 9117–9123 (2015).
Yoshida, M., Suzuki, R., Zhang, Y., Nakano, M. & Iwasa, Y. Memristive phase switching in two-dimensional 1T-TaS2 crystals. Sci. Adv. 1, e1500606 (2015).
Nakata, Y. et al. Monolayer 1T-NbSe2 as a Mott insulator. NPG Asia Mater. 8, e321 (2016).
Brec, R. & Rouxel, J., Synthesis and characterization of new intercalated lithium cathodes. New Ways to Save Energy 620–630, https://www.springer.com/us/book/9789027710789 (Springer, The Netherlands, 1980).
Ichimura, K. & Sano, M. Electrical conductivity of layered transition-metal phosphorus trisulfide crystals. Synth. Met. 45, 203–211 (1991).
Chittari, B. L. et al. Electronic and magnetic properties of single-layer MPX3 metal phosphorous trichalcogenides. Phys. Rev. B 18, 184428 (2016).
Mao, H. K. et al. High-pressure phase diagram and equation of state of solid helium from single-crystal x-ray diffraction to 23.3 GPa. Phys. Rev. Lett. 60, 2649–2652 (1988).
Mott, N. F. Metal-Insulator Transitions. (Taylor and Francis, London, 1990).
Kurosaki, Y., Shimizu, Y., Miyagawa, K., Kanoda, K. & Saito, G. Mott transition from a spin liquid to a Fermi liquid in the spin-frustrated organic conductorκ-(ET)2Cu2(CN)3. Phys. Rev. Lett. 95, 177001 (2005).
Nayak, A. P. et al. Pressure-induced semiconducting to metallic transition in multilayered molybdenum disulphide. Nat. Commun 5, 3731 (2014).
Kondo, J. Resistance minimum in dilute magnetic alloys. Prog. Theor. Phys. 32, 37–49 (1964).
Mott, N. F. Charge transport in non-crystalline semiconductors. Festkorper Probleme IX 22–45, https://doi.org/10.1016/b978-0-08-015543-2.50005-x (Elsevier, 1969).
Hill, R. M. Variable-range hopping. Phys. Status Solidi (a) 34, 601–613 (1976).
Van Keuls, F. W., Hu, X. L., Jiang, H. W. & Dahm, A. J. Screening of the Coulomb interaction in two-dimensional variable-range hopping. Phys. Rev. B 56, 1161–1169 (1997).
Lee, S., Colombet, P., Ouvrard, G. & Brec, R. A new chain compound of vanadium (III): structure, metal ordering, and magnetic properties. Mater. Res. Bull. 21, 917–928 (1986).
Efros, A. L. & Shklovskii, B. I. Coulomb gap and low temperature conductivity of disordered systems. J. Phys. C Solid State Phys. 8, L49–L51 (1975).
Li, Z. et al. Transition between Efros–Shklovskii and Mott variable-range hopping conduction in polycrystalline germanium thin films. Semicond. Sci. Technol. 32, 035010 (2017).
Rosenbaum, R. Crossover from Mott to Efros–Shklovskii variable-range-hopping conductivity in InxOy films. Phys. Rev. B 44, 3599–3603 (1991).
Pollak, M. & Shklovskii, B., Hopping Transport In Solids (Elsevier, 1991).
Pergament, A. L., Stefanovich, G. B., Kuldin, N. A. & Velichko, A. A. On the problem of metal–insulator transitions in vanadium oxides. ISRN Condens. Matter. Phys. 960627, 1–6 (2013).
Affleck, I., Kennedy, T., Lieb, E. H. & Tasaki, H. Rigorous results on valence-bond ground states in antiferromagnets. Phys. Rev. Lett. 57, 799–802 (1987).
Mao, H. K., Xu, J. & Bell, P. M. Calibration of the ruby pressure gauge to 800 kbar under quasi-hydrostatic conditions. J. Geophys. Res. 91, 4673–4676 (1986).
Filik, J. et al. Processing two-dimensional X-ray diffraction and small-angle scattering data in DAWN 2. J. Appl Crystallogr. 50, 959–966 (2017).
Toby, B. H. & Von Dreele, R. B. GSAS-II: the genesis of a modern open-source all purpose crystallography software package. J. Appl. Crystallogr. 46, 544–549 (2013).
Momma, K. & Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl Crystallogr. 44, 1272–1276 (2011).
Dunstan, D. J. & Spain, I. L. Technology of diamond anvil high-pressure cells: I. Principles, design and construction. J. Phys. E Sci. Instrum. 22, 913–923 (1989).
Spain, I. L. & Dunstan, D. J. The technology of diamond anvil high-pressure cells: II. Operation and use. J. Phys. E Sci. Instrum. 22, 923–933 (1989).
Acknowledgements
This work was carried out with the support of the Diamond Light Source and we acknowledge the provision of beamtime at I15 under proposal number NT21368. The authors would like to thank P.A.C. Brown, S.E. Dutton, I. Hwang, D. Jarvis, and Y. Noda for their generous help and discussions. We would also like to acknowledge support from Jesus College of the University of Cambridge, IHT KAZATOMPROM and the CHT Uzbekistan program. The work was carried out with financial support from the Ministry of Education and Science of the Russian Federation in the framework of Increase Competitiveness Program of NUST MISiS (No K2-2017-024). This work was supported by the Institute for Basic Science (IBS) in Korea (Grant no. IBS-R009-G1).
Author information
Authors and Affiliations
Contributions
M.J.C. carried out the resistivity measurements and wrote the paper. M.J.C. and S.S. performed the crystal growth. D.D. carried out the x-ray measurements. H.H., C.R.S.H., and M.J.C. analyzed the x-ray data and structures. P.L.A., C.R.S.H., C.L., and M.J.C. designed and set up the pressure apparatus. M.J.C., J.G.P., C.R.S.H., C.L., A.R.W., and S.S.S. analyzed and interpreted the results. S.S.S. and J.G.P. conceived and supervised the study.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Coak, M.J., Son, S., Daisenberger, D. et al. Isostructural Mott transition in 2D honeycomb antiferromagnet V0.9PS3. npj Quantum Mater. 4, 38 (2019). https://doi.org/10.1038/s41535-019-0178-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-019-0178-8
This article is cited by
-
Insulator–metal transition in CrSiTe3 triggered by structural distortion under pressure
npj 2D Materials and Applications (2023)
-
Symmetry progression and possible polar metallicity in NiPS3 under pressure
npj 2D Materials and Applications (2022)
-
Dimensional crossover tuned by pressure in layered magnetic NiPS3
Science China Physics, Mechanics & Astronomy (2021)
-
Absence of superconductivity in bulk Nd1−xSrxNiO2
Communications Materials (2020)