Abstract
The Hall coefficient RH of Sr2RuO4 exhibits a non-monotonic temperature dependence with two sign reversals. We show that this puzzling behavior is the signature of two crossovers, which are key to the physics of this material. The increase of RH and the first sign change upon cooling are associated with a crossover into a regime of coherent quasiparticles with strong orbital differentiation of the inelastic scattering rates. The eventual decrease and the second sign change at lower temperature are driven by the crossover from inelastic to impurity-dominated scattering. This qualitative picture is supported by quantitative calculations of RH(T) using the Boltzmann transport theory in combination with dynamical mean-field theory, taking into account the effect of spin–orbit coupling. Our insights shed new light on the temperature dependence of the Hall coefficient in materials with strong orbital differentiation, as observed in Hund’s metals.
Similar content being viewed by others
Introduction
Measuring the Hall coefficient RH is a standard way of characterizing charge carriers in quantum materials. For free carriers of a single type, the Hall coefficient RH is simply given by the inverse of the density of carriers n and their charge e. In principle, RH is negative for an electron-like Fermi surface (FS) and positive for a hole-like FS, respectively. Sign changes of RH can occur, for example, if the FS evolves from an electron-like to a hole-like one with temperature.1 However, in complex materials with a FS composed of multiple sheets, interpreting RH can be more complicated and also provides richer information when both electron-like and hole-like carriers are present simultaneously. For instance, in the case of one hole-like and one electron-like FS sheet, the corresponding Hall coefficient is given by an average of RH,e <0 and RH,h >0:
weighted by the squares of the individual hole and electron conductivities, σh and σe, respectively. Hence, the ratio of scattering rates between the two types of carriers enters in a key manner to determine both the overall sign and magnitude of the Hall coefficient.
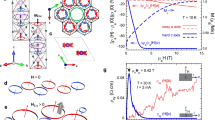
The 4d transition metal oxide Sr2RuO4 is such a complex material: with low-energy bands built out of three Ru-t2g orbitals (dxy, dyz, dxz) hybridized with O–2p states, it has a FS comprising two electron-like sheets, β and γ, and one hole pocket, α.2,3,4 Indeed, experiments5,6,7 have observed a particularly intriguing temperature dependence of RH in Sr2RuO4, as depicted in Fig. 1. RH increases from a negative value of about −1 × 10–10 m3 C−1 at low temperatures (values between −1.37 × 10−10 and −0.7 × 10−10 m3 C−1 for T → 0 have been reported,5,6,7,8) exhibit a sign change at T1 = 30 K (in the cleanest samples), reaches a positive maximum at about 80 K, changes sign a second time around T2 = 120 K, and eventually saturates to a slightly negative value for T > 200 K.
Sketch of the temperature dependence of the Hall coefficient RH and the different transport/electronic regimes in Sr2RuO4. The solid line shows the non-monotonic temperature behavior of RH with two sign reversals at about 30 and 120 K after experimental data from refs. 5,6,7 The sign changes can be suppressed by adding small amounts of Al impurities (dashed lines)7
Shirakawa et al.5 suggested early on that the rich temperature dependence of RH in Sr2RuO4 points to the multi-carrier nature of this material. This conclusion, reached by considering a Drude model with two types of carriers, was later refined in several works9,10,11 using Boltzmann transport theory calculations for tight-binding models assuming scattering rates 1/τν = Aν + BνT2 for the different FS sheets ν = {α, β, γ}, with adjustable parameters Aν and Bν. The overall take-home message of these phenomenological models is that RH is highly sensitive to the precise details of the FS sheets and also to the temperature and sheet dependence of the scattering rates.
Another remarkable experimental finding provides insight in interpreting the temperature dependence of RH:7 adding small amounts of Al impurities has a drastic impact on the intermediate temperature regime such that RH no longer turns positive and instead increases monotonically from the low-T to the high-T limit, as indicated by dotted lines in Fig. 1. Arguably, the similarity of the low-T values of RH for different impurity concentrations provides evidence that the elastic-scattering regime has been reached where RH is mainly determined by FS properties (see also ref. 6). In contrast, the temperature dependence itself must be due to inelastic scattering, possibly associated with electronic correlations.7
In this work, we address this rich temperature dependence of RH in Sr2RuO4 and provide a clear interpretation of its physical meaning. We show that the two sign changes of RH(T) in clean samples are the signatures of two important crossovers in the physics of this material. The increase of RH upon cooling from high temperature signals the gradual formation of coherent quasiparticles, which is associated with a strong temperature dependence of the ratio of inelastic scattering rates between the xy and xz/yz orbitals. At low temperatures the decrease of RH is due to the crossover from inelastic to impurity-dominated scattering. These qualitative insights have relevance to a wide class of materials with orbital differentiation.
Our qualitative picture is supported by a quantitative calculation of RH(T) using Boltzmann transport theory in combination with dynamical mean-field theory (DMFT),12 taking into account the electronic structure of the material. The spin–orbit coupling (SOC) is found to play a key role,13,14 because it has a strong influence on the shape of the FS and also controls the manner in which the scattering rates associated with the different orbitals combine into k-dependent quasiparticle scattering rates at a given point on the FS.13,14,15
Results
Dependence on scattering rate ratios
The orbital dependence of scattering rates is crucial for the understanding of the Hall effect. Therefore, we introduce a localized basis set of t2g-like orbitals |χm〉 with basis functions labeled as m = {xy, xz, yz}, using maximally localized Wannier orbitals16,17 constructed from the Kohn–Sham eigenbasis of a non-SOC density functional theory (DFT) calculation. We treat SOC by adding an atomic SOC term for the t2g subspace with an effective strength of λ = 200 meV, which takes already the correlation enhancement of the SOC by a factor of about two into account.15,18,19,20 We assign scattering rates ηxy, ηxz, and ηyz (due to crystal symmetries ηxz = ηyz) to each orbital, irrespective of the microscopic details of the underlying scattering mechanisms, which will be addressed at a later stage. Then, these scattering rates are converted into k-dependent scattering rates for each band ν:
The overlap elements |〈χm(k)|ψν(k)〉|2 correspond to the orbital character of the eigenstates |ψν(k)〉 of the Hamiltonian at a given momentum k. The orbital character for points on the FS is shown in the inset of Fig. 2. With the Hamiltonian and the scattering rates ην(k), we calculate RH within Boltzmann transport theory using the BoltzTraP2 package.21,22 Further details on Eq. (2), the Hamiltonian construction and the transport calculations, are provided in the Methods section.
In the Boltzmann transport theory, RH only depends on the scattering rates through their ratio ξ = ηxy/ηxz/yz and not through their absolute magnitude; a point we verified in our calculations. This also implies that within the constant isotropic scattering rate approximation, that is, ξ = 1, the full temperature dependence of RH cannot be explained. The calculated RH as a function of the scattering rate ratio ξ is displayed in Fig. 2. Without SOC RH remains negative for all values of ξ and approaches zero as \(\xi \gg 1\). In this limit the γ sheet drops out and the contributions of the hole-like α sheet and electron-like β sheet compensate each other. This means that it is not possible to explain the positive value of RH observed experimentally in clean samples for T1 < T < T2 (Fig. 1) without taking SOC into account. With SOC we observe a very different behavior of RH(ξ); it turns from negative to positive at \(\xi \simeq 2.6\). This is a result of two effects13,14,15 (see Fig. 2, inset): First, SOC changes the shape and size of the FS sheets, and second, it induces a mixing between different orbital characters, which varies for each point on the FS. Thus, the manner in which the scattering rates associated with the different orbitals combine into k-dependent quasiparticle scattering rates (Eq. (2) is controlled by the SOC. From the calculated dependence of RH(ξ) in the presence of SOC, we deduce that agreement with experiments would require ξ to be smaller than 2.6 at high temperatures, increase above this value at ~T2, and then decrease again to reach a value close to unity at low temperatures.
Inelastic electron–electron scattering
We turn now to microscopic calculations by first considering inelastic electron–electron scattering ratios calculated with DMFT (see Methods). These calculations consider the t2g subspace of states with Hubbard–Kanamori interactions of U = 2.3 eV and J = 0.4 eV.23 The calculated ξ(T) from inelastic scattering only is displayed in Fig. 3a. In agreement with previous studies,23,24 we find that the xy orbital is less coherent than xz/yz at all temperatures and ηxy > ηxz/yz. In Sr2RuO4 the crossover from the low-T coherent Fermi liquid regime with \(\eta \sim T^2\) to an incoherent regime with a quasilinear temperature dependence of the scattering rate is well documented23,25 and also manifested in deviations of the resistivity from a low-temperature quadratic behavior to a linear one.26 Importantly, this coherence-to-incoherence crossover as well as the corresponding coherence scales are strongly orbital dependent. When approaching the Fermi liquid regime (TFL ≈ 25 K26,27,28) the scattering rate ratio reaches a value as large as \(\xi ^{\mathrm{FL}}\sim 3\) (Fig. 3a), but decreases rapidly upon heating with ξ = 1.8 at 300 K. We do not find a substantial change for even higher temperatures; at 500 K the scattering rate ratio is ξ = 1.6.
Influence of inelastic electron–electron scattering on the temperature dependence of RH. a Inelastic scattering rate ratios extracted from dynamical mean-field theory (DMFT) self-energies extrapolated to zero frequency (see Methods). The error bars represent the standard deviation of nine consecutive DMFT iterations. b RH(T) considering the DMFT inelastic electron–electron scattering rate ratios. c Scattering rates ην(θ) on the three Fermi surface sheets ν = {α, β, γ} for kz = 0 along the angle θ from 0° (Γ–M) to 45° (Γ–X) under consideration of the orbital character shown in the right inset of Fig. 2. The scattering rates at 29 K (blue) are multiplied by a factor of 44, chosen such that ηα(45°) coincides with the result at 310 K (red). d Color map of RH assuming constant sheet-dependent scattering rate ratios. The solid black line indicates RH = 0 and the dashed black line marks ηα = ηβ
Connecting these results to the discussion of Fig. 2 above, the temperature dependence of ξ directly translates into that of RH, as shown in Fig. 3b. Like in experiments, RH is negative at high temperatures, but when the temperature is lowered it increases and crosses zero at 110 K. This demonstrates that electronic correlations are indeed able to turn RH positive and suggests the following physical picture: the electronic transport in Sr2RuO4 crosses from a regime governed by incoherent electrons at high temperatures, connected to a weaker orbital differentiation of scattering rates and a negative RH, over to a coherent Fermi liquid regime, with a stronger orbital differentiation and positive RH. The resulting sign change at 110 K can be seen as a direct consequence of this coherence-to-incoherence crossover. We emphasize that this sign change is only observed when SOC is taken into account. Without SOC RH is purely negative and shows only a weak temperature dependence (Fig. 3b, dashed line).
When moving along the FS from Γ–M (θ = 0°) to Γ−X (θ = 45°), the mixing of the orbital character induced by SOC (Eq. (2)) leads to angular-dependent scattering rates ην(θ) (Fig. 3c). At θ = 0° the ratio of scattering rates between the γ and β sheets is large, because these bands still have mainly xy and xz/yz character, respectively (Fig. 2, inset). As expected from Fig. 3a, this sheet dependence decreases with increasing temperature. On the other hand, at θ = 45° the ratio is small, due to a very similar orbital composition of the γ and β sheets. The α pocket (being almost entirely xz/yz) has the lowest scattering rate and turns RH positive when ξ becomes large enough at low temperatures. To shed more light on the interplay of the individual FS sheets, we can phenomenologically assign constant scattering rates to each FS sheet, as shown in Fig. 3d. We see that for RH to be positive a necessary condition is ηβ > ηα. This again highlights the importance of SOC, because without SOC the α and β sheets have entirely xz/yz orbital character, and thus ηα = ηβ. Should one make this assumption also in the presence of SOC, it would not result in RH > 0 for any ratio ηγ/ηα (Fig. 3d, dashed line).
Impurity-dominated scattering
Considering inelastic scattering only would yield a positive RH at even lower temperatures deep in the Fermi liquid regime. However, at such low temperatures elastic scattering is expected to dominate over inelastic scattering. The extracted DMFT scattering rates at 29 K with 5.5 meV for the xy and 1.9 meV for the xz/yz orbitals are of the order of the impurity scattering for “clean” samples with residual resistivities of \(\sim {\hskip -1pt} 0.5\,{\mathrm{\mu}}\Omega \,{\mathrm{cm}}\). Therefore, we add a constant elastic scattering ηel. to the orbital-dependent inelastic scattering \(\eta _m^{{\mathrm{inel}}{\mathrm{.}}}\). This elastic term is assumed to be isotropic: \(\eta _{xy}^{{\mathrm{el}}{\mathrm{.}}} = \eta _{xz/yz}^{{\mathrm{el}}{\mathrm{.}}}\). The resulting temperature dependence of RH for values of ηel. ranging from 0.1 to 10 meV is shown in Fig. 4. The dashed lines are calculated with the Fermi liquid form \(\eta _m^{{\mathrm{inel}}{\mathrm{.}}} = A_mT^2\) and parameters Am determined from the calculated inelastic scattering rates at 29 K.
Full temperature dependence of the Hall coefficient RH with added elastic scattering ηel. ranging from 0.1 to 10 meV. The dashed lines indicate the Fermi liquid regime with parameters determined from the dynamical mean-field theory (DMFT) result at 29 K. The inset shows the experimentally measured RH from ref. 7 for samples with different residual resistivities ρ obtained by introducing small amounts of Al impurities
For small enough ηel. we observe a second zero crossing of RH(T) and a regime with RH < 0 at low temperatures, which is consistent with RH(T) depicted in Fig. 1. For T → 0 the fully elastic-scattering regime is reached, and thus RH is not influenced by the magnitude of the (isotropic) scattering rate, but rather by the shape of the FS only. This regime corresponds to ξ = 1 in Fig. 2, for which we obtain RH = −0.94 × 10−10 m3 C−1, in good quantitative agreement with experiments.5,6,7,8 With increasing temperature the influence of elastic scattering fades away and the precise interplay with inelastic scattering shapes the overall temperature dependence of RH. Hence, we see that also the low-temperature zero crossing has a simple physical interpretation: it signals the crossover between the regime dominated by elastic scattering at low temperatures and the regime dominated by inelastic scattering at higher temperatures. Matching the two terms in the scattering rate, a simple estimate of the corresponding crossover scale is \(T_1\sim \sqrt {\eta ^{{\mathrm{el}}{\mathrm{.}}}/A_{xy}} \sim \sqrt {\eta ^{{\mathrm{el}}{\mathrm{.}}}T_{{\mathrm{FL}}}}\). This scale obviously depends on the elastic-scattering rate, and coincides approximately with the Fermi liquid coherence scale TFL only for the cleanest samples reported in which \(\eta ^{{\mathrm{el}}{\mathrm{.}}}\sim T_{{\mathrm{FL}}}\). For even cleaner samples we predict T1 < TFL.
On the contrary, for larger ηel. we find that RH(T) ceases to exhibit any zero crossing and is negative in the whole temperature range. Only in very clean samples can the inelastic scattering rate sufficiently exceed the elastic one for the sign changes of RH to occur. This is further substantiated by experimental Hall measurements for samples where the residual resistivity was altered by introducing different amounts of Al impurities, cf. the dependence of RH on ηel. in Fig. 4 and the inset with experimental data from ref. 7
In the high-T limit, we obtain a value of RH, which is more negative and temperature dependent than the one reported in experiments.5,6,7 Within the Boltzmann transport theory this would imply that a larger ratio ηxy/ηxz/yz is needed. Likewise, resistivities are significantly underestimated in DMFT transport calculations for T > 300 K in this material.24 A possible explanation is that other sources of inelastic scattering, for example, electron–phonon scattering, could play an important role in the high-T regime. We emphasize, however, that all experimental evidence points towards negligible magnetic contribution (due to processes like skew scattering) and a standard orbital-dominated Hall effect in Sr2RuO4.6,8,10
Discussion
In summary, our quantitative calculations and qualitative interpretations explain the highly unusual temperature dependence of the Hall coefficient of Sr2RuO4. The high-T sign change of RH(T) in clean samples is the direct consequence of the crossover from a high-T incoherent regime to a coherent regime with orbital differentiation. The orbital composition of each quasiparticle state on the FS, as well as the distinct scattering rates of the different orbitals, is crucial to this phenomenon and are properly captured by DMFT. This is in line with recent insights from angle-resolved photoemission spectroscopy.15 In turn, the low-T sign change is due to the crossover from inelastic to impurity-dominated scattering, which is further substantiated by comparing our results to experimental data on samples with a higher impurity concentration. Because it directly affects the shape of the FS sheets and strongly mixes their orbital character, SOC is found to be essential in explaining RH(T).
Orbital differentiation is actually a general feature common to Hund’s metals,23,29,30,31,32 a broad class of materials in which the electronic correlations are governed by the Hund’s coupling, comprising for example transition metal oxides of the 4d series as well as iron-based superconductors.33,34,35,36 We note that a non-monotonic temperature dependence of the Hall coefficient has also been reported for Sr3Ru2O7.37 Beyond ruthenates, LiFeAs and FeSe are two compounds without FS reconstruction due to long-range magnetic order, which display striking similarities to Sr2RuO4 in many regards. The FS of these superconductors is also composed of multiple electron- and hole-like sheets with distinct orbital composition and strong orbital differentiation.31,32 Indeed, the Hall coefficient of LiFeAs has a strong temperature dependence38 and that of FeSe displays two sign changes in the tetragonal phase.39,40 These examples show that strongly correlated materials with multiple FS sheets of different or mixed orbital character and a orbital-differentiated coherence-to-incoherence crossover are expected to show a pronounced temperature dependence of the Hall coefficient. Sign changes then emerge in materials with balanced electron and hole-like contributions. These observations point to a wide relevance of our findings beyond the specific case of Sr2RuO4.
Methods
Hamiltonian and SOC
We use a maximally localized Wannier function construction16,17 to obtain an effective low-energy Hamiltonian for the three t2g-like orbitals centered on the Ru atoms. This construction is based on a non-SOC DFT calculation, using the software packages WIEN2k41 with GGA-PBE,42 wien2wannier,43 and wannier90.44 We incorporate the SOC as an additional local term, where we neglect the coupling to eg orbitals, as these are well separated in energy. It has been shown that electronic correlations lead to an effective enhancement of the SOC in Sr2RuO4 by nearly a factor of two.18,19,20 As the corresponding off-diagonal elements of the self-energy (in the orbital basis) are approximately frequency independent,20 we model the effect of correlations by using a static effective SOC strength of λ = 200 meV, instead of the DFT value of about λDFT = 100 meV. This is crucial to obtain precise agreement with the FS recently measured with photoemission experiments.15 We point out that even when using λDFT we find the same qualitative conclusions for the sign changes of RH. We refer to ref. 15 for further details on the DFT calculation and the Hamiltonian construction.
Dynamical mean-field theory
For the DMFT calculations we use the TRIQS library45 in combination with the TRIQS/DFTTools46 package and the TRIQS/CTHYB47 impurity solver (3.85 × 109 measurements). Due to the fermionic sign problem of the TRIQS/CTHYB solver, low temperatures are only accessible without SOC. However, in Sr2RuO4 the diagonal parts of the self-energy are, to a good approximation, unchanged upon the inclusion of SOC.20,48 Therefore, we perform one-shot DMFT calculation using the Hamiltonian without SOC and added Hubbard–Kanamori interactions (including spin-flip and pair-hopping terms) with U = 2.3 eV and J = 0.4 eV from cRPA.23 Inelastic scattering rates ηm are extracted from non-SOC self-energies Σm(iωn) by fitting a polynomial of 4th order to the lowest 6 Matsubara points and extrapolating Im[Σm(iωn → 0)], a procedure used in ref. 23 We calculate the standard deviation with nine consecutive DMFT iterations to obtain error bars for the inelastic scattering rate ratios. Note that Im[Σm(iωn)] is diagonal in the orbitals m, and thus ηmm′ = 0 for m ≠ m′.
Transport
We calculate RH using Boltzmann transport theory as implemented in the BoltzTraP2 package and described in the corresponding refs. 21,22 We use a 46 × 46 × 46 input k-grid, which is interpolated on a five times denser grid with BoltzTraP2. From Eq. (2) we obtain a scattering rate for each band and k point, which we set in BoltzTraP2 as scattering_model. Off-diagonal elements of the scattering rates, ηνν′(k) and ηmm′, are not captured by Eq. (2). In the case of Sr2RuO4 the scattering rates in the orbital basis ηmm′ are indeed diagonal (see above). The off-diagonal elements of ηνν′(k) and possible inter-band transitions are not considered in BoltzTraP2, but we verified with Kubo transport calculations (TRIQS/DFTTools46) that these are negligible for the ordinary conductivity σxx. We also calculated RH with the Kubo formula without SOC using the DMFT spectral functions A(k, ω) and neglecting inter-band transitions.1 The results at T = 464.2, 232.1 and 116.0 K differ from Boltzmann transport theory by <0.025 × 10−10 m3 C−1, that is, <10%. Boltzmann transport theory results are accurate because the relatively sharp (resilient) quasiparticle peaks persist up to high temperatures,1,23,49,50 which was recently discussed for other ruthenate compounds,51 too. We note that recently interest has been devoted to the theoretical descriptions of the Hall effect in strongly correlated systems beyond Boltzmann transport theory.52,53,54
Data availability
All data generated and analyzed during this study are available from the corresponding author upon reasonable request.
References
Xu, W., Haule, K. & Kotliar, G. Hidden Fermi liquid, scattering rate saturation, and Nernst effect: a dynamical mean-field theory perspective. Phys. Rev. Lett. 111, 036401 (2013).
Mackenzie, A. P. et al. Quantum oscillations in the layered perovskite superconductor Sr2RuO4. Phys. Rev. Lett. 76, 3786–3789 (1996).
Bergemann, C., Julian, S., Mackenzie, A., NishiZaki, S. & Maeno, Y. Detailed topography of the Fermi surface of Sr2RuO4. Phys. Rev. Lett. 84, 2662–2665 (2000).
Damascelli, A. et al. Fermi surface, surface states, and surface reconstruction in Sr2RuO4. Phys. Rev. Lett. 85, 5194–5197 (2000).
Shirakawa, N. et al. Novel Hall-coefficient behavior in superconducting Sr2RuO4. J. Phys. Soc. Jpn. 64, 1072–1075 (1995).
Mackenzie, A. P. et al. Hall effect in the two-dimensional metal Sr2RuO4. Phys. Rev. B 54, 7425–7429 (1996).
Galvin, L. M. et al. Hall effect in single crystal Ca2−xSrxRuO4. Phys. Rev. B 63, 161102 (2001).
Kikugawa, N., Mackenzie, A. P., Bergemann, C. & Maeno, Y. Low-temperature Hall effect in substituted Sr2RuO4. Phys. Rev. B 70, 174501 (2004).
Mazin, I. I., Papaconstantopoulos, D. A. & Singh, D. J. Tight-binding Hamiltonians for Sr-filled ruthenates: application to the gap anisotropy and Hall coefficient in Sr2RuO4. Phys. Rev. B 61, 5223–5228 (2000).
Noce, C. & Cuoco, M. Phenomenological model for magnetotransport in a multiorbital system. Phys. Rev. B 62, 9884–9887 (2000).
Noce, C. & Cuoco, M. Energy bands and Fermi surface of Sr2RuO4. Phys. Rev. B 59, 2659–2666 (1999).
Georges, A., Kotliar, G., Krauth, W. & Rozenberg, M. J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 68, 13–125 (1996).
Haverkort, M. W., Elfimov, I. S., Tjeng, L. H., Sawatzky, G. A. & Damascelli, A. Strong spin–orbit coupling effects on the Fermi surface of Sr2RuO4 and Sr2RhO4. Phys. Rev. Lett. 101, 026406 (2008).
Veenstra, C. N. et al. Spin-orbital entanglement and the breakdown of singlets and triplets in Sr2RuO4 revealed by spin- and angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 112, 127002 (2014).
Tamai, A. et al. High-resolution photoemission on Sr2RuO4 reveals correlation-enhanced effective spin–orbit coupling and dominantly local self-energies. Phys. Rev. X 9, 021048 (2019).
Marzari, N. & Vanderbilt, D. Maximally localized generalized Wannier functions for composite energy bands. Phys. Rev. B 56, 12847–12865 (1997).
Souza, I., Marzari, N. & Vanderbilt, D. Maximally localized Wannier functions for entangled energy bands. Phys. Rev. B 65, 035109 (2001).
Liu, G.-Q., Antonov, V. N., Jepsen, O. & Andersen., O. K. Coulomb-enhanced spin–orbit splitting: the missing piece in the Sr2RuO4 puzzle. Phys. Rev. Lett. 101, 026408 (2008).
Zhang, G., Gorelov, E., Sarvestani, E. & Pavarini, E. Fermi surface of Sr2RuO4: spin–orbit and anisotropic Coulomb interaction effects. Phys. Rev. Lett. 116, 106402 (2016).
Kim, M., Mravlje, J., Ferrero, M., Parcollet, O. & Georges, A. Spin–orbit coupling and electronic correlations in Sr2RuO4. Phys. Rev. Lett. 120, 126401 (2018).
Madsen, G. K. & Singh, D. J. BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 175, 67–71 (2006).
Madsen, G. K., Carrete, J. & Verstraete, M. J. BoltzTraP2, a program for interpolating band structures and calculating semi-classical transport coefficients. Comput. Phys. Commun. 231, 140–145 (2018).
Mravlje, J. et al. Coherence–incoherence crossover and the mass-renormalization puzzles in Sr2RuO4. Phys. Rev. Lett. 106, 096401 (2011).
Deng, X., Haule, K. & Kotliar, G. Transport properties of metallic ruthenates: DFT + DMFT investigation. Phys. Rev. Lett. 116, 256401 (2016).
Stricker, D. et al. Optical response of Sr2RuO4 reveals universal Fermi-liquid scaling and quasiparticles beyond Landau theory. Phys. Rev. Lett. 113, 087404 (2014).
Hussey, N. E. et al. Normal-state magnetoresistance of Sr2RuO4. Phys. Rev. B 57, 5505–5511 (1998).
Maeno, Y. et al. Two-dimensional Fermi liquid behavior of the superconductor Sr2RuO4. J. Phys. Soc. Jpn. 66, 1405–1408 (1997).
Mackenzie, A. P. & Maeno, Y. The superconductivity of Sr2RuO4 and the physics of spin-triplet pairing. Rev. Mod. Phys. 75, 657–712 (2003).
Aichhorn, M., Biermann, S., Miyake, T., Georges, A. & Imada, M. Theoretical evidence for strong correlations and incoherent metallic state in FeSe. Phys. Rev. B 82, 064504 (2010).
Lanatà, N. et al. Orbital selectivity in Hund’s metals: the iron chalcogenides. Phys. Rev. B 87, 045122 (2013).
Miao, H. et al. Orbital-differentiated coherence–incoherence crossover identified by photoemission spectroscopy in LiFeAs. Phys. Rev. B 94, 201109 (2016).
Kostin, A. et al. Imaging orbital-selective quasiparticles in the Hund’s metal state of FeSe. Nat. Mater. 17, 869–874 (2018).
Werner, P., Gull, E., Troyer, M. & Millis, A. J. Spin freezing transition and non-Fermi-liquid self-energy in a three-orbital model. Phys. Rev. Lett. 101, 166405 (2008).
Haule, K. & Kotliar, G. Coherence-incoherence crossover in the normal state of iron oxypnictides and importance of Hund’s rule coupling. N. J. Phys. 11, 025021 (2009).
Yin, Z. P., Haule, K. & Kotliar, G. Kinetic frustration and the nature of the magnetic and paramagnetic states in iron pnictides and iron chalcogenides. Nat. Mater. 10, 932–935 (2011).
Georges, A., de’ Medici, L. & Mravlje, J. Strong correlations from Hund’s coupling. Annu. Rev. Condens. Matter Phys. 4, 137–178 (2013).
Perry, R. et al. Hall effect of Sr3Ru2O7. Phys. B 284-288, 1469–1470 (2000).
Heyer, O. et al. Resistivity and Hall effect of LiFeAs: evidence for electron–electron scattering. Phys. Rev. B 84, 064512 (2011).
Watson, M. D. et al. Dichotomy between the hole and electron behavior in multiband superconductor FeSe probed by ultrahigh magnetic fields. Phys. Rev. Lett. 115, 027006 (2015).
Sun, J. P. et al. High-T c superconductivity in FeSe at high pressure: dominant hole carriers and enhanced spin fluctuations. Phys. Rev. Lett. 118, 147004 (2017).
Blaha, P. et al. WIEN2k, An Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties (Techn. Univ. Wien, Austria, 2018).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Kuneš, K. et al. Wien2wannier: from linearized augmented plane waves to maximally localized Wannier functions. Comput. Phys. Commun. 181, 1888–1895 (2010).
Mostofi, A. A. et al. An updated version of wannier90: a tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 185, 2309–2310 (2014).
Parcollet, O. et al. TRIQS: a toolbox for research on interacting quantum systems. Comput. Phys. Commun. 196, 398–415 (2015).
Aichhorn, M. et al. TRIQS/DFTTools: a TRIQS application for ab initio calculations of correlated materials. Comput. Phys. Commun. 204, 200–208 (2016).
Seth, P., Krivenko, I., Ferrero, M. & Parcollet, O. TRIQS/CTHYB: a continuous-time quantum Monte Carlo hybridisation expansion solver for quantum impurity problems. Comput. Phys. Commun. 200, 274–284 (2016).
Linden, N.-O. Dynamical Mean-Field Theory Studies on Real Materials. Ph.D. thesis, Ludwig-Maximilians-Univ., Munich (2019).
Wang, S.-C. et al. Quasiparticle line shape of Sr2RuO4 and its relation to anisotropic transport. Phys. Rev. Lett. 92, 137002 (2004).
Deng, X. et al. How bad metals turn good: spectroscopic signatures of resilient quasiparticles. Phys. Rev. Lett. 110, 086401 (2013).
Liu, Y., Nair, H. P., Ruf, J. P., Schlom, D. G. & Shen, K. M. Revealing the hidden heavy Fermi liquid in CaRuO3. Phys. Rev. B 98, 041110 (2018).
Auerbach, A. Hall number of strongly correlated metals. Phys. Rev. Lett. 121, 066601 (2018).
Nourafkan, R. & Tremblay, A.-M. S. Hall and Faraday effects in interacting multiband systems with arbitrary band topology and spin-orbit coupling. Phys. Rev. B 98, 165130 (2018).
Mitscherling, J. & Metzner, W. Longitudinal conductivity and Hall coefficient in two-dimensional metals with spiral magnetic order. Phys. Rev. B 98, 195126 (2018).
Acknowledgements
We gratefully acknowledge useful discussions with Gabriel Kotliar, Andrew Mackenzie, Hugo Strand, Andrea Damascelli, Reza Nourafkan, André-Marie Tremblay. J.M. is supported by the Slovenian Research Agency (ARRS) under Program P1-0044. M.A. acknowledges support from the Austrian Science Fund (FWF), project Y746, and NAWI Graz. This work was supported in part by the European Research Council grant ERC-319286-QMAC. The Flatiron Institute is a division of the Simons Foundation.
Author information
Authors and Affiliations
Contributions
M.Z. performed all calculations and the results were analyzed by M.Z. and A.G. All authors discussed and interpreted the results at different stages. The whole project was initiated by A.G. The manuscript was written by M.Z. with the help of all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zingl, M., Mravlje, J., Aichhorn, M. et al. Hall coefficient signals orbital differentiation in the Hund’s metal Sr2RuO4. npj Quantum Mater. 4, 35 (2019). https://doi.org/10.1038/s41535-019-0175-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-019-0175-y
This article is cited by
-
Emergence of flat bands and ferromagnetic fluctuations via orbital-selective electron correlations in Mn-based kagome metal
Nature Communications (2024)
-
Tuning the Fermi liquid crossover in Sr2RuO4 with uniaxial stress
npj Quantum Materials (2022)
-
Direct observation of a uniaxial stress-driven Lifshitz transition in Sr2RuO4
npj Quantum Materials (2019)