Abstract
At temperatures above the superconducting transition temperature, the pairfield susceptibility provides information on the nature of the pairfield fluctuations. Here, we study the d-wave pairfield susceptibility of a 2D Hubbard model for a doping which has a pseudogap (PG) and for a doping which does not. In both cases, there will be a region of Kosterlitz–Thouless fluctuations as the transition at TKT is approached. Above this region, we find evidence for pairfield-order parameter-phase fluctuations for dopings with a PG and BCS Cooper pair fluctuations for dopings without a PG.
Similar content being viewed by others
Introduction
Tunneling experiments have been used to study pairfield fluctuations in both the underdoped and overdoped cuprates.1,2 In these experiments, the tunneling current I versus voltage V between an optimally doped YBCO \((T_c^{{\mathrm{High}}}\sim 90\,{\mathrm{K}})\) electrode and an underdoped or overdoped \((T_c^{{\mathrm{Low}}}\sim 50\,{\mathrm{K}})\) electrode was measured. The change in the I−V characteristic ΔI(V) with the application of a small magnetic field or under microwave irradiation, which suppresses the pairfield current, gives the contribution associated with the transfer of pairs from the higher Tc electrode to the fluctuating pairfield of the lower Tc electrode. Similar phenomena are well known in the traditional low Tc superconductors3 where the fluctuating pairfield is well described by Cooper pair fluctuations,4 with parameters set by the lattice phonon spectrum and the Fermi liquid, out of which the superconducting state emerges. However, the cuprates are quasi-two-dimensional d-wave superconductors with a nearby Mott antiferromagnetic phase, and depending upon the doping, the superconducting phase can emerge from a pseudogap (PG) phase or a non-PG phase.
Various authors5,6,7 have discussed the possibility of using pair tunneling as a probe to study the differences in the pairfield fluctuations between the PG and non-PG regions. Here, after introducing the pairfield susceptibility and describing the type of experiment which motivated this study, we use the dynamic cluster approximation (DCA) with a continuous-time auxiliary-field quantum Monte-Carlo (QMC) solver to study the pairfield fluctuations for a 2D Hubbard model, with an on-site Coulomb interaction U/t = 7 and a next-nearest-neighbor hopping t′/t = −0.15 in units of the nearest-neighbor hopping amplitude t. Previous calculations have shown that in the underdoped regime, this model exhibits a peak in the spin susceptibility8,9 and an antinodal gap in the single-particle spectral weight10,11 characteristic of a PG. Our aim is to compare the nature of the pairfield fluctuations, as the superconducting phase is approached for a filling which exhibits a PG with that of a filling which does not.
In weak coupling, the dynamic d-wave pairfield susceptibility χd(ω, T) is given by the Fourier transform of the pairfield response function
with
Here, the momentum dependence of the gap function has been taken to have the leading d-wave form and its frequency dependence is absorbed as a cutoff which enters Tc. In the ladder approximation4,12
with
and Γ0 = 8Tc/π.
As schematically illustrated in Fig. 1, tunneling experiments1,2,3 between a superconducting film S below its transition temperature and a film S′ above its transition temperature find an excess current. This excess current is associated with the transfer of pairs from the superconducting side to the fluctuating pairfield on the non-superconducting side.13,14 This current varies as Imχ(ω = 2 eV), which from Eq. (3) gives
Illustration of a pair-tunneling experiment. A tunnel junction separates two films S and S′. The temperature T is such that it is lower than the transition temperature Tc of the film S on the right and higher than the transition temperature \(T_c^\prime\) of the film S′ on the left. In this case, there will be an excess current associated with electron pairs from S tunneling to the fluctuating pairfield of S′
The temperature dependence of the peak in ΔI(V) at 2 eV = Γ0ε0(T) provides information on the nature of the pairfield fluctuations on the non-superconducting side. Independent of the TDGL approximation, in general, the voltage integral of ΔI(V)/V is proportional to χd(ω = 0,T).
Such experiments require a careful choice of materials and special fabrication techniques. In addition, the measurements are limited to temperatures below the Tc of the higher transition temperature film and require the careful separation of the excess pair current from the quasi-particle background. Here, motivated by these experiments, we will carry out a numerical study of the d-wave pairfield fluctuations for a 2D Hubbard model. While this will not have the same limitations as the experiment, it is limited by our choice of the 2D Hubbard model, by the DCA approximation, and by the fact that the simulation works with Matsubara frequencies. As one knows, this basic model exhibits features seen in the cuprate materials and the DCA approximation allows us to go beyond the ladder result. We will avoid the problem of analytic continuation of the Matsubara frequencies by calculating the ω = 0 response, which as noted is proportional to the voltage integral of ΔI(V)/V.
Results and discussion
The d-wave pairfield susceptibility that we will study is given by
with
Here, G(k) is the dressed single-particle propagator and λd(T) and ϕd(k) are the d-wave eigenvalue and eigenfunction form factor, respectively, obtained from the Bethe–Salpeter equation
with Γpp the irreducible particle–particle vertex. The notation k denotes both the momentum k and fermion Matsubara frequency ωn = (2n + 1)πT. These quantities are evaluated using a DCA QMC approximation.15
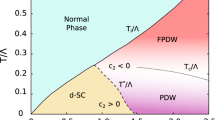
A schematic temperature-doping phase diagram estimated from these calculations is shown in Fig. 2. At half-filling, the ground state has a long-range AF order which is absent at finite temperature, because of the continuous rotational spin symmetry. For low doping, DCA8,9 calculations find a peak in the q = 0 spin susceptibility χs(T). There is also evidence for the opening of an antinodal gap in the single-particle spectral weight,10,11 as the temperature drops below T✶. The results for χs(T) for U/t = 7 and t′/t = −0.15 are shown in Fig. 3. Here, we will consider two dopings 〈n〉 = 0.93 and 〈n〉 = 0.85. For 〈n〉 = 0.93, the spin susceptibility χs(T) peaks and then decreases below a temperature T✶, which marks the opening of a PG. The behavior of the spin susceptibility χs(T) for 〈n〉 = 0.85 is consistent with a doping that is beyond the PG region.
Schematic temperature-filling phase diagram of the 2D Hubbard model. There is long-range AF order at T = 0 for 〈n〉 = 1, a superconducting region with a Kosterlitz–Thouless18 transition line denoted by black circles, and a dashed T✶ pseudogap (PG) line marked by orange diamonds, where the q = 0 spin susceptibility peaks. The orange diamonds mark the peaks of the spin susceptibility shown in Fig. 2, and the black circles mark the temperature at which the extrapolation of the d-wave eigenvalue λd(T) reaches one. The vertical lines indicate the two fillings 〈n〉 = 0.93 and 0.85, for which the pairfield fluctuations will be studied
At lower temperatures, dynamic cluster calculations also find evidence for d-wave superconductivity,16,17 which for a 2D system will occur at a Kosterlitz–Thouless18 transition TKT. Here, we are interested in comparing the manner in which the pairfield fluctuations develop as the temperature is lowered toward TKT for a doping 〈n〉 = 0.93, where the superconducting phase is approached from the PG phase, with a doping 〈n〉 = 0.85, which does not have a PG.
If the dynamics is described by the diffusive form Eq. (3), then the peak in ΔI(V,T) will occur at a voltage which varies as ε(T) = 1 − λd(T). However, even if the dynamic structure of Imχd(ω) is not adequately described by Eq. (3),2,5,7 the voltage integral of ΔI(V,T)/V will be proportional to ε−1(T). As discussed in the Supplemental Material, the numerator of Eq. (6) is slowly varying with T, so that the dominant temperature dependence arises from 1 − λd(T). The results for χd(T) for various dopings are shown in the Supplemental Material. Plots of ε(T) = 1 − λd(T) are shown in Fig. 4 for 〈n〉 = 0.93 and 0.85. The inset in Fig. 4a shows Monte-Carlo results for the inverse spin susceptibility χ−1(T) of the classical 2D xy model. Here, one sees that there is a Curie–Weiss regime at higher temperatures associated with Emery–Kivelson phase fluctuations,19 which then crosses over to the low-temperature vortex–antivortex KT behavior
as TKT is approached.
Temperature dependence of ε(T) = 1 − λd(T) for the 2D Hubbard model. Here, ε(T) is normalized to its value at T/t = 0.2. a ε(T) for 〈n〉 = 0.93 and b for 〈n〉 = 0.85. The inset in a shows Monte-Carlo results for the susceptibility of a 2D xy model, which has a fixed amplitude with only a phase degree of freedom that can fluctuate. The dashed curves in a show the linear Curie–Weiss behavior, while in b, they show the BCS Cooper pair fluctuation result \({\mathrm{ln}}\left( {T/T_c^{MF}} \right)\)
We believe that the change in curvature of ε(T) as the temperature decreases for the 〈n〉 = 0.93 doping reflects the onset of phase fluctuations19 as T decreases. This behavior is analogous to that of a granular superconductor, in which at higher temperatures, one has a BCS \({\mathrm{log}}(T/T_c^{{\mathrm{MF}}})\) behavior associated with a single grain followed by an xy Curie–Weiss behavior associated with pair-phase fluctuations for a range of temperatures, until the KT behavior is reached.20 We note that this change in curvature and the upturn at low temperatures is not seen in DCA calculations using a four-site cluster (2 × 2–plaquette). In addition, in this case, DCA calculations find that Tc(〈n〉) has a maximum for 〈n〉 = 0.95 and falls to zero very close to 〈n〉 = 1,21 i.e., different from the 12-site cluster results displayed in Fig. 2. We believe that this is due to the fact that (spatial) phase fluctuations and KT behavior, which reduce Tc, are absent in small clusters. This characteristic change in behavior as the cluster size is increased provides further support for the presence of phase fluctuations in the underdoped PG region of the Hubbard model.
In contrast, for 〈n〉 = 0.85, the superconducting transition is approached from a region without a PG. In this doping regime, the meanfield temperature \(T_c^{{\mathrm{MF}}}\) is close to the Kosterlitz–Thouless temperature and over most of the temperature range above a narrow region, set by the Ginzburg parameter, ε(T) has the BCS form \({\mathrm{ln}}(T/T_c^{{\mathrm{MF}}})\) as shown by the dashed curve in Fig. 4b.
Finally, although it is difficult to experimentally measure the large q pairfield fluctuations2 which are necessary to determine the short-distance pairfield susceptibility, in the numerical simulations, this can be done. With \({\mathrm{\Delta }}_{\ell + x,\ell }^\dagger = (c_{\ell + x \uparrow }^\dagger c_{\ell \downarrow }^\dagger - c_{\ell + x \downarrow }^\dagger c_{\ell \uparrow }^\dagger )\) creating a pair between site \(\ell\) and its next-nearest-neighbor site in the x-direction \(\ell + x\), we have calculated the local χyx(r = 0, T) pairfield susceptibility
This measures the local pairfield induced on the \((\ell ,\ell + y)\) link when a singlet pair is created on the adjacent \((\ell ,\ell + x)\) link. Its negative sign clearly shows the d-wave character of the local pairfield. The presence of such pairfield fluctuations in the underdoped PG regime is also indicated by the observations of the persistence of a gap node in the ARPES spectrum at a temperature well above Tc.22 We have chosen to study χyx(r = 0, T) rather than the local d-wave susceptibility, because χyx(r = 0, T) avoids a remnant of the equal time expectation value \(\langle {\mathrm{\Delta }}_{\ell + x,x}{\mathrm{\Delta }}_{\ell + x,\ell }^\dagger \rangle = - 2\langle s_{\ell + x} \cdot s_\ell \rangle + \frac{1}{2}\langle n_{\ell + x}n_\ell \rangle\), which is associated with the local spin and charge correlations.8
The results for χyx(T) are shown in Fig. 5. For the 〈n〉 = 0.85 doping, the local χyx(T) pairfield susceptibility grows as T decreases. However, for the underdoped case with 〈n〉 = 0.93, χyx(T) saturates as the temperature decreases and the system enters the PG regime. In this case, the amplitude of the induced local pairfield is limited by the opening of the PG. Note however, as seen in Fig. 4a, χd(T)~ε−1(T) continues to increase as T decreases and the fluctuations of the phase of the pairfield-order parameter decrease. Additional results for χyx(T) for various dopings are shown in the Supplemental Material.
To conclude, above a region of KT fluctuations, the nature of the pairfield fluctuations of a 2D Hubbard model depend upon whether the superconducting phase is approached from a PG or non-PG regime. For an overdoped case 〈n〉 = 0.85, without a PG, we find BCS Cooper pair fluctuations.4,12 For an underdoped 〈n〉 = 0.93 filling which exhibits a PG, we find evidence of phase fluctuations of a pairfield-order parameter.19
Methods
In the DCA QMC approximation, the momentum space is coarse-grained to map the problem onto a finite-size cluster embedded in a mean field, which represents the lattice degrees of freedom not included on the cluster. The effective cluster problem is then solved with a continuous-time auxiliary-field QMC algorithm.23 Here, we use a 12-site cluster (see Fig. 1 in ref. 16), which allows us to study the effects of nonlocal fluctuations, and for which the Fermion sign problem of the QMC solver is manageable down to temperatures close to the superconducting instability.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
The computer code DCA++ that was used to generate the results reported in this paper is available at https://github.com/CompFUSE/DCA.
References
Bergeal, N. et al. Pairing fluctuations in the pseudogap state of copper-oxide superconductors probed by the Josephson effect. Nat. Phys. 4, 608–611 (2008).
Koren, G. & Lee, P. A. Observation of two distinct pairs fluctuation lifetimes and supercurrents in the pseudogap regime of cuprate junctions. Phys. Rev. B 94, 174515 (2016).
Anderson, J. T. & Goldman, A. M. Experimental determination of the pair susceptibility of a superconductor. Phys. Rev. Lett. 25, 743–747 (1970).
Abrahams, E. & Tsuneto, T. Time variation of the Ginzburg-Landau order parameter. Phys. Rev. 152, 416–432 (1966).
Jankó, B., Kosztin, I., Levin, K., Norman, M. R. & Scalapino, D. J. Incoherent pair tunneling as a probe of the cuprate pseudogap. Phys. Rev. Lett. 82, 4304–4307 (1999).
Kwon, H.-J., Dorsey, A. T. & Hirschfeld, P. J. Observability of quantum phase fluctuations in cuprate superconductors. Phys. Rev. Lett. 86, 3875–3878 (2001).
She, J. H. et al. Observing the origin of superconductivity in quantum critical metals. Phys. Rev. B 84, 144527 (2011).
Maier, T. A. et al. Pairing in a dry Fermi sea. Nat. Commun. 7, 11875 (2016).
Chen, X., LeBlanc, J. P. F. & Gull, E. Simulation of the NMR response in the pseudogap regime of the cuprates. Nat. Commun. 8, 14986 (2017).
Senechal, D., Lavertu, P., Marois, M. & Tremblay, A. Competition between antiferromagnetism and superconductivity in high T c cuprates. Phys. Rev. Lett. 94, 156404 (2005).
Macridin, A., Jarrell, M., Maier, T., Kent, P. R. C. & D’Azevedo, E. Pseudogap and antiferromagnetic correlations in the Hubbard model. Phys. Rev. Lett. 97, 036401 (2006).
Aslamasov, L. G. & Larkin, A. I. The influence of fluctuation pairing of electrons on the conductivity of normal metal. Phys. Lett. A 26, 238–239 (1968).
Ferrell, R. A. Fluctuations and the superconducting phase transition: II. Onset of Josephson tunneling and paraconductivity of a junction. J. Low Temp. Phys. 1, 423–442 (1969).
Scalapino, D. J. Pair tunneling as a probe of fluctuations in superconductors. Phys. Rev. Lett. 24, 1052–1055 (1970).
Maier, T., Jarrell, M., Pruschke, T. & Hettler, M. Quantum cluster theories. Rev. Mod. Phys. 77, 1027–1080 (2005).
Maier, T. A., Jarrell, M., Schulthess, T. C., Kent, P. R. C. & White, J. B. Systematic study of d-wave superconductivity in the 2D repulsive Hubbard model. Phys. Rev. Lett. 95, 237001 (2005).
Staar, P., Maier, T. & Schulthess, T. C. Two-particle correlations in a dynamic cluster approximation with continuous momentum dependence: Superconductivity in the two-dimensional Hubbard model. Phys. Rev. B 89, 195133 (2014).
Kosterlitz, J. & Thouless, D. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C. 6, 1181–1181 (1973).
Emery, V. J. & Kivelson, S. A. Importance of phase fluctuations in superconductors with small superfluid density. Nature 374, 434–437 (1995).
Kapitulnik, A., Kivelson, S. A. & Spivak, B. Colloquium: anomalous metals: failed superconductors. Rev. Mod. Phys. 91, 011002 (2019).
Jarrell, M., Maier, T., Hettler, M. H. & Tahvildarzadeh, A. Phase diagram of the Hubbard model: beyond the dynamical mean field. Europhys. Lett. 56, 563–569 (2001).
Kondo, T. et al. Point nodes persisting far beyond T c in Bi2212. Nat. Commun. 6, 7699 (2015).
Gull, E., Werner, P., Parcollet, O. & Troyer, M. Continuous-time auxiliary-field Monte Carlo for quantum impurity models. Europhys. Lett. 82, 57003 (2008).
Acknowledgements
The authors would like to thank E. Abrahams, I. Bozovic, I. Esterlis, M. Fisher, S. Kivelson, P.A. Lee, and A.-M. Tremblay for useful comments. We also thank I. Esterlis for the xy Monte-Carlo results shown in Fig. 4 and S. Kivelson for his comment regarding the relationship of this work to granular superconducting films. This work was supported by the Scientific Discovery through Advanced Computing (SciDAC) program funded by the U.S. Department of Energy, Office of Science, Advanced Scientific Computing Research and Basic Energy Sciences, and Division of Materials Sciences and Engineering. An award of computer time was provided by the INCITE program. This research used resources of the Oak Ridge Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract DE-AC05-00OR22725.
Author information
Authors and Affiliations
Contributions
Both T.A.M. and D.J.S. conceived the project. T.A.M. performed the numerical calculations and D.J.S. and T.A.M. analyzed and interpreted the numerical data. D.J.S. wrote the paper with input from T.A.M.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Maier, T.A., Scalapino, D.J. Pairfield fluctuations of a 2D Hubbard model. npj Quantum Mater. 4, 30 (2019). https://doi.org/10.1038/s41535-019-0169-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-019-0169-9
This article is cited by
-
Explaining the pseudogap through damping and antidamping on the Fermi surface by imaginary spin scattering
Communications Physics (2022)