Abstract
Charge density waves (CDWs), periodic modulations of the charge density, are among the most abundant and non-trivial ordered phases in condensed matter. Here we demonstrate the occurrence of multi-valley charge density waves (MV-CDW) on the semimetal Sb(111), a phenomenon previously observed at semiconductor surface inversion layers. The topological nature of the pocket surface states in Sb(111) ensures perfect nesting conditions giving rise to sharp peaks in helium atom scattering (HAS) diffraction spectra. The peculiar temperature dependence permits to distinctly associate the diffraction peaks with surface electron and hole-pocket states due to the non-trivial surface electronic band structure known from recent experimental data and present ab-initio calculations. Inelastic HAS spectra, besides providing the surface phonon dispersion curves in agreement with density functional perturbation theory calculations, reveal two additional dispersion curves of elementary excitations in the gap well below Rayleigh waves. They are attributed to collective excitations of the quasi-commensurate MV-CDWs associated with the surface electron M-pocket states at the Fermi level. These findings suggest that HAS can be regarded as a choice spectroscopy for the investigation of surface electronic excitations in the THz domain, opening up a new window for the search of collective phases at surfaces.
Similar content being viewed by others
Introduction
Fermi level multivalley states occurring around distinct wavevectors of some semimetal surfaces provide a basis for the occurrence of charge density waves (CDWs).1,2,3 The mechanism of multivalley CDWs at semiconductor surfaces, first described by Kelly and Falicov in the 70 s is conceptually similar to that of 1D Peierls CDWs.4 Both mechanisms are based on an almost perfect nesting between states with wavevectors k concentrated around well-defined values at the Fermi level. In the ordinary two (three)-dimensional case, where nesting is defined by stationary diameters across the Fermi contour (surface), fluctuations admix states with any Δk connecting the continuum of states at the Fermi level. In multivalley systems with narrow pockets, fluctuations can only mix states with Δk either very small or close to the intervalley nesting vectors, thus making intervalley CDWs more robust against fluctuations. Notably, in semiconductors and semimetals the Fermi level shifts substantially with temperature, so that the critical behaviour of a multivalley CDW is not just a matter of fluctuations as for ordinary CDWs. In addition, multivalley CDWs are generally, albeit not necessarily, stabilised by electron–phonon (e–ph) interaction.3,5,6,7
Helium atom scattering (HAS) has been recently recognised as a powerful tool to investigate the mode-selected e–ph interaction at the surface of conducting or highly polarisable surfaces.8,9,10 The ability relies on the fact that the exchange of energy and parallel momentum between the neutral probe atom and the atoms of the solid can only occur via the interposed surface electrons whose wave functions extend outward up to the scattering atom turning point. More precisely the inelastic-scattering amplitudes from surface phonons are proportional to the phonon-induced surface charge density oscillations, and therefore to the mode-selected e–ph interaction.9,11
Given this mechanism, a natural question is whether the energy and parallel momentum provided by the atom can be retained by low-energy surface electronic excitations, rather than being transmitted to phonons, and reveal their dispersion curves. Since the band structure at the Fermi level of semimetal surfaces like Bi(111) and Sb(111) is characterised by sets of narrow surface electron and hole pockets in the reciprocal space,12,13,14 multivalley CDWs are expected to be observed in HAS diffraction patterns.
The high sensitivity of HAS to CDWs as compared to other surface probes allowing for a precise determination of the transition temperatures and critical exponents was demonstrated long ago for layered chalcogenides15,16 as well as recently for the 1D topological metal Bi(114).17 The observation of phason dispersion curves with HAS was previously reported for the long-period reconstruction of the Au(111) \(23 \times \sqrt 3\) surface18 and another hint comes from the non-adiabatic Kohn-anomalies observed for Mo(110):H and W(110):H19,20,21,22 which are associated with electron–hole pair excitations. However, a signature of collective surface electronic excitations in elastic atom–surface scattering spectra has remained missing up to date.
With regard to the ideal surfaces, there is some consensus about whether CDWs can exist in Bi(111),12,13 whereas they seemed to be excluded in Sb(111).13 On the other hand the spin–orbit (SO) coupling, which makes Sb(111) a weak topological insulator with spin-split bands around the zone centre,23 can in principle support a spin-density wave.14
Here we show that the spin-selected nesting between the states of narrow pockets at the Fermi level, peculiar of topological semimetals, yields sharp features in the HAS diffraction spectra corresponding to multivalley CDWs, and clear signatures of collective phase and amplitude CDW excitations in the THz spectral region. Inelastic HAS measurements on Sb(111) at two different temperatures reveal two additional branches in the gap below the Rayleigh wave branch. On the basis of density functional perturbation theory (DFPT) calculations of the surface phonon dispersion curves of Sb(111),23 it appears that the two low-energy branches cannot be attributed to any possible phonon branch of the ideal surface. Their dispersion curves appear to be compatible with the Brillouin zone (BZ) of the commensurate surface electron CDW lattice, which suggests their assignment to a phason/ampliton pair.
Sb(111) exhibits a rhombohedral crystal structure (A7, space group \({\mathrm{R}}\overline {\mathrm{3}} {\mathrm{m}}\)), where atoms are arranged in bilayers normal to the [111]-direction.24,25 Intralayer bonding is mostly covalent, whereas bilayers are held together by weaker interactions which permits an easy cleavage, giving rise to the hexagonal surface unit cell of Sb(111) with a lattice constant a = 4.308 Å26 (see Fig. 1b).
Measurement principle and diffraction scans showing the CDW periodicity. a Schematic overview of the apparatus. A supersonic helium beam is produced in a source chamber, before scattering from the Sb(111) sample. The scattered beam is detected in a mass-spectrometer detector. Momentum transfer ΔK occurs due to scattering of the He beam from the crystal, at a certain incident angle ϑi, through a fixed total scattering angle. Energy resolution is optionally added by chopping the He beam with a chopper and measuring the time-of-flight. b The crystal structure of Sb(111) showing the first bilayer (dark and light blue atoms) and the first atomic plane of the second bilayer (grey atoms), with the surface unit cell (full line; lattice constant a = 4.308 Å) and the \((2/\sqrt 3 \times 2/\sqrt 3 )\)R30° surface unit cell of the electron pocket multivalley CDW (broken line; CDW lattice constant \(a_{\rm{CDW}} = 2a/\sqrt 3\)). c Diffraction scans for Sb(111) along the \(\overline {\Gamma {\mathrm{K}}}\) azimuth for different surface temperatures and beam energies. The vertical-dashed lines show the momentum transfers corresponding to the interpocket transitions as illustrated in Fig. 2. Note the slight shift to smaller absolute values of ΔK of the hole-pocket peaks with increasing TS. The small peak D corresponds to transitions between equivalent spots on the Dirac ring
There are no significant changes in terms of the structure upon truncation of bulk Sb,26,27 in contrast to the electronic properties, which change significantly depending on the crystal thickness. While bulk Sb(111) is a topological semimetal,28,29 Sb thin films are predicted to become a topological insulator at a thickness under 22 layers, to exhibit a quantum spin Hall phase below 8 layers28,30 and finally to be a semiconductor at bilayer thickness.31,32 For a bismuth monolayer lattice on top of an insulator, a quantum spin hall phase at room temperature has also been recently predicted.33
A previous HAS analysis of the surface structure, step height, and terrace distribution of Sb(111) provided a surface corrugation of about 13% of the lattice constant, and confirmed the occurrence of bilayer steps, with 14% of specular reflection from surface portions including one-bilayer step, and only 2% from two-bilayer steps.34 For a HAS coherence length of the order of 50 Å the terrace width can be estimated based on the width of the specular peak, with 40–80 nm throughout several scans.35
Results
Elastic scattering
Figure 1c shows three HAS diffraction patterns of Sb(111) plotted versus the parallel momentum transfer ΔK. For elastic scattering ΔK is given by:
with ki, the incident wave vector, and ϑi and ϑf the incident and final angle with respect to the surface normal, respectively (see Fig. 1a). Figure 1c shows scans along the \(\overline {\Gamma {\mathrm{K}}}\) azimuth plotted versus ΔK, measured for an incident energy Ei varying between 11.85 and 22 meV and three different surface temperatures TS from 121 to 405 K. The intensity scale has been expanded to show additional features with smaller intensity. Besides some features assigned to bound-state resonances (e.g. the peak R) and kinematical focusing (KF), which are easily recognised due to the strong dependence of their position on the incident energy,36 there are features that occur at fixed values of ΔK, independently of the incident energy, and are therefore assigned to elastic diffraction processes, just as the two main diffraction peaks at ΔK = ±2.90 Å–1 corresponding to the periodicity of the surface atomic lattice. The additional weaker diffraction peaks occur at ΔK = ±1.45 Å–1 and ΔK = ±0.3 Å–1 (with an uncertainty of about ±0.04 Å–1).
The intensity of the sharp peaks at ΔK = ±1.45 Å–1 falling at one half of the G-vector along \(\overline {\Gamma {\mathrm{K}}}\) decreases rapidly with temperature, faster than for the ordinary specular and diffraction peaks37 (see also the SI for an analysis of the temperature dependence). It might also be associated with a surface reconstruction disappearing above a certain temperature, however, the temperature dependence in Fig. 1c is inconsistent with that scenario. The intensity of the satellite diffraction peaks at ±0.3 Å–1 increases with temperature, contrary to the expected Debye–Waller attenuation. Since HAS is basically diffracted by the surface electron charge density, the interpretation of such superstructure should be searched for in the peculiar surface electronic structure of Sb(111) which is characterised by narrow electron and hole pockets at the Fermi level,13,38 potentially responsible for the presence of CDWs.
The diffraction patterns along the \(\overline {\Gamma {\mathrm{M}}}\) direction36 (not reported here) show prominent features, besides the specular and diffraction peaks, which can all be assigned to bound-state resonances or kinematical focusing, from their dependence on the incident energy. Only a weak feature at –3G/2 ≈ –2.6 Å–1 (but not at +3G/2) appears to be persistent for varying incident energy, and is also vanishing for increasing temperature like that at G/2 along \(\overline {\Gamma {\mathrm{K}}}\). The following analysis shows that the peculiar surface electronic structure of Sb(111) explains the HAS diffraction patterns measured at different surface temperatures in the \(\overline {\Gamma {\mathrm{K}}}\) direction.
Surface electronic structure of Sb(111)
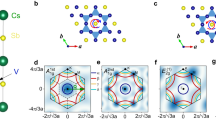
The electronic surface states of Sb(111) have been analysed previously by Höchst and Ast38 and by Sugawara et al.13 with angle-resolved photoemission spectroscopy (ARPES) and later by Xie et al. with laser-based ARPES.39 Sb(111) exhibits a non-trivial surface electronic structure as seen in the DFT calculations including SO coupling of the band structure around the Fermi level depicted in Fig. 2a. It appears that, starting from a Dirac point at the zone centre (\(\overline \Gamma\)), two spin-split surface bands generate a narrow electron pocket at \(\overline \Gamma\), a hole pocket in each of the six \(\overline {\Gamma {\mathrm{M}}}\) directions and another electron pocket at the six \(\overline {\mathrm{M}}\) symmetry points. The corresponding Fermi contours at the Fermi level are shown in Fig. 2c. They are found in excellent agreement with Xie et al. laser-based ARPES39 (Fig. 2b) and Sugawara et al. ARPES data13 (Fig. 2d).
Surface electronic band structure of Sb(111) together with an illustration of the interpocket transitions. a Details of the surface electronic band structure of Sb(111) calculated with DFT-SO showing the two surface spin-split bands in the \(\overline {\Gamma {\mathrm{M}}}\) direction and a portion along \(\overline {\Gamma {\mathrm{K}}}\). The colour shadows give the degree of surface localisation and linewidths. At the Fermi level the surface bands form a quasi-isotropic electron pocket at \(\overline \Gamma\) (Dirac ring) and along \(\overline {\Gamma {\mathrm{M}}}\) an elongated hole pocket, with a pronounced surface character at small wavevectors, and another electron pocket centred at the \(\overline {\mathrm{M}} _{}^{}\)-point. b Laser-based ARPES band profiles measured by Xie et al.39 show excellent agreement with the calculated band structure in a. c Calculated pocket Fermi contours: The orientations of pocket hole and electron spins depend on whether pockets are in the \(\overline {\Gamma {\mathrm{M}}}\) or the \(\overline {\Gamma {\mathrm{M}}}\)′ direction. The removal of spin degeneracy lowers the surface hexagonal symmetry to trigonal. d ARPES data by Sugawara et al.13 (reproduced with permission, copyright 2006 by the American Physical Society). Pockets with the same spin show intense spots, reflecting the trigonal symmetry, in closer agreement with the theoretical positions, and shapes shown in c than with bulk LAPW-LDA calculations reported by Sugawara et al.13 (light blue contours shown in panel d). Similar results have been reported by Xie et al.39 The interpocket transitions in the \(\overline {\Gamma {\mathrm{K}}}\) direction and the respective ΔK values corresponding to the peaks in the diffraction spectrum of Fig. 1c are indicated as double arrows in d
As seen in Fig. 2d, in addition to the quasi-hexagonal Dirac ring around \(\overline \Gamma\) (radius ≈0.07 Å–1), high-intensity spots from the pocket states crossing the Fermi level are observed in the \(\overline {\Gamma {\mathrm{M}}}\) directions as described by DFT calculations, corresponding to hole pockets and electron pockets with maximum intensity at \(\overline {\mathrm{M}}\). As appears in Fig. 2a the hole-pocket states have a prominent surface density of states (DOS) around the edge at Kh ≈ 0.15 Å–1 in good agreement with ARPES observation in Fig. 2d.
The presence of electron pockets at the \(\overline {\mathrm{M}}\)-points and of hole-pockets at \(\approx \overline {\Gamma {\mathrm{M}}} /4\), and the close correspondence between the positions of the additional diffraction peaks and the corresponding intervalley separations ΔK in the \(\overline {\Gamma {\mathrm{K}}}\) direction is a compelling evidence for multi-valley CDWs. As shown by Kelly and Falicov1, this is possible, provided the electron–phonon contribution to the intervalley exchange interaction is sufficiently strong. The authors remark that “the electron–electron interaction, via phonons is known to be the dominant intervalley exchange effect; it leads to superconductivity in some many-valley degenerate semiconductors,40 but is large and attractive even in materials which are not superconducting”. The antimony (111) surface clearly belongs to this family.
The basic mechanism for the formation of a multivalley CDW associated with the electron pockets at the \(\overline {\mathrm{M}}\)-points (K = G/2) can be understood by considering the three degenerate free-electron pocket states of equal spin at the Fermi level exp[iKx] and exp[iK\((x/2 \pm \sqrt 3 y/2)\)] with K = G/2 and their three linear combinations A, E1, and E2 dictated by the crystal point symmetry. The density associated to each linear combination shows a CDW modulation, whereas their sum with equal weights gives a uniform density. Any perturbation, e.g. electron–phonon interaction causing a splitting of the states, and their different population at finite temperature yields a CDW. A totally symmetric ground state, would give a CDW shape:
Equation (2) defines a hexagonal surface CDW lattice rotated 30° with respect to the crystal lattice and a lattice constant \(a_{{\rm{CDW}}} = 2a/\sqrt 3 = 4.97\) Å (Fig. 1b). A similar argument holds for a CDW associated with the hole states, where K = G/2 is replaced by Kh. The construction of a CDW originating from the superposition of free-electron waves from electron- and hole-pockets would lead of course to a more complex CDW lattice and a larger period. However, the temperature dependence of the diffraction spectra indicates that at low temperature the hole-pocket states play a negligible role.
The association of the additional diffraction peaks to the electron and hole-pockets stems from the peculiar temperature dependence of their intensities. On the one hand, the hole-pocket peaks increase with surface temperature, unlike ordinary diffraction peak intensities which decrease with increasing TS. On the other hand, the \(\overline {\mathrm{M}}\) electron pocket peaks decrease faster than the ordinary diffraction peaks, possibly disappearing at ≈450 K. An analysis of the temperature dependence and the critical exponent based on the corresponding order parameter can be found in the SI. Such an anomalous temperature dependence may be attributed to a downward shift of the Fermi energy for increasing TS, which has the effect of increasing the DOS in the hole pocket and decreasing that of the \(\overline {\mathrm{M}}\) electron pockets.
The DFT calculation tells that both pockets are already there at 0 K and the \(\overline {\mathrm{M}}\) electron pocket minimum is at about –0.1 eV below the Fermi level (Fig. 2a). Thus a temperature increase of ≈450 K which gives rise to the disappearance of the \(\overline {\mathrm{M}}\) electron pocket peaks, corresponds to a work function change rate of dϕ/dTS ≈ 0.22 meV K–1. The value of dϕ/dTS falls just in the range of other p-band metals, e.g. 0.22 meV K–1 for Sn and 0.20 meV K–1 for Bi41 and agrees with measurements of ϕ for Sb thin films at 77 and 300 K giving dϕ/dTS ≈ 0.18 meV K–1.42 The downward shift of the Fermi level is also responsible for the slight shift of the hole-pocket peaks to smaller absolute values of ΔK with increasing temperature (see Fig. 1c).
The above described analysis makes the CDW scenario the most plausible, despite previous indications that no CDW occurs in Sb(111). The fact that the presence of a CDW in Sb(111) has so far gone unnoticed in investigations with other experimental techniques may be explained by the higher sensitivity of HAS to charge density modulations. The smallest charge density modulation Δn detectable with HAS can be estimated based on an energy resolution ΔE ≈ 1 meV divided by the Esbjerg–Nørskov constant for low-energy He atoms, A = 750 eV/a.u.,43 yielding Δn ≈ 1.3 × 10–6 atomic units. Nevertheless, a very recent scanning tunnelling microscopy study44 has revealed for Sb(111) at a temperature of about 5 K a (2 × 2) surface structure, which is the minimum periodicity common to the \((2/\sqrt 3 \times 2/\sqrt 3 )\)R30° CDW and the Sb(111)(1 × 1) lattice (for a short discussion see the SI, in particular Fig. S5). It follows from the above, that experimental techniques which distinctly probe the charge density over the topmost atomic layer seem to be better suited for the search of surface CDWs compared to techniques which imply some penetration depth into the bulk.
There is however, another possible explanation of the observed diffraction spectra not requiring CDWs: the quasi-elastic collisions of pocket electrons with the flying-by He atom and consequent spin-conserving intervalley transitions. A simple classical calculation conserving total energy and parallel momentum (the atom normal momentum change is as usual absorbed by the crystal center of mass) shows that for an incident He-atom energy of 15 meV, the electron energy for the ΔK = ±1.4 Å–1 transitions changes by –6.0 and +5.0 meV, respectively. These are small amounts as compared to the Fermi energy relative to the \(\overline {\mathrm{M}}\)-pocket bottom, at least at low temperature, but cause some asymmetry in the two diffraction amplitudes. Some asymmetry is noticed in Fig. 1c, but not at high temperature, where it should be more pronounced. The hole intervalley transitions would imply a much smaller energy transfer of the order of ±1 meV, whereas in the \(\overline {\Gamma {\mathrm{M}}}\) direction the –3G/2 inter-pocket transition with larger energy transfer would cause large asymmetry, perhaps explaining the absence of the +3G/2 spot. It should be noted that in this direction the shortest inter-pocket transitions ΔK = ±G/2 would be spin forbidden and the same would hold for ΔK = ±3G/2 (the ΔK = ±G transition is covered by the lattice diffraction). Hence, since ΔK = ±3G/2 is just the shortest reciprocal vector GCDW of the CDW lattice in its [110]CDW direction the observation of a feature at –3G/2 supports the CDW scenario.
Moreover, for the alternative scenario without a CDW, inelastic transitions at special values of ΔK corresponding to single-particle inter-pocket transitions would be detected in time-of-flight (TOF) measurements. On the contrary, as shown in the following section, TOF spectra give, besides a complete set of surface phonon dispersion curves, two low-energy branches which can be assigned to the expected ampliton and phason excitations of the electron CDW lattice.45,46,47 The ability of inelastic HAS in its high-resolution 3He spin-echo version to observe phasons associated with misfit dislocations in the long-period \(23 \times \sqrt 3\) reconstructed Au(111) surface was demonstrated by McIntosh et al.18 recently, while here CDW phasons and amplitons are observed with ordinary HAS spectroscopy.
Dispersion curves
The dispersion curves of elementary excitations have been obtained by transforming TOF spectra of the scattered He atoms to energy transfer spectra (see Fig. S2 in the Supplementary Information). The experimental dispersion curves of surface phonons and the two additional low-energy branches assigned to phasons and amplitons measured at both 170 (only acoustic region) and 300 K (whole spectrum) are plotted in Fig. 3. The symbols represent the experimental data while the background lines correspond to the DFPT calculations. The colour scale of the DFPT calculations corresponds to the intensity of the phonon modes projected onto the first surface layer. The experimental data points are labelled according to their proximity to the calculated phonon modes, with either prominently shear vertical (SV) or longitudinal (L) polarisation on the first or third atomic layer, respectively.
Measured surface phonon dispersion of Sb(111) in comparison with DFPT calculations. The data points have been extracted from measurements at 170 K in (a) and at 300 K in (b). They are plotted on top of the theoretical DFPT dispersion curves, with the corresponding DOS projected onto the first surface layer and given by colour code. All phonon polarisations accessible using the present scattering geometry are superimposed and the measured data points are labelled by proximity to the calculated phonon modes. SV1 or SV3 denote surface (quasi-) shear-vertical modes with the largest amplitudes at the surface layer (bilayer) or at the third layer (second bilayer), respectively. Similarly L1 (L3) denote surface (quasi-) longitudinal modes with the largest amplitude on the first (second) bilayer. Shear-horizontal modes are not plotted. The grey data points (crosses) are attributed to phasons and amplitons of the multi-valley CDW associated with the Fermi surface \(\overline {\mathrm{M}}\)-point electron pockets. The inset at the top-right shows the BZ of the surface CDW lattice inscribed into the crystallographic surface BZ. The CDW symmetry point \(\overline {\mathrm{M}} _{{\rm{CDW}}}\) corresponds to a maximum in the phason/ampliton branches (green arrow in a)
As already observed in the surface phonon dispersion of Bi(111),10 the e–ph interaction on Sb(111) is sufficiently large to make vibrational modes that are mainly localised at the third layer (SV3, L3) visible for HAS. Due to the e–ph interaction, large modulations of the surface charge density are induced,10 which is also important in observing comparatively large inelastic intensities from surface optical modes.48 The property is common to other layered structures, as recently shown theoretically49 and experimentally50,51 for Bi2Te3(111) and Bi2Se3(111). In general the overall agreement of the measurements with the calculations is very good.
In addition to the data points which are reproduced by the DFPT calculations, there are data points plotted as grey stars in Fig. 3, which cannot be assigned to any surface vibrational mode. These data points form two separate branches, the aforementioned phasons and amplitons, which becomes particularly evident for the measurements at TS = 170 K along the \(\overline {\Gamma {\mathrm{KM}}}\) direction. The features leading to these modes are small in intensity but consistently present over the whole measuring range as can be seen in the SI (Figs. S2 and S3). The broad maximum, falling in both branches at one half of the \(\overline {\Gamma {\mathrm{KM}}}\) segment, is seen to occur at 0.7 Å–1 (green arrow in Fig. 3a), which is the \(\overline {\mathrm{M}} _{{\rm{CDW}}}\) symmetry point of the CDW BZ (Fig. 3, inset). This correspondence and the approximate specularity of the branches with respect to \(\overline {\mathrm{M}} _{\rm{CDW}}\) suggest to assign the two branches to CDW excitations, i.e. phasons and amplitons. Note that the commensurate excitations of a commensurate electron CDW have a finite energy at ΔK = 0 (here also at the \(\overline {\mathrm{M}} \equiv \overline \Gamma _{\rm{CDW}}\) point) due to the pinning to the lattice.
For a phenomenological description of CDW excitations the multipole expansion (ME) model52 is applied to the M-electron CDW lattice, viewed as a 2D periodic lattice of electron shells subject to dynamical multipolar deformations. In the simplest picture the latter are restricted to dipolar deformations (rigid displacements) either normal (amplitons) or parallel longitudinal (phasons) to the surface. While the corresponding degrees of freedom are endowed with an effective inertial mass μ, the atomic lattice is assumed to be rigid (infinite mass) so as to ensure adiabaticity, and to exert on the electron shells an isotropic pinning force constant f0 (see “CDW structure and dynamics within the ME model” in the SI). The two dispersion curves can then be fairly well reproduced with just nearest neighbour (nn) and next nn (2n) force constants for normal (ampliton) and parallel longitudinal (phason) shell (dipolar) displacements, f1α and f1φ, and f2α and f2φ, respectively. The fit shown in Fig. 4 (effective masses = 1) is obtained (see SI) with f0 = 12, f1α = 3, f2α = –2 and f1φ = 1, f2φ = –1, all in meV2/μ units.
The measured low-energy branches fitted with the ME model. The additional low-energy branches measured with HAS in Sb(111) at two different surface temperatures are attributed to the elementary excitations of the commensurate electron multi-valley CDW: a amplitons, b phasons. The upper abscissa shows the symmetry points of the CDW lattice. The full lines show fits based on the ME model with dipolar coordinates and nearest (nn) and next-nearest (2n) interactions (see SI)
The deviations, notably the small dips at \(\overline {\mathrm{K}}\) may be due to the coupling either with the hole pockets, which would introduce short-period oscillations in the dispersion curves, or with phonons. A possible coupling to phonons as the cause of dips at \(\overline {\mathrm{K}}\) in the CDW branches (and apparently also in the lowest phonon branch) deserves further investigation. The physical meaning of the fitting parameter values does not seem to be trivial, especially the fact that the 2n force constants remain comparable to the nn ones, while having opposite signs. For a pure dipole–dipole interaction f1α and f2α should both be positive with a ratio \(f_{1\alpha }/f_{2\alpha } = \sqrt {27}\), while f1φ and f2φ should be negative and in the same ratio. Pauli repulsion for in-plane shell displacements, many-body effects and dispersion forces, as well as the amplification/depression of interactions at different distances due to the interference of the electron CDW with that of the pocket holes (see “CDW structure and dynamics within the ME model” in the SI), are expected to play a role in the effective force constants of the ME model—an issue worth being investigated from first principles.
Discussion
In summary, we have shown that additional elastic peaks which are observed in HAS diffraction spectra from Sb(111) can be assigned, on the basis of their peculiar temperature dependence, to electron and hole multi-valley CDWs. The multi-valley structure at the Fermi level consists of six electron pockets at the \(\overline {\mathrm{M}}\) symmetry points of the surface BZ, and six hole pockets at about 1/5 of the \(\overline {{\mathrm{KM}}}\) segments of alternate spins, as found in existing ARPES data and present DFT calculations including SO coupling.
Furthermore, inelastic HAS spectra, besides providing the surface phonon dispersion curves in agreement with DFPT + SOC calculations, reveal two additional dispersion curves of elementary excitations in the energy region well below the Rayleigh mode. They can be associated to phasons and amplitons of the multi-valley CDW associated with the electron pockets. The fact that inelastic HAS from surface phonons exclusively occurs, for a conducting surface, through the e–ph interaction8,9,10,11 implies that also the dispersion of low-energy surface electron collective excitations can be measured by HAS. It is expected that ordinary HAS, as well as its ultrahigh-resolution 3He spin-echo version,53,54 will be regarded as a choice spectroscopy for the investigation of surface electronic excitations in the THz domain.
Methods
Experimental details
The experiments were carried out on the helium-atom-scattering apparatus H.A.N.S which has been described in greater detail in earlier publications.55 Figure 1a shows a schematics of the experimental setup. The energetically narrow He-atom beam (ΔE/E ≈ 2%) is created by a supersonic expansion of He-gas and scattered off the surface in a fixed 91.5° source-sample-detector geometry. Energy dispersive measurements for inelastic scattering are performed using TOF measurements with a pseudo-random chopper disc.
The sample under investigation was an antimony (Sb) single crystal cleaved in the (111) direction in shape of a disc of 15 mm diameter and 2 mm thickness. The crystal was cleaned by several cycles of Ar+ sputtering and subsequent annealing at 475 K. The contamination and cleanness were checked by auger electron spectroscopy and the intensity of the diffuse elastic peak. The sample holder can be cooled using liquid nitrogen and heated using a button heater while the temperature is measured by a type K thermocouple. The used He beam energies range from 11.8 to 36.6 meV and the experiments were carried out at constant surface temperatures between 120 and 405 K.
Computational details
Calculations have been performed within DFT by using a norm conserving fully relativistic pseudopotential and the Perdew–Burke–Ernzerhof generalised gradient approximation for the exchange and correlation functional.56 SO coupling effects are taken into account self-consistently with the formalism of non-collinear spin magnetisation as implemented in the QE distribution.57 The Kohn–Sham wave functions are expanded in plane waves up to a kinetic-energy cutoff of 45 Ry. A Gaussian smearing of 0.01 Ry is used to deal with the metallic character of Sb.
In accordance with Campi et al.,23 the Sb(111) surface is modelled by a slab geometry with a single atom per layer and 24 layers. The periodic images of the slab are separated by a vacuum region 12 Å wide. The band structure and the Fermi energy are calculated for the optimised slab geometry.23 To resolve the fine details of the electronic properties of interest, we first performed a self-consistent calculation with integration of the BZ over a (48 × 48 × 1) Monkhorst–Pack58 mesh followed by non self-consistent calculations over highly dense meshes.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Kelly, M. J. & Falicov, L. M. Electronic structure of inversion layers in many-valley semiconductors. Phys. Rev. Lett. 37, 1021–1024 (1976).
Kelly, M. J. & Falicov, L. M. Electronic ground state of inversion layers in many-valley semiconductors. Phys. Rev. B 15, 1974–1982 (1977).
Kelly, M. J. & Falicov, L. M. Optical properties of charge-density-wave ground states for inversion layers in many-valley semiconductors. Phys. Rev. B 15, 1983–1987 (1977).
Grüner, G. Density Waves in Solids, vol. 89 of Frontiers in Physics (Perseus Publishing, Cambridge, Massachusetts, 1994).
Aruga, T. Charge-density waves on metal surfaces. J. Phys. Condes. Matter 14, 8393 (2002).
Zhu, X., Cao, Y., Zhang, J., Plummer, E. W. & Guo, J. Classification of charge density waves based on their nature. Proc. Natl Acad. Sci. USA. 112, 2367–2371 (2015).
Xi, X. et al. Strongly enhanced charge-density-wave order in monolayer NbSe2. Nat. Nanotechnol. 10, 765 (2015).
Sklyadneva, I. Y. et al. Mode-selected electron-phonon coupling in superconducting Pb nanofilms determined from He atom scattering. Phys. Rev. Lett. 107, 095502 (2011).
Benedek, G. et al. Unveiling mode-selected electron-phonon interactions in metal films by helium atom scattering. Phys. Chem. Chem. Phys. 16, 7159–7172 (2014).
Tamtögl, A. et al. Surface and subsurface phonons of Bi(111) measured with helium atom scattering. Phys. Rev. B 87, 035410 (2013).
Manson, J. R., Benedek, G. & Miret-Artés, S. Electron-phonon coupling strength at metal surfaces directly determined from the helium atom scattering Debye-Waller Factor. J. Phys. Chem. Lett. 7, 1016–1021 (2016).
Ast, C. R. & Höchst, H. Indication of charge-density-wave formation in Bi(111). Phys. Rev. Lett. 90, 016403 (2003).
Sugawara, K. et al. Fermi surface and anisotropic spin-orbit coupling of Sb(111) studied by angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 96, 046411 (2006).
Koroteev, Y. M. et al. Strong spin-orbit splitting on Bi surfaces. Phys. Rev. Lett. 93, 046403 (2004).
Benedek, G. et al. Shifted surface-phonon anomaly in 2H-TaSe2. Phys. Rev. Lett. 60, 1037–1040 (1988).
Brusdeylins, G. et al. Determination of the critical exponent for a charge density wave transition in 2H-TaSe2 by helium atom scattering. EPL 9, 563 (1989).
Hofmann, P. et al. Strong-coupling charge density wave in a one-dimensional topological metal. Phys. Rev. B 99, 035438 (2019).
McIntosh, E. M. et al. Measurement of the phason dispersion of misfit dislocations on the Au(111) Surface. Phys. Rev. Lett. 110, 086103 (2013).
Hulpke, E. & Lüdecke, J. Hydrogen-induced phonon anomaly on the W(110) surface. Phys. Rev. Lett. 68, 4 (1992).
Hulpke, E. & Lüdecke, J. The giant surface phonon anomaly on hydrogen saturated W(110) and Mo(110). Surf. Sci. 287, 837–841 (1993).
Plummer, E., Shi, J., Tang, S.-J., Rotenberg, E. & Kevan, S. Enhanced electron-phonon coupling at metal surfaces. Prog. Surf. Sci. 74, 251–268 (2003).
Kröger, J. Electron-phonon coupling at metal surfaces. Rep. Prog. Phys. 69, 899 (2006).
Campi, D., Bernasconi, M. & Benedek, G. Phonon and electron-phonon interaction at the Sb(111) surface. Phys. Rev. B 86, 7 (2012).
Barrett, C. S., Cucka, P. & Haefner, K. The crystal structure of antimony at 4.2, 78 298° K. Acta Crystallogr. 16, 451–453 (1963).
Schiferl, D. & Barrett, C. S. The crystal structure of arsenic at 4.2, 78 and 299 °K. J. Appl. Crystallogr. 2, 30–36 (1969).
Bengió, S. et al. The structure of Sb(111) determined by photoelectron diffraction. Surf. Sci. 601, 2908–2911 (2007).
Stegemann, B., Ritter, C., Kaiser, B. & Rademann, K. Characterization of the (0001) cleavage surface of antimony single crystals using scanning probe microscopy: atomic structure, vacancies, cleavage steps, and twinned interlayers. Phys. Rev. B 69, 155432 (2004).
Zhang, P., Liu, Z., Duan, W., Liu, F. & Wu, J. Topological and electronic transitions in a Sb(111) nanofilm: the interplay between quantum confinement and surface effect. Phys. Rev. B 85, 201410 (2012).
Soumyanarayanan, A. & Hoffman, J. E. Momentum-resolved STM studies of Rashba-split surface states on the topological semimetal Sb. J. Electron Spectrosc. Relat. Phenom. 201, 66–73 (2015).
Kim, S. H. et al. Topological phase transition and quantum spin Hall edge states of antimony few layers. Sci. Rep. 6, 33193 (2016).
Wang, G., Pandey, R. & Karna, S. P. Atomically thin group V elemental films: theoretical investigations of antimonene allotropes. ACS Appl. Mater. Interfaces 7, 11490–11496 (2015).
Fortin-Deschênes, M. et al. Synthesis of antimonene on germanium. Nano Lett. 17, 4970–4975 (2017).
Reis, F. et al. Bismuthene on a SiC substrate: a candidate for a high-temperature quantum spin Hall material. Science 357, 287–290 (2017).
Mayrhofer-Reinhartshuber, M., Tamtögl, A., Kraus, P. & Ernst, W. E. Helium atom scattering investigation of the Sb(111) surface. J. Phys. 25, 395002 (2013).
Farías, D. & Rieder, K.-H. Atomic beam diffraction from solid surfaces. Rep. Prog. Phys. 61, 1575 (1998).
Mayrhofer-Reinhartshuber, M., Kraus, P., Tamtögl, A., Miret-Artés, S. & Ernst, W. E. Helium-surface interaction potential of Sb(111) from scattering experiments and close-coupling calculations. Phys. Rev. B 88, 205425 (2013).
Tamtögl, A., Mayrhofer-Reinhartshuber, M., Kraus, P. & Ernst, W. E. Surface Debye temperature and vibrational dynamics of Antimony(111) from helium atom scattering measurements. Surf. Sci. 617, 225–228 (2013).
Höchst, H. & Ast, C. R. The Fermi surfaces of thin Sb(111) films. J. Electron Spectrosc. Relat. Phenom. 137-140, 441–444 (2004).
Zhuo-Jin, X. et al. Weak electron-phonon coupling and unusual electron scattering of topological surface states in Sb(111) by laser-based angle-resolved photoemission spectroscopy. Chin. Phys. Lett. 31, 067305 (2014).
Cohen, M. L. Superconductivity in many-valley semiconductors and in semimetals. Phys. Rev. 134, A511–A521 (1964).
Ibragimov, K. I. & Korol’kov, V. A. Temperature dependence of the work function of metals and binary alloys. Inorg. Mater. 37, 567–572 (2001).
Fahrenbruch, A. L. Photoelectric Properties Of Evaporated Antimony Films As A Function Of Film Thickness. Master’s thesis (Oregon State University, Corvallis, 1967).
Esbjerg, N. & Nørskov, J. K. Dependence of the He-scattering potential at surfaces on the surface-electron-density profile. Phys. Rev. Lett. 45, 807–810 (1980).
Yam, Y. -C. et al. Unexpected zero bias conductance peak on the topological semimetal Sb (111) with a broken bilayer. Preprint at https://arxiv.org/abs/1810.13390 (2018).
Vallade, M., Dvorak, V. & Lajzerowicz, J. Amplitudons and phasons in the triple-k incommensurate phase of quartz-type crystals. J. de. Phys. 48, 1171–1179 (1987).
Grüner, G. The dynamics of charge-density waves. Rev. Mod. Phys. 60, 1129–1181 (1988).
Torchinsky, D. H., Mahmood, F., Bollinger, A. T., Božović, I. & Gedik, N. Fluctuating charge-density waves in a cuprate superconductor. Nat. Mater. 12, 387–391 (2013).
Kraus, P., Tamtögl, A., Mayrhofer-Reinhartshuber, M., Benedek, G. & Ernst, W. E. Resonance-enhanced inelastic He-atom scattering from subsurface optical phonons of Bi(111). Phys. Rev. B 87, 245433 (2013).
Heid, R., Sklyadneva, I. Y. & Chulkov, E. V. Electron-phonon coupling in topological surface states: the role of polar optical modes. Sci. Rep. 7, 1095 (2017).
Tamtögl, A. et al. Electron-phonon coupling and surface Debye temperature of Bi2Te3(111) from helium atom scattering. Phys. Rev. B 95, 195401 (2017).
Tamtögl, A. et al. Nanoscale surface dynamics of Bi2Te3 (111): observation of a prominent surface acoustic wave and the role of van der Waals interactions. Nanoscale 10, 14627–14636 (2018).
Jayanthi, C. S., Bilz, H., Kress, W. & Benedek, G. Nature of surface-phonon anomalies in noble metals. Phys. Rev. Lett. 59, 795–798 (1987).
Jardine, A., Hedgeland, H., Alexandrowicz, G., Allison, W. & Ellis, J. Helium-3 spin-echo: principles and application to dynamics at surfaces. Prog. Surf. Sci. 84, 323 (2009).
Jones, A., Tamtögl, A., Calvo-Almazán, I. & Hansen, A. Continuous compressed sensing for surface dynamical processes with helium atom scattering. Sci. Rep. 6, 27776 (2016).
Tamtögl, A., Mayrhofer-Reinhartshuber, M., Balak, N., Ernst, W. E. & Rieder, K. H. Elastic and inelastic scattering of He atoms from Bi(111). J. Phys. Condes. Matter 22, 1–6 (2010).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condes. Matter 21, 395502 (2009).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976).
Acknowledgements
This research was supported by the European Commission and the Styrian Government within the ERDF program. A.T. acknowledges financial support provided by the FWF (Austrian Science Fund) within the project J3479-N20. A.T. and W.E.E. gratefully acknowledge support by the FWF within the project P29641-N36, as well as by NAWI Graz.
Author information
Authors and Affiliations
Contributions
A.T., P.K. and M.M.-R. performed the experimental measurements under the supervision of W.E.E. The analysis of the experimental data was carried out by A.T., P.K. and G.B. D.D. and M.B. performed the DFT calculations while D.C. ran the DFPT calculations and G.B. implemented the ME model. G.B. co-wrote the paper with A.T. and all authors contributed to the discussion and preparation of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tamtögl, A., Kraus, P., Mayrhofer-Reinhartshuber, M. et al. Statics and dynamics of multivalley charge density waves in Sb(111). npj Quantum Mater. 4, 28 (2019). https://doi.org/10.1038/s41535-019-0168-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-019-0168-x
This article is cited by
-
Evidence for a spin acoustic surface plasmon from inelastic atom scattering
Scientific Reports (2021)
-
Electron–phonon coupling in superconducting 1T-PdTe2
npj 2D Materials and Applications (2021)