Abstract
The intertwined charge, spin, orbital, and lattice degrees of freedom could endow 5d compounds with exotic properties. Current interest is focused on electromagnetic interactions in these materials, whereas the important role of lattice geometry remains to be fully recognized. For this sake, we investigate pressure-induced phase transitions in the spin-orbit Mott insulator Sr3Ir2O7 with Raman, electrical resistance, and x-ray diffraction measurements. We reveal an interesting magnetic transition coinciding with a structural transition at 14.4 GPa, but without a concurrent insulator-metal transition. The conventional correlation between magnetic and Mott insulating states is thereby absent. The observed softening of the one-magnon mode can be explained by a reduced tetragonal distortion, while the actual magnetic transition is associated with tilting of the IrO6 octahedra. This work highlights the critical role of lattice frustration in determining the high-pressure phases of Sr3Ir2O7. The ability to control electromagnetic properties via manipulating the crystal structure with pressure promises a new way to explore new quantum states in spin-orbit Mott insulators.
Similar content being viewed by others
Introduction
Exotic ground states in 5d quantum materials, such as spin liquids,1,2 Weyl semimetals,3 topological insulators,4,5 and superconductors,6,7 are commonly believed to be driven by the competition between electron interaction U, spin-orbit coupling (SOC) ξ, and hopping amplitude t. In particular, for Ir5+ atoms in octahedral crystal field, the 5d orbital degeneracy is lifted by the strong on-site SOC, and the ground state is formed by effective S = 1/2 pseudospins.8 The lattice degree of freedom and its coupling to electron orbital angular momenta therefore have long been thought to play a trivial role.9
However, recently it has been recognized that pseudospin-lattice coupling may have strong impact on the low-energy physics of 5d materials.10 In the single-layer perovskite Sr2IrO4, canted S = 1/2 pseudospins in the antiferromagnetic phase are shown to rigidly lock to IrO6 octahedra due to strong SOC, and the pseudospin orientations rotate together with the octahedra under applied electric current.11 Moreover, pseudospin-lattice coupling can induce a tetragonal-to-orthorhombic structural transition and explain the in-plane magnon gaps of Sr2IrO4.12 Jahn–Teller effect also can explain some high energy features of different iridates in resonant inelastic x-ray scattering (RIXS),13 and the avoidance of metallization of Sr2IrO4 under pressure.14 These findings suggest that subtle structural changes may influence critically the low-energy Hamiltonian. While determining the exact role of lattice variable in 5d materials remains a challenge, applying pressure opens up an avenue for such research, since it could possibly decouple entangled degrees of freedom during phase transitions.15
In this work, we apply pressure to the double-layered perovskite Sr3Ir2O7, which is the middle member of the Ruddlesden-Popper series Srn+1IrnO3n+1 (n = 1, 2, ∞). This material provides an interesting playground to study phase transitions, as it is considered in the weak Mott limit16 with a relatively small charge gap and tiny magnetic moment.17 Sr3Ir2O7 has been extensively studied recently,8,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31 and its crystal structure is commonly reported to stabilize in I4/mmm symmetry.18 However, when the rotation angle α (describing in-plane IrO6 rotation, ~11–12°) and the tilt angle β (describing the deviation of IrO6 c-axis from the z-direction, ~less than 1°) are taken into account, the symmetry is reduced to Bbca,17 or Bbcb,19 or even C2/c.20 Furthermore, the IrO6 octahedron itself has a slight tetragonal distortion. Therefore, Sr3Ir2O7 serves as an ideal candidate for studying how lattice frustrations affect the electromagnetic properties and structural stability at high pressure.
Results and discussion
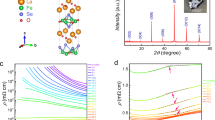
Figure 1 shows the temperature-dependent Raman spectra of Sr3Ir2O7 at ambient pressure. Six Raman modes are identified, respectively, at 146, 181, 269, 392, 592, and 1360 cm−1 based on the room-temperature spectrum. The frequencies are close to those reported in the literature.21 As temperature decreases, a new Raman peak appears at 780 ± 8 cm−1 (96.7 ± 1.4 meV) at 270 K. We assign this new peak to the one-magnon mode, as its peak intensity decreases significantly with increasing temperature, and its energy is also consistent with the zone-center magnon excitation (~90 meV) reported in RIXS studies of Sr3Ir2O7.22,23 The one-magnon peak exhibits an asymmetric Fano-like line shape, which could result from interaction with a continuum of excitations. Above TN ~285 K,17 the magnon peak disappears.
a Temperature-dependent Raman spectra of Sr3Ir2O7 at ambient pressure. The direction of decreasing temperature is indicated by the dashed arrow line. Five major vibrational modes are identified, and their atomic motions in the polyhedral are represented at the top of the figure. b Raman spectra of Sr3Ir2O7 for selected pressures at 10 K. The dotted lines are guides to the eye, showing the evolution of three A1g modes, respectively, at 152, 288 and 595 cm−1. The dashed curve tracks the pressure dependence of the one-magnon peak. Since the two-magnon mode merges with the first order Raman mode of diamond, we cannot study its high-pressure behavior. Two additional phonon modes appearing at 14.4 GPa are indicated by dots. Additional modes occurring at 1.9 GPa close to the A1g (187 cm−1) and B2g (403 cm−1) modes are indicated by arrow and asterisk, respectively
The Raman spectra also reveal a two-magnon mode at 1360 ± 2.3 cm−1 (168.62 ± 0.3 meV) [Fig. 1a], which is different from the previously reported energy ~1500 cm−1 (~185 meV) measured by 632.8 nm laser.21 The two-magnon peak increases slowly with decreasing temperature, and its intensity remains appreciable even at room temperature, suggesting a short-range spin-correlation character. In contrast, the previously reported two-magnon mode was strongly suppressed with temperature and vanished at TN = 285 K.21 Given that the two-magnon mode in our study also could be excited by 488 nm laser, different excitation source is probably not the reason for the observed discrepancy. Rather, the discrepancy could originate from subtle variation in the compositions of different samples.
Apart from the assigned magnon modes at 780 and 1360 cm−1, the other five Raman peaks are assigned to phonon modes, which could be indexed according to the I4/mmm space group of tetragonal symmetry.18 The fourteen Raman active modes expected from group theory include ΓRaman = 5A1g + 2B1g + 1B2g + 6Eg.24 However, only one B2g mode at 392 cm−1 and four A1g phonon modes are observable in our Raman experiments, whereas the rest of the modes are absent probably due to their weak Raman scattering cross sections.
As previously reported, the A1g mode at 146 cm−1 corresponds to the stretching of Sr atoms against the IrO6 octahedra.24 The A1g mode at 181 cm−1 involves displacements of Sr atoms along the c-axis with antiphase motion of adjacent layers and in-plane rotations of O atoms.21 The A1g mode at 269 cm−1 is attributed to the bending of the Ir–O–Ir bond21,24 due to IrO6 rotation, and the B2g mode at 392 cm−1 is associated with some out-of-plane atomic displacement of in-plane oxygens.21 Finally, the A1g mode at 592 cm−1 originates from the vibration of apical oxygen atoms in IrO6 octahedra.32 These modes are illustrated in Fig. 1a. When cooled down to 10 K, these Raman modes shift to higher frequencies as shown in Fig. 1b.
Figure 1b shows the pressure-dependent Raman spectra of Sr3Ir2O7 at 10 K. First, we note that two weak phonon modes emerge close to the A1g mode (187 cm−1) and B2g mode (403 cm−1) at 1.9 GPa. These two emergent modes, indicated by arrow and asterisk, respectively, in Fig. 1b, have been discovered previously24 and are visible below TN owing to magnetic interaction. Second, the one-magnon peak softens continuously and broadens with increasing pressure; the peak eventually disappears around 14.4 GPa, evincing a magnetic transition. In addition, two new modes appear below 152 cm−1 and the above A1g mode weakens at around 14.4 GPa. Similarly, the A1g mode at 288 cm−1 (the bending of the Ir–O–Ir bond) and 595 cm−1 (the vibration of apical oxygens in IrO6 octahedra) harden with pressure prior to almost vanishing around 14.4 GPa, which indicates increased IrO6 rotation and tilt angles at high pressure. These changes in phonon modes suggest a structural transition concurring with the magnetic transition around 14.4 GPa. We also performed room temperature and high-pressure Raman measurements to provide further evidence of the structural transition at 23.2 GPa. The results are given in the Supplementary Material in Fig. S2.
The pressure-induced structural phase transition is also confirmed by X-ray diffraction (XRD) at room temperature. The XRD measurements are performed on single crystals, and the results confirm that the sample is stable in an I4/mmm phase up to 21.2 GPa at room temperature, while the new phase was fitted with space group C2 (Fig. 2b). The integrated XRD patterns of Sr3Ir2O7 up to 33.2 GPa are presented in the Supplementary Material in Fig. S3a. At 33.2 GPa, the X-ray diffraction pattern fitting using the symmetry of I4/mmm starts to fail (see Fig. S3b in the Supplementary Material), suggesting the structures of the new phase should adopt a lower symmetry, i.e., C2. Detailed XRD analysis of the Sr3Ir2O7 crystal performed to exclude possible admixture of Sr2IrO4 is also shown in the Supplementary Material in Fig. S4.
a Le Bail fitting of the tetragonal I4/mmm phase of Sr3Ir2O7 at 11.7 GPa. b Le bail fitting of the higher-pressure monoclinic C2 phase of Sr3Ir2O7 at 33.2 GPa. The lattice parameters of each phase are written, respectively, at the top-right corner of each panel. In a and b the red circles are background subtracted data points, the black solid line presents the Le Bail fitting, blue tick marks are the calculated Bragg reflections, and the residuals of the fitting are shown by the black line beneath
Our discovery of magnetic and structural transitions at 14.4 GPa now could explain the mysterious origin of a second-order phase transition reported by Zhao et al.25 In their work, the second-order transition derived from the P-V data was attributed to an insulator-metal like transition at ~13 GPa,26 but they also suspected that magnetic transition might be a possible cause.25 To investigate if there is a concurring insulator-metal transition (similar to that observed by in pump-probe experiment at ambient conditions27), we also perform electrical transport measurement on a Sr3Ir2O7 single crystal. The results are plotted in Fig. 3a.
a Temperature-dependent electrical resistance of Sr3Ir2O7 along the a-b plane (Rab) plotted in log scale for selected pressures. Sr3Ir2O7 remains in an insulating state even after the magnetic transition at ~14.4 GPa. b Pressure (P) vs. charge gap energy (Δ) of Sr3Ir2O7. The critical pressure for reaching the metallic state can be estimated by the following empirical relation: Δ(P) = Δ0 exp(−χ P), where Δ0 is the gap energy at ambient-pressure and χ determines the rate of decrease of Δ with P. A fitting (red line) using the above equation results in χ = 0.09976 GPa−1 and P1meV = 55.6 GPa. This critical pressure 55.6 GPa for metallization is close to that reported in previous experiments.26,28,29
The electrical resistance within the a-b plane follows an activation law Ra–b (T) = exp (Δ/2kBT), where Δ is the charge gap and kB is the Boltzmann’s constant.26,33 We obtain the value of Δ at each pressure point from linear fitting of lnR (T) vs. 1/T. The gap energy (black square) as a function of pressure is plotted in Fig. 3b. From this analysis, Sr3Ir2O7 remains an insulator even when the structural and magnetic transitions concur at 14.4 GPa. It is expected to metalize at 55.6 GPa, which is close to the critical pressure reported previously.26,28,29 Pressure thus decouples the insulator-metal transition from the magnetic and structural transitions in Sr3Ir2O7, while these transitions remain coupled in pump-probe measurements.27
To further address how lattice frustration affects the magnetic order, we use spin-wave theory to study the magnon excitations. In particular, we adopt the magnetic exchange Hamiltonian from the reference,22 which describes well the spin-wave dispersion of Sr3Ir2O7 in RIXS measurements. The pressure evolution of magnon dispersion could originate from a change in three microscopic parameters: the ratio of Hund’s coupling to the on-site Coulomb interaction η (=JH/U), the IrO6 rotation angle α, and the effective tetragonal distortion θ that parametrizes the tetragonal splitting of t2g levels. It is important to understand which parameter dominates the softening of single-magnon energy under pressure.
First, pressure could enhance η via screening the Hubbard U while leaving JH nearly unchanged. Since we do not observe any metallization at 14.4 Gpa, the impact of pressure on η should be small. Second, it has been shown that pressure can increase the rotation angle α by a few degrees.28 However, our numerical calculations indicate that such a small change in α only lowers the magnon frequency by a few percent (see Fig. 4), which is not enough to account for the experimentally observed magnon softening. On the other hand, decreasing θ can significantly reduce the zone-center magnon energy and lift the degeneracy of the magnon branches (see Fig. S1 in the Supplementary Material). The evidence for reduced tetragonal distortion at high pressure is indeed found in the RIXS experiment by Ding et al.,28 in which the peak width of spin-orbiton excitation at ~0.5 eV reduces from 0.56 eV at 0.98 GPa to 0.48 eV at 12.4 GPa. Such a reduction strongly suggests a reduced tetragonal distortion, as in principle the peak width should have increased under pressure due to the broadening of Jeff = 1/2 and Jeff = 3/2 bands. We thus conclude that one major effect of pressure on the material is to reduce the anisotropy arising from tetragonal distortion of IrO6 octahedra (see Fig. 4).
Spin-wave theory prediction for the one-magnon energy at the Brillouin zone center as a function of tetrahedral distortion (θ) for selected IrO6 octahedron rotation angles (α). The ratio of Hund’s coupling to the on-site Coulomb interaction η = (JH/U) is fixed. The theoretical model and parameters for ambient pressure are adopted from the ref. 22
Although the model could explain the magnon softening, it is unable to illustrate the disappearance of magnon. To explain this effect, the IrO6 tilting angle β should be considered. It already has been reported that the actual symmetry of Sr3Ir2O7 should be C2/c with a tilting angle β less than 1 degree.20 Such a small tilting usually has been regarded as having a trivial effect. In our high-pressure study, however, the tilting appears to be important. In fact, the observed blue shift and disappearance of the 152 cm−1 and 595 cm−1 Raman modes suggest that pressure enhances both α and β, which could induce buckling or disordering of IrO6 octahedra along the c-axis and results in a local symmetry breaking (structural transition). The antiferromagnetic order (that gives rise to the magnon dispersion) in Sr3Ir2O7 stems from the interlayer exchange coupling Jc between Ir atoms mediated through apical oxygens.30 A strong IrO6 tilting could suppress Jc and result in the disappearance of magnon excitation. In principle, full suppression of the magnon peak also could arise from other effects, such as staggered distortions where the intralayer interactions change differently in two neighboring layers. Spin-phonon coupling mediated by single-ion anisotropy also can induce a small in the spin gap, although the phonon renormalization after magnetic transition in Sr3Ir2O7 appears weaker compared with that in other 5d compounds, such as Cd2Os2O7.34,35,36,37,38 A future comprehensive theoretical investigation of these effects is greatly needed.
Finally, we summarize our findings in a phase diagram shown in Fig. 5. After the magnetic transition at 14.4 GPa and 10 K, Sr3Ir2O7 is still an insulator. It remains challenging to characterize the magnetic structure and the underlying mechanism of phase transition. Based on similar phenomena observed in doping experiments, the insulating phase above 14.4 GPa could be paramagnetic, spin frustrated,31 or even a totally new quantum state that has never been reported. Sr3Ir2O7 at ambient conditions is located approximately at the center of the phase diagram plotted as functions of U/t and ξ/t.9 When pressure increases, both U/t and ξ/t could decrease, and the system could eventually reach the metallic region. We have reported previously an insulator-metal transition in Sr3Ir2O7 around 55–59.5 GPa,28 which is consistent with other studies.26,29 According to Fig. 5, the pathway for such a pressure evolution could possibly pass though the axion insulator phase3 before it reaches the metallic regime. Therefore, it is not impossible that the insulating phase discovered here might be an axion state. We speculate that applying pressure could be a promising way to search for various predicted phases in 5d spin-orbit materials.9
Schematic P-T phase diagram of Sr3Ir2O7. The phase boundary (TN) of paramagnetic (PM) insulator phase and magnetically ordered insulator phase and also the structural phase transition boundary (TS) are based on our Raman data (squares and asterisks on the phase boundary). The black dot on the TN (or TS) phase boundary represents the structural phase transition reported in the reference.25 The insulator to metal transition (IMT) region is taken from the references.26,28,29
In summary, we have revealed an interesting magnetic transition that concurs with a structural transition around 14.4 GPa by Raman measurements on Sr3Ir2O7. We attribute the origin of these transitions to pressure-enhanced rotation and tilt angles of IrO6 octahedra. The magnetic transition is shown to decouple from insulator-metal transition. The absence of usual correlation between magnetic and insulating phases in Sr3Ir2O7 is similar to that in Sr2IrO4.39,40 Our high-pressure study together with previous discoveries manifests the critical role of lattice frustration in determining the ground state properties of Sr3Ir2O7, and maybe generically of 5d materials. Our work calls for more theoretical studies to unravel the interplay of intertwined degrees of freedom in spin-orbit systems and the exact mechanism of their phase transitions.
Methods
Sample synthesis
Sr3Ir2O7 single crystal was grown from flux method. High-purity SrCO3, IrO2 and SrCl2·6H2O powders were mixed together and placed in platinum crucible. The molar ratios of the source materials was 2:1:20. The crucible was heated to 1573 K and dwelt for 10 h and then slowly cooled down to room temperature. After that the single crystals were separated from the flux by washing with deionized water. The obtained single crystal had typical dimensions 0.8 × 0.8 × 0.3 mm3. The experimental XRD pattern of Sr3Ir2O7 and calculated pattern based on the standard ICSD (075587) date are shown in the Supplementary Material in Fig. S4a. This result indicated that our sample is tetragonal phase (space group I4/mmm) at ambient condition and has good quality.
High-pressure Raman measurements
Raman spectra were collected on a single-crystal Sr3Ir2O7 at beamline 22-IR-1 of the National Synchrotron Light Source II, Brookhaven National laboratory. The sample was loaded inside a symmetric-type diamond anvil cell (DAC) and the DAC was placed in a microscopy cryostat system (Cryo Industries of America, Inc.). A pair of ultralow fluorescence type II diamonds with culet size ~300 μm were used. A Spectra-Physics Excelsior solid-state laser with a wavelength of 532 nm was used in the Raman measurement. Potassium bromide (KBr) was used as the pressure transmitting medium, and the pressure inside the cell was determined by the shift of the ruby fluorescence line. The laser power was less than 1 mW. In our measurements, 300 grooves/mm grating and ~1–3 μm beam spot were applied.
High-pressure transport measurements
Electrical resistance was measured with a standard four-probe-electrode circuit on a single-crystal Sr3Ir2O7. A T301 stainless steel gasket with cubic boron nitride/epoxy mixture powder inserts was used. Si oil was used as a pressure medium and the pressure was determined using ruby fluorescence technique. Four thin gold probes were attached to the samples with silver glue to measure the resistance.
High-pressure synchrotron diffraction measurements
The in situ high-pressure XRD measurements were carried out on a single-crystal Sr3Ir2O7 at beamline 16-BM-D of the Advanced Photon Source (APS), Argonne National Laboratory. A symmetric type DAC with culet size of 300 μm was used for the measurement. Neon was used as a pressure medium and the pressure was determined using ruby fluorescence technique. The incident monochromatic x-ray beam energy was set to 30 keV (λ = 0.4133 Ǻ). Diffraction patterns were recorded on a MAR345 image plate. We aligned the sample to the vertical-rotation axis and collected diffraction patterns in a step-scan method (1.5 s/step) with 1.0° step over the range from −20° to 20° up to 33.2 GPa, similar to the “rotation method” used in conventional single crystal crystallography.
Model Hamiltonian and spin-wave theory
We describe the pressure evolution of magnon excitation using the spin model reported in the ref. 22 Below we review the interaction terms in the model, which includes both intralayer (Hab) and interlayer (Hc) Hamiltonians:
where <i,j>, <<i,j>>, and <<< i,j >>> denote the first, second, and third nearest neighbors within the a-b plane. J, J2, and J3 represent the isotropic coupling constants. The anisotropic coupling term Γ stems from Hund’s exchange interaction and staggered rotations of octahedra. The latter also results in a Dzyaloshinsky-Moriya (DM) interaction,22 characterized by the constant D. For the nearest-interlayer interactions, Jc, Γc, and Dc were adopted for the similar coupling constants along the c-axis, while J2c stands for the next-nearest-neighbor interlayer coupling. All these isotropic and anisotropic exchange coupling constants (except for the long-range interactions J2, J3, and J2c) can be expressed in terms of the three microscopic parameters: the IrO6 rotation angle α, the effective tetragonal distortion θ, and the ratio of Hund’s coupling to onsite Coulomb interaction η = (JH/U). Here, we use the parameters in the reference for ambient pressure. We also assume J2c = 0.25 Jc and keep J2 = 11.9 meV, J3 = 14.6 meV, and η as constants.22
Within linear spin-wave theory (applicable in the antiferromagnetic phase), the single-magnon excitation energy in the Brillouin zone center (i.e., that observed by Raman measurements) is expressed by \(\omega = 1/2\sqrt {\left( {4\Gamma + \Gamma _c} \right)\left( {8J + 2J_c + 4\Gamma + \Gamma _c} \right) - \left( {4D + D_c} \right)^2}\). Our calculations reveal that the major influence of pressure is to reduce the anisotropic coupling Γ, e.g., from 4.4 meV at ambient pressure to 2.0 meV at around 20 GPa. Also, both Jc and Dc are enhanced, while other coupling constants are only slightly affected. We notice that tilting of the IrO6 octahedra along the c-axis can reduce the interlayer coupling Jc and thus soften the magnon energy, although overall Jc is enhanced due to a pressure-enhanced bandwidth.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Wang, F. & Senthil, T. Twisted Hubbard model for Sr2IrO4: magnetism and possible high temperature superconductivity. Phys. Rev. Lett. 106, 136402 (2011).
Kitagawa, K. et al. A spin-orbital-entangled quantum liquid on a honeycomb lattice. Nature 554, 341–345 (2018).
Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Price, C. C. & Perkins, N. B. Critical properties of the Kitaev-Heisenberg model. Phys. Rev. Lett. 109, 187201 (2012).
Chaloupka, J., Jackeli, G. & Khaliullin, G. Zigzag magnetic order in the iridium oxide Na2IrO3. Phys. Rev. Lett. 110, 097204 (2013).
Watanabe, H., Shirakawa, T. & Yunoki, S. Monte Carlo study of an unconventional superconducting phase in iridium oxide J eff=1/2 Mott insulators induced by carrier doping. Phys. Rev. Lett. 110, 027002 (2013).
Yonezawa, S., Muraoka, Y., Matsushita, Y. & Hiroi, Z. Superconductivity in a pyrochlore-related oxide KOs2O6. J. Phys. Condens. Matter 16, L9–L12 (2004).
Jackeli, G. & Khaliullin, G. Mott insulators in the strong spin-orbit coupling limit: from Heisenberg to a quantum compass and Kitaev models. Phys. Rev. Lett. 102, 017205 (2009).
Witczak-Krempa, W., Chen, G., Kim, Y. B. & Balents, L. Correlated quantum phenomena in the strong spin-orbit regime. Annu. Rev. Conden. Ma. P. 5, 57–82 (2014).
Cao, G. & Schlottmann, P. The challenge of spin-orbit-tuned ground states in iridates: a key issues review. Rep. Prog. Phys. 81, 042502 (2018).
Cao, G. et al. Electrical control of structural and physical properties via strong spin-orbit interactions in Sr2IrO4. Phys. Rev. Lett. 120, 017201 (2018).
Liu, H. & Khaliullin, G. Pseudo Jahn-Teller effect and magnetoelastic coupling in spin-orbit Mott insulators. Phys. Rev. Lett. 122, 057203 (2019).
Plotnikova, E. M., Daghofer, M., van den Brink, J. & Wohlfeld, K. Jahn-Teller effect in systems with strong on-site spin-orbit coupling. Phys. Rev. Lett. 116, 106401 (2016).
Samanta, K., Ardito, F. M., Souza-Neto, N. M. & Granado, E. First-order structural transition and pressure-induced lattice/phonon anomalies in Sr2IrO4. Phys. Rev. B 98, 094101 (2018).
Ding, Y. et al. Novel high-pressure monoclinic metallic phase of V2O3. Phys. Rev. Lett. 112, 056401 (2014).
Hogan, T. et al. First-order melting of a weak spin-orbit Mott insulator into a correlated metal. Phys. Rev. Lett. 114, 257203 (2015).
Cao, G. et al. Anomalous magnetic and transport behavior in the magnetic insulator Sr3Ir2O7. Phys. Rev. B 66, 214412 (2002).
Subramanian, M. A., Crawford, M. K. & Harlow, R. L. Single crystal structure determination of double layered strontium iridium oxide Sr3Ir2O7. Mater. Res. Bull. 29, 645–650 (1994).
Matsuhata, H. et al. Crystal structure of Sr3Ir2O7 investigated by transmission electron microscopy. J. Solid. State Chem. 177, 3776–3783 (2004).
Hogan, T. et al. Structural investigation of the bilayer iridate Sr3Ir2O7. Phys. Rev. B 93, 134110 (2016).
Gretarsson, H. et al. Two-magnon raman scattering and pseudospin-lattice interactions in Sr2IrO4 and Sr3Ir2O7. Phys. Rev. Lett. 116, 136401 (2016).
Kim, J. et al. Large spin-wave energy gap in the bilayer iridate Sr3Ir2O7: evidence for enhanced dipolar interactions near the Mott metal-insulator transition. Phys. Rev. Lett. 109, 157402 (2012).
Moretti Sala, M. et al. Evidence of quantum dimer excitations in Sr3Ir2O7. Phys. Rev. B 92, 024405 (2015).
Cetin, M. F. Light scattering in spin orbit coupling dominated systems. Ph.D thesis, Technische Universitaet Carolo-Wilhelmina zu Braunschweig (2012).
Zhao, Z. et al. Pressure induced second-order structural transition in Sr3Ir2O7. J. Phys. Condens. Matter 26, 215402 (2014).
Li, L. et al. Tuning the J eff=1/2 insulating state via electron doping and pressure in the double-layered iridate Sr3Ir2O7. Phys. Rev. B 87, 235127 (2013).
Chu, H. et al. A charge density wave-like instability in a doped spin-orbit-assisted weak Mott insulator. Nat. Mater. 16, 200–203 (2017).
Ding, Y. et al. Pressure-induced confined metal from the Mott insulator Sr3Ir2O7. Phys. Rev. Lett. 116, 216402 (2016).
Donnerer, C. et al. Pressure dependence of the structure and electronic properties of Sr3Ir2O7. Phys. Rev. B 93, 174118 (2016).
Kim, J. W. et al. Dimensionality driven spin-flop transition in layered iridates. Phys. Rev. Lett. 109, 037204 (2012).
Qi, T. F. et al. Spin-orbit tuned metal-insulator transitions in single-crystal Sr2Ir1−xRhxO4(0≤x≤1). Phys. Rev. B 86, 125105 (2012).
Cetin, M. F. et al. Crossover from coherent to incoherent scattering in spin-orbit dominated Sr2IrO4. Phys. Rev. B 85, 195148 (2012).
Zocco, D. A. et al. Persistent non-metallic behavior in Sr2IrO4 and Sr3Ir2O7 at high pressures. J. Phys. Condens. Matter 26, 255603 (2014).
Yamaura, J. et al. Tetrahedral magnetic order and the metal-insulator transition in the pyrochlore lattice of Cd2Os2O7. Phys. Rev. Lett. 108, 247205 (2012).
Sohn, C. H. et al. Strong spin-phonon coupling mediated by single ion anisotropy in the all-in-all-out pyrochlore magnet Cd2Os2O7. Phys. Rev. Lett. 118, 117201 (2017).
Tardif, S. et al. All-in-all-out magnetic domains: x-ray diffraction imaging and magnetic field control. Phys. Rev. Lett. 114, 147205 (2015).
Shinaoka, H., Miyake, T. & Ishibashi, S. Noncollinear magnetism and spin-orbit coupling in 5d pyrochlore oxide Cd2Os2O7. Phys. Rev. Lett. 108, 247204 (2012).
Bogdanov, N. A. et al. Magnetic state of pyrochlore Cd2Os2O7 emerging from strong competition of ligand distortions and longer-range crystalline anisotropy. Phys. Rev. Lett. 110, 127206 (2013).
Ge, M. et al. Lattice-driven magnetoresistivity and metal-insulator transition in single-layered iridates. Phys. Rev. B 84, 100402 (2011).
Haskel, D. et al. Pressure tuning of the spin-orbit coupled ground state in Sr2IrO4. Phys. Rev. Lett. 109, 027204 (2012).
Acknowledgements
This work is supported by National Key R&D Program of China No. 2018YFA0305703. The x-ray diffraction measurements were performed at sectors 16 BM-D of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science user facility operated by Argonne National Laboratory (ANL) supported by the U.S. DOE Award No. DE-AC02-06CH11357. The Raman experiments were performed at beamline 22-IR-1 of the National Synchrotron Light Source II (NSLS-II), Brookhaven National Laboratory, supported by NSF (Cooperative Agreement EAR 1606856, COMPRES) and DOE/NNSA (DE-NA-0002006, CDAC). NSLS-II is supported by the DOE/BES (DE-SC0012704). The electric transport measurements were performed at the Center for High-Pressure Science and Technology Advanced Research. The authors thank S. Tkachev for help with the gas loading at the Advanced Photon Source. Y.D. and H.-k. M. acknowledges the support from DOE-BES under Award No. DE-FG02-99ER45775 and NSFC Grant No. U1530402. This work is also supported by National Key R&D Program of China No. 2016YFA0300604, 2017YFA0302901, and the National Natural Science Foundation of China No. 11774399, 11474330, 91750111, and Science Challenge Project, No. TZ2016001, and the Fundamental Research Funds for the Central Universities, China, No. GK201801009.
Author information
Authors and Affiliations
Contributions
Y.D. and J.Z. designed the project. J.Z., H.D., and Z.L. performed the Raman measurements. J.Z., S.Y., and H.D. carried out the XRD and transport measurements. C.Y., D.Y., and Y.S. synthesized the single crystals. J.C. performed the theoretical calculations. J.Z., Y.D., and J.C. analyzed the data. Y.D. supervised the project. All the authors helped with the project and read and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, J., Yan, D., Yesudhas, S. et al. Lattice frustration in spin-orbit Mott insulator Sr3Ir2O7 at high pressure. npj Quantum Mater. 4, 23 (2019). https://doi.org/10.1038/s41535-019-0162-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-019-0162-3
This article is cited by
-
Evolution of electronic and magnetic properties of Sr2IrO4 under strain
npj Quantum Materials (2022)