Abstract
Transition metal oxides of the 4d and 5d block have recently become the targets of materials discovery, largely due to their strong spin–orbit coupling that can generate exotic magnetic and electronic states. Here, we report the high-pressure synthesis of Lu2Rh2O7, a new cubic pyrochlore oxide based on 4d5 Rh4+, and characterizations via thermodynamic, electrical transport, and muon spin relaxation measurements. Magnetic susceptibility measurements reveal a large temperature-independent Pauli paramagnetic contribution, while heat capacity shows an enhanced Sommerfeld coefficient, γ = 21.8(1) mJ/mol-Rh K2. Muon spin relaxation measurements confirm that Lu2Rh2O7 remains paramagnetic down to 2 K. Taken in combination, these three measurements suggest that Lu2Rh2O7 is a correlated paramagnetic metal with a Wilson ratio of RW = 2.5. However, electric transport measurements present a striking contradiction as the resistivity of Lu2Rh2O7 is observed to monotonically increase with decreasing temperature, indicative of a nonmetallic state. Furthermore, although the magnitude of the resistivity is that of a semiconductor, the temperature dependence does not obey any conventional form. Thus, we propose that Lu2Rh2O7 may belong to the same novel class of non-Fermi liquids as the nonmetallic metal FeCrAs.
Similar content being viewed by others
Introduction
The electronic and magnetic properties of many transition metal oxides can be understood by considering three energy scales: (i) the on-site Coulomb repulsion, Hubbard U, (ii) the band width, W, and (iii) the spin–orbit coupling, λ. The strong-coupling limit of this paradigm occurs for 3d oxides where Hubbard repulsion dominates \(\left( {U/W \gg 1} \right)\) and spin–orbit coupling (λ ∝ Z4) is negligible. As a consequence, Mott insulating states are observed in many materials that one would expect to be metals from band theory, as exemplified by the parent compounds of the high-temperature cuprate superconductors.1 The opposing limit occurs for 5d oxides, where the d electron orbitals are far more spatially delocalized such that U decreases while W increases (U/W ≈ 1). At the same time, the large mass enhancement brings spin–orbit coupling to the forefront, giving rise to remarkable correlated states such as topological insulators, Weyl semi-metals, and spin–orbit assisted Mott insulators.2 Intermediate to these two limits is the 4d oxides, where U, W, and λ can all be comparable in magnitude.
The chemically versatile pyrochlore oxides, A2B2O7, are an excellent family of materials to explore the competition between U, W, and λ. In this structure, the A site is usually occupied by a rare earth cation, while the B site can be occupied by transition or post-transition metals from the 3d, 4d, or 5d block. Consequently, a wide assortment of electronic behaviors are observed, ranging from band insulators to correlated metals. Pyrochlores are also of significant interest for their magnetic properties. The corner-sharing tetrahedral arrangement of the A and B cation sublattices is prone to intense geometric frustration, which has been extensively studied in the insulating families.3 The metallic pyrochlore oxides provide an intriguing platform for studying the interplay of geometric frustration and metallic degrees of freedom, an emerging topic that has begun to garner significant attention.4,5,6,7,8,9 Whereas frustration in local moment systems can straightforwardly be identified via the so-called frustration index, f = |θCW|TN,10 no equivalent metric has yet been established for itinerant magnetic materials. Hence, how to unambiguously identify the presence of frustration in an itinerant system remains an open problem. A recent study broached this topic by using inelastic neutron scattering to extract exchange couplings which were then compared to a local moment picture.9
In the rare earth pyrochlores, the 4f electrons from the A-site cation are highly localized and do not participate in electrical conduction. Thus, the electronic properties of pyrochlore materials are largely governed by the choice of B-site cation.11 Insulating states are expected and observed in cases where there are no partially filled d-electron orbitals, such as when B = Ti4+, Ge4+, Sn4+, and Zr4+. Due to their dominant Hubbard U, insulating or semiconducting states are also found in the majority of cases where B has a partially occupied 3d shell, such as B = Mn4+ and Cr4+. Semiconducting states are found for a number of pyrochlores with partially filled 4d or 5d-shells, such as those with B = Mo4+, Ru4+, and Pt4+. Pyrochlores with metallic states are fewer in number, with notable examples being found amongst the B = Os5+, Re5+, and Ir4+ families. In these systems, large spin–orbit coupling results in fascinating correlated electron phenomena. For instance, the iridate family of pyrochlores have been lauded as candidates for topological electronic states.12 Meanwhile, Cd2Re2O7 is a moderately heavy fermion metal, γ = 13.3 mJ/mol-Re K2,13 with a superconducting transition at TC = 1.47 K.14 In the case of Cd2Os2O7, the entanglement of spin, orbital, and lattice degrees of freedom drives a metal-to-insulator transition at 226 K concomitant with antiferromagnetic order.15,16,17,18 Here, we introduce a new 4d pyrochlore, Lu2Rh2O7, where we expect that U, W, and λ are all comparable in magnitude, giving rise to an exotic non-Fermi liquid state.
The magnetism in Lu2Rh2O7 originates from 4d5 Rh4+ while 4f14 Lu3+ is non-magnetic. Although several 4d5 rhodate pyrochlores have been previously reported,19,20 their characterization has been negligible, especially in contrast to their 5d5 iridate analogs. This can, in part, be attributed to the difficulty in stabilizing rhodium in its 4+ oxidation state, which we overcome using high-pressure methods. In the pyrochlore lattice, Rh4+ sits at the center of a trigonally distorted octahedral oxygen environment with D3d point group symmetry. As schematically presented in Fig. 1a, the crystal electric field and moderately strong spin–orbit coupling (λ = 0.19 eV for Rh in contrast with λ = 0.40 eV for Ir21) split the d electron states into a filled jeff = 3/2 band and a half-occupied jeff = 1/2 band. Thus, akin to the 5d5 iridates,22 the 4d5 rhodates can have a jeff = 1/2 magnetic degree of freedom, leading to a spin–orbit induced Mott insulating state.23 Both theoretical calculations and direct spectroscopic measurements have confirmed the applicability of the jeff = 1/2 picture in other rhodate materials.17,24 However, even in cases where λ is not large enough to reach the pure jeff = 1/2 limit, as is likely the case in Lu2Rh2O7, the influences of spin–orbit coupling are still strongly felt.25,26 We have characterized the magnetic and electronic properties of Lu2Rh2O7 with magnetic susceptibility, heat capacity, resistivity, and muon spin relaxation (μSR) measurements. These measurements reveal an apparent contradiction: magnetic susceptibility, heat capacity, and μSR are consistent with a strongly correlated paramagnetic metal. Resistivity data on the other hand suggests an unconventional semiconducting state and hence, a gap in the density of states. Thus, we propose that Lu2Rh2O7 belongs to the class of “nonmetallic metals” a term coined to describe the behavior of FeCrAs.27,28
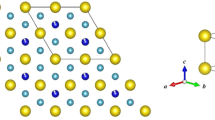
a The 4d5 Rh4+ cations in Lu2Rh2O7 sit at the center of a trigonally distorted (D3d) octahedral oxygen environment. Strong spin–orbit coupling will further split the t2g states into a filled jeff = 3/2 and a half-filled jeff = 1/2 state; however, this limit may not be fully reached for Rh4+ with moderate spin–orbit coupling. b Powder x-ray diffraction pattern and Rietveld refinement for Lu2Rh2O7 measured at T = 300 K with a copper Kα1 wavelength (λ = 1.5406 Å). The Bragg peak positions for the Fd3̄m pyrochlore phase are indicated by the upper set of crosses. The lower set of crosses are from a minor RhO2 impurity accounting for 2% of the sample volume. The results of the refinement are shown in Table 1
Results
Under strongly oxidizing conditions, Lu2Rh2O7 crystallizes in the pyrochlore structure (space group Fd3̄m). The powder x-ray diffraction pattern, which is presented in Fig. 1b, was analyzed via Rietveld refinement, giving a cubic lattice parameter of a = 10.0265(1) Å. The ratio of the ionic radii for Lu3+ (86.1 pm) and Rh4+ (60 pm) is within the stability range for the pyrochlore structure.11 Thus, significant levels of A/B site mixing are neither expected nor observed. The only adjustable coordinate within the pyrochlore structure is the O2 x position, which we refine to x = 0.3296(5). When x = 0.3125, the oxygen environment at the B-site is an ideal octahedron (point group Oh). Deviations from this value induce a compression along the local [111] axis, as shown in Fig. 1a, such that the six equidistant oxygen ions have alternating bond angles of 93.5° and 86.5° with the central Rh4+ cation (point group D3d). A small RhO2 impurity, comprising 2.1(2)% of the total sample volume, was included as a second phase in the Rietveld refinements (a tetragonal structure with space group P42/mnm).29,30 RhO2 is a high-pressure metallic oxide phase which is insoluble in aqua regia and could not be removed from our samples. The results of the Rietveld refinement, including the goodness-of-fit parameters, are listed in Table 1.
The magnetic susceptibility of Lu2Rh2O7 measured in an H = 1 T field is presented in Fig. 2. We have corrected the data for core diamagnetism using the values tabulated in ref. 31, which gives χD = −1.54 ⋅ 10−4 emu/F.U. There is no appreciable difference between data collected under zero-field cooled or field cooled conditions. Lu2Rh2O7 is paramagnetic down to the lowest measured temperature, with no evidence for magnetic ordering or spin freezing down to 2 K. The susceptibility is dominated by a large nearly temperature independent Pauli paramagnetic contribution. Below 10 K, the intrinsic susceptibility is obscured by a Curie-tail. We observe a shallow, broad hump in the susceptibility centered near 50 K. As can be seen in Fig. 2, the inverse susceptibility between 100 and 300 K is reasonably well-described by a Curie–Weiss equation, \(\chi = \frac{C}{{T - \theta }}\), where we obtain θ = −1393(2) K and \(\mu _{{\mathrm{eff}}} = \sqrt {8C} = 3.1(1)\,\mu _B\). Clearly, this magnitude of θ is not physically meaningful as the susceptibility is dominated by the Pauli paramagnetic contribution. However, attempts to model the susceptibility to a modified Curie–Weiss law, \(\chi = \frac{C}{{T - \theta }} + \chi _0\), failed to produce a unique solution. Instead, we proceed by subtracting the Curie-tail contribution, which we fit to \(\chi \propto \frac{C}{T}\), allowing us to estimate the low-temperature Pauli paramagnetic contribution as χP = 7.6 ⋅ 10−4 emu/mol-Rh. This value is nearly an order of magnitude larger than in typical metals, signaling strong electron correlation effects. The induced magnetization at 2 K and 7 T is only 0.01 μB/Rh4+, consistent with an itinerant paramagnetic state (inset of Fig. 2). The susceptibility and magnetization data for Lu2Rh2O7 bear a striking resemblance to that of SrRhO3, another Rh4+-based paramagnetic metal.32 The unusual properties of SrRhO3 have been argued to emerge as the result of proximity to a quantum critical point.33
The magnetic susceptibility of Lu2Rh2O7, which was measured at H = 1 T, is dominated by a largely temperature independent Pauli paramagnetic contribution. The full symbols and the left hand axis are the susceptibility, χ, while the open symbols and the right hand axis give the inverse susceptibility, χ−1. The yellow dashed line is the as-measured susceptibility data, prior to the Curie tail subtraction. The red line is a fit to the Curie–Weiss equation. The inset shows magnetization measurements at T = 2 and 25 K
The heat capacity of Lu2Rh2O7 is presented in Fig. 3, where no phase transitions are observed between 2 and 300 K. For comparison, we plot alongside this data the scaled heat capacity of Lu2Ti2O7, which is an insulating lattice analog with no unpaired d electrons.34 The heat capacity of Lu2Ti2O7 was scaled by \(\mu = \sqrt {M_{LRO}/ {M_{LTO}}}\) where MLRO and MLTO are the molecular weights of Lu2Rh2O7 and Lu2Ti2O7, respectively. These two data sets are largely consistent, confirming that the high-temperature heat capacity of Lu2Rh2O7 can be accounted for by lattice degrees of freedom. The scaled heat capacity of Lu2Ti2O7 is observed to slightly exceed that of Lu2Rh2O7 below 50 K. This difference can be understood to originate from anharmonic effects, which are known to be significant in rare earth pyrochlores,35 and will vary between compounds dependent on the details of the phonon interactions. Indeed, the heat capacity of Lu2Ti2O7 is also observed to exceed that of Dy2Ti2O7 in the same temperature interval.34 At the lowest temperatures, Fermi liquid behavior is observed for Lu2Rh2O7, where C/T is linear with respect to T2 up to T = 10 K (inset of Fig. 3). The fitted value for the Sommerfeld coefficient is γ = 21.8(1) mJ/mol-Rh K2, which is large and comparable to values observed in other strongly correlated rhodates and ruthenates.36,37,38
The heat capacity of Lu2Rh2O7 measured in zero field, with the scaled heat capacity of Lu2Ti2O7 from ref. 34 shown for reference. The inset shows a fit of C/T = γ + βT2 over the shaded region, which yields a large Sommerfeld coefficient, γ = 21.8(1) mJ/mol-Rh K2
Enhanced electron masses are most commonly associated with heavy fermion physics in f-electron metals.39 However, there are several notable examples of d-electron systems with anomalously large Sommerfeld coefficients, including Y1−xScxMn240 and LiV2O4.41 In both Y1−xScxMn2 (a cubic Laves phase) and LiV2O4 (a spinel), the underlying magnetic sublattice is a pyrochlore-like network of corner-sharing tetrahedra. It has been proposed that geometric frustration plays a central role in their electronic properties. Frustration tends to suppress conventional magnetic order, giving rise to strong spin fluctuations, while the itinerant nature of the electrons results in large spin disorder entropy at low temperatures, which gives rise to an enhanced linear contribution to the specific heat.42 Indeed, the values for γ in Y1−xScxMn2 (140 mJ/mol K2 for x = 0.0343) and LiV2O4 (420 mJ/mol K241) are comparable to some of the best known examples of f-electron heavy fermion systems, such as URu2Si2 (180 mJ/mol K244) and UPt3 (420 mJ/mol K245) Given that the magnetic sublattice of Lu2Rh2O7 shares this frustrated architecture, similar mechanisms may be responsible for its enhanced Sommerfeld coefficient.
We have also performed zero field μSR measurements on Lu2Rh2O7. While the bulk probes employed thus far all indicate the absence of magnetic order, muons as a local probe are highly sensitive to very small ordered moments, even those below 0.1 μB. Muon decay asymmetry spectra were collected between 2 and 250 K, and several representative data sets are presented in Fig. 4a. The relaxation, which is weak at all measured temperatures, is observed to gradually increase with decreasing temperature. We do not observe any sharp increase in relaxation or spontaneous oscillations, as would be expected in the case of long-range magnetic order. As a function of temperature, the relaxation evolves from more Gaussian-like at high temperatures to Lorentzian at the lowest temperatures. Thus, we fitted the asymmetry spectra to a stretched exponential function
where λ is the relaxation rate and the stretching parameter was constrained to lie between β = 1 (Lorentzian) and β = 2 (Gaussian). The non-relaxing background asymmetry, ABG, accounts for muons which land outside the sample. The total asymmetry was constrained by fitting the precessing signal at high temperature in a weak field applied transverse to the muon’s spin. The temperature dependence of both λ and β are presented in Fig. 4b. The relaxation rate gradually grows below 200 K, reaching a maximum value of 0.15 μs−1 at 2 K. There is a concomitant decrease of the stretching parameter, which plateaus at β = 1 below 20 K. This can be understood in terms of a crossover, where at high temperatures more Gaussian relaxation is observed due to fluctuating nuclear dipoles whereas at lower temperatures the signal is dominated by slowing spin dynamics. The decrease in β may share an origin with the broad hump in the susceptibility in the same temperature interval. Moreover, these μSR measurements confirm that Lu2Rh2O7 remains paramagnetic, with no evidence for magnetic order or spin freezing down to 2 K.
a Several representative asymmetry spectra from muon spin relaxation measurements on Lu2Rh2O7. Error bars are derived from \(\sqrt N \) counting statistics. The solid lines are fits to a stretched exponential function. b The temperature dependence of the fitted relaxation rate, λ, and the stretching parameter, β, reveal weak spin dynamics and a crossover from more Gaussian-like relaxation to Lorentzian relaxation
Electrical resistivity measurements were carried out using a conventional four-terminal method on a cold-pressed pellet46 of Lu2Rh2O7, which was annealed in air at 600 °C for 10 h to minimize grain boundary effects. X-ray diffraction measurements were performed before and after the annealing protocol to confirm that it did not result in any degradation of the sample. In striking contrast to the magnetic susceptibility and heat capacity, which would both suggest a metallic state, the room temperature resistivity is 0.36 Ω-cm, which is typical of a semiconducting state. Furthermore, the temperature dependence of the resistivity monotonically increases with decreasing temperature (i.e., dρ/dT < 0). The resistivity is observed to diverge below 10 K. The inset of Fig. 5 shows that this resistivity does not obey a thermally activated Arrhenius behavior for a very large range of temperatures. The data can be fit between 200 and 300 K to ρ ∝ ρa ⋅ exp(−Δ/2kBT), yielding a very small gap of Δ = 37(1) meV. There are several factors worth considering in the quantitative interpretation of this data. First is that this sample is a pressed pellet and thus, scattering from grain boundaries may be expected to uniformly increase the resistivity. However, the cold-pressing and annealing protocol followed here has been demonstrated to provide nearly intrinsic transport measurements in other transition metal oxides, including samples that are far softer and more porous than the one measured here.46 Moreover, even without the cold-pressing technique, conventional metallic resistivity (i.e., dρ/dT > 0) has been measured in numerous polycrystalline samples of rhodates synthesized via the same high-pressure techniques used here.32,47,48,49,50 It is also worth mentioning that our minor impurity phase, RhO2, is known to be a metal.30 Thus, the nonmetallic resistivity is clearly intrinsic to Lu2Rh2O7, a remarkable result in a material that all other probes suggest is metallic.
Discussion
Our characterizations have revealed that Lu2Rh2O7 possesses a highly unusual non-Fermi liquid state. While both heat capacity and magnetic susceptibility indicate a finite density of states at the Fermi energy, the temperature dependence of the resistivity appears more consistent with a semiconducting gap. Moreover, even for a semiconductor, the temperature dependence of the resistivity is unconventional. It is instructive to consider a comparison with the “nonmetallic metal” FeCrAs. First, an important structural commonality is that in both materials, the magnetic constituent(s) are connected in triangular motifs that can be prone to geometric magnetic frustration. In the case of Lu2Rh2O7 this is the corner-sharing tetrahedral pyrochlore sublattice and in the case of FeCrAs the non-magnetic Fe atoms occupy a triangular network of trimers while the magnetic Cr atoms form a distorted Kagome network. In regards to their electronic properties, the magnetic susceptibility of both materials is dominated by a largely temperature independent Pauli paramagnetic contribution.27 Secondly, both materials have a Sommerfeld coefficient, as determined by heat capacity measurements, significantly larger than typically expected for a d electron system, γ = 21.8(1) mJ/mol-Rh K2 and 31.6 mJ/mol K2 for Lu2Rh2O7 and FeCrAs, respectively. However, the Wilson ratio \(\left( {R_W = 4\pi ^2k_B^2\chi _P/3(g\mu _B)^2\gamma } \right)\) for FeCrAs, RW = 4–5 27 is larger than our computed value of RW = 2.5 for Lu2Rh2O7. A third commonality is the temperature dependence of the resistivity, where dρ/dT is negative, nominally indicative of a gap in the density of states. However, the room temperature resistivity for FeCrAs is approximately 0.4 m Ω-cm, approximately three orders of magnitude smaller than our value of 0.4 Ω-cm. Another significant difference between these two materials is that the Cr moments in FeCrAs undergo a long-range antiferromagnetic ordering transition at TN = 125 K,27 while no magnetic order is observed in Lu2Rh2O7 down to at least 2 K.
Several compelling explanations have been put forward to explain the nonmetallic metallic state in FeCrAs, which are worth examining in the current context of our results on Lu2Rh2O7. The first proposal, which comes from Rau and Kee, suggests a hidden spin liquid state for the non-magnetic Fe trimers.51 They propose that the electrons residing on these trimers are close to a metal-insulator quantum critical point, such that charge fluctuations strongly renormalize the transport behavior while only minimally affecting the thermodynamic properties. A second proposal that does not rely on proximity to a Mott insulating state, but instead attributes the unusual qualities of FeCrAs to it being a Hund’s metal.52 In a Hund’s metal, non-Fermi liquid properties emerge due to strong intra-atomic exchange in a multiorbital material, such as ruthenates and iron pnictides.53 The result of strong Hund’s coupling in these materials is that a subset of the d orbitals are pushed towards the local limit while maintaining strong coupling to other itinerant electrons. Several arguments make this second scenario less favorable in the case of Lu2Rh2O7. First, Hund’s coupling generally plays a weaker role in 4d5 Rh4+.53 Secondly, this model is expected to give a large Wilson ratio,28 as indeed observed in FeCrAs where RW = 4–5,27 whereas in Lu2Rh2O7, RW = 2.5. Recent inelastic neutron scattering experiments have revealed high energy itinerant-like spin excitations, which Plumb et al. propose may account for the nonmetallic resistivity.54 Further study of the spin dynamics in Lu2Rh2O7 are called for, a task which would be greatly benefited by the availability of large single crystal samples. While no single crystals of rhodate pyrochlores have been reported to date, a route similar to that used for Sr2RhO4 may prove fruitful.38
Using high-pressure methods, we have synthesized a new pyrochlore Lu2Rh2O7, in which jeff = 1/2 Rh4+ occupies a frustrated corner-sharing tetrahedral lattice. No magnetic order is observed down to 2 K in μSR measurements. Heat capacity and magnetic susceptibility measurements both indicate strong electron correlations, with a large temperature independent Pauli paramagnetic response and an enhanced Sommerfeld coefficient, γ = 21.8(1) mJ/mol-Rh K2. Resistivity measurements, in contrast, suggest nonmetallic behavior (dρ/dT < 0) in the full measured temperature range, 2–300 K. Thus, Lu2Rh2O7 has a non-Fermi liquid state, sharing many commonalities with the nonmetallic metal FeCrAs.
Methods
High-pressure synthetic techniques are often required to stabilize Rh4+ compounds,19,20,29,30,32,47,48 as Rh3+ is the more common oxidation state. The cubic pyrochlore Lu2Rh2O7 was prepared using a belt-type high-pressure apparatus at the National Institute for Materials Science in Tsukuba, Japan. Lu2O3 was thoroughly dried prior to the reaction. Rhodium metal was first oxidized to Rh2O3 by reacting under flowing oxygen at 1000 °C for 72 h. The reaction into the pyrochlore phase was completed using KClO4 as an oxidizing agent to promote the Rh4+ oxidation state. The precursors (Lu2O3, Rh2O3, KClO4 in a 1:1:\(\frac{3}{8}\) ratio) were thoroughly ground together and sealed in a platinum capsule. The reaction was completed at 1700 °C and 6 GPa of applied pressure for 2 h, after which the sample was quenched to room temperature before the pressure was released. The final product was repeatedly washed with water to remove KCl and then dried. The resulting 0.5 g sample is made up of sub-micron sized black crystallites. Once prepared, this material is stable in air on a timescale of years.
X-ray diffraction measurements were performed using a PANalytical diffractometer with copper Kα1 radiation, λ = 1.540560 Å. Rietveld refinement was performed using FullProf.55 Magnetic susceptibility, resistivity, and heat capacity measurements between 2 and 300 K were completed using a Quantum Design Physical Property Measurement System. Zero field μSR measurements were performed at the M20 surface muon channel at TRIUMF in the LAMPF Spectrometer. The μSR data were fitted over the full measured time interval, up to 9.5 μs, using the muSRfit software package.
Data availability
The crystal structure of Lu2Rh2O7, as determined by Rietveld refinement of the powder x-ray diffraction data, is available at the Cambridge Crystallographic Data Centre with deposition number CSD 1895045. All other data is available from the authors on reasonable request.
References
Lee, P. A., Nagaosa, N. & Wen, X.-G. Doping a Mott insulator: physics of high-temperature superconductivity. Rev. Mod. Phys. 78, 17–85 (2006).
Witczak-Krempa, W., Chen, G., Kim, Y. B. & Balents, L. Correlated quantum phenomena inthe strong spin–orbit regime. Annu. Rev. Condens. Matter Phys. 5, 57–82 (2014).
Gardner, J. S., Gingras, M. J. P. & Greedan, J. E. Magnetic pyrochlore oxides. Rev. Mod. Phys. 82, 53–107 (2010).
Nakatsuji, S. et al. Metallic spin-liquid behavior of the geometrically frustrated kondo lattice Pr2lr2O7. Phys. Rev. Lett. 96, 087204 (2006).
Lacroix, C. Frustrated metallic systems: a review of some peculiar behavior. J. Phys. Soc. Jpn. 79, 011008 (2010).
Julian, S. & Kee, H. Y. Frustrated metallic magnets. Phys. Can. 68, 95–98 (2012).
Paddison, J. A. M. et al. Emergent frustration in co-doped β-Mn. Phys. Rev. Lett. 110, 267207 (2013).
Billington, D. et al. Magnetic frustration, short-range correlations and the role of the paramagnetic fermi surface of PdCrO2. Sci. Rep. 5, 12428 (2015).
Sapkota, A. et al. Effective one-dimensional coupling in the highly frustrated square-lattice itinerant magnet CaCo2−yAs2. Phys. Rev. Lett. 119, 147201 (2017).
Ramirez, A. P. Strongly geometrically frustrated magnets. Annu. Rev. Mater. Sci. 24, 453–480 (1994).
Subramanian, M. A., Aravamudan, G. & Subba Rao, G. V. Oxide pyrochlores: a review. Prog. Solid State Chem. 15, 55–143 (1983).
Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and Fermi-arcsurface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Blacklock, K. & White, H. W. Specific heats of the pyrochlore compounds Cd2Re2O7 and Cd2Ru2Oz. J. Chem. Phys. 71, 5287–5289 (1979).
Sakai, H. et al. Superconductivity in a pyrochlore oxide, Cd2Re2O7. J. Phys. Condens. Matter 13, L785–L790 (2001).
Sleight, A. W., Gillson, J. L., Weiher, J. F. & Bindloss, W. Semiconductor–metal transition in novel Cd2Os2O7. Solid State Commun. 14, 357–359 (1974).
Mandrus, D. et al. Continuous metal–insulator transition in the pyrochlore Cd2Os2O7. Phys. Rev. B 63, 195104 (2001).
Calder, S. et al. Spin–orbit-driven magnetic structure and excitation in the 5d pyrochlore Cd2Os2O7. Nat. Commun. 7, 11651 (2016).
Sohn, C. H. et al. Strong spin–phonon coupling mediated by single ion anisotropy in the all-in-all-out pyrochlore magnet Cd2Os2O7. Phys. Rev. Lett. 118, 117201 (2017).
Sleight, A. W. & Gillson, J. L. Platinum metal pyrochlores of the type Tl2M2O7. Mater. Res. Bull. 6, 781–784 (1971).
Lazarev, V. B. & Shaplygin, I. S. Electrical properties of mixed oxides containing a platinum metal and a non-noble metal. Russ. J. Inorg. Chem. 23, 163–170 (1978).
Martins, C., Aichhorn, M. & Biermann, S. Coulomb correlations in 4d and 5d oxides from first principles or how spin–orbit materials choose their effective orbital degeneracies. J. Phys. Condens. Matter 29, 263001 (2017).
Uematsu, D. et al. Large trigonal-field effect on spin–orbit coupled states in a pyrochlore iridate. Phys. Rev. B 92, 094405 (2015).
Rau, J. G., Lee, E. K. H. & Kee, H.-Y. Spin–orbit physics giving rise to novel phases in correlated systems: iridates and related materials. Annu. Rev. Condens. Matter Phys. 7, 195–221 (2016).
Birol, T. & Haule, K. J eff = 1/2 Mott-insulating state in Rh and Ir fluorides. Phys. Rev. Lett. 114, 096403 (2015).
Martins, C., Aichhorn, M., Vaugier, L. & Biermann, S. Reduced effective spin-orbital degeneracy and spin-orbital ordering in paramagnetic transition-metal oxides: Sr2IrO4 versus Sr2RhO4. Phys. Rev. Lett. 107, 266404 (2011).
Luo, Y. et al. Li2RhO3: a spin-glassy relativistic Mott insulator. Phys. Rev. B 87, 161121 (2013).
Wu, W., McCollam, A., Swainson, I., Rancourt, D. G. & Julian, S. R. A novel non-Fermi-liquid state in the iron-pnictide FeCrAs. Europhys. Lett. 85, 17009 (2009).
Akrap, A., Dai, Y. M., Wu, W., Julian, S. R. & Homes, C. C. Optical properties and electronic structure of the nonmetallic metal FeCrAs. Phys. Rev. B 89, 125115 (2014).
Muller, O. & Roy, R. Formation and stability of the platinum and rhodium oxides at high oxygen pressures and the structures of Pt3O4, β-PtO2 and RhO2. J. Less Common Met. 16, 129–146 (1968).
Shannon, R. D. Synthesis and properties of two new members of the rutile family RhO2 and PtO2. Solid State Commun. 6, 139–143 (1968).
Bain, G. A. & Berry, J. F. Diamagnetic corrections and Pascal’s constants. J. Chem. Educ. 85, 532–536 (2008).
Yamaura, K. & Takayama-Muromachi, E. Enhanced paramagnetism of the 4d itinerant electrons in the rhodium oxide perovskite SrRhO3. Phys. Rev. B 64, 224424 (2001).
Singh, D. J. Prospects for quantum criticality in perovskite SrRhO3. Phys. Rev. B 67, 054507 (2003).
Saha, S. et al. Temperature-dependent Raman and x-ray studies of the spin-ice pyrochlore Dy2Ti2O7 and nonmagnetic pyrochlore Lu2Ti2O7. Phys. Rev. B 78, 214102 (2008).
Maczka, M. et al. Temperature-dependent Raman scattering studies of the geometrically frustrated pyrochlores Dy2Ti2O7, Gd2Ti2O7 and Er2Ti2O7. J. Raman Spectrosc. 39, 537–544 (2008).
Maeno, Y. et al. Two-dimensional Fermi liquid behavior of the superconductor Sr2RuO4. J. Phys. Soc. Jpn. 66, 1405–1408 (1997).
Park, J. et al. Robust singlet dimers with fragile ordering in two-dimensional honeycomb lattice of Li2RuO3. Sci. Rep. 6, 25238 (2016).
Perry, R. S. et al. Sr2RhO4: a new, clean correlated electron metal. New J. Phys. 8, 175 (2006).
Stewart, G. R. Heavy-fermion systems. Rev. Mod. Phys. 56, 755–787 (1984).
Shiga, M., Fujisawa, K. & Wada, H. Spin liquid behavior of highly frustrated Y(Sc)Mn2 and effects of nonmagnetic impurity. J. Phys. Soc. Jpn. 62, 1329–1336 (1993).
Kondo, S. et al. LiV2O4: a heavy fermion transition metal oxide. Phys. Rev. Lett. 78, 372–373 (1997).
Lacroix, C. Heavy-fermion behavior of itinerant frustrated systems: β-Mn, Y(Sc)Mn2, and LiV2O4. Can. J. Phys. 79, 1469–1473 (2001).
Wada, H. et al. Spin fluctuations of Y(Mn1−xAlx)2 and Y1−xScxMn2. J. Magn. Magn. Mater. 70, 17–19 (1987).
Palstra, T. T. M. et al. Superconducting and magnetic transitions in the heavy-fermion system URu2Si2. Phys. Rev. Lett. 55, 2727–2730 (1985).
Frings, P. H., Franse, J. J. M., De Boer, F. R. & Menovsky, A. Magnetic properties of UxPty compounds. J. Magn. Magn. Mater. 31, 240–242 (1983).
Zhou, J.-S., Goodenough, J. B. & Dabrowski, B. Transition from Curie–Weiss to enhanced Pauli paramagnetism in RNiO3 (R = La, Pr, Gd). Phys. Rev. B 67, 020404 (2003).
Yamaura, K., Huang, Q., Young, D. P., Noguchi, Y. & Takayama-Muromachi, E. Crystal structure and electronic and magnetic properties of the bilayered rhodium oxide Sr3Rh2O7. Phys. Rev. B 66, 134431 (2002).
Yamaura, K., Huang, Q., Young, D. P. & Takayama-Muromachi, E. Crystal structure and magnetic properties of the trilayered perovskite Sr4Rh3O10: a new member of the strontium rhodate family. Chem. Mater. 16, 3424–3430 (2004).
Yamaura, K. et al. High-pressure synthesis, crystal structure determination, and a Ca substitution study of the metallic rhodium oxide NaRh2O4. Chem. Mater. 17, 359–365 (2005).
Yamaura, K. & Takayama-Muromachi, E. High-pressure synthesis of the perovskite rhodate CaRhO3. Phys. C 445, 54–56 (2006).
Rau, J. G. & Kee, H.-Y. Hidden spin liquid in an antiferromagnet: applications to FeCrAs. Phys. Rev. B 84, 104448 (2011).
Nevidomskyy, A. H. & Coleman, P. Kondo resonance narrowing in d- and f-electron systems. Phys. Rev. Lett. 103, 147205 (2009).
Georges, A., de’Medici, L. & Mravlje, J. Strong correlations from Hunds coupling. Annu. Rev. Condens. Matter Phys. 4, 137–178 (2013).
Plumb, K. W. et al. From mean-field localized magnetism to itinerant spin fluctuations in the nonmetallic metal FeCrAs. Phys. Rev. B 97, 184431 (2018).
Rodriguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Phys. B Condens. Matter 192, 55–69 (1993).
Acknowledgements
The authors gratefully acknowledge useful conversations with Yipeng Cai, Jonathan Gaudet, John Greedan, Chien-Lung Huang, and Murray Wilson. The authors thank Bassam Hitti and Gerald Morris from TRIUMF for their support with the μSR experiment. A.M.H. thanks the National Institute for Materials Science (NIMS) for their hospitality and support through the NIMS Internship Program. This work was supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) and Canada Foundation for Innovation. C.R.W. is additionally supported by the Canada Research Chair (Tier II) program and the Canadian Institute for Advanced Research. Q.C. and H.D.Z. are supported by the National Science Foundation (NSF-DMR-1350002).
Author information
Authors and Affiliations
Contributions
The high-pressure synthesis and x-ray diffraction were performed by A.M.H. and M.T. Magnetic susceptibility and electric resistivity measurements, and their analysis, were performed by Q.C., H.D.Z., C.M., P.M.S., J.P.A., A.M.H., and C.R.W. Heat capacity measurements were performed by A.Z.S. and C.R.W. μSR measurements were performed and analyzed by A.M.H. and G.M.L. with assistance from C.D. and Z.G. The manuscript was written by A.M.H. and C.R.W. with input from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hallas, A.M., Sharma, A.Z., Mauws, C. et al. Coexistence of metallic and nonmetallic properties in the pyrochlore Lu2Rh2O7. npj Quantum Mater. 4, 9 (2019). https://doi.org/10.1038/s41535-019-0148-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-019-0148-1
This article is cited by
-
Peculiar magnetotransport properties in epitaxially stabilized orthorhombic Ru3+ perovskite LaRuO3 and NdRuO3
Communications Materials (2024)
-
Structural and magnetic properties of ferromagnetic pyrochlore Lu2V2O7
Indian Journal of Physics (2024)