Abstract
The determination of the symmetry of the energy gap is crucial for research on the microscopic mechanisms of unconventional superconductivity. Here, we demonstrate experimentally that high-resolution resonant inelastic X-ray scattering at the Cu L3 edge can serve as a momentum-resolved, bulk-sensitive probe of the superconducting gap. We studied two optimally doped cuprates Bi2Sr2CaCu2O8+δ and Bi2Sr2Ca2Cu3O10+δ, in which we observe a strongly momentum dependent reduction of the spectral weight upon entering the superconducting state, with a maximum for momenta connecting antinodal regions of the Fermi surface. Based on a comparison with the calculated charge susceptibility and electronic Raman scattering data, we interpret our observation as a renormalization of the non-local charge susceptibility due to the superconducting gap opening. Our data demonstrate the methodological potential of resonant inelastic X-ray scattering as a versatile probe of the energy gap of high-temperature superconductors, including buried interfaces in heterostructures which are inaccessible to angle-resolved photoemission spectroscopy.
Similar content being viewed by others
Introduction
The experimental determination of the superconducting (SC) order parameter is one of the most essential steps in identifying the microscopic mechanism of superconductivity. For the cuprates and other unconventional superconductors, this problem is particularly challenging, because the order parameter is strongly momentum dependent, and because different order parameters coexist and compete with the SC state.1 Various spin and charge spectroscopies have been used to address this challenge. In the spin channel, inelastic neutron scattering (INS) has detected a pronounced rearrangement of the dynamical susceptibility and the emergence of a collective “resonance” mode upon cooling into the SC state.2,3 In the charge channel, optical spectroscopy and Raman scattering of photons in the visible range have been employed to study the excitations across the SC gap.4,5,6 Although these techniques are sensitive to the bulk of the material and can reach energy resolutions below 1 meV, INS requires large single crystals to get a workable signal, whereas the use of visible laser light in optical spectroscopy and Raman scattering limits the accessible momentum transfer q to the Brillouin zone (BZ) center. Angle-resolved photoemission spectroscopy (ARPES), a momentum-resolved probe of single-particle charge excitations, can probe the formation of the Bogoliubov quasiparticles and the momentum dependence of the order parameter. In the cuprates, it has contributed to the understanding of the universal \(d_{x^2 - y^2}\)-wave symmetry, as well as deviations from the ideal \(d_{x^2 - y^2}\)-wave due to the so-called pseudogap in the antinodal region of the Fermi surface (FS).7,8 However, due to its intrinsic surface sensitivity, the distinction between surface and bulk electronic states with ARPES remains technically challenging. Moreover, the necessity of single crystals with a natural cleavage plane severely limits the applicability of this method to different systems, confining it principally to Bi-based cuprates. Furthermore, research on SC electronics and spintronics9 requires information on SC correlations at buried interfaces, which ARPES is unable to provide. It is therefore desirable to establish a momentum-resolved, bulk-sensitive experimental approach to the low-energy charge and spin excitations in a large set of superconductors.
Resonant inelastic X-ray scattering (RIXS) has proven to be a powerful tool for studying elementary excitations.10,11 Being a photon-in, photon-out technique in the soft X-ray regime, RIXS is bulk-sensitive and naturally includes the charge response of the system.12,13 The substantial momentum of X-ray photons makes it possible to map out dispersive charge excitations in a wide region of the BZ.14,15 When RIXS is performed at the L edge, the strong spin–orbit coupling in the 2p core hole makes the cross section sensitive also to spin-flip scattering,16,17 which allows the observation of collective magnetic excitations.18,19 This versatile capability of RIXS leads to the possibility of measuring the modifications of charge and spin susceptibilities induced by the SC gap opening. Indeed, Marra et al.20 have theoretically proposed that RIXS can serve as a probe of the symmetry and phase of the SC order parameter, given that the coherence factors in the charge and spin susceptibilities in the SC state reflect not only the amplitude but also the phase of the order parameter.21 However, this perspective has not been realized to date because of the limited energy resolution of the available instruments, combined with the small energy scales associated with superconductivity.
In the present work, by taking advantage of the high energy resolution of the new ERIXS spectrometer at the beam line ID32 of the European Synchrotron Radiation Facility (ESRF), and the relatively large SC gaps of the optimally-doped double- and triple-layer Bi-based cuprates Bi2Sr2CaCu2O8+δ (Bi2212, Tc = 90 K) and Bi2Sr2Ca2Cu3O10+δ (Bi2223, Tc = 110 K), we show that RIXS has the capability to measure the SC gap. These systems have the double advantage that their energy gaps (including the pseudogap) extend up to 40 and 80 meV, respectively, which are comparable to the resolution of ERIXS, and that their single-particle spectra have already been characterized by ARPES.22,23 In order to facilitate the interpretation of the experimental data, we complement the RIXS experiment with electronic Raman scattering (ERS) in the visible range measured in the B1g geometry, which yields information about the electronic excitations predominantly from the antinodal region5 (see Methods).
Results
Charge susceptibility
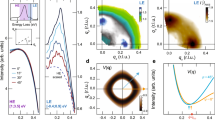
In the scattering geometry used for our experiments, the RIXS intensity is dominated by charge excitations (see Methods). Unlike ARPES that is a single particle probe, RIXS measures a two particle correlation function, for which the momentum dependence of the SC-induced renormalization is less intuitive. To get an idea of the momenta where major modifications of the RIXS spectra are expected, it is useful to estimate the charge susceptibility [χc(q, ω)] of the system. Here, q and ω correspond to the momentum and energy transfers from the X-ray photons to the sample. Figure 1a, b shows the imaginary part of the calculated χc(q, ω) for Bi2212 in the normal and SC states, respectively. Explicitly, it is expressed as20
Calculated charge susceptibility for Bi2212. a, b Imaginary part of calculated charge susceptibility [χc(q, ω)] along the Cu-O direction [q = (h, 0)] and the diagonal direction [q = (h, h)] in the normal a and superconducting (SC) b states in Bi2Sr2CaCu2O8+δ (Bi2212). The calculations are performed for a tight-binding band structure with a d-wave SC order parameter Δk = Δ[cos(kxa) − cos(kya)]/2. Tight-binding hopping parameters are taken from ref. 24 and Δ is set to 30 meV. c–e Constant-q cut of Imχc(q, ω) in the SC and normal states, and their difference at momentum transfers investigated in the RIXS measurement. Numerical data are convoluted with the experimental resolution of 50 meV. Corresponding momenta are indicated by dotted lines in a, b
The calculation was performed using a tight-binding band structure εk, whose hopping parameters were taken from the ARPES data in ref. 24. In the SC state, the d-wave SC order parameter Δk = Δ[cos(kxa) − cos(kya)]/2 is employed with the amplitude Δ = 30 meV.22 \(E_{\boldsymbol{k}} = \sqrt {\varepsilon _{\boldsymbol{k}}^2 + {\mathrm{\Delta }}_{\boldsymbol{k}}^2}\) is the energy dispersion of the Bogoliubov quasiparticles. The summation is taken over the entire BZ. Upon cooling below Tc, the low-energy spectral weight between 0 and ~0.1 eV is transferred to higher energy loss, reflecting the increased excitation energy required for creating particle-hole pairs across the d-wave SC gap, whereas the spectra above 0.2 eV are almost unchanged. Furthermore, major modifications are observed close to the Γ point, where the coherence factors are large in the charge channel (square brackets in Eq. (1)). We select three representative momentum transfers that are accessible to Cu L3 RIXS and show different modifications, as indicated by dotted lines. The constant q cuts of Imχc(q, ω) at these momenta convoluted with the experimental resolution of 50 meV are plotted in Fig. 1c–e. At q = (0.15, 0) (Fig. 1c), a momentum close to that connecting the antinodal region of two neighboring FSs,24 we observe a clear spectral weight transfer. At a larger momentum transfer q = (0.4, 0) (Fig. 1d), the SC-induced changes are much smaller, as this momentum does not significantly connect different parts of the FS. Along the diagonal direction q = (0.1, 0.1) (Fig. 1e), we observe a moderate spectral weight transfer. In the following, we shall test the capability of RIXS to experimentally detect the SC gap opening, by investigating modifications of the RIXS spectra below and above Tc at these momentum transfers.
We also show in Fig. 2a, b Imχc(q, ω) for Bi2223 in the normal and SC states. The hopping parameters extracted by the tight-binding fitting of ARPES band structure23 are used in the calculation. In the SC state, the d-wave order parameter Δk = Δ[cos(kxa) − cos(kya)]/2 is employed with the amplitude Δ = 60 meV. In the triple-layer Bi2223, there are inequivalent inner and outer CuO2 planes. Here we have chosen the SC gap value for the inner CuO2 planes, which possess the larger SC gap than that of the outer ones (Δ = 43 meV). In Fig. 2c, we also plot a constant q plot of Imχc(q, ω) for the momentum transfer q = (0.15, 0), which is investigated in the RIXS experiment.
Calculated charge susceptibility for Bi2223. a, b Calculated charge susceptibility along the Cu-O direction [q = (h, 0)] and the diagonal direction [q = (h, h)] in the normal a and superconducting (SC) b states in Bi2223. The calculations are performed for a tight-binding band structure with a d-wave SC order parameter Δk = Δ[cos(kxa) − cos(kya)]/2. Tight-binding hopping parameters are taken from ref. 23 and Δ is set to 60 meV. The dotted lines indicate the constant q cut plotted in c. c Constant q plot of Imχc(q, ω) at q = (0.15, 0) in the SC and normal states, and their difference spectrum
Electronic Raman scattering in the B 1g geometry
In order to provide a baseline for our approach, we show in Fig. 3 the electronic Raman susceptibility ImχERS(q = 0, ω) measured in the B1g geometry for Bi2212 and Bi2223 at 10 K and at Tc. The difference spectra between these two temperatures are also shown as black lines. In Bi2212 (Fig. 3a), the spectral weight below 50 meV is suppressed and transferred to higher energy loss, leading to the so-called “2Δ” peak at ~70 meV, consistent with previous reports.25,26,27,28 In Bi2223 (Fig. 3b), we also observe a spectral weight reduction in the low energy (E < 50 meV) and a broader increase in the higher energy (50 < E < 130 meV) ranges. There is a peak at ~70 meV and a small bump at ~90 meV, as indicated by open triangles. The triple-layer Bi2223 has inequivalent inner and outer CuO2 planes. The peak at 70 meV is assigned to the response from the SC condensate in the outer CuO2 planes with a smaller SC gap, whereas the bump at 90 meV is assigned to that in the inner CuO2 planes with a larger SC gap. The peak energy of 70 meV is in good agreement with prior work.29 These ERS results, together with the calculated susceptibility, set the energy scale expected for our RIXS experiment.
Electronic Raman scattering spectra for Bi2212 and Bi2223. a, b B1g Raman response of optimally-doped Bi2212 and Bi2Sr2Ca2Cu3O10+δ (Bi2223), respectively, at 10 K and Tc. Data are presented as Raman susceptibility ImχERS(q = 0, ω). The difference spectra between these two temperatures are also shown as black lines. The locations of the “2Δ” peaks are indicated by open triangles
RIXS spectra at the Cu L 3 edge
Figure 4a, b shows the RIXS spectra of Bi2212 and Bi2223 at q = (0.15, 0) for different temperatures across Tc. The spectra include an elastic line (originating mostly from thermal diffuse scattering, surface roughness, and the tail from specular reflectivity) and a broad high-energy feature that is composed of paramagnons,18,19 multimagnon excitations as well as low-energy interband transitions. Both for Bi2212 and Bi2223, the RIXS spectral weight between the elastic line and the high-energy peak decreases markedly with decreasing temperature, whereas the intensity at higher energies remains substantially unchanged. At the same time, the intensity of the elastic line, due to the contribution from thermal diffuse scattering, increases with temperature. In order to extract the spectral change originating from the low-energy electronic excitations, we have fitted the elastic lines with Gaussian functions, as shown by the dotted curves (see Methods for the procedure for determining elastic lines). Note that the spectral shapes of the energy-gain part are almost identical between different temperatures. RIXS spectra after the subtraction of the elasic lines are shown in Fig. 4c, d. The remaining spectral modifications demonstrate that the low-energy electronic excitations are temperature dependent. The difference spectra from the highest temperature data are shown in Fig. 4e, f. The difference spectra are evaluated after subtracting the elastic lines. For clarity we show smoothed data as solid lines and the original difference spectra as dotted lines. The spectral reduction starts around zero energy, has a maximum at 32 meV in Bi2212 and at 42 meV in Bi2223, and extends up to ~100 meV. Remarkably, the minima of the difference spectra obtained from the calculated susceptibility are located at 25 meV in Bi2212 (Fig. 1c) and at 50 meV in Bi2223 (Fig. 2c), in good agreement with those in the RIXS data. Furthermore, the reduction of spectral weight monotonically decreases with increasing temperature, in accordance with the monotonic closing of both SC gap and pseudogap. Note that the onset of the spectral weight reduction is visible already above Tc, at 150 K for Bi2212 and 120 K for Bi2223. Considering that q = (0.15, 0) approximately connects the antinodal region of the FS, this observation is consistent with the pseudogap remaining open in the antinodal region at these temperatures. Moreover, we note here that the spectral weight suppression is more pronounced in Bi2212 than in Bi2223. This could be a consequence of a higher level of impurities present in the Bi2223 crystals and/or to the fact that the reference spectrum used for the subtraction in Bi2212 was collected at a higher temperature.
RIXS spectra at q = (0.15, 0) for Bi2212 and Bi2223. a, b Cu L3-edge resonant inelastic x-ray scattering (RIXS) spectra for Bi2212 and Bi2223, respectively, at q = (0.15, 0). Gaussian functions representing the elastic lines are shown by dotted curves. c, d RIXS spectra after the subtraction of the elastic lines. e, f Difference spectra from the highest temperature. Smoothed data are represented by the solid lines and the original difference spectra by the dotted lines. The difference spectra are evaluated after subtracting the elastic lines
The low-energy range also includes other spectral contributions, such as phonons and the tail of the high-energy peak. In order to evaluate the possible influence of these contributions on the observed spectral-weight rearrangement, we have investigated RIXS spectra at q = (0.4, 0) and (0.1, 0.1) in Bi2212. While the optical phonon branches are expected to be weakly dispersing as a function of q, the particle-hole excitations across the d-wave SC gap are strongly q-dependent, as shown in Fig. 1. Figure 5a, b shows the RIXS spectra for Bi2212 at q = (0.4, 0) and (0.1, 0.1), respectively, below and above Tc. At q = (0.4, 0), the calculation predicts that the low-energy modification in Imχc(q, ω) is small (Fig. 1d). This is indeed observed in the RIXS data in Fig. 5a: the RIXS intensity remains unchanged within the experimental error between 20 and 150 K. This is also evident from the elastic-subtracted spectra shown in Fig. 5c and the difference spectrum plotted at the bottom of Fig. 5a. On the other hand, along the diagonal of the BZ at q = (0.1, 0.1), a moderate spectral weight transfer is expected (Fig. 1e). In the RIXS data in Fig.5b, we indeed observe a considerable spectral-weight reduction between the high-energy peak and the zero loss line, which is also clear from the elastic-subtracted spectra in Fig. 5d. Moreover, the minimum of the difference RIXS spectra (bottom of Fig. 5b) is located at ~70 meV, in good agreement with 67 meV in Imχc(q, ω). These results provide evidence that the spectral modifications originate not from thermal population of optical phonons but dominantly from the q dependence of electronic excitations across the SC gap.
Discussion
In the RIXS spectra we have clearly observed the spectral weight reduction at low temperatures at q = (0.15, 0) and (0.1, 0.1). This demonstrates that RIXS at the Cu L3 edge can detect the opening of SC gap of the cuprates, in a momentum-resolved and bulk-sensitive manner. Meanwhile, one also notices that the concomitant increase of spectral weight on the higher energy side (“2Δ” coherence peak) has not been clearly detected, in contrast to the peaks in the B1g ERS data in Fig. 3. The absence of 2Δ peaks in the RIXS data suggests that the spectral weight is not conserved between different temperatures in the investigated energy range. Note that the Bose factor correction to the RIXS data does not significantly modify the lineshapes of difference spectra above 50 meV. We plot in Fig. 6 the difference RIXS spectra at q = (0.15, 0) after the Bose factor correction. Here we first removed the elastic lines from the raw spectra, divided the spectra by the Bose population factor for positive energy loss region, and subtracted the high temperature spectra. The difference spectra for 20 K without Bose factor correction are also plotted as dotted lines. It is clear from the spectra for 20 K that the correction has little effect above 50 meV both in Bi2212 and Bi2223, where the Bose factor is close to unity. Therefore, the absence of the 2Δ peak in the RIXS spectra is not ascribed to the Bose population factor.
Before addressing the absence of the 2Δ peak in detail, we stress that the RIXS process is exactly described by a low energy susceptibility, albeit not equivalent to the charge susceptibility
with εi (εf) the polarization of the incoming (scattered) light, ωi the energy of the incoming photons and ω the energy loss of the scattered photon. The full q-dependent effective RIXS operator \(R_{\omega _i,{\boldsymbol{q}}}^{\varepsilon _i,\varepsilon _f}\) introduced in ref. 17 includes possible excitations on all sites and is obtained by a Fourier transform of the real-space operator, i.e., \(R_{\omega _i,{\boldsymbol{q}}}^{\varepsilon _i,\varepsilon _f} = \mathop {\sum}\nolimits_j {\kern 1pt} e^{{\mathrm{i}}{\boldsymbol{q}} \cdot {\boldsymbol{r}}_j}R_{\omega _i,j}^{\varepsilon _i,\varepsilon _f}\), in which the core hole is created and annihilated on site j.
With the definition of RIXS susceptibility, we discuss the relationship between the RIXS at low q and the B1g ERS. The full Raman susceptibility is composed of the bare response term and the other “backflow” terms, which originate from the screening by the long-range Coulomb interaction.30,31 The backflow terms are relevant when the polarization configurations transform according to the lattice symmetry, such as A1g in the D4h point group of the cuprates. It is known that the backflow terms, at least theoretically, strongly renormalize the singularity of the 2Δ ERS response expected from the bare Raman term.32 On the other hand, the B1g ERS cross section does not receive corrections by the backflow terms, since the backflow terms for crossed polarizations with q = 0 are identically zero by symmetry. Therefore, the experimental energy scale of the 2Δ peaks in the B1g Raman data in Fig. 3 can be directly associated with that of the SC gap in the antinodal region.
On the other hand, regarding the RIXS data, we performed the measurements without polarization analysis with less symmetric geometry (as detailed in Methods) than the conventional ERS setup (the light paths are aligned along the c-axis with the in-plane polarization vectors). Although the RIXS susceptibility for nonzero q including the screening effect has not been well formulated at this stage, the backflow terms are likely to be nonzero for the present geometry, particularly for the parallel polarization channel. It is probable that the backflow terms strongly renormalize the 2Δ RIXS response, as in the case of the A1g Raman. Therefore, the absence of the 2Δ peak in the RIXS data may indicate the importance of the backflow terms in the RIXS cross section.
Additionally, we discuss the non-local nature of the RIXS process as a major difference between the RIXS and ERS cross sections. To understand the RIXS susceptibility more quantitatively, we express the RIXS process by a series of low-energy effective operators.13 If we, for simplicity, focus on effective operators leading to a single particle susceptibility, we find for the charge scattering with ε = εi = εf:
which includes hopping between the core hole site j and its neighboring sites separated at a distance rl. α(rl, ωi, ε) describes the energy and polarization dependence of the RIXS process. Off resonance, i.e., for ωi below the resonant energy (ωL), the RIXS susceptibility is equivalent to the susceptibility measured by non-resonant ERS. In this case, α(rl, ωi < ωL) is proportional to \(\delta _{{\boldsymbol{r}}_l,0}\), which makes \(R_{\omega _i,j}^\varepsilon\) equivalent to the local density operator, and thereby also the scattering spectra to the charge susceptibility. When ωi is tuned to resonance and the excited core electron is placed near the Fermi energy, the electron can move away from the core hole site up to a distance ~vFτ, where vF is the Fermi velocity and τ the core-hole-state lifetime. This leads to non-zero α(r, ωi) for rl up to several lattice spacings.13 The resulting non-local contributions to the RIXS operator give rise to large spectral weight at low energy, which may lead to significant deviations of the measured intensities from those obtained from the charge susceptibility.13,33 The direct calculation of the RIXS cross section in the SC state is highly nontrivial and beyond the scope of the present work.
Whether the spectral weight removed from the SC gap reappears as a peak at the energy scale of 2Δ or as incoherent spectral weight at higher energies depends sensitively on the impurity concentrations. With large impurity concentrations the 2Δ peak disappears in ERS, albeit at different impurity concentrations for excitations in the B1g or A1g symmetry.34,35,36 Since electrons can be moved by a distance rl during the RIXS process, in contrast to ERS where the electron is created and annihilated on the same site, it is probable that these excitations are more vulnerable to scattering placing the lost spectral weight from within the SC gap not at 2Δ, but into an incoherent excitation smeared over a large energy scale of the interaction strengths in the bare Hamiltonian. A superconductivity-induced spectral weight transfer involving an energy scale above 1 eV is also observed in the optical conductivity of Bi221237 and YBa2Cu3O6.9.38
In conclusion, we have measured the charge and magnetic excitations of optimally-doped Bi2212 and Bi2223 by high-resolution RIXS at the Cu L3 edge. We have observed a reduction of RIXS spectral weight across the SC transition at q = (0.15, 0) in an energy range that matches the SC energy gap. The spectral reduction decreases with increasing temperature but remains nonzero somewhat above Tc, consistent with the closure of the SC gap and the residual pseudogap opening above Tc. Furthermore, the Bi2212 data at q = (0.4, 0) show little modification across Tc, whereas the spectrum at the BZ diagonal direction q = (0.1, 0.1) exhibits a moderate reduction, in good agreement with the modifications of charge susceptibility. We ascribe the absence of the 2Δ peak in the RIXS spectra to the screening effect by the backflow terms and to the non-local nature of the RIXS operator. The present demonstration of the feasibility of detecting the energy gap by the bulk-sensitive RIXS technique is of great methodological importance, as it will open the way to new studies of the SC gap in cuprates where reliable ARPES results are absent, such as YBa2Cu3O6+x, and in buried interfaces in heterostructures, which are inaccessible to ARPES. Furthermore, the capability to access both spin and charge excitations over a larger (q, ω) space than INS and Raman scattering will allow one to connect the renormalization of the susceptibilities across the SC transition to the phase competition between superconductivity, charge- and spin density waves in the cuprate phase diagram, all with a single experimental probe.
Methods
RIXS measurements
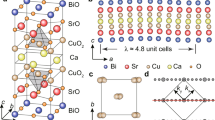
The RIXS measurements were performed at the beam line ID32 of ESRF (The European Synchrotron Radiation Facility, Grenoble, France), using the new high-resolution ERIXS spectrometer. The incident x-ray energy was tuned to the Cu L3 peak (~931 eV) of the absorption spectra measured in total electron yield. The zero energy loss and the energy resolution were determined by measuring non-resonant elastic scattering from silver paint deposited next to the samples. The energy resolution was ~50 meV (full width at half maximum of the Gaussian elastic profile), which allowed us to detect small spectral modifications across the SC transition while having a sufficient photon flux on the samples. The incoming x-rays were linearly polarized perpendicular to the scattering plane (σ polarization). The polarization of scattered x-rays was not analyzed. The scattering angle 2θ was fixed at 150° and the in-plane momentum transfer q was changed by rotating the sample angle θ. The single crystals were cleaved ex situ before mounting them in the measurement chamber in order to obtain fresh surfaces. Data are normalized to the ring current, and presented in reciprocal lattice units (r.l.u.) defined with respect to the pseudotetragonal unit cell with lattice constants a = b = 3.82 Å and c = 30.84 Å for Bi2212 and a = b = 3.82 Å and c = 37.16 Å for Bi2223, respectively. The growth conditions of the Bi2212 and Bi2223 samples follow procedures described in refs. 39,40.
Charge and spin susceptibilities
In principle, RIXS is sensitive to both charge and spin excitations, but charge excitations dominate the response in our experiments. Near the Γ-point [i.e., for the data points at q = (0.15, 0) and (0.1, 0.1) in our experiments], the coherence factor of the spin excitations nearly vanishes20 whereas the one for charge excitations is nearly maximal (Eq. (1)). For q = (0.4, 0), where both susceptibilities are significant, the polarization factor in the RIXS cross section greatly favors charge excitations. Specifically, we chose a geometry close to grazing emission, that is, θ is larger than half of 2θ (specular condition). Prior experiments on YBa2Cu3O6+x with full polarization analysis41 have demonstrated that in this geometry, the low-energy spectral weight is dominated by scattering from charge excitations which preserves the photon polarization.
Determination of elastic peaks
The precise determination of the elastic line is crucial to quantify the spectral modification at different temperatures. We have determined the elastic peak in the following procedure: (1) determine the zero energy loss from the nonresonant spectra of the silver paint deposited next to the samples, which are accumulated before and after the sample scan (~1 h each). The validity of the method is confirmed by the fact that the leading edges of the elastic spectra match very well between different temperatures. (2) Fit the energy gain part (E < 0) of the spectra to a Gaussian function, with the center fixed at E = 0 and the width confined in the interval 45 < ΔE < 55 meV. Our fitting procedure involves only one free parameter that can siginificantly vary, i.e., the height of the Gaussian, thus making the fitting process quite robust. Note that we did not perform the decomposition of the spectra including the tail of the paramagnon peak, which involves large uncertainties. Based on this analysis, it is clear that the peaks of the asymmetric quasi-elastic lines are located at positive energy. Importantly, the minima of the spectral depletion are located near the dip of the low-temperature spectra, much above the maxima of the quasi-elastic lines.
ERS measurements
The ERS measurements were performed in backscattering geometry using a Jobin Yvon LabRam HR800 single-grating spectrometer. We employed the λ = 632.8 nm (red) line from a He-Ne laser for excitation, which induces resonant enhancement of electronic signals.42 The B1g geometry was realized by selecting the linear polarization of the incoming photons to be 45° from the Cu-O direction, and that of the outgoing photons to be perpendicular to that of incoming photons [z(X′Y′)z in Porto’s notation]. The data are presented as the Raman susceptibility ImχERS(q = 0, ω), which is derived by correcting the raw data by the spectrometer efficiency, subtracting a constant background, binning adjacent data points, and dividing it by the Bose population factor.
Data availability
Raw RIXS data were generated at the European Synchrotron Radiation Facility. Derived data supporting the findings of this study are available from the corresponding author upon reasonable request.
References
Keimer, B., Kivelson, S. A., Norman, M. R., Uchida, S. & Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015).
Eschrig, M. The effect of collective spin-1 excitations on electronic spectra in high-T c superconductors. Adv. Phys. 55, 47–183 (2006).
Inosov, D. S. et al. Normal-state spin dynamics and temperature-dependent spin-resonance energy in optimally doped BaFe1.85Co0.15As2. Nat. Phys. 6, 178–181 (2010).
Basov, D. N., Averitt, R. D., van der Marel, D., Dressel, M. & Haule, K. Electrodynamics of correlated electron materials. Rev. Mod. Phys. 83, 471–541 (2011).
Devereaux, T. P. & Hackl, R. Inelastic light scattering from correlated electrons. Rev. Mod. Phys. 79, 175–233 (2007).
Sidis, Y. et al. Magnetic resonant excitations in high-T c superconductors. Phys. Status Solidi B 241, 1204–1210 (2004).
Damascelli, A., Hussain, Z. & Shen, Z.-X. Angle-resolved photoemission studies of the cuprate superconductors. Rev. Mod. Phys. 75, 473–541 (2003).
Hashimoto, M., Vishik, I. M., He, R.-H., Devereaux, T. P. & Shen, Z.-X. Energy gaps in high-transition-temperature cuprate superconductors. Nat. Phys. 10, 483–495 (2014).
Linder, J. & Robinson, J. W. A. Superconducting spintronics. Nat. Phys. 11, 307–315 (2015).
Kotani, A. & Shin, S. Resonant inelastic X-ray scattering spectra for electrons in solids. Rev. Mod. Phys. 73, 203–246 (2001).
Ament, L. J. P., van Veenendaal, M., Devereaux, T. P., Hill, J. P. & van den Brink, J. Resonant inelastic X-ray scattering studies of elementary excitations. Rev. Mod. Phys. 83, 705–767 (2011).
Jia, C., Wohlfeld, K., Wang, Y., Moritz, B. & Devereaux, T. P. Using RIXS to uncover elementary charge and spin excitations. Phys. Rev. X 6, 021020 (2016).
Lu, Y. & Haverkort, M. W. Nonperturbative series expansion of Green’s functions: the anatomy of resonant inelastic x-ray scattering in the doped Hubbard model. Phys. Rev. Lett. 119, 256401 (2017).
Kim, Y.-J. et al. Doping dependence of charge-transfer excitations in La2−xSrxCuO4. Phys. Rev. B 70, 094524 (2004).
Ishii, K. et al. Mott gap excitations in twin-free YBa2CuO7−δ (T c = 93 K) studied by resonant inelastic x-ray scattering. Phys. Rev. Lett. 94, 187002 (2005).
Ament, L. J. P., Ghiringhelli, G., Sala, M. M., Braicovich, L. & van den Brink, J. Theoretical demonstration of how the dispersion of magnetic excitations in cuprate compounds can be determined using resonant inelastic X-ray scattering. Phys. Rev. Lett. 103, 117003 (2009).
Haverkort, M. W. Theory of resonant inelastic x-ray scattering by collective magnetic excitations. Phys. Rev. Lett. 105, 167404 (2010).
Braicovich, L. et al. Dispersion of magnetic excitations in the cuprate La2CuO4 and CaCuO2 compounds measured using resonant x-ray scattering. Phys. Rev. Lett. 102, 167401 (2009).
Le Tacon, M. et al. Intense paramagnon excitations in a large family of high-temperature superconductors. Nat. Phys. 7, 725–730 (2011).
Marra, P., Sykora, S., Wohlfeld, K. & van den Brink, J. Resonant inelastic X-ray scattering as a probe of the phase and excitations of the order parameter of superconductors. Phys. Rev. Lett. 110, 117005 (2013).
Kee, H.-Y. & Varma, C. M. Polarizability and single-particle spectra of two-dimensional s- and d-wave superconductors. Phys. Rev. B 58, 15035–15044 (1998).
Vishik, I. M. et al. Phase competition in trisected superconducting dome. Proc. Natl Acad. Sci. USA 109, 18332–18337 (2012).
Ideta, S. et al. Enhanced superconducting gaps in the trilayer high-temperature Bi2Sr2Ca2Cu3O10+δ cuprate superconductor. Phys. Rev. Lett. 104, 227001 (2010).
Norman, M. R., Randeria, M., Ding, H. & Campuzano, J. C. Phenomenological models for the gap anisotropy of Bi2Sr2CaCu2O8 as measured by angle-resolved photoemission spectroscopy. Phys. Rev. B 52, 615–622 (1995).
Staufer, T., Nemetschek, R., Hackl, R., Müller, P. & Veith, H. Investigation of the superconducting order parameter in Bi2Sr2CaCu2O8 single crystals. Phys. Rev. Lett. 68, 1069–1072 (1992).
Venturini, F. et al. Doping dependence of the electronic Raman spectra in cuprates. J. Phys. Chem. Solids 63, 2345–2348 (2002).
Blanc, S. et al. Quantitative Raman measurement of the evolution of the cooper-pair density with doping in Bi2Sr2CaCu2O8+δ superconductors. Phys. Rev. B 80, 140502 (2009).
Murai, N. et al. Electronic Raman scattering on out-of-plane disordered Bi2Sr2CaCu2O8+δ: How the pseudogap affects the superconducting Raman response. Phys. Rev. B 91, 214520 (2015).
Limonov, M., Lee, S., Tajima, S. & Yamanaka, A. Superconductivity-induced resonant Raman scattering in multilayer high-T c superconductors. Phys. Rev. B 66, 054509 (2002).
Monien, H. & Zawadowski, A. Theory of Raman scattering with final-state interaction in high-t c bcs superconductors: collective modes. Phys. Rev. B 41, 8798–8810 (1990).
Devereaux, T. P. & Einzel, D. Electronic Raman scattering in superconductors as a probe of anisotropic electron pairing. Phys. Rev. B 51, 16336–16357 (1995).
Devereaux, T. P., Virosztek, A. & Zawadowski, A. Multiband electronic Raman scattering in bilayer superconductors. Phys. Rev. B 54, 12523–12534 (1996).
Tsutsui, K. & Tohyama, T. Incident-energy-dependent spectral weight of resonant inelastic x-ray scattering in doped cuprates. Phys. Rev. B 94, 085144 (2016).
Devereaux, T. P. Theory for the effects of impurities on the Raman spectra of superconductors. Phys. Rev. B 45, 12965–12975 (1992).
Devereaux, T. P. Theory of electronic Raman scattering in disordered unconventional superconductors. Phys. Rev. Lett. 74, 4313–4316 (1995).
Misochko, O. V., Sakai, K., Nakashima, S. & Gu, G. Pairing symmetry and localization probed by electronic Raman scattering in disordered high-T c superconductors. Phys. Rev. B 60, 1326–1331 (1999).
Molegraaf, H. J. A., Presura, C., van der Marel, D., Kes, P. H. & Li, M. Superconductivity-induced transfer of in-plane spectral weight in Bi2Sr2CaCu2O8+δ. Science 295, 2239–2241 (2002).
Boris, A. V. et al. In-plane spectral weight shift of charge carriers in YBa2Cu3O6.9. Science 304, 708–710 (2004).
Wen, J. et al. Large Bi-2212 single crystal growth by the floating-zone technique. J. Cryst. Growth 310, 1401–1404 (2008).
Fujii, T., Watanabe, T. & Matsuda, A. Single-crystal growth of Bi2Sr2Ca2Cu3O10+δ (Bi-2223) by TSFZ method. J. Cryst. Growth 223, 175–180 (2001).
Minola, M. et al. Collective nature of spin excitations in superconducting cuprates probed by resonant inelastic x-ray scattering. Phys. Rev. Lett. 114, 217003 (2015).
Le Tacon, M. et al. Two energy scales and two distinct quasiparticle dynamics in the superconducting state of underdoped cuprates. Nat. Phys. 2, 537–543 (2006).
Acknowledgements
H.S. acknowledges financial support from the JSPS Research Fellowship for Research Abroad. M.M. was partially supported by the Alexander von Humboldt Foundation. G.G. and Y.Y.P. were partially supported by the Fondazione CARIPLO and Regione Lombardia, Italy, through the ERC-P-ReXS project (2016-0790).
Author information
Authors and Affiliations
Contributions
H.S., M.M., L.B., G.G., M.L.T., and B.K. designed the experiments. H.S., M.M., Y.Y.P., R.F., E.L., L.B., and G.G. performed the RIXS experiments assisted by K.K., D.B., and N.B.B. S.I., H.E., C.H., and X.J.Z. grew the single crystals and performed sample characterization. H.S., T.L., and J.P. performed the annealing of samples before the RIXS experiments. H.S. and M.M. performed ERS experiments with the help of M.L.T. H.S. analyzed the experimental data. Y.L. and M.W.H. carried out the theoretical calculations. H.S., M.M., and B.K. wrote the manuscript with comments from all co-authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Suzuki, H., Minola, M., Lu, Y. et al. Probing the energy gap of high-temperature cuprate superconductors by resonant inelastic x-ray scattering. npj Quant Mater 3, 65 (2018). https://doi.org/10.1038/s41535-018-0139-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-018-0139-7
This article is cited by
-
Unconventional exciton evolution from the pseudogap to superconducting phases in cuprates
Nature Communications (2022)
-
Probing light-driven quantum materials with ultrafast resonant inelastic X-ray scattering
Communications Physics (2020)