Abstract
The single-band, quasi-two dimensional metals PdCoO2 and PtCoO2 have recently come to prominence because of their extremely long mean free paths, which establish them as some of the most electronically pure materials known, and as potential hosts of previously unobservable regimes of electronic transport. To fully establish their magnetotransport properties, we have studied the magnetoresistance and Hall effect in bulk single crystals to which electrical contacts have been made with high precision using focused ion beam machining. We observe a strong temperature dependence of the Hall resistivity in small applied fields, linked to a large violation of Kohler’s rule in the magnetoresistance. We discuss the extent to which these observations can be accounted for by standard transport theory.
Similar content being viewed by others
Introduction
Recent years have seen a rapid growth of research on unusual regimes of electronic transport.1 Of particular interest is one in which the mean free path deduced from standard measurements of electrical resistivity is very long. As is well known from the physics observed in high purity semiconductor two-dimensional electron gases and graphene, a host of novel physics can be seen in this high purity limit.2,3,4 In bulk systems, there has been a renaissance of research into ultrapure Bi,5 and the extremely low resistivity observed at low temperatures in compound metals such as Cd3As2, NbP, and WP2, is also generating considerable attention.6,7,8
The majority of the bulk metals with extremely long mean free paths are either low carrier density semi-metals or materials with fairly complex multi-sheet Fermi surfaces and both electron- and hole-like carriers. It is highly desirable, therefore, to identify high carrier density metals with simple, single-sheet Fermi surfaces and long resistive mean free paths, to provide benchmark systems for understanding electrical transport. An additional benefit is quasi-two-dimensional conduction, to provide information at high carrier density to complement observations in the low density two dimensional systems.
The non-magnetic delafossite metals PtCoO2 and PdCoO2 satisfy all the above criteria. Conduction takes place in triangular lattice Pt and Pd layers, with a single conduction band crossing the Fermi level. The electrical conductivity of both materials is remarkably high. At room temperature PtCoO2 has the longest mean free path of any monovalent or divalent metal (longer even than those in elemental Cu or Ag).9 Low temperature mean free paths of tens of microns have been observed in PdCoO2,10 and there is evidence that in this regime, there is strong phonon drag, in which the phonons gain net momentum when a current flows, meaning that normal electron-phonon scattering processes do not contribute to the observed resistivity.10,11
The extremely long relaxation times seen at low temperatures in PdCoO2 have been exploited in studies of out of plane magnetoresistance12,13 and electrical flow in mesoscopic channels of restricted width,14 with the latter experiments uncovering evidence for hydrodynamic flow from analysis of zero field data. However, no comprehensive study of in-plane magneto transport has been reported. This is important both in its own right and because of recent theoretical work highlighting the possibility that hydrodynamic effects are in principle observable by comparing data from mesoscopic samples under applied magnetic fields with those seen in bulk samples,15,16 experiments which require detailed knowledge of the bulk properties.
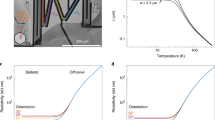
PdCoO2 and PtCoO2 are also attractive for study because of the remarkable simplicity of their basic electronic structure.9 The single, highly two-dimensional band with dominantly Pt or Pd character that crosses the Fermi level results in the Fermi surfaces shown in Fig. 1a and b. Both have been extensively characterized by the de Haas-van Alphen effect, angle-resolved photoemission measurements and electronic structure calculations.10,17,18,19,20,21 The results of experiment and theory are in excellent agreement, as long as the correlations in the transition metal layers are taken into account so that the small deviations from perfect two-dimensionality due to interplane coherence are correctly reproduced.19,22 Once this is done, both the calculations and direct photoemission experiments show that, in a two-dimensional approximation, the Fermi velocity is constant around the Fermi surface to within ±5% (Fig. 1c). PdCoO2 and PtCoO2 are therefore ideal materials on which to test the predictions of transport theory.
The Fermi surfaces of PtCoO2 a and PdCoO2 b as determined by angle-resolved photoemission. Both are highly two-dimensional and nearly hexagonal, with slight differences in curvature between the two compounds. c The Fermi velocities vF for the two compounds, obtained from electronic structure calculations optimized to match the experimentally determined band parameters, projected into a two-dimensional Brillouin zone. In both cases vF varies around only by ±5% of its mean value, with the maximum along Γ- K in PtCoO2 and Γ- M in PdCoO2
Results
As described in the Methods section below, the extremely high conductivity of PdCoO2 and PtCoO2 means that devices with precisely defined geometries are required for accurate measurements; this was achieved by sculpting single crystals using focused ion beams. In total, 3 devices of this kind were made from PdCoO2 and 3 from PtCoO2 for this project; representative devices of each material are shown in Fig. 2a and b, respectively, with measured zero-field resistivity shown in Fig. 2c and d. Averaged across all measured devices, measured room temperature resistivity was 3.05 ± 0.07 μΩcm for PdCoO2 and 1.82 ± 0.13 μΩcm for PtCoO2, with intersample thickness variation the main source of experimental error. Given the precision with which the new devices were prepared, the above values should replace the previous best estimates [2.6 μΩcm10 and 2.1 μΩcm19] for the room temperature resistivities of the two compounds. At low temperature the resistivity of the two samples shown in Fig. 2 is 8.1 nΩcm and 80 nΩcm, respectively at the low and high end of the ranges (8.1–29.3 nΩcm and 20–80 nΩcm) observed for the two compounds.
The resistivity of the PdCoO2 a and PtCoO2 b devices, shown in panels c and d, respectively. Each device was sculpted from a single crystal using focused ion beam milling. Electrical contact is made to the crystal via a layer of sputtered gold applied to the top surface. To ensure current homogeneity through the thickness of the measurement channel the current passes along a meander track before entering that channel. The longitudinal and Hall contact pairs for which ρxx(H) and ρxy(H) data are shown in this paper are marked, but the multi-contact geometry allowed for checks that these data were consistent across each sample
Throughout this paper we will discuss the analysis of transport data using expressions that, while commonly used, require precise definition. We adopt the following convention: ‘Boltzmann’ theory refers to solutions of the Boltzmann equation in the relaxation time approximation in which all scattering is momentum-relaxing, but the resulting mean free path can vary as a function of wave vector k around the Fermi surface. A ‘Drude’ expression is more restrictive, assuming the existence of a single, k-independent relaxation time. Since the Fermi velocity is so weakly k-dependent in PdCoO2 and PtCoO2 (Fig. 1c), a single relaxation time is equivalent to a single mean free path to a good approximation. The low temperature resistivity of the PdCoO2 crystal (Fig. 2a) is particularly noteworthy because in a standard Drude analysis it corresponds to a mean free path of 20.3 μm and, therefore, to extremely weak momentum-relaxing scattering.
The Hall resistivity for the two samples is shown in Fig. 3a and b for a range of temperatures between 2 K and 300 K. As emphasized by the derivative plots shown in Fig. 3c and d, there is a clear, temperature-dependent separation between low-field and high-field behavior. At 2 K the derivative of approximately 0.027 μΩcm/T corresponds to a Hall coefficient (RH) of 2.7 × 10−10 m3/C and Hall number of 2.3 × 1028 m−3, within a few per cent of the Drude expectation for the carrier concentration of metals with Fermi surfaces of the volume established by the de Haas-van Alphen experiments.9,10,19 As the temperature is raised, the low-field value of RH drops, below a crossover field that is strongly temperature-dependent, but the high-field derivative remains approximately temperature independent for T < 150 K. At higher temperatures, the high-field regime is not reached within our range of applied magnetic fields. Perhaps surprisingly for a single-band material with such a simple Fermi surface, the low field value of RH is as much as a factor of three smaller than the high field one. The measured magnetoresistance (MR) of PdCoO2 and PtCoO2 is shown in Fig. 4a and b. At all temperatures, the scale of the MR is small, never exceeding 30% at 9 T. The overall scale of the magnetoresistance at 2 K in PdCoO2 is noticeably smaller than that at all temperatures lower than 100 K. This strong additional depression of the MR correlates empirically with the extremely high conductivity of this ultra-pure PdCoO2 sample at 2 K; in samples of lower purity, the effect is much weaker.
The Hall resistivity ρxy for PdCoO2 a and PtCoO2 b at nine temperatures between 2 K and 300 K, offset for clarity. In all cases the field H is applied parallel to the crystallographic c axis, perpendicular to the conducting planes. A pronounced decrease in gradient is seen at low fields, with a characteristic field width that grows rapidly with temperature. This is illustrated in panels c and d, showing color scale plots of dρxy /dH as a function of field and temperature, produced by interpolating numerical derivatives of the data shown in panels a and b. The large decrease in gradient is preceded by a much weaker increase in gradient seen in, for example, the 100 K data for fields between 6 and 9 T in panels a and b, and the black bands in panels c and d
The magnetoresistance of PdCoO2 a and PtCoO2 b at nine temperatures between 2 K and 300 K, expressed in the conventional manner as Δρ/ρ. Voltage noise levels in all cases were 1.5 nV/√Hz in the 10-channel lock-in setup that we were using; the higher noise levels on the 30 K and 2 K data reflect the extremely low resistance of the PdCoO2 sample when its resistivity falls to 10 nΩcm and below. In panels c and d we show the strong violation of Kohler’s rule below 100 K and 150 K in PdCoO2 and PtCoO2, respectively
Discussion
Independent of any specific framework of analysis, the data shown in Figs. 3 and 4 imply several things. Firstly, the transport must be controlled by more than one characteristic microscopic length scale. This can be deduced directly from the Hall effect data. The weak-field Hall coefficient can in principle differ from the high-field one because it is sensitive to details of scattering.23 However, if that scattering has only one characteristic length scale, i.e. the system is controlled by a single mean free path in a Drude picture, the length scale cancels from the expression for the weak-field Hall coefficient and the weak- and strong-field Hall coefficients must both equal 1/ne where e is the electronic charge and n the carrier density. The observation of the crossover in the Hall effect data therefore necessarily implies more than one length scale. Since the crossover field can be associated with a length set by the cyclotron radius rc = ħkF/eB (where ħ is Planck’s constant divided by 2π and kF is the average Fermi wave vector) which decreases with increasing field, the strong temperature-dependent increase of the crossover field implies that at least one of the microscopic length scales decreases rapidly with increasing temperature.
The existence of more than one length scale around the Fermi surface is also consistent with the observation of magnetoresistance, because within the Drude theory of a single-band material with only one microscopic length scale the MR vanishes. If there are two distinct scales, the MR will be non-zero and be related to their difference, while the resistivity in zero field will depend on some weighted average of the two. If the two scales have the same temperature dependence, MR data measured at different temperatures will collapse when plotted as Δρ(B)/ρ(0) against [B/ρ(0)]2. This collapse, often referred to as Kohler’s rule, is obeyed above approximately 150 K in PdCoO2 and PtCoO2, but is violated quite strongly below 150 K, as shown in Fig. 4c and d.
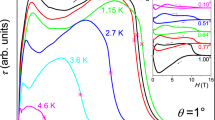
The fact that the low temperature MR data fall below the Kohler-collapsed data implies that the separation of length scales that exists for T > 150 K is becoming smaller. This would be qualitatively expected to reduce the depression of the weak-field Hall coefficient from its high-field Drude value, and this is clearly observed in the data: in Fig. 5a, we show the temperature dependence for T < 150 K of two factors, α(T) = \(\mathop {{\lim }}\limits_{B \to 0} R_H(T)/R_H(2K)\) and β(T) = \(\mathop {{\lim }}\limits_{\frac{B}{\rho } \to 0} \frac{{{\mathrm{\Delta }}\rho /\rho (0)}}{{\left( {B/\rho (0)} \right)^2}}(2K)/\frac{{{\mathrm{\Delta }}\rho /\rho (0)}}{{\left( {B/\rho (0)} \right)^2}}(T)\). The similarity between the trends in α(T) and β(T) is quantitative as well as qualitative, implying that a single temperature-dependent scale controls the weak field MR and Hall effect. The violation of Kohler’s rule in this temperature range further implies that the scale that controls α(T) and β(T) becomes significantly different from the scale that controls ρ(0).
a The factors α (circles) and β (triangles) as defined in the main text for PtCoO2 (orange) and PdCoO2 (purple), respectively. Data for β for PdCoO2 are included for completeness, but are less reliable because the extremely low resistivity at low temperatures leads to larger relative error in its estimation. In panel b we show the results of model calculations (described in Methods) for the ratio r of the weak- to strong-field Hall coefficients predicted for a Fermi surface approximated to a hexagon with rounded corners. Because the weak-field Hall conductivity is dominated by regions of high Fermi surface curvature, whereas the high-field Hall coefficient is independent of Fermi surface topography, the experimentally observed value of r = 0.3 (dotted line) can phenomenologically be accounted for by a factor δ suppressing the mean free path on the Fermi surface corners relative to that on the faces. Depending on the value chosen for the curvature factor η, δ varies between 0.3 and 0.6
The data in Figs. 2–4, combined with Fig. 5a and the deductions made above, represent the main experimental results and model-free conclusions that we report in this paper. We close with a discussion of the extent to which they can be reconciled in a conventional picture of k-dependent scattering.
Accounting for the observations in a conventional Boltzmann framework relies on the fact that the Fermi surfaces of Fig. 1a and b are non-circular. The weak-field Hall coefficient RH ~ σxy/σxx2, where σxy and σxx are the Hall and magnetoresistive conductivities, respectively. In the relaxation time approximation with only standard momentum-relaxing scattering, the length scales referred to in the above discussions are expressed as mean free paths \(\ell\). If there is only one value of \(\ell\), RH is independent of scattering, because \(\sigma _{{\mathrm{xy}}} \sim \ell ^2\) and \(\sigma _{{\mathrm{xx}}} \sim \ell\). However, the elegant geometrical construction of ref. 23 for interpreting the weak-field Hall effect in two-dimensional metals highlights the fact that for Fermi surfaces around which the curvature varies, the high curvature regions dominate σxy while an average around the whole Fermi surface determines σxx. If the mean free path \(\ell _1\) on the high curvature regions is smaller than that \((\ell _0)\) on the low curvature regions, and the curvature changes strongly around the Fermi surface, RH is suppressed from its high field value by a factor proportional to \((\ell _1/\ell _0)^2\). We have constructed an explicit, simplified model of the delafossite Fermi surface as a hexagon with corners of varying curvature, with \(\ell _1 = \delta \ell _0\) on the curved regions, and \(\ell _0\) on the straight ones (see Methods). Using this simple model, it is straightforward to show that for realistic values of curvature, the Hall effect is accounted for with δ ~ 0.3-0.6 (Fig. 5b).
The observation of weak field MR in a material with a single two-dimensional Fermi surface requires, within Boltzmann theory, that \(\ell\) varies around that Fermi surface.24 Some MR is expected, therefore, if \(\ell _0 \ne \ell _1\), with its value being determined by details of the change from \(\ell _0\) to \(\ell _1\) around the Fermi surface. If δ becomes closer to 1 at low temperatures, the weak field Hall coefficient rises and the magnitude of MR is qualitatively expected to fall. The close correlation evident in Fig. 5a would, however, be the result of some fine-tuning, because the MR and Hall effect depend differently on the details of how the variation around the Fermi surface takes place.
Although the above discussion shows that it is possible to construct a model within conventional Boltzmann theory that can capture the main features of our observations, a microscopic justification would be required for at least two of the necessary ingredients of the model. Firstly, it is not clear why there should be a factor of two change in \(\ell\) around two-dimensional Fermi surfaces around which the changes of vF are much smaller, and are oriented differently between PdCoO2 and PtCoO2 (see Fig. 1c). Secondly, it is far from obvious that δ should be so strongly temperature dependent below 150 K, rising from approximately 0.5 at 150 K to 1 by 30 K. More generally, the fact that both the Fermi surface shape and vF variation differ between PdCoO2 and PtCoO2 is in tension with an explanation of their similar magneto-transport properties that essentially makes use of detail. For these reasons, we do not put the above model forward as a definitive explanation of the data, but as a guide to the assumptions required to make a standard Boltzmann analysis consistent with the observations.
In conclusion, we have measured the bulk in-plane Hall effect and MR of the ultrapure metals PdCoO2 and PtCoO2, by performing simultaneous multi-channel low-noise transport measurements on microstructured single crystals. Model-free examination of the data reveals the existence of two microscopic length scales, each with a strong temperature dependence. More detailed analysis in the standard relaxation-time approximation shows that aspects of the data can be reconciled to some degree with conventional theory, but an analysis of this kind is not fully satisfactory. We note that in metals with low rates of momentum relaxing scattering, more exotic contributions beyond standard Boltzmann transport in the relaxation time approximation can also in principle play a role in determining transport properties.25,26,27,28 We hope that our experimental findings motivate further theoretical work on these fascinating two-dimensional metals.
Methods
Device preparation and measurement
Single crystals of PdCoO2 and PtCoO2 were grown in sealed quartz tubes using methods discussed in.19,29 The focused ion beam sculpting of these crystals to well-defined defined device geometries was performed in a dual beam liquid gallium FIB (FEI Helios) using adaptations of methods described in detail in refs 14,30 Electronic band structure calculations were performed using methods described in refs 19,22 with the resulting Fermi velocities averaged across the kz direction of the Brillouin zone to produce the two-dimensional projections summarized in Fig. 1c.
Experimentally, nearly two-dimensional metals with extremely high electrical conductivity are in a fairly unusual regime, and measuring the intrinsic bulk transport properties requires special care. Injection of current through top contacts can result in an inhomogeneous depth distribution of current in the measurement channel; we avoid this by patterning in the long meanders between the current injection point and the channel, confirming with simulations and multi-contact measurements that homogeneous in-channel currents have been achieved. To probe the ohmic rather than the ballistic regime both the width of the sample and the spacing between voltage contacts should be as large as possible. To ensure that the magnetotransport data are a good approximation to the bulk limit, even when the mean free path is as large as 20 μm, large channel widths (155 μm and 190 μm for PdCoO2 and PtCoO2, respectively) and longitudinal voltage contact separation (204 μm and 244 μm or PdCoO2 and PtCoO2 respectively) were used. However, for as-grown crystals of PdCoO2 with a typical thickness 10-20 μm, wide crystals have very low resistance at low temperatures, so good voltage resolution is required. Another issue is the relative scale of resistance and Hall resistance. In most metals in standard configurations for transport measurements, the resistance is much larger than the Hall resistance for magnetic fields B in the range −10 T < B < 10 T, but in these delafossites the situation is reversed, and even tiny thickness variations can lead to a pronounced odd-in-field contribution to the magnetoresistance. Surprisingly, an apparent odd contribution to magnetoresistance does not violate Onsager’s relations in exotic cases for which transport is non-local,31 so differentiating between this possibility and effects caused by non-ideal crystal shapes requires precise sample preparation and geometrical characterization. For that reason we performed the measurements described here on crystals carefully selected for uniform thickness, and sculpted to well-defined geometries using focused ion beam milling. Measuring thickness across large samples is not always easy, so all measurements were made in multi-contact configurations to check for consistency. To avoid this becoming prohibitively time-consuming we designed a bespoke probe and readout system featuring a Synktek 10 channel lock-in amplifier, and studied all relevant configurations simultaneously with a voltage noise level of 1.5 nVHz-1/2 using standard a.c. methods at a measurement frequency of 73.3 Hz for PdCoO2 and 177.7 for PtCoO2 and current of 1 mA. Fine temperature control and all readout was achieved with this home-built system; field and coarse temperature control were obtained by mounting the measurement probe in a 9 T Quantum Design Physical Property Measurement System.
Modeling the low-field Hall slope
The ratio of the low field Hall slope to the high field Hall slope is given by
where \({\mathrm{\Gamma }} = \frac{{4\pi A}}{{S^2}}\), A is the area enclosed by the Fermi surface, S is the perimeter of the Fermi surface, A, is the area enclosed by the “\(\ell\)-surface” (see23), and \(\ell _{{\mathrm{av}}}\) is the average
mean free path:
where p is a parametrization of the Fermi surface and \(\ell (p)\) is the mean free path at point p.
We consider a rounded hexagon for the Fermi surface, with side c and radius of curvature R (Fig. 6). This leads to
We use a simple model for a momentum-dependent mean free path:
on flat edges and \(\ell ({\bf{k}}) = \ell _1 = \delta \ell _0\) on rounded corners
This leads to
and
Combining everything, we find the ratio of the low field Hall slope to the high field Hall slope to be
where η=R/c.
References
Hartnoll, S. A. Theory of universal incoherent metallic transport. Nat. Phys. 11, 54–61 (2015).
Stormer, H. et al. Fractional quantization of the Hall-effect. Phys. Rev. Lett. 50, 1953–1956 (1983).
Molenkamp, L. W. & de Jong, M. J. M. Electron-electron-scattering-induced size effects in a two-dimensional wire. Phys. Rev. B. 49, 5038–5041 (1994).
Novoselov, K. S. et al. Room-temperature quantum hall effect in graphene. Science 315, 1379–1379 (2007).
Collaudin, A., Fauque, B., Fuseya, Y., Kang, W. & Behnia, K. Angle dependence of the orbital magnetoresistance in Bismuth. Phys. Rev. X. 5, 021022 (2015).
Liang, T. et al. Ultrahigh mobility and giant magnetoresistance in the Dirac semimetal Cd3As2. Nat. Mater. 14, 280–284 (2015).
Shekhar, C. et al. Extremely large magnetoresistance and ultrahigh mobility in the topological Weyl semimetal candidate NbP. Nat. Phys. 11, 645–649 (2015).
Kumar, N. et al. Extremely high magnetoresistance and conductivity in the type-II Weyl semimetals WP2 and MoP2. Nat. Commun. 8, 1642 (2017).
Mackenzie, A. P. The properties of ultrapure delafossite metals. Rep. Prog. Phys. 80, 032501 (2017).
Hicks, C. W. et al. Quantum oscillations and high carrier mobility in the delafossite PdCoO2. Phys. Rev. Lett. 109, 116401 (2012).
Daou, R., Frésard, R., Hébert, S. & Maignan, A. Large anisotropic thermal conductivity of the intrinsically two-dimensional metallic oxide PdCoO2. Phys. Rev. B 91, 041113 (2015).
Takatsu, H. et al. Extremely large magnetoresistance in the nonmagnetic metal PdCoO2. Phys. Rev. Lett. 111, 056601 (2013).
Kikugawa, N. et al. Interplanar coupling-dependent magnetoresistivity in high-purity layered metals. Nat. Commun. 7, 10903 (2016).
Moll, P. J. W., Kushwaha, P., Nandi, N., Schmidt, B. & Mackenzie, A. P. Evidence for hydrodynamic electron flow in PdCoO2. Science 351, 1061–1064 (2016).
Alekseev, P. S. Negative magnetoresistance in viscous flow of two-dimensional electrons. Phys. Rev. Lett. 117, 166601 (2016).
Scaffidi, T., Nandi, N., Schmidt, B., Mackenzie, A. P. & Moore, J. E. Hydrodynamic electron flow and Hall viscosity. Phys. Rev. Lett. 118, 226601 (2017).
Eyert, V., Frésard, R. & Maignan, A. On the metallic conductivity of the delafossites PdCoO2 and PtCoO2. Chem. Mater. 20, 2370–2373 (2008).
Kim, K., Choi, H. C. & Min, B. I. Fermi surface and surface electronic structure of delafossite PdCoO2. Phys. Rev. B 80, 035116 (2009).
Kushwaha, P. et al. Nearly free electrons in a 5d delafossite oxide metal. Sci. Adv. 1, e1500692 (2015).
Ong, K. P., Singh, D. J. & Wu, P. Unusual transport and strongly anisotropic thermopower in PtCoO2 and PdCoO2. Phys. Rev. Lett. 104, 176601 (2010).
Ong, K. P., Zhang, J., Tse, J. S. & Wu, P. Origin of anisotropy and metallic behavior in delafossite PdCoO2. Phys. Rev. B 81, 115120 (2010).
Arnold, F. et al. Quasi-two-dimensional Fermi surface topography of the delafossite PdRhO2. Phys. Rev. B 96, 075163 (2017).
Ong, N. P. Geometric interpretation of the weak-field Hall conductivity in two-dimensional metals with arbitrary Fermi surface. Phys. Rev. B 43, 193–201 (1991).
Harris, J. et al. Violation of Kohler's rule in the normal-state magnetoresistance of YBa2Cu3O7-δ and La2SrxCuO4. Phys. Rev. Lett. 75, 1391–1394 (1995).
Hruska, M. & Spivak, B. Conductivity of the classical two-dimensional electron gas. Phys. Rev. B 65, 033315 (2002).
Lucas, A. & Sachdev, S. Memory matrix theory of magnetotransport in strange metals. Phys. Rev. B 91, 195122 (2015).
Lucas, A. & Hartnoll, S. A. Kinetic theory of transport for inhomogeneous electron fluids. Preprint at ArXiv http://arxiv.org/abs/1706.04621 (2017).
Hartnoll, S. A., Lucas, A., Sachdev, S. Holographic quantum matter. Preprint at ArXiv:161207324 (2016).
Kushwaha, P. et al. Single crystal growth, structure, and electronic properties of metallic delafossite PdRhO2. Cryst. Growth Des. 17, 4144–4150 (2017).
Moll, P. J. W. Focused ion beam microstructuring of quantum matter. Annu. Rev. Condens. Matter Phys. 9, 147–162 (2018).
Buttiker, M. Symmetry of electrical-conduction. Ibm J. Res. Dev. 32, 317–334 (1988).
Acknowledgements
We gratefully acknowledge the technical assistance of S. Seifert, and interesting discussions with P. Surowka, P. Witkowski and R. Moessner. We acknowledge the support of the Max Planck Society, support from the European Research Council (through the QUESTDO project), and the Engineering and Physical Sciences Research Council, UK (grant no. EP/I031014/1). T.S. acknowledges support from the Emergent Phenomena in Quantum Systems initiative of the Gordon and Betty Moore Foundation, V.S. thanks EPSRC for PhD studentship support through grant number EP/L015110/1 and J.E.M acknowledges the support of NSF DMR-1507141.
Author information
Authors and Affiliations
Contributions
N.N. performed the microstructuring and magneto-transport measurements, with help from M.E.B., P.J.W.M., and M.K. P.K. and S.K. grew the single crystals, and V.S, F.M., and P.D.C.K. performed the photoemission experiments. H.R. carried out electronic structure calculations, T.S. performed Hall effect modeling within Boltzmann transport theory, and T.S., S.A.H., and J.E.M. contributed to data interpretation. A.P.M. led the overall project and the drafting of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nandi, N., Scaffidi, T., Kushwaha, P. et al. Unconventional magneto-transport in ultrapure PdCoO2 and PtCoO2. npj Quant Mater 3, 66 (2018). https://doi.org/10.1038/s41535-018-0138-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-018-0138-8
This article is cited by
-
Crystal-chemical origins of the ultrahigh conductivity of metallic delafossites
Nature Communications (2024)
-
Interaction of in-plane Drude carrier with c-axis phonon in PdCoO2
npj Quantum Materials (2023)
-
Directional ballistic transport in the two-dimensional metal PdCoO2
Nature Physics (2022)
-
Hydrodynamic approach to two-dimensional electron systems
La Rivista del Nuovo Cimento (2022)
-
Evidence of a coupled electron-phonon liquid in NbGe2
Nature Communications (2021)