Abstract
Topological superconductivity with Majorana bound states, which are critical to implement nonabelian quantum computation, may be realized in three-dimensional semimetals with nontrivial topological feature, when superconducting transition occurs in the bulk. Here, we report pressure-induced superconductivity in a transition-metal dipnictide NbAs2. The emergence of superconductivity is not accompanied by any structural phase transition up to the maximum experimental pressure of 29.8 GPa, as supported by pressure-dependent synchrotron X-ray diffraction and Raman spectroscopy. Intriguingly, the Raman study reveals rapid phonon mode hardening and broadening above 10 GPa, in coincident with the superconducting transition. Using first-principle calculations, we determine Fermi surface change induced by pressure, which steadily increases the density of states without breaking the electron–hole compensation. Noticeably, the main hole pocket of NbAs2 encloses one time-reversal-invariant momenta of the monoclinic lattice, suggesting NbAs2 as a candidate of topological superconductors.
Similar content being viewed by others
Introduction
There have been various proposals in search of quasiparticle excitations of Majorana fermions (MFs) in solids, which are the subject of both fundamental research and error-tolerant topological quantum computing.1,2 Superconductor–topological insulator (TI) heterostructures turn the surface Dirac fermions of topological insulators (TIs) into p-wave-like Cooper pairs.3 Majorana zero modes by this superconducting proximity approach have been observed in vortices by scanning tunneling microscopy in Bi2Te3/NbSe2 heterostructures.4,5 Superconducting proximity effects may also create MFs in semiconducting nanowires with strong spin–orbital coupling,6,7 or in ferromagnetic atomic chains.8 Alternatively, chiral Majorana edge states are expected in two-dimensional (2D) chiral topological superconductors, consisting of a topological insulator in proximity to an s-wave superconductor.9,10,11,12 It is intriguing that superconducting phase transitions are widely observed in many topological materials when high pressure is applied, such as type II Weyl semimetals of MoTe213 and WTe2,14,15 Dirac semimetals of Cd3As216 and ZrTe5,17 and topological insulators of Bi2Se3,18 Bi2Te3,19 and Sb2Te3.20 Recently tip-induced superconductivity (SC) has attracted much attention because it could offer a new platform to study topological SC (TSC) in Dirac21 and Weyl semimetals.22 Charge carrier doping is the another effective method to induce TSC in topological insulators such as in CuxBi2Se323 and SrxBi2Se3.24 The experimental observations strongly suggest the feasibility to realize TSC25,26 in novel topological materials with nontrivial topological features. However, before the emergence of SC, most of these topological compounds undergo structural phase transitions, which usually change the topological states.
Very recently, transition-metal dipnictides of the MPn2 family,27,28,29,30,31,32,33 where M represents Mo, Nb, or Ta atom, and Pn is As or Sb atom, respectively, generate a wide interest as a new prototype of topological semimetals with extremely large magnetoresistance (XMR). When spin–orbital coupling is included, the band anticrossing in MPn2 between the M-dxy and \(M - d_{x^2 - y^2}\) orbitals along the I–L–I′ direction are fully gapped,34 resulting in weak topological insulator invariants of \({\Bbb Z}_2 = [0;111]\).28,31,35 Another interesting point in the MPn2 family is that magnetic field could induce Weyl points.36 With its monoclinic lattice (Space group No. 12), which is normally stable under very high pressure,16,17 it is tempting to study the physical properties of MPn2 under high pressure.
In this work, we report pressure-dependent transport measurement and structure evolution in NbAs2, using the diamond-anvil-cell (DAC) technique to continuously tune the electronic structure. Superconducting transition has been successfully observed at 12.8 GPa with a critical temperature (Tc) of 2.63 K. Further increase in pressure gradually suppresses Tc, which disappears completely at 27.9 GPa when bad metal (BM) behavior dominates below the helium temperature. Using high-pressure X-ray diffraction (XRD) and Raman scattering, we confirm that there is no structural phase transition up to the maximum experimental pressure of 29.8 GPa, which implies that the topological state maybe remain undisturbed under high pressure. Intriguingly, the electron-hole compensation in NbAs2 changes little even in the superconducting region, as suggested by first-principle calculations, although the electron–hole compensation under pressure is not so perfect. Instead, the dwindling of XMR and the emergence of SC are characterized by continuous Fermi surface change and gradual growth in density of state. Our results thus indicate the coexistence of XMR and SC. The growing density of states is usually beneficial to the occurrence of SC. Moreover, the Cooper pair formation in NbAs2 may also be correlated to the enhanced electron–phonon coupling under high pressure, since the Raman studies reveal significant phonon mode hardening and broadening above 10 GPa. It is noteworthy that, in the SC region, the main hole pocket of NbAs2 encloses the time-reversal-invariant (TRI) momenta M. These suggest NbAs2 as a candidate of TRI topological superconductors.
Results and discussion
Pressure-dependent structure analysis
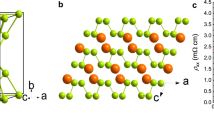
The structure evolution of NbAs2 under pressure is determined by synchrotron radiation-based high-pressure XRD and Raman spectroscopy, as shown in Fig. 1. The XRD data are refined using the Rietveld method, and the Bragg peaks are well indexed by the space group C2/m for both the 0.6 and 25.3 GPa data (See Supplementary Fig. S1). Within 30 GPa, the pressure-induced lattice changes are reversible. In Fig. 1a, we show the XRD results of NbAs2 when the DAC is slowly decompressed from 29.8 to 0.3 GPa. The data are essentially identical to the bottom curve of 0.6 GPa. In Fig. 1b, the high pressure dependent unit-cell volumes can be fitted by the third-order Birch–Murnaghan equation of state,37 and no distinct drop of the unit-cell volume is observed with the increase of pressure, which suggests stability of this structure. The monoclinic lattice is also manifested in pressure-dependent Raman scattering measurements, showing six fingerprinting peaks between 180 and 350 cm−1, namely A2g, A3g, B3g, A4g, A5g, and A6g, respectively (see Fig. 1c). It is intriguing that Raman spectroscopy shows distinctive enhancement of A2g, A3g, B3g, A4g, and A5g above 10 GPa, when the data are normalized by the A2g peak intensity. The distinct broadening in A2g, A4g and A5g, which could be an indication of stronger electron–phonon coupling or pressure-enhanced defect scattering,38 is also discernable above 10 GPa.
High pressure structure of NbAs2. a X-ray diffraction patterns of NbAs2 at various pressures display no structural phase transition. b Unit-cell volume decreases with increasing pressure, while the volume diminishes by 13% at 25.3 GPa. c The Raman shifts at various pressures show the hardening and broadening of Raman scattering peaks
Resistivity measurements
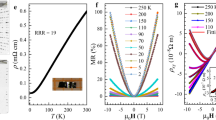
Figure 2a, b summarize the resistance vs. temperature (R–T) characteristics of NbAs2 at various pressures from 0.5 to 27.9 GPa. Below 9.8 GPa, NbAs2 shows typical metallic behavior, which is characterized by monotonic increase in resistance with increasing temperature, and exhibits a lower residual-resistivity-ratio with enhancement of pressure. The trend is reversed at 9.8 GPa, when the whole R–T curve is upshifted by \(\sim 0.03{\kern 1pt} {\mathrm{\Omega }}\) compared to 6.1 GPa. SC with a transition temperature of 2.63 K emerges at 12.8 GPa, but the resistance does not drop to zero even at 1.8 K (Fig. 2a). Further increase in pressure surprisingly starts to suppress Tc, although the SC transition becomes sharper, and zero-resistance behavior is observed at 16 GPa. Noticeably, the zero-resistance transition is accompanied by a positive resistance kink, which is very sharp and only extends within a temperature range of 0.2 K. Subsequently, the superconducting transition is gradually suppressed when the positive resistance kink becomes broader and its onset shifts to lower T. Above 23 GPa, the positive-resistance kink completely dominates.
Pressure-induced superconductivity in single-crystal NbAs2. a Temperature-dependent resistance is measured from 0.5 to 14.6 GPa and superconducting transition appears at 12.8 GPa. The enlarged view of low temperature resistance is shown in the inset. b The resistance as a function of temperature at different pressures between 16 and 27.9 GPa is displayed with a enlarged plot around the superconducting transition in the inset. c Magnetoresistance (MR = (R(8T) − R(0T))/R(0T)) at 4.5 K is suppressed slowly as pressure increases from 0.5 to 14.6 GPa. The MR at 12.8 GPa and 8T is nearly 22%, which is still very large. d Average mobility \(\bar \mu\) obtained by fitting to the formula \({\mathrm{MR}} = (\bar \mu B)^{1.43}\) decreases monotonously with increasing pressure
In previous studies, the emergence of SC is generally accompanied with a suppression of the XMR effect in topological semimetals.14,15,39 There are different interpretations in the XMR suppression mechanism. Cai et al.39 suggest that pressure weakens the electron–hole compensation in WTe2 by gradually decreasing the hole carrier population. In situ pressure-dependent Hall measurements by Kang et al.14 indeed observe the change from a positive sign to negative sign in the Hall coefficients, suggesting increasing population of the electron carriers and decreasing hole carriers density. Moreover, Pan et al. report that the SC transition is induced by rapid increase in the density of states at the Fermi surface, as a result of the compression of the unit cell,15 while the difference between hole pockets and electron pockets is enhanced with applied pressure.
NbAs2 is a well compensated semimetal at ambient pressure.28 When high pressure is applied, XMR at 8 T is effectively suppressed from 5.16 at 0.5 GPa to 0.08 at 14.6 GPa, as shown in Fig. 2c. The dwindling of XMR as a function of pressure can be explained well by pressure-induced decrease in the average mobility \(\bar \mu\),40 using the power-law relation of \({\mathrm{MR}} = (\bar \mu B)^l\). Using logarithmic scale (see the inset of Fig. 2c), it is clear that the XMR curves at different pressures have nearly the same linear slope (l = 1.43), which is a simple measure of the electron–hole compensation accuracy,34 and the electron–hole compensation here is not so perfect. By fitting the experimental data to the aforementioned equation, we found that \(\bar \mu\) decreases quasi-linearly as a function of pressure, and only shows a slight upward curvature as entering the SC region above 10 GPa (see Fig. 2d). Our results thus imply that a distinct phase boundary does not exist between SC and XMR, and the mechanism of SC in NbAs2 may be different compared to other topological semimetals.14
The positive resistance kinks, which become broader and shift to lower temperature as a function of pressure (P), may be rooted in different mechanisms, such as superconductor to metal transition in disordered system,41 a probable foreshadow of p-wave SC in superconductor–ferromagnet nanowires structure,42 or highly anisotropic superconducting gap,43 but should not be the same as the semiconductor-like behavior in LaO0.5F0.5BiSe2.44 When external magnetic field (B) is applied, Tc monotonically shifts to lower temperatures and the positive resistance kinks gradually become predominant. As shown in Fig. 3a, it is surprising that the superconducting transition at 16 GPa is completely suppressed at 1000 Oe. This may be due to the predominant resistivity upturn, which pushes Tc to below 1.8 K. Nevertheless, with the available experimental data, we can define an empirical critical \(T_{\mathrm{c}}^{90\% }\) by those points at which R is 90% of the normal state, as seen in the inset of Fig. 3b. In Fig. 3b, the deduced \(T_{\mathrm{c}}^{90\% }\) can be well fitted by the Werthamer–Helfand–Hohenberg (WHH) model,45 which yields the orbital-limited upper critical field in dirty-limited system by \(H_{c2}^{orb}(0) \simeq \left. { - 0.69{\kern 1pt} T_c \times dH_{c2}/dT} \right|_{T = T_{\mathrm{c}}} = 2288\) Oe.
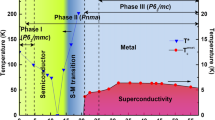
Determination of upper critical field for superconductivity and temperature-pressure phase diagram of NbAs2. a Temperature-dependent resistance at different magnetic fields is measured at 16 GPa. b Hc2 as a function of temperature and its WHH fitting are displayed. The inset shows the definition of different superconducting transition temperatures and transition temperature of bad metal. c Resistance at 4.5, 100, 200, and 300 K in the normal state at different pressures shows the peak near 12.8 GPa where superconducting transition emerges. d Calculated density of states of NbAs2 at the Fermi level vs. pressure. The squares are the density of states as a function of pressure, and the red line indicates the tendency of density of state under the pressure. e Tc is plotted against pressure as well as evolution of MR, and superconductivity appears at 12.8 GPa following the suppression of XMR with increasing pressure. The BM transition appears after 16 GPa. The regions of XRM, SC, and BM in the phase diagram are marked by blue, magenta, and green colors, respectively
Interestingly, by plotting the pressure-dependent R at different T (4.5, 100, 200, and 300 K, respectively) in Fig. 3c, we are able to clearly see an anomaly at 12.8 GPa, which corresponds to the emergence of SC. However, there is no structural phase transition up to 29.8 GPa, so the origin of this behavior needs further investigation. By including the characteristic parameters of XMR, \({T}_{\mathrm{c}}^{90\% }\) as a function of pressure, we can draw the P–T phase diagram for NbAs2. As summarized in Fig. 3e, high pressure suppresses the XMR effect (the blue region) by reducing the average mobility \(\bar \mu\). The emergence of SC may be related to the enhancement of density of states,15,46 and calculated density of states increase as a function of pressure, as seen in Fig. 3d. Moveover, there is a significant overlap between the XMR (the blue region) and SC region (the magenta region) when SC emerges at 12.8 GPa. Such a coexistence of XMR and SC is in contrast to the other cases like WTe2 where XMR is significantly suppressed as entering the SC state under high pressure.14 Above 16 GPa, there is a probable phase competition between SC and the BM transition (the green region), which maybe lead to the vanishing of Tc at 27.9 GPa.
Electronic structures under pressure
To get insights into the aforementioned experimental results, we have studied the pressure-dependent electronic structure of NbAs2 using density–functional theory (DFT) calculations, which adopt the experimental lattice parameters determined by XRD. Figure 4 displays the DFT calculations at ambient pressure, 15.6, and 22.7 GPa, respectively. In excellent agreement with the XMR measurements, the DFT results confirm that pressure simultaneously increases electron and hole populations in NbAs2, which is displayed in Fig. 4d–f where the electron pockets (magenta) and hole pockets (blue) all enlarge with increasing pressure. This is not surprising since the monoclinic lattice is retained under high pressure. Equally important, the steady growth in charge carrier does not show any anomaly, neither in density of states in Fig. 3d nor in Fermi surface topology, in the vicinity of 12.8 GPa when SC starts to emerge. According to the proposed theory by Fu et al.,26 time-reversal-invariant topological SC in a centrosymmetry system requires odd-parity spin pairing and an Fermi surface enclosing an odd number of TRIM points. Although the pairing symmetry is not explicitly known, the latter condition is well satisfied in NbAs2. As shown in Fig. 4, the main hole pocket of NbAs2 enlarges under pressure, centering the TRIM point of M. In addition, the electronic specific-heat coefficient of γ = 0.45 mJ/mol/K2 is observed from the specific heat measurements (see Fig. S3 in Supplementary Materials), suggesting weak electronic correlation in NbAs2 at ambient pressure. With increasing pressure, the sudden hardening and broadening phonon modes may start to play a critical role in the emergence of SC, and the phonon-mediated pairing maybe have an odd-parity symmetry in NbAs2 if there is a singular behavior of the electron–phonon interaction at long wavelength.47,48 In addition, no structural transition is observed as entering the superconducting states with increasing pressure and thus the topological surface state should remain undisturbed at high pressure, which suggests the possibility of topologically superconducting surface states in NbAs2 because of superconducting proximity effect.3 Therefore, NbAs2 with time-reversal and inversion symmetries may be a candidate for topological superconductor. It is necessary to be checked by further experiments.
Pressure-dependent band structures of NbAs2, showing increasing electron and hole pockets. a–c Band structures in NbAs2 are shown at ambient pressure, 15.6 and 22.7 GPa, respectively. The red points are TRIM points. d–f 3D Fermi surface diagram at ambient pressure, 15.6 and 22.7 GPa indicates that the TRIM (M) is enclosed by the hole-type Fermi surface (the magenta pockets), and blue pockets are electron-type Fermi surface. TRIM points are marked in the Fig. 4d
In summary, we study the high pressure-induced SC in topological semimetal NbAs2, which shows a superconducting transition temperature of 2.63 K at 12.8 GPa. Unlike previously reported topological semimetals, no structural phase transition occurs near the superconducting region, which is supported both by the high-pressure synchrotron XRD and Raman data. Raman spectroscopy, resistance and specific heat data all suggest the critical importance of electron-phonon interactions on the SC pairing in NbAs2, which may be a candidate of time-reversal-invariant topological superconductor with odd spin paring parity. Strikingly, the SC phase emerges with a nearly invariable electron-hole compensation and shows no anomaly in the density of states in the vicinity of the critical pressure of 12.8 GPa. Our results illustrate that high-pressure induced SC may be more complex in physical origins than the prevailing explanations, and the monoclinic family of MPn2 may provide a platform to test various theoretical proposals and to search for topological SC.
Methods
Samples and experimental technique
Single crystals of NbAs2 were grown by means of a vapor transport technique.28 High pressure was generated by a screw-pressure-type DAC consisting of nonmagnetic Cu–Be alloy and two diamonds with the culet of 300μm diameter. A T301 stainless-steel gasket with a 280 μm diameter hole was used for different runs of high-pressure resistance measurement by the standard four-probe method. The single crystal was placed in the hole and a mixture of fine cubic boron nitride powder with epoxy was compressed firmly to insulate the electrodes from the gasket. Pressure medium was daphne 7373 oil and some ruby powder was applied to demarcate the pressure by the ruby fluorescence method at room temperature. High-pressure synchrotron powder XRD (λ = 0.4246 Å) was performed at room temperature at the beamline 16 BM-D,49 High Pressure Collaborative Access Team (HPCAT).
DFT calculations
The electron structure calculations were performed with the Vienna ab initio simulation package50,51 by the method of the projector augmented wave52 and the generalized gradient approximation53 in order to introduce the exchange-correlation potential. Spin–orbit coupling has been included using the second variation perturbation method.54 In addition, the plane-wave cutoff energy is setting about 500 eV and 21 × 21 × 13 k-points sampling is performed based on the Monkhorst-Pack scheme.55 The total energy is ensured to be converged within 10−6 eV. We use the structure parameters of high-pressure synchrotron XRD to relax the structure with the tolerance of 0.01 eV/Å s
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Das Sarma, S. Non-abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008).
Wilczek, F. Majorana returns. Nat. Phys. 5, 614–618 (2009).
Fu, L. & Kane, C. L. Superconducting proximity effect and Majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 100, 096407 (2008).
Xu, J. P. et al. Experimental detection of a Majorana mode in the core of a magnetic vortex inside a topological insulator-superconductor Bi2Te3/NbSe2 heterostructure. Phys. Rev. Lett. 114, 017001 (2015).
Sun, H. H. et al. Majorana zero mode detected with spin selective andreev reflection in the vortex of a topological superconductor. Phys. Rev. Lett. 116, 257003 (2016).
Sau, J. D., Lutchyn, R. M., Tewari, S. & Sarma, S. D. Generic new platform for topological quantum computation using semiconductor heterostructures. Phys. Rev. Lett. 104, 040502 (2010).
Lutchyn, R. M., Sau, J. D. & Sarma, S. D. Majorana fermions and a topological phase transition in semiconductor–superconductor heterostructures. Phys. Rev. Lett. 105, 077001 (2010).
Nadj-Perge, S. et al. Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor. Science 346, 602–607 (2014).
Qi, X. L., Hughes, T. L. & Zhang, S. C. Chiral topological superconductor from the quantum Hall state. Phys. Rev. B 82, 184516 (2010).
Chung, S. B., Qi, X. L., Maciejko, J. & Zhang, S. C. Conductance and noise signatures of Majorana backscattering. Phys. Rev. B 83, 100512(R) (2011).
Wang, J., Zhou, Q., Lian, B. & Zhang, S. C. Chiral topological superconductor and half-integer conductance plateau from quantum anomalous Hall plateau transition. Phys. Rev. B 92, 064520 (2015).
He, Q. L. et al. Chiral Majorana fermion modes in a quantum anomalous Hall insulator–superconductor structure. Science 357, 294–299 (2017).
Qi, Y. et al. Superconductivity in Weyl semimetal candidate MoTe2. Nat. Commun. 7, 11038 (2015).
Kang, D. et al. Superconductivity emerging from a suppressed large magnetoresistant state in tungsten ditelluride. Nat. Commun. 6, 7804 (2015).
Pan, X. C. et al. Pressure-driven dome-shaped superconductivity and electronic structural evolution in tungsten ditelluride. Nat. Commun. 6, 7805 (2015).
He, L. P. et al. Pressure-induced superconductivity in the three-dimensional dirac semimetal Cd3As2. NPJ Quantum Mater. 1, 16014 (2016).
Zhou, Y. H. et al. Pressure-induced superconductivity in a three-dimensional topological material ZrTe5. Proc. Natl Acad. Sci. USA 113, 2904–2909 (2016).
Kirshenbaum, K. et al. Pressure-induced unconventional superconducting phase in the topological insulator Bi2Se3. Phys. Rev. Lett. 111, 087001 (2013).
Zhang, J. L. et al. Pressure-induced superconductivity in topological parent compound Bi2Te3. Proc. Natl Acad. Sci. USA 108, 24–28 (2011).
Zhu, J. et al. Superconductivity in topological insulator Sb2Te3 induced by pressure. Sci. Rep. 3, 2016 (2013).
Wang, H. et al. Observation of superconductivity induced by a point contact on 3D Dirac semimetal Cd3As2 crystals. Nat. Mater. 15, 38 (2016).
Wang, H. et al. Discovery of tip induced unconventional superconductivity on Weyl semimetal. Sci. Bull. 62, 425–430 (2017).
Hor, Y. S. et al. Superconductivity in CuxBi2Se3 and its implications for pairing in the undoped topological insulator. Phys. Rev. Lett. 104, 057001 (2010).
Shruti, Maurya, Neha, V. K., Srivastava, P. & Patnaik, S. Superconductivity by Sr intercalation in the layered topological insulator Bi2Se3. Phys. Rev. B 92, 020506 (2015).
Qi, X. L., Hughes, T. L., Raghu, S. & Zhang, S. C. Time-reversal-invariant topological superconductors and superfluids in two and three dimensions. Phys. Rev. Lett. 102, 187001 (2009).
Fu, L. & Berg, E. Odd-parity topological superconductors: Theory and application to CuxBi2Se3. Phys. Rev. Lett. 105, 097001 (2010).
Li, Y. K. et al. Resistivity plateau and negative magnetoresistance in the topological semimetal TaSb2. Phys. Rev. B 94, 121115(R) (2016).
Li, Y. P. et al. Negative magnetoresistance in topological semimetals of transition-metal dipnictides with nontrivial Z 2 indices. arXiv:1603.04056 (2016).
Shen, B., Deng, X. Y., Kotliar, G. & Ni, N. Fermi surface topology and negative longitudinal magnetoresistance observed in the semimetal NbAs2. Phys. Rev. B 93, 195119 (2016).
Wu, D. S. et al. Giant semiclassical magnetoresistance in high mobility TaAs2 semimetal. Appl. Phys. Lett. 108, 042105 (2016).
Luo, Y. K. et al. Anomalous electronic structure and magnetoresistance in TaAs2. Sci. Rep. 6, 27294 (2016).
Yuan, Z. J., Lu, H., Liu, Y. J., Wang, J. F. & Jia, S. Large magnetoresistance in compensated semimetals TaAs2 and NbAs2. Phys. Rev. B 93, 184405 (2016).
Wang, Y. Y., Yu, Q. H., Guo, P. J., Liu, K. & Xia, T. L. Resistivity plateau and extremely large magnetoresistance in NbAs2 and TaAs2. Phys. Rev. B 94, 041103 (2016).
Wang, Z. et al. Topological phase transition induced extreme magnetoresistance in TaSb2. arXiv:1603.01717 (2016).
Xu, C. C. et al. Electronic structures of transition metal dipnictides XPn2 (X = Ta, Nb; Pn = P, As, Sb). Phys. Rev. B 93, 195106 (2016).
Gresch, D., Wu, Q., Winkler, G. W. & Soluyanov, A. A. Hidden Weyl points in centrosymmetric paramagnetic metals. New J. Phys. 19, 035001 (2017).
Birch, F. Finite elastic strain of cubic crystals. Phys. Rev. 71, 809–824 (1947).
Jin, F. et al. Raman scattering study of large magnetoresistance semimetals TaAs2 and NbAs2. Phys. Rev. B 94, 094302 (2016).
Cai, P. L. et al. Drastic pressure effect on the extremely large magnetoresistance in WTe2: quantum oscillation study. Phys. Rev. Lett. 115, 057202 (2015).
Zhu, Z. W. et al. Quantum oscillations, thermoelectric coefficients, and the Fermi surface of semimetallic WTe2. Phys. Rev. Lett. 114, 176601 (2015).
Xing, Y. et al. Quantum griffiths singularity of superconductor-metal transition in Ga thin films. Science 350, 542–545 (2015).
Wang, J. et al. Interplay between superconductivity and ferromagnetism in crystalline nanowires. Nat. Phys. 6, 389–394 (2010).
Du, G. et al. Superconductivity with two-fold symmetry in topological superconductor SrxBi2Se3. Sci. China Phys. Mech. Astron. 60, 037411 (2017).
Liu, J. Z., Li, S., Li, Y. F., Zhu, X. Y. & Wen, H. H. Pressure-tuned enhancement of superconductivity and change of ground state properties in LaO0.5F0.5BiSe2 single crystals. Phys. Rev. B 90, 094507 (2014).
Werthamer, N. R., Helfand, E. & Hohenberg, P. C. Temperature and purity dependence of the superconducting critical field, H c2. III. electron spin and spin–orbit effects. Phys. Rev. 147, 295–302 (1966).
Ueno, K. et al. Discovery of superconductivity in KTaO3 by electrostatic carrier doping. Nat. Nanotechnol. 6, 408–412 (2011).
Wan, X. G. & Savrasov, S. Y. Turning a band insulator into an exotic superconductor. Nat. Commun. 5, 4144 (2014).
Brydon, P. M. R., Das Sarma, S., Hui, H. Y. & Sau, J. D. Odd-parity superconductivity from phonon-mediated pairing: application to CuxBi2Se3. Phys. Rev. B 90, 184512 (2014).
Park, C. Y. et al. New developments in micro-X-ray diffraction and X-ray absorption spectroscopy for high-pressure research at 16-BM-D at the advanced photon source. Rev. Sci. Instrum. 86, 072205 (2015).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Koelling, D. D. & Harmon, B. N. A technique for relativistic spin-polarised calculations. J. Phys. C 10, 3107–3114 (1977).
Monkhorst, H. J. & Pack, J. D. Special points for brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976).
Acknowledgments
This work was supported by the National Key R&D Program of China (Grant nos. 2016YFA0300204, 2016YFA0300402, and 2017YFA0303002), the National Basic Research Program of China (Grant no. 2014CB921203), and the National Science Foundation of China (Grant nos. U1332209, 11574264, and 11774305). Y.Z. acknowledges the start funding support from the Thousand Talents Plan. The X-ray work was performed at HPCAT (Sector 16), Advanced Photon Source, Argonne National Laboratory. HPCAT operations are supported by DOE-NNSA under Award No. DE-NA0001974 and DOE-BES under Award No. DE-FG02-99ER45775, with partial instrumentation funding by NSF. The Advanced Photon Source is a US Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357.
Author information
Authors and Affiliations
Contributions
Y.P. Li synthesized and characterized the single crystals. C. An, Y.H. Zhou, and Z.R. Yang conducted the high-pressure transport measurements. Y. Zhou, C. An, and R.R. Zhang carried out the Raman experiments, X.L. Chen and C.Y. Park performed the high-pressure synchrotron X-ray diffraction experiments. C.Q. Hua and Y.H. Lu did the DFT calculations. Y.P. Li, C.Q. Hua, Y.H. Lu, Z.R. Yang, Y. Zheng, and Z.A. Xu wrote the paper. All the authors analyzed the data and discussed the results. Y.P. Li, C. An, and C.Q. Hua were co-first authors to this work. Z.R. Yang and Z.A. Xu co-supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, Y., An, C., Hua, C. et al. Pressure-induced superconductivity in topological semimetal NbAs2. npj Quant Mater 3, 58 (2018). https://doi.org/10.1038/s41535-018-0132-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-018-0132-1
This article is cited by
-
Electronic, optical and mechanical properties of MAs2 (M = W, Cr, Mo): a first-principles study
Indian Journal of Physics (2024)
-
Superconducting and structural properties of the phosphorus-rich Nb2P5 superconductor under high pressure
Tungsten (2023)