Abstract
Interaction-driven metal–insulator transitions or Mott transitions are widely observed in condensed matter systems. In multi-orbital systems, many-body physics is richer in which an orbital-selective metal–insulator transition is an intriguing and unique phenomenon. Here we use first-principles calculations to show that a magnetic transition (from paramagnetic to long-range magnetically ordered) can simultaneously induce an orbital-selective insulator–metal transition in rock-salt ordered double perovskite oxides A2BB′O6, where B is a non-magnetic ion (Y3+ and Sc3+) and B′ a magnetic ion with a d3 electronic configuration (Ru5+ and Os5+). The orbital-selectivity originates from geometrical frustration of a face-centered-cubic lattice on which the magnetic ions B′ reside. Including realistic structural distortions and spin-orbit interaction do not affect the transition. The predicted orbital-selective transition naturally explains the anomaly observed in the electric resistivity of Sr2YRuO6. Implications of other available experimental data are also discussed. This work shows that by exploiting geometrical frustration on non-bipartite lattices, new electronic/magnetic/orbital-coupled phase transitions can occur in correlated materials that are in the vicinity of metal–insulator phase boundary.
Similar content being viewed by others
Introduction
Interaction-driven metal–insulator transition (so-called Mott transition) is one of the most striking phenomena in condensed matter systems.1 With the development of many-body methods such as dynamical mean field theory, we can coherently describe the Mott transition using a single-orbital Hubbard model.2,3
In multi-orbital systems, more complicated Mott physics emerges and the orbital-selective Mott transition (OSMT) is a most intriguing phenomenon.4 OSMT refers to the phenomenon in which as the transition occurs, conduction electrons become localized on some orbitals and remain itinerant on other orbitals. The idea, which was first introduced to explain the transport properties of Ca2−xSrxRuO4,4,5,6,7 has stimulated many theoretical investigations8,9,10,11,12,13,14 and different mechanisms underlying this phenomenon have been proposed: for example different orbitals have different intrinisic band widths,4 different on-site energies,15 different p-d hybridization16, and/or different band degeneracies.17
In this work, we use first-principles calculations to introduce a new approach to induce orbital-selective insulator–metal transition in multi-orbital systems. We show that in a multi-orbital Mott insulator with its magnetic ions residing on a non-bipartite lattice, the occurrence of long-range magnetic ordering can drive electrons on one orbital into a metallic state while leaving electrons on other orbitals insulating. The orbital-selectivity originates from ‘geometrical frustration’ of non-bipartite lattices, which enforces some magnetic moments to be ferromagnetically coupled in an antiferromagnetic ordering.
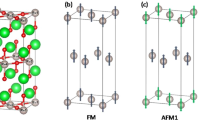
Figure 1a shows the crystal structure of a rock-salt ordered double perovskite oxide A2BB′O6. Blue and brown oxygen octahedra enclose two different types of transition metal ions B and B′. Green balls are A ions and red balls are oxygen ions. In panels b and c of Fig. 1, we show a simplified structure of an ordered double perovskite oxide in which only transition metal ions B and B′ are shown. The small blue balls are non-magnetic transition metal ions B and the large black balls are magnetic transition metal ions B′. The red arrows denote magnetic moments of B′ ions. The magnetic ions B′ reside on a face-centered-cubic (fcc) lattice. Panel b shows a schematic of a paramagnetic state in which magnetic moments on B′ ions have random orientations and fluctuate in time. Panel c shows a schematic of an antiferromagnetic state. We note that if nearest-neighbor exchange is antiferromagnetic in nature, it is impossible to have a ‘complete’ antiferromagnetic ordering on a fcc lattice in which each pair of nearest-neighbor magnetic moments is antiferromagnetically coupled because fcc lattice has ‘geometrical frustration’.18,19 Instead a so-called type-I antiferromagnetic ordering is widely observed in ordered double perovskite oxides.20,21,22,23,24,25,26,27 This ordering is shown in panel c, in which magnetic moments alternate their directions between adjacent atomic planes along the z-axis. Mathematically the magnetic moment configuration is characterized by an ordering wave vector \({\mathbf{Q}} = \frac{{2\pi }}{a}(001)\), where a is the lattice constant. Our first-principles calculations show that ordered double perovskite oxides which contain magnetic Ru5+ and Os5+ ions are promising candidate materials which are Mott insulators in high-temperature paramagnetic state but undergo the aforementioned orbital-selective insulator–metal transition as the type-I antiferromagnetic ordering occurs at low temperatures. Experimental evidence for this transition and implications of other available experiment data will be discussed.
a A full crystal structure of ordered double perovskite oxides A2BB′O6. The blue and brown oxygen octahedra enclose two different types of transition metal ions B and B′. The green balls are A ions and red balls are oxygen ions. b, c A simplified crystal structure of an ordered double perovskite oxide, in which only transition metal ions B and B′ are shown. The small blue balls are non-magnetic transition metal ions B and the large black balls are magnetic transition metal ions B′. The red arrows denote magnetic moments of B′ ions. Panel b shows a paramagnetic state in which magnetic moments have random orientations and fluctuate in time. c Shows a type-I antiferromagnetic state in which magnetic moments alternate their directions between adjacent atomic layers along the z-axis (the ordering wave vector \({\mathbf{Q}} = \frac{{2\pi }}{a}(001)\), where a is the lattice constant)
The computational details of our first-principles calculations are found in Methods Section.
Results
Table 1 lists five candidate materials in this study. In those ordered double perovskite oxides, Ru5+ and Os5+ are magnetic, and Y3+ and Sc3+ are non-magnetic. Both Ru5+ and Os5+ have a d3 configuration in which, due to Hund’s rule, three d electrons fill three t2g orbitals and form a spin \(S = \frac{3}{2}\).28 All those four ordered double perovskite oxides exhibit type-I antiferromagnetic ordering below Néel temperature TN.20,21,22,23,24,25,26,27 For clarity, we first study Ba2YRuO6 as a representative material. We discuss other four materials in section Discussion. Ref. 20 shows that Ba2YRuO6 crystallizes in a cubic Fm-3m structure (space group No. 225) and retains Fm-3m symmetry from room temperature down to 2.8 K (below TN). The change in lattice constant due to thermal expansion is very small (<0.15%). Experimentally, it is found that Y3+ and Ru5+ site mixing is negligible or at most very low (about 1%)20 because the size difference between Y3+ and Ru5+ is significant (0.260 Å), which stabilizes the ordered structure.29 Our calculations use its experimental low-temperature ordered structure (the details are shown in Supplementary Materials).
Spectral functions
We show in Fig. 2 spectral functions of Ba2YRuO6 in both paramagnetic state (panel a) and type-I antiferromagnetic state (panel b) (A spin-resolved spectral function of a single Ru atom in the type-I antiferromagnetic state is shown in Supplementary Materials). The blue curves are total spectral functions and the red curves are Ru t2g projected spectral functions. The paramagnetic state is insulating with a Mott gap of about 0.2 eV. However, the type-I antiferromagnetic state shows interesting properties: the lower and upper Hubbard bands of Ru t2g states exhibit sharper peaks, compared to those in the paramagnetic state, but the Mott gap is closed and the state is metallic.
Spectral functions of ordered double perovskite Ba2YRuO6 calculated using DFT + DMFT with URu = 2.3 eV and JRu = 0.3 eV. a Shows the spectral function of paramagnetic state (PM) and b shows the spectral function of type-I antiferromagnetic state (AFM). The blue and red curves are total and Ru t2g projected spectral functions, respectively. The Fermi level is at ω = 0 eV. Spin up and spin down are summed for both PM and AFM states
We first note that the transition shown in Fig. 2 is opposite to Slater transition.30,31 Whereas both transitions are driven by antiferromagnetic ordering, in Slater transition a gap is opened in a paramagnetic metal with the occurrence of antiferromagnetic ordering, whereas Fig. 2 shows that the appearance of antiferromagnetic ordering closes the gap of a paramagnetic insulator and induces a metallic state.
Second, we show that the gap closing has nothing to do with charge transfer between Ru5+ and Y3+ ions.32,33 In Fig. 3, we show the spectral functions of Ba2YRuO6 in a larger energy window. In addition to total and Ru t2g projected spectral functions, we also show Ru eg projected spectral function (green), Y t2g projected spectral function (purple) and O p projected spectral function (orange). We find that Ru eg states have higher energy than Ru t2g states due to crystal field splitting, and Y t2g state have even higher energy than Ru eg states. This is consistent with the nominally empty d configuration of Y3+. We note that even in plain DFT-PBE calculations (without Hubbard U), Y t2g states have higher energy than Ru t2g and eg states (see Fig. 1 in Supplementary Materials). This indicates that there is no charge transfer between Y3+ and Ru5+ ions in both paramagnetic and type-I antiferromagnetic states of Ba2YRuO6.
Spectral functions of ordered double perovskite Ba2YRuO6 in a large energy window (note that the ω axis is broken). a Shows the spectral function of paramagnetic state (PM) and b shows the spectral function of type-I antiferromagnetic state (AFM). The blue curves are total spectral functions; the red curves are Ru t2g projected spectral functions; the green curves are Ru eg projected spectral functions; the purple curves are Y t2g states; the orange curves are O p projected spectral functions. The Fermi level is at ω = 0 eV. Spin up and spin down are summed for both PM and AFM states
Orbital-selective transition
In this section, we show that the gap closing in Ba2YRuO6 is driven by the orbital-selective insulator–metal transition as we mentioned in the Introduction. Figure 4 is the key result, in which we decompose the spectral function of Ba2YRuO6 into three Ru t2g orbital projections, in the paramagnetic state and in the type-I antiferromagnetic state (the ordering wave vector \({\mathbf{Q}} = \frac{{2\pi }}{a}(001)\)). We can see that in the paramagnetic state, three Ru t2g orbitals have identical projected spectral functions due to cubic symmetry. A small Mott gap is opened up in the paramagnetic state. However, in the type-I antiferromagnetic state, three Ru t2g orbitals have different projected spectral functions. Ru dxy orbital exhibits metallic property with the gap closed, in contrast to Ru dxy orbital in the paramagnetic state (column 1 of Fig. 4). On the other hand, Ru dxz and Ru dyz orbitals show stronger insulating property with the gap size increased and the peaks of lower/upper Hubbard bands becoming sharper (columns 2 and 3 of Fig. 4).
Spectral functions of double perovskite Ba2YRuO6 in paramagnetic state (PM, a) and in type-I antiferromagnetic state (AFM, b). The ordering wave vector is \({\mathbf{Q}} = \frac{{2\pi }}{a}(001)\), where a is the lattice constant. a1 and b1 Ru dxy projected spectral functions. a2 and b2 Ru dxz projected spectral functions. a3 and b3 Ru dyz projected spectral functions. The Fermi level is at ω = 0 eV. Spin up and spin down are summed for both PM and type-I AFM states
The orbital-selectivity, i.e. which Ru t2g orbital undergoes the insulator–metal transition with the occurrence of type-I antiferromagnetic ordering is related to the Ru magnetic moment configuration, which is characterized by the ordering wave vector Q. For type-I antiferromagnetic ordering, there are three ordering wave vectors: \({\mathbf{Q}} = \frac{{2\pi }}{a}(001)\), \(\frac{{2\pi }}{a}(010)\) or \(\frac{{2\pi }}{a}(100)\), where a is the lattice constant. They correspond to different axes along which Ru magnetic moments alternate their directions between adjacent atomic planes. As is shown in Fig. 5, for each ordering wave vector Q, Ru magnetic moments are parallel in \(\frac{1}{3}\) of nearest-neighbor Ru pairs and are anti-parallel in the other \(\frac{2}{3}\) of nearest-neighbor Ru pairs. The Ru magnetic moments that are parallel single out a plane and the Ru t2g orbital that lies in the plane (rather than out of the plane) undergoes an insulator–metal transition. For example, in Fig. 5a, the ordering wave vector \({\mathbf{Q}} = \frac{{2\pi }}{a}(001)\) and the parallel Ru magnetic moments single out xy plane. Together, we show an iso-value surface, which is the spin-resolved (orange and green) integrated local spectral function around the Fermi level (Supplementary Materials for details). The shape of the iso-value surface clearly indicates that the many-body density of states close to the Fermi level has a dxy character, which is consistent with Fig. 5. In Fig. 5b, c, we repeat the calculations with different ordering wave vectors \({\mathbf{Q}} = \frac{{2\pi }}{a}(010)\) and \(\frac{{2\pi }}{a}(100)\). As we change Q, the states at the Fermi surface show dxz and dyz orbital character, respectively. This partial ‘ferromagnetic coupling’ in the type-I antiferromagnetic ordering is the key to explain the orbital-selective insulator–metal transition. In Fig. 5a, the Ru magnetic moments are ferromagnetically coupled in the xy plane and antiferromagnetically coupled in the xz and yz planes. The largest hopping matrix element for Ru dxy orbital is the one in the xy plane between the Ru nearest-neighbors. In the xy plane, the parallel Ru magnetic moments facilitate scattering upon excitation and thus increase coherence and band width for Ru dxy orbital34. If the band width is large enough, the Mott gap is closed for the Ru dxy orbital, which is exactly what Fig. 4b1 shows. Similarly, for Ru dxz (dyz) orbital, the largest hopping matrix element is the one in xz (yz) plane, but in that plane the Ru t2g magnetic moments are anti-parallel, which hinders scattering upon excitation and thus decreases band width and further increases band gap34 (A simple material with a half-filled t2g shell is studied in Supplemenatray Materials to demonstrate the correlation between long-range magnetic ordering and band widths). We note in Fig. 4 that compared to the paramagnetic state, in the type-I antiferromagnetic state, the gaps of Ru dxz and dyz orbitals are indeed larger and the peaks of lower/upper Hubbard bands of Ru dxz and dyz orbitals become sharper. Applying the same analysis to different magnetic configurations in Fig. 5b, c shows that Ru dxz (dyz) undergoes the insulator–metal transition with the occurrence of type-I antiferromagnetic ordering of \({\mathbf{Q}} = \frac{{2\pi }}{a}(010)\) \(\left( {{\mathbf{Q}} = \frac{{2\pi }}{a}(100)} \right)\). We emphasize here that because both paramagnetic state and antiferromagnetic state in Fig. 4 are calculated at the same low temperature, it indicates that the occurrence of type-I antiferromagnetic ordering is the driving force to induce the orbital-selective insulator–metal transition.
Different magnetic configurations in ordered double perovskite Ba2YRuO6. The red arrows denote Ru t2g magnetic moments. For clarity, only Ru (large black balls) and Y (small blue balls) are explicitly shown. The orange and green shades are spin-resolved iso-value surface of integrated local spectral function for Ba2YRuO6 in the type-I antiferromagnetic state. The integral runs from EF − 0.05 eV to EF, where EF is the Fermi level. The orange (green) color indicates the spectral function of spin up (down). a The ordering wave vector \({\mathbf{Q}} = \frac{{2\pi }}{a}(001)\) and the integrated local spectral function close to the Femi level shows a dxy character; b The ordering wave vector \({\mathbf{Q}} = \frac{{2\pi }}{a}(010)\) and the integrated local spectral function close to the Femi level shows a dxz character; c The ordering wave vector \({\mathbf{Q}} = \frac{{2\pi }}{a}(100)\) and the integrated local spectral function close to the Femi level shows a dyz character
Electric conductivity
A direct consequence of the electronic structure shown in Fig. 4 is anisotropic transport properties of Ba2YRuO6 in a type-I antiferromagnetic state. We calculate electric conductivity using DFT + U method within linear response theory and semi-classical approximation framework.35,36 We explain that for long-range magnetically ordered states, because the self-energy is small and its frequency dependence is weak, DFT + DMFT and DFT + U methods yield very similar results.
In DFT + U method, electric conductivity origins from intra-band transitions, which can be calculated from band structure. Using linear response theory and semi-classical approximation, we have:35,36
where f(ε) is the Fermi-Dirac distribution, α, β = x, y, z, and τ is the relaxation time. Note that τ is not directly calculated by DFT + U method, but is treated as a parameter. Our calculations find that the off-diagonal components of electric conductivity vanish due to crystal symmetry (Ba2YRuO6 has a Fm-3m structure). The diagonal components of electric conductivity have two independent values: σxx = σyy and σzz. This is because type-I antiferromagnetic ordering breaks cubic symmetry (given \(\frac{{2\pi }}{a}\) (001) ordering wave vector). Anisotropy in electric conductivity arises from the fact that in a type-I antiferromagnetic state (given \(\frac{{2\pi }}{a}\) (001) ordering wave vector), Ru dxy orbital is metallic while Ru dxz and dyz orbitals are insulating. This means that intra-band transitions contribute to σxx and σyy, but not to σzz. Our calculations find a finite electric conductivity σxx = σyy (Fig. 6) and a vanishing electric conductivity σzz = 0.
Magnetic energetics
We have shown that an orbital-selective insulator–metal transition can occur in ordered double perovskite Ba2YRuO6 as the material transitions from the paramagnetic state into the type-I antiferromagnetic (AFM) state with decreasing temperatures. Although type-I AFM ordering has been observed in experiment (Table 1), as a self-consistent check, we calculate other types of long-range magnetic orderings: ferromagnetic ordering (FM) and antiferromagnetic ordering with magnetic moments alternating directions along (111) axis (the ordering wave vector \({\mathbf{Q}} = \frac{{2\pi }}{a}\left( {\frac{1}{2}\frac{1}{2}\frac{1}{2}} \right)\) and we refer to it as type-II AFM) (Supplementary Materials for details). We use DFT + U method (with the same URu and JRu) to calculate the energy difference between these magnetic orderings because technically (i) DFT + U method can calculate larger systems than DFT + DMFT method (we need an 80-atom cell to calculate type-II antiferromagnetic ordering37); (ii) DFT + U method can achieve much higher accuracy than CTQMC-based DFT + DMFT method.38 Due to the quantum Monte Carlo nature of CTQMC algorithm, the accuracy we can obtain from DFT + DMFT method is on the order of 10 meV per cell. DFT + U method can converge a total energy of 1 meV per cell accuracy or even higher. In addition, as we have mentioned in the previous section, DFT + DMFT and DFT + U methods produce consistent results for long-range ordered states. That is the physical reason why we may alternatively use DFT + U method to calculate the total energy for magnetically ordered states.
Using type-I AFM state as the reference, we find FM and type-II AFM are higher in energy than type-I AFM by 110 meV/f.u. and 37 meV/f.u., respectively. The result that FM has higher energy than type-I AFM shows that the nearest-neighbor exchange coupling is indeed antiferromagnetic in nature. The reason that type-I AFM is more stable than type-II AFM is because in type-I AFM state, for each Ru magnetic moment, \(\frac{2}{3}\) of its nearest-neighbor magnetic moments are anti-parallel and the other \(\frac{1}{3}\) of its nearest-neighbor magnetic moments are parallel; in type-II AFM state, for each Ru magnetic moment, half of its nearest-neighbor magnetic moments are anti-parallel and the other half are parallel. As the nearest-neighbor Ru exchange coupling is intrinsically antiferromagnetic, and type-I AFM ordering has more antiferromagnetic coupled nearest-neighbor pairs of Ru magnetic moments than type-II AFM ordering, this explains why type-I AFM ordering is more stable. Our results are consistent with the experimental measurements.20,21,22
We note that the fcc lattice on which the magnetic ion Ru resides has ‘geometrical frustration’, therefore complicated magnetic orderings (non-collinear and/or non-coplanar etc.) are possible in the ground state.28,39,40 However, at finite temperatures, by the mechanism of ‘order by disorder’, collinear magnetic orderings are favored by thermal fluctuations18,19 and collinear type-I AFM ordering is indeed observed in experiments.20,21,22 In our current study, it is the first long-range magnetic ordering which emerges from a paramagnetic state that is relevant to the orbital-selective insulator–metal transition.
Spin-orbit interaction
We notice that Ru has 4d orbitals and spin-orbit (SO) interaction plays a more pronounced role in 4d and 5d magnetic ions than 3d magnetic ions. In this section, we discuss whether spin-orbit interaction may affect the magnetically driven orbital-selective insulator–metal transition.
We note that currently DFT + DMFT + SO method is not feasible in multi-orbital systems because spin-orbit interaction induces an intrinsic sign problem in the CTQMC algorithm.38 But we find that in the antiferromagnetic (AFM) ordered state, the frequency dependence in the self-energy is much weaker than that in the paramagnetic state (see the Supplementary Materials for details). This indicates that Hartree-Fock approximation is as good as DMFT to describe the AFM ordered state. Therefore we compare DFT + U and DFT + U + SO methods.
In the presence of spin-orbit interaction, spin is directly coupled to crystal lattice. In type-I AFM state with \({\mathbf{Q}} = \frac{{2\pi }}{a}(001)\), we globally rotate all Ru magnetic moments in real space and find that they are stabilized along the z-axis.
Figure 7 shows the spectral functions for type-I AFM state of Ba2YRuO6 (with an ordering wave vector \({\mathbf{Q}} = \frac{{2\pi }}{a}(001)\)), calculated using DFT + U method (panel a) and DFT + U + SO method (panel b). The red, blue, and green lines are the spectral functions projected onto Ru dxy, Ru dxz, and Ru dyz orbitals, respectively. Using both methods, we find that with the ordering wave vector \({\mathbf{Q}} = \frac{{2\pi }}{a}(001)\), Ru dxz and Ru dyz orbitals are insulating while Ru dxy orbital is metallic. This orbital-dependent feature is also consistent with the spectral function calculated by DFT + DMFT method (Fig. 4).
Spectral function A(ω) for type-I antiferromagnetic Ba2YRuO6 with the ordering wave vector \({\mathbf{Q}} = \frac{{2\pi }}{a}(001)\), where a is the lattice constant. The Fermi level is at ω = 0 eV. a Calculated by DFT + U method and b is calculated by DFT + U + SO method. The red, blue, and green lines are Ru dxy, Ru dxz, and Ru dyz projected spectral functions, respectively. For DFT + U calculations, spin up and spin down are summed up. For DFT + U + SO calculations, the spins are aligned along the z-axis
This result is in fact not surprising because in the current study, the magnetic ions of double perovskite oxides have a d3 configuration. Due to Hund’s rule, the three electrons fill three t2g orbitals and form a spin \(S = \frac{3}{2}\) state. The orbital degree of freedom is completely quenched and the system is presumably well described by a spin-only Hamiltonian.28,40 Therefore including spin-orbit interaction does not significantly change the electronic structure, as is shown in Fig. 7.
Phase diagram with Hubbard U
In the previous sections, we use a single value of Hubbard URu to perform all the calculations. Now, we discuss the phase diagram as a function of Hubbard URu with JRu fixed at 0.3 eV, calculated by DFT + DMFT method. We find that there are two critical values of Hubbard U (Fig. 8): (i) as U > Uc1, both the high-temperature paramagnetic state (PM) and the low-temperature type-I antiferromagnetic state (AFM) are insulating; (ii) as U < Uc2, both the high-temperature PM and low-temperature AFM states are metallic and (iii) as Uc2 < U < Uc1, the high-temperature PM state is insulating and the low-temperature AFM state is metallic. It is precisely in the region of Uc2 < U < Uc1 that the magnetically driven orbital-selective insulator–metal transition can occur at the magnetic critical temperature TN. For Ba2YRuO6, we find Uc1 = 3.2 eV and Uc2 = 1.5 eV. Although the accurate value of Hubbard U for Ru is yet to be determined, the range set by Uc1 and Uc2 is achievable for a 4d transition metal ion. We also note that Fig. 8 shows two types of phase transition. One is the AFM-metallic to AFM-insulating transition on the Hubbard U axis (at low temperatures). The other is the PM-insulator to AFM-metal state transition as temperature decreases. Both types of phase transition are continuous. The U-driven phase transition is continuous because increasing U gradually separates the majority and minority spins of Ru dxy orbital (given a \(\frac{{2\pi }}{a}\) (001) ordering wave vector) and eventually opens a gap. The PM-insulator to AFM-metal transition is continuous too, because the gap closing of Ru dxy orbital (given a \(\frac{{2\pi }}{a}\) (001) ordering wave vector) is achieved by gradually aligning the Ru dxy moments and increasing the band width of Ru dxy orbital till the majority and minority spins of Ru dxy orbital overlap in energy.
Phase diagram of Ba2YRuO6, Ba2ScRuO6, Sr2YRuO6, Sr2ScOsO6, and Sr2YOsO6 as a function of Hubbard U on magnetic ions Ru5+ and Os5+. The Hund’s JRu and JOs are fixed at 0.3 eV. There are two critical values of U. As U > Uc1 (green part), both high-temperature paramagnetic (PM) and low-temperature type-I antiferromagnetic (AFM) states are insulating. As U < Uc2 (blue part), both high-temperature PM and low-temperature type-I AFM states are metallic. As Uc2 < U < Uc1, high-temperature PM state is insulating and low-temperature type-I AFM state is metallic. The critical values of Uc1 and Uc2 (in unit of eV) are (3.2, 1.5) for Ba2YRuO6, (3.9, 2.3) for Ba2ScRuO6, (3.1, 1.2) for Sr2YRuO6, (2.9, 1.0) for Sr2ScOsO6, and (1.9, 1.0) for Sr2YOsO6
Discussion
We have provided a comprehensive study on the magnetically driven orbital-selective insulator–metal transition in Ba2YRuO6 in section Results. However, the transition is not unique to Ba2YRuO6; it is general to ordered double perovskite oxides with one d3 magnetic ion and one non-magnetic ion as long as the material is a Mott insulator that lies close to the metal-insulator phase boundary in the paramagnetic state.
In this section, we study other four ordered double perovskite oxides that are listed in Table 1 and discuss the connection of our theoretical results to the available experimental data. Ba2ScRuO6, Sr2YRuO6, Sr2ScOsO6, and Sr2YOsO6 have been synthesized and their experimental structures (used in the calculations) are shown in Supplementary Materials. We use DFT + DMFT method to calculate the U phase diagram for these four double perovskite oxides (the Hund’s JRu and JOs are fixed at 0.3 eV41,42,43). The results are shown in Fig. 8. Like Ba2YRuO6, Ba2ScRuO6 also crystallizes in the cubic Fm-3m structure (space group No. 225 Fm-3m).23 However, the lattice constant of Ba2ScRuO6 is smaller than that of Ba2YRuO6 by about 2%,20,23 which leads to larger hopping matrix elements. Therefore the critical Hubbard Uc1 and Uc2 for Ba2ScRuO6 are both larger than those for Ba2YRuO6. On the other hand, Sr2YRuO6, Sr2ScOsO6 and Sr2YOsO6 all crystallize in a distorted structure (space group No. 14 P21/n).24,25,26,27 Due to rotations and tilts of RuO6 and OsO6 oxygen octahedra, metal-oxygen-metal bond angle is smaller than that in a cubic structure (In Sr2YRuO6, Sr2ScOsO6, and Sr2YOsO6, the average metal-oxygen-metal bond angle is about 160°, while in Ba2YruO6 and Ba2ScRuO6, the metal-oxygen-metal bond angle is 180°). This results in reduced hopping and therefore the critical Hubbard Uc1 and Uc2 for all three double perovskite oxides are smaller than those for Ba2YRuO6. We note that while in our calculations there is uncertainty about the accurate value of Hubbard U on transition metal ions (Ru5+ and Os5+), different ‘iso-electronic’ materials (Table 1) provide a fairly large range of U in which the predicted transition can occur (shown in Fig. 8).
Next we turn to available experimental data. Magnetic properties of the five materials listed in Table 1 have been carefully studied.21,22,23,24,25,26,27 Type-I antiferromagnetic ordering has been observed in all these double perovskite oxides. Remarkably, Cao et al. observes a sharp anomaly in the electric resistivity ρ(T) of Sr2YRuO6 at the magnetic ordering temperature TN.26 Ref. 26 measures two types of resistivity: ρab(T) for the basal plane and ρc(T) for the out-of-plane c-axis. As the temperature T is above the Néel temperature TN, both ρab(T) and ρc(T) exhibit insulating properties: they rapidly increase as the temperature decreases. However, just below TN, ρab(T) exhibits a clear anomaly: it changes the sign of its slope and slowly decreases with lowering temperatures (a metallic-like behavior). Interestingly, this anomaly is only evident in ρab(T) but is absent in ρc(T). ρc(T) exhibits insulating property both above and below TN with a weak “kink” feature at TN. Just below TN, ρc(T) increases slightly faster with decreasing temperatures than it does just above TN. Our predicted phase transition provides an explanation for the anomaly observed in the resistivity of Sr2YRuO6 at TN. Considering that the magnetic ordering wave vector is along the c-axis,26 the anomaly in ρab(T) shows that Ru dxy orbital (which lies in the ab plane) undergoes an insulator–metal transition at TN (see panel 1 of Fig. 4). On the other hand, Ru dxz and dyz orbitals remain insulating at TN and therefore the anomaly is not observed in ρc(T). The gap size associated with Ru dxz and dyz orbitals increases at TN (see panels 2 and 3 of Fig. 4), which explains the “kink” behavior at TN.
However, as the temperature further decreases, ρab of Sr2YRuO6 undergoes a second phase transition from an antiferromagnetic metal to an antiferromagnetic insulator.26 According to the authors of ref. 26 the second phase transition arises from the fact that Dzyaloshinskii–Moriya interaction (DM-interaction) cants Ru spins and induces weak ferromagnetism, which eventually reopens the gap.
The second phase transition is interesting by itself and deserves further investigation, but is outside the scope of our current study. In our calculations, we consider type-I antiferromagnetic state (no weak ferromagnetism) in all material candidates.
Because, Sr2YRuO6 has a distorted structure and the presence of DM-interaction complicates the analysis of transport measurements, we suggest that a very similar compound Ba2YRuO6 is a cleaner system to observe our predicted phase transition. Ba2YRuO6 has a cubic structure (space group Fm-3m) and inversion symmetry of Fm-3m space group forbids DM-interaction. Without the second phase transition, ρab should show a turning-point at TN (this has already been observed in Sr2YRuO6) and then monotonically decrease with decreasing temperatures.
Another cleaner material candidate is probably Ba2ScRuO6, which also crystallizes in a Fm-3m structure. Ref. 23 shows that in double perovskite Ba2ScRuO6, a double-kink feature is observed in its magnetic susceptibility, which indicates two ordering temperatures (TN = 31 and 44 K). However, only one peak is observed in its heat capacity, which corresponds to the higher ordering temperature. The origin of the transition at the lower ordering temperature is not clear. A measurement of low-temperature electric resistivity for Ba2ScRuO6 is desirable, which will probe the predicted orbital-selective transition and may help unlock the puzzle of two ordering temperatures.
Finally, we mention that in order to observe the transition, we need the material to lie close to the metal-insulator phase boundary in the paramagnetic state (but still on the insulating side). Therefore, for 3d transition metal ions such as Mn4+ (d shell configuration 3d3), because a typical U is about 4–5 eV (larger than all the Uc1 calculated), we do not expect to observe the orbital-selective insulator–metal transition in 3d double perovskite oxides, such as Sr2TiMnO6. For 4d, 5d transition metal ions such as Ru5+ and Os5+, because the Hubbard U gets smaller and the metal d band width gets larger, complex oxides that contain 4d and 5d transition metal ions are much closer to metal-insulator phase boundary in paramagnetic state and therefore they are more promising candidate materials to observe the transition we predict here.
In conclusion, we use first-principles calculations to demonstrate a magnetically driven orbital-selective insulator–metal transition in ordered double perovskite oxides A2BB′O6 with a non-magnetic ion B (Y3+ and Sc3+) and a d3 magnetic ion B′ (Ru5+ and Os5+). With decreasing temperatures, as the material transitions from paramagnetic insulating (Mott) state to type-I antiferromagnetic (AFM) state, one t2g orbital of the magnetic ion becomes metallic while the other two t2g orbitals of the magnetic ion become more insulating. The origin of the transition arises from ‘geometric frustration’ of a fcc lattice, which enforces some magnetic moments to be ferromagnetically coupled in an antiferromagnetic ordering. The orbital-selectivity is associated with the ordering wave vector Q of type-I AFM state. We hope our study can stimulate further experiments to provide more compelling evidence for the predicted electronic phase transition in ordered double perovskite oxides that contain 4d and 5d transition metal ions.
Methods
We perform first-principles calculations by using density functional theory (DFT)44,45 plus Hubbard U correction (DFT + U),46 DFT plus Hubbard U correction and spin-orbit interaction (DFT + U + SO)47 and DFT plus dynamical mean field theory (DFT + DMFT).3 Both DFT + U and DFT + U + SO methods are implemented in the Vienna Ab initio Simulation Package (VASP).48,49 In DMFT method, a continuous-time quantum Monte Carlo algorithm (CTQMC)50 is used to solve the impurity problem.38 The impurity solver was developed by K. Haule’s group at Rutgers University.51 In DMFT calculations, both paramagnetic and antiferromagnetic states for all material candidates are computed at a temperature of 116 K. Convergence of key results is checked at 58 K and no significant changes are observed in electronic structure.
For long-range magnetically ordered calculations using DFT + U, DFT + U + SO and DFT + DMFT as well as paramagnetic calculations using DFT + DMFT, a non-spin-polarized exchange correlation functional is used in the DFT component.52,53 The spin symmetry is broken by the Hubbard U and Hund’s J interactions.
Electronic structures are calculated using DFT + DMFT method. Magnetic energy differences are calculated using DFT + U method and effects of spin-orbit (SO) coupling are studied by using DFT + U + SO method.
In the DFT part, we use generalized gradient approximation with Perdew–Burke–Ernzerhof (PBE) parametrization54 for the exchange correlation functional. For DFT + DMFT calculations, the correlated metal d orbitals and the oxygen p orbitals are constructed using maximally localized Wannier functions.55 As for the interaction strengths, we first use one set of interaction parameters URu = 2.3 eV and JRu = 0.3 eV to show the representative electronic structure and then study Hubbard U dependence. We show that the transition we predict can occur in a range of interaction strength for all candidate materials. We note that recent calculations of SrRu2O656,57,58 show that for a t2g-p model, URu is about 5 eV from constrained random-phase-approximation (cRPA),57,58 which is larger than the upper limit Uc1 below which our predicted transition can be observed. However, the “kink” observed in the resistivity of Sr2YRuO6 indicates that the antiferromagnetic ordered state of Sr2YRuO6 exhibits metal-like behavior around TN, implying that the interaction strength URu in Sr2YRuO6 might be smaller than that in SrRu2O6 probably due to different crystal structure, or single-site DMFT method with a cRPA value of interaction strength may favor the insulating phase. This deserves further study in future work.
In DFT + U, DFT + U + SOC and DFT + DMFT calculations, we use a charge-only exchange correlation functional (i.e. not depending on spin density) in the DFT component. A charge-only double counting is also used in all methods. Previous works show that this choice can avoid an unphysically large exchange-splitting in spin-dependent exchange correlation functionals.52,53,59
More computational details are found in Supplementary Materials.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Imada, M., Fujimori, A. & Tokura, Y. Metal-insulator transitions. Rev. Mod. Phys. 70, 1039–1263 (1998).
Georges, A., Kotliar, G., Krauth, W. & Rozenberg, M. J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 68, 13–125 (1996).
Kotliar, G. et al. Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 78, 865–951 (2006).
Anisimov, V. I., Nekrasov, I. A., Kondakov, D. E., Rice, T. M. & Sigrist, M. Orbital-selective Mott-insulator transition in Ca2−xSrxRuO4. Eur. Phys. J. B 25, 191–201 (2002).
Nakatsuji, S. & Maeno, Y. Quasi-two-dimensional Mott transition system. Phys. Rev. Lett. 84, 2666–2669 (2000).
Fang, Z., Nagaosa, N. & Terakura, K. Orbital dependent phase control in Ca2−xSrxRuO4. Phys. Rev. B 69, 045116 (2004).
Ko, E., Kim, B. J., Kim, C. & Choi, H. J. Strong orbital-dependent d-band hybridization and fermi-surface reconstruction in metallic Ca2−xSrxRuO4. Phys. Rev. Lett. 98, 226401 (2007).
Koga, A., Kawakami, N., Rice, T. M. & Sigrist, M. Orbital-selective Mott transitions in the degenerate Hubbard model. Phys. Rev. Lett. 92, 216402 (2004).
De’Medici, L., Georges, A. & Biermann, S. Orbital-selective Mott transition in multiband systems: slave-spin representation and dynamical mean-field theory. Phys. Rev. B 72, 205124 (2005).
Ferrero, M., Becca, F., Fabrizio, M. & Capone, M. Dynamical behavior across the Mott transition of two bands with different bandwidths. Phys. Rev. B 72, 205126 (2005).
Liebsch, A. Novel Mott transitions in a nonisotropic two-band Hubbard model. Phys. Rev. Lett. 95, 116402 (2005).
Biermann, S., de’ Medici, L. & Georges, A. Non-fermi-liquid behavior and double-exchange physics in orbital-selective Mott systems. Phys. Rev. Lett. 95, 206401 (2005).
Liebsch, A. & Ishida, H. Subband Filling and Mott transition in Ca2−xSrxRuO4. Phys. Rev. Lett. 98, 216403 (2007).
Hoshino, S. & Werner, P. Spontaneous orbital-selective Mott transitions and the jahn-teller metal of A 3C60. Phys. Rev. Lett. 118, 177002 (2017).
Werner, P. & Millis, A. J. High-spin to low-spin and orbital polarization transitions in multiorbital Mott systems. Phys. Rev. Lett. 99, 126405 (2007).
Wu, J., Phillips, P. & Castro Neto, A. H. Theory of the magnetic moment in iron pnictides. Phys. Rev. Lett. 101, 126401 (2008).
De’Medici, L., Hassan, S. R., Capone, M. & Dai, X. Orbital-selective Mott transition out of band degeneracy lifting. Phys. Rev. Lett. 102, 126401 (2009).
Henley, C. L. Ordering by disorder: ground-state selection in fcc vector antiferromagnets. J. Appl. Phys. 61, 3962–3964 (1987).
Henley, C. L. Ordering due to disorder in a frustrated vector antiferromagnet. Phys. Rev. Lett. 62, 2056–2059 (1989).
Aharen, T. et al. Magnetic properties of the S = 3/2 geometrically frustrated double perovskites La2LiRuO6 and Ba2YRuO6. Phys. Rev. B 80, 134423 (2009).
Battle, P. & Jones, C. The crystal and magnetic structures of Sr2LuRuO6, Ba2YRuO6, and Ba2LuRuO6. J. Solid State Chem. 78, 108–116 (1989).
Carlo, J. P. et al. Spin gap and the nature of the 4d 3 magnetic ground state in the frustrated fcc antiferromagnet Ba2YRuO6. Phys. Rev. B 88, 024418 (2013).
Kayser, P. et al. Magnetic and structural studies of Sc containing ruthenate double perovskites A2ScRuO6 (A = Ba, Sr). Inorg. Chem. 56, 9009–9018 (2017).
Taylor, A. E. et al. Magnetic order and electronic structure of the 5d 3 double perovskite Sr2ScOsO6. Phys. Rev. B 91 100406(R) (2015).
Paul, A. K. et al. Magnetically frustrated double perovskites: synthesis, structural properties, and magnetic order of Sr2 BOsO6 (b = Y, In, Sc). Z. für Anorg. und Allg. Chem. 641, 197–205 (2015).
Cao, G., Xin, Y., Alexander, C. S. & Crow, J. E. Weak ferromagnetism and spin-charge coupling in single-crystal Sr2YRuO6. Phys. Rev. B 63, 184432 (2001).
Battle, P. & Macklin, W. The crystal and magnetic structures of Sr2YRuO6. J. Solid State Chem. 52, 138–145 (1984).
Chen, G. & Balents, L. Spin-orbit coupling in d 2 ordered double perovskites. Phys. Rev. B 84, 094402 (2011).
Barnes, P. W., Lufaso, M. W. & Woodward, P. M. Structure determination of A 2 M 3+TaO6 and A2M3+NbO6 ordered perovskites: octahedral tilting and pseudosymmetry. Acta Crystallogr. Sect. B 62, 384–396 (2006).
Slater, J. C. Magnetic effects and the Hartree-Fock equation. Phys. Rev. 82, 538–541 (1951).
Calder, S. et al. Magnetically driven metal-insulator transition in NaOsO3. Phys. Rev. Lett. 108, 257209 (2012).
Chen, H., Millis, A. & Marianetti, C. Engineering correlation effects via artificially designed oxide superlattices. Phys. Rev. Lett. 111, 116403 (2013).
Kleibeuker, J. E. et al. Electronic reconstruction at the isopolar LaTiO3/LaFeO3 interface: an X-ray photoemission and density-functional theory study. Phys. Rev. Lett. 113, 237402 (2014).
Salamon, M. B. & Jaime, M. The physics of manganites: structure and transport. Rev. Mod. Phys. 73, 583–628 (2001).
Gajdoš, M., Hummer, K., Kresse, G., Furthmüller, J. & Bechstedt, F. Linear optical properties in the projector-augmented wave methodology. Phys. Rev. B 73, 045112 (2006).
Judith Harl’s thesis (http://othes.univie.ac.at/2622/).
Vasala, S. & Karppinen, M. A 2 B′B″O6 perovskites: a review. Prog. Solid State Chem. 43, 1–36 (2015).
Gull, E. et al. Continuous-time Monte Carlo methods for quantum impurity models. Rev. Mod. Phys. 83, 349–404 (2011).
Tiwari, R. & Majumdar, P. Noncollinear magnetic order in the double perovskites: double exchange on a geometrically frustrated lattice. Int. J. Mod. Phys. B 27, 1350018 (2013).
Chen, G., Pereira, R. & Balents, L. Exotic phases induced by strong spin-orbit coupling in ordered double perovskites. Phys. Rev. B 82, 174440 (2010).
Dang, H. T., Mravlje, J., Georges, A. & Millis, A. J. Electronic correlations, magnetism, and Hund’s rule coupling in the ruthenium perovskites SrRuO3 and CaRuO3. Phys. Rev. B 91, 195149 (2015).
Han, Q., Dang, H. T. & Millis, A. J. Ferromagnetism and correlation strength in cubic barium ruthenate in comparison to strontium and calcium ruthenate: a dynamical mean-field study. Phys. Rev. B 93, 155103 (2016).
Lo Vecchio, I. et al. Electronic correlations in the ferroelectric metallic state of LiOsO3. Phys. Rev. B 93, 161113 (2016).
Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev. 136, B864–B871 (1964).
Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133 (1965).
Liechtenstein, A. I., Anisimov, V. I. & Zaanen, J. Density-functional theory and strong interactions: orbital ordering in Mott-Hubbard insulators. Phys. Rev. B 52, R5467 (1995).
Takeda, T. The scalar relativistic approximation. Z. für Phys. B Condens. Matter Quanta 32, 43–48 (1978).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Werner, P., Comanac, A., De’ Medici, L., Troyer, M. & Millis, A. J. Continuous-time solver for quantum impurity models. Phys. Rev. Lett. 97, 076405 (2006).
Haule, K. Quantum Monte Carlo impurity solver for cluster dynamical mean-field theory and electronic structure calculations with adjustable cluster base. Phys. Rev. B 75, 155113 (2007).
Park, H., Millis, A. J. & Marianetti, C. A. Density functional versus spin-density functional and the choice of correlated subspace in multivariable effective action theories of electronic structure. Phys. Rev. B 92, 035146 (2015).
Chen, H. & Millis, A. J. Spin-density functional theories and their +U and +J extensions: a comparative study of transition metals and transition metal oxides. Phys. Rev. B 93, 045133 (2016).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Marzari, N., Mostofi, A. A., Yates, J. R., Souza, I. & Vanderbilt, D. Maximally localized Wannier functions: theory and applications. Rev. Mod. Phys. 84, 1419–1475 (2012).
Streltsov, S., Mazin, I. I. & Foyevtsova, K. Localized itinerant electrons and unique magnetic properties of SrRu2O6. Phys. Rev. B 92, 134408 (2015).
Hariki, A., Hausoel, A., Sangiovanni, G. & Kuneš, J. DFT + DMFT study on soft moment magnetism and covalent bonding in SrRu2O6. Phys. Rev. B 96, 155135 (2017).
Okamoto, S., Ochi, M., Arita, R., Yan, J. & Trivedi, N. Localized-itinerant dichotomy and unconventional magnetism in SrRu2O6. Sci. Rep. 7, 11742 (2017).
Chen, J., Millis, A. J. & Marianetti, C. A. Density functional plus dynamical mean-field theory of the spin-crossover molecule Fe(phen)2(NCS)2. Phys. Rev. B 91, 241111 (2015).
Acknowledgements
We are grateful to useful discussion with Andrew J. Millis, Jernej Mravlje, Sohrab Ismail-Beigi, Gang Chen, Yuan Li, and Hongjun Xiang. The work is funded by the National Science Foundation of China under the grant No. 11774236. Computational facilities are provided via Extreme Science and Engineering Discovery Environment (XSEDE).
Author information
Authors and Affiliations
Contributions
H.C. conceived the project, performed first-principles calculations, analyzed data, and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The author declares no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, H. Magnetically driven orbital-selective insulator–metal transition in double perovskite oxides. npj Quant Mater 3, 57 (2018). https://doi.org/10.1038/s41535-018-0131-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-018-0131-2