Abstract
Topological nodal-line semimetals are characterized by line-contact bulk band crossings and topological surface states. Breaking certain protecting symmetry turns this system into a Dirac semimetal or Weyl semimetal that hosts zero-dimensional isolated nodal points. Recent advances in band theory predicted a topological nodal-line semimetal state possessing a new type of nodal line in AlB2-type diborides. Here, we report an experimental realization of nodal-line fermions and associated surface states near the Fermi energy in ZrB2 by angle-resolved photoemission spectroscopy combined with first-principles calculations. The Dirac nodal lines in ZrB2 wind into two groups of nodal rings, which are linked together along the Γ-K direction. We further observe a distinct surface state connecting to each nodal line, indicative of the nontrivial topological nature of the bulk nodal lines. Therefore, our results provide convincing experimental evidence of nodal-line semimetal states in ZrB2 both in the bulk and on the surface, suggesting ZrB2 as a remarkable platform for discovering unique phenomena induced by nodal-line fermions.
Similar content being viewed by others
Introduction
The realization of novel quantum states of matter with nontrivial topology beyond topological insulators has become a significant objective in current condensed-matter physics research.1,2,3 Very recently, the discovery of topological semimetals has achieved this goal, which ignites extensive work focusing on the exotic topological properties and their underlying connection with the electronic structure.4 The topological semimetal states host nontrivial bulk band-crossing points in crystal momentum space.5,6 Characterized by the degeneracy, distribution of the band-crossing points in the Brillouin zone (BZ), and the associated topological boundary states, the topological semimetals can be classified into three categories: Dirac, Weyl, and nodal-line semimetals. In Dirac and Weyl semimetals, the bulk nodes are discrete in the BZ and their surface projections are connected by surface Fermi arcs.4 While in nodal-line semimetals, the bulk nodes extend along one-dimensional curves and the corresponding surface states are flat in dispersion according to the previous nodal-line modelings,7 where the band crossings of a nodal line should occur at zero energy with a constraint chiral symmetry. Hence the flat surface bands are dubbed the drumhead states. However, the chiral symmetry is not exact in a real crystal, resulting in the nodal line does not generally occur at a constant energy, thus the associated topological surface states are not flat either.8,9
The Dirac semimetal and Weyl semimetal states have been theoretically predicted and experimentally verified in various families of compounds.10,11,12,13,14,15,16,17,18,19,20,21 Although there have been several theoretical proposals for the material realization of topological nodal-line semimetal states,4,8,22,23,24 the conclusive experimental proof remains absent until recent angle-resolved photoemission spectroscopy (ARPES) measurements on TiB2,25 showing a tangible realization of bulk nodal-line fermions. Since the surface states associated with the nodal lines are not observed in TiB2,25 the confirmation of the topological nodal-line semimetal state by the coexistence of bulk evidence and surface signature is still desired. In this work, we investigate the electronic structure of ZrB2, which is predicted to host similar nodal-line configurations and surface states to that of TiB2.26,27 By using ARPES and first-principles calculations, we clearly observe two groups of nodal rings embedded in different mirror planes. These rings are further found to be linked with each other along the Γ-K direction. More importantly, we identify distinct surface states emanating from the bulk nodal lines, the surface signatures demonstrate the nontrivial topology of the nodal-line semimetal states in ZrB2.
Compared with the previous nodal-line candidates CaAgAs, PbTaSe2, and the ZrSiS family,28,29,30,31,32,33 ZrB2 has the following advantages: (1) the whole band-crossing features forming the nodal lines are clearly resolved below the Fermi energy (EF) in ZrB2, while the nodes of CaAgAs,28 PbTaSe2,29 and the ZrSiS family30,31,32,33 cannot be observed by ARPES with the crossings located above EF; (2) the nodal-line fermions and their connections with the surface states are observed without any interference from other bands in ZrB2, while in PbTaSe229 and the ZrSiS family,30,31,32,33 the observation of bulk nodal lines is seriously obstructed by surface states. Thus, our experimental discovery in ZrB2 establishes a unique system that has the conclusive evidence of topological nodal-line semimetal states both in the bulk and on the surface.
Results
Structure and transport properties of ZrB2
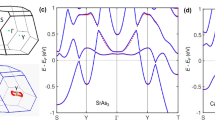
As illustrated in Fig. 1a, ZrB2 crystallizes in a hexagonal lattice system with the space group P6/mmm (No. 191).34 The corresponding bulk and (001)-projected surface BZs are shown in Fig. 1b, where the Γ-K-M and Γ-A-H planes are two mirror planes of D6h group. The flat and shiny surface (inset of Fig. 1c) for our ARPES measurements is the (00l) plane, demonstrated by the single crystal x-ray diffraction (XRD) pattern in Fig. 1c. To further check the chemical composition of our samples, we display the core-level photoemission spectrum in Fig. 1d, where the characteristic peaks of Zr-4p, Zr-5s, and B-2p orbitals are clearly revealed.
Single crystal and electronic structure of ZrB2. a Schematic crystal structure of ZrB2. b Bulk and (001) surface BZs for a hexagonal close-packed structure. c XRD pattern on the (00l) surface. Inset: Picture of a ZrB2 crystal. d The core-level photoemission spectrum measured with 132-eV photons. e Magnetic field dependences of the resistivity and Hall resistivity (inset) at T = 2.5 K, displayed as blue and black curves, respectively. The magnetic field is parallel to the c-axis. The superimposed red curves are the fitting results using the two-carrier model. f Calculated bulk band structure along the high-symmetry lines without SOC. The near-EF band-crossing features of α, β, γ, and δ are indicated
The magnetic field dependences of the resistivity (ρxx) and Hall resistivity (ρxy) at T = 2.5 K are depicted in Fig. 1e and the inset of Fig. 1e, respectively. By fitting the experimental curves with the two-carrier model,35 the estimated densities of electron-type and hole-type carriers are 1.156 (5) × 1021 and 1.153 (5) × 1021 cm−3, respectively, comparable to that of TiB2 (ne, nh ~ 1021 cm−3)25 and the ZrSiS family (ne, nh ~ 1020 cm−3).36,37 Figure 1f presents an overview of the calculated bulk band structure for ZrB2 without the spin-orbit coupling (SOC) effect. Four Dirac-like band-crossing features, which are denoted as α, β, γ, and δ, respectively, give rise to two groups of nodal rings embedded in different mirror planes. When the SOC is included in the calculation, small energy gaps (~40 meV) open at these band crossings.38 We will proceed to a detailed discussion on the nodal-line semimetal states by systematic electronic structure investigations in the following.
Fermi surface (FS) topologies in four high-symmetry planes
We present the measured and calculated FS topologies in Fig. 2. Figure 2d–f shows the FSs recorded with three different photon energies, hν = 132, 94, and 70 eV, which are close to the kz ~ π (FS3), ~0 (FS1), and ~−π (FS2) planes, respectively. By continuously varying the photon energy, we are able to map out the FS in the Γ-A-H plane (FS4), as displayed in Fig. 2b. From the FS1 in the kz ~ 0 plane (Fig. 2e), the r1 nodal rings formed by α and β are clearly observed surrounding K points. From the FS2 and FS3 in the kz ~ ±π planes (Fig. 2d, f), triangular FSs are resolved at H points, which are attributed as the surface states and discussed later, but no sign of the r1 nodal ring is revealed. Another major contrast between FS1 and FS2/FS3 is the absence of intensity around Γ point for the former, and the presence of a circular FS centered at A point for the latter. This difference could be further illuminated by the FS4 in the Γ-A-H plane (Fig. 2b). The FS around A point, which agreeing well with the green-colored FS sheet in the calculation (Fig. 2c, g), arises from a hole-like band presented in Fig. 4. Characterized by these features in experiment, the electronic structure exhibits a prominent three-dimensional (3D) nature, as confirmed by the calculated 3D FSs (Fig. 2g) and their projections on the Γ-A-H plane (Fig. 2c). Since the r2 nodal ring in the Γ-A-H plane formed by γ and δ also pass through the Fermi wave vectors of β, thereby the β band-crossing feature belongs to both the r1 and r2 nodal rings. Consequently, the 3D FS is a nodal-link structure composed of these two nodal rings. Due to the kz broadening effect, which is prominent in ARPES measurements with vacuum ultraviolet light,31,39,40 the ARPES spectra reflects the electronic states integrated over a certain kz region of bulk BZ. Therefore, the (001)-projected r2 nodal rings around Γ/A points are clearly resolved in FS1-FS3 (Fig. 2d–f). Furthermore, the nodal-link point (J) of the r1 and r2 nodal rings along the Γ-K direction is unambiguously recognized in FS1 (Fig. 2e). All the above observations are consistent with the calculated bulk FSs shown in Fig. 2c, g, h.
Experimental and theoretical FSs of ZrB2. a 3D bulk BZ with four high-symmetry planes, which illustrate the momentum locations of the measured FSs in (b, d–f). Cuts 1, 2 and 3–5 indicate the locations of the experimental band structures in Figs. 3 and 4, respectively. b ARPES intensity map [FS4 in (a)] at EF in the hν-k|| plane, where k|| is oriented along the Γ-K (A-H) direction, recorded with various photon energies. a′ = \(\sqrt 3 a\)/2 (a = 3.169 Å). The purple dashed ellipses indicate the hole-like FSs at A points, serving as guides to the eye. c Projections of calculated 3D FSs on the Γ-A-H plane. d–f ARPES intensity plots obtained by hν = 132, 94, and 70 eV, showing FS3, FS1, and FS2 indicated in (a), respectively. The red solid lines indicate the first BZs projected on the (001) surfaces. Two groups of Dirac nodal rings, r1 and r2 [(001)-projection], are resolved. The link points (denoted as J point) of r1 and r2 are indicated by black dashed circles in (e). The blue dashed triangles in (d, f) are guides to the eye for the triangular FSs around H points. g Calculated 3D bulk FSs. h The top view of the calculated 3D FSs, namely the two-dimensional FSs projected on the (001) surface. i Calculated FS contours of the (001) surface for a 20-unit-cell-thick slab with Zr terminations. The intensity of the red color scales the spectral weight projected to the topmost unit cell. The blue solid lines represent the (001) surface BZs
In addition, we observe that some FS features in the kz ~ ±π planes (FS2 and FS3) are absent in the calculated bulk FSs, i.e., the triangular FSs around H points, the FS sheets between two H points, and the hexagonal FS centered at A point (relatively weak in FS3 due to the matrix element effect and its presence can be proved in Fig. 2b). As illustrated in the hν-k|| [k|| is oriented along the Γ-K (A-H) direction] ARPES intensity plot in Fig. 2b, the Fermi crossings of the hexagonal FS do not show noticeable photon-energy dependence over a wide range (65–140 eV), which is an indication of surface state. This result inspires us to carry out surface state spectrum calculations for a (001)-oriented 20-unit-cell-thick slab terminated by Zr layers. The calculated surface state FSs presented in Fig. 2i well reproduce these three experimental FS topologies, demonstrating their surface state origins.
Presence of bulk nodal-line fermions below E F
Based on the discussion above, the r1 nodal rings can only be observed in the kz ~ 0 plane. This character establishes an excellent system to separately investigate the bulk nodal lines and electronic surface states. Now we record the near-EF ARPES spectra along the Γ-K and M-K directions, which are indicated as cuts 1 and 2 in Fig. 2a, respectively, in the kz ~ 0 plane (FS1) to prove the presence of bulk nodal-line fermions in ZrB2. The intensity plots and corresponding second derivative plots are shown in Fig. 3a–d. The electronic structure near EF is only composed of the α and β band-crossing features forming the r1 nodal rings, except a band dispersing from the crossing point of β along the Γ-K direction, which is relatively weak when crossing EF due to the matrix element effect and thus not resolved in the FS mapping data in Fig. 2e. This band is identified as the surface state and discussed later. We then plot the momentum distribution curves (MDCs) of β and α in Fig. 3e, f, respectively. The linear dispersions in a large energy range with the crossing points below EF are unambiguously recognized. By comparing with the superimposed bulk band calculations in Fig. 3b, d one can obtain a high consistency between experiment and theory, which provides further evidence for the experimental realization of bulk nodal-line fermions in ZrB2. As for the hole-like band ~2.5 eV below EF at M point (Fig. 3c, d), due to the kz broadening effect in ARPES, it derives from the projection of the band along the H-L-H direction with a similar feature in Fig. 4c, which is well reproduced by the calculation.
Band structure of the r1 nodal ring. a, b Photoemission intensity plot and corresponding second derivative plot along the Γ-K direction (cut 1 in Fig. 2a) recorded with hν = 94 eV, respectively, where SS is short for surface state. (c, d) Same as (a, b), respectively, but along the M-K direction (cut 2 in Fig. 2a). The appended red curves in (b, d) are calculated bulk band dispersions without SOC. The band-crossing features along the M-K and Γ-K directions are denoted as α and β, respectively. e, f MDC plots of β and α, which are taken around the right ones in (a, c), respectively. The blue dashed lines indicate the linear dispersions. The band-crossing points are highlighted by the black curves. The solid triangles in (e) are extracted peak positions, serving as guides to the eye for the surface state emanating from the node of β
Electronic surface states in the kz ~ −π plane. a, c, e Photoemission intensity plots along the A-H, L-H, and A-L directions (cuts 3–5 in Fig. 2a) measured with hν = 70 eV, respectively. The appended red curves are calculated bulk band dispersions without SOC. The white dashed curves in (a, e) indicate the SS3 at A point, serving as guides to the eye. The red and blue solid circles in (a, c) represent the crossing points of β and α, whose positions are determined by the MDCs in Fig. 3e, f, respectively. b, d, f Calculated band structure along the \({\bar{\mathrm \Gamma }}\)-\(\bar K\), \(\bar M\)-\(\bar K\), and \({\bar{\mathrm \Gamma }}\)-\(\bar M\) directions for a 20-unit-cell-thick (001) slab with Zr terminations, respectively. The intensity of the red color scales the spectral weight projected to the topmost unit cell
Electronic surface states associated with the bulk nodal lines
Next, from the perspective of surface signature, we demonstrate the nontrivial topology of the nodal-line semimetal states in ZrB2 by investigating the surface states revealed in the kz ~ −π plane (FS2). In Fig. 4a, c, e, we present the experimental band dispersions with overlapped bulk band calculations along the A-H, L-H, and A-L directions, as indicated by cuts 3–5 in Fig. 2a, respectively. Besides the well-reproduced bulk bands, there are some extra bands (SS1–SS3) not existing in the bulk calculations. According to the experimental FSs measured in the kz ~ ±π planes (FS2 and FS3), we can determine the origins of the crossing-EF ones among these bands, i.e., the SS1 corresponds to the triangular FS around H point, and the SS2 forms the hexagonal FS surrounding A point and the FS sheet between two H points, respectively. To further understand the three extra bands, we perform 20-unit-cell-thick slab model calculations with Zr-terminated layers. The calculated band dispersions along the \({\bar{\mathrm \Gamma }}\)-\(\bar K\), \(\bar M\)-\(\bar K\), and \({\bar{\mathrm \Gamma }}\)-\(\bar M\) directions with spectral weight from the topmost unit cell are plotted in Fig. 4b, d, f, respectively, which can reproduce SS1–SS3 very well and confirm their surface state nature.
Discussion
In order to clarify the nontrivial topology of the bulk nodal lines realized in ZrB2, which are protected by the mirror-reflection symmetries and the combination of spatial-inversion symmetry (P) and time-reversal symmetry (T), i.e., the P·T symmetry, here we illustrate the connection between the nodal lines and the surface states by combining both the bulk and surface observations. We plot the crossing points of β and α as the red and blue solid circles in Fig. 4a, c, whose positions are extracted from the MDCs in Fig. 3e, f, respectively. We can observe that the bulk nodes of β and α exactly locate on the loci of the surface states resolved in the kz ~ −π plane. Along the A-H direction (Fig. 4a), starting from the node of β, the SS2 disperses inwards with respect to A point. This behavior resembles that of the extra band observed along the Γ-K direction in Fig. 3, showing its (the extra band around Γ point) surface state origin associated with the bulk nodal line. Along the L-H direction (Fig. 4c), the SS1 passing through the node of α disperses outwards with respect to L point. The bulk nodes and the surface state spectra are obtained from two independent measurements carried out in different high-symmetry planes, therefore the discovery of their well match provides convincing evidence for the topological nature (the bulk-boundary correspondence8,22,41) of the nodal-line semimetal states in ZrB2.
In summary, our direct experimental observation by ARPES presents conclusive evidence of the bulk nodal-line fermions in ZrB2 with negligible SOC effect. Under the protection of the mirror-reflection symmetries and the P·T symmetry, the electronic structure hosts two groups of Dirac nodal rings, which are linked together along the Γ-K direction. Meanwhile, we clearly resolve electronic surface state emanating from each nodal line, proving the nontrivial topology of the bulk nodal lines. With the experimental realization of topological nodal-line semimetal states in ZrB2 powerfully supported by both the bulk evidence and the surface signature, we establish an ideal material platform for studying the novel physics and exotic properties related to nodal lines.
Methods
Sample synthesis
High-quality single crystals of ZrB2 were grown via the Fe flux method.38 The starting elements of Zr (99.95%), B (99.99%), and Fe (99.98%) were put into an alumina crucible, with a molar ratio of Zr:B:Fe = 3:6:17. The mixture was heated up to 1873 K in a high-purity argon atmosphere and then slowly cooled down to 1623 K at a rate of 4 K/h. The ZrB2 single crystals were separated from the Fe flux using the hot hydrochloric acid solution.
ARPES measurements
ARPES measurements were performed at the Dreamline beamline of the Shanghai Synchrotron Radiation Facility using a Scienta D80 analyzer and at the beamline 13U of the National Synchrotron Radiation Laboratory equipped with a Scienta R4000 analyzer. The energy and angular resolutions were set to 25 meV and 0.2°, respectively. Fresh surfaces for ARPES measurements were obtained by cleaving the samples in situ along the (001) plane. All spectra presented in this work were recorded at T = 20 K in a working vacuum better than 5 × 10−11 Torr.
Band structure calculations
First-principles calculations were carried out with the projector augmented-wave method42,43 as implemented in the Vienna ab initio Simulation Package.44 The generalized gradient approximation of Perdew-Burke-Ernzerhof formula45 was adopted for the exchange-correlation functional. The kinetic energy cutoff of the plane-wave basis was set to be 420 eV. A 20 × 20 × 20 k-point mesh was utilized for the BZ sampling. The bulk FSs were investigated by adopting the maximally localized Wannier function method.46 A slab with thickness of 20 unit cells along the [001] direction was used in our surface state calculations. The slabs were separated by a vacuum layer of 20 Å, which was sufficient to avoid the interactions between different slabs. SOC effect38 was not taken into account in all the above calculations.
Data availability
All relevant data are available from the corresponding authors upon request.
Change history
12 October 2018
The original version of this Article did not acknowledge Qi Wang as an equally contributing author. This has now been corrected in the HTML and PDF versions of the Article.
References
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045 (2010).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057 (2011).
Weng, H., Dai, X. & Fang, Z. Exploration and prediction of topological electronic materials based on first-principles calculations. MRS Bull. 39, 849–858 (2014).
Weng, H., Dai, X. & Fang, Z. Topological semimetals predicted from first-principles calculations. J. Phys. Condens. Matter 28, 303001 (2016).
Volovik, G. E. The Universe in a Helium Droplet. (Oxford University Press, Oxford, 2009).
Fang, Z. et al. The anomalous Hall effect and magnetic monopoles in momentum space. Science 302, 92–95 (2003).
Ryu, S. & Hatsugai, Y. Topological origin of zero-energy edge states in particle-hole symmetric systems. Phys. Rev. Lett. 89, 077002 (2002).
Fang, C., Weng, H. M., Dai, X. & Fang, Z. Topological nodal line semimetals. Chin. Phys. B 25, 117106 (2016).
Li, R. et al. Dirac node lines in pure alkali earth metals. Phys. Rev. Lett. 117, 096401 (2016).
Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Wang, Z. et al. Dirac semimetal and topological phase transitions in A 3Bi (A = Na, K, Rb). Phys. Rev. B 85, 195320 (2012).
Weng, H., Fang, C., Fang, Z., Bernevig, B. A. & Dai, X. Weyl semimetal phase in noncentrosymmetric transition-metal monophosphides. Phys. Rev. X 5, 011029 (2015).
Huang, S.-M. et al. A Weyl Fermion semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class. Nat. Commun. 6, 7373 (2015).
Soluyanov, A. A., Gresch, D., Wang, Z., Wu, Q. S. & Troyer, M. Type-II Weyl semimetals. Nature 527, 495–498 (2015).
Chang, G. et al. Universal topological electronic properties of nonmagnetic chiral crystals. arXiv 1611.07925 (2016).
Liu, Z. K. et al. Discovery of a three-dimensional topological Dirac semimetal, Na3Bi. Science 343, 864–867 (2014).
Borisenko, S. et al. Experimental realization of a three-dimensional Dirac semimetal. Phys. Rev. Lett. 113, 027603 (2014).
Lv, B. Q. et al. Experimental discovery of Weyl semimetal TaAs. Phys. Rev. X 5, 031013 (2015).
Xu, S.-Y. et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 349, 613–617 (2015).
Lv, B. Q. et al. Observation of Weyl nodes in TaAs. Nat. Phys. 11, 724–727 (2015).
Yang, L. X. et al. Weyl semimetal phase in the non-centrosymmetric compound TaAs. Nat. Phys. 11, 728–732 (2015).
Burkov, A. A., Hook, M. D. & Balents, L. Topological nodal semimetals. Phys. Rev. B 84, 235126 (2011).
Yang, S.-Y. et al. Symmetry demanded topological nodal-line materials. Adv. Phys.: X 3, 1414631 (2018).
Yu, R., Fang, Z., Dai, X. & Weng, H. Topological nodal line semimetals predicted from first-principles calculations. Front. Phys. 12, 127202 (2017).
Liu, Z.-H. et al. Experimental observation of Dirac nodal links in centrosymmetric semimetal TiB2. Phys. Rev. X, 8, 031044 (2018).
Zhang, X., Yu, Z. M., Sheng, X. L., Yang, H. Y. & Yang, S. A. Coexistence of four-band nodal rings and triply degenerate nodal points in centrosymmetric metal diborides. Phys. Rev. B 95, 235116 (2017).
Feng, X., Yue, C., Song, Z., Wu, Q. & Wen, B. Topological Dirac nodal-net fermions in AlB2-type TiB2 and ZrB2. Phys. Rev. Mater. 2, 014202 (2018).
Wang, X.-B. et al. Topological surface electronic states in candidate nodal-line semimetal CaAgAs. Phys. Rev. B 96, 161112(R) (2017).
Bian, G. et al. Topological nodal-line fermions in spin-orbit metal PbTaSe2. Nat. Commun. 7, 10556 (2016).
Schoop, L. M. et al. Dirac cone protected by non-symmorphic symmetry and three-dimensional Dirac line node in ZrSiS. Nat. Commun. 7, 11696 (2016).
Takane, D. et al. Dirac-node arc in the topological line-node semimetal HfSiS. Phys. Rev. B 94, 121108(R) (2016).
Lou, R. et al. Emergence of topological bands on the surface of ZrSnTe crystal. Phys. Rev. B 93, 241104(R) (2016).
Hosen, M. M. et al. Tunability of the topological nodal-line semimetal phase in ZrSiX-type materials (X = S, Se, Te). Phys. Rev. B 95, 161101(R) (2017).
Post, B., Glaser, F. W. & Moskowitz, D. Transition metal diborides. Acta Metall. 2, 20–25 (1954).
Xia, B. et al. Indications of surface-dominated transport in single crystalline nanoflake devices of topological insulator Bi1.5Sb0.5Te1.8Se1.2. Phys. Rev. B 87, 085442 (2013).
Hu, J. et al. Evidence of topological nodal-line fermions in ZrSiSe and ZrSiTe. Phys. Rev. Lett. 117, 016602 (2016).
Hu, J. et al. Nearly massless Dirac fermions and strong Zeeman splitting in the nodal-line semimetal ZrSiS probed by de Haas-van Alphen quantum oscillations. Phys. Rev. B 96, 045127 (2017).
Wang, Q. et al. Extremely large magnetoresistance and high-density Dirac-like fermions in ZrB2. Phys. Rev. B 97, 205105 (2018).
Strocov, V. N. Intrinsic accuracy in 3-dimensional photoemission band mapping. J. Electron Spectrosc. Relat. Phenom. 130, 65–78 (2003).
Kumigashira, H. et al. High-resolution angle-resolved photoemission study of LaSb. Phys. Rev. B 58, 7675 (1998).
Weng, H. et al. Topological node-line semimetal in three-dimensional graphene networks. Phys. Rev. B 92, 045108 (2015).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 48, 13115 (1993).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Souza, I., Marzari, N. & Vanderbilt, D. Maximally localized Wannier functions for entangled energy bands. Phys. Rev. B 65, 035109 (2001).
Acknowledgements
The work was supported by the National Key R&D Program of China (Grants No. 2016YFA0300504 and No. 2017YFA0302903), the National Natural Science Foundation of China (Grants No. 11774421, No. 11574394, No. 11774423, No. 11774424, No. 11227902, and No. 11704394), and the Chinese Academy of Sciences (CAS) (Project No. XDB07000000). R.L., K.L., and H.L. were supported by the Fundamental Research Funds for the Central Universities, and the Research Funds of Renmin University of China (RUC) (Grants No. 17XNH055, No. 14XNLQ03, No. 15XNLF06, and No. 15XNLQ07). Y.H. was supported by the CAS Pioneer Hundred Talents Program. Z.L. acknowledges Shanghai Sailing Program (No. 17YF1422900).
Author information
Authors and Affiliations
Contributions
R.L., H.C.L., Y.B.H., H.D., and S.C.W. conceived the experiments. R.L. performed ARPES measurements with the assistance of M.L., Z.H.L., X.C.W., Z.L.W., Z.S., and D.W.S. P.J.G., K.L., and Z.Y.L. performed first-principles calculations. Q.W., S.S.S., C.H.L., and H.C.L. synthesized the single crystals. R.L., H.C.L., and S.C.W. analysed the experimental data. R.L. plotted the figures. R.L. and S.C.W. wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lou, R., Guo, P., Li, M. et al. Experimental observation of bulk nodal lines and electronic surface states in ZrB2. npj Quant Mater 3, 43 (2018). https://doi.org/10.1038/s41535-018-0121-4
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-018-0121-4
This article is cited by
-
Ultrafast relaxation of acoustic and optical phonons in a topological nodal-line semimetal ZrSiS
Communications Physics (2022)
-
Low-dimensional electronic state at the surface of a transparent conductive oxide
Communications Physics (2022)
-
Hidden bulk and surface effects in the spin polarization of the nodal-line semimetal ZrSiTe
Communications Physics (2021)
-
Intrinsic in-plane nodal chain and generalized quaternion charge protected nodal link in photonics
Light: Science & Applications (2021)
-
Topological materials discovery from crystal symmetry
Nature Reviews Materials (2021)