Abstract
Resolving the microscopic pairing mechanism and its experimental identification in unconventional superconductors is among the most vexing problems of contemporary condensed matter physics. We show that Raman spectroscopy provides an avenue towards this aim by probing the structure of the pairing interaction at play in an unconventional superconductor. As we study the spectra of the prototypical Fe-based superconductor Ba1−xKxFe2As2 for 0.22 ≤ x ≤ 0.70 in all symmetry channels, Raman spectroscopy allows us to distill the leading s-wave state. In addition, the spectra collected in the B1g symmetry channel reveal the existence of two collective modes which are indicative of the presence of two competing, yet sub-dominant, pairing tendencies of \(d_{x^2 - y^2}\) symmetry type. A comprehensive functional Renormalization Group and random-phase approximation study on this compound confirms the presence of the two sub-leading channels, and consistently matches the experimental doping dependence of the related modes. The consistency between the experimental observations and the theoretical modeling suggests that spin fluctuations play a significant role in superconducting pairing.
Similar content being viewed by others
Introduction
In superconductors such as the cuprates, ferro-pnictides, ruthenates, or heavy-fermion systems, the pairing mechanism is believed to be unconventional and related to direct electronic interactions rather than conventional electron–phonon mediated couplings. Yet, the precise microscopic mechanism, the “glue” that binds electrons into Cooper pairs, remains elusive. Measurements of the superconducting ground state alone are insufficient to unambiguously determine whether a superconductor has a conventional or unconventional pairing mechanism. Raman spectroscopy provides the avenue for gathering the missing information in both dominant and sub-dominant pairing channels.
In comparison to other techniques, Raman spectroscopy (which involves inelastic scattering of light) is rather unique as it provides access to both the energy gaps of a superconductor and to bound states inside the gaps1 that serve as signposts marking the strength of a given pairing interaction.
These bound states were predicted a long time ago by Bardasis and Schrieffer (BS)2 and are collective excitations that correspond to the phase oscillations of the ground state order parameter triggered by the sub-dominant (d-wave) interactions. The BS modes or particle-particle excitons couple to the Raman probe, but there is no consensus yet about their observation in conventional superconductors.3,4 Fe-based superconductors (FeSCs), however, presented a more favorable scenario to search for this physics as many of them are believed to exhibit s± pairing (with an order parameter that may change sign between Fermi surface pockets5,6,7,8,9) and also a sub-leading d-wave pairing interaction that can be strongly competitive. Theoretical calculations based on spin fluctuations have even argued that d-wave could become the ground state for sufficiently strong hole-doping.10,11
For these reasons, Scalapino and Devereaux12 performed a “bare-bones” calculation for a typical FeSC electronic structure with s± symmetry of the ground state and anisotropic gaps, showing that the mode frequency should depend on 1/λd − 1/λs, where λd and λs are the respective coupling strengths of the electrons to the glue that binds the Cooper pair in the d-wave and the s-wave channel. Recent measurements on Ba1−xKxFe2As2,4,13,14 NaFe1−xCoxAs,15 Ba(Fe1−xCox)2As216,17 found peaks in the B1g spectrum which were consistent with a collective mode, but its direct association with a BS mode was unclear.
In this work, we confirm the presence of two sub-dominant pairing interactions, as predicted theoretically, by providing an identification of multiple BS modes in the B1g spectrum of the prototypical ferro-pnictide Ba1−xKxFe2As2 (BKFA). Each sub-dominant pairing interaction results in a BS mode.18 This perspective underlies our identification of the two new peaks in the Raman spectrum with B1g BS modes. The analysis of our experimental peak energies also supports this scenario and even allows us to empirically extract the relative coupling strengths, λd(1)/λs and λd(2)/λs, of the two distinct B1g \(\left( {d_{x^2 - y^2}} \right)\) pairing channels competing with the s± ground state. We could reproduce the presence of all three pairing channels by performing a functional Renormalization Group (fRG) as well as a Random Phase Approximation (RPA) study. Since the fRG calculation includes the leading fluctuations (magnetic, superconducting, charge density wave etc.) whereas the RPA is distinctly based on magnetically driven (i.e., spin-fluctuation-induced) pairing, the agreement of both approaches with each other and the experiment strongly points to a spin-fluctuation scenario in BKFA. Since a direct observation of spin fluctuations below Tc is not achievable by Raman scattering (the relevant scattering states are gapped out) we study the BS modes which remain as the fingerprints of the microscopic pairing interactions.
Results
Experiments
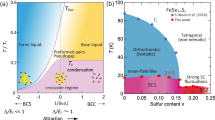
To this end we measured eight samples of BKFA in the wide doping range 0.22 ≤ x ≤ 0.70 as indicated in Fig. 1a and described in detail in Sec. II of the Supplementary Information. BKFA forms high quality single crystals19,20,21 and fairly clean and isotropic gaps.22,23 In the samples with x = 0.22 and x = 0.25 superconductivity and the spin density wave (SDW) state coexist. The samples with x = 0.62 and x = 0.70 are above the doping level of x = 0.6, where EF reaches the bottom of the inner electron band and the topology of the Fermi surface changes qualitatively.24 To present the case for the physics of sub-dominant pairing interactions, we wish to stay away from special effects arising from magnetism or disappearance of pockets and focus on the samples with x = 0.35, 0.40, 0.43, 0.48. In this range, the Raman spectra in the B1g symmetry channel (1 Fe unit cell) change continuously as shown in Fig. 2a–d. Spectra of the other symmetries and outside the range 0.35 ≤ x ≤ 0.48 are compiled in Sec. IV of the Supplementary Information.
Phase diagram and schematics of doping dependent Fermi surfaces in Ba1−xKxFe2As2. a The sampling points of the measurements are compiled in the phase diagram38 as blue and red dots deep in the superconducting state and slightly above Tc, respectively. b, c Schematic Brillouin zone and Fermi surface in the 1 Fe unit cell. With increasing hole-doping x the hole pockets (blue) grow and the electron pockets (red) shrink (changes exaggerated)
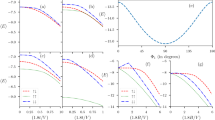
Doping dependence of the Raman spectra in B1g symmetry. a–d Raman response Rχ″(Ω, T, x) (raw data after division by the Bose–Einstein factor) of Ba1−xKxFe2As2 in B1g symmetry above (red) and below (blue) Tc close to optimal doping in the range x = 0.35 to x = 0.48. e Difference spectra ΔRχ″(Ω, x) in B1g symmetry. The energy scale is normalized to the respective Tc values of the differently doped samples. The intensities are off-set, the dashed horizontal lines mark zero. The purple arrows indicate the pair-breaking features at high energy. Green and orange arrows mark two BS modes pulled off the energy gap. They correspond to the sub-dominant channels d(1) and d(2), respectively
The spectra above the superconducting transition temperature Tc are dominated by the electron-hole continua. Below Tc additional (symmetry-dependent) structures appear in the energy range up to ~300 cm−1, and the spectral weight is redistributed from below twice the superconducting gap 2Δ to energies above. New features arise from pair breaking, excitations across the gap, and exciton-like bound states.1,4,18 With increasing doping and a concomitant reduction of Tc, the peaks move to lower energies.
To illustrate why BKFA is a model superconductor for investigating BS modes we highlight the changes in the electronic spectra below Tc. For this purpose we subtract the normal state response from the superconducting spectra. This procedure elimantes temperature-independent components of the spectra like phonons in A1g and B2g symmetry (see Sec. IV of the Supplementary Information). By plotting the difference \({\mathrm{\Delta }}R\chi ^{\prime\prime} ({\tilde{\mathrm \Omega }})\) ≡ \(R\chi ^{\prime\prime} ({\tilde{\mathrm \Omega }},T \leq 10{\kern 1pt} {\mathrm{K}})\) − \(R\chi ^{\prime\prime} ({\tilde{\mathrm \Omega }},T \geq T_c)\) in Fig. 2e with \({\tilde{\mathrm \Omega }}\) = ħΩ/kBTc we extract superconductivity-induced features of pure B1g symmetry. Due to the full gap, the difference spectra become negative at low energies and three pronounced peaks are observed. The differences between normal and superconducting spectra disappear (ΔRχ″ → 0) close to \({\tilde{\mathrm \Omega }} = 8\). The highest peak (purple arrows in Fig. 2e) at ~6.2, which we identify with the maximal gap, depends weakly on doping. The range of 2Δ/kBTc ≃ 6.2 is in qualitative agreement with the results from other methods.22,23,25 There are two additional narrow lines in the ranges 1.5–3 (green arrows) and 4–5.5 (orange arrows) displaying a strong monotonic downshift with increasing K content. At optimal doping (x = 0.40), evidence was furnished that the narrow line at \({\tilde{\mathrm \Omega }} = 5.3\) (140 cm−1 in Fig. 2b) results from a bound state of two electrons of a broken Cooper pair.4
Along with the line at \({\tilde{\mathrm \Omega }} = 5.3\), we find another narrow line in B1g symmetry at \({\tilde{\mathrm \Omega }} = 2.8\) (75 cm−1 in Fig. 2b), which is difficult to properly assign on the basis of just one doping level. In ref.4 it was suggested that this peak originates in pair-breaking. However, upon studying several doping levels and all symmetries (Secs. IV and V of the Supplementary Information) we find the following systematics in favor of two BS modes: (i) The two in-gap modes appear only in B1g symmetry. (ii) As opposed to the pair-breaking maxima at ~6kBTc there are no other gap energies observed the two sharp modes could correspond to. (iii) The spectral weights of both modes depend on their binding energies as predicted by theory (see Sec. VI of the Supplementary Information). (iv) Upon doping K for Ba the in-gap modes increasingly split off of the pair-breaking maximum. The nearly identical doping dependences of the two modes and the absence of pair-breaking features in other symmetries suggest that both modes are linked to the maximal gap. The unique appearance of narrow BS modes in B1g symmetry for 0.35 ≤ x ≤ 0.48 indicates that there are sub-dominant interactions with d-wave symmetry. We label the corresponding sub-leading B1g channels as d(1) and d(2) for the lower- and the higher-energy line, respectively.
In Fig. 3a we compile experimental peak energies derived from Fig. 2. The difference between 2Δ (purple) and the BS modes in the range 1.5–5.5kBTc (green and orange) corresponds to the binding energies Eb(i) = 2Δ − ΩBS(i) with i = 1, 2 of the bound states. The ratios of the relative coupling strengths λd(i)/λs are estimated from Eb(i)/2Δ using the results of refs.3,4,12 and λs = 0.7 from refs.26,27. Note that we used a doping-independent value of 0.7 for this estimate as the ratios λd(i)/λs are weakly sensitive to small changes of λs (see Sec. VI of the Supplementary Information). This analysis enables us to check the validity of the RPA and fRG approaches in a system with intermediate coupling strength.
Gap energies and relative coupling strengths. a Doping dependence of the characteristic B1g gap energies. The highest pair-breaking energy ΩPB scales approximately with Tc. The maxima at ΩBS(1) and ΩBS(2) inside the gap decrease faster than Tc. b, c Relative coupling parameters of the sub-dominant (λd(i)) and the dominant (λs) channel. With a dominant interaction of λs = 0.7,26,27 the ratios for λd(i)/λs are extracted from the experiment (open green and orange symbols, corresponding to d(1) and d(2), respectively). The green and orange dots represent results from fRG and RPA18 calculations in panels (b, c), respectively
Theory
According to ref.18, the presence of two BS modes in the same symmetry channel must imply the presence of two pairing interactions with different form factors competing with the ground state. Thus in addition to the ratios λd(i)/λs derived from experiment, we show in Fig. 3b, c the results of two microscopic studies using fRG and RPA schemes that precisely identify these pairing channels and also provide an estimate for λd(i)/λs.
In order to determine the hierarchy of pairing interactions from the effective pairing vertex V from either fRG or RPA, we decompose this pairing channel into eigenmodes, which is tantamount to solving an eigenvalue problem of the form
where k comprises momentum, band, and spin degrees of freedom, and α is the index consecutively numbering the different eigenvalues. We assume α to be ordered according to the magnitude of eigenvalues λα. gα(k) is the pairing eigenvector along the Fermi surfaces specifying the symmetry of the pairing. More details can be found in Sec. I of the Supplementary Information.
From both fRG and RPA, we find λs, gs(k) (α = 1) to be the dominant superconducting pairing of A1g (s±) type and λd(1,2), gd(1,2)(k) (α = 2, 3) the sub-leading B1g type couplings. Schematic eigenvectors gα(k) for α = 1, 2, 3 are shown as insets in Fig. 3a. These results apply to both \(V \equiv V_{{\mathrm{fRG}}}^{\mathrm{\Lambda }}\) and V ≡ VRPA when used in Eq. (1), where Λ is the low-energy cutoff in the fRG flow that serves as an upper bound for the transition temperature28,29 (see also Sec. I of the Supplementary Information). The leading eigenvalue λs ≡ λ1 in Eq. (1), which is a function of Λ in the case of fRG, then determines the leading Fermi surface instability. The ratios of the eigenvalues λd(1,2)/λs ≡ λ2,3/λ1 determine the peak positions of the BS modes and are shown along with the experiments in Fig. 3b, c. Note that λ2 ≡ λd1 fits the extended d-wave harmonic form predicted in ref.10.
Discussion
Arguably the most critical and presumably controversial part of this research is the identification of the in-gap modes observed in B1g symmetry. There are essentially four proposals for the explanation of narrow modes close to or below the gap edge 2Δ, where we assume that the gap on a given band is nearly isotropic in BKFA in accordance with experiment:25 (i) Josephson-like number-phase oscillations of Cooper pairs between the electronic bands are expected for a multi-band system (Leggett mode).30 In the ferro-pnictides they appear in A1g symmetry close to 2Δ for the dominating interband pairing and are strongly damped.31 Experimentally they cannot be distinguished from the pair-breaking peak since the relative intensity of the two effects is not obvious. (ii) For an s± gap an exciton-like narrow mode is predicted to appear in A1g symmetry below the pair-breaking peak.32 Since the materials are very clean with the elastic scattering rate ħ/τ much smaller than Δ it should not be overdamped and be as clearly visible as the B1g collective modes. We did not find indications thereof even upon using various laser lines (see Sec. III of the Supplementary Information). (iii) In the presence of nematic fluctuations the intensity close to the gap edge is predicted to be enhanced in the related B1g channel at a putative quantum critical point.17 In Ba(Fe1−xCox)2As2 the intensity of the B1g response is indeed enhanced close to optimal doping. However, the A1g intensity follows the B1g intensity33 in contrast to the expectation. In NaFe1−xCoxAs a very strong mode close to the gap edge was observed below Tc. The mode appears only along with the response of nematic fluctuations above Tc.15 Yet, the variation with doping of both intensity and energy of this mode is distinctly different from that in BKFA. In addition, the response from fluctuations in BKFA is already very weak for x = 0.2233 and can safely be excluded to exist for 0.35 ≤ x ≤ 0.7. Therefore, the modes in NaFe1−xCoxAs have an origin different from that in BKFA. (iv) Phase oscillations of the order parameter first described by Bardasis and Schrieffer2 entail δ-like in-gap modes in the case of a clean gap appearing in symmetry channels orthogonal to that of the ground state. For the Fermi surface structure of the ferro-pnictides they are expected in B1g symmetry as observed experimentally here. We provide additional arguments in favor of this interpretation now thus extending the detailed quantitative discussion of ref.4 to all doping levels relevant here.
Bound states are generally expected in the presence of competing interactions.2,12 They complete the excitation spectrum of a superconductor and are similar to excitons in a semiconductor. The identification of BS modes and their differentiation from other collective excitations is possible through various characteristic properties. These include the BCS-like temperature dependence of a resolution-limited line in materials having a clean gap. In contrast, the pair-breaking maximum is broad and does not normally follow the BCS prediction4 since the peak energy depends on the gap, the concentration of impurities,34 and on interactions.35 In addition, the BS mode drains spectral weight from the pair-breaking maximum in agreement with theoretical predictions3,12 (see Fig. S10a1–d3 of the Supplementary Information). The transfer of spectral weight and the fitting of the two BS modes is only qualitatively captured by the phenomenology proposed earlier (see Fig. S10e of the Supplementary Information) and may eventually be improved by future 3D calculations. Finally, the spectral weight of BS modes does not increase monotonically with increasing coupling strength of the bound state but, rather, has a maximum for intermediate coupling (see Fig. S9 of the Supplementary Information). Obviously all criteria could be observed experimentally and we feel on safe ground for comparing the doping dependences of the observed modes with model calculations based on fRG and RPA schemes.
The comparison of the two independent theoretical approaches allows us to pin down the origin of the leading pairing channel since the fRG includes all interactions28,29, whereas the RPA focuses on the spin sector as spelled out in detail in Sec. I of the Supplementary Information. Another difference becomes apparent in the procedure used to determine the effective interaction potential. The fRG analysis is designed to start its unbiased Renormalization Group flow already at energies above the bandwidth while the effective model scale entering the RPA resummation has to be chosen at comparably lower energies (see Sec. I of the Supplementary Information). As it turns out, however, in spite of these differing initializations, transcending further down to energies at which superconductivity occurs yields similar findings for both methods.
From the plethora of theories intended to describe the iron-based superconductors, the comparison with the experiment now enables us, as a first step, to verify the validity of fRG and RPA for the intermediately coupled electronic system of BKFA. We find in accordance with our experiments that both approaches predict an s-wave ground state and the two strongest sub-leading channels to be of d-wave symmetry. Furthermore, the theoretical predictions for the relative coupling parameters as shown in Fig. 3 are in good agreement with the experiment. The fRG results are in quantitative agreement, the RPA values systematically underestimate the relative coupling strength but are still close to the experiment. Hence we conclude that fRG and RPA are suitable to describe the experiment around optimal doping, 0.35 ≤ x ≤ 0.48, where the two collective BS modes can be identified. Besides the agreement with the experiment the fRG interaction eigenvectors gα(k) match very well with those obtained from the spin-fluctuation-based RPA analysis in all three channels (α = 1, 2, 3). These agreements indicate that spin fluctuations are an important if not the leading interaction in the system under consideration.
The results presented here put narrow constraints on the description of the Raman data and render differing interpretations15,17 rather unlikely to be applicable to BKFA. Hence, the observation of two collective modes inside the gap of a superconductor establishes a novelty in terms of experimental analysis which promises to have an impact on the general understanding of unconventional superconductivity. Along with the magnitude of the gap, the modes reveal the hierarchy of pairing states in a prototypical material, in full agreement with microscopic predictions. As a result, our experiment demonstrates the unique possibilities of using light scattering as a probe for observing unconventional pairing fingerprints.
Methods
In this joint experimental and theoretical study we compare results of electronic Raman spectroscopy with predictions of two independent simulations, a fRG analysis and spin-fluctuation theory in the RPA.
Light scattering
The experiments were performed with calibrated light scattering equipment.1 For excitation a solid state laser (Coherent, Genesis MX SLM) was used emitting at 575 nm. A few experiments at optimal doping (x = 0.40) were performed with additional laser lines at 532 (Coherent, Sapphire 532 SF), 514 and 458 nm (Coherent, Innova 304C) in order to scrutinize the resonance behavior as described in Sec. III of the Supplementary Information. The samples were mounted on the cold finger of a He-flow cryostat in a cryogenically pumped vacuum. The laser-induced heating was determined experimentally to be close to 1 K per mW absorbed laser power (see ref.36). Spectra were measured in the four polarization configurations xy, x′y′, RR, and RL where x and y are along the Fe-Fe bonds, \(x^\prime = 1{\mathrm{/}}\sqrt 2 \left( {x + y} \right)\), \(y^\prime = 1{\mathrm{/}}\sqrt 2 \left( {y - x} \right)\), and \(R{\mathrm{/}}L = 1{\mathrm{/}}\sqrt 2 \left( {x \pm iy} \right)\). All symmetry components (A1g, A2g, B1g, and B2g for tetragonal Ba1−xKxFe2As2) can be extracted using linear combinations of the experimental spectra. For the symmetry assignment we use the 1 Fe per unit cell (cf. Fig. 1b for the corresponding BZ).16,37 The spectra we show within this work represent the response Rχ″(Ω, T) which is obtained by dividing the cross section by the Bose–Einstein factor {1 + n(T, Ω)} = [1 − exp(−ħΩ/kBT)]−1 in which R is an experimental constant. In some cases we isolate superconductivity-induced contributions by subtracting the response measured at T ≳ Tc from the spectra taken at \(T \ll T_c\) and label the difference spectra ΔRχ″(Ω, T).
Theory
For analyzing the Cooper pairing in the ferro-pnictides we studied two microscopic models which allow us to disentangle the various contributions to the interaction potential \(V_{{\bf{k}},{\bf{k}}^\prime }\). This disentanglement becomes possible since the scheme of the fRG analysis28,29 includes all possible interactions a priori in an unbiased fashion whereas the RPA scheme focusses on spin fluctuations. We are aware that both models are valid only in the weak coupling limit but we believe that the essential physics is captured correctly. Either approach leads to an eigenvalue equation (see Eq. (1)) which yields a hierarchy of eigenvalues and the related eigenvectors. (For technical details see Sec. I of the Supplementary Information.) Upon comparing the results the relative influence of the various pairing tendencies can be estimated.
Data availability
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Devereaux, T. P. & Hackl, R. Inelastic light scattering from correlated electrons. Rev. Mod. Phys. 79, 175 (2007).
Bardasis, A. & Schrieffer, J. R. Excitons and plasmons in superconductors. Phys. Rev. 121, 1050–1062 (1961).
Monien, H. & Zawadowski, A. Theory of Raman scattering with final-state interaction in high-T c BCS superconductors: collective modes. Phys. Rev. B 41, 8798–8810 (1990).
Böhm, T. et al. Balancing act: evidence for a strong subdominant d-wave pairing channel in Ba0.6K0.4Fe2As2. Phys. Rev. X 4, 041046 (2014).
Mazin, I. I., Singh, D. J., Johannes, M. D. & Du, M. H. Unconventional superconductivity with a sign reversal in the order parameter of LaFeAsO1−xFx. Phys. Rev. Lett. 101, 057003 (2008).
Hosono, H. & Kuroki, K. Iron-based superconductors: current status of materials and pairing mechanism. Phys. C. 514, 399–422 (2015).
Chubukov, A. V., Fernandes, R. M. & Schmalian, J. Origin of nematic order in FeSe. Phys. Rev. B 91, 201105 (2015).
Hirschfeld, P. J. Using gap symmetry and structure to reveal the pairing mechanism in Fe-based superconductors. C. R. Phys. 17, 197–231 (2016).
Si, Q., Yu, R. & Abrahams, E. High-temperature superconductivity in iron pnictides and chalcogenides. Nat. Rev. Mater. 1, 16017 (2016).
Thomale, R., Platt, C., Hu, J., Honerkamp, C. & Bernevig, B. A. Functional renormalization-group study of the doping dependence of pairing symmetry in the iron pnictide superconductors. Phys. Rev. B 80, 180505 (2009).
Thomale, R., Platt, C., Hanke, W., Hu, J. & Bernevig, B. A. Exotic d-wave superconducting state of strongly hole-doped KxBa1−xFe2As2. Phys. Rev. Lett. 107, 117001 (2011).
Scalapino, D. J. & Devereaux, T. P. Collective d-wave exciton modes in the calculated Raman spectrum of Fe-based superconductors. Phys. Rev. B 80, 140512 (2009).
Kretzschmar, F. et al. Raman-scattering detection of nearly degenerate s-wave and d-wave pairing channels in iron-based Ba0.6K0.4Fe2As2 and Rb0.8Fe1.6As2 superconductors. Phys. Rev. Lett. 110, 187002 (2013).
Wu, S.-F. et al. Superconductivity and electronic fluctuations in Ba1−xKxFe2As2 studied by Raman scattering. Phys. Rev. B 95, 085125 (2017).
Thorsmølle, V. K. et al. Critical quadrupole fluctuations and collective modes in iron pnictide superconductors. Phys. Rev. B 93, 054515 (2016).
Muschler, B. et al. Band- and momentum-dependent electron dynamics in superconducting Ba(Fe1−xCox)2As2 as seen via electronic Raman scattering. Phys. Rev. B 80, 180510 (2009).
Gallais, Y., Paul, I., Chauvière, L. & Schmalian, J. Nematic resonance in the Raman response of iron-based superconductors. Phys. Rev. Lett. 116, 017001 (2016).
Maiti, S., Maier, T. A., Böhm, T., Hackl, R. & Hirschfeld, P. J. Probing the pairing interaction and multiple Bardasis-Schrieffer modes using Raman spectroscopy. Phys. Rev. Lett. 117, 257001 (2016).
Rotter, M., Tegel, M. & Johrendt, D. Superconductivity at 38 K in the iron arsenide (Ba1−xKx)Fe2As2. Phys. Rev. Lett. 101, 107006 (2008).
Shen, B. et al. Transport properties and asymmetric scattering in Ba1−xKxFe2As2 single crystals compared to the electron doped counterparts Ba(Fe1−xCox)2As2. Phys. Rev. B 84, 184512 (2011).
Karkin, A. E., Wolf, T. & Goshchitskii, B. N. Superconducting properties of (Ba−K)Fe2As2 single crystals disordered with fast neutron irradiation. J. Phys. Condens. Matter 26, 275702 (2014).
Evtushinsky, D. V. et al. Momentum dependence of the superconducting gap in Ba1−xKxFe2As2. Phys. Rev. B 79, 054517 (2009).
Nakayama, K. et al. Universality of superconducting gaps in overdoped Ba0.3K0.7Fe2As2 observed by angle-resolved photoemission spectroscopy. Phys. Rev. B 83, 020501 (2011).
Xu, N. et al. Possible nodal superconducting gap and Lifshitz transition in heavily hole-doped Ba0.1K0.9Fe2As2. Phys. Rev. B 88, 220508 (2013).
Hardy, F. et al. Strong correlations, strong coupling, and s-wave superconductivity in hole-doped BaFe2As2 single crystals. Phys. Rev. B 94, 205113 (2016).
Ikeda, H., Arita, R. & Kuneš, J. Phase diagram and gap anisotropy in iron-pnictide superconductors. Phys. Rev. B 81, 054502 (2010).
Kuroki, K., Usui, H., Onari, S., Arita, R. & Aoki, H. Pnictogen height as a possible switch between high-T c nodeless and low-T c nodal pairings in the iron-based superconductors. Phys. Rev. B 79, 224511 (2009).
Metzner, W., Salmhofer, M., Honerkamp, C., Meden, V. & Schönhammer, K. Functional renormalization group approach to correlated fermion systems. Rev. Mod. Phys. 84, 299–352 (2012).
Platt, C., Hanke, W. & Thomale, R. Functional renormalization group for multi-orbital Fermi surface instabilities. Adv. Phys. 62, 453–562 (2014).
Leggett, A. J. Number-phase fluctuations in two-band superconductors. Prog. Theor. Phys. 36, 901 (1966).
Cea, T. & Benfatto, L. Signature of the Leggett mode in the A 1g Raman response: from MgB2 to iron-based superconductors. Phys. Rev. B 94, 064512 (2016).
Chubukov, A. V., Eremin, I. & Korshunov, M. M. Theory of Raman response of a superconductor with extended s-wave symmetry: application to the iron pnictides. Phys. Rev. B 79, 220501 (2009).
Böhm, T. et al. Superconductivity and fluctuations in Ba1−pKpFe2As2 and Ba(Fe1−nCon)2As2. Phys. Status Solidi (b) 254, 1600308 (2017).
Devereaux, T. P. Theory of electronic Raman scattering in disordered unconventional superconductors. Phys. Rev. Lett. 74, 4313 (1995).
Manske D. Theory of Unconventional Superconductors. Springer Tracts in Modern Physics. 202, Springer Verlag GmbH: Berlin, 2004.
Kretzschmar, F. et al. Critical spin fluctuations and the origin of nematic order in Ba(Fe1−xCox)2As2. Nat. Phys. 12, 560–563 (2016).
Mazin, I. I. et al. Pinpointing gap minima in Ba(Fe0.94Co0.06)2As2 via band-structure calculations and electronic Raman scattering. Phys. Rev. B 82, 180502 (2010).
Böhmer, A. E. et al. Nematic susceptibility of hole-doped and electron-doped BaFe2As2 iron-based superconductors from shear modulus measurements. Phys. Rev. Lett. 112, 047001 (2014).
Acknowledgements
We acknowledge useful discussions with L. Benfatto, A. Eberlein, D. Einzel, S. A. Kivelson, C. Meingast, and I. Tüttő. W.H. gratefully acknowledges the hospitality of the Institute for Theoretical Physics at the University of California Santa Barbara. Financial support for the work came from the Deutsche Forschungsgemeinschaft (DFG) via the Priority Program SPP 1458 (T.B., A.B., R.H., C.P. and W.H., project nos. HA 2071/7-2 and HA 1537/24-2), the Collaborative Research Centers SFB 1170 (W.H., C.P., and R.T.), and TRR 80 (F.K. and R.H.), the Bavaria California Technology Center BaCaTeC (T.B. and R.H., project no. A5 [2012-2]), the European Research Council (ERC) through ERC-StG-Thomale-TOPOLECTRICS (R.T.), and from the U.S. Department of Energy (DOE), Office of Basic Energy Sciences, Division of Materials Sciences and Engineering, under Contract Nos. DE-AC02-76SF00515 (B.M. and T.P.D.) and DE-FG02-05ER46236 (P.J.H. and S.M.). The RPA calculations were conducted at the Center for Nanophase Materials Sciences, which is a DOE Office of Science User Facility. The work in China (H.-H.W.) was supported by the National Key Research and Development Program of China (2016YFA0300401), and the National Natural Science Foundation of China (NSFC) via projects A0402/11534005 and A0402/11374144.
Author information
Authors and Affiliations
Contributions
T.B. and R.H. conceived the experiments. R.T., T.A.M., W.H., T.P.D., D.J.S., S.M. and P.J.H. developed the theoretical concept. P.A., T.W. and H.-H.W. prepared the samples. T.B., F.K., A.B., M.R., D.J. and R.H.A. performed the experiments. T.B. developed the phenomeology and fitted the data. C.P., T.A.M., B.M. and S.M. performed the numerical work. T.B., R.T., W.H., B.M., T.P.D., D.J.S., S.M., P.J.H., and R.H. analyzed the results and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Böhm, T., Kretzschmar, F., Baum, A. et al. Microscopic origin of Cooper pairing in the iron-based superconductor Ba1−xKxFe2As2. npj Quant Mater 3, 48 (2018). https://doi.org/10.1038/s41535-018-0118-z
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-018-0118-z
This article is cited by
-
Terahertz pulse-driven collective mode in the nematic superconducting state of Ba1−xKxFe2As2
npj Quantum Materials (2022)
-
Classification and characterization of nonequilibrium Higgs modes in unconventional superconductors
Nature Communications (2020)
-
Pairing mechanism in multiband superconductors
Scientific Reports (2020)