Abstract
In the thin film limit, the surface state of a three-dimensional topological insulator gives rise to two parallel conduction channels at the top and bottom surface of the film, which are difficult to disentangle in transport experiments. Here, we present gate-dependent multi-tip scanning tunneling microscope transport measurements combined with photoemission experiments all performed in situ on pristine BiSbTe3 thin films. To analyze the data, we develop a generic transport model including quantum capacitance effects. This approach allows us to quantify the gate-dependent conductivities, charge carrier concentrations, and mobilities for all relevant transport channels of three-dimensional topological insulator thin films (i.e., the two topological surface state channels, as well as the interior of the film). For the present sample, we find that the conductivity in the bottom surface state channel is minimized below a gate voltage of Vgate = −34 V and the top surface state channel dominates the transport through the film.
Similar content being viewed by others
Introduction
Understanding the behavior of topological insulators under the influence of an electric field is of fundamental interest for the application of the unique electronic properties of their topological surface states (TSS) in future electronic devices.1,2 Among the most promising three-dimensional topological insulators (3D-TI) are the compounds Bi2Se3, Bi2Te3, and Sb2Te3 because of their pronounced band gap of up to 300 meV, which makes them applicable at room temperature.1,3 However, it has become clear that the aforementioned binary materials often suffer from unintentional doping by crystal lattice defects.1,4,5 This doping can shift the Fermi level EF into the bulk conduction/valence bands and may result in predominant bulk transport, bypassing the auspicious TSS.6 One way to reduce the bulk transport is to alloy different binary TIs into ternary or even quaternary compounds,6,7,8 shifting EF back into the bulk bandgap.9 Another aspect is that the electronic bands at the surface of a TI are typically shifted with respect to the bulk due to surface band bending.8,10,11 This effect renders it difficult to simultaneously achieve a low-conducting bulk and a surface electronic configuration where EF only cuts the TSS.
Thin films of the ternary compound (Bi1−xSbx)2Te3 with x ≈ 0.5, in the following referred to as BiSbTe3, have proven to have low bulk conductivities, and also at their surface, EF lies inside the bandgap of the bent bulk bands.7,12,13 Furthermore, the existence of conduction channels at the substrate interface, besides the TSS, can be excluded,14 which makes BiSbTe3 a promising candidate for future applications, as a lateral current through the material is expected to be transmitted predominantly by the TSS.
In the present work, we use a combination of angle-resolved photoemission spectroscopy (ARPES) and gated four-tip scanning tunneling microscopy (STM) to characterize the electronic and transport properties of pristine epitaxial BiSbTe3 thin films under ultra-high vacuum (UHV) conditions. This approach gives us direct access to the filling level of the TSS at the surface of the same sample on which we also perform transport measurements. In this way, a comprehensive analysis of the transport properties of the TSS becomes possible. We interpret gate-dependent four-probe measurements by using a generic parallel channel transport model. The three channels of the model represent the two TSS channels, formed by the TSS at the top and bottom surfaces of the thin film and the bulk channel which corresponds to the interior of the film. We determine the gate-dependent carrier concentrations in each of the three channels by using a gating model, which includes quantum capacitance effects and band bending calculations. As a result, we are able to describe the experimental data and determine the carrier concentrations and carrier mobilities in each of the three transport channels.
Results
Angle-resolved photoemission spectroscopy
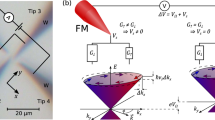
Figure 1a shows a schematic of the combined transport and photoemission measurement setup, which we use to analyze a d = 10 nm thin film of BiSbTe3. ARPES results obtained at hv = 8.4 eV are shown in Fig. 1b, c. We find a linear dispersion of the TSS with a filling level of the Dirac cone of \(E_{{\mathrm{top}}}^0\) = 250(20) meV, as determined from the intersection of the two dashed lines with respect to the Fermi energy. The cone slope corresponds to a Fermi velocity of vF = 5.6(2) × 105 ms−1, in agreement with the literature.1,3,15 We further find that the position of the Dirac point coincides with the valence band edge (solid red line in Fig. 1c). A cut through the Dirac cone at EF (Fig. 1b) shows a circular Fermi surface with a Fermi radius of kF = 0.07(1) Å−1. Spin-resolved energy distribution curves reveal a high spin polarization of the Dirac cone of up to 50%, consistent with the topological nature of the observed surface state (see Supplementary Note 1 and Supplementary Fig. 1). Using the Fermi wave vector kF, we determine the carrier concentration in the TSS at the top surface of the sample, without a gate voltage applied, as \(n_{{\mathrm{top}}}^0 = k_{\mathrm{F}}^2{\mathrm{/}}4\pi\) = 4(1) × 1012 cm−2 (ref. 9 and Supplementary Note 2). ARPES measurements were performed after the transport measurements to ensure the pristine sample quality throughout the measurements.
Schematic of the measurement geometry and results obtained by photoemission spectroscopy and four-probe measurements. a Measurement setup consisting of a BiSbTe3 thin film grown on a silicon-on-insulator substrate (thicknesses not to scale). The tips of a four-tip scanning tunneling microscope contact the thin film surface while a gate voltage Vgate is applied to the back side of the substrate. b ARPES measurement of the k||,x/k||,y plane at the Fermi energy with a fit to the Fermi surface (dashed circle), without gating. c Corresponding photoemission intensity as a function of binding energy in k||,x direction with the Dirac cone indicated by dotted red lines. d In situ four-probe I/V measurement of the TI film. e Scanning electron microscopy image of the four-probe setup with equidistant tip spacing. Scale bar: 100 µm
Transport measurements
Contacting the TI thin film with the tips of a four-tip STM results in a measurement geometry that resembles an in situ realization of a TI field-effect transistor. Four-probe I/V measurements of the TI film at Vgate = 0 V, shown in Fig. 1d, reveal a linear current–voltage characteristic, corresponding to a sheet conductivity of σtotal = 0.44(5) mS ⎕−1. The error of σtotal includes the positioning errors of the tips.
In the next step, we determine the TI film conductivity as a function of the gate voltage Vgate, resulting in the black squares in Fig. 2. In the data, we observe a transition between two distinct gating regimes: for gate voltages larger than Vgate ≈ −34 V, the TI sheet conductivity shows a clear increase with Vgate, while for lower gate voltages, the conductivity saturates and forms a plateau at σtotal = 0.34(5) mS ⎕−1. The crucial advantage of the present study is the possibility to grow and characterize samples without breaking the vacuum. This is important because sample processing under ambient conditions, such as lithography, is reported to alter the electronic properties of TI samples10,16,17,18,19,20 and thus, the results of in situ photoemission measurements and ex situ transport measurements cannot be directly compared. In contrast, our seamless in situ approach allows a direct comparison of the respective results and enables the comprehensive analysis of our gate-dependent transport data.
Measurement of the gate-dependent TI film sheet conductivity σtotal (black squares) and fit of the transport model given by Eq. (1) in the text (solid red line). The individual contributions of the model σtop, σbot, and σfilm are also plotted (note the axis break). The colored lines in the inset show current paths through the individual channels. Note that the film thickness d = 10 nm is much smaller than the tip spacing s = 100 μm, which we use in the transport measurement
Transport model
The conduction in a TI thin film can be described by three parallel conduction channels—the two TSS channels at the top and bottom surfaces of the film and one in the interior of the film, in the following referred to as “bulk channel”. Here, our gate-dependent transport measurements in combination with ARPES and a detailed transport model allow us to disentangle the contributions of the individual conduction channels. Specifically, the sample conductivity σtotal in the model is given by
where σtop, σbot, and σfilm are the conductivities of the two TSS channels and the bulk channel, μtop, μbot, and μfilm are the respective carrier mobilities, \(n_{{\mathrm{top}}}^0\), \(n_{{\mathrm{bot}}}^0\), and \(n_{{\mathrm{film}}}^0\) are the initial carrier concentrations without gating (i.e., Vgate = 0 V), and ntop, nbot, and nfilm are the corresponding gate-induced carrier concentrations, respectively. Note that there is a minimum carrier concentration in the TSS which is typically dominated by charge fluctuations in the film, e.g., due to charge puddles.21 For the present sample, we assume a minimum charge carrier density of 0.5 × 1012 cm−2 based on the literature12,21 but we also show that varying this value does not have a large influence on the results obtained from applying the transport model to the present sample (see Supplementary Note 3, Supplementary Fig. 2 and Supplementary Table 1).
While \(n_{{\mathrm{top}}}^0\) is readily extracted from the ARPES measurements, \(n_{{\mathrm{bot}}}^0\) is difficult to access experimentally. For a freestanding topological insulator film and without gating, the position of the Fermi level relative to the Dirac point should be identical for the top and bottom TSS channels and correspondingly \(n_{{\mathrm{bot}}}^0\) = \(n_{{\mathrm{top}}}^0\). However, it has become clear that this is typically not the case in experiments.12,22 The different environments which the top and bottom TSS channels are exposed to result in different conductivities; e.g., at the bottom surface, the substrate may influence the carrier concentration in the TSS.16,18,19
When gating the TI film, the carrier concentration in each of the three transport channels changes due to quantum capacitance effects, i.e., the gate-electric field penetrates through the TSS at the bottom surface of the film23 (see also Supplementary Note 4). These effects occur because, as charges are transferred to the TSS, higher energy levels must be populated due to the small density of states (DOS) in the TSS. Thus, part of the applied gate voltage is consumed by filling higher energy levels and, as a result, the gate effect is attenuated compared with a sample with a large DOS. In the corresponding equivalent circuit diagram, the quantum capacitance is described by an additional capacitance CQ = e2n/E in series with the ordinary geometric capacitance, with n being the number of induced charge carriers on the capacitor plate and E the resulting shift of the filling level (see Supplementary Note 4 and Supplementary Fig. 3). For small changes in the carrier concentration, this expression can be approximated to \(C_{\mathrm{Q}} \approx e^2{\textstyle{{\partial n} \over {\partial E}}} = e^2\rho\), where ρ is the DOS at the Fermi level.21,24 In the following, we lift this approximation for CQ and implement an explicit treatment of the quantum capacitance in the form of the gate-dependent change of the TSS filling level. To include the quantum capacitance effect of the top and bottom TSS channels, we use a gating model given by the equivalent circuit diagram shown in Fig. 3a, after refs. 15,21,24. In this description, we use capacitances per unit area and assume that the current injecting tips contact both TSS channels (close to ground potential) due to a finite conductance of the bulk channel.
Gating model and band schematics. a Equivalent circuit diagram of the present sample geometry. b Band schematic in the TI film at Vgate = 0 V. The bulk conduction band and valence bands are shown in blue and red, with the position of the band edges at each surface indicated by arrows, respectively. The relative position of the bands with respect to EF at the top TSS channel is known from ARPES. c Band schematic of the TI film under negative gate voltage Vgate ≤ −34 V. The bulk valence band edge at the bottom of the film is shifted to the Fermi energy
Gate-dependent carrier concentrations
From the equivalent circuit model shown in Fig. 3a and charge conservation it holds15,21,24
Using the definition of capacitance, the charge carrier densities on the capacitors Cgate and CTI can be written as a function of the potential differences across them
For the present sample, we determine CTI = εTI/d ≈ 8 μF cm−2 from the TI film thickness d and the dielectric constant εTI = 100 εo (ref. 21). Note that the reported values for the dielectric constant of TIs fluctuate in the range εTI ≈ 50–200 εo (ref. 25), and that we have also investigated the dependence of our model on this parameter (see Supplementary Note 5 and Supplementary Fig. 4). Due to the linear dispersion of TSS, the filling level with respect to the Dirac point \(E_{{\mathrm{top}}}^0\) is furthermore related to the charge carrier density \(n_{{\mathrm{top}}}^0\) (for Vgate = 0 V) by
and in the same way \(E_{{\mathrm{bot}}}^0\) = \(a\sqrt {n_{{\mathrm{bot}}}^0}\) (see Supplementary Note 2 and refs. 9,12,26). A change in the carrier concentration \(n_{{\mathrm{top}}}^0 \to n_{{\mathrm{top}}}^0 + n_{{\mathrm{top}}}\) according to Eq. (4) therefore results in a change of the filling level Etop given by \(E_{{\mathrm{top}}}^0 + E_{{\mathrm{top}}}\) = \(a\sqrt {n_{{\mathrm{top}}}^0 + n_{{\mathrm{top.}}}}\)
From this, we obtain
and an equivalent expression for Ebot. Combining Eqs. (2), (3), and (5), we find the explicit equations
and
(Supplementary Note 6). We evaluate Eqs. (6) and (7) numerically, which gives us ntop and nbot as a function of Vgate and the parameter \(n_{{\mathrm{bot}}}^0\), while \(n_{{\mathrm{top}}}^0\) is provided by ARPES. For a given value of \(n_{{\mathrm{bot}}}^0\), which we determine later by fitting the experimental data, we calculate the band bending in the TI film as a function of the applied gate voltage by modeling the TI film as a 10 nm thin small bandgap semiconductor (Egap = 260 meV, according to our ARPES results) and solving Poisson’s equation (see Supplementary Note 7, Supplementary Fig. 5 and refs. 27,28,29). As a result, we obtain the gate-dependent total charge carrier density in the bulk channel \(n_{{\mathrm{film}}}^0 + n_{{\mathrm{film}}}\left( {V_{{\mathrm{gate}}}} \right)\).
Before applying Eq. (1) to our data, note that Eqs. (6) and (7) are only valid if on each surface the Fermi level cuts the TSS, as depicted in Fig. 3b. However, gating can result in a case where the bulk bands are shifted to EF at one or the other surface of the thin film, as depicted for the valence band in Fig. 3c. In this case, the gate induces charge carriers predominantly in the corresponding bulk band due to the large DOS there. The high DOS of the bulk bands corresponds to a large quantum capacitance of the respective surface and results in a complete screening of the gate electric field at this surface.23 For the present sample, this leads to a constant, gate-independent carrier concentration in the top TSS channel for gate voltages lower than Vgate = −34 V. Thus, further decreasing the gate voltage will not lead to any further shift of the bands with respect to EF. Combining the solution of Eqs. (6) and (7), when the Fermi level lies in the band gap, with the constant band positions once the bulk bands reach the Fermi level allows us to describe the entire range of experimental data, as shown in the following.
Disentanglement of the transport channels
We now turn to the quantitative analysis of the data in Fig. 2 using Eq. (1) in combination with \(n_{{\mathrm{top}}}^0\), obtained from ARPES, the gate-dependent carrier concentrations nbot, ntop, which we receive from Eqs. (6) and (7), and \(n_{{\mathrm{film}}}^0 + n_{{\mathrm{film}}}\) determined by the band bending calculations. From a fit of Eq. (1) to the data, we determine the four remaining parameters of the transport model, i.e., \(n_{{\mathrm{bot}}}^0\), μbot, μtop, and μfilm. The results are \(n_{{\mathrm{bot}}}^0\) = 1.7 × 1012 cm−2, μbot = 184 cm2 V−1 s−1, μtop = 578 cm2 V−1 s−1, and μfilm < 2 cm2 V−1 s−1. The resulting graph of Eq. (1) is shown as solid red line in Fig. 2. Additionally, we plot the individual contributions of the transport model σtop, σbot, and σfilm. We find that the four parameters determined by the fit correspond to four specific signatures of the gate-dependent conductivity: (a) \(n_{{\mathrm{bot}}}^0\) is mainly determined by the gate voltage at which the kink in the conductivity occurs (Vgate = −34 V), (b) μtop is mainly determined by the conductivity value at the kink together with \(n_{{\mathrm{top}}}^0\) = 4 × 1012 cm−2 obtained from ARPES, (c) μbot is determined by the slope of the conductivity graph right of the kink, and (d) μfilm is determined by the slope of the graph left of the kink. At this point, we would like to stress that without the knowledge of \(n_{{\mathrm{top}}}^0\), from the in situ ARPES measurements, the fit of the transport model to the experimental data would be underdetermined and would not result in a unique solution for the fit parameters. Note also that the gating model reproduces the experimentally observed negative curvature of the conductivity graph above Vgate = −34 V, which is a direct result of the quantum capacitance and in marked contrast to the expected linear graph if only the bottom TSS channel would be affected by the gate.
Resulting from the fit of our transport model we find that for gate voltages below Vgate = −34 V, the current through the sample is almost exclusively transmitted by the top TSS channel. Beyond this gate voltage the conductivity of the bottom TSS channel is minimized because the Dirac point is located at the Fermi level, as depicted in Fig. 3c. At this filling level and in the absence of scattering, the conductance of the TSS is 2e2/h (ref. 30). However, it was recently shown that there is a significant amount of scattering of the TSS at defects in the present samples.31 In combination with the large probe spacing in the present experiment (100 µm), this results in a minimum TSS channel conductance smaller than the conductance quantum. For calculations assuming a minimum conductance of the conductance quantum, see Supplementary Note 3 and Supplementary Fig. 2. Below Vgate = −34 V, the only remaining gate-dependent transport channel is the bulk channel due to the valence band edge at the bottom of the film being located at the Fermi level. As we observe a constant conductivity below Vgate = −34 V, we obtain a lower limit for the film mobility μfilm < 2 cm2 V−1 s−1. Our result for μfilm is two orders of magnitude smaller than the TSS mobility. In the literature, the bulk mobility is reported to be only one order of magnitude lower than the corresponding TSS mobility.32 We explain our observed lower bulk mobility by the fact that our transport experiments were performed at room temperature, resulting in an increased phonon scattering in the bulk compared with experiments performed at low temperature. In contrast, the mobility in the TSS is reported to be rather insensitive to phonon scattering.33 The bulk charge carrier densities obtained from our gate-dependent band bending calculations agree with typical carrier densities reported in the literature.13 In combination with the estimated low mobility, this results in a negligible film conductivity as evident in Fig. 2. We can exclude possible screening effects of the substrate and its interface to the TI, as we have measured several samples of different thicknesses and compositions on identically prepared substrates which all show distinctly different gate-dependent conductivities (see Supplementary Note 8, Supplementary Figs. 6–8 and Supplementary Table 2).
In general, our transport model describes the experimental data in Fig. 2 very well, with only small deviations between the experimental and calculated graph when the filling in the bottom TSS channel approaches the Dirac point. This observation can be explained by a smooth transition between the gating regimes in the experiments due to the room temperature conditions and the resulting smeared-out Fermi edge. A width of the Fermi edge of ~4kBT, i.e., Ebot ± ~2kBT, translates to a broadening of the charge carrier density nbot according to Eq. (4), and therefore after Eq. (2) and (3), it leads to a broadening of Vgate by ±~5 V at room temperature. This value fits the experimentally observed transition region in Fig. 2 reasonably well. Another effect which can contribute to the smeared-out transition is local variations in the band positions within the TI, e.g., due to charge puddles.15
Figure 4a shows the disentangled gate-dependent valence and conduction band positions which we calculate from the fitted transport model after Eqs. (6) and (7). We find that while the bottom TSS channel band positions \(E_{{\mathrm{vb}}}^{{\mathrm{bot}}}\), \(E_{{\mathrm{cb}}}^{{\mathrm{bot}}}\) shift considerably as a function of gate voltage, the band positions in the top TSS channel changes only by an amount of ΔE < 50 meV in the experimentally applicable gate voltage range. This agrees with the partial screening of the gate-induced electric field by the bottom TSS channel (due to the quantum capacitance) and the larger initial filling level of the top TSS channel, which results in a slower change of the band positions as charges are induced, as a result of the square-root dependence of the TSS filling level on the carrier concentration (Eq. (4)). For Vgate ≤ −34 V, the bulk valence band at the bottom of the film is located at the Fermi level and the band positions are constant as a result of the large DOS in this band.
Gate-dependent band positions. a Band positions relative to the Fermi level in the top and bottom TSS channel as a function of gate voltage calculated from the transport model. b Depth-dependent position of the bulk valence band edge Evb and bulk conduction band edge Ecb relative to the Fermi level, without gating. The corresponding TSS filling levels at the top and bottom surfaces of the film are indicated left and right of the graph, respectively. c Corresponding band profile at Vgate = −34 V
While Fig. 3b, c showed only a qualitative sketch of the band positions in the film, we can now calculate the exact band positions from the fitted transport model. Figure 4b, c show the calculated depth-dependent profiles of the valence band edge Evb and conduction band edge Ecb throughout the thin film at Vgate = 0 V and Vgate = −34 V, respectively. From these graphs, it is evident that the Dirac point of the bottom TSS channel is shifted to the Fermi level by gating, resulting in a minimal bottom TSS channel conductivity at Vgate = −34 V, while at the top surface, EF lies within the bulk bandgap, with the largely filled TSS dominating the conduction through the TI thin film. Furthermore, it is evident that the bands show only a weak curvature, which is the result of the long screening length compared with the film thickness.24,34
Discussion
Our generic transport model shows that the influence of the gate voltage on the conductivity of each of the two TSS channels in a TI thin film can vary from strong to negligible, depending on the alignment of the bulk bands with respect to EF at each surface. In detail, we find three possible cases: (1) If the Dirac points of both TSS channels are located well within the bandgap, the influence of the gate voltage is strong and controls the charge transport though both TSS channels.15,24 (2) If the gate shifts the bands such that the Fermi level enters at one or both surfaces into the bulk bands, a further gate-induced shift of the bands relative to the Fermi level is inhibited and the conductance of the respective TSS cannot be influenced by the gate anymore. This occurs as the gate induces charges predominantly in the bulk bands, which have a high DOS. (2a) If this occurs at the TSS channel more distant from the gate electrode, this TSS channel becomes insensitive to gate voltages, as it was observed in refs. 12,13. (2b) If the gate-induced shift of the TSS channel closest to the gate is inhibited due to the bulk bands (as it is the case in our sample for Vgate ≤ −34 V), both TSS channel fillings become independent of the gate voltage because the high DOS of the bulk bands at this surface screens the gate electric field completely. This effect explains also the often-reported negligible gate-dependence in first-generation TI samples, where strong doping resulted in EF being located well within the valence/conduction bands in the range of applicable gate voltages.1,35 Our transport model can capture all these cases of band alignments quantitatively. The comparison between the model and the experiment would greatly benefit from facilitating gate-dependent ARPES measurements, which would allow to determine ntop(Vgate) directly. However, such experiments were not possible in the present study because the gate electric fields need to be well screened to not influence the ARPES measurements, and this would have required elaborate changes to the experimental setup.
In conclusion, by combining in situ gate-dependent transport measurements with photoemission spectroscopy, we are able to disentangle the transport through all of the conduction channels of a BiSbTe3 thin film, namely the top and the bottom TSS channels, as well as the interior of the film. The use of a generic transport model, which includes gate-dependent quantum capacitances, gives access to the carrier concentrations and respective mobilities in each of the three channels. Application of the model to the experimental data shows that for the present sample the conductivity in the bottom TSS channel is minimized below a gate voltage of Vgate = −34 V, resulting in the top TSS channel dominating the transport through the film. The reason for this behavior is a high DOS in the bulk bands of the TI, which prevents a gate-induced shift of the bulk band edges past the Fermi energy, in combination with the Dirac point being located at the bulk valence band edge in the present sample. The demonstrated experimental techniques and data analysis procedures are generic and allow to determine the detailed transport properties of pristine samples with short turnaround times.
Methods
Sample preparation
We prepared a d = 10 nm thin film of (Bi0.53Sb0.47)2Te3 on a silicon-on-insulator (SOI) wafer by molecular beam epitaxy. The SiO2 thickness is 300 nm, while the template layer on which the TI film is grown consists of undoped Si(111) with 70 nm thickness. For further details see Supplementary Note 9.
Angle-resolved photoemission spectroscopy
ARPES measurements were performed at 30 K with a MBS A-1 hemispherical energy analyzer that was set to 40 meV energy resolution. Monochromatic VUV light with hν = 8.4 eV came from a microwave-driven Xe discharge lamp. Fermi surface maps were obtained by rotating the sample around the in-plane sample axis that is parallel to the analyzers entrance slit.
Four-probe measurement
For transport measurements, we use an mProbes room-temperature four-tip STM.36 This instrument allows individual positioning of the tips on the sample surface under scanning electron microscope monitoring. To measure the sample conductivity, the tips are lowered out of tunneling contact until a soft but stable contact to the sample surface is formed. Details on the measurement technique can be found, e.g., in ref. 37. For all STM experiments, we used electrochemically etched tungsten tips.
Data availability
Data within the manuscript, and its Supplementary Information is available from the corresponding author upon reasonable request.
References
Chen, Y. L. et al. Experimental realization of a three-dimensional topological insulator, Bi2Te3. Science 325, 178–181 (2009).
Roushan, P. et al. Topological surface states protected from backscattering by chiral spin texture. Nature 460, 1106–1109 (2009).
Zhang, H. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438–442 (2009).
Hsieh, D. et al. A tunable topological insulator in the spin helical Dirac transport regime. Nature 460, 1101–1105 (2009).
Jiang, Y. et al. Landau quantization and the thickness limit of topological insulator thin films of Bi2Te3. Phys. Rev. Lett. 108, 016401 (2012).
Ren, Z., Taskin, A. A., Sasaki, S., Segawa, K. & Ando, Y. Large bulk resistivity and surface quantum oscillations in the topological insulator Bi2Te2Se. Phys. Rev. B 82, 241306 (2010).
Kong, D. et al. Ambipolar field effect in the ternary topological insulator (Bi1-xSbx)Te3 by composition tuning. Nat. Nanotechnol. 6, 705–709 (2011).
Taskin, A. A., Ren, Z., Sasaki, S., Segawa, K. & Ando, Y. Observation of Dirac holes and electrons in a topological insulator. Phys. Rev. Lett. 107, 016801 (2011).
Zhang, J. et al. Band structure engineering in (Bi1−xSbx)Te3 ternary topological insulators. Nat. Commun. 2, 574 (2011).
Analytis, J. G. et al. Bulk Fermi surface coexistence with Dirac surface state in Bi2Se3: a comparison of photoemission and Shubnikov-de Haas measurements. Phys. Rev. B 81, 205407 (2010).
Eschbach, M. et al. Realization of a vertical topological p-n junction in epitaxial Sb2Te3/Bi2Te3 heterostructures. Nat. Commun. 6, 8816 (2015).
He, L. et al. Evidence of the two surface states of (Bi0.53Sb0.47)2Te3 films grown by van der Waals epitaxy. Sci. Rep. 3, 3406 (2013).
Weyrich, C. et al. Growth, characterization, and transport properties of ternary (Bi1-xSbx)Te3 topological insulator layers. J. Phys. Condens. Matter 28, 495501 (2016).
Lüpke, F. et al. Chalcogenide-based van der Waals epitaxy: interface conductivity of tellurium on Si(111). Phys. Rev. B 96, 035301 (2017).
Fatemi, V. et al. Electrostatic coupling between two surfaces of a topological insulator nanodevice. Phys. Rev. Lett. 113, 206801 (2014).
Brahlek, M., Kim, Y. S., Bansal, N., Edrey, E. & Oh, S. Surface versus bulk state in topological insulator Bi2Se3 under environmental disorder. Appl. Phys. Lett. 99, 012109 (2011).
Durand, C. et al. Differentiation of surface and bulk conductivities in topological insulators via four-probe spectroscopy. Nano Lett. 16, 2213–2220 (2016).
Hoefer, K. et al. Intrinsic conduction through topological surface states of insulating Bi2Te3 epitaxial thin films. Proc. Natl Acad. Sci. USA 111, 14979–14984 (2014).
Kong, D. et al. Rapid surface oxidation as a source of surface degradation factor for Bi2Se3. ACS Nano 5, 4698–4703 (2011).
Park, S. H., Hamh, S. Y., Park, J., Kim, J. S. & Lee, J. S. Possible flat band bending of the Bi1.5Sb0.5Te1.7Se1.3 crystal cleaved in an ambient air probed by terahertz emission spectroscopy. Sci. Rep. 6, 36343 (2016).
Kim, D. et al. Surface conduction of topological Dirac electrons in bulk insulating Bi2Se3. Nat. Phys. 8, 459–463 (2012).
He, X. et al. Highly tunable electron transport in epitaxial topological insulator (Bi1-xSbx)2Te3 thin films. Appl. Phys. Lett. 101, 123111 (2012).
Luryi, S. Quantum capacitance devices. Appl. Phys. Lett. 52, 501–503 (1988).
Yang, F. et al. Dual-gated topological insulator thin-film device for efficient fermi-level tuning. ACS Nano 9, 4050–4055 (2015).
Richter, W. & Becker, C. R. A Raman and far‐infrared investigation of phonons in the rhombohedral V2–VI3 compounds Bi2Te3, Bi2Se3, Sb2Te3 and Bi2(Te1−xSex)3 (0<x<1), (Bi1−ySby)2Te3 (0<y<1). Phys. Status Solidi B 84, 619–628 (1977).
Novoselov, K. S. et al. Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197–200 (2005).
Just, S. et al. Surface and step conductivities on Si(111) surfaces. Phys. Rev. Lett. 115, 066801 (2015).
Lüth, H. Solid Surfaces, Interfaces and Thin Films (Springer, 2014) https://www.springer.com/us/book/9783319107554.
Zhang, P. et al. Electrical conductivity in silicon nanomembranes. New J. Phys. 8, 200 (2006).
Xu, Y., Miotkowski, I. & Chen, Y. P. Quantum transport of two-species Dirac fermions in dual-gated three-dimensional topological insulators. Nat. Commun. 7, 11434 (2016).
Lüpke, F. et al. Electrical resistance of individual defects at a topological insulator surface. Nat. Commun. 8, 15704 (2017).
He, L. et al. Surface-dominated conduction in a 6 nm thick Bi2Se3 thin film. Nano Lett. 12, 1486–1490 (2012).
Dankert, A., Geurs, J., Kamalakar, M. V., Charpentier, S. & Dash, S. P. Room temperature electrical detection of spin polarized currents in topological insulators. Nano Lett. 15, 7976–7981 (2015).
ViolBarbosa, C. E. et al. Direct observation of band bending in the topological insulator Bi2Se3. Phys. Rev. B 88, 195128 (2013).
Bianchi, M. et al. Coexistence of the topological state and a two-dimensional electron gas on the surface of Bi2Se3. Nat. Commun. 1, 128 (2010).
Cherepanov, V. et al. Ultra compact multitip scanning tunneling microscope with a diameter of 50 mm. Rev. Sci. Instrum. 83, 033707 (2012).
Miccoli, I., Edler, F., Pfnür, H. & Tegenkamp, C. The 100th anniversary of the four-point probe technique: the role of probe geometries in isotropic and anisotropic systems. J. Phys. Condens. Matter 27, 223201 (2015).
Acknowledgements
We gratefully acknowledge Helmut Stollwerk and Franz-Peter Coenen for technical assistance.
Author information
Authors and Affiliations
Contributions
F.L., S.J., M.E., T.H., E.M., M.L., and N.v.d.D. performed the experiments and evaluated the data. F.L., V.C., and B.V. designed the transport experiment. M.E., T.H., E.M., L.P., and C.M.S. designed the photoemission experiment. M.L., P.S., D.R., N.v.d.D., G.M., and D.G. developed and fabricated the samples. The manuscript was written by F.L., S.J., M.E., T.H., M.L., F.S.T., and B.V. All authors discussed and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lüpke, F., Just, S., Eschbach, M. et al. In situ disentangling surface state transport channels of a topological insulator thin film by gating. npj Quant Mater 3, 46 (2018). https://doi.org/10.1038/s41535-018-0116-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-018-0116-1
This article is cited by
-
Room temperature in-situ measurement of the spin voltage of a BiSbTe3 thin film
Scientific Reports (2020)