Abstract
The Kondo insulator SmB6 is purported to develop into a robust topological insulator at low temperatures. Yet there are several puzzling and unexplained physical properties of the insulating bulk. It has been proposed that bulk spin excitons may be the source of these anomalies and may also adversely affect the topologically protected metallic surface states. Here, we report muon spin rotation measurements of SmB6 that show thermally activated behavior for the temperature dependence of the transverse-field relaxation rate below 20 K and a decreasing contact hyperfine field contribution to the positive muon Knight shift below 5–6 K. Our data are consistent with the freezing out of a bulk low-energy (~1 meV) spin exciton concurrent with the appearance of metallic surface conductivity. Furthermore, our results support the idea that spin excitons play some role in the anomalous low-temperature bulk properties of SmB6.
Similar content being viewed by others
Introduction
Due to a combination of spin–orbit coupling and time reversal symmetry, a topological insulator (TI) supports protected metallic edge and surface states in two-dimensional (2D) and three-dimensional (3D) systems, respectively.1 The ideal 3D TI has a truly insulating bulk gap, as this restricts applications of the transport properties to the topologically protected surface, where the electron spin is uniquely locked to the charge momentum. Yet true bulk insulating behavior is not realized in established TIs due to bulk impurity conduction.2 The homogeneous intermediate-valence compound SmB6 is a strong candidate for a 3D TI with a robust bulk insulating gap.3 In contrast to a conventional band insulator, the insulating gap in SmB6 is created via Kondo hybridization of localized Sm-4f and itinerant Sm-5d electrons, with the Fermi level residing in the hybridization gap.
Experimental evidence for SmB6 being a TI is provided by transport measurements that have demonstrated predominant surface electrical conduction below ~5–7 K,4,5,6 and the detection of in-gap surface states by angle-resolved photoemission spectroscopy (ARPES).7,8,9,10,11 However, recent high-resolution ARPES results suggest that the surface conductivity is not associated with topological surface states.12 Moreover, at low T, there is a sizable metallic-like T-linear specific heat of bulk origin,13 and significant bulk ac-conduction.14 Quantum oscillations are observed in the magnetization of SmB6 as expected for 2D metallic surface states,15 but subsequent measurements suggest that the origin is a bulk 3D Fermi surface.16 These findings have raised the possibility of charge-neutral fermions in the insulating bulk.17,18,19
The Sm ions in SmB6 rapidly fluctuate between non-magnetic Sm2+ (4f6) and magnetic Sm3+ (4f55d1) electronic configurations, resulting in an average intermediate valence that varies with temperature.20,21 Interestingly, SmB6 exhibits magnetic fluctuations below 20–25 K where the Kondo gap is fully formed, as observed by muon spin rotation (μSR).22,23 This was first presumed22 to be due to the bulk magnetic in-gap states detected by nuclear magnetic resonance below 20 K,24 and later specifically speculated to be due to bulk spin excitonic excitations.25 Spin excitons in SmB6 are induced by residual dynamic AFM exchange interactions between the hybridized quasiparticles and are a precursor to an AFM instability.26,27 A 14 meV bulk collective mode observed within the hybridization gap by inelastic neutron scattering (INS) has been interpreted as a spin exciton.28,29 Bulk spin excitons are expected to adversely affect the protected topological order by causing spin-flip scattering of the surface states.30 There is some indirect evidence for this from angle-integrated photoemission31 and planar tunneling32 spectroscopy studies.
Since an implanted positive muon (μ+) does not create a spin-exciton excitation, μSR is only sensitive to thermally activated spin excitons. Consequently, the 14 meV bulk spin exciton observed by INS should not be detectable by μSR below 20–25 K. An additional lower energy (≤1 meV) spin-exciton branch has recently been predicted and suggested to contribute to bulk quantum oscillations and cause the anomalous upturn in the specific heat at low T.33 On the other hand, the low-T specific heat is enhanced by Gd impurities34 and drastically reduced in isotopically enriched SmB6,35 suggesting that magnetic impurities play some role but spin excitons do not. Nevertheless, decoupling of the surface states from an ~4 meV bulk spin exciton has been argued to explain the rapid increase in the surface conductance below 5–6 K and subsequent saturation below 4 K.32 While the reduction in energy from 14 to 4 meV is assumed to be due to a diminished Kondo temperature at the surface,30 a distinct low-energy bulk spin exciton is another possibility.
Here, we report high transverse-field (TF)-μSR measurements of the μ+-Knight shift in Al-flux grown SmB6 single crystals that provide evidence for a bulk spin exciton of energy much lower than 14 meV. Specifically, our data demonstrate the occurrence of thermally activated low-energy magnetic excitations that are characteristic of an ~1 meV spin exciton.
Results
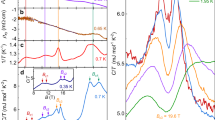
Figure 1 shows the temperature dependence of the bulk magnetic susceptibility χmol at different magnetic fields H applied parallel to the c-axis. At high temperature, χmol exhibits Curie–Weiss behavior indicative of paramagnetic Sm ions. Opening of the hybridization gap below 110 K gives rise to the broad maximum, followed by a field-dependent upturn below T ~17 K that masks the expected low-T van-Vleck saturation. The upturn has previously been attributed to impurities.36,37
In the absence of spontaneous magnetic order, the applied field polarizes the conduction electrons and induces spin polarization of the localized Sm-4f magnetic moments. The local field Bμ sensed by the μ+ is the vector sum of the dipolar field Bdip from the Sm-4f magnetic moments and a contact hyperfine field Bc. At high T where SmB6 behaves as a poor metal, the muon’s positive charge is screened by a cloud of conduction electrons. The screening electron cloud acquires a finite spin density due to the Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction with the spin-polarized Sm-4f moments, and by direct contact generates a hyperfine field at the μ+ site. This is expected to vanish with the development of a bulk insulating gap at lower T. In an insulating state, Bc may instead originate from direct overlap of the μ+ with the wavefunction of localized magnetic electrons, or from bonding of the μ+ to an ion that is covalently bonded to a local atomic magnetic moment.38
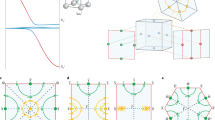
Figure 2 shows Fourier transforms of TF-μSR time spectra recorded on SmB6 at H = 6 T. Due to the apodization necessary to remove ringing artifacts caused by the short muon time window (~10 μs) and noise caused by fewer counts at later times (due to the short muon lifetime), the Fourier transforms are a broadened visual approximation of the internal magnetic field distribution. Consequently, analysis of the TF-μSR signals was done in the time domain (see Supplementary Information for representative fits). At T = 200 K, there are three well-separated peaks in the Fourier transform. The central peak arises from muons stopping in the Ag backing plate. The left and right peaks have an amplitude ratio of 2:1, and are consistent with the μ+ stopping at the midpoint of the horizontal or vertical edges of the cubic Sm-ion sublattice. This is in agreement with the identified μ+ site in CeB6.39 Moreover, we have verified the μ+ site assignment by TF-μSR measurements with H applied at 45° with respect to the c-axis (see Fig. S3).
In a field applied parallel to the c-axis, the μ+ site is magnetically inequivalent on the horizontal and vertical edges of the cubic Sm sublattice. The dipole field generated by polarization of the Sm-4f moments along the c-axis direction is equivalent and antiparallel to H at the (⊥) sites \(\left( {\frac{1}{2},0,0} \right)\) and \(\left( {0,\frac{1}{2},0} \right)\), and different in magnitude and parallel to H at the (∥) site \(\left( {0,0,\frac{1}{2}} \right)\) (see Fig. 3a inset). Consequently, the TF-μSR time spectra were fit to an asymmetry function with a two-component sample contribution (see Fig. S4).
Here, As and AAg denote the initial asymmetries of the sample and Ag backing plate contributions, respectively. Also, νi = (γμ/2π)Bμ,i and \({\mathrm{\Delta }}_i^2 = \gamma _\mu ^2\left\langle {{\mathbf{B}}_{\mu ,i}^2} \right\rangle\), where γμ/2π = 135.54 MHz/T is the muon gyromagnetic ratio, and Bμ,i and \(\left\langle {{\mathbf{B}}_{\mu ,i}^2} \right\rangle\) are the local magnetic field and width of the field distribution at the μ+ sites (i = ⊥, ∥, and Ag), respectively. The initial phase of the muon spin polarization is denoted by ϕ. As the temperature is lowered, ν⊥ (ν∥) increases (decreases), and below T ~30 K the ⊥ (∥) peak in the Fourier transform broadens and moves to the far right (left). Even so, the two sample components are observed to maintain a population ratio of 2:1 down to 1.9 K. We note that the 6 T applied magnetic field is far below the field of 80–90 T required to close the insulating gap.40
Time domain TF-μSR signal fitting results. Temperature dependence of a the μ+-Knight shifts, and b the TF-μSR relaxation rates at magnetic fields of 4 T and 6 T applied parallel to the c-axis. Data at H = 2 T are also shown in a for T ≥ 50 K, below which the different components of the TF-μSR signal are not clearly resolved. The error bars in a represent the uncertainties in the parameters νi and ν0, and in b the uncertainty in Δi from the fits in the time domain. The inset in a shows the two magnetically inequivalent muon sites on the vertical (∥) and horizontal edges (⊥) of the Sm-ion cubic sublattice. The inset in b shows a semi-log plot of Δ⊥ (minus a constant) vs. 1/T, for 4.2 ≤ T ≤ 17.6 K. The straight dashed line is a fit of the data for T ≥ 5 K to a thermally activated function: Δ⊥ = A + Bexp(EA/kBT)
The relative frequency shift is defined as Kμ,i = (νi − ν0)/ν0, where ν0 = (γμ/2π)H. After correcting for the demagnetization and Lorentz fields, the μ+-Knight shift at the magnetically inequivalent muon sites is:
where \(A_{\mathrm{c}}^i\) and Adip are the contact hyperfine and dipolar coupling constants, χ4f = χmol − χ0 is the local 4f magnetic susceptibility, and χ0 and \(K_0^i\) are the Pauli paramagnetic susceptibility and the corresponding Knight shifts, respectively.
Figure 3 shows the temperature dependence of the Knight shifts Ki and TF relaxation rates Δi. In contrast to χmol, the Knight shifts below 17 K do not exhibit an appreciable field dependence. We attribute the large uncertainty and jump or dip in Δ⊥ and Δ∥ between 20 and 40 K to fit parameters playing off against each other, as ν⊥ ≈ ν∥ in this temperature range.
Figure 4a shows the Knight shift data plotted vs. χmol with temperature as an implicit parameter (a so-called Clogston–Jaccarino plot). We find that a plot of K⊥ − K∥ vs. χmol above 110 K (not shown) is linear as expected from Eqs. (2a) and (2b), but has a slope and intercept incompatible with Ac and K0 being isotropic. Using the calculated value Adip = 0.395 T/μB for the μ+ site, linear fits of the Knight shifts in SmB6 above 110 K to Eqs. (2a) and (2b) yield \(A_{\mathrm{c}}^ \bot = 0.346\,{\mathrm{T}}/{\mathrm{\mu }}_{\mathrm{B}}\) and \(A_{\mathrm{c}}^\parallel = - 0.378\,{\mathrm{T}}/{\mathrm{\mu }}_{\mathrm{B}}\). This anisotropy can be explained by the influence of the Sm 4f5-shell electric quadrupole moment41 on the conduction electron spin polarization at the μ+ site, which has been observed in other compounds with non-spherical f-electron distributions.42
Comparison of the μ+-Knight shift to the bulk magnetic susceptibility and surface conductivity. a Ki at the two magnetically inequivalent μ+ sites vs. χmol for H = 6 T. Temperature is an implicit parameter. The straight black lines are fits to Eqs. (2a) and (2b). Temperature dependences of b the ratio K⊥/K∥ below 30 K, and c K⊥ and the electrical sheet resistance below 13 K. The red curve is a fit of the K⊥ data for T ≤ 5 K to a thermally activated Arrhenius equation, assuming an activation energy EA = 0.99 meV. The error bars for Ki represent the uncertainties in the parameters νi and ν0 from the fits in the time domain
Below 110 K, the Ki vs. χmol plots deviate from linearity (see Fig. 4a). Point-contact spectroscopy43 and ARPES44 measurements on SmB6 show that the hybridization gap develops over a fairly wide temperature range of 30 K ≤ T ≤ 110 K. This results in a loss of scaling between Ki and χmol, due to a gradual reduction of both the Pauli susceptibility \(\left( { \propto K_0^i} \right)\) and the electronic spin density at the μ+ sites \(\left( { \propto A_{\mathrm{c}}^i} \right)\). Near 30 K, the simultaneous vanishing of K⊥ and K∥ implies \(K_0^i = 0\) and χ4f = 0 in Eqs. (2a) and (2b).
Below T ~25 K, a μ+-Knight shift reappears, which does not linearly scale with χmol (Fig. 4a) and is accompanied by an increase in the TF relaxation rates with decreasing T (Fig. 3b).
Discussion
The μ+-Knight shift below 25 K is a property of the insulating bulk. In insulators and semiconductors, the μ+ sometimes forms a bound state with an electron, known as a muonium atom (Mu).38 The signature of Mu in high TF is a pair of frequencies separated by the Mu hyperfine splitting and centered on the precession frequency of the free μ+ in the applied field—the latter being close to the μ+ precession frequency in the Ag backing plate. This is clearly not observed in Fig. 2. Consequently, the μ+-Knight shift must still be induced by the Sm-4f moments.
The lack of scaling of Ki with the bulk magnetic susceptibility χmol below 25 K could potentially arise from the charged muon significantly altering the Sm3+ crystal electric field (CEF) level scheme and hence χ4f. A significant influence of the μ+ on the local magnetic susceptibility has been identified in a few Pr3+-ion systems.45,46 The CEF level scheme of Sm3+ (4f5) in SmB6 is similar to Ce3+ (4f1) in CeB6. In both cases, the spin–orbit interaction splits the 4f states into J = 5/2 and J = 7/2 multiplets. The J = 5/2 multiplet is further split in the cubic crystalline field into a Γ7 doublet, and a ground-state Γ8 quartet that has magnetic and quadrupolar moments. The energy difference between the Γ8 quartet and excited Γ7 doublet is about 15 meV in SmB6,47 and 46 meV in CeB6,48 which in both compounds exceeds the Kondo energy scale (temperature). Thus, only modifications of the Zeeman split Γ8 quartet are relevant in the low T regime. In CeB6, which does not develop a Kondo insulating gap, Ki linearly scales with χmol above 10 K. Hence, it is unlikely that the μ+ induces the Knight shift observed in SmB6 below 20 K. We note that the loss of scaling between Ki and χmol in CeB6 below 10 K is due to the development of antiferroquadrupolar ordering,49 which does not occur in SmB6.
According to Eqs. (2a) and (2b), there must be a new contact hyperfine field Bc to cause the sign change in the values of K⊥ and K∥ below 25 K. As mentioned earlier, in an insulating state, this may result from the μ+ bonding to an ion that is covalently bonded to a localized magnetic electron. A super-transferred hyperfine field at the μ+ site through a Sm-B-μ+ connection could arise from field-induced moments at the B sites. In CeB6, field-induced magnetic moments inside or around the B6 octahedron have been ruled out by polarized neutron diffraction,50 which is presumably also the case in SmB6. Moreover, the formation of a B-μ+ bond is incompatible with the μ+ site, which is ~2 Å from the nearest B atom.
The alternative possibility in an insulating state is that Bc originates from direct overlap of the μ+ with the wavefunction of the localized magnetic electrons. While the Sm-4f orbitals are highly localized, the 5d orbitals of the nearest-neighbor Sm ions partially overlap the μ+ site. In a spin exciton, the spin polarization of the bound 5d electron is coherently coupled to the localized 4f electrons, and a contact hyperfine field may result from an exchange interaction between the μ+ and the extended magnetic 5d electrons.
The temperature dependence of the TF-μSR relaxation rate (Fig. 3b) provides evidence for a low-energy spin exciton. The marked increase of Δ⊥ and Δ∥ below 20 K corresponds to an increase in the width of the local field distribution, indicative of a gradual slowing down of magnetic fluctuations. As shown in the inset of Fig. 3b, the H = 6 T data for Δ⊥ above 5 K can be fit with a thermally activated law: Δ⊥ = A + Bexp(EA/kBT), yielding A = 0.35 ± 0.07 μs−1, B = 0.12 ± 0.04 μs−1, and EA = 0.99 ± 0.12 meV. The temperature-independent contribution comes from the nuclear dipole moments and the spatial inhomogeneity of the applied magnetic field. The thermally activated decrease of Δ⊥ is consistent with a rising fluctuation rate 1/τ, where 1/τ∝exp(−EA/kBT) and τ is the average correlation time. Spin excitons create fluctuating regions of AFM correlations extending over a few unit cells, which modify the local field sensed by the μ+. The increase in Δi is explained by AFM amplitude fluctuations perpendicular to H, producing a small temporary canted moment. This is presumably of order H/JRKKY, where JRKKY is the virtual RKKY-like magnetic exchange interaction between the 4f moments in the theory of Riseborough.26,27 The nearly constant difference between Δi at 6 T and 4 T above 6 K is primarily caused by a difference in the inhomogeneity of the applied field. Below 5–6 K, however, Δi saturates and exhibits an intrinsic increase with H. The saturation indicates that the average fluctuation period of the spin excitons (τ) has become large with respect to the muon time window, such that Δi is no longer significantly affected by fluctuations. The corresponding field dependence of Δi below 5–6 K reflects an inhomogeneous broadening of the local field distribution.
Figure 4b shows a strong temperature dependence of K⊥/K∥ at 6 ≤ T ≤ 20 K, which with \(K_0^i = 0\) reflects the behavior of \(\left( {A_{\mathrm{c}}^ \bot - A_{{\mathrm{dip}}}/2} \right)/\left( {A_{\mathrm{c}}^\parallel + A_{{\mathrm{dip}}}} \right)\). Changes in the lattice parameter20,51,52 below 20 K are too small to cause an appreciable change in Adip. The remaining possibility is that \(A_{\mathrm{c}}^ \bot\) and \(A_{\mathrm{c}}^\parallel\) change with decreasing temperature. The anisotropy of Ac above 110 K indicates coupling of the non-spherical 4f-electron distribution to the field-induced Sm magnetic moments. Hence, the strong temperature dependence of \(A_{\mathrm{c}}^ \bot\) and \(A_{\mathrm{c}}^\parallel\) below 20 K is likely due to a rotation of the 4f-electron distribution with the canted moment induced by AFM fluctuations. We note that the values of \(A_{\mathrm{c}}^i\) are dependent on the overlap integral of the non-spherical 4f-electron distribution and the 5d electrons with wavefunctions that overlap the μ+ site. Below 6 K, there is an abrupt increase in K⊥/K∥ to a value comparable to that at 25 K. This suggests that the 4f-electron distribution returns to being more closely aligned with the applied field.
As shown in Fig. 3a, there is an abrupt decrease (increase) in K⊥ (K∥) below 5–6 K. According to Eqs. (2a) and (2b), these simultaneous behaviors cannot be explained by a rapid change in χ4f(T). Instead, these behaviors appear to reflect the temperature dependence of K⊥/K∥ (and hence \(A_{\mathrm{c}}^ \bot\) and \(A_{\mathrm{c}}^\parallel\)) that is apparent at T ≤ 5 K in Fig. 4b. As shown in Fig. 4, the temperature dependence of K⊥ for T ≤ 5 K is well fit with a thermally activated Arrhenius equation: K⊥(T) = K⊥(0) + Cexp(−EA/kBT) that assumes the same value EA = 0.99 meV obtained from the fit of the temperature dependence of Δ⊥. This suggests that unlike the TF-μSR relaxation rate, the μ+-Knight shift is sensitive to thermal activation of the spin exciton below 6 K, and in particular the shift in the time-average and field sensed by the muon ensemble associated with the hyperfine coupling between the μ+ and the bound 5d electron of the spin exciton. Nevertheless, there are insuffient μ+-Knight shift data points below 6 K to establish true exponential-activated behavior.
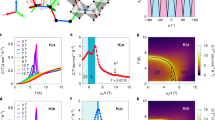
The dynamic relaxation rate λZF observed by zero-field (ZF) μSR develops below 20–25 K,22 exhibits a short anomalous peak near 4 K, and subsequently saturates. Our findings here suggest that the saturation is due to the freezing out of a bulk spin exciton of much lower energy than that observed by INS, giving way to AFM quantum spin fluctuations. We note that the peak in λZF(T) near 4 K vanishes with the addition of a 0.5% Fe impurity.23 This is likely due to the predicted adverse effect of impurities on a fully developed spin exciton.27 We have carried out similar TF-μSR measurements on the 0.5% Fe-doped sample. Figure 5 shows a comparison of the low-temperature results with those for the pure compound. While the bulk magnetic susceptibility is significantly modified by the impurities, the changes to the temperature dependences of Δ⊥ and K⊥ are more subtle. A fit of the Δ⊥ vs. T data for the Fe-doped sample above 5 K to the thermally activated law described earlier yields EA = 0.75 ± 0.16 meV. The smaller activation energy compared to pure SmB6 is consistent with the expected impurity-induced broadening and decrease of the binding energy of the spin exciton.27 Furthermore, the substantial effect of the dilute Fe impurity is consistent with the finding that impurities on the level of 1% are enough to destroy the spin exciton feature observed by Raman spectroscopy.53
Comparison between pure and Fe-doped SmB6. Temperature dependences of the low-temperature a bulk magnetic susceptibility, b TF-μSR relaxation rate Δ⊥, and c Knight shift K⊥ in pure and 0.5% Fe-doped SmB6 for H = 6 T. The dashed curves in b are fits of the Δ⊥ data above 5 K to a thermally activated function: Δ⊥ = A + Bexp(EA/kBT). The dashed curves in c are fits of the K⊥ data at T ≤ 5 K to a thermally activated Arrhenius equation: K⊥(T) = K⊥(0) + Cexp(−EA/kBT) assuming the values of EA from the fits in b. The error bars for Ki represent the uncertainties in the parameters νi and ν0 from the fits in the time domain. Likewise, the error bars for Δi represent the uncertainty from the fits in the time domain
Our experiments provide evidence for thermally activated low-energy magnetic excitations in SmB6. The results support the theoretical prediction of a low-energy spin exciton (≤1 meV) in SmB6, which has been argued to account for certain low-temperature thermodynamic and transport anomalies.33 As shown in Fig. 4c, the saturation of the electrical sheet resistance Rs occurs below 4 K, where K⊥ is greatly reduced. This observation suggests that the resistivity plateau develops when spin exciton scattering of the metallic surface states becomes insignificant.
Methods
Samples and experimental technique
The growth and characterization of the crystals were previously reported.23 The high TF μ+-Knight shift measurements were performed on a 5 × 5-mm2 mosaic of single crystals aligned with the c-axis parallel to the applied field and mounted on a pure Ag backing plate. The measurements utilized a He-gas flow cryostat and the so-called “NuTime” spectrometer at TRIUMF in Vancouver, Canada. All of the high TF-μSR measurements were recorded with the initial muon spin polarization P(0) perpendicular to the external magnetic field H, which was applied parallel to the muon beam momentum. Figure S1 shows a schematic of a custom sample holder designed for the μ+-Knight shift measurements.
The value of the muon spin precession frequency in the applied magnetic field H alone, ν0 = (γμ/2π)H, was accurately determined by first simultaneously recording the TF-μSR signal in a 99.998% pure Ag mask located upstream of the sample. To correct for the difference in the external field at the Ag mask and sample locations, TF-μSR measurements were also simultaneously performed on the Ag mask with Ag in place of SmB6 at the sample location.
Data availability
All relevant data are available from the authors upon request.
References
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Ando, Y. Topological insulator materials. J. Phys. Soc. Jpn. 82, 102001 (2013).
Dzero, M., Xia, J., Galitski, V. & Coleman, P. Topological Kondo insulators. Annu. Rev. Condens. Matter Phys. 7, 249–280 (2016).
Kim, D. J., Thomas, S., Grant, T., Botimer, J., Fisk, Z. & Xia, J. Surface Hall effect and nonlocal transport in SmB6: evidence for surface conduction. Sci. Rep. 3, 3150 (2013).
Wolgast, S. et al. Low-temperature surface conduction in the Kondo insulator SmB6. Phys. Rev. B 88, 180405(R) (2013).
Kim, D. J., Xian, J. & Fisk, Z. Topological surface state in the Kondo insulator samarium hexaboride. Nat. Mater. 13, 466–470 (2014).
Jiang, J. et al. Observation of possible topological in-gap surface states in the Kondo insulator SmB6 by photoemission. Nat. Commun. 4, 3010 (2013).
Xu, N. et al. Surface and bulk electronic structure of the strongly correlated system SmB6 and implications for a topological Kondo insulator. Phys. Rev. B 88, 121102(R) (2013).
Neupane, M. et al. Surface electronic structure of the topological Kondo-insulator candidate correlated electron system SmB6. Nat. Commun. 4, 2991 (2013).
Frantzeskakis, E. et al. Kondo hybridization and the origin of metallic states at the (001) surface of SmB6. Phys. Rev. X 3, 041024 (2013).
Xu, N. et al. Direct observation of the spin texture in SmB6 as evidence of the topological Kondo insulator. Nat. Commun. 5, 4566 (2014).
Hlawenka, P. et al. Samarium hexaboride is a trivial surface conductor. Nat. Commun. 9, 517 (2018).
Wakeham, N. et al. Low-temperature conducting state in two candidate topological Kondo insulators: SmB6 and Ce3Bi4Pt3. Phys. Rev. B 94, 035127 (2016).
Laurita, N. J. et al. Anomalous three-dimensional bulk ac conduction within the Kondo gap of SmB6 single crystals. Phys. Rev. B 94, 165154 (2016).
Li, G. et al. Two-dimensional Fermi surfaces in Kondo insulator SmB6. Science 346, 1208–1212 (2014).
Tan, B. S. et al. Unconventional Fermi surface in an insulating state. Science 349, 287–290 (2015).
Baskaran, G. Majorana Fermi sea in insulating SmB6: a proposal and a theory of quantum oscillations in Kondo insulators. Preprint at https://arxiv.org/abs/1507.03477 (2015).
Erten, O., Chang, P.-Y., Coleman, P. & Tsvelik, A. M. Skyrme Insulators: Insulators at the brink of superconductivity. Phys. Rev. Lett. 119, 057603 (2017).
Chowdhury, D., Sodemann, I. & Senthil, T. Mixed-valence insulators with neutral Fermi surfaces. Nat. Commun. 9, 1766 (2018).
Tarascon, J. M. et al. Temperature dependence of the samarium oxidation state in SmB6 and Sm1-xLaxB6. J. Phys. 41, 1141–1145 (1980).
Mizumaki, M., Tsutsui, S. & Iga, F. Temperature dependence of Sm valence in SmB6 studied by X-ray absorption spectroscopy. J. Phys. Conf. Ser. 176, 012034 (2009).
Biswas, P. K. et al. Low-temperature magnetic fluctuations in the Kondo insulator SmB6. Phys. Rev. B 89, 161107 (2014).
Akintola, K. et al. Quantum spin fluctuations in the bulk insulating state of pure and Fe-doped SmB6. Phys. Rev. B 95, 245107 (2017).
Caldwell, T. et al. High-field suppression of in-gap states in the Kondo insulator SmB6. Phys. Rev. B 75, 075106 (2007).
Biswas, P. K. et al. Suppression of magnetic excitations near the surface of the topological Kondo insulator SmB6. Phys. Rev. B 95, 020410(R) (2017).
Riseborough, P. S. Magnetic bound states in SmB6. Ann. Phys. 9, 813–820 (2000).
Riseborough, P. S. Collapse of the coherence gap in Kondo semiconductors. Phys. Rev. B 68, 235213 (2003).
Alekseev, P. A. et al. Magnetic excitation spectrum of mixed-valence SmB6 studied by neutron scattering on a single crystal. J. Phys. Condens. Matter 7, 289–305 (1995).
Fuhrman, W. T. et al. Interaction driven subgap spin exciton in the Kondo insulator SmB6. Phys. Rev. Lett. 114, 036401 (2015).
Kapilevich, G. A. et al. Incomplete protection of the surface Weyl cones of the Kondo insulator SmB6: spin exciton scattering. Phys. Rev. B 92, 085133 (2015).
Arab, A. et al. Effects of spin excitons on the surface states of SmB6: a photoemission study. Phys. Rev. B 94, 235125 (2016).
Park, W. K. et al. Topological surface states interacting with bulk excitations in the Kondo insulator SmB6 revealed via planar tunneling spectroscopy. Proc. Natl Acad. Sci. USA 113, 6599–6604 (2016).
Knolle, J. & Cooper, N. R. Excitons in topological Kondo insulators: theory of thermodynamic and transport anomalies in SmB6. Phys. Rev. Lett. 118, 096604 (2017).
Fuhrman, W. T. et al. Screened moments and extrinsic in-gap states in samarium hexaboride. Nat. Commun. 9, 1539 (2018).
Orendáč, M. et al. Isosbestic points in doped SmB6 as features of universality and property tuning. Phys. Rev. B 96, 115101 (2017).
Roman, J. et al. Low temperature magnetic properties of samarium hexaboride. Czech. J. Phys. 46, 1983–1984 (1996).
Gabáni, S. et al. Magnetic properties of SmB6 and Sm1-xLaxB6 solid solutions. Czech. J. Phys. 52, A225–A228 (2002).
Schenck, A.Muon Spin Rotation Spectroscopy: Principles and Applications in Solid State Physics. (Adam Hilger Ltd., Bristol, 1985).
Schenck, A., Gygax, F. N. & Kunii, S. Field-induced magnetization distribution and antiferroquadrupolar order in CeB6. Phys. Rev. Lett. 89, 037201 (2002).
Cooley, J. C. et al. High field gap closure in the Kondo insulator SmB6. J. Supercond. 12, 171–173 (1999).
Delyagin, N. N. & Erzinkyan, A. L. The impact of quadrupole moment of 4f shell on the hyperfine interactions anisotropy in RAl2 (R=Sm, Tb) intermetallic compounds. Solid State Commun. 230, 16–19 (2016).
Schenck, A., Gygax, F. N., Andreica, D. & Onuki, Y. J. Interplay of quadrupolar order, Ce 4f spin dynamics and RKKY induced conduction electron spin polarization in CeAg. Phys. Condens. Matter 15, 8599–8617 (2003).
Zhang, X. et al. Hybridization, inter-ion correlation, and surface states in the Kondo insulator SmB6. Phys. Rev. X 3, 011011 (2013).
Xu, N. et al. Exotic Kondo crossover in a wide temperature region in the topological Kondo insulator SmB6 revealed by high-resolution ARPES. Phys. Rev. B 90, 085148 (2014).
Feyerherm, R. et al. Crystal electric field next to a hydrogen-like interstitial—μ+ in PrNi5. Z. Phys. B 99, 3–13 (1995).
Tashma, T. et al. Electronic changes induced by μ+ in PrIn3: muon-spin-rotation observation and crystalline-electric-field model calculation. Phys. Rev. B 56, 9397 (1997).
Sundermann, M. et al. 4f crystal field ground state of the strongly correlated topological insulator SmB6. Phys. Rev. Lett. 120, 016402 (2018).
Sundermann, M. et al. The quartet ground state in CeB6: an inelastic X-ray scattering study. Europhys. Lett. 117, 17003 (2017).
Schenck, A., Gygax, F. N., Solt, G., Zaharko, O. & Kunii, S. Temperature and field dependence of the order parameter in the antiferroquadrupolar phase of CeB6 from μ+ Knight Shift measurements. Phys. Rev. Lett. 93, 257601 (2004).
Givord, F., Boucherle, J.-X., Burlet, P., Gillon, B. & Kunii, S. Non-anomalous magnetization density distribution in CeB6. J. Phys. Condens. Matter 15, 3095 (2003).
Sirota, N. N., Novikov, V. V., Vinokurov, V. A. & Paderno, Yu. B. Temperature dependence of the heat capacity and lattice constant of lanthanum and samarium hexaborides. Phys. Solid State 40, 1856–1858 (1998).
Mandrus, D. et al. Low-temperature thermal expansion of SmB6: evidence for a single energy scale in the thermodynamics of Kondo insulators. Phys. Rev. B 49, 16809 (2002).
Valentine, M. E. et al. Breakdown of the Kondo insulating state in SmB6 by introducing Sm vacancies. Phys. Rev. B 94, 075102 (2016).
Acknowledgements
This work was performed at TRIUMF, the University of Maryland (UofM), and Simon Fraser University (SFU). The authors wish to thank E. Mun, J.S. Dodge, and P.S. Riseborough for informative discussions. J.E.S. acknowledges support from NSERC of Canada. J.P. acknowledges support from AFOSR through Grant No. FA9550-14-1-0332 and the Gordon and Betty Moore Foundation’s EPiQS Initiative through Grant No. GBMF4419.
Author information
Authors and Affiliations
Contributions
S.R.S., X.F.W., and J.P. grew and characterized the sample. K.A. performed the bulk magnetic susceptibility measurements. K.A., A.P., S.R.D., A.C.Y.F., M.P., S.R.S., and J.E.S. performed the high TF-μSR measurements at TRIUMF. K.A. and J.E.S. carried out the data analysis. K.A. and J.E.S. wrote the manuscript with input from all co-authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Akintola, K., Pal, A., Dunsiger, S.R. et al. Freezing out of a low-energy bulk spin exciton in SmB6. npj Quant Mater 3, 36 (2018). https://doi.org/10.1038/s41535-018-0110-7
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-018-0110-7