Abstract
Honeycomb-lattice quantum magnets with strong spin-orbit coupling are promising candidates for realizing a Kitaev quantum spin liquid. Although iridate materials such as Li2IrO3 and Na2IrO3 have been extensively investigated in this context, there is still considerable debate as to whether a localized relativistic wavefunction (Jeff = 1/2) provides a suitable description for the electronic ground state of these materials. To address this question, we have studied the evolution of the structural and electronic properties of α-Li2IrO3 as a function of applied hydrostatic pressure using a combination of x-ray diffraction and x-ray spectroscopy techniques. We observe striking changes even under the application of only small hydrostatic pressure (P ≤ 0.1 GPa): a distortion of the Ir honeycomb lattice (via X-ray diffraction), a dramatic decrease in the strength of spin-orbit coupling effects (via X-ray absorption spectroscopy), and a significant increase in non-cubic crystal electric field splitting (via resonant inelastic X-ray scattering). Our data indicate that α-Li2IrO3 is best described by a Jeff = 1/2 state at ambient pressure, but demonstrate that this state is extremely fragile and collapses under the influence of applied pressure.
Similar content being viewed by others
Introduction
The electronic ground state in many iridate materials is described by a complex wave-function in which spin and orbital angular momenta are entangled due to relativistic spin-orbit coupling (SOC).1,2 Such a localized electronic state carries an effective total angular momentum of Jeff = 1/2.3,4 In materials with an edge-sharing octahedral crystal structure, such as the honeycomb iridates α-Li2IrO3 and Na2IrO3, these Jeff = 1/2 moments are expected to be coupled through a special bond-dependent magnetic interaction,5,6,7 which is a necessary condition for the realization of a Kitaev quantum spin liquid.8 However, this relativistic electron picture is challenged by an alternate description, in which itinerant electrons are confined to a benzene-like hexagon, keeping the system insulating despite the delocalized nature of the electrons.9,10 In this quasi-molecular orbital (QMO) picture, the honeycomb iridates are an unlikely choice for a Kitaev spin liquid.
The Jeff = 1/2 ground state arises from a very specific hierarchy of energy scales, set by crystal electric field, spin-orbit coupling, and electronic correlation effects. These energy scales can be probed by resonant inelastic X-ray scattering (RIXS), which is sensitive to d−d transitions involving the Ir 5d valence levels (both within the t2g manifold and between the t2g and eg manifolds).11,12,13,14,15 At ambient pressure, high resolution RIXS measurements on α-Li2IrO311 have shown that this material occupies a regime where octahedral crystal field splitting ≫ spin-orbit coupling ≫ trigonal crystal field splitting. These measurements indicate that the splitting of the lower Jeff = 3/2 levels (∆~0.11 meV) is small compared to the splitting between the Jeff = 3/2 and Jeff = 1/2 levels (3λ/2 ~ 0.78 eV), providing some of the most compelling evidence in favor of the Jeff = 1/2 description of this compound. Another experimental signature often associated with the Jeff = 1/2 relativistic electronic ground state is an unusually large difference between the X-ray absorption spectroscopy (XAS) “white line” intensity observed at the Ir L3 (2p3/2 → 5d) and L2 (2p1/2 → 5d) absorption edges.16,17,18 The ratio of these intensities is known as the L3/L2 branching ratio (BR), and provides a direct measure of 〈L⋅S〉, the angular part of the expectation value for the spin orbit operator.19,20 In the absence of SOC, one expects BR = 2, reflecting the fact that there are twice as many states in 2p3/2 as in 2p1/2. In a wide range of iridate materials, including Na2IrO3, large BR ranging from 4 to 6 have been observed, and have been interpreted as evidence for the Jeff = 1/2 state.18
Experimentally distinguishing between the localized Jeff = 1/2 and itinerant QMO descriptions of the honeycomb iridates is complicated by the complex hierarchy of energy scales involved. In fact, Foyevtsova and coworkers have argued that the aforementioned X-ray spectroscopy results are not incompatible with a QMO-based picture.10 However, the nature of the wavefunction can often be revealed indirectly when an appropriate tuning parameter is used to vary the electronic properties of the system. Hydrostatic pressure is a particularly effective tuning parameter, as it can be used to directly modify the overlap between electronic orbitals, and thereby control the electronic bandwidth or correlation strength.17,21,22 In recent theoretical work by Kim et al.23 it has been suggested that the honeycomb iridates could be tuned between the localized Jeff = 1/2 and itinerant QMO regimes by varying the energy scale associated with either the spin-orbit coupling or the electronic correlations. Therefore, hydrostatic pressure may provide an ideal experimental knob to switch between these two pictures.
We have studied the evolution of the structural and electronic properties of the honeycomb lattice iridate α-Li2IrO3 as a function of applied hydrostatic pressure using three complementary synchrotron x-ray techniques. In addition to RIXS and XAS, we used conventional x-ray powder diffraction (XRD) to study the crystal structure of this material. The pressure of the sample was tuned from ambient pressure up to 10 GPa using a diamond anvil cell (DAC). We observe dramatic suppression of the XAS branching ratio with the application of small (~0.1 GPa) hydrostatic pressure, which arises from a pressure-induced structural distortion of the ideal honeycomb lattice. These changes occur at pressures well below the structural phase transition into a dimerized phase (Pc≈3 GPa), indicating the fragility of the Jeff = 1/2 state. The RIXS data also show strong, non-trivial pressure dependence, which will be discussed with the aid of density functional calculations.
Results
X-ray absorption spectroscopy
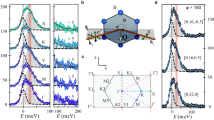
The pressure dependence of the x-ray absorption spectra for α-Li2IrO3 is provided in Fig. 1. The large branching ratio observed at ambient pressure (BR = 5.1±0.4) is consistent with a Jeff = 1/2 state, and is similar to previously reported BR for other spin-orbit-driven iridates such as Sr2IrO4.17,18 However, the BR of α-Li2IrO3 drops precipitously under applied pressure, falling to less than 2/3 of its original value by P = 1.1 GPa. The BR continues to decrease more gradually up to ~3 GPa, and ultimately plateaus at a high pressure value of 2.8±0.1 GPa. Although dramatically reduced from ambient pressure, this value still exceeds the statistical branching ratio (BR = 2) expected in the limit of negligible SOC. In fact, it is strikingly similar to that of iridium metal (BR ~ 3),18,24,25 a material which exhibits significant SOC, but which does not harbour a Jeff = 1/2 ground state. As a result, these data suggest that applied pressure results in a collapse of the Jeff = 1/2 ground state in α-Li2IrO3 by P = 1.1 GPa.
X-ray absorption spectroscopy (XAS) can be used to probe the relativistic Jeff = 1/2 ground state of α-Li2IrO3. At ambient pressure, XAS measurements reveal an anomalously large intensity difference between the main white line features observed at a the Ir L3 (2p3/2 → 5d) and b Ir L2 (2p1/2 → 5d) absorption edges. This large L3/L2 branching ratio is a strong signature of the Jeff = 1/2 ground state. c Under applied pressure, the branching ratio decreases rapidly, approaching a value reminiscent of elemental iridium. The high pressure branching ratio remains greater than the statistical ratio of 2, but falls well below the values reported for other spin-orbit-driven Jeff = 1/2 systems. (Inset) This qualitative trend is also captured by quantum chemistry calculations based on the experimental crystal structure
The abrupt drop in branching ratio is also qualitatively reproduced by ab initio quantum chemistry calculations, as shown in the inset of Fig. 1c and described in the “Methods” section. In fact, these calculations, which are based on the experimental crystal structures determined from XRD, suggest that the drop in branching ratio actually occurs at significantly lower pressures, close to P = 0.1 GPa. We have carried out high pressure electrical resistance measurements on α-Li2IrO3 (provided in the SM), which indicate that the sample remains insulating up to 7 GPa. This confirms that it is the Jeff = 1/2 character of the ground state, and not its insulating properties, that is disrupted by applied pressure.
The pressure scale associated with this change in BR is quite remarkable in comparison with other iridates. In Sr2IrO4 for example, the BR remains essentially unchanged up to 30 GPa,17 and an applied pressure of 70 GPa is required to produce a decrease similar to what is observed in Fig. 1. This suggests that α-Li2IrO3 is situated much closer to the boundary of the Jeff = 1/2 relativistic electronic state, and shows that it is possible to tune the system into a new electronic ground state under the influence of applied pressure.
X-ray Diffraction
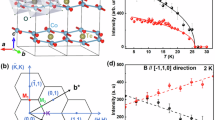
In order to elucidate the role of structure in these electronic changes, we performed x-ray powder diffraction measurements, as shown in Fig. 2. These measurements reveal that α-Li2IrO3 undergoes a series of two structural distortions as a function of pressure. The first of these distortions, which arises at P ~ 0.1 GPa, is characterized by a gradual elongation of the Ir honeycomb lattice. At ambient pressure, α-Li2IrO3 displays an almost ideal, undistorted Ir honeycomb lattice,11,26,27 with 6 equal Ir-Ir bond lengths of 2.98 Å. By 0.1 GPa, we find that this honeycomb lattice has begun to distort, forming 2 long bonds (3.08 Å) and 4 short bonds (2.92 Å) on each Ir hexagon. Such a distortion is fully allowed under the C2/m space group reported for this compound at ambient pressure.
a High pressure X-ray powder diffraction measurements reveal a series of pressure-induced structural distortions in α-Li2IrO3. b At ambient pressure, α-Li2IrO3 displays an almost ideal undistorted Ir honeycomb lattice. c As the pressure increases, the honeycomb lattice distorts, forming four shorter bonds and 2 longer bonds on each Ir hexagon. d Above 3 GPa, the honeycomb lattice buckles and begins to dimerize, with each hexagon developing 2 short bonds, 2 medium bonds, and 2 long bonds
This initial distortion is followed by a much larger distortion, which takes place during a first order structural phase transition at 3 GPa. This transition is evident from peak splitting in the observed diffraction patterns (Fig. 2a), a discontinuous jump in lattice parameters (see SM), and an extended phase coexistence region from P ~ 3 to 5 GPa. Structural refinements indicate that this transition is associated with a distortion that lowers the crystal symmetry from monoclinic (C2/m) to triclinic (P-1). This causes the honeycomb lattice to stretch and buckle, with each Ir hexagon developing 2 short bonds, 2 intermediate bonds, and 2 long bonds. The length of the 2 short bonds in the triclinic structure is remarkably small (2.31 Å), which strongly suggests the formation of Ir-Ir dimers at high pressures. After the original submission of this article, high pressure x-ray diffraction measurements on single crystal α-Li2IrO3 were reported by V. Hermann et al.28 These measurements confirm the presence of a high pressure structural phase transition, with lattice dimerization occurring at Pc ~ 3.8 GPa. A similar case of structural dimerization has also been reported in the honeycomb lattice ruthenate Li2RuO3.29,30,31 In Li2RuO3, the Ru honeycomb lattice exhibits a strong tendency to form local dimers and covalent Ru-Ru bonds,31 with the development of long-range dimer order occurring below TC ~ 540 K.29,31 Interestingly, we note that the rapid drop in branching ratio in α-Li2IrO3 appears to coincide with the small initial distortion at 0.1 GPa, rather than the much more obvious transition associated with the structural dimerization at 3 GPa.
Resonant inelastic X-ray scattering
The pressure dependence of the RIXS spectra for α-Li2IrO3 is shown in Fig. 3. We note that the data shown here were obtained using a higher flux/lower resolution experimental configuration compared to earlier ambient pressure measurements on this compound.11 However, this energy resolution is sufficient to show that the d–d excitations are very sensitive to applied pressure, with significant changes in the distribution of spectral weight associated with transitions between the Ir t2g levels. In particular, the strong energy loss peak at \(\hbar \omega = E_i - E_f = 0.78_{}^{}\) eV (associated with transitions between the Jeff = 3/2 and Jeff = 1/2 levels) gradually decreases in intensity, while a new inelastic peak develops at \(\hbar \omega \sim 1.40_{}^{}\) eV. The total spectral weight of these two features is approximately constant as a function of pressure (shown in the inset of Fig. 3a), implying that spectral weight transfers from the low energy peak to the high energy peak, presumably due to a reorganization of the t2g energy levels. The most obvious consequence of this new energy level scheme is that the trigonal crystal field splitting becomes larger than the spin-orbit coupling, confirming that the Jeff = 1/2 model is no longer a valid description for this system. We note that the peak at 1.40 eV first appears at the lowest applied pressure, but that the largest change in spectral weight coincides with the structural transition at P ~ 3 GPa.
Resonant inelastic X-ray scattering (RIXS) reveals the pressure dependence of the d–d transitions and crystal electric field splittings in α-Li2IrO3. a At ambient pressure, there is one strong peak (A), which corresponds to intra-t2g transitions between the Jeff = 3/2 and Jeff = 1/2 levels. Note that the small splitting of peak A is not observed in our low resolution setup. As the pressure increases, this peak drops rapidly in intensity, with a new peak (B) appearing at higher energies. As shown in the inset, the combined spectral weight of these two features is approximately constant. Quantitative analysis of the high pressure RIXS spectra is consistent with a three-transition energy level scheme, indicating a significant increase in non-cubic crystal electric field splitting and a clear departure from the Jeff = 1/2 model. The solid lines represent fits carried out using the procedure described in the Supplementary Material. A comparison of potential t2g energy level schemes is provided for α-Li2IrO3 at (b) ambient pressure (localized Jeff = 1/2), (c) P = 2.9 GPa (localized pseudospin S = 1/2), and (d) P = 2.9 GPa (itinerant QMO picture). These levels are illustrated in the hole representation, where a single t2g hole can be excited from the lowest energy level to the higher excited states
A comparison of t2g energy level schemes corresponding to the localized Jeff = 1/2, localized pseudospin S = 1/2, and itinerant QMO models is provided in Fig. 3b–d. Under moderate pressure (0.2 < P < 2.0 GPa), the RIXS spectra can be fit equally well using either the itinerant QMO model or the pseudospin S = 1/2 model, a localized electron picture which applies in the limit of large non-cubic crystal electric field (Δ > 3λ/2).32 However, the pressure-induced peak at 1.40 eV develops an increasingly asymmetric lineshape at higher pressure, and above ~2 GPa it cannot be accurately fit using a single symmetric lineshape (see Supplementary Materials for further details). The quality-of-fit is significantly improved by introducing a third inelastic peak at slightly higher energies (\(\hbar \omega \sim 1.60_{}^{}\) eV). Such a three-peak spectrum cannot be justified in the localized electron model, but it is one of the distinguishing features of the itinerant QMO model.
In the QMO model originally proposed for Na2IrO3 by Mazin et al.9 each Ir hexagon forms a series of six QMOs which are organized into four distinct energy levels as shown in Fig. 3. These orbitals are occupied by 5 Ir valence electrons, giving rise to three possible d–d transitions within the t2g manifold. Furthermore, the QMO theory predicts that the energies of these four levels are based on only two independent parameters: the nearest neighbor (NN) and next nearest neighbor (NNN) O-assisted hopping terms, \(t\prime _1\) and \(t\prime _2\). The high pressure RIXS spectra can be fit to a model based on this QMO energy level scheme with remarkably good agreement. The experimental values of the hopping parameters extracted from these fits are \(t\prime _1 = 0.27\) eV and \(t\prime _2 = 0.15\) eV at 2.4 GPa (monoclinic phase) and \(t\prime _1 = 0.33\) eV and \(t\prime _2 = 0.11\) eV at 4.8 GPa (triclinic phase). These values can be compared to the theoretical estimates of \(t\prime _1 = 0.27\) eV and \(t\prime _2 = 0.075\) eV predicted for Na2IrO3 at ambient pressure.9
Although the RIXS spectra collected in the high pressure triclinic phase are still well described by the same three transition energy level scheme, it should be noted that the original QMO picture may no longer be valid within this regime. In particular, the dimerization of the honeycomb lattice may be expected to alter the character of the molecular orbitals that make up these states. However, in spite of the large lattice distortion at 3 GPa, we find that the RIXS spectra evolves very smoothly as a function of pressure, showing similar qualitative features above and below the structural transition.
Discussion
The electronic structure of α-Li2IrO3 can be investigated more closely with the aid of density functional calculations, as shown in Fig. 4. As the experimental data suggests, these calculations indicate that the electronic density of states (DOS) is very sensitive to the effect of applied pressure. At ambient pressure (Fig. 4a), the DOS resembles that of a localized Jeff = 1/2 spin-orbital Mott insulator.11 As the pressure increases towards 2.8 GPa (Fig. 4b, c), a series of four peaks gradually develop in the vicinity of the Fermi level, with three peaks below Ef and one peak above. This DOS appears to be consistent with the energy level scheme suggested by the RIXS data, and is reminiscent of an itinerant QMO insulator with a gap of ~0.2 eV. The development of a QMO-like state is supported by previous DFT calculations by Foyevtsova et al.10 which suggest that moderate structural distortions act to enhance effective intrahexagon hopping parameters, while reducing the interhexagon hopping parameters. As a result, the overall effect of the primary distortions that occur in the honeycomb iridate crystal structure—orthorhombic distortions, trigonal distortions, and rotations of the IrO6 octahedra—is believed to enhance the QMO character of these materials.
The pressure dependence of the density of states (DOS) in α-Li2IrO3 can be investigated with density functional theory calculations (GGA + SOC + U, with Hubbard U = 2.0 eV and Hund’s J = 0.5 eV) performed using the experimental crystal structures determined at a ambient, b P = 0.1 GPa, c P = 2.8 GPa, and d P = 5.2 GPa. The solid curve represents the full DOS, while the shaded area represents the contribution due to the Ir electrons. These calculations demonstrate that the electronic band structure of α-Li2IrO3 is very sensitive to applied pressure, with substantial changes to the DOS emerging even at 0.1 GPa. Although the size of the insulating gap is reduced with applied pressure, the system remains insulating through the collapse of the Jeff = 1/2 ground state (P ≤ 0.1 GPa) and the structural phase transition at P ~3 GPa. The overlap between peaks in the DOS increases significantly within the dimerized triclinic phase (P = 5.2 GPa)
As noted above, a QMO-like state is unlikely to survive into the heavily distorted triclinic phase without substantial modification. Indeed, the calculated DOS in the dimerized phase (Fig. 4d) appears to have lost much of its QMO character, as the overlap between t2g bands below Ef becomes significantly larger. The DFT results also suggest that α-Li2IrO3 remains insulating within the dimerized phase, in agreement with our high pressure electrical resistance measurements. The detailed properties of the dimerized phase are clearly a subject that requires further investigation. It is intriguing to note that the energy level scheme and calculated DOS for dimerized Li2RuO330 also bear strong similarities to the QMO model.
Figure 5 presents a comparison of pressure scales identified by our three primary experimental techniques. The pressure scales identified by XAS are illustrated by the pressure dependence of the Ir L2 and L3-edge white line intensities (Fig. 5a), the pressure scales identified by XRD are illustrated by the evolution of the Ir-Ir bond lengths (Fig. 5b), and the pressure scales identified by RIXS are illustrated by the evolution of the inelastic peak positions which correspond to energies of the intra-t2g transitions (Fig. 5c). Taken in combination, these measurements point towards the following four distinct regimes:
-
(1)
P ≲ 0.1 GPa—characterized by a high branching ratio, undistorted honeycomb lattice, and 2 peak RIXS spectrum. These properties are consistent with a localized relativistic Jeff = 1/2 ground state, as has generally been assumed for α-Li2IrO3 under ambient pressure conditions.
-
(2)
0.1 GPa ≲ P ≲ 2 GPa—characterized by a low branching ratio, slightly distorted honeycomb lattice, and 2 peak RIXS spectrum. The drop in branching ratio implies a breakdown of the relativistic Jeff = 1/2 ground state, and the energy level scheme can be explained in terms of either a localized pseudospin S = 1/2 model32 or an itinerant QMO model.9 The localized S = 1/2 picture appears to be favored by the relatively small change in bandwidth predicted by DFT.
-
(3)
2 GPa ≲ P ≲ 3 GPa—characterized by a low branching ratio, slightly distorted honeycomb lattice, and 3 peak RIXS spectrum. The evolution of the RIXS spectrum can no longer be explained in terms of a purely localized model, and is most naturally attributed to the development of an itinerant QMO-like state.
-
(4)
P ≳ 3 GPa—characterized by a low branching ratio, highly distorted honeycomb lattice, and 3 peak RIXS spectrum. The large distortion of the crystal structure points towards the development of a dimerized ground state. DFT calculations predict a breakdown of the QMO-like state, and the energy level scheme appears similar to the dimerized molecular orbital state of Li2RuO3.30
A comparison of major pressure scales in α-Li2IrO3 identified by XAS, XRD, and RIXS. a Pressure dependence of the Ir L2 and L3 edge white line intensity obtained from XAS. b Pressure dependence of the Ir-Ir bond lengths determined from XRD. c Pressure dependence of the inelastic peak positions (or intra-t2g transition energies) determined from RIXS. The experimental data highlights four different regimes, which we attribute to: a localized Jeff = 1/2 state (unshaded), a localized pseudospin S = 1/2 state (shaded red), an itinerant QMO state (shaded green), and a highly distorted dimerized state (shaded blue)
In summary, we present compelling experimental evidence of a pressure-driven collapse of the localized Jeff = 1/2 relativistic electronic ground state in the honeycomb lattice iridate α-Li2IrO3. Under the application of modest hydrostatic pressure, our complimentary x-ray diffraction and spectroscopy data reveals a structural distortion which coincides with the development of a new electronic ground state; one that is dominated by non-cubic crystal electric field effects rather than strong spin-orbit coupling. These results show that the Jeff = 1/2 state found in α-Li2IrO3 at ambient pressure is extremely fragile, since it can be disrupted by a remarkably small applied pressure of 0.1 GPa. Such fragility of the relativistic ground state could have important implications for the understanding of pressure-driven magnetic transitions in other Kitaev magnets.
Methods
Experimental Methods
X-ray absorption spectroscopy measurements were performed using the Hard X-Ray MicroAnalysis (HXMA) beamline 06ID-1 at the Canadian Light Source. The data were collected in fluorescence yield detection mode, using a 32 element Ge detector. The incident energy was selected using a Si (111) monochromator, and the higher harmonic contributions were suppressed by a combination of Rh-coated mirrors and a 50% detuning of the wiggler.
X-ray powder diffraction measurements were performed using HXMA at the CLS. The data were collected with angle dispersive techniques,33 using high energy x-rays (Ei = 24.35 keV, λ = 0.509176 Å) and a MAR345 image plate detector. Full Rietveld refinements were performed using the GSAS software package.34
Resonant inelastic X-ray scattering measurements were performed using the MERIX spectrometer on beamline 30-ID-B at the Advanced Photon Source. A diamond (111) primary monochromator, silicon (220) secondary monochromator, and spherical (2 m radius) diced silicon (844) analyzer were used to produce a high flux, medium resolution instrument configuration. The overall energy resolution [full width at half maximum (FWHM)] in this configuration was 110 meV. In order to minimize the elastic background intensity, measurements were carried out in horizontal scattering geometry with a scattering angle close to 2θ = 90°.
All measurements were performed at room temperature. Loose powder samples were loaded into a diamond anvil cell, using either panoramic (XAS, RIXS) or transmission (XRD) cell geometries. The pressure was tuned with a precision of ±0.2 GPa using the R1 fluorescent line from a ruby chip placed inside the sample space. To ensure reproducibility, high pressure measurements were repeated using a series of different pressure transmitting media. XAS measurements were carried out using low viscosity silicone fluid, XRD measurements were carried out using high viscosity silicone fluid, nitrogen gas, and water, and RIXS measurements were carried out using neon gas. Over these pressure ranges, all four pressure transmitting media are expected to deliver reasonable, quasi-hydrostatic performance. The reversibility of the pressure-induced changes was verified by performing measurements at partial and full pressure release after the highest pressure data points had been collected. Due to the presence of hysteresis effects associated with the first order structural transition at 3 GPa, all measurements presented here have been obtained under increasing pressure conditions (unless explicitly stated otherwise).
First Principles Calculations
Density functional theory (DFT) calculations were carried out within the local (spin) density approximation [L(S)DA] using the Full Potential Local Orbital band structure Package (FPLO).35 A k-mesh of 6 × 6 × 6 k-points in the whole Brillouin zone was employed. In order to account for correlation effects in the Ir 5d-shell we adopted the L(S)DA + U scheme. Due to the rather sizable spin-orbit interaction of the Ir atoms the full relativistic four-component Dirac scheme was used.
Similar to other iridates, the LDA results suggest a metallic state. To obtain an insulating ground state, one needs to take into account strong correlations in mean field approximation (LDA + U). We introduce a Hubbard U = 2.0 eV and Hund’s coupling of J = 0.5 eV for the Ir 5d-shell.
In order to extract theoretical values for the Ir L3/L2 branching ratio, the quantity which is experimentally probed by XAS, ab initio calculations were performed using many-body quantum chemistry methods. These calculations were performed on a finite cluster of atoms consisting of one IrO6 reference octahedron, four nearest-neighbor (NN) IrO6 octahedra, and fifteen adjacent Li ions. The latter accounts for the finite charge distribution in the immediate neighborhood of the central IrO6 unit. The remaining part of the lattice was modeled by point charges fit to reproduce the ionic Madelung potential in the cluster region. Energy-consistent relativistic pseudopotentials and basis functions of quadruple-zeta quality36 were used to describe the valence shell of the central Ir ion, while all-electron basis sets of triple-zeta quality37 were applied for the ligands corresponding to the reference octahedron. The NN Ir ions were represented by closed-shell Pt4+ \(t_{2g}^6\) species, using relativistic pseudopotentials and triple-zeta basis functions for the valence shell.36 For the oxygen sites corresponding to the NN octahedra, all-electron minimal atomic-natural-orbital basis sets were employed.38 Total-ion effective potentials along with a single s valence function were used for the adjacent Li species.39
All computations were carried out with the molpro quantum chemistry package.40 Multiconfigurational wave functions were first obtained using the complete-active-space self-consistent-field (CASSCF) approach. The CASSCF optimization was carried out for an average of the \(^2T_{2g}\;(t_{2g}^5)\), \(^4T_{1g}\;(t_{2g}^4e_g^1)\), \(^4T_{2g}\;(t_{2g}^4e_g^1)\), and \(^6A_{1g}\;(t_{2g}^3e_g^2)\) states. In the final multireference configuration-interaction (MRCI) calculations,41,42 single and double excitations were allowed from the O 2p and Ir 5d orbitals of the reference octahedron. All the aforementioned states entered the spin-orbit treatment, carried out as described in Ref.43. The branching ratios were derived at the MRCI level, following the procedure described in Ref.44.
Representative crystal structures determined from XRD measurements at ambient pressure, 0.1 GPa, 0.6 GPa, and 2.8 GPa were used as input for the quantum chemistry calculations. The resulting MRCI branching ratios are plotted in the inset of Fig. 1 in the main text. It is clear that the computed values capture the same qualitative trend as the experimental data but systematically underestimate the observed branching ratios. It has been shown that better agreement with the experimental data can be obtained by including more excited states in the spin-orbit treatment,44 however, this aspect of the calculation falls beyond the scope of the present study.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Witczak-Krempa, W., Chen, G., Kim, Y. B. & Balents, L. Correlated quantum phenomena in the strong spin-orbit regime. Annu. Rev. Condens. Matter Phys. 5, 57–82 (2014).
Rau, J. G., Lee, E. K.-H. & Kee, H.-Y. Spin-orbit physics giving rise to novel phases in correlated systems: iridates and related materials. Annu. Rev. Condens. Matter Phys. 7, 195–221 (2016).
Kim, B. J. et al. Novel J eff = 1/2 Mott state induced by relativistic spin-orbit coupling in Sr2IrO4. Phys. Rev. Lett. 101, 076402 (2008).
Kim, B. J. et al. Phase-sensitive observation of a spin-orbital mott state in Sr2IrO4. Science 323, 1329–1332 (2009).
Jackeli, G. & Khaliullin, G. Mott insulators in the strong spin-orbit coupling limit: from Heisenberg to a quantum compass and Kitaev models. Phys. Rev. Lett. 102, 017205 (2009).
Chaloupka, J., Jackeli, G. & Khaliullin, G. Kitaev-Heisenberg model on a honeycomb lattice: possible exotic phases in iridium oxides A2IrO3. Phys. Rev. Lett. 105, 027204 (2010).
Singh, Y. et al. Relevance of the Heisenberg-Kitaev model for the honeycomb lattice iridates A2IrO3. Phys. Rev. Lett. 108, 127203 (2012).
Kitaev, A. Anyons in an exactly solved model and beyond. Ann. Phys. 321, 2–111 (2006).
Mazin, I. I., Jeschke, H. O., Foyevtsova, K., Valenti, R. & Khomskii, D. I. Na2IrO3 as a molecular orbital crystal. Phys. Rev. Lett. 109, 197201 (2012).
Foyevtsova, K., Jeschke, H. O., Mazin, I. I., Khomskii, D. I. & Valenti, R. Ab initio analysis of the tight-binding parameters and magnetic interactions in Na2IrO3. Phys. Rev. B 88, 035107 (2013).
Gretarsson, H. et al. Crystal-field splitting and correlation effect on the electronic structure of A2IrO3. Phys. Rev. Lett. 110, 076402 (2013).
Kim, J. et al. Magnetic excitation spectra of Sr2IrO4 probed by resonant inelastic X-ray scattering: establishing links to cuprate superconductors. Phys. Rev. Lett. 108, 177003 (2012).
Liu, X. et al. Long-range magnetic ordering in Na2IrO3. Phys. Rev. Lett. 109, 157401 (2012).
Hozoi, L. et al. Longer-range lattice anisotropy strongly competing with spin-orbit interactions in pyrochlore iridates. Phys. Rev. B 89, 115111 (2014).
Kim, J. et al. Excitonic quasiparticles in a spin-orbit Mott insulator. Nat. Comm. 5, 4453 (2014).
Laguna-Marco, M. A. et al. Orbital magnetism and spin-orbit effects in the electronic structure of BaIrO3. Phys. Rev. Lett. 105, 216407 (2010).
Haskel, D. et al. Pressure tuning of the spin-orbit coupled ground state in Sr2IrO4. Phys. Rev. Lett. 109, 027204 (2012).
Clancy, J. P. et al. Spin-orbit coupling in iridium-based 5d compounds probed by x-ray absorption spectroscopy. Phys. Rev. B 86, 195131 (2012).
van der Laan, G. & Thole, B. T. Local probe for spin-orbit interaction. Phys. Rev. Lett. 60, 1977–1980 (1988).
Thole, B. T. & van der Laan, G. Branching ratio in x-ray absorption spectroscopy. Phys. Rev. B 38, 3158–3171 (1988).
Tafti, F. F., Ishikawa, J. J., McCollam, A., Nakatsuji, S. & Julian, S. R. Pressure-tuned insulator to metal transition in Eu2Ir2O7. Phys. Rev. B 85, 205104 (2012).
Clancy, J. P. et al. X-ray scattering study of pyrochlore iridates: crystal structure, electronic, and magnetic excitations. Phys. Rev. B 94, 024408 (2016).
Kim, B. H., Shirakawa, T., & Yunoki, S. From a quasimolecular band insulator to a relativistic Mott insulator in equation 17 systems with a honeycomb lattice structure. Phys. Rev. Lett. 117, 187201 (2016).
Qi, B., Perez, I., Ansari, P. H., Lu, F. & Croft, M. L2 and L3 measurements of transition-metal 5d orbital occupancy, spin-orbit effects, and chemical bonding. Phys. Rev. B 36, 2972–2975 (1987).
Jeon, Y., Qi, B., Lu, F. & Croft, M. Transition-metal (Au, Pt, Ir, Re) bonding to Al, Si, Ge: X-ray-absorption studies. Phys. Rev. B 40, 1538–1545 (1989).
O’Malley, M. J., Verweij, H. & Woodward, P. M. Structure and properties of ordered Li2IrO3 and Li2PtO3. J. Solid State Chem. 181, 1803–1809 (2008).
Freund, F. et al. Single crystal growth from separated educts and its application to lithium transition-metal oxides. Sci. Rep. 6, 35362 (2016).
Hermann, V. et al. Competition between spin-orbit coupling, magnetism, and dimerization in the honeycomb iridates: α-Li2IrO3 under pressure. Phys. Rev. B 97, 020104(R) (2018).
Miura, Y., Yasui, Y., Sato, M., Igawa, N. & Kakurai, K. New-type phase transition of Li2RuO3 with Honeycomb structure. J. Phys. Soc. Jpn. 76, 033705 (2007).
Johannes, M. D., Stux, A. M. & Swider-Lyons, K. E. Electronic structure and properties of Li-insertion materials: Li2RuO3 and RuO2. Phys. Rev. B 77, 075124 (2008).
Kimber, S. A. J. et al. Valence bond liquid phase in the honeycomb lattice material Li2RuO3. Phys. Rev. B 89, 081408(R) (2014).
Bhattacharjee, S., Lee, S.-S. & Kim, Y. B. Spin-orbital locking, emergent pseudo-spin and magnetic order in honeycomb lattice iridates. New J. Phys. 14, 073015 (2012).
Smith, J. S. & Desgreniers, S. Selected techniques in diamond anvil cell crystallography I: centring samples using x-ray transmission and rocking samples to improve x-ray diffraction image quality. J. Synchrotron Rad. 16, 83–96 (2009).
Larson, A. C. & Van Dreele, R. B. General Structure Analysis System (GSAS). Los Alamos National Laboratory, Los Alamos, NM. Report No. LAUR 86-748 (2004).
Koepernik, K. & Eschrig, H. Full-potential nonorthogonal local-orbital minimum-basis band-structure scheme. Phys. Rev. B 59, 1743–1757 (1999).
Figgen, D., Peterson, K. A., Dolg, M. & Stoll, H. Energy-consistent pseudopotentials and correlation consistent basis sets for the 5d elements Hf-Pt. J. Chem. Phys. 130, 164108 (2009).
Dunning, T. H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 90, 1007–1023 (1989).
Pierloot, K., Dumez, B., Widmark, P.-O. & Roos, B. O. Density matrix averaged atomic natural orbital (ANO) basis sets for correlated molecular wave functions. Theor. Chim. Acta 90, 87–114 (1995).
Fuentealba, P., Preuss, H., Stoll, H. & Szentpaly, L. V. A proper account of core-polarization with pseudopotentials: single valence-electron alkali compounds. Chem. Phys. Lett. 89, 418–422 (1982).
Werner, H.-J., Knowles, P. J., Knizia, G., Manby, F. R. & Schütz, M. Molpro: a general-purpose quantum chemistry program package. WIREs Comput. Mol. Sci. 2, 242–253 (2012).
Werner, H.-J. & Knowles, P. J. An efficient internally contracted multiconfiguration-reference configuration interaction method. J. Chem. Phys. 89, 5803–5814 (1988).
Knowles, P. J. & Werner, H.-J. Internally contracted multiconfiguration-reference configuration interaction calculations for excited states. Theor. Chim. Acta 84, 95–103 (1992).
Berning, A., Schweizer, M., Werner, H.-J., Knowles, P. J. & Palmieri, P. Spin-orbit matrix elements for internally contracted multireference configuration interaction wavefunctions. Mol. Phys. 98, 1823–1833 (2000).
Katukuri, V. M. et al. Electronic structure of low-dimensional 4d5 oxides: interplay of ligand distortions, overall lattice anisotropy, and spin-orbit interactions. Inorg. Chem. 53, 4833–4839 (2014).
Acknowledgements
Work at the University of Toronto was supported by the Natural Science and Engineering Research Council (NSERC) of Canada through the Collaborative Research and Training Experience (CREATE) program (432242-2013) and a Discovery Grant (RGPIN-2014-06071). Y.S. acknowledges DST, India for support through DST Grant No. SB/S2/CMP-001/2013. S. D. acknowledges support from NSERC. K.M. acknowledges UGC-CSIR India for a fellowship. G. R. acknowledges Israeli Science Foundation Grant #1189/14. Y.D is supported by NSFC Grant No. U1530402, National Key R & D Program of China 2018YFA0305703 and the Science Challenge Project, No. TZ2016001. Y.L. thanks the support by the National Research Foundation of Korea (NRF) grant (No. 2018R1A3B1052042) funded by the Korea government (MSIP). Research described in this paper was performed at the Canadian Light Source, which is supported by the Canada Foundation for Innovation, the Natural Sciences and Engineering Research Council of Canada, the University of Saskatchewan, the Government of Saskatchewan, Western Economic Diversification Canada, the National Research Council Canada, and the Canadian Institutes of Health Research. In addition, this research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357.
Author information
Authors and Affiliations
Contributions
Experiments were conceived by J.P.C., H.G., Y.S., S.D., Y.D., N.C. and Y.-J.K. Samples were synthesized by Y.S. and K.M. High pressure X-ray absorption spectroscopy measurements were performed by J.P.C., J.A.S., S.D., and N.C. High pressure X-ray diffraction measurements were performed by J.P.C., J.A.S., Y.S. S.D., S.L., G.K.R., J.I. and Y.L. High pressure resonant inelastic X-ray scattering measurements were performed by J.P.C., H.G., J.S., Y.D., M.H.U. and D.C. High pressure electrical resistivity measurements were performed by Y.S. and S.L. DFT and ab initio quantum chemistry calculations were performed by R.Y., L.H., D.E., and J.v.d.B. The data analysis was carried out by J.P.C. Manuscript was prepared by J.P.C. and Y.-J.K. with contributions from all co-authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Clancy, J.P., Gretarsson, H., Sears, J.A. et al. Pressure-driven collapse of the relativistic electronic ground state in a honeycomb iridate. npj Quant Mater 3, 35 (2018). https://doi.org/10.1038/s41535-018-0109-0
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-018-0109-0
This article is cited by
-
Mechanism of the insulator-to-metal transition and superconductivity in the spin liquid candidate NaYbSe2 under pressure
npj Quantum Materials (2022)
-
Spin–lattice and electron–phonon coupling in 3d/5d hybrid Sr3NiIrO6
npj Quantum Materials (2019)
-
Concept and realization of Kitaev quantum spin liquids
Nature Reviews Physics (2019)