Abstract
The direct domain coupling of spontaneous ferroelectric polarization and net magnetic moment can result in giant magnetoelectric (ME) coupling, which is essential to achieve mutual control and practical applications of multiferroics. Recently, the possible bulk domain coupling, the mutual control of ferroelectricity (FE) and weak ferromagnetism (WFM) have been theoretically predicted in hexagonal LuFeO3. Here, we report the first successful growth of highly-cleavable Sc-stabilized hexagonal Lu0.6Sc0.4FeO3 (h-LSFO) single crystals, as well as the first visualization of their intrinsic cloverleaf pattern of vortex FE domains and large-loop WFM domains. The vortex FE domains are on the order of 0.1–1 μm in size. On the other hand, the loop WFM domains are ~100 μm in size, and there exists no interlocking of FE and WFM domain walls. These strongly manifest the decoupling between FE and WFM in h-LSFO. The domain decoupling can be explained as the consequence of the structure-mediated coupling between polarization and dominant in-plane antiferromagnetic spins according to the theoretical prediction, which reveals intriguing interplays between FE, WFM, and antiferromagnetic orders in h-LSFO. Our results also indicate that the magnetic topological charge tends to be identical to the structural topological charge. This could provide new insights into the induction of direct coupling between magnetism and ferroelectricity mediated by structural distortions, which will be useful for the future applications of multiferroics.
Similar content being viewed by others
Introduction
Multiferroic materials, in which two or multiple ferroic orders coexist, have drawn a great deal of attentions due to their fundamental importance and potentials for the next generation devices.1,2,3 However, in most multiferroics, the magnetoelectric (ME) coupling strength is quite weak, especially in linear-ME materials,4 which limits their practical applications. Therefore, multiferroics with the direct domain coupling between spontaneous magnetization (M) and polarization (P) are highly sought after. The direct domain coupling can result in giant ME coupling, enabling the mutual control in the sense that flipping one of M or P can induce the flipping of the other. This direct domain coupling effect has been partially achieved, for example, at the hetero-interfaces of bilayer films. M in one film layer can be flipped by flipping P in the other film layer by electrical fields, however not the other way around.5 The similar situation has also been discovered in single-phase Dy0.7Tb0.3FeO3 and Dy0.75Gd0.25FeO3 where only the flipping of M by electrical fields is reported.6 Other examples in single-phase bulk systems are very limited. CoCr2O47,8 and Mn2GeO49 appear to be the only two single-phase materials that contain spontaneous M and magnetism-induced P, which can be flipped by the magnetic field. However, their P magnitude is tiny for any applications, and flipping P (thus, M) with electrical fields cannot be achieved due to the small magnitude of P. Recently, a theoretical study suggests that the single-phase hexagonal LuFeO3 (h-LuFeO3) system may have the potential to realize this ideal effect with the direct domain coupling between its ferroelectricity (FE) and weak ferromagnetism (WFM).10 Thus, it is of great importance to study experimentally the possibility of a direct domain coupling effect in h-LuFeO3, which is energy efficient and highly desirable for future applications. Meanwhile, the recent ME coupling study on h-LuFeO3/LuFe2O4 superlattices11 demonstrates the capability of electrical field control of magnetism near the room temperature, which indicates h-LuFeO3 and its related compounds are promising for future applications. However, with little knowledge of the intrinsic ME coupling of h-LuFeO3 itself, a full understanding of the ME coupling in superlattices and other related materials is unrealistic.
For the possible giant ME coupling, h-LuFeO3 systems in the P63cm polar structure (Fig. 1a) has attracted a significant research attentions, since this metastable hexagonal phase of its orthorhombic bulk form was reported to be stabilized in thin film form by epitaxial strain12,13 or in bulk by Sc or Mn doping.14,15,16 Samples in both forms are believed to show similar physical properties despite different approaches used for the synthesis (see Supplementary Information, note 1 for details). They exhibit robust FE well above room temperature, similar to the well-studied multiferroic hexagonal RMnO3 (h-RMnO3, R = rare earth).17,18 Their improper FE due to the structural instability is associated with the structural trimerization. The trimerization drives the FE transition from the non-polar P63/mmc to the polar P63cm structure and results in a two-up/one-down (or two-down/one-up) displacement of R-site ions, which, in turn, leads to ferroelectric polarization along the c axis. Note that alternating FE domains are clamped to the six structural vortex domains around one topological defect, forming an intriguing cloverleaf pattern in h-RMnO3 (ref. 19). Although magnetic domains in h-RMnO3 can be coupled with FE domains,20,21 there exists no bulk spontaneous M in h-RMnO3.
The structure of h-(Lu, Sc)FeO3. (a) Crystallographic structure of h-(Lu, Sc)FeO3 in P63cm space group. Yellow balls indicate Lu or Sc atoms, while grey and blue balls stand for Fe and O atoms respectively. The black arrows show the displacement directions of Lu or Sc atoms with a two-down/one-up case. Trimerized Fe atoms are illustrated with green bonds. (b) 3D magnetic structure of h-(Lu, Sc)FeO3 in A2 phase, which enables the spin canting along the c axis. Ordered Fe spins in two adjacent layers are shown with red open arrows, and the Fe trimerization of Z = 0 layer is labeled with green bonds. (c) X-ray diffraction of the Lu0.6Sc0.4FeO3 single crystal ground powders which shows the pure hexagonal phase in P63cm space group. The refinement was done by Reitica with the simulated lattice constant a = 5.879 Å and c = 11.695 Å, the standard deviation Rp = 6.851, Rwp = 10.62 and χ2 = 0.514. (d) Optical microscope image of a cleaved Lu0.6Sc0.4FeO3 surface (LSFO1). Scale bar is 200 μm. The image of the whole crystal before cleaving is shown in the inset
Compared with h-RMnO3, the strong magnetic interaction between Fe3+ spins in h-LuFeO3 induces a high antiferromagnetic ordering temperature (TN = 440 K in ref.12, 170 K in ref. 13). Even though the exact TN is still under debate, the presence of net ferromagnetic moment along the c axis is evident below 160–170 K. The magnetic state below 160–170 K is confirmed in both theory and experiment to be the A2-dominant spin configuration (Fig. 1b),10,15 which results in a significant canted-antiferromagnetic (or WFM) moment along the c axis. Both large spontaneous P and M do coexist below 160–170 K. More importantly, a theoretical study predicts the presence of a bulk linear ME coupling or even the direct coupling between polarization and WFM domains in h-LuFeO3 (ref. 10). Therefore, h-LuFeO3 is a unique candidate where a direct mutual control of P and M domains can be explored.
Results
Despite all of these extensive investigations, the intrinsic FE domain structure in h-LuFeO3 is still unexplored, and the direct experimental study of the ME coupling in h-LuFeO3 is absent. One of the main reasons is the instability of the h-LuFeO3 phase at ambient synthesis conditions, which makes it challenging to synthesize bulk single crystals. Here, we report a successful growth of high-quality highly-cleavable h-Lu1-xScxFeO3 (nominal x = 0.4) single crystals for the first time, using a floating zone technique and subsequent extensive annealing with different cooling rates (see 'Methods' and Supplementary Information, note 2). The X-ray spectrum obtained using a PANalytical diffractometer (Fig. 1c) is consistent with the pure h-Lu0.6Sc0.4FeO3 phase,14,16 and does not exhibit any measurable peak broadening or the presence of any second phases, indicating the high quality of crystals. Three 1 °C/h-cooled h-Lu0.6Sc0.4FeO3 specimens (LSFO1-3) were prepared by mechanical cleaving to expose hexagonal a–b surfaces, and used for most of our scanning experiments. A large and flat surface of LSFO1 after cleaving is shown in Fig. 1d, while an image of the whole as-grown crystal is shown in the inset. From room-temperature piezoresponse force microscopy (PFM) studies, we have visualized a cloverleaf pattern of vortex FE domains in h-Lu0.6Sc0.4FeO3 for the first time, which is absent in epitaxial h-LuFeO3 thin films. Furthermore, low-temperature magnetic force microscopy (MFM) studies on the same surfaces suggest that WFM domains are distinct from FE domains in terms of the size and shape, and there exists no mutual locking between FE and WFM domain walls. These observations undoubtedly indicate a complete decoupling between FE and WFM.
Ferroelectricity
Fig. 2a–c are the PFM images of cleaved h-Lu0.6Sc0.4FeO3 surfaces with different cooling rates in the 1200–1400 °C range, in which FE Curie temperature (TC) locates (see Supplementary Information, note 2). The fast-cooled sample (100 °C/h) shows small disordered FE domains on a ~100 nm scale (Fig. 2a). Additional dark field transmission electron microscopy (DF-TEM) studies confirm that a 100 °C/h-cooled h-Lu0.5Sc0.5FeO3 crystal also exhibits irregular-shape and disordered FE domains on a similar scale (Supplementary Information, Figure S1), possibly due to a large amount of chemical/structural disorders (e.g., partial edge dislocations22 and large line defects23). A cloverleaf pattern of vortex FE domains, similar to that in h-RMnO3 (ref. 19), is now visible in the 10 °C/h-cooled specimen (Fig. 2b). A well-organized micron-size cloverleaf pattern of vortex FE domains (Fig. 2c, d) is evident in the 1 °C/h-cooled LSFO1 (area A). We found that vortex FE domains distribute uniformly across the whole cleaved surface. For example, Fig. 2f shows the PFM image of another area (area B, far away from area A) of LSFO1, resembling those of area A. These results demonstrate that the intrinsic FE domain structure in h-Lu0.6Sc0.4FeO3 is a topological vortex configuration, which is sensitive to chemical/structural disorders. Their relevant length scale can be systematically tuned by the cooling rate across the FE Curie temperature, which is in the range of 1400–1200 °C. Although most of our samples have FE domains with +P and –P domains in 50/50 ratio, known as type-I domains, some cleaved samples closed to the surface of crystals do show type-II narrow domains (Figure S2) due to the self-poling effect during the annealing process, which is also commonly observed in h-RMnO3 compounds.24
The ferroelectricity and vortex ferroelectric domains of h-Lu0.6Sc0.4FeO3. Room-temperature PFM images of cleaved surfaces of crystals after a 100 °C/h, b 10 °C/h, and c 1 °C/h cooling in the 1400–1200 °C temperature range. (d) The large-range PFM image of the area A of LSFO1 (the black dashed square corresponds to (c)). (e) The density of defects as a function of cooling rates. Error bars of the defect density for 1 °C/h, 10 °C/h, and 100 °C/h cooling are ±0.005 μm−2, ±0.16 μm−2, and ±0.4 μm−2 respectively. Data of ErMnO3 and TmMnO3 is obtained from ref. 25. (f) PFM image of another area in LSFO1 (area B). (g) Room-temperature P-E loops of LSMO2 at 2702 Hz, which prove its robust and switchable ferroelectricity. Scale bars are 2 μm in a, b and c, 5 μm in d and f
We plotted the density of topological defects (vortices and antivortices) in PFM images vs. the cooling rate (Fig. 2e). The h-Lu0.6Sc0.4FeO3 tends to show a much higher density of topological defects, compared with h-RMnO3 (e.g., ErMnO3 and TmMnO3, data obtained from ref. 25), even though it has a higher TC than, e.g., ErMnO3 (TC ≈ 1129 °C). Note that a higher- TC h-RMnO3 tends to exhibit a lower density of topological defects. The estimated linear slope of ~0.88 is significantly larger than the slope (~0.59) predicted by the Kibble-Zurek mechanism (KZM) in h-RMnO3 (ref. 25). This discrepancy is likely due to the high density of chemical/structural disorders in fast-cooled h-Lu0.6Sc0.4FeO3, which can be annealed away through the slow cooling at the high-temperature range. This disorder is probably related to the metastable nature of the hexagonal phase of LuFeO3, unlike the stable h-RMnO3 phase. Meanwhile, the poor R-Square value (~0.84) of the linear fitting in h-Lu0.6Sc0.4FeO3 (Fig. 2e) also suggests that the density of topological defects is likely affected by extrinsic effects such as pinning by structural defects. Therefore, the intrinsic slope of h-Lu0.6Sc0.4FeO3 needs to be further studied in the future, especially in the slowly-cooled range where the pinning effect by structural defects are minimized. We emphasize that we have observed the cloverleaf-pattern FE domains in h-LSFO, which has not been reported before, e.g., in epitaxial h-LuFeO3 thin films.12 Note that h-LuFeO3 films are typically synthesized at 700–900 °C, which is well below the TC. Thus, it is possible that films may have significant chemical/structural disorders, resulting in ultra-fine irregular FE domains or single FE domain due to surface boundary conditions.
We obtained good polarization loops (Fig. 2g) of another 1 °C/h-cooled specimen (LSFO2) using a Ferroelectric Material Test System (FMTS, Radiant), demonstrating the presence of switchable ferroelectric polarization. Complimentary polarization loops as a function of the frequency are also provided in the Supplementary Information Figure S3a. Their consistency and similarities at different frequencies suggest that the measured loops reflect their intrinsic polarizations without artifacts. The permittivity and the loss tangent as a function of frequency and temperature are shown in Figure S3b and S3c respectively. The low loss at the room temperature and its continuous drop at low temperatures indicate h-Lu0.6Sc0.4FeO3 is a good insulator.
Magnetism
The magnetic susceptibility of LSFO2 in magnetic fields along and perpendicular to the c axis (Fig. 3a), measured by a Magnetic Property Measurement System (Quantum Design), demonstrate the existence of the canted antiferromagnetic (or WFM) moment along the c axis below 163 K, which is consistent with the presence of the A2 spin order. A smooth reduction of magnetic susceptibility below 75 K upon cooling may indicate the presence of a spin reorientation transition away from the A2 spin order, which has been reported in Lu0.5Sc0.5FeO3 (ref. 15). This behavior is also evident in the M-H curves at 5 K and 130 K (Fig. 3b). Thus, WFM domain structures were examined by a low-temperature MFM (Attocube) at the liquid nitrogen temperature (~78 K), where the A2 phase (thus, WFM moment) is dominant. Compared with the micron-size vortex FE domains, large loop-like WFM domains (Fig. 3c) without any hint of cloverleaf cores are clearly observed in LSFO1 (area C, Fig. 3d). To further confirm the magnetic origin of these MFM contrasts, the specimen was warmed up to 200 K (above the A2-phase transition temperature of 163 K) and cooled back to 78 K. After this new thermal cycle, the WFM domain structure of the same area has completely changed (Fig. 3e, f). For a clear view of WFM domain structure, a large-range mosaic MFM image around the area C is shown in Fig. 3g. The vortex FE domains at the lower-left corner of Fig. 3g, reproduced from Fig. 2d, are distinct from the large WFM domains. The size of these WFM domains is roughly ~100 μm, while FE domains are on the order of ~1 μm. Furthermore, the WFM domain wall thickness is as large as 2–4 μm (Figure S4), which is also distinct from the almost-atomically-sharp FE domain walls.
Magnetic properties and magnetic domains of h-Lu0.6Sc0.4FeO3. (a) magnetic susceptibility of LSFO2 in 2 kOe (H⊥c; open squares, and H//c; red circles) as a function of temperature. (b) Out-of-plane magnetization (H//c) of LSFO2 as a function of magnetic field at 130 K (red circles) and 5 K (black triangles), and linear in-plane magnetization (H⊥c) at 5 K (blue open squares). (c) MFM image and d corresponding topography of LSFO1 (area C) at 78 K. (e) MFM image and f its topography of the same area C at 78 K after a new thermal cycle. (g) Large-range MFM image collage around the area C, which is shown with the black dashed square. PFM image of LSFO1 (area A) is shown in the black square at the left-lower corner with the same scale for comparison. Large loop-shape WFM domains are clearly visible in ~100 μm scale. Scale bars are 20 μm
Moreover, our in situ PFM images at the room temperature (Figure S5a and S5b) and 78 K (Figure S5c and S5d) show an identical domain pattern at both temperatures. Considering that WFM domains change in different thermal cycles (Fig. 3c–e) while FE domains should remain unchanged, we could confidently draw the conclusion that they are decoupled.
ME coupling
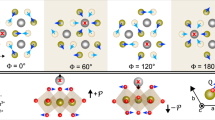
There are two and only two possible types of coupling among ferroelectric polarization, structural antiphases, and A2-type antiferromagnetic spins that have been theoretically proposed.10 They may result in different relationships among FE (P = ±P), WFM (Mc = ±Mc, magnetization along the c axis), and ME (αc = ±αc, ME coefficient along the c axis) domains, where P = αc • Mc. First, note that within unit-cell translation, structural distortions such as oxygen distortions rotate |π/3| across one FE domain wall, which is a structural antiphase boundary at the same time, so that the six domain structure in Fig. 4 is a topological vortex. Now, in the first case (Fig. 4a), in-plane spins rotate |ΔΦ| = 2π/3 across one FE domain wall. In this case, FE domains are directly coupled with WFM domains but decoupled from ME domains. So WFM domains and FE domains must exhibit an identical pattern. In the other case (Fig. 4b), in-plane spins rotate |ΔΦ| = π/3 across one FE domain wall, which is in the same manner as structural distortions. So FE domains will be decoupled with WFM domains and coupled with ME domains. Our experimental findings clearly indicate the decoupling between FE and WFM domains (Fig. 4b). It can be summarized in the cartoon of Fig. 4c, obtained by combining Figs. 2d and 3e. Note that similar PFM and MFM results have been reproduced in another cleaved crystal (LSFO3) of the same batch (Figure S6). Moreover, the similar magnetic susceptibility and PE loop can also be reproduced in different crystal pieces (Figure S7) that are cleaved from the same batch, which is an indication of uniform ferroelectric and magnetic properties within the batch. Figure 4d illustrates the zoom-in view of the dotted area in Fig. 4c, and the 3D spin configurations of trimerized Fe3+ are drawn for each domain. Another evidence of this domain decoupling between FE and WFM is the absence of ME current (or P switching) when Mc is switched by magnetic fields (see Figure S8 and Supplementary Information note 3 for details).
Magnetoelectric coupling of h-Lu0.6Sc0.4FeO3. Possible in-plane magnetic structures of coupled a and decoupled b cases between FE and WFM domains. Blue (black) dashed lines show the FE (WFM) domain walls. Dark circles are Fe3+ ions, and the red open arrows illustrate their in-plane spins. Black arrows stand for the structural distortions of top-apical oxygen ions. Trimerized Fe3+ ions are labeled with green bonds. The blue (+P, −Mc), yellow (+P, +Mc), orange (−P, +Mc) and purple (−P, −Mc) background colors represent the four possible FE and WFM domain combinations. αc is the ME coefficient along the c axis. The α+ domain is chosen to be the same for clear comparison. Spins in dark grey triangle backgrounds are supposedly identical by unit-cell translations, rotate |ΔΦ| = 2π/3 for a and |ΔΦ| = π/3 for b across an FE domain wall. (c) Cartoon of real FE and WFM domain distributions drawn by combining Fig. 2d and 3e in the same scale. (d) Zoom-in cartoon of the black dotted area in c, and the 3D cartoon of spin configurations for four different domains. Spins are shown by the red open arrows, and other symbols remain the same as in a and b, except that red (black) solid arrows are now the c-direction canted magnetic moments (electric polarizations). The domain decoupled case of b corresponds to the experimental result of c or d, which demonstrates decoupling between FE and WFM domains
Discussion
Our results of decoupled FE and WFM domains can be understood in terms of magnetic domain wall energy. It is expected that the domain wall energy with the in-plane spin rotation of large |2π/3| likely costs larger than that with the small |π/3| rotation. This can also be understood in terms of topology. Structural distortions such as oxygen distortions all the way around one vortex (antivortex) core rotate by +(−)2π, so the relevant structural topological charge (or the winding number, ns) of one vortex (antivortex) is +(−)1. Similarly, magnetic topological charge (or the winding number, nm) for the in-plane spins of a vortex (antivortex) in the domain-decoupled case (Fig. 4b) is +(−)1. On the other hand, nm is +(−)2 in the domain-coupled case (Fig. 4a), which is different from ns and likely not favored topologically. As a consequence of this coupling between structural distortions and in-plane antiferromagnetic spins, the out-of-plane spins (WFM) are decoupled with FE domains as observed experimentally. Though a further experimental proof of this coupling is needed in the future, the statement above is still logically true as the coupling between structural distortions and in-plane antiferromagnetic spins is the only possibility based on theoretical predictions (ref. 10). This is also consistent with the situation in YMnO3 where FE domains are found to be coupled to its in-plane antiferromagnetic domains.21 We want to emphasize that the spin-canting angle in h-Lu0.6Sc0.4FeO3, estimated from the observed remnant magnetization (~0.01 μB/Fe), is tiny (<1°). Therefore, antiferromagnetic in-plane spins are still dominant. So it is natural to have nm = ns, which leads to the decoupling between FE and WFM domains, since WFM is only a small out-of-plane spin component of the dominant in-plane spins.
In summary, we have found that the intrinsic FE domain structure of h-LSFO is of fine topological vortex configuration. In contrast, weak ferromagnetic domains are of a loop shape with a much larger size. The distinct sizes and shapes demonstrate the decoupling between FE and out-of-plane WFM, even though in-plane antiferromagnetic spins likely correlate with structural modulations around topological vortices according to theoretical predictions. Our results indicate that the magnetic topological charge tends to be identical with the structural topological charge. This observation is consistent with the absence of any FE and WFM domain-coupled ME effects in h-LSFO. Our results provide new insights into induction of direct coupling between magnetism and FE mediated through structural distortions, which will be useful for the future applications of multiferroics.
Methods
Crystal growth
High-quality h-Lu0.6Sc0.4FeO3 single crystals were grown using a floating zone method under 0.8 MPa O2 atmosphere. The feed rods were prepared using the standard solid-state reaction (ref. 14). The as-grown crystals were annealed at 1400 °C in air for 24 h to enhance crystallinity, and then cooled down to 1200 °C with different cooling rates (100 °C/h, 10 °C/h and 1 °C/h). Afterward, they were cooled to room temperature at the same cooling rate of 100 °C/h. Finally, they were further annealed under 20 MPa O2 pressure at 1000 °C in a high-pressure oxygen furnace to remove any oxygen vacancies and thus enhance resistance. In similar h-RMnO3 compounds, it is well known that the topological vortex density can be symmetrically tuned by different cooling rates near their FE Curie temperatures (ref. 23). As different densities of vortex FE domains are observed in samples with different rates for the 1200–1400 °C cooling in this work, the FE Curie temperature of h-Lu0.6Sc0.4FeO3 is in the range of 1200–1400 °C.
PFM and MFM measurements
For all the PFM measurements, AC 5 V at 68 kHz was applied to a tip (a commercial conductive AFM tip) while sample backside is grounded. Before the MFM measurement, a 20 nm gold film was sputtered onto the same cleaved surface of LSFO1 after PFM experiments to eliminate any electrostatic signal from FE domains during the MFM scanning (ref. 20). All the MFM images are obtained using a dual pass mode with a lift height of 50 nm.
PE measurements
PE loops were measured on a polished thin sample by the “PUND” method provide in the Ferroelectric Material Test System (RADIANT TECHNOLOGIES INC.). The remanent-only polarization hysteresis loop is finally derived. (Also see the reference in Supplementary information note 2).
Data availability
All relevant data are available from the authors upon request.
References
Cheong, S.-W. & Mostovoy, M. Multiferroics: a magnetic twist for ferroelectricity. Nat. Mater. 6, 13–20 (2007).
Ramesh, R. & Spaldin, N. A. Multiferroics: progress and prospects in thin films. Nat. Mater. 6, 21–29 (2007).
Khomskii, D. Classifying multiferroics: mechanisms and effects. Phys. (Coll. Park. Md). 2, 20 (2009).
Tokunaga, Y. et al. Composite domain walls in a multiferroic perovskite ferrite. Nat. Mater. 8, 558–562 (2009).
Heron, J. T. et al. Deterministic switching of ferromagnetism at room temperature using an electric field. Nature 516, 370–373 (2014).
Tokunaga, Y., Taguchi, Y., Arima, T. & Tokura, Y. Electric-field-induced generation and reversal of ferromagnetic moment in ferrites. Nat. Phys. 8, 838–844 (2012).
Yamasaki, Y. et al. Magnetic reversal of the ferroelectric polarization in a multiferroic spinel oxide. Phys. Rev. Lett. 96, 207204 (2006).
Lawes, G. et al. Dielectric anomalies and spiral magnetic order in CoCr2O4. Phys. Rev. B 74, 24413 (2006).
White, J. S. et al. Coupling of magnetic and ferroelectric hysteresis by a multicomponent magnetic structure in Mn2GeO4. Phys. Rev. Lett. 108, 77204 (2012).
Das, H., Wysocki, A. L., Geng, Y., Wu, W. & Fennie, C. J. Bulk magnetoelectricity in the hexagonal manganites and ferrites. Nat. Commun. 5, 2998 (2014).
Mundy, J. A. et al. Atomically engineered ferroic layers yield a room-temperature magnetoelectric multiferroic. Nature 537, 523–527 (2016).
Wang, W. et al. Room-temperature multiferroic hexagonal LuFeO3 films. Phys. Rev. Lett. 110, 237601 (2013).
Disseler, S. M. et al. Magnetic structure and ordering of multiferroic hexagonal LuFeO3. Phys. Rev. Lett. 114, 217602 (2015).
Masuno, A. et al. Weak ferromagnetic transition with a dielectric anomaly in hexagonal Lu0.5Sc0.5FeO3. Inorg. Chem. 52, 11889–11894 (2013).
Disseler, S. M. et al. Multiferroicity in doped hexagonal LuFeO3. Phys. Rev. B 92, 54435 (2015).
Lin, L. et al. Hexagonal phase stabilization and magnetic orders of multiferroic Lu1−xScxFeO3. Phys. Rev. B 93, 75146 (2016).
Abrahams, S. C. Ferroelectricity and structure in the YMnO3 family. Acta Crystallogr. B57, 485–490 (2001).
Koehler, W. C., Yakel, H. L., Wollan, E. O. & Cable, J. W. A note on the magnetic structures of rare earth manganese oxides. Phys. Lett. 9, 93–95 (1964).
Choi, T. et al. Insulating interlocked ferroelectric and structural antiphase domain walls in multiferroic YMnO3. Nat. Mater. 9, 253–258 (2010).
Geng, Y., Lee, N., Choi, Y. J., Cheong, S.-W. & Wu, W. Collective magnetism at multiferroic vortex domain walls. Nano Lett. 12, 6055–6059 (2012).
Fiebig, M., Lottermoser, T., Fröhlich, D., Goltsev, A. V. & Pisarev, R. V. Observation of coupled magnetic and electric domains. Nature 419, 818–820 (2002).
Cheng, S. et al. Topologically allowed nonsixfold vortices in a sixfold multiferroic material: observation and classification. Phys. Rev. Lett. 118, 145501 (2017).
Chae, S. C. et al. Direct observation of the proliferation of ferroelectric loop domains and vortex-antivortex pairs. Phys. Rev. Lett. 108, 167603 (2012).
Wang, X., Huang, F.-T., Hu, R., Fan, F. & Cheong, S.-W. Self-poling with oxygen off-stoichiometry in ferroelectric hexagonal manganites. APL Mater. 3, 41505 (2015).
Lin, S.-Z. et al. Topological defects as relics of emergent continuous symmetry and Higgs condensation of disorder in ferroelectrics. Nat. Phys. 10, 970–977 (2014).
Acknowledgements
We would like to thank M. Mostovoy for insightful discussions. This work was supported by the Gordon and Betty Moore Foundation’s EPiQS Initiative through Grant GBMF4413 to the Rutgers Center for Emergent Materials.
Author information
Authors and Affiliations
Contributions
B. G., K.D., X. X., and R.H. prepared the samples; F.H. performed the TEM investigation; Y.W. and J.K. measured P-E loops and magnetic properties; K.D. did PFM and MFM measurements; S.C. guided the project; K.D. and S.C. analysed the data and wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Du, K., Gao, B., Wang, Y. et al. Vortex ferroelectric domains, large-loop weak ferromagnetic domains, and their decoupling in hexagonal (Lu, Sc)FeO3. npj Quant Mater 3, 33 (2018). https://doi.org/10.1038/s41535-018-0106-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-018-0106-3
This article is cited by
-
Altermagnetism with non-collinear spins
npj Quantum Materials (2024)
-
Domain-wall magnetoelectric coupling in multiferroic hexagonal YbFeO3 films
Scientific Reports (2023)
-
Magnetoelectric coupling of domains, domain walls and vortices in a multiferroic with independent magnetic and electric order
Nature Communications (2021)
-
Quasi-one-dimensional metallic conduction channels in exotic ferroelectric topological defects
Nature Communications (2021)
-
Permutable SOS (symmetry operational similarity)
npj Quantum Materials (2021)