Abstract
Coupled localized electron spins hosted by defects in semiconductors implement quantum bits with the potential to revolutionize nanoscale sensors and quantum information processing. The present understanding of optical means of spin state manipulation and read-out calls for quantitative theoretical description of the active states, built-up from correlated electrons in a bath of extended electron states. Hitherto we propose a first-principles scheme based on many body perturbation theory and configuration interaction and address two room temperature point defect qubits, the nitrogen vacancy in diamond and the divacancy in silicon carbide. We provide a complete quantitative description of the electronic structure and analyze the crossings and local minima of the energy surface of triplet and singlet states. Our numerical results not only extend the knowledge of the spin-dependent optical cycle of these defects, but also demonstrate the potential of our method for quantitative theoretical studies of point defect qubits.
Similar content being viewed by others
Introduction
Calculation of highly correlated electron states in contact with a bath of extended states is a long-standing problem1 that is of immediate importance in such divers fields as the description of exotic phases in transition metal oxides2,3,4 or the mangeto-optical properties of point defects in semiconductors5,6,7,8 that comprise transitions between correlated localized in-gap levels and delocalized defect resonances placed in the range of extended states. To this end, we have developed a practical first principles method that can be employed for large systems including ~2300 electrons. Here, we demonstrate on the most prominent point defects acting as solid state quantum bits, i.e., the nitrogen-vacancy center in diamond9 and the divacancy in silicon carbide,10,11 that highly correlated electron states occur in these quantum bits that significantly interact with the electron bath of the solids. Their electronic states also strongly couple to the coordinates of the nuclei constituting the defects. Such electronic correlation and electron-vibration coupling play an essential role in the spin-selective non-radiative decay from the optically allowed excited state of these point defects that is the key of quantum bit initialization and readout.
The highly correlated electron states are built-up from localized orbitals with strong mutual Coulomb interaction, which is responsible for the high correlation. Such localized orbitals appear in the dangling bond orbitals of vacancies in covalent solids, for instance, nitrogen-vacancy (NV) center of diamond12 and divacancy (VCVSi) in silicon carbide (SiC).13 In the former, the vacancy sits near a nitrogen atom that substitutes one carbon atom in the diamond lattice with an extra electron donated by other defects; in the latter two nearby vacancies form the neutral divacancy complex in SiC. In both cases, the optical and magnetic activity of the defects are related to the deep levels of the defects, particularly, caused by the dangling bonds of the carbon vacancy (see Fig. 1). These electrons form high-spin S = 1 states and highly correlated low-spin S = 0 multiplets (see Fig. 2) where the S = 0 1A1 multiplet is known to be responsible for the spin selective non-radiative decay from the S = 1 3E optically allowed excited state of NV center.14,15,16 The non-radiative decay is mediated by intersystem crossing (ISC) involving spin-orbit and electron–phonon couplings between the triplet and singlet states. Thanks to the effective ISC in these defects,9,14,15,17 their electron spin can be initialized and read out optically, which makes it possible to apply single NV centers in diamond and divacancies in SiC as qubits. These solid state qubits are strong candidates to realize nanoscale sensors18,19,20,21 and quantum communication devices.22,23 It is an immediate quest to calculate these processes ab initio, in order to predict how to optimize the qubit operation for known qubits, and find new candidates.24,25,26 The inevitable first step in determining the ISC routes and processes is to accurately calculate the highly correlated states and their energies as a function of the nuclei coordinates of the point defects.
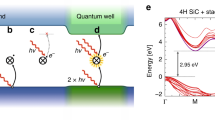
Defects for quantum computing. a Nitrogen-vacancy center in diamond. b Divacancy in SiC. The position of vacancies is depicted by a small dots. The C3 symmetry axis of the C3v symmetry is also shown. The spin density is localized on the carbon dangling bonds (pink lobes) in both defects. We show the hh configuration of divacancy in 4H polytype of SiC (see Supplementary Information for more details about the 4H polytype and the different divacancy configurations). The schematic diagram of the calculated spinpolarized DFT Kohn–Sham levels in the band gap is depicted for c NV center and d divacancy. The double lines for the e levels represent the double degenerate {e x , e y } states that can be occupied by two electrons in each spin channel. The a state transforms as a1 in C3v symmetry. The subscripts text of these labels represents the localization of the dangling bonds, i.e., C orbitals or Si orbitals. The eSi orbitals do not contribute to the qubit operation of the defect and can be ignored in the context. The similarity in the electronic structure of the two defects is apparent. VB and CB represent valence and conduction bands, respectively
Effect of dynamic correlation on multiplets of the NV-center. Comparison of multiplet levels obtained with CI with bare Coulomb interaction and effective Coulomb interaction screened with CRPA and RPA dielectric functions with earlier approaches. a CI-cluster model of NV−.6 b extended Hubbard model fitted to GW-calculations 8 using CI or BSE approaches. c combined G0W0-BSE approach.5 d an extended Hubbard cluster model.7 The CI with bare Coulomb interaction is executed with a basis including the a and e levels as well as valence band states with EVBM − 3.0 eV < E < EVBM. The results for this basis are not fully converged regarding the 1A1 state but match a full CI calculation for a small cluster of ref.6
A state-of-the-art route to calculate the excitation energies and states of defects in semiconductors27,28 at ab initio level is the many-body perturbation theory within the GW approach and solving the Bethe Salpeter equation (BSE).29,30 However, GW+BSE method yields results for the NV center in diamond5 that are at variance with the models derived from experimental data.16 Configurational interaction (CI) quantum chemistry calculations6,31 on tiny diamond clusters and parameterized semi-empirical Hubbard-model calculations indicate7,8 that BSE is unable to treat the highly correlated states arising in NV center. Nevertheless, unrealistically small defect models or methods with inherent semi-empirical parameters do not allow systematic calculations of highly correlated states. An alternative route to defects in solids3 is indicated by dynamic mean field theory where the physics of strong local correlation in the material is mapped to an effective local Anderson impurity problem with a few strongly interacting localized (d or f) orbitals of the host atoms (or the impurity atom) and an interaction with a bath of interant electrons.2 The effective interaction can be constructed from ab initio for instance within the constrained RPA32 and a solution of the impurity problem can be obtained via a truncated configuration interaction approach.33 In case of the defects of interest in our work the strong correlation arises from the interaction of the defect orbitals with extended defect resonances and band states. The proper choice of the impurity problem thus is a task.
Motivated by the dynamic meanfield theory we have developed a methodology based on an screened effective interaction derived from many body theory and a configuration interaction approach that is free from empirical parameters and is applicable to necessarily large clusters, including periodic boundary conditions, to calculate the states and energies of highly correlated states. With this method we explore the magneto-optical properties and spin–relaxation dynamics of the two leading solid state qubits.
Results and discussion
CI-CRPA approach
Description of the multiplet levels of the defect is equivalent to treat static correlation among the localized defect states within the band gap and extended defect resonances via the many-electron hamiltonian
where \(\hat a^\dagger\), \(\hat a\) are the creation and annihilation operators, respectively, acting on the single electron states i, j, k, l, and t ij accounts for a single electron part and the second term describes the electron-electron interaction via the bare Coulomb term (V) or as implemented here by an effective screened interaction (Veff) as described below. Inclusion of the latter is essential for a tractable basis of single particle states allowing for a minimal subset of physically well motivated states, namely the defect states within the band gap and ideally only a few defect resonances, valence or conduction band states (see Fig. S1 in the Supplementary Information). The effective interaction Veff is treated within the constrained random phase approximation (CRPA).32 It is the screened Coulomb interaction using the CRPA dielectric function εCRPA, i.e. \(V_{{\mathrm{eff}}} = \varepsilon _{{\mathrm{CRPA}}}^{ - 1}V\). εCRPA is calculated like the RPA one but excluding transitions among those Kohn-Sham states that form the CI basis. Veff employed together with the RPA screening of the subspace \(\varepsilon _{{\mathrm{RPA}}}^{{\mathrm{subspace}}}\) reproduces the self-energy in the single-shot GW approximation of the full system,32 i.e., the self-energy \({\sum} { = \varepsilon _{{\mathrm{RPA}}}^{ - 1}V} {\mathrm{ = }}\varepsilon _{{\mathrm{RPA}}}^{{\mathrm{subspace}} - 1\,}V_{{\mathrm{eff}}}\).
The CI basis is constructed from Kohn–Sham orbitals of the defect ground state employing hybrid density functional theory (DFT) as outlined in Methods. For intrinsic defects in diamond and SiC, this approach yields band gaps and defect levels in good agreement with experimental findings and sophisticated GW calculations.34 Spin-symmetry in the many body hamiltonian is enforced by utilizing a spin-restricted DFT calculation with equal occupation of both spin channels.
The matrix elements t ij include the kinetic energy and interaction with the ion cores in a full CI approach. We here employ a limited basis set and therefore also include the interaction with the remaining itinerant electrons via the DFT mean field potential. As we outline in the Supplementary Information, we express the matrix by \(t_{ij} = \varepsilon _i^{{\mathrm{HSE}}}\,\delta _{ij} - h_{ij}^{{\mathrm{dc}}}\) using the Kohn–Sham eigenvalues \(\varepsilon _i^{{\mathrm{HSE}}}\) and a double counting correction for the electron–electron interaction between the basis states.
Multiplet states of NV− and VCVSi
We first demonstrate our ab initio methodology on the NV center in diamond that was modeled in a 512-atom supercell containing 2046 valence electrons in the system (see also Methods section). We are able to set the level of approximations and compare the results obtained by previous methods (see Fig. 2). This comparison highlights the complex physics of highly correlated states of defects for quantum applications and the need of parameter free treatment in realistically large cluster to treat these states. Particularly, our findings indicate that the screened interaction is a pivotal ingredient. We calculated the multiplet spectrum for the bare Coulomb interaction (denoted CI in Fig. 2) and effective interaction screened with the CRPA or RPA dielectric functions (CI-CRPA and CI-RPA, respectively). For the 3E and 1E states results from CI (2.2 and 0.7 eV) and CI-RPA (1.9 and 0.4 eV) are found within 0.2 eV of the CI-CRPA value. The most striking differences are found for the 1A1, which is relevant for the ISC, and 1E′ states. CI-RPA suffers overscreening effect because of double counting (see Supplementary Information). The molecular cluster calculations using full CI calculations6 or cluster Hubbard-model7 predict unreliable energy for the critical 1A1 state. In such small clusters bulk-like states are not fully developed both with respect to their extent and the energy separation between occupied and empty states, which yields a dynamical screening distinct from that of bulk diamond. Our CI-CRPA results for 1A1 and 1E qualitatively agree with the GW + BSE periodic cluster approach (refs.5,8 see “ext. Hub. BSE column” in Fig. 2 for the latter), however, 3E and 1E′ are found at different energies, mainly as the BSE basis set is limited to electron–hole pairs that is insufficient for highly correlated states. Our CI-CRPA hamiltonian reproduces the results obtained for an extended Hubbard hamiltonian.8 There the hamiltonian parameters were fitted such as to reproduce GW quasiparticle energies of the localized defect levels and a resonance. However, this fitting procedure may be ambiguous as the number of resonant states needed for the correct description of the system cannot be defined in a consistent manner. Our method does not contain any fitting procedure and the number of states in the CI basis can be chosen to achieve convergent results (see Fig. S1 in Supplementary Information). In the particular case of the NV center, by taking only the in-gap defect states in the CI basis and the corresponding Veff already produce near convergent multiplet energies within 80 meV. This explains the success of the extended Hubbard hamiltonian approach8 for this particular defect. Nevertheless, the defect orbitals (dangling bonds) can principally hybridize with the valence band electrons into several relevant defect resonances, thus any methodology with simple fit to a single resonant state does not provide consistent results in general as we show below.
We also employed our CI-CRPA method for the divacancies in 4H SiC. Among the four distinct configurations of the defect we here focus on the axial divacancy at hexagonal sites (see Supplementary Information for the divacancy configurations in 4H SiC and results for all configurations) that we briefly call here divacancy in the context. It is modeled in a 576-atom periodic cluster involving 2296 valence electrons. The CI-CRPA basis has to include valence bands and resonant states down to EV − 0.9 eV, specifically the aC resonance that is subject to a substantial exchange splitting in spinpolarized DFT (cf. Figure 1), in order to yield consistent and convergent results for this defect in SiC. This finding underlines the necessity for such methodology that does not contain any fitting parameters in the description of highly correlated electron states. The calculated low energy spectrum, including the highly correlated multiplets, is indeed very similar for diamond NV and SiC divacancy, just the energies of divacancy’s states are scaled down. The divacancy’s eSi-related many electron states are well decoupled from this range of the spectrum. This result fully demonstrates from ab initio that the NV center in diamond and the divacancy in SiC are indeed similar systems. This has been confirmed in recent resonant photoluminescence excitation experiments.17 We find that the m s = ±1 3E states are built-up from a single Slater-determinant, thus the constraint DFT approach (see Methods) is justified to explore the adiabatic potential energy surface (PES) of the 3E excited state. 3E and 1E states are subject to Jahn–Teller distortion35,36 where the energy of the multiplets is calculated as a function of the coordinates of the nuclei along the PES to minimize the energy of the 3E state with the stable minimum ES2 − cf. Figure 3. Furthermore a second metastable configuration ES1 arises from non-linear Jahn–Teller coupling and many body effects as this was first discussed for the negative vacancy in silicon37 (cf. Fig. S2 and the Supplementary Information for a detailed discussion of all Jahn–Teller distortions). Here we first focus on the minimum ES2.
Potential energy surfaces of the lowest lying multiplet states of the centers as obtained in the adiabatic approximation. a NV− and b VCVSi hh vs. the displacement Q along the linear path connecting the ground and Jahn–Teller distorted excited state geometries (GS and ES2 repectively, QGS = 0). In c, d a schematic comparison of the optical excitation and spin relaxation paths (solid and dashed red arrows) of NV− and VCVSi for the lowest states including non-radiative relaxation (blue arrow) is shown
For the NV center, the calculated zero-phonon line (ZPL) energies of the transitions 3E → 3A2 and 1A1 → 1E are about 0.2 eV lower in energy than the experimental values but the relaxation energy upon optical excitation of about 0.255 eV is well reproduced. The calculated energy difference of 0.5 eV between the 3E and 1A1 states in the groundstate geometry of NV is in the right energy region estimated from experimental data.16 The 1E′ state lies high in energy and corroborates the expectation38 of a strong 1E → 1E′ transition that could not be observed below a photon energy at and below 2 eV. It is, however, located above the ionization threshold to NV0 at 2.2 eV. In the case of divacancies in 4H SiC experimental data is available for the ZPL energies that are reproduced within 0.1 eV by CI-CRPA (see Supplementary Information). The small and consistent discrepancy between the theoretical data and CI-CRPA results on ZPL energies might partially come from the employed approximation in the calculation of electron correlation but also from the strong electron–phonon renormalization effect known in diamond39 where the latter is beyond the scope of this study.
Spin relaxation dynamics
The spin selective non-radiative decay is a key mechanism for spin state initialization and readout of NV center and divacancy in qubit applications and has not been fully understood. The dynamics of the decay process depends on the coupling and ISCs of the triplet and singlet states and the interplay with phonon modes. The most important phonons are those that govern the Jahn–Teller distortion of the triplet and, as we discuss, give rise to a crucial pseudo Jahn–Teller coupling40 among the singlet states. In the group theory approach to the spin-relaxation dynamics14,15,16 multiplet states are identified with fundamental multiplet states of the high symmetry ground state, so far neglecting further coupling among states of the same representation via the Coulomb interaction or Jahn–Teller coupling. Here we advance the understanding of the relaxation dynamics using the adiabatic picture and based on the coupled fundamental multiplet states that are eigenstates of our CI-CRPA hamiltonian. The picture that arises from this analysis is depicted in Fig. 3c and d. The multiplet wavefunction of the singlet states in the ground and excited state configuration ES1 and ES2 of the NV center and divacancy can be seen in Supplementary Tables S5 and S6. The possible decay processes in the low energy branch in the NV center have not been completely understood so far, thus we consider these first. We find that the 1E state, which splits to 1A and 1A′ in low symmetry Jahn–Teller configurations, already contains a contribution from the \(\left| {a\bar e_{x\left( y \right)}} \right\rangle - \left| {a\bar e_{x\left( y \right)}} \right\rangle\) multiplets (within the hole notation, e x (e y ) as indicated in the insets of Fig. S2) in the ground state geometry, thus the 1E state is connected to the mS = ±1 state of the ground state 3A2 triplet via the perpendicular component of the spin-orbit coupling. Furthermore, the dominant contribution to 1A1, the \(\left| {e_x\bar e_x} \right\rangle + \left| {\bar e_ye_y} \right\rangle\) determinant, dynamically couples to the 1E singlet state through a pseudo Jahn–Teller effect40 driven by e symmetric localized phonon modes (compare 1A1 and 1A states for the undistorted GS and distorted configurations ES1 and ES2 in Table S5). At the distorted configurations we observe a contribution of ≈13%. Since, \(\left| {e_x\bar e_x} \right\rangle + \left| {\bar e_ye_y} \right\rangle\) and the mS = 0 spin state of 3A2 are coupled through the parallel component of the spin-orbit coupling, our results demonstrate a link between 1E and the mS = 0 spin state of the triplet ground state. These results explain the experimental observations of decay processes between 1E and all the spin states of 3A2 state14 and extend the theory of spin state initialization and readout of the NV center. The spin selective decay in the high energy branch of the NV center has been recently discussed in the literature,16,41 however, the contribution of the \(\left| {a\bar a} \right\rangle\) multiplet has been neglected so far. Our results show non-negligible (3.5%) contribution from this multiplet to the 1A1 state, which decreases the calculated coupling strength of 1A1 to the mS = ±1 states of 3E, thus it reduces the rate of the spin selective decay as well.
From the comparison of the singlet wavefunctions of the NV center in diamond and divacancy in 4H SiC, one can see that both defects exhibit similar shelving states. The only notable difference is the stronger mixing of 1A1 state and the 1E state in divacancy, which may result in faster decay from the 1E state toward the mS = 0 spin state of the 3A2 ground state. From the calculated energy gap Δ of the 3E and 1E levels of the NV center in diamond and divacancy in 4H SiC, one can see that in the latter case the gap is much smaller, only 0.7 eV. The phonon spectral function of the divacancy for Δ = 0.7 eV is non-negligible, thus there is non-zero overlap of 3E state and the phonon sideband of 1E that give rise to an additional decay path between these states. The additional decay path explains the deduced rate of 15 MHz for the 3E mS = 0 to singlets and 21 MHz 3E mS = ±1 to singlets transitions in divacancy of 3C SiC17 which has a similar electronic structure to that of the considered divacancy configuration in 4H SiC.42 Note that, in the case of NV center in diamond, the 3E mS = 0 to singlets transition rate is two orders of magnitude smaller than the 3E mS = ±1 to singlets transition rate.
The above arguments show that decay rates depend not only on the matrix elements provided here but also on the spin-orbit coupling strength, non-radiative matrix elements, and the phonon spectral density. The complex PESs of the 3E and 1E with two distinct minima that arise from (pseudo) Jahn–Teller coupling (see Supplementary Information) as well as the coupling of multiplet states with two sets of E modes require further attention. In case of the spin-dependent relaxation rates of the divacancy, only the full set of E modes enables the proper inclusion of the ISCs that occurs between 1E and 3A2 along the path GS-ES1 (cf. Fig. S2) and between 3E and 1A1 at ES1 and ES2. Neglect of the former would lead to underestimated transition rates. The ISC between 1E and 3A2 along GS-ES1 is absent in case of the NV center and given the much smaller Jahn–Teller coupling in the 1E mode a description with two E modes35,41 should effectively cover the main physical mechanisms. Nevertheless, these findings require further investigations, in particular, regarding the calculation of spin-selective decay rates and non-adiabatic coupling that are beyond the scope of the present work.
Optical transitions
Optical transitions are at the heart of the photon–spin interface of qubit defects. These include radiative lifetimes and give access to spin-manipulation and charge state control. In the following and the Supplementary Information we employ ab initio multiplet states for the investigation of such optical properties.
In the case of NV center we calculated optical transitions from in-gap states to the diamond bands (see Supplementary Information) that are relevant for the optical excitation43 and electrical readout44 of the center. From these data one can calculate the radiative lifetimes τNV of the excited states (see Fig. S4 and the Supplementary Information). The calculated \({}^{^3{\mathrm{E}}}\tau _{{\mathrm{NV}}}\) = 8 ns is close to the experimental value at ≈12 ns.16,45 For the singlet we obtain \({}^{^1{\mathrm{A}}_1}\tau _{{\mathrm{NV}}}\) = 1878 ns that is two orders of magnitude longer than that for the triplet. This ab initio result sheds light on the experimental fact that not just the competition with non-radiative decay but the inherently tiny optical transition dipole moment is responsible for the very weak infrared PL signal of NV center (cf. the absorption spectrum in Fig. S4b). This result clearly indicates that sensing protocols based on infrared absorption of NV center46 have serious limitation. The calculated absorption from the shelving 1E state to the conduction band is considerable, and its transition energy is close to the energy of the 532-nm laser that is often applied in NV experiments. Taking into account the consistent underestimation of the optical transition energies, it can be concluded that 532-nm optical excitation cannot ionize NV center from the shelving state which explains the negative contrast in the electrically detected magnetic resonance spectrum.44 Optical ionization or the strong transition 1E → 1E′ require larger photon energies. Since the 1E → 1E′ transition is embedded in the continuum of bound to free transitions just below an even stronger transition to the conduction bands at 2.62 eV (cf. Fig. S4b), excitation protocols utilizing this transition have to deal with competing ionization via non-radiative processes.
For the divacancy in 4 H SiC we obtain the lifetimes \({}^{^3{\mathrm{E}}}\tau _{{\mathrm{V}}_{\mathrm{C}}{\mathrm{V}}_{{\mathrm{Si}}}}\) = 63 ns and \(^{^{1}{\mathrm A}_{1}}\tau{{\mathrm{V}}_{\mathrm{C}}{\mathrm{V}}_{{\mathrm{Si}}}}\) = 3109 ns, respectively, where the known PL lifetime of 3E state is 15 ± 3 ns19 that inherits direct radiative and non-radiative processes between the triplet excited state and ground state, and the non-radiative ISC processes via the singlets. It has been recently found in experiments17 that the direct rate consisting of both the radiative and non-radiative ones and the ISC rate is about the same in divacancy. This results in ≈30 ns lifetime associated with the direct decay processes which is still about a factor of 2 shorter than the calculated direct radiative decay. We argue that the phonon-mediated direct non-radiative decay from 3E to 3A2 is much more competitive in the SiC divacancy than that in NV diamond which naturally explains this discrepancy. In NV diamond, the optical transition energy (≈1.94 eV) is about twice larger than that of SiC divacancy (≈1.1 eV) but with similar optical transition dipole moments and phonon energies. This implies that the direct non-radiative decay by phonons are strongly suppressed in NV diamond while it is relatively efficient in SiC divacancy. We further note that the ≈0.7 eV 1A1 → 1E optical transition does not likely occur in SiC divacancy because of the very slow radiative rate.
The present ab initio method employed here to analyze and predict properties of prototypical examples of qubits in solid can be applied to a broad class of materials with using realistically large models that exhibit highly correlated electron states interacting with extended electrons.
Methods
The defect centers are analyzed in four stages: (i) The high spin ground state and the relaxed geometry of defects is obtained via spin polarized hybrid-DFT calculations. (ii) The lowest optically excited electronic configurations are determined by our DFT-based CI-method. (iii) Within the constraint DFT (CDFT) approach we occupy the defect states according to these excited states and relax the geometry of the defect in these states. This approach already proved to be successful.25,26 (iv) The ground state and excited state geometries are connected by a linear path. For a few (i.e., 4–6) distinct geometries along this path we calculate the excitation spectrum using the CI-method (cf. main text and Supplementary Information). In the step (i) to (iv) all DFT-calculations were performed within the adiabatic approximation. Thus the potential energy surfaces obtained in step (iv) also rely on the adiabatic approximation.
With our CI-method we thus obtain high-spin and intermediate low-spin excited states as well as the important ISCs. The defect centers and their environment are represented in large super cells containing 512 atoms for the NV center and 576 atoms for the defects in 4 H SiC. The projector-augmented plane-wave method along with the screened hybrid exchange-correlation-functional HSE0647,48 are employed as implemented in VASP.49,50,51 VASP was extended to calculate the CRPA response function and the matrix elements of the electron-electron interaction. We applied 420 eV plane wave cutoff and the usual carbon, nitrogen, and silicon PAW potentials provided by the VASP package. In the geometry optimization procedure the threshold on the forces acting on the atoms was set to 0.005 eVÅ. These parameters provided convergent results.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Grimme, S. & Waletzke, M. A combination of Kohn-Sham density functional theory and multi-reference configuration interaction methods. J. Chem. Phys. 111, 5645–5655 (1999).
Biermann, S. Dynamical screening effects in correlated electron materials–a progress report on combined many-body perturbation and dynamical mean field theory: GW+DMFT. J. Phys. Condens. Matter 26, 173202 (2014).
Schüler, M., Renk, C. & Wehling, T. O. Variational exact diagonalization method for Anderson impurity models. Phys. Rev. B 91, 235142 (2015).
Tomczak, J. M., Liu, P., Toschi, A., Kresse, G. & Held, K. Merging GW with DMFT and non-local correlations beyond. Eur. Phys. J. Spec. Top. 226, 2565–2590 (2017).
Ma, Y., Rohlfing, M. & Gali, A. Excited states of the negatively charged nitrogen-vacancy color center in diamond. Phys. Rev. B 81, 041204 (2010).
Delaney, P., Greer, J. C. & Larsson, J. A. Spin-polarization mechanisms of the nitrogen-vacancy center in diamond. Nano Lett. 10, 610–614 (2010).
Ranjbar, A. et al. Many-electron states of nitrogen-vacancy centers in diamond and spin density calculations. Phys. Rev. B 84, 165212 (2011).
Choi, S., Jain, M. & Louie, S. G. Mechanism for optical initialization of spin in NV− center in diamond. Phys. Rev. B 86, 041202(R) (2012).
Childress, L. et al. Coherent dynamics of coupled electron and nuclear spin qubits in diamond. Science 314, 281–285 (2006).
Koehl, W. F., Buckley, B. B., Heremans, F. J., Calusine, G. & Awschalom, D. D. Room temperature coherent control of defect spin qubits in silicon carbide. Nature 479, 84–88 (2011).
Christle, D. J. et al. Isolated electron spins in silicon carbide with millisecond coherence times. Nat. Mater. 14, 160–163 (2015).
Davies, G. & Hamer, M. F. H. Optical studies of the 1.945 eV vibronic band in diamond. Proc. R. Soc. Lond. A 348, 285–298 (1976).
Son, N. T. et al. Divacancy in 4H-SiC. Phys. Rev. Lett. 96, 055501 (2006).
Maze, J. R. et al. Properties of nitrogen-vacancy centers in diamond: the group theoretic approach. New J. Phys. 13, 025025 (2011).
Doherty, M. W., Manson, N. B., Delaney, P. & Hollenberg, L. C. L. The negatively charged nitrogen-vacancy centre in diamond: the electronic solution. New J. Phys. 13, 025019 (2011).
Goldman, M. L. et al. State selective intersystem crossing in nitrogen-vacancy centers. Phys. Rev. B 91, 165201 (2015).
Christle, D. J. et al. Isolated spin qubits in SiC with a high-fidelity infrared spin-to-photon interface. Phys. Rev. X 7, 021046 (2017).
Rondin, L. et al. Magnetometry with nitrogen-vacancy defects in diamond. Rep. Progress. Phys. 77, 056503 (2014).
Falk, A. L. et al. Electrically and mechanically tunable electron spins in silicon carbide color centers. Phys. Rev. Lett. 112, 187601 (2014).
Calusine, G., Politi, A. & Awschalom, D. D. Silicon carbide photonic crystal cavities with integrated color centers. Appl. Phys. Lett. 105, 011123 (2014).
Falk, A. L. et al. Optical polarization of nuclear spins in silicon carbide. Phys. Rev. Lett. 114, 247603 (2015).
Hensen, B. et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 526, 682–686 (2015).
Kalb, N. et al. Entanglement distillation between solid-state quantum network nodes. Science 356, 928–932 (2017).
Weber, J. R. et al. Quantum computing with defects. Proc. Natl Acad. Sci. USA 107, 8513–8518 (2010).
Gali, A. Time-dependent density functional study on the excitation spectrum of point defects in semiconductors. Phys. Status Solidi B 248, 1337–1346 (2011).
Gali, A. Excitation spectrum of point defects in semiconductors studied by time-dependent density functional theory. J. Mater. Res. 27, 897–909 (2012).
Ma, Y. & Rohlfing, M. Optical excitation of deep defect levels in insulators within many-body perturbation theory: the F center in calcium fluoride. Phys. Rev. B 77, 115118 (2008).
Bockstedte, M., Marini, A., Pankratov, O. & Rubio, A. Many-body effects in the excitation spectrum of a defect in SiC. Phys. Rev. Lett. 105, 026401 (2010).
Onida, G., Reining, L. & Rubio, A. Electronic excitations: density-functional versus many-body Green’s-function approaches. Rev. Mod. Phys. 74, 601–659 (2002).
Freysoldt, C. et al. First-principles calculations for point defects in solids. Rev. Mod. Phys. 86, 253–305 (2014).
Zyubin, A. S., Mebel, A. M., Hayashi, M., Chang, H.-C. & Lin, S. H. Quantum chemical modeling of photoabsorption properties of the nitrogen-vacancy point defect in diamond. J. Comput. Chem. 30, 119–131 (2009).
Aryasetiawan, F. et al. Frequency-dependent local interactions and low-energy effective models from electronic structure calculations. Phys. Rev. B 70, 195194 (2004).
Zgid, D., Gull, E. & Chan, G. K.-L. Truncated configuration interaction expansions as solvers for correlated quantum impurity models and dynamical mean-field theory. Phys. Rev. B 86, 165128 (2012).
Deák, P., Aradi, B., Frauenheim, T., Janzén, E. & Gali, A. Accurate defect levels obtained from the HSE06 range-separated hybrid functional. Phys. Rev. B 81, 153203 (2010).
Abtew, T. A. et al. Dynamic jahn-teller effect in the NV− center in diamond. Phys. Rev. Lett. 107, 146403 (2011).
Rogers, L. J. et al. Singlet levels of the NV− centre in diamond. New J. Phys. 17, 013048 (2015).
Anderson, F. G., Ham, F. S. & Grossmann, G. Lattice distortions and electronic structure in the negative silicon vacancy. Phys. Rev. B 53, 7205–7216 (1996).
Kehayias, P. et al. Infrared absorption band and vibronic structure of the nitrogen-vacancy center in diamond. Phys. Rev. B 88, 165202 (2013).
Gali, A. et al. Electron-vibration coupling induced renormalization in the photoemission spectrum of diamondoids. Nat. Commun. 7, 11327 (2016).
Bersurker, I. The Jahn-Teller Effect (Cambridge University Press 2006).
Thiering, G. & Gali, A. Ab initio calculation of spin-orbit coupling for an NV center in diamond exhibiting dynamic Jahn-Teller effect. Phys. Rev. B 96, 081115(R) (2017).
Gordon, L., Janotti, A. & Van de Walle, C. G. Defects as qubits in 3C- and 4H-SiC. Phys. Rev. B 92, 045208 (2015).
Siyushev, P. et al. Optically controlled switching of the charge state of a single nitrogen-vacancy center in diamond at cryogenic temperatures. Phys. Rev. Lett. 110, 167402 (2013).
Bourgeois, E. et al. Photoelectric detection of electron spin resonance of nitrogen-vacancy centres in diamond. Nat. Commun. 6, 8577 (2015).
Batalov, A. et al. Temporal coherence of photons emitted by single nitrogen-vacancy defect centers in diamond using optical rabi-oscillations. Phys. Rev. Lett. 100, 077401 (2008).
Dumeige, Y. et al. Magnetometry with nitrogen-vacancy ensembles in diamond based on infrared absorption in a doubly resonant optical cavity. Phys. Rev. B 87, 155202 (2013).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened coulomb potential. J. Chem. Phys. 118, 8207–8215 (2003).
Krukau, A. V., Vydrov, O. A., Izmaylov, A. F. & Scuseria, G. E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 125, 224106 (2006).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Paier, J., Hirschl, R., Marsman, M. & Kresse, G. The Perdew-Burke-Ernzerhof exchange-correlation functional applied to the G2-1 test set using a plane-wave basis set. J. Chem. Phys. 122, 234102 (2005).
Acknowledgements
Our work profited from discussions with Patrik Rinke, Pedro Brana Coto, Tim Wehling, and Gabriel Bester. Financial support by the Open Access Publication Fund of the University of Salzburg is gratefully acknowledged. Supercomputer time was granted on the HPC cluster of the RRZE of the Friedrich-Alexander Universität, Erlangen-Nürnberg, the Doppler-Cluster of the Paris-Lodron University Salzburg and the SNIC2013-1-331 supercomputer time at the National Supercomputer in Linköping. We acknowledge the support from the MTA Lendület program of the Hungarian Academy of Sciences, EU Commission (DIADEMS project, Contract No. 611147), the National Research Development and Innovation Office of Hungary within the Quantum Technology National Excellence Program (Project No. 2017-1.2.1-NKP-2017-00001), the Knut and Alice Wallenberg Fundation. Use of the Center for Nanoscale Informations was supported by the U. S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under contract No. DE-AC02-06CH11357.
Author information
Authors and Affiliations
Contributions
M.B. and A.G. conceived, designed, and led the project and co-wrote the article. M.B. deviced the CI-CRPA approach. F.Sch., Th.G., and M.B. implemented the method, performed the calculations of CI states and optical spectra. M.B., I.V., and A.G. contributed to the underlying DFT calculations and the analysis of the results.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bockstedte, M., Schütz, F., Garratt, T. et al. Ab initio description of highly correlated states in defects for realizing quantum bits. npj Quant Mater 3, 31 (2018). https://doi.org/10.1038/s41535-018-0103-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-018-0103-6
This article is cited by
-
Downfolding from ab initio to interacting model Hamiltonians: comprehensive analysis and benchmarking of the DFT+cRPA approach
npj Computational Materials (2024)
-
Dynamical downfolding for localized quantum states
npj Computational Materials (2023)
-
Vibrationally resolved optical excitations of the nitrogen-vacancy center in diamond
npj Computational Materials (2022)
-
Quantum guidelines for solid-state spin defects
Nature Reviews Materials (2021)
-
Ab initio theory of the negatively charged boron vacancy qubit in hexagonal boron nitride
npj Computational Materials (2020)