Abstract
Similar to chemical doping, pressure produces and stabilizes new phases of known materials, whose properties may differ greatly from those of their standard counterparts. Here, by considering a series of LaFeAs1−xP x O iron-pnictides synthesized under high-pressure high-temperature conditions, we investigate the simultaneous effects of pressure and isoelectronic doping in the 1111 family. Results of numerous macroscopic and microscopic technique measurements unambiguously show a radically different phase diagram for the pressure-grown materials, characterized by the lack of magnetic order and the persistence of superconductivity across the whole 0.3 ≤ x ≤ 0.7 doping range. This unexpected scenario is accompanied by a branching in the electronic properties across x = 0.5, involving both the normal and superconducting phases. Most notably, the superconducting order parameter evolves from nodal (for x < 0.5) to nodeless (for x ≥ 0.5), in clear contrast to other 1111 and 122 iron-based materials grown under ambient-pressure conditions.
Similar content being viewed by others
Introduction
Superconductivity (SC) in LaFePO,1 a compound first synthesized by Zimmer et al.,2 sets in at a modest T c of only 3.2 K. However, the significantly higher T c = 26 K, reported later for F-doped LaFeAsO,3 brought to attention a whole new class of compounds, the iron-based layered pnictides and chalcogenides, whose complex magnetic and superconducting properties are still being investigated.4,5,6 Although the electronic spin fluctuations are widely acknowledged as responsible for the pairing mechanism in the superconducting phase,7 many issues still remain open.8 For instance, surprisingly, two rather similar, isostructural and isovalent 1111 compounds, such as LaFePO and LaFeAsO, exhibit strikingly different properties. While the first is paramagnetic and becomes superconducting below 5 K1,9 (with indications that oxygen vacancies might also influence T c ),10,11 the second compound orders antiferromagnetically below TN = 140 K,12 with no traces of SC at lower temperatures.
Due to initial difficulties in preparing high-quality 1111 materials, this puzzling behavior attracted first only the attention of theorists. By means of ab initio density-functional methods, the electronic structures and the magnetic properties of LaFePO and LaFeAsO were calculated in considerable detail.13,14 It turned out that pnictogen atoms play a key role in establishing the Fe–P (or Fe–As) distance, giving rise to an unusual sensitivity of material’s properties to an apparently minor detail.15 This conclusion was reinforced by later work, where an interpretation based on quantum criticality (QC) was put forward.16 In a QC scenario, the proximity of iron-based materials to a Mott transition implies that, by increasing the ratio of kinetic energy to Coulomb repulsion, one can pass from an antiferromagnetic to a paramagnetic state. Detailed calculations in the related F-doped LaFeAsO materials showed the proximity of the latter to a quantum tricritical point, with an anomalously flat energy landscape, implying that even weak perturbations can induce significant changes in the physical properties.17 Magnetic frustration is believed to cause such behavior, since the large degeneracy of the ground state close to a quantum critical point (QCP), (i.e., entropy accumulation) can be relieved by a low-temperature transition to the superconducting state.6
In LaFeAsO, the most obvious way to induce such a quantum-critical transition is the isoelectronic substitution of phosphorus for arsenic. Indeed, the smaller ionic radius of phosphorus leads to a smaller cell volume and, hence, to an enhanced kinetic energy and to reduced electronic correlations. Amid the antiferromagnetic and paramagnetic behavior of the pristine As and P compounds, respectively, one expects a superconducting dome, with the highest T c being reached at the QCP.16
These predictions were first tested in a systematic study of the LaFeAs1−xP x O series, which focused on x-ray structural analysis, bulk resistivity, and magnetometry measurements.18 By partially substituting P for As, the Fe2As2 layers were reported to contract, while the La2O2 layers to expand along the c-axis. SC occurred in a narrow range around x = 0.3, with a rather low maximum T c of 10 K. The absence of SC above x = 0.4, yet its reappearance in LaFePO, i.e., for x = 1, remained an open issue. No experimental evidence indicating the occurrence of a QCP at x = 0.3 was found. On the other hand, the As-for-P substitution in 122 systems, such as BaFe2(As1−xP x )2, showed that the AFM phase at x = 0 was gradually replaced by a superconducting phase at x = 1, with a putative QCP occurring at x = 0.3.19
More recent efforts included microscopic investigations of the LaFeAs1−xP x O series via 31P nuclear magnetic resonance (NMR).20 In this case, resonance-width data suggested the onset of antiferromagnetism in different ranges of x substitutions, with the resulting phase diagram not showing a clearcut QCP, but rather AF zones separated by SC “pockets”. Very recently, similar SC “pockets” were also found in the rather complex hole-doped and electron-doped (La,Sr)FeAs1−xP x (O,F/H) system.21
To address the many issues mentioned above, such as the reasons for the very different electronic properties of LaFeAsO and LaFePO, the unusual sensitivity to structural modifications, and the occurrence of QC, we investigated a new batch of LaFeAs1−xP x O compounds, grown under high-pressure conditions. These conditions are known to stabilize otherwise unstable (or energetically unfavorable) phases and allowed us to study the consequences of the simultaneous occurrence of chemical-pressure (via substitution) and physical (during synthesis) pressure. As we show here, the latter leads to surprising results in the 1111 class. Thus, by employing local microscopic techniques, such as muon-spin rotation (μSR) and NMR, we obtain a radically revised low-temperature LaFeAs1−xP x O phase diagram, characterized by the lack of antiferromagnetic transitions at intermediate x values (between 0.3 and 0.7). In addition, on the basis of new data, we bring new evidence about the interplay of magnetic fluctuations and SC. Most importantly, coherent experimental results indicate a clear change in the character of the superconducting order parameter, which appears to evolve from nodal to nodeless as x increases, the exact opposite with respect to standard ambient-pressure grown samples.22,23
Results
Structural, magnetic, and transport properties
The x-ray powder diffraction patterns of LaFeAs1−xP x O are shown in the Supplementary Fig. 1 and confirm that the studied compounds adopt the expected overall structure. Indeed, our specimens, grown via high-pressure synthesis, reveal diffraction patterns that are almost indistinguishable from those of samples grown under standard conditions.18 Yet, the detailed evolution with x of the multiple peaks close to 30 degrees is different in our case, indicating different local environments. As we show below, this leads to a radically different phase diagram and SC properties. The tetragonal (P4/nmm) crystal structure of LaFeAs1−xP x O evolves smoothly from a = 4.03 Å and c = 8.72 Å for x = 0 to a = 3.96 Å and c = 8.51 Å for x = 1, the decrease in lattice parameters reflecting the smaller ionic radius of P with respect to As. The absence of substantial structural differences between samples of this series indicates that the observed changes in the electronic properties and, hence, the adopted ordered phases at low temperatures, are related to electron-correlation effects. How these tiny structural differences cause the alleged variation in electron correlations is the challenging task for future refined studies.
The superconducting critical temperatures T c were determined by means of SQUID magnetometry and radio-frequency detuning of the NMR resonant circuit (see Supplementary Fig. 2), with all samples exhibiting large fractions of magnetic shielding and the maximum T c being reached at x = 0.5 (see Supplementary Fig. 3). This is a surprising result, clearly departing from known phase diagrams of La-1111 samples grown at ambient pressure,24 for which no SC is observed in the x = 0.4 to 0.7 range. In our case, low-temperature, low-field susceptibility data show a relatively steep decrease of χ(T) below T c and a significant diamagnetic response close to T = 0, indicating a good chemical homogeneity and bulk SC, respectively. From the depression of T c with increasing magnetic fields we estimate an Hc2(0) ~ 70 T, a value that matches data reported in the literature for various La-1111 compounds.25,26
The temperature dependence of resistivity ρ(T) is shown in Fig. 1. Unlike previously reported results (see, e.g., ref.18), all our (high-pressure grown) samples are superconductors with T c values in the 15–20 K range. Likewise, all of them exhibit a shallow maximum at T m , just above the superconducting transition, related to increased electronic correlations (see below). By normalizing ρ(T) to the peak occurring at T m [and not to the usual ρ(300 K) value], we find an intriguing splitting into two branches. Samples with x ≤ 0.5 show a rather weak temperature dependence and aggregate into the lower branch, while those with x > 0.5 exhibit a stronger T-dependence and populate the upper branch. This is a remarkable result, indicating a profound change in the electronic correlations across the x = 0.5 boundary, confirmed also by microscopic probes (see next sections). Note that, by plotting existing data18 in the same way produces only uniformly spaced curves, thus indicating the particular nature of the high-pressure grown samples.
Split resistivity curves. Normalized resistivity vs. temperature for the LaFeAs1−xP x O series synthesized under high-pressure conditions. All samples become superconducting after reaching a local maximum at T m . Notice the different behavior of samples with x ≤ 0.5 from those with x > 0.5, highlighted by two different color hues
Absence of magnetic order from zero-field μSR
To reveal the magnetic and superconducting behavior of the LaFeAs1−xP x O series, we investigated systematically the temperature dependence of the muon-spin relaxation in zero- and in applied magnetic fields, respectively. As a local microscopic technique, muon-spin rotation/relaxation (μSR), relies on the detection of muon-decay positrons, emitted preferentially along the muon-spin direction.27,28 Given the absence of perturbing applied fields, zero-field (ZF) μSR represents a uniquely sensitive probe of the intrinsic magnetic properties, in many respects complementary to NMR/NQR.
Typical ZF-μSR data for the x = 0.55 case are shown in Fig. 2a. The μSR asymmetry spectra at 32 and 1.6 K, i.e., above and below T c and/or a possible magnetic ordering temperature T*, do not exhibit any oscillations, but only a weak decay, best described by a Kubo-Toyabe relaxation function28 multiplied by an exponential decay:
Here A0 is the initial asymmetry parameter, while a and λZF are the muon-spin relaxation rates due to static nuclear moments and electronic moments, respectively. The nuclear contribution is small, almost temperature independent, and accounts for the initial Gaussian-like decay. Hence, the observed depolarization is mostly determined by contributions from the electronic magnetic moments. The key feature of the data shown in Fig. 2a is the unchanged relaxation rate above and below T c (T*). This is remarkable since, at low temperatures, most iron-based superconductors exhibit antiferromagnetic order which, depending on whether long-ranged or short-ranged, implies either muon-spin asymmetry oscillations or a strong increase in damping, respectively (see, e.g., refs.29,30). The absence of either of them in the investigated LaFeAs1−xP x O series rules out the onset of a possible magnetic order, in clear contrast with other cases, where a magnetic order (long-ranged or short-ranged) is established, alone or in coexistence with SC.31,32 Yet, as shown in Fig. 2b, the relaxation rates still exhibit a small hump close to T* (corresponding to a maximum in the electronic spin fluctuations), showing up prominently in the NMR relaxation data (see further). The origin of the hump relates to the competing SC and magnetic order in superconductors with s± pairing, which below T c tends to suppress the magnetically induced increase in relaxation rate, thus giving rise to a cusp in the relaxation data.33
Zero-field μSR relaxation. a Representative LaFeAs1−xP x O zero-field μSR spectra above and below T c , for x = 0.55, fitted by means of Eq. (1). b For many samples the relaxation is rather inconspicuous, yet it invariably shows a tiny peak close to T* (arrows), corresponding to a maximum in electronic spin fluctuations (see text). Lines are guides to the eye
Change of SC pairing characteristics revealed via TF-μSR
Transverse-field (TF) μSR is among the standard techniques for studying the superconducting phase. When an external magnetic field is applied to a field-cooled type-II superconductor, the resulting flux-line lattice (FLL) modulates the local field. Implanted muons sense uniformly the SC-related field inhomogeneity, which is detected as an additional Gaussian relaxation σsc. Figure 3a clearly illustrates this by means of typical TF-μSR spectra for x = 0.7, measured at μ0H = 20 mT, both above and below T c (15 K). As the temperature is lowered below T c , the asymmetry relaxation rate increases significantly. In the TF-μSR case, the time-domain μSR data were fitted using:28
Here ATF(0) is the initial asymmetry, γ μ = 2π × 135.53 MHz/T is the muon gyromagnetic ratio, B μ is the local field at the implanted-muon site, ϕ is the initial phase, and λZF and σ are an exponential and a Gaussian relaxation rate, respectively. The weak exponential relaxation 0.56λZF28 was chosen in agreement with the ZF data analysis and is considerably smaller than the Gaussian relaxation rate σ. The latter contains contributions from both the FLL (σsc) and a small temperature-independent relaxation due to nuclear moments (σn). The FLL contribution below T c was derived by subtracting the nuclear contribution from the Gaussian relaxation rate, i.e., \(\sigma _{{\mathrm{sc}}}^2 = \sigma ^2 - \sigma _{\mathrm{n}}^2\), where σn was kept fixed at its value above T c . In all cases we observe a clear diamagnetic shift in the superconducting phase, determined as the difference between the applied and the sensed magnetic fields. This can also be seen directly in Fig. 3a, where at long times the low-temperature oscillations show a reduced frequency. Besides diamagnetism, the development of a FLL below T c implies the appearance of σsc, in turn reflecting the increase in 1/λ2 [see Fig. 3bc], the two being related by:34,35
with Φ0 = 2.068 × 10−3 T μm2 the magnetic-flux quantum and λ ≡ λeff the effective magnetic-field penetration depth. In anisotropic polycrystalline superconducting samples (as is the case for LaFeAs1−xP x O) the effective penetration depth is determined mostly by the shortest penetration depth λ ab , the relation between the two being λeff = 31/4λab.36
Changing nature of SC from TF-μSR data. a Representative LaFeAs1−xP x O μSR spectra for x = 0.7, taken above and below T c in a 20-mT transverse field. The onset of superconductivity upon lowering the temperature is reflected in a faster decay of the asymmetry. Temperature dependence of λ−2 for x = 0.4 (b) and x = 0.65 (c) measured at μ0H = 20 mT. Solid lines indicate fits by means of s-wave and d-wave SC pairings. Notice the change in pairing character across x = 0.5. See text for details
Figure 3b,c shows the temperature dependence of λ−2(T), proportional to the effective superfluid density λ−2 ∝ ρ s , for two representative samples, x = 0.4 and 0.65. In the latter case λ−2(T) is clearly constant at low temperatures, (below T c /3), hence indicating a fully-gapped superconductor (i.e., one with a nodeless SC gap). Conversely, the x = 0.4 sample, which does not exhibit any saturation of λ−2, even close to T = 0 K, behaves as a superconductor with an anisotropic (nodal) gap (most probably of d type). This remarkable change in the symmetry of pairing in the superconducting phase, seems to reflect the diverse normal-state properties of samples across the x = 0.5 composition, as already determined from resistivity measurements (see Fig. 1). Indeed, the experimental λ−2(T) values could only be fitted by mutually exclusive s-wave or d-wave models which, as shown in Fig. 3, provide Δ d (0) = 3.10(3) meV and Δ s (0) = 2.51(2) meV for the x = 0.4 and 0.65 case, respectively (fit details are reported in the appendix).
NMR line shapes confirm lack of magnetic order
NMR is a powerful yet complementary technique to μSR, with respect to probe location, presence of polarizing fields, time scale, etc. By using mostly 31P-NMR measurements, we investigate both the static (line widths and -shifts) as well as the dynamic (spin-lattice relaxation) properties of the LaFeAs1−xP x O series.
In all cases the 31P NMR lines are narrow (about 20 kHz) and evolve smoothly with temperature (a typical dataset is shown in Supplementary Fig. 4). Given the powder nature of the samples, a linewidth of only 160 ppm indicates a good crystalline quality. An analysis of line shifts and widths for various samples and applied fields reveals a number of interesting features (see Fig. 4).
Weakly increasing linewidths reflect lack of magnetic order. Representative 31P NMR shifts (a) and line widths (b) vs. temperature, measured at 3.5 and 7 T. The full lines are guides to the eye. A drop in shift below T c (arrow) is observed only at 3.5 T (inset). The line widths show only a moderate increase below T* for all x values and applied fields
The Knight shift, which probes the intrinsic uniform susceptibility, is defined as K = (fr − f0)/f0, with f0 the reference frequency of the bare nucleus in an applied field μ0H and fr the observed NMR frequency. In our case, the average K values are ~ 0.1%, with K(T) decreasing upon reducing the temperature and a trend to saturation below 50 K. Significantly enhanced K(T) values, with a maximum at ca. 125 K were previously reported in similar compounds, but synthesized at ambient pressure (e.g., for x = 0.7).24 Such only partial agreement with our 31P NMR results most likely reflects the different sample-synthesis conditions. The datasets collected at 3.5 T (see inset), show an additional drop in Knight shift upon entering the superconducting phase in two representative cases, x = 0.6 and 0.7. Besides being compatible with the s-wave nature of SC in the LaFeAs1−xP x O family, this last feature, missing in both our high-field dataset as well as in those reported in the literature24 (taken at 12 T), suggests an active role of the applied field, consisting not merely in the well-known lowering of T c . A final interesting feature of the reported Knight-shift data is a temperature-independent offset between the x = 0.3 and the 0.7 datasets (main panel in Fig. 4a). The overall decrease in K(T) for x = 0.3 corresponds to a reduction of the uniform spin susceptibility and is compatible with enhanced antiferromagnetic correlations, tending towards the AF order, as observed in the x = 0 case. Incidentally, given the symmetric compositions (with respect to x = 0.5) of the x = 0.3 and 0.7 compounds, their non-overlapping K(T) curves suggest a different strength/nature of electronic correlations, above and below x = 0.5, as we discuss below.
The linewidth data, reported in Fig. 4b, are also quite informative. In general, samples with x = 0.5 or close to it exhibit the largest linewidths, compatible with an enhanced degree of disorder.37 The increase in FWHM with decreasing temperature—often an indication of a possible magnetic order—in our case is smooth, with only a minor enhancement at the lowest temperatures (as identified by arrows in Fig. 4b). This behavior is in good agreement with our ZF-μSR data, showing only minor changes in the relaxation rate across a presumed TN (see Fig. 4b). At the same time, our FWHM data are in stark contrast with those of samples synthesized at ambient pressure,24 where a tenfold (or higher) increase in linewidth is observed upon entering the antiferromagnetic phase. The lack of appreciable variations of FWHM vs. T strongly suggests that samples synthesized under high-pressure do not exhibit any AF order at intermediate x values but, as we show below, at most sustain (significant) AF fluctuations.
NMR relaxation rates and AF spin fluctuations
The 31P spin-lattice relaxation times T1 were evaluated from magnetization-recovery curves M z (t), such as those shown in the inset of Fig. 5, by using the standard expression for the exponential recovery of spin-1/2 nuclei. For the central transition of the spin-3/2 75As nuclei we use:38
Here \(M_z^0\) represents the saturation value of magnetization at thermal equilibrium, f is the inversion factor (exactly 2 for a complete inversion), and β is a stretching exponent. The latter is required, since for samples with intrinsic disorder multiple relaxation times are expected. Indeed, as shown in the inset of Fig. 5, the recovery occurs over many decades, reflecting a wide distribution of relaxation rates.
The simultaneous presence of As and P atoms implies a strongly stretched NMR relaxation. The stretched-exponential coefficient β shows a monotonic decrease as the temperature is lowered, starting well above T c , yet distinct for samples with x values above and below x = 0.5. Inset: the recovery of magnetization in a typical 31P NMR spin-lattice relaxation experiment below T c spans several decades
The evolution of β with temperature indicates a smooth decrease from 1, the canonical value for simple disorder-free metals, to almost 0.5 close to T = 0 K. Such a strong reduction of β is typical of samples with disorder, where the inequivalence of NMR sites increases as the temperature is lowered.37 As shown in Fig. 5, samples having the same degree of disorder exhibit a very similar β(T) dependence. Yet, the vertical offset, most likely indicates again a different degree of electronic correlations above and below x = 0.5.
Peak in 1/T1T hints at significant spin fluctuations, as confirmed by comparison with Knight-shift data. a 1/(T1T) vs. temperature for all the samples. While the datasets at 3.5 and 7 T for the same sample coincide, the height and position of maxima depend strongly on x. Inset: Below T c (arrows) the lowest 1/(T1T) value is achieved for the sample with the highest T c (x = 0.5). b Left scale (circles): 1/(T1T) vs. temperature in LaFeAs0.7P0.3O measured via 31P and 75As NMR at 7.066 T. In spite of the very different Larmor frequencies, the comparison shows closely matching features and similar 1/(T1T) magnitudes. Given the absence of quadrupole effects for the I = 1/2 31P nucleus, this similarity hints at a magnetic origin of nuclear relaxation, i.e., related to AF electron-spin fluctuations. Right scale: A comparison of the temperature dependences of 1/(T1T) (circles) and 31K2 (squares). The significant departure of the two curves below ca. 120 K indicates the development of strong AF fluctuations
Figure 6a summarizes the extensive 1/(T1T) dataset, collected at both fields and for all the samples. Unlike the Knight-shift and linewidth data, the 1/(T1T) vs. T curves are practically independent of the applied field for all the investigated x values. We recall that \(1{\mathrm{/}}(T_1T)\) = \(\mathop {\sum}\nolimits_q {\kern 1pt} F(q)\chi \prime\prime \left( {q,f_{\mathrm{r}}} \right){\mathrm{/}}f_{\mathrm{r}}\) probes the fluctuating hyperfine fields at a nuclear site and, as such, it represents a measure of the dynamic correlations. Here, F is the tensor of the hyperfine form-factor, while χ″ represents the imaginary part of the dynamical electronic susceptibility. The main feature of the reported (T1T)−1(T) data is the presence of low-temperature peaks of varying magnitude. The substantial increase of (T1T)−1 upon lowering the temperature indicates an increase in the dynamical susceptibility, typical of a magnetic instability and/or spin fluctuations.39 The successive steep decrease upon further cooling suggests instead a progressive slowing down of spin fluctuations, associated to a short-range diffusive dynamics in the MHz range, involving wall motions of nematic domains.40,41 Since such a slow dynamics cannot be captured by faster techniques such as μSR, a much less pronounced peak is observed in the ZF-μSR relaxation rates (see Fig. 2b). This is further confirmed by the prompt decoupling of muon spins in longitudinal-field μSR measurements (not shown).
By comparing the T c values vs. x (as determined via susceptibility measurements—see Supplementary Fig. 3) we note that the sample with the highest T c does not display the most intense spin fluctuations, but rather the opposite is true. The complete set of 1/(T1T) data shows that, as in case of Knight shifts, samples with x values above and below x = 0.5 do not exhibit the same relaxation curves. This persistent lack of symmetry indicates a significant change in the electronic properties of the LaFeAs1−xP x O series across the x = 0.5 demarcation line.
Further insight into the electronic correlations and spin fluctuations across the LaFeAs1−xP x O series is obtained from two instructive comparisons, both presented in Fig. 6b. First, we compare the K2(T) behavior with the temperature dependence of 1/(T1T). Since in simple metals, both the Knight shift and the relaxation rate depend essentially on the electronic density of states at the Fermi level, N(EF), the two curves should adopt a similar functional form, as expected from the Korringa relation K2 = S · 1/(T1T), with S a constant.42 The Knight shift probes only the uniform susceptibility, whereas 1/(T1T) depends also on the electron-spin dynamics. A clear departure of the two, as observed in our case below 90 K, indicates the development of significant antiferromagnetic spin fluctuations. The peak in 1/(T1T) correlates with the onset of an NMR line broadening (see Fig. 4b), which at first might suggests the onset of an AF order. However, the tiny increase in FWHM and the practically constant μSR relaxation with temperature (see Fig. 2), both rule out the occurrence of a proper magnetic order, indicating instead a spin-fluctuation dominated scenario, with the opening of a spin-gap below T*.
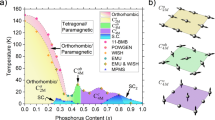
Phase diagram of LaFeAs1−xP x O showing the critical temperature T c and that of the spin-fluctuation maxima T* at different applied fields (vertical arrow: 0, 3.5, and 7 T), measured via magnetometry and NMR, respectively. While the onset of superconductivity is suppressed by the applied field, the T* values remain unaffected. Empty symbols and dashed lines refer to the phase diagram of the material grown at ambient pressure,24 exhibiting two SC phases separated by an antiferromagentic phase. For clarity, the latter temperature values were reduced by half
The spin-fluctuation driven relaxation is confirmed also by a second comparison, that of the 31P and 75As NMR relaxation rates. Both of them are plotted in Fig. 6b as 1/(T1T) vs. T for the x = 0.3 case. Although the resonance frequencies differ by more than a factor of 2, the two datasets almost coincide. This is true not only for the position of the 1/(T1T) peaks, but suprisingly also with regard to the almost equal magnitudes. Since the two nuclei have spins I = 1/2 and 3/2, they can relax by means of magnetic-only and magnetic and quadrupole relaxation channels, respectively.
The practically overlapping 1/(T1T) peaks indicate that quadrupole effects play no (or only a minor) role in the relaxation of 75As nuclei. Therefore, the only remaining relaxation channel, available in both cases, is that dominated by magnetic interactions, which in our case can be identified with spin fluctuations.
Discussion
To summarize the results of the different measurements on the LaFeAs1−xP x O series reported above, we provide an overview in the form of the phase diagram shown in Fig. 7. We notice that: (a) T c reaches a maximum for x = 0.5, (b) the diagram is not symmetric with respect to this value, and (c) the phase diagram is very different from that of samples grown at ambient pressure.
The reason for the maximum T c being reached for x = 0.5 is most likely related to the pnictogen-height value hPn over the iron plane. Detailed structural analyses of a similarly synthesized 1111 family with isolectronic pnictogen substitution have shown that the x = 0.5 composition corresponds to the highest T c and to hPn = 1.32 Å.43 The latter is very close to the optimal \(h_{{\mathrm{Pn}}}^{{\mathrm{opt}}} = 1.38\) Å value, known to produce the highest T c s in many classes of iron-based superconductors.44 On the theoretical side, models of SC based on a spin-fluctuation mediated pairing correlate \(h_{{\mathrm{Pn}}}^{{\mathrm{opt}}}\) with the electron-hole interband scattering rate (see, e.g., ref.45), with the optimum value achieved exactly in the symmetric x = 0.5 case. In our case this would imply that, in spite of a spin-gap opening below T*(>T c ), it would still allow for the formation of a superconducting state below T c .
The phase diagram asymmetry, instead, may reflect a symmetry change in the superconducting order parameter, from nodal to nodeless, when x increases from 0 in LaFeAsO to 1 in LaFePO. Indeed, it has been pointed out that the transition between the two different types of SC order parameter occurs at hPn = 1.33 Å,22,46 practically coincident with the \(h_{{\mathrm{Pn}}}^{{\mathrm{opt}}}\) value reported above, although the change in SC character is opposite in our case, probably due to the high-pressure synthesis conditions. Since \(h_{{\mathrm{Pn}}}^{{\mathrm{opt}}}\) corresponds to x = 0.5 in our case, this implies that compounds such as LaFeAs0.6P0.4O and LaFeAs0.4P0.6O, deviating by ±0.1 from x = 0.5, should behave differently. Indeed, the data reported above show clear variations across x = 0.5 in the temperature dependences of resistivities, K-shift values, and 1/(T1T) rates, as well as in the TF-μSR parameters. Our results, therefore, provide strong support in favor of hPn acting as a switch between the nodal and nodeless pairings,46 with hPn being determined by the As-to-P substitution ratio. Ultimately, it is the change in the lattice structure which modifies the nesting among disconnected parts of the Fermi surface (FS). This makes the Fermi-surface topology one of the key parameters to determine the occurrence of SC, whereas the exchange interaction between localized Fe2+ moments in the 3d orbitals is the other one.47,48
The above mentioned orbital effects are crucial to understand why a maximum T c is achieved at intermediate x values (x = 0.5, in our case). Upon increasing the As/P ratio, the hybridization between the d XZ and d YZ orbitals (a 45-degree rotated version of the standard d xz and d yz orbitals) is enhanced.48 On the one hand, hybridization optimizes the orbital matching between the electron- and hole Fermi surfaces and enhances the spin fluctuations within the orbitals, in turn acting as mediators of the SC. An increased hybridization also decreases the intersection of the two relevant ellipse-shaped Fermi surfaces, generating a favorable nesting for SC. On the other hand, the hybridization splits the two bands, with the more dispersive inner band achieving a lower density of states, thus implying lower T c values. The final outcome of these opposing trends upon isoelectronic doping is a compromise between orbital matching and a reduction in the density of states, which results in an optimal T c at intermediate As/P ratios, as observed experimentally.
Finally, we emphasize that a phase diagram, where SC is found for all the x values between 0.3 and 0.7, is very different from the multi-dome diagram found for samples synthesized at ambient pressure.21,24 Since quenching is known to stabilize otherwise metastable states obtained under high-pressure high-temperature conditions, this can explain the essential differences observed in the two cases.
In conclusion, by using different microscopic and macroscopic techniques, we investigated the electronic properties of the LaFeAs1−xP x O family of 1111 iron-based superconductors. Our results, show that samples from the same family when synthesized under high-pressure, differ in fundamental ways from those synthesized under ambient-pressure conditions. Our key finding, supported by both ZF-μSR and NMR results, is the lack of antiferromagnetic order in all the compounds covered in our investigation. Instead, we find clear evidence of significant spin fluctuations across the 0.3 ≤ x ≤ 0.7 range of the series. In addition, unlike in the previously reported results, we find an onset of SC for all our samples, with T c values depending on x, lying at or slightly below the temperatures where relaxation rates due to spin fluctuations reach their maxima. This proximity suggests a close competition between the incipient magnetic order and SC, with the latter most likely being mediated by spin fluctuations. Finally, the asymmetric character of the LaFeAs1−xP x O phase diagram, as well as the distinctly different NMR datasets for samples with nominally symmetric compositions with respect to x = 0.5, indicate the different nature of the superconducting order parameter across the x = 0.5 boundary, evolving from nodal to nodeless as x increases. The peculiar behavior of La-1111 grown under high pressure conditions, implies that even nominally identical As concentrations can produce very different local environments and, therefore, give rise to a different evolution of T c as hPn is modified via chemical substitution.43 In view of this, other high-pressure grown iron-based superconductors are expected to be in for new surprises.
Methods
Sample preparation and characterization
A series of polycrystalline LaFeAs1−xP x O samples was prepared by using the cubic-anvil high-pressure and high-temperature technique.49,50,51 Due to the toxicity of arsenic, all procedures related to the sample preparation were performed in a glove box. Pellets containing the high-purity (>99.95%) precursors (La2As, LaP2, Fe2O3, As, and Fe) were enclosed in a boron nitride container and placed into a graphite heater. A pressure of 3 GPa was applied at room temperature. Then, by keeping the pressure constant, the temperature was ramped up to 1320 °C in 2 h, maintained there for 12 h, and finally abruptly quenched to room temperature. Once the pressure was released, the sample was removed. The structural characterization was performed by means of standard powder x-ray diffraction (XRD) measurements carried out at room temperature, which confirmed the single-phase nature of the samples, as well as the absence of impurities (below the 1% level). Temperature-dependent DC magnetization measurements were performed by means of a superconducting quantum interference device (SQUID) magnetometer (Quantum Design), while the electrical resistivity of pressed powder specimens was measured in a four-point probe configuration. Finally, energy-dispersive x-ray (EDX) spectroscopy was used to quantitatively analyze the chemical composition of the synthesized samples.
NMR and μSR measurements
For the microscopic investigation of LaFeAs1−xP x O, with 0.3 ≤ x ≤ 0.7, in both the normal and the superconducting phase, we employed first 31P NMR. With an isotopic abundance of 100% and a high gyromagnetic ratio (γ/2π = 17.254 MHz/T), this I = 1/2 nucleus provides a favorable local probe. In selected cases we also performed 75As NMR measurements. A good signal-to-noise (S/N) ratio was achieved by using samples in the form of loose powders, which reduces the electrical contacts between grains. The NMR spectra in the 2–300 K range were obtained by fast Fourier transformation (FFT) of the spin-echo signals generated by π/2 − π rf pulses with 50 μs of typical delay between the pulses. Given the short rf pulse length (tπ/2 ~ 3 μs), frequency sweeps were not necessary for acquiring the 31P NMR lines. Since samples with intermediate x contain two independent NMR-active nuclei, in selected cases we also performed 75As-NMR measurements. Given the nuclear spin I = 3/2 and related quadrupole effects for 75As, this allows for an instructive comparison with the purely-magnetic spin-1/2 31P data (see above). In addition, we investigated the effects of the applied magnetic field, by acquiring NMR data at μ0H = 7.066 T and 3.505 T. Nuclear spin-lattice relaxation times T1 were measured following a standard inversion-recovery procedure with spin-echo detection at variable delays. The magnetic field was calibrated using 27Al NMR on pure aluminum, whose gyromagnetic ratio and Knight shift are known to high precision.
The μSR measurements were performed at the general-purpose spectrometer (GPS) of Paul Scherrer Institut, PSI, Villigen (Switzerland). Various powder samples from the LaFeAs1−xP x O series were mounted on copper forks by using aluminated mylar and kapton foils. This setup up, combined with active vetoing, resulted in very low spurious background signals. Due to active compensation coils, true zero-field conditions were achieved during the ZF-μSR experiments. The ZF and TF-μSR measurements were carried out between 1.5 and 30 K, the lowest temperatures being reached by using a pumped He-4 cryostat.
The error bars in case of μSR measurements were obtained from the raw data counting statistics, while for the NMR they were derived from the NMR-signal noise levels. The reported error bars were calculated by using the standard methods of error propagation.
Fitting formulae for the superconducting gap
TF-μSR measurements give access to λ−2(T), which is proportional to the effective superfluid density, ρ s ∝ λ−2. Hence, a study of the temperature dependence of λ−2(T) can reveal the symmetry of the superconducting gap (i.e., of the electronic density of states in the proximity of the Fermi energy below T c ). As shown in Fig. 2c (solid dark line), the experimental λ−2(T) data for x > 0.5 are consistent with a nodeless superconducting gap with s-wave symmetry, which in the clean limit regime (l > ξ) gives:52
Here λ−2(0) is the zero-temperature value of the magnetic penetration depth and f = [1 + exp(E/kBT)]−1 represents the Fermi distribution. The temperature dependence of the superconducting gap can be approximated analytically as:53
with Δ0 the gap value at zero temperature.
In the x < 0.5 case, however, the nodeless s-wave model in Eq. (4) cannot fit the data (see Fig. 2b, solid gray line). Only a d-wave based model, which contains nodes, can account for the experimental λ−2(T) data. In this case the superconducting gap Δ = Δ(T, ϕ) acquires an additional \(\left| {{\mathrm{cos}}(2\phi )} \right|\) angular factor and the temperature dependence of λ−2(T) becomes:
The fits with an s-wave model for x > 0.5 and a d-wave model for x < 0.5, give λ(0) = 391(10) nm and Δ s (0) = 2.51(2) meV for x = 0.65 and λ(0) = 476(10) nm and Δ d (0) = 3.10(3) meV for x = 0.4. Considering the similar T c values, the 2Δ(0)/kBT c ratios are 3.6 and 5.3, respectively, to be compared with 3.52 of the standard BCS theory.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Kamihara, Y. et al. Iron-based layered superconductor: LaOFeP. J. Am. Chem. Soc. 128, 10012–10013 (2006).
Zimmer, B. I., Jeitschko, W., Albering, J. H., Glaum, R. & Reehuis, M. The rare earth transition metal phosphide oxides LnFePO, LnRuPO and LnCoPO with ZrCuSiAs type structure. J. Alloy Compd. 229, 238–242 (1995).
Kamihara, Y., Watanabe, T., Hirano, M. & Hosono, H. Iron-based layered superconductor La[O1–x F x ]FeAs (x = 0.05–0.12) with T c = 26 K. J. Am. Chem. Soc 130, 3296–3297 (2008).
Johnston, D. C. The puzzle of high temperature superconductivity in layered iron pnictides and chalcogenides. Adv. Phys. 59, 803–1061 (2010).
Paglione, J. & Greene, R. L. High-temperature superconductivity in iron-based materials. Nat. Phys. 6, 645–658 (2010).
Si, Q., Yu, R. & Abrahams, E. High-temperature superconductivity in iron pnictides and chalcogenides. Nat. Rev. Mater. 1, 16017 (2016).
Inosov, D. S. Spin fluctuations in iron pnictides and chalcogenides: from antiferromagnetism to superconductivity. C. R. Phys. 17, 60–89 (2016).
Borisenko, S. V. et al. Direct observation of spin-orbit coupling in iron-based superconductors. Nat. Phys. 12, 311–317 (2016).
Hamlin, J. J., Baumbach, R. E., Zocco, D. A., Sayles, T. A. & Maple, M. B. Superconductivity in single crystals of LaFePO. J. Phys.: Cond. Matter 20, 365220 (2008).
McQueen, T. M. et al. Intrinsic properties of stoichiometric LaFePO. Phys. Rev. B 78, 024521 (2008).
Analytis, J. G. et al. Bulk superconductivity and disorder in single crystals of LaFePO. ArXiv e-prints (2008). arXiv:0810.5368 [cond-mat.supr-con].
de la Cruz, C. et al. Magnetic order close to superconductivity in the iron-based layered LaO1−xF x FeAs systems. Nature 453, 899–902 (2008).
Singh, D. J. & Du, M.-H. Density functional study of LaFeAsO1−xF x : a low carrier density superconductor near itinerant magnetism. Phys. Rev. Lett. 100, 237003 (2008).
Lebègue, S. Electronic structure and properties of the Fermi surface of the superconductor LaOFeP. Phys. Rev. B 75, 035110 (2007).
Lebègue, S., Yin, Z. P. & Pickett, W. E. The delicate electronic and magnetic structure of the LaFePnO system (Pn = pnicogen). New J. Phys. 11, 025004 (2009).
Abrahams, E. & Si, Q. Quantum criticality in the iron pnictides and chalcogenides. J. Phys.: Cond. Matter 23, 223201 (2011).
Giovannetti, G. et al. Proximity of iron pnictide superconductors to a quantum tricritical point. Nat. Commun. 2, 398 (2011).
Wang, C. et al. Superconductivity in LaFeAs1−xP x O: effect of chemical pressures and bond covalency. Europhys. Lett. 86, 47002 (2009).
Kasahara, S. et al. Evolution from non-Fermi- to Fermi-liquid transport via isovalent doping in BaFe2(As1−xP x )2 superconductors. Phys. Rev. B 81, 184519 (2010).
Kitagawa, S. et al. Relationship between superconductivity and antiferromagnetism in LaFeOAs1−xP x revealed by 31P-NMR. J. Phys. Soc. Jpn. 83, 023707 (2014).
Miyasaka, S. et al. Three superconducting phases with different categories of pairing in hole- and electron-doped LaFeAs1−xP x O. Phys. Rev. B 95, 214515 (2017).
Hashimoto, K. et al. Nodal versus nodeless behaviors of the order parameters of LiFeP and LiFeAs superconductors from magnetic penetration-depth measurements. Phys. Rev. Lett. 108, 047003 (2012).
Nourafkan, R. Nodal versus nodeless superconductivity in isoelectronic LiFeP and LiFeAs. Phys. Rev. B 93, 241116 (2016).
Mukuda, H. et al. Emergence of novel antiferromagnetic order intervening between two superconducting phases in LaFe(As1−xP x )O: 31P-NMR studies. J. Phys. Soc. Jpn. 83, 083702 (2014).
Prakash, J., Singh, S. J., Samal, S. L., Patnaik, S. & Ganguli, A. K. Potassium fluoride doped LaOFeAs multi-band superconductor: Evidence of extremely high upper critical field. Europhys. Lett. 84, 57003 (2008).
Singh, S. J., Prakash, J., Maurya, V. K., Ganguli, A. K. & Patnaik, S. Study of upper critical field in 1111-ferropnictide superconductors. AIP Conf. Proc. 1447, 905–906 (2012).
Blundell, S. J. Spin-polarized muons in condensed matter physics. Contemp. Phys. 40, 175–192 (1999).
Yaouanc, A. & de Réotier, P. D. Muon Spin Rotation, Relaxation, and Resonance: Applications to Condensed Matter. (Oxford University Press, Oxford, 2011).
Luetkens, H. et al. The electronic phase diagram of the LaO1−xF x FeAs superconductor. Nat. Mater. 8, 305–309 (2009).
Drew, A. J. et al. Coexistence of static magnetism and superconductivity in SmFeAsO1−xF x as revealed by muon spin rotation. Nat. Mater. 8, 310–314 (2009).
Shiroka, T. et al. Long- to short-range magnetic order in fluorine-doped CeFeAsO. Phys. Rev. B 84, 195123 (2011).
Lamura, G. et al. Slow magnetic fluctuations and superconductivity in fluorine-doped NdFeAsO. Phys. Rev. B 91, 024513 (2015).
Fernandes, R. M. et al. Unconventional pairing in the iron arsenide superconductors. Phys. Rev. B 81, 140501(R) (2010).
Barford, W. & Gunn, J. M. F. The theory of the measurement of the London penetration depth in uniaxial type II superconductors by muon spin rotation. Phys. C. 156, 515–522 (1988).
Brandt, E. H. Properties of the ideal Ginzburg-Landau vortex lattice. Phys. Rev. B 68, 054506 (2003).
Fesenko, V. I., Gorbunov, V. N. & Smilga, V. P. Analytical properties of muon polarization spectra in type-II superconductors and experimental data interpretation for mono- and polycrystalline HTSCs. Phys. C 176, 551–558 (1991).
Shiroka, T. et al. Distribution of NMR relaxations in a random Heisenberg chain. Phys. Rev. Lett. 106, 137202 (2011).
McDowell, A. F. Magnetization-recovery curves for quadrupolar spins. J. Magn. Reson., Ser. A 113, 242–246 (1995).
Oka, T., Li, Z., Kawasaki, S., Chen, G. F. & Wang, N. L. & Guo-qing Zheng. Antiferromagnetic spin fluctuations above the dome-shaped and full-gap superconducting states of LaFeAsO1−xF x revealed by 75As-nuclear quadrupole resonance. Phys. Rev. Lett. 108, 047001 (2012).
Hammerath, F. et al. Progressive slowing down of spin fluctuations in underdoped LaFeAsO1−xF x . Phys. Rev. B 88, 104503 (2013).
Bossoni, L. et al. Persistence of slow fluctuations in the overdoped regime of Ba(Fe1−xRh x )2As2 superconductors. Phys. Rev. B 93, 224517 (2016).
Korringa, J. Nuclear magnetic relaxation and resonance line shift in metals. Physica 16, 601–610 (1950).
Zhigadlo, N. D. et al. Interplay of composition, structure, magnetism, and superconductivity in SmFeAs1−xPxO1−y. Phys. Rev. B 84, 134526 (2011).
Mizuguchi, Y. et al. Anion height dependence of T c for the Fe-based superconductor. Supercond. Sci. Technol 23, 054013 (2010).
Thomale, R., Platt, C., Hanke, W. & Bernevig, A. B. Mechanism for explaining differences in the order parameters of FeAs-based and FeP-based pnictide superconductors. Phys. Rev. Lett. 106, 187003 (2011).
Kuroki, K., Usui, H., Onari, S., Arita, R. & Aoki, H. Pnictogen height as a possible switch between high-Tc nodeless and low-T c nodal pairings in the iron-based superconductors. Phys. Rev. B 79, 224511 (2009).
Arita, R. & Ikeda, H. Is Fermi-surface nesting the origin of superconductivity in iron pnictides?: A fluctuation exchange approximation study. J. Phys. Soc. Jpn. 78, 113707 (2009).
Usui, H., Suzuki, K. & Kuroki, K. Origin of the non-monotonic variance of T c in the 1111 iron based superconductors with isovalent doping. Sci. Rep. 5, 11399 (2015).
Zhigadlo, N. D. et al. High-pressure flux growth, structural, and superconducting properties of LnFeAsO (Ln = Pr, Nd, Sm) single crystals. Phys. Rev. B 86, 214509 (2012).
Zhigadlo, N. D. Growth of whisker-like and bulk single crystals of PrFeAs(O,F) under high pressure. J. Cryst. Growth 382, 75–79 (2013).
Zhigadlo, N. D. High pressure crystal growth of the antiperovskite centrosymmetric superconductor SrPt3P. J. Cryst. Growth 455, 94–98 (2016).
Tinkham, M. Introduction to Superconductivity. 2nd edn, (Dover Publications, New York, 1996).
Carrington, A. & Manzano, F. Magnetic penetration depth of MgB2. Physica C 385, 205–214 (2003).
Acknowledgements
The authors thank A. Amato (Paul Scherrer Institut) for the assistance during the experiments and P. Macchi for useful discussions. This work was financially supported in part by the Schweizerische Nationalfonds zur Förderung der Wissenschaftlichen Forschung (SNF).
Author information
Authors and Affiliations
Contributions
Project planning: T.S. Sample synthesis and characterization: N.D.Z. μSR experiments were carried out by R.K.; NMR measurements and data analysis by T.S. and N.B. The manuscript was drafted by T.S. and H.R.O. and was completed with input from all the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Shiroka, T., Barbero, N., Khasanov, R. et al. Nodal-to-nodeless superconducting order parameter in LaFeAs1−xP x O synthesized under high pressure. npj Quant Mater 3, 25 (2018). https://doi.org/10.1038/s41535-018-0099-y
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-018-0099-y
This article is cited by
-
Superconductivity in the crystallogenide LaFeSiO1−δ with squeezed FeSi layers
npj Quantum Materials (2022)