Polaron freezing and the quantum liquid-crystal phase in the ferromagnetic metallic La_0.67Ca_0.33MnO₃

Abstract

The remarkable electronic properties of colossal magnetoresistive manganites are widely believed to be caused by the competition between a ferromagnetic metallic state and an antiferromagnetic insulating state with complex spin, charge, and orbital ordering. However, the physics underlying their magnetotransport properties is still not clear, especially the role of correlated Jahn–Teller polarons, which depending on temperature and doping, might form a liquid, glass or stripe polaron state. This question touches one of the most fundamental problems in the physics of doped Mott insulators, i.e. understanding the mechanism that chemical doping makes an insulator becoming superconductive as in the case of cuprates, or exhibiting the colossal magnetoresistance effect, as in the case of manganites. Here, by using ¹³⁹La NMR and high resolution transmission electron microscopy in the temperature range 3.2–1000 K, we have monitored the formation and evolution of CE-type polarons in optimally doped La_0.67Ca_0.33MnO₃. While NMR experiments show that correlated polarons dominate electron spin dynamics in the ferromagnetic phase, at very low temperatures they appear to form a quantum liquid-crystal like ferromagnetic phase, embedded into a ferromagnetic matrix with 3D polaron correlations. This is evidence that similarly to high T_c cuprates, quantum soft phases underlie the exotic physical properties of colossal magnetoresistive manganites.

Introduction

Polarons, moving electrons dressed in a cloth of lattice distortions, are key ingredient in the fascinating physics of transition metal oxides, such as high T_c superconducting cuprates, nickelates, and colossal magnetoresistive (CMR) manganites.^{1,2,3,4,5,6,7,8,9} The concept of polarons was first introduced by Landau in 1933.¹⁰ If an electron is placed into the conduction band of an ionic crystal, the electron is trapped by digging its own hole due to the strong coulombic interaction of the electron with its surrounding positive ions. The electron together with the lattice distortions induced by itself is called polaron (lattice polaron). In addition to this static effect, moving electrons induce dynamic lattice distortions; they are accompanied by lattice vibrations, i.e. phonons. Considering that Cu²⁺ and Mn³⁺ are among the strongest Jahn–Teller (JT) ions, a great effort has been devoted to understand the role of JT polarons in the superconducting pairing of high T_c cuprates,^1,2,3,4 and its normal state analog, the CMR effect in manganites.^5,6,7,8,9

Important role in the efforts to understand superconductivity has been played by the discovery of the hole stripe phase in underdoped cuprates.^11,12 When adding holes into the antiferromagnetic (AFM) insulating parent cuprate, the AFM phase breaks into domains, which are separated by hole-rich metallic clumps (stripes) with a rapid change of the phase of the background spins and orbitals at the domain boundary.^11,12,13 At the same time a weak energy gap emerges at temperatures 2–3 times T_c,^1,14 giving rise to the so called pseudogap phase. A plausible explanation of the hole-striped phase is in terms of inter-site JT bipolarons.^1,15 At high temperatures bipolarons occupy random positions, which are accompanied by large strain fields, while by decreasing temperature bipolarons are organized into hole-stripes minimizing their strain energy.

However, in the last years there is compelling evidence that hole assembling in the pseudogap phase of cuprate superconductors is organized in an electronic liquid crystal phase (ELC).^16,17,18,19 Scanning tunneling microscopy (STM) experiments demonstrated the formation of large electron nematic domains (>40 nm) on the surface of the BSCCO superconductor.²⁰ Theoretical calculations have shown that the formation of an ELC state is possible in a hole-doped Mott insulator if zero point transverse stripe fluctuations are above a certain threshold. Then, a novel smectic quantum phase is formed with crystalline order in one direction, and liquid-like correlations in the other two directions.²¹

In the case of hole-doped manganites, exemplified by the prototype La_1−xCa _x MnO₃ (LCMO) family, charge segregation phenomena might be viewed with a similar rationale.²² Manganites resemble in many aspects the cuprate compounds, despite the absence of superconductivity. Like cuprates, manganites are JT active, so there is a certain doping regime, where electron–phonon coupling dominates the electronic and structural properties. Furthermore, they acquire high volume density of dynamic and static JT polarons, which give rise to strong correlation effects.^8,23,24 For example, dynamic short-range polaron correlations give rise to a polaron liquid,^6,25 which by lowering temperature freezes into a polaron glass,^5,9 while in other cases static long-range ordering drives them into a polaron solid.²⁶ Besides, experiments provide evidence about the presence of a pseudogap-like phase, which is interwoven with polaron ordering,^6,27,28,29 and the appearance of charge and orbital stripes.^25,30,31 This sets into question the assumption that the pseudogap state is a hallmark of high T_c superconductivity state, suggesting that it is probably a more general phenomenon characteristic of hole-doped AFM Mott insulators. Most important, neutron scattering³² and high resolution TEM³³ experiments indicate the presence of a smectic³² and nematic³³ liquid crystal state in the charge stripe phase of manganites. It is thus of fundamental importance to examine in more detail the role of polarons in charge segregation effects, especially the relation of polarons with the formation of an ELC state.

Crucial role in these effects is played by the CE type spin, charge, and orbital ordering, exemplified by the half doped La_0.5Ca_0.5MnO₃ (LCMO(0.5)).³⁴ The low temperature charge and spin structure in this system is dominated by the CE AFM ordering comprised of alternating Mn³⁺ and Mn⁴⁺ ions in a zig-zag arrangement on the (001) plane, whereas successive planes are AFM ordered. In addition, a minority ferromagnetic (FM) phase has been observed coexisting with the CE AFM phase.^35,36 Most spectacular, Fresnel imaging and electron holography experiments have shown that the FM minority phase comprises of FM metallic and FM charge ordered regions separated by boundaries with antiphase spin orientation.³⁷ The question thus rises whether “FM charge ordered—FM metallic” phase segregation in AFM background is present at optimal doping x = 0.33, as foreseen by theory,³⁶ and the relation it might have with the CE-type short range correlated polarons (i.e. short zig-zag chains of alternating Mn³⁺ and Mn⁴⁺ ions) detected in the PM phase.⁹ Most important, in view of the common trends, which have been observed in different doped Mott insulators, to examine whether polaron ordering in manganites might lead to a quantum ELC state at low temperatures.

Here, by using ¹³⁹La NMR and high resolution transmission electron microscopy (HRTEM) in the temperature range 3.2–1000 K, we succeeded to detect the formation of nanoscopic regions with CE-type charge ordering in the PM phase of LCMO(0.33) and to monitor the evolution of their dynamics by cooling. According to the NMR relaxation experiments, the mechanism of the electron spin dynamics remains unchanged in the FM phase, manifesting the dominant role of correlated polarons down to the lowest temperature of NMR measurements. Remarkably, by decreasing temperature the FM phase is shown to split into two components; a slow relaxing one with extremely low magnetic anisotropy resembling an electron spin liquid crystal phase, and a fast relaxing FM component with relatively high magnetic anisotropy, belonging to the initial FM phase with 3D polaronic correlations. At T = 3.2 K a weak NMR signal from AFM CE-type ordered regions was detected, which shows that charge ordering survives down to the lowest temperature of NMR measurements. Most notable, the rapid increase of the low magnetic anisotropy NMR signal component is strong indication that the ground state of FM metallic manganites might be a quantum ELC state, as predicted by theory for doped Mott insulators.²¹

Results

The local static and dynamic magnetic and structural properties of the LCMO(0.33) have been investigated by applying ¹³⁹La NMR in magnetic field 9.4 T, in the temperature range 3.2 K up to 900 K. In the presence of an external magnetic field B, ¹³⁹La(I = 7/2) nuclei experience the Zeeman interaction, which splits the nuclear energy levels into 2I + 1 equidistant energy levels, with energies E_m = mγħB. In addition, the ¹³⁹La nucleus is coupled to the local electric field gradient (EFG) tensor, through its electric quadrupole moment Q. In the presence of both the Zeeman and Quadrupolar interactions the frequency of the NMR spectrum corresponding to transitions between levels m and m − 1 is given by, $\omega _{\rm m} = \gamma B + \frac{3}{2}\frac{{e^2qQ}}{{4\hbar I\left( {2I - 1} \right)}}$(3cos² θ − 1 − ηsin² θcos² ϕ)(2m − 1), where e is the charge of the electron, eq is equal to V _zz , η is the asymmetry parameter of the EFG tensor $\eta = \frac{{\left| {V_{yy} - V_{xx}} \right|}}{{V_{zz}}}$, and θ, ϕ are the angles between the principal axis of the EFG tensor and the magnetic field. According to this equation, the transition between the m = +1/2 and m = −1/2 levels (the so called central transition) is unaffected by the electric quadrupole interaction to first order, while the distance in frequency of all other transitions (satellites) from the central transition, depends solely on the quadrupolar interaction. In case of a powder sample, as in our case, the crystal axes, and hence the EFG, are distributed at random angles with respect to the applied magnetic field. The angular average of the satellite patterns gives rise to a characteristic frequency distribution. The width of the sattelite frequency distribution (SFD) is proportional to the EFG (and consequently to the lattice distortions) and independent of the magnetic field. It is furthermore noticed that for T < T_c the magnetic field B at the site of the La nuclei is equal to the sum of the applied external field B and the transferred hyperfine field $B_{{\rm hf}} = (1{\mathrm{/}}\gamma \hbar )A\left\langle S \right\rangle$, where A is the hyperfine coupling constant and $\left\langle S \right\rangle$ the average electronic spin of the eight nearest Mn neighbors.^38,39

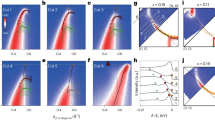
Figure 1a demonstrates ¹³⁹La NMR spectra of the LCMO(0.33) system in the temperature range 3.2–900 K. LCMO(0.33) undergoes two major phase transitions: a structural one from the high temperature $R\bar 3c$ rhombohedral phase to the low temperature orthorombic Pnma phase at T_RO ≈ 710 K,^39,40 and a paramagnetic to FM (PM–FM) one at T_c = 267 K, as shown in Figures S3.1, S3.2 and S5.1 of the Supplementary Information. The critical temperature of the PM–FM phase transition T_c, defined as the inflection point of the frequency vs. T plot, in the magnetic field of 9.4 T is found to be T_c ≈ 300 K (right bottom inset), sufficiently higher than in zero external magnetic field. At high temperatures spectra show the characteristic NMR powder pattern consisting of a narrow central line and the broad SFD. However, by approaching T_c from above, the narrow central line starts to broaden and for T ≤ 320 K becomes indistinguishable from the SFD. The inset at the top left side of Fig. 1a shows the SFD as a function of temperature. By decreasing temperature, at T ≈ 710 K, an abrupt increase of the SFD width is observed, which marks the transition from the $R\bar 3c$ to the Pnma crystal structure and the onset of strong incoherent JT displacements.^39,40 Neutron scattering experiments indicate that the appearance of the JT distortions is related with the formation of uncorrelated dynamic JT polarons right below T_RO, which by further decreasing temperature freeze into a CE-type polaron glassy state with correlation length of ≈1 nm.⁹ Most notable, for T < 100 K spectra start to broaden and shift to higher frequency, which might indicate the onset of an until now unnoticed novel FM phase. Furthermore, at T = 3.2 K, in addition to the FM ¹³⁹La NMR signal at ≈79 MHz, a weak signal is observed at frequency ≈58 MHz, which corresponds to the CE-type AFM spin arrangement, as clearly seen in Fig. 1b,c. For reasons of comparison the CE-type AFM NMR signal at T = 3.2 K of LCMO(0.50) and LCMO(0.41) are shown in Fig. 1d,e. This result corroborates with theoretical predictions, which show that the FM metallic state of the LCMO family, might be more complicated than initially thought, with the ground state at certain doping concentrations consisting of a CE-type matrix with FM metallic stripes.³⁶

Fig. 1

a ¹³⁹La NMR spectra in magnetic field 9.4 T, in the temperature range 3.2 K up to 900 K. The yellow points show the plot of the NMR frequency as a function of temperature. The upper left inset demonstrates the width of the satellite frequency distribution (SFD) as function of temperature. The bottom right inset shows the derivative of the SFD width (yellow points) and of the NMR signal frequency (white points) as a function of temperature. The structural transition at T ≈ 710 K and the PM–FM magnetic transition at ≈300 K are nicely detected. In addition, a second magnetic phase transition is observed to take place at ≈100 K. b ¹³⁹La NMR spectra of LCMO(0.33) at 3.2 K. A weak CE-type AFM signal is observed at frequency 57.782 MHz. c The ¹³⁹La NMR spin-echo signal at 57.782 MHz. d,e For reasons of comparison the ¹³⁹La NMR signal of LCMO(0.50) and LCMO(0.41) are presented. In case of LCMO(0.50) a strong AFM CE-type NMR signal is observed at frequency ≈57.6 MHz, together with the FM signal at ≈79 MHz³⁵

To get insight into the evolution of the magnetic interactions in the static polaron regime of the PM phase the inverse NMR central line width 1/w, which is proportional to the inverse of the magnetic susceptibility χ⁻¹,⁴¹ is plotted as a function of temperature in Fig. 2. For reasons of comparison 1/w vs. T curves of LCMO with x = 0.23, 0.41, and La_0.70Sr_0.30MnO₃ (LSMO(0.30)), from previous ¹³⁹La NMR line shape measurements³⁹ are presented. In case of the LSMO(0.30) system, which remains in the $R\bar 3c$ crystallographic phase at all temperatures, 1/w vs. T follows a linear Curie–Weiss law, crossing the horizontal T axis at T_c ≈ 400 K. Similarly, LCMO(0.41), which shows only dynamic CE-type polaronic distortions in the PM phase,⁹ and no SFD was observed in the relevant ¹³⁹La NMR spectra, 1/w follows the Curie–Weiss law down to T_c ≈ 300 K. However, in case of LCMO(0.23) and LCMO(0.33), where JT static polarons have been detected with neutron scattering experiments,⁹ strong deviation from the linear Curie–Weiss relation is observed in the temperature range 400–550 K, in agreement with magnetic susceptibility measurements.⁴⁰ This deviation signalizes the transition from the dynamic to the static polaron regime.^9,39,40 It is also tempting to consider that for T > 550 K electron spin dynamics in both the LCMO(0.23,0.33) systems are dominated by magnetic correlations of the high temperature $R\bar 3c$ phase, while for T < 400 K the formation of the static CE-type polaronic distortions dominates their magnetic properties.

Fig. 2

Formation of static JT polarons affects the inverse ¹³⁹La NMR linewidth 1/w, which is proportional to the inverse magnetic susceptibility χ⁻¹.⁴¹ Presented are 1/w vs. T curves for LCMO(0.25,0.33,0.41) and LSMO(0.3) in the temperature range 80–900 K and 9.4 T external magnetic field. Strong deviation from the Curie–Weiss law is observed at T ≈ 550 K for LCMO (0.23, 0.33). The dashed lines are guides to the eye

The Pnma to $R\bar 3c$ phase transition at T = 710 K in LCMO(0.33) was identified by applying HRTEM. Since these two phases are very similar, a detailed simulation of their selected area electron diffraction patterns was performed in order to identify zones axes with prominent differences. Using the hexagonal description of the unit cell, two equivalent zone axes are the [111]_Pnma, which is parallel to $\left[ {\overline 1 11} \right]_{{\mathrm{R}}\overline {\mathrm{3}} {\mathrm{c}}}$. Figure 3a shows a HRTEM image at room temperature parallel to [111]_Pnma, while Fig. 3c is the relevant FFT. It should be noted that as an aid to the reader, the usual grey-scale contrast of the HRTEM images in Fig. 3 are converted to a color-scale image, using the temperature color look-up table palette of the Gatan Digital Micrograph software, in order to enhance the contrast details of the HRTEM images (details are presented in Figure S2.6). After heating the same crystal to 800 K the HRTEM image of Fig. 3b was obtained, with the FFT shown in Fig. 3d. The main difference between the two FFTs is that two rows of spots in the [111]_Pnma zone axis disappear at 800 K, and the later FFT can only be indexed as the $[\overline 1 11]_{{\mathrm{R}}\overline 3 {\mathrm{c}}}$ zone axis, i.e. the crystal structure at 800 K has changed to the $R\overline 3 c$. HRTEM images in Figures S2.3, S2.4, and S2.5 of the Supplementary Information confirm that for T < 700 K the system is in the Pnma phase.

Fig. 3

HRTEM detection of the Pnma to $R\overline 3 c$ phase transition of LCMO(0.33) (T_c ≈ 710 K). a,b HRTEM images at T = 296 K and T = 800 K. c,d The relevant fast Fourier transforms. e Comparison of the d-spacing along the $(10 \overline 1)_{{\rm Pnma}}//\left( {\overline 1 1\overline 2 } \right)_{{{\rm{R}}\overline 3{\rm{c}}}}$ planes. HRTEM measurements in the temperature range 110–1000 K are provided in the Supplementary Information

Apart the above crystalline phase transition, another interesting observation was made regarding the Pnma phase at room temperature. Figure 4 presents the HRTEM image parallel to the [113]_Pnma zone axis, which provides a clear view of the Mn ions on the $(\overline 2 20)$ planes. Line profile analysis along the $(\overline 1 \overline 2 1)$ planes, shows the presence of nanoscopic regions with size ≈1–2 nm, acquiring alternating profile intensity at the position of successive Mn ions, as shown in the upper yellow intensity profile, while in other regions the profile does not show this type of alteration, as can be seen in the left yellow intensity profile. The green rectangle inset in Fig. 4 is the relevant calculated HRTEM image, which was structurally refined by varying the atomic positions, and by including bond-valence sum optimization to consider the presence of Mn³⁺/Mn⁴⁺ ions (Figure S2.7 in the Supplementary Information). Clearly, there exist regions, where the experimental profiles match with the calculated one, indicating the presence of nanosized charge ordered regions in agreement with previous reports.^34,42

Fig. 4

HRTEM indication of short range charge ordering in the PM phase of LCMO (0.33). a HRTEM image parallel to the [113]_Pnma zone axis at T = 296 K. Intensity profiles along the $(\overline 1 \overline 2 1)$ planes are shown in yellow color. The image section in the green rectangle inset is the relevant calculated HRTEM image, as obtained with the MacTempasX software, after performing structural refinement, and including bond-valence sum optimization to consider the presence of Mn³⁺/Mn⁴⁺ ions. Comparison of the experimental profiles with the calculated one shows the presence of nanoscopic regions where the two profiles match (upper yellow color profile), indicating the presence of short range charge ordering, as well as regions with no charge ordering (left yellow color profile). b The fast Fourier transform of the HRTEM image

In order to monitor the evolution of the polaron dynamics across the PM–FM phase transition and in the FM metallic phase, the ¹³⁹La spin-lattice and spin-spin relaxation (SLR/SSR) rates $T_{1,2}^{ - 1}$ of the central transition were measured as a function of T by lowering temperature from 900 K down to 3.2 K (Fig. 5a). The pulse sequences and fitting procedures to acquire the T₁ and T₂ relaxation times are described in the Methods section and in ref. ⁴³. The SLR rate depends on the amplitude and the frequency of the local magnetic field fluctuations δω₀ at the position of the La nuclei, created (i) by the fluctuating part of the transferred hyperfine interaction of the Mn^3+,4+ ions, and (ii) by the fluctuating part of the dipolar field of the Mn^3+,4+ ions. According to the literature this can be described as^41,43

$$\frac{1}{T}_1 = \frac{{2\left( {\delta \omega _0} \right)^2\tau }}{{1 + \left( {\omega _{\rm e}\tau } \right)^2}}$$

(1)

where δω₀ = 2πμ_BA∑ δS _j , δS _j is the amplitude of the electron spin fluctuation, A is the hyperfine coupling constant, μ_B is the Bohr magneton, ω_e is the electron Larmor frequency, and the correlation time τ = τ₀ exp(E_a/k_BT), which describes polaron hopping through an energy barrier E_a.

Fig. 5

¹³⁹La NMR relaxation studies of LCMO(0.33), in external magnetic field of 9.4 T. a ¹³⁹La NMR $T_1^{ - 1}$ (white points) and $T_2^{ - 1}{\mathrm{/}}16$ (yellow points) as a function of temperature in the temperature range 3.2–900 K. In the FM phase, $T_2^{ - 1}$ splits into two components; a fast fluctuating, exponentially decaying one (yellow points) and a slow fluctuating, Gaussian decaying one (orange color points). b The decay curves of the ¹³⁹La NMR transverse magnetization M _xy of LCMO(0.33) in external magnetic field of 9.4 T, at three characteristic temperatures. 2τ is the time of refocusing of the nuclear spin echo, as described in the Methods section. c ⁵⁷Fe Moessbauer spectroscopy of La_0.67Ca_0.32Fe_0.01MnO₃ as a function of temperature. Measurements confirm the presence of two relaxing components at low temperatures

Besides, in case of the ¹³⁹La nuclear sites with I = 7/2 the T₁ contribution to the SSR rate is given by $T_2^{ - 1}$ = (I + 1/2)²$T_1^{ - 1}$ = $16T_1^{ - 1}$.⁴³

According to Fig. 5a, by lowering temperature both $T_{1,2}^{ - 1}$ increase gradually until they reach a maximum value $T_{1,{\rm max}}^{ - 1} = T_{2,{\rm max}}^{ - 1}$/16 ≈ 10⁻² μs⁻¹ at 400 K, which corresponds to ω_eτ ≈ 1. By further decreasing temperature both SLR and SSR rates decrease abruptly, entering into the slow fluctuating regime, where ω_eτ ≥ 1. No sign of a ferromagnetic critical divergence of the relaxation rates is observed at T_c = 300 K, in agreement with previous measurements,⁴³ which is expected for a soft ferromagnet like LCMO(0.33) in an external magnetic field of 9.4 T. Notably, according to Savosta et al.⁴⁴ in the slow fluctuating regime the activation energy E_a of hopping electrons, acquires a quadratic dependence on temperature, E_a ∝ T², which is attributed to a polaron hopping mechanism for T₁.⁴⁴ Comparing the relaxation rates below and above the PM–FM transition, it is evident that for T < 400 K the same relaxation mechanism governs electron-spin dynamics in both phases. Remarkably, for T < 250 K a second slow relaxing component appears in the SSR rate; This is clearly seen in Fig. 5b which demonstrates the nuclear spin-echo decay curves at three different temperatures in the FMM phase. Right below T_c the spin-echo decays follow a single exponential law and SSR is controlled solely by the SLR contribution, which implies that polaron hopping dominates electron spin dynamics. However, for T < 120 K nuclear magnetization is shown to decay with a Gaussian function, which indicates the presence of slow quasistatic electron spin arrangements, resembling the ⁶³Cu nuclear quadrupole resonance (NQR) and NMR spin echo decay of slowly fluctuating stripes in superconducting cuprates.^45,46 In the temperature range 120 K ≤ T ≤ 250 K both the single exponential and Gaussian $T_{2R}^{ - 1}$ and $T_{2G}^{ - 1}$ relaxation mechanisms are present. Remarkably, no change in the SLR rate by cooling is observed, which means that both fast and slow relaxing components are related to the polaron spin dynamics mechanism. The appearance of two phase components with slow and fast dynamics is further confirmed with ⁵⁷Fe Moessbauer spectroscopy performed on La_0.67Ca_0.33Mn_0.99Fe_0.01O₃, as presented in Fig. 5c. This system exhibits a PM–FM phase transition at T_c = 228 K, which is sufficiently lower than that of the undoped system.⁴⁷ Moessbauer spectroscopy, in the ferromagnetic state, measures the hyperfine field B_hf via the line splitting at the iron sites. For a typical isotropic ferromagnet, such as α-Fe, Moessbauer spectra (MS) below the critical temperature consist of a sextet with narrow Lorentzian lines, while in the PM phase spectra consist of a single narrow absorption line, which reflects the quadrupolar interactions and the electronic environment via the quadrupolar split and the isomeric shift.⁴⁷ The inset in Fig. 5c presents selected MS in the temperature range 20–200 K. At 20 K the spectrum shows two signal components with the characteristic FM sextet, while at higher temperatures they both display an asymmetric line broadening, with dominant the two central lines of the magnetic sextet. Close to T_c the two central lines appear to collapse partially into a broad single line. This behavior can be excellently fitted with the relaxation model developed by van der Woude and Dekker,⁴⁸ unveiling the presence of two different relaxation mechanisms. Specifically, the main plot in Fig. 5c shows the evolution of the relaxation rates of the two Moessbauer signal components with the temperature. While at elevated temperatures a single relaxation rate is observed, at ≈100 K the two signals decompose into a fast and slow relaxing components, in similarity with the ¹³⁹La NMR SSR rate measurements.

The detection of two FM phase components with different spin dynamics corroborates with previous results showing the formation of two FM phase components at low temperatures with different magnetic anisotropy.⁴⁹ In order to correlate the two differently relaxing FM components with possible differences in the magnetic anisotropy, the NMR radiofrequency (rf) enhancement technique was implemented. In FM materials, very strong NMR signals are produced at extremely low rf irradiation fields B₁, due to the coupling of the rf field with the magnetic moments of the unpaired electrons.⁵⁰ In this way B₁ is strongly enhanced by the rf enhancement factor n = B_hf/(1 + Nχ)B_A, where N is the demagnetizing factor, χ the magnetic susceptibility, and B_A the magnetic anisotropy field. Correspondingly, the NMR signal is amplified by the oscillating electron moments, thus giving rise to the strong NMR signals that characterize FM materials. Experimentally, the rf enhancement factor is obtained by recording the ¹³⁹La NMR signal intensity I as a function of B₁ at the peak of the NMR spectra.⁵⁰ Since application of an external magnetic field pins electron spins, rf enhancement experiments are performed in zero external magnetic field. The inset in Fig. 6a presents the zero field ¹³⁹La NMR spectrum of LCMO(0.33) at 5 K. The signal consists of a single broad Gaussian centered at ≈21 MHz. The relevant main plot shows the 2D contour plot of the signal intensity vs. B₁ and T. At very low temperatures two signal components are observed at B₁ ≈ 0.1 and 1.5 G, unveiling the presence of two FM configurations with different magnetic anisotropy. The two signal components correlate excellently with the NMR relaxation and Mossbauer data. It is worth to notice that the signal component with maximum at B₁ ≈ 0.1, corresponds to FM ordered electron spins responding almost freely to the external rf field, i.e. they possess liquid-like electron spin correlations. By raising temperature this signal decreases in intensity and is not observed for T > 100 K (inset in Figure S6.1a), most probably due to the extremely short T₂ value. Furthermore, by increasing the Ca doping the liquid-like signal component exists even in the AFM LCMO(0.55) system, as presented in Figure S6.1b. At this doping, neutron scattering experiments show only CE-type AFM long-range order (ref. ¹² in Supplementary Information). This is evidence that for x = 0.55 the detected liquid-like ¹³⁹La NMR signal is produced in nanoscopic FM regions dispersed in the AFM phase, which are not detectable in neutron scattering experiments. In view of this fact, the observation of the weak CE-type AFM ¹³⁹La NMR signal in the x = 0.33 system indicates that the free responding FM signal is produced in liquid-like FM nanodomains in a background, where AFM CE-type correlations are important. Notably, the planar zig-zag propagation of the CE-type ordering in the (001) plane, make reasonable to consider that the spin-liquid FM nanodomains are ordered into either in-plane nematic threads or smectic (i.e. planar liquid) nanodomains.

Fig. 6

a 2D contour plot of the ¹³⁹La NMR signal intensity in zero external magnetic field as a function of the rf field B₁ at various temperatures. Measurements were performed at the maximum intensity of the ¹³⁹La NMR signal at frequency ≈21 MHz, as shown in the inset. By lowering temperature a signal component grows for T < 100 K, which is excited at extremely low B₁ values. This signal component corresponds to a quantum spin liquid crystal phase, as explained in the text. b The temperature vs. Ca doping T − x phase diagram of the La_1−xCa _x MnO₃. A low temperature region of a mixed quantum liquid crystal/FM metallic phase is observed in the doping range 0.2 ≤ x ≤ 0.5

Discussion

A plausible scenario explaining these results is as follows: static CE-type polarons are formed in the Pnma phase of the LCMO(0.33) system for T < 550 K. In the high temperature rhombohedral $R\overline 3 c$ phase JT distortions are forbidden by symmetry, while right below the T_RO transition temperature, dynamic JT polarons were detected with the help of neutron scattering experiments.⁹ Interestingly, the HRTEM results at room temperature in Fig. 4 indicates the formation of nanoscopic charge ordered regions, with size ≈1–2 nm. It is noticed that the CE phase consists of diagonal stripes of alternating zig-zag Mn³⁺ and Mn⁴⁺ charges (as well as d(3x² − r²) and d(3y² − r²)) on the (001) plane, which from the TEM point of view would give rise to an alternating line profile intensity at the position of the Mn ions on successive $(\overline 2 20)$ planes. This is similar to the line profile intensity of the calculated HRTEM images in Fig. 4a and S2.7. At this point it should be mentioned that since HRTEM images are phase contrast sensitive, further work is needed to confirm this result. The formation of CE-type polarons corroborates also with the electrical resistivity measurements in zero external magnetic field presented in Figure S4.1 of the Supplementary Information. Specifically, for T < 300 K, an anomalous increase of the electrical resistance is observed, which is in agreement with the presence of short-range-ordered polarons, while for T < T_c ≈ 265 K, the resistivity decreases initially abruptly, and subsequently gradually following a non-metallic temperature dependence. The abrupt decrease of the resistivity right below T_c is evidence that part of the static polaron regions melt into a polaron bad metal. Another interesting result is that the appearance of static polarons in the PM phase has strong impact on the magnetic susceptibility, as seen in the inverse ¹³⁹La line width 1/w vs. T curve, which is observed to deviate strongly from the Curie–Weiss law for T < 550 K. Most notably, the ¹³⁹La NMR SLR data in Fig. 5a show that polaron dynamics follow the same law in both the PM and FMM phases, suggesting that spatially extended polaron correlations survive down to the lowest measured temperature. A similar temperature dependence was observed in the ¹³⁹La NMR SLR rate of La_1−xNa _x MnO₃, which was acquired in zero external magnetic field for T < T_c.⁴⁴ For T < 200 K the ¹³⁹La NMR spin echo decay envelope becomes gradually Gaussian, as observed in Fig. 4b, which is evidence that polaron dynamics freeze down. A slow relaxing FM phase component is detected at low temperatures with novel features: (i) it has extremely low magnetic anisotropy, as shown by the ¹³⁹ La NMR rf enhancement experiments, and (ii) it shows enhanced spin polarization in an external magnetic field, as implied by the ¹³⁹ La NMR signal frequency shift in Fig. 1a. At the same time a weak AFM CE-type ¹³⁹La NMR signal has been observed at 3.2 K, which is strong indication that there exist nanoscopic regions, where the CE-type zig-zag spin and charge ordering survives down to the lowest measured temperature. A reasonable assumption to explain the extremely low magnetic field anisotropy in conjunction with CE-type ordering is that at low temperatures, in the FM metallic phase an electron spin liquid crystal phase component appears, which is comprised of uncorrelated CE-type zig-zag FM polaron chains. Notably, the strong enhancement of the intensity of the NMR signal from the low magnetic anisotropy regions by cooling down to the lowest measured temperature of 5 K, as presented in the inset of Figure S7.1a, is indication that the electron spin liquid crystal phase might be the ground state of this system. The above scenario is comprehenced into the phase diagram presented in Fig. 6b, where a region with mixed FM metallic spin crystalline/FM quantum spin liquid crystal phase is observed to exist in the doping region 0.2 ≤ x ≤ 0.5.

In summary, by using ¹³⁹La NMR and HRTEM in the temperature range 3.2–900 K, we succeeded to elucidate important aspects on the role of polarons in the intriguing physical properties of optimally doped FM LCMO(0.33). We present strong indications that for T < 550 K, the PM phase is organized into quasistatic CE-type correlated polarons, while for T < T_c these regions transform into a bad polaronic metal, possibly on a dynamic CE-type background. This is reminiscence of the STM and ARPES study of La_2−2xSr_1+2xMn₂O₇, which uncover this system as a pseudogaped bad polaronic metal.⁶ Most important, suppressing thermal fluctuations by decreasing temperature, polarons are shown to organize into a quantum spin liquid crystal phase, presumably of uncorrelated CE-type polaron chains. This is important information in the emerging field of quantum liquid crystal systems.

Methods

La_0.67Ca_0.33MnO₃ powder sample was prepared by thoroughly mixing high-purity stoichiometric amounts of CaCO₃, La₂O₃, and MnO₂. The mixed powder reacted in air up to 1400 °C for several days with intermediate grinding. The sample was then slowly cooled to 25 °C. In order to secure stoichiometry of the sample, additional annealing in He atmosphere was applied. More specifically, in the final preparation step the sample was heated under He flow up to 1100 °C for 48 h followed by rapid cooling to room temperature.

Powder X-ray diffraction (XRD) patterns were acquired at room temperature using a Siemens D500 diffractometer, with Cu K radiation (λ = 1.5418 Å). XRD patterns were recorded in 2θ ranging from 10° to 120°, at a scanning rate of 0.03°/min. The crystal structure and the exact structural parameters were determined with Rietveld refinement. Simulated XRD patterns were produced by the Fullprof software package (Figure S1.1 in the Supplementary Information).

Samples for electron microscopy were prepared by suspending the LCMO powder in ethanol, followed by air evaporation of a droplet on an ultra thin carbon-supported Cu grid (TED PELLA, Inc.). In-situ TEM investigation of LCMO nano-powders was carried out using the high voltage electron microscope (JEM-ARM1300S, 1250 kV) installed at Korea Basic Science Institute in the temperature range from 100 to 1000 K. The LCMO nano-powders in HVEM were heated/cooled at a rate of 10 K/min and a holding time of 30 min at each temperature. The structure modeling of two phases LCMO crystals was performed according to previous result⁴⁰ and the drawing of atomic structure was performed using program VESTA. The quality of all high-resolution electron microscopy (HREM) images was enhanced by using bandpass and mask filtering method with fast Fourier transform (FFT) data of HREM images. Calculated HRTEM images were obtained with the help of the MacTempasX software, Total Resolution LLC. Structural refinement was performed by varying the atomic positions, including bond-valence sum optimization to unveil the Mn³⁺, Mn⁴⁺ ordering. The simulated electron diffraction pattern images were obtained with the SingleCrystal software (CrystalMaker Software Ltd.).

¹³⁹La NMR experiments were performed on a home-built broadband spectrometer operating in the frequency range 5–800 MHz, in 9.4 T and zero external magnetic field. Because the NMR spectra are extremely broad, the 90° − τ − 180° spin-echo point by point method was employed, which is based on recording the spin echo signal, while sweeping the spectrometer frequency. An Oxford 1200CF continuous flow cryostat was employed for measurements in the temperature range 3.2–350 K and an Oxford HT1000V furnace for measurements in the range 300–900 K. In case of the NMR measurements in the 9.4 T external magnetic field, pulse widths were set to 7 and 14 μsec, respectively. In case of the NMR measurements in zero external magnetic field the pulse widths were set at 0.6 and 1.2 μsec and very-low rf power level (B₁ in the range 0.05–5 G) was applied, due to the very strong rf-enhancement factor which characterizes magnetic materials in the absence of a strong external magnetic field. ¹³⁹La NMR spin-lattice T₁ measurements were performed by using a 90° − t − 90° − τ − 180° pulse sequence, comprised of a saturation recovery two-pulse sequence, followed by a 180° pulse to record the spin echo signal. ¹³⁹La NMR spin-spin T₂ measurements were performed by using the conventional 90° − τ − 180° Hahn spin echo pulse sequence.

Absorption MS were collected with a ⁵⁷Co(Rh) source moving at room temperature, while the absorbers were in a variable temperature cryostat.

DC magnetization measurements, electrical resistance and heat capacity measurements, which are presented in the Supplementary Information, were performed on a Quantum Design, Physical Property Measuring System (PPMS-9T) operating in magnetic fields 0–9 T and in the temperature range 2–350 K. Specifically, for the electrical resistance measurements the van der Pauw four-point technique in the PPMS was applied on pelletized samples (Figures S3.1, S3.2, S4.1, and S5.1 in the Supplementary Information).

Data availability

The authors declare that the data supporting the findings of this study are available within the article and its Supplementary Information files.