Abstract
The quantum anomalous Hall effect in thin film magnetic topological insulators (MTIs) is characterized by chiral, one-dimensional conduction along the film edges when the sample is uniformly magnetized. This has been experimentally confirmed by measurements of quantized Hall resistance and near-vanishing longitudinal resistivity in magnetically doped (Bi,Sb)2Te3. Similar chiral conduction is expected along magnetic domain walls, but clear detection of these modes in MTIs has proven challenging. Here, we intentionally create a magnetic domain wall in an MTI, and study electrical transport along the domain wall. In agreement with theoretical predictions, we observe chiral transport along a domain wall. We present further evidence that two modes equilibrate while co-propagating along the length of the domain wall.
Similar content being viewed by others
Introduction
The recent prediction1 and subsequent discovery2 of the quantum anomalous Hall (QAH) effect in thin films of the three-dimensional magnetic topological insulator (MTI) (Cr y Bi x Sb1−x−y )2Te3 has opened new possibilities for chiral-edge-state-based devices in zero external magnetic field. Like the ν = 1 quantum Hall (QH) system, the QAH system is predicted to have a single chiral edge mode circulating along the boundary of the film. Backscattering of the chiral edge mode should be suppressed, as recently verified by the observation of well-quantized Hall resistivities |ρ yx | = (1 ± 10−6) h/e 2, along with longitudinal resistivities as low as 10 mΩ.3,4,5 Dissipationless, chiral 1D conduction is also expected along magnetic domain walls,6,7,8,9 but explicit experimental confirmation of this prediction has proven elusive.
Edge conduction in the QAH system is a consequence of the system’s topological non-triviality.10 The QAH system is topologically classified by the Chern number C = ±1, corresponding to upwards or downwards magnetization, respectively. At the interface between MTI and vacuum, the Chern number transitions from C = ±1 to the topologically trivial C = 0; one chiral edge mode propagates along this interface. At a magnetic domain wall, however, the Chern number changes by two, from C = +1 to C = −1. Accordingly, two chiral modes should co-propagate along this interface.7,11,12 If the domain does not reach the film’s edge, the modes at the domain wall should simply circle the domain, having no effect on transport. But if the domain wall connects two of the device’s edges or contacts, it may affect two- and/or four-terminal resistances. Analogous transport has been studied in the QH effect in graphene-based two-dimensional electron gases, where patterned gates can produce adjacent regions of different density and hence different filling factor.13,14
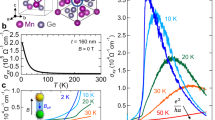
Previously, the magnetization of MTIs has been flipped without spatial control, by sweeping a homogenous external magnetic field through the coercive field \(H_{C}^{\rm {TI}}\). For most MTIs that display the QAH effect, ρ yx transitions from \(\mp\) h/e 2 to ±h/e 2 over a substantial range of field (H = 150 to H = 200 mT for the material used in the work), and ρ xx has a maximum in this field range.15,16,17,18,19,20 Hysteresis loops of the four-terminal resistances of a 50 μm wide Hall bar of MTI film are shown in Fig. 1a. In some samples and in some temperature ranges, R yx jumps in discrete steps when the external field is swept through \(H_{C}^{\rm {TI}}\) (see Supplementary Material).21 Each jump likely represents rearrangement of the magnetic domain structure. Since within a domain the 2D bulk of an MTI is highly insulating at the lowest temperatures,3,4 these jumps suggest that domain walls host conductive modes. The set of discrete R yx values is not reproducible between separate magnetic field sweeps, suggesting that the network of magnetic domain walls is complex.
Experimental summary. a Hysteresis curves of the Hall (red) and longitudinal (blue) resistivities in a top-gated Hall bar of the magnetic topological insulator (Cr0.12Bi0.26Sb0.62)2Te3. b Schematic side view of a superconducting cylinder screening magnetic flux lines away from a thin MTI film (purple) on a GaAs substrate (blue). The cylinder and MTI are separated by an alumina dielectric (brown) and a top gate (gold). Dimensions are not to scale. c Schematic top view of Device A. d Schematic top view of Device B. e, f Schematics of the expected chiral electrical transport in the presence of magnetic domain walls (dotted lines), when M z = −1 and \(M_{z}^{\rm {SC}} = 1\), in Devices A and B. The orange arrows indicate a single chiral mode each, and the red and blue vectors indicate the direction of magnetization.
To better study transport along domain walls, we intentionally engineered a magnetic domain wall in six quintuple layer (Cr0.12Bi0.26Sb0.62)2Te3 by spatially modulating the external magnetic field H, and then measured electronic transport along the domain wall at H = 0. Our results confirm chiral transport along magnetic domain walls in the quantum anomalous Hall system, and support the prediction12 that domain walls host two co-propagating modes whose carriers equilibrate.
Results and discussion
We spatially modulate the magnetic field applied to the MTI film using Meissner repulsion from a bulk superconductor.22 A niobium cylinder of 1.5 mm diameter and 2 mm height partially covers the surface of a patterned MTI film, but is not in electrical contact. When superconducting, the niobium cylinder screens a portion of the external magnetic field, as sketched in Fig. 1b. Far from the cylinder, the external magnetic field is unscreened and the magnetization of the MTI film switches direction when the external field reaches \(H_{C}^{\rm {TI}}\). The screened portion of the MTI film, underneath the cylinder, does not switch magnetization until the external magnetic field reaches a higher value. We define M z = M/|M| = 1(−1) to represent upwards- (downwards-) pointing magnetization of the MTI film away from the superconductor. \(M_{z}^{\rm {SC}}\) represents the equivalent quantity in the screened region of the MTI.
To create a domain wall, the MTI film is first fully magnetized downwards \(M_z = M_{z}^{\rm {SC}} = - 1\) with a large external field. A positive field slightly above \(H_{C}^{\rm {TI}}\), typically between μ 0 H = 180 mT and 200 mT, is then applied. Only the unscreened region switches magnetization, so that M z = 1, and \(M_{z}^{\rm {SC}} = - 1\). This process forms a domain wall near the boundary of the superconductor; its exact position depends on the geometric demagnetization of the superconductor. Applying oppositely signed fields forms the magnetic configuration M z = −1, \(M_{z}^{\rm {SC}} = 1\). Domains are formed with the sample held between 25 and 200 mK; this process is detailed in the Supplementary Material.
We study the transport properties of the domain wall at zero field in two geometries. Device A (Fig. 1c, schematic) is a Hall bar with eight voltage terminals and two current contacts. A niobium cylinder placed on the device’s surface covers the leftmost four voltage terminals. Device B (Fig. 1d, schematic) consists of four etched regions inside a large region of MTI. Electrical contact is made to the boundary of each etched region. Since the contacts are not connected by an edge of the MTI, no conductive channel connects the contacts when Device B is uniformly magnetized, and the resistance between pairs of contacts exceeds 8 MΩ at T = 25 mK. The boundary of a niobium cylinder overlaps all four etched regions to form a magnetic domain wall connecting them. The MTI’s Fermi level in Device B is tuned with an electrostatic top gate with an alumina dielectric (see Methods); Device A’s top gate, however, is unintentionally shorted to one contact and is left at zero volts during measurements.
Preliminarily, Device A is fully magnetized downwards by an external field μ 0 H = −1 T and then returned to μ 0 H = 0. At base temperature, the Hall resistance approaches −h/e 2 both underneath and away from the superconducting cylinder, as indicated in Table 1. In both regions, the measured longitudinal resistance is small compared to h/e 2, indicating nearly dissipationless conduction along the edges of the device.
Next, the external magnetic field is swept, as detailed previously, to attempt to create a magnetic domain. After returning to zero field, we find oppositely signed Hall resistivities in the screened and unscreened regions of Device A, confirming the formation of distinct magnetic domains in the Hall bar. Again, the measured longitudinal resistance is small compared to h/e 2 in both regions, indicating nearly dissipationless conduction along edges within the domains. In the configuration M z = −1, \(M_{z}^{\rm {SC}} = 1\), the longitudinal resistance away from the niobium cylinder R xx is somewhat larger than R xx in the configuration \(M_z = M_{z}^{\rm {SC}} = - 1\), suggesting slightly incomplete reversal of the magnetization in the region outside the superconductor. Were the Fermi level optimized by the top gate, the longitudinal resistances might be further reduced in all measurements. Four-terminal resistances in Device A, in various magnetic configurations, are presented in Table 1.
Having confirmed the creation of a magnetic domain wall, we study the equilibration of the two chiral modes expected to co-propagate along the domain wall. Consider carriers traveling along the domain walls sketched in Fig. 1e. For sufficiently long domain walls, we expect full equilibration, meaning that carriers leaving the domain walls move rightwards and leftwards along the device’s edges with equal probability.12 For full equilibration, the Landauer-Büttiker formalism predicts four-terminal longitudinal resistances \(R_{xx}^{\rm {top}}\) and \(R_{xx}^{\rm {bottom}}\), measured across the domain wall, of 0 and 2h/e 2 (see Supplementary Material), in reasonable agreement with our results as shown in Table 1. The measured resistances slightly exceed the predicted values, which could result either from slightly incomplete equilibration, or from the presence of an extra dissipative channel related to a reduction in the exchange-induced gap in a stripe around the domain wall (see Supplementary Material).
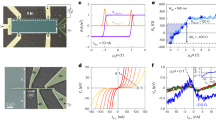
Using Device B, we examine how carriers propagate along domain walls. The effective longitudinal resistance R 14,23 quantifies dissipation along the domain wall, and the effective Hall resistance R 13,24 and its mirror R 42,31 establish the chirality of the conductive modes. These four-terminal measurements are not standard longitudinal and Hall measurements, but are topologically analogous to typical R xx and R yx measurements in the ν = 2 QH system if indeed two chiral modes co-propagate along the interface between two insulating domains. R 14,23, shown in Fig. 2a as a function of gate voltage, is smallest when the gate voltage is −8 V; here, the Fermi level presumably sits in the center of the gap. The low longitudinal resistance at the optimum gate voltage and base temperature, as shown in Table 2, indicates nearly dissipationless conduction along the domain wall.
Longitudinal resistance along a domain wall. a The resistance R 14,23 of Device B as a function of gate voltage at temperatures between 25 mK and 674 mK. The magnetization is M z = 1 and \(M_{z}^{\rm {SC}} = - 1\), such that a domain wall with clockwise chirality connects the contacts. b R 14,23 at gate voltage −8 V, shown on an Arrhenius plot. Only data at temperatures exceeding 150 mK are included in the fit to an Arrhenius law
Dissipation along the domain wall appears thermally activated above T = 150 mK (Fig. 2b). The longitudinal resistance R 14,23 increases with rising temperature according to an Arrhenius law R 14,23 ∝ exp(−T 0/T) with an activation gap T 0 = 0.41 K. Arrhenius activation with a comparable gap size is observed in the material’s sheet conductivity σ, measured in the Corbino geometry (see Supplementary Material). The temperature dependence of R 14,23 flattens below T = 150 mK; the cause of this behavior is unclear. The consistent Arrhenius activation between R 14,23 and σ suggests that dissipation in transport along the domain wall is caused by carriers scattering between the 1D chiral modes and thermally activated 2D bulk states.
The effective Hall resistances R 13,24 and R 42,31 are oppositely-signed; further, their signs switch when the device’s magnetic configuration is reversed. This confirms the chirality of conduction along the domain wall. The magnitudes of R 13,24 and R 42,31 at the optimum gate voltage, detailed in Table 2, are close to (but slightly exceed) 0.5h/e 2, the expected value for two chiral modes. As shown in Fig. 3, R 13,24 and R 42,31 converge as the temperature rises, with R 13,24 ≈ R 42,31 ≈ 0.25h/e 2 at T = 770 mK. Here, conduction through the 2D bulk dominates and the two resistances are no longer analogous to Hall measurements; instead, they saturate at a positive value reflecting the sheet conductivity σ and the device geometry.
Effective Hall resistances of conduction along a domain wall. The resistances of Device B, a R 13,24 and b R 42,31, as a function of gate voltage at temperatures between 25 mK and 882 mK. The magnetization is M z = 1 and \(M_{z}^{\rm {SC}} = - 1\), such that a domain wall with clockwise chirality connects the contacts. c R 13,24 and R 42,31 at gate voltage −8 V, as a function of temperature, for the magnetic configurations M z = −1 and \(M_{z}^{\rm {SC}} = + 1\) (solid markers), and M z = 1 and \(M_{z}^{\rm {SC}} = - 1\) (hollow markers)
We have shown that magnetic domain walls in quantum anomalous Hall insulators conduct through chiral modes, which are expected to be topological in origin. Two modes are predicted to propagate along domain walls, thus we expect the effective Hall resistances of Device B to saturate at h/2e 2 at low temperatures. Though we do not observe such saturation, the measured effective Hall resistances at the optimum gate voltage are near the predicted value.
To explain the discrepancy, we propose that the magnetic exchange interaction, needed to open a gap in the MTI’s surface states,1 is reduced around the domain wall, allowing the formation of a compressible stripe. In Device A, the stripe would increase the measured values \(R_{xx}^{\rm {top}}\) and \(R_{xx}^{\rm {bottom}}\), while in Device B, the stripe could perturb R 13,24 and R 42,31 from h/2e 2 without imparting a significant contribution to the longitudinal resistance (see Supplementary Material). The width of the compressible stripe is presumably related to the spatial profile of the applied magnetic field, which varies over hundreds of microns near the edge of the superconductor (see Supplementary Material).
After completion of this work, we learned of a study by Yasuda et al. that also investigated conduction in an MTI along magnetic domain walls, formed by a different approach.23
Methods
Material growth
Measurements were performed on high quality single crystalline (Cr0.12Bi0.26Sb0.62)2Te3 films 6 quintuple layers (QLs) in thickness. Films were grown on a semi-insulating GaAs (111)B substrate in a Perkin-Elmer ultra-high-vacuum molecular beam epitaxy system. The substrate was annealed at 580 °C in a Se-rich environment to remove the native oxide. The MTI film was grown with the substrate held at 200 °C with the Cr, Bi, Sb, and Te source shutters simultaneously open. Growth was monitored using in situ reflection high-energy electron diffraction (RHEED). After growth, a 2 nm Al layer was evaporated in situ at room temperature and later allowed to oxidize in air to passivate the surface, protecting the film from unwanted environmental doping or aging effects.
Device fabrication
Devices were patterned using contact photolithography. For each patterning step, a hexamethyldisilazane adhesion layer was spin coated, followed by Megaposit SPR 3612 photoresist. The pre-exposure bake of 80 °C for 120 s was chosen to avoid thermal damage to the film. The photoresist was exposed under an ultraviolet mercury vapor lamp at approximately 70 mJ/cm2 and was developed in Microposit developer CD-30 for 35 s. The device mesas were defined after patterning by etching the surrounding film with an Ar ion mill. Ohmic contacts were made by first cleaning the area with a brief exposure to an in situ Ar ion source, and then evaporating 5 nm Ti and 100 nm Au, followed by liftoff. To realize a robust top gate, a dielectric was grown uniformly across the film by evaporating a 1 nm Al seed layer, which was allowed to oxidize, and then depositing approximately 40 nm of alumina by atomic layer deposition. The top gate was then fabricated by evaporating 5 nm Ti and 85 nm Au, followed by liftoff. Excess alumina dielectric on the surrounding area was etched using Microposit developer CD-26 (tetramethylammonium hydroxide based, metal ion free). Metal was evaporated using a Kurt Lesker electron beam evaporator with an in situ Ar ion source. Atomic layer deposition used trimethylaluminum precursor and water as the oxidizer in a nitrogen purged vacuum chamber.
Lock-in measurements
Four-terminal resistances were measured using a typical lock-in measurement setup in a dilution refrigerator at a base temperature of 25 mK. Devices A and B were measured in separate cooldowns. All measurements were current biased with a 5 nA AC bias, which was applied to the device by sourcing 5 V RMS across a 1 GΩ resistor. The current traveling through the device and out of the drain terminal was measured with an Ithaco 1211 current preamplifier with 200 Ω input impedance, set to −107 V/A gain. Differential voltages V xx and V yx were measured with NF Corporation LI-75A voltage preamplifiers and Stanford Research Systems SR830 digital lock-in amplifiers. The excitation frequency was between 1 and 10 Hz; at higher frequencies, large phase differences developed between the excitation and measurement.
The amplifier chain in the measurement setup requires calibration for precise measurement due to uncertainty in the amplifiers’ gains. Approximately four months prior to collection of data in this work, the amplifiers were calibrated to the Hall resistance of a quantum anomalous Hall device. Comparison of the QAH device’s Hall resistance to the resistance of a standard resistor, using a cryogenic current comparator, verified its precise quantization to h/e 2. The amplifier chain used in lock-in measurements gives the uncalibrated measurement for the Hall resistance V yx /I = 26.75 kΩ, which is 3.6% higher than h/e 2 = 25.81 kΩ. All resistances presented in this work were multiplied by 0.965 to correct for this inaccuracy. Current measurements all used the same amplifier chain, whereas multiple amplifier chains were used to make simultaneous voltage measurements. To estimate the systematic deviation between voltage measurements, we measured an identical voltage with each amplifier chain, finding less than 0.4% variation in the measured value, which serves as a bound for the error of the corrected resistance values. The statistical error of the lock-in measurements is lower than one part in 1000.
Data availability
The data supporting the findings of this study are available from the corresponding author upon reasonable request.
References
Yu, R. et al. Quantized anomalous Hall effect in magnetic topological insulators. Science 329, 61–64 (2010).
Chang, C.-Z. et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 340, 167–170 (2013).
Bestwick, A. J. et al. Precise quantization of the anomalous Hall effect near zero magnetic field. Phys. Rev. Lett. 114, 187201 (2015).
Fox, E. J. et al. Part-per-million quantization and current-induced breakdown of the quantum anomalous Hall effect. Preprint at https://arxiv.org/abs/1710.01850 (2017).
Chang, C.-Z. et al. High-precision realization of robust quantum anomalous Hall state in a hard ferromagnetic topological insulator. Nat. Mater. 14, 473–477 (2015).
Qi, X.-L., Hughes, T. L., Raghu, S. & Zhang, S.-C. Time-reversal-invariant topological superconductors and superfluids in two and three dimensions. Phys. Rev. Lett. 102, 187001 (2009).
Wang, J., Lian, B. & Zhang, S.-C. Universal scaling of the quantum anomalous Hall plateau transition. Phys. Rev. B 89, 085106 (2014).
Checkelsky, J. G., Ye, J., Onose, Y., Iwasa, Y. & Tokura, Y. Dirac-fermion-mediated ferromagnetism in a topological insulator. Nat. Phys. 8, 729–733 (2012).
Wakatsuki, R., Ezawa, M. & Nagaosa, N. Domain wall of a ferromagnet on a three-dimensional topological insulator. Sci. Rep. 5, 13638 (2015).
Qi, X.-L., Wu, Y.-S. & Zhang, S.-C. Topological quantization of the spin Hall effect in two-dimensional paramagnetic semiconductors. Phys. Rev. B 74, 085308 (2006).
Nomura, K. & Nagaosa, N. Surface-quantized anomalous Hall current and the magnetoelectric effect in magnetically disordered topological insulators. Phys. Rev. Lett. 106, 166802 (2011).
Upadhyaya, P. & Tserkovnyak, Y. Domain wall in a quantum anomalous Hall insulator as a magnetoelectric piston. Phys. Rev. B 94, 020411 (2016).
Williams, J. R., DiCarlo, L. & Marcus, C. M. Quantum Hall effect in a gate-controlled p-n junction of graphene. Science 317, 638–641 (2007).
Amet, F., Williams, J. R., Watanabe, K., Taniguchi, T. & Goldhaber-Gordon, D. Selective equilibration of spin-polarized quantum Hall edge states in graphene. Phys. Rev. Lett. 112, 196601 (2014).
Checkelsky, J. G. et al. Trajectory of the anomalous Hall effect towards the quantized state in a ferromagnetic topological insulator. Nat. Phys. 10, 731–736 (2014).
Kou, X. et al. Scale-invariant quantum anomalous Hall effect in magnetic topological insulators beyond the two-dimensional limit. Phys. Rev. Lett. 113, 137201 (2014).
Mogi, M. et al. Magnetic modulation doping in topological insulators toward higher-temperature quantum anomalous Hall effect. Appl. Phys. Lett. 107, 182401 (2015).
Kandala, A., Richardella, A., Kempinger, S., Liu, C.-X. & Samarth, N. Giant anisotropic magnetoresistance in a quantum anomalous Hall insulator. Nat. Commun. 6, 7434 (2015).
Lachman, E. O. et al. Visualization of superparamagnetic dynamics in magnetic topological insulators. Sci. Adv. 1, e1500740 (2015).
Kou, X. et al. Metal-to-insulator switching in quantum anomalous Hall states. Nat. Commun. 6, 8474 (2015).
Liu, M. et al. Large discrete jumps observed in the transition between Chern states in a ferromagnetic topological insulator. Sci. Adv. 2, e1600167 (2016).
Carmona, H. A. et al. Two dimensional electrons in a lateral magnetic superlattice. Phys. Rev. Lett. 74, 3009–3012 (1995).
Yasuda, K. et al. Quantized chiral edge conduction on reconfigurable domain walls of a magnetic topological insulator. Preprint at https://arxiv.org/abs/1707.09105 (2017).
Acknowledgements
The authors acknowledge Andrew J. Bestwick for his contributions to the instrumentation and procedures used in this work, Elliott Rosenberg for assisting with magnetism measurements, and Marc Kastner, Francesco Giazotto, Malcolm Beasley, and Inti Sodemann for insightful discussions. Device fabrication and measurement was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division, under Contract DE-AC02-76SF00515. Infrastructure and cryostat support were funded in part by the Gordon and Betty Moore Foundation through Grant No. GBMF3429. X. K., L. P., and K. L. W. acknowledge support from FAME, one of six centers of STARnet, a Semiconductor Research Corporation program sponsored by MARCO and DARPA; and from the Army Research Office under Grant Numbers W911NF-16-1-0472 and W911NF-15-1-0561:P00001. X. K. acknowledges support from the Chinese National Thousand Young Talents Program and Shanghai Sailing Program under Grant Number 17YF1429200. Part of this work was performed at the Stanford Nano Shared Facilities (SNSF), supported by the National Science Foundation under award ECCS-1542152.
Author information
Authors and Affiliations
Contributions
X.K., L.P., and K.L.W. grew and characterized the material. I.T.R. and E.J.F. fabricated the devices and performed the measurements. I.T.R., E.J.F., and D.G.-G. contributed to measurement analysis and wrote the paper with contributions from all co-authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rosen, I.T., Fox, E.J., Kou, X. et al. Chiral transport along magnetic domain walls in the quantum anomalous Hall effect. npj Quant Mater 2, 69 (2017). https://doi.org/10.1038/s41535-017-0073-0
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-017-0073-0
This article is cited by
-
Creation of chiral interface channels for quantized transport in magnetic topological insulator multilayer heterostructures
Nature Communications (2023)
-
Topological current divider in a Chern insulator junction
Nature Communications (2022)
-
Topological spintronics and magnetoelectronics
Nature Materials (2022)
-
Evidence for one-dimensional chiral edge states in a magnetic Weyl semimetal Co3Sn2S2
Nature Communications (2021)
-
Nanoscale imaging of equilibrium quantum Hall edge currents and of the magnetic monopole response in graphene
Nature Physics (2020)