Abstract
A nematic topological superconductor has an order parameter symmetry, which spontaneously breaks the crystalline symmetry in its superconducting state. This state can be observed, for example, by thermodynamic or upper critical field experiments in which a magnetic field is rotated with respect to the crystalline axes. The corresponding physical quantity then directly reflects the symmetry of the order parameter. We present a study on the superconducting upper critical field of the Nb-doped topological insulator NbxBi2Se3 for various magnetic field orientations parallel and perpendicular to the basal plane of the Bi2Se3 layers. The data were obtained by two complementary experimental techniques, magnetoresistance and DC magnetization, on three different single crystalline samples of the same batch. Both methods and all samples show with perfect agreement that the in-plane upper critical fields clearly demonstrate a two-fold symmetry that breaks the three-fold crystal symmetry. The two-fold symmetry is also found in the absolute value of the magnetization of the initial zero-field-cooled branch of the hysteresis loop and in the value of the thermodynamic contribution above the irreversibility field, but also in the irreversible properties such as the value of the characteristic irreversibility field and in the width of the hysteresis loop. This provides strong experimental evidence that Nb-doped Bi2Se3 is a nematic topological superconductor similar to the Cu- and Sr-doped Bi2Se3.
Similar content being viewed by others
Introduction
The search for topological superconductors, which support Majorana bound states as low energy excitations, is one of the central topics of current research.1,2,3,4,5 This is because of the fact that Majorana bound states are non-Abelian particles that have potential applications in engineering in the form of topologically protected qubits for quantum computation.6,7,8 A promising approach to the realization of topological superconductors is to use s-wave superconductors to induce superconducting pairing on topological insulators9 or systems with strong Rashba spin–orbit coupling.10,11,12,13,14,15,16,17,18 This results in effective p-wave topological superconductors which support Majorana fermions.
Importantly, as shown by many experimental groups recently, topological insulators such as Bi2Se3 can become superconducting when doped by metals such as Cu, Sr and Nb.19,20,21,22,23,24,25 Due to the non-trivial topology in the normal state band structures, the nature of pairing in these superconducting states has attracted much interest. In particular, it was proposed that Cu-doped Bi2Se3 could be a topological superconductor with odd parity pairing, which belongs to the Au representation of the D3d point group.26 There are Majorana surface states associated with these superconducting phases that should cause zero-bias conductance peaks in tunneling experiments.21 However, the zero-bias conductance peak found in an early experiment on CuxBi2Se3 is missing in more surface sensitive scanning tunneling experiments.27
On the other hand, recent measurements on Cu-doped and Sr-doped Bi2Se3 observed that the in-plane three-fold rotational symmetry is spontaneously broken into a two-fold rotational symmetry below the superconducting transition temperature.28,29,30,31 This spontaneous breaking of rotational symmetry can be explained if the superconducting phase is in the nematic phase, which belongs to the two-component Eu representation of the point group.32,33
Interestingly, the Eu representation, which is a two-dimensional representation, allows another topological superconducting phase, which spontaneously breaks the time-reversal symmetry. This phase is a nodal Weyl superconductor that supports Majorana arcs on the surfaces.33,34,35,36,37 It was proposed by Qiu et al.25 that Nb-doped Bi2Se3 spontaneously breaks time-reversal symmetry below T c. The Nb-doped case may be special because of the finite magnetic moments of the Nb atoms intercalated in the van der Waals gap between the Bi2Se3 layers,25 which may enhance this Weyl superconducting phase.34 On the other hand, other recent experiments on Nb-doped Bi2Se3, including torque magnetometry,24 penetration depth measurements,38,39 and Andreev reflection spectroscopy,40 suggested that the system is in the nematic phase. However, only the torque experiments were directly probing the in-plane anisotropy, but the measurement were carried out in the irreversible regime and the results are difficult to interpret. In order to settle this issue we have measured the upper critical fields for magnetic fields applied in different directions in the basal plane, using magnetoresistance and DC magnetization measurements, and found a strong evidence of a two-fold rotational symmetry below T c. The two-fold symmetry is further reflected in the DC magnetization value of the initial branch of the hysteresis loop after zero-field cooling, in the reversible thermodynamic contribution above the irreversibility field, as well as in the irreversible properties, such as the width of the hysteresis loop at a fixed magnetic field value. Our work thus provides further evidence that Nb-doped Bi2Se3 is in the odd-parity nematic superconducting phase. Due to the large superconducting volume fraction in Nb-doped Bi2Se3 compared to the Cu- and Sr-doped cases, Nb-doped Bi2Se3 can be an ideal material to investigate the topological properties of this nematic phase.
Results
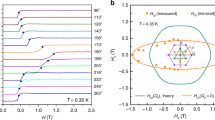
The electric resistivity of Nb0.25Bi2Se3 (Sample 1) in zero magnetic field shows a superconducting transition in form of a sharp drop with onset at 3.2 K (see inset of Fig. 1). In Fig. 1 we show magnetoresistance data taken at fixed temperature of 0.34 K for different directions of in-plane magnetic fields varying over more than 180°. A significant angular variation of the field-driven transition can be seen. The resistive increase occurs at ~ 0.4 T for orientations around 0°, and is shifted to higher fields until the field of the midpoint approximately doubles with a value exceeding 1.4 T peaking at ±90°. To define the upper critical field transition we used different criteria to determine characteristic fields from the data at which for each angle a certain fixed percentage of the normal state resistance is reached: 50, 75 and 90%. The so defined characteristic fields are presented in Fig. 2 as a function of the in-plane magnetic field orientation. The inset shows the same data in form of a polar plot. Centered at 0° a broad and rounded minimum is observed, while sharp peaks occur at ±90°. No signature of the three-fold crystalline symmetry is obvious. The data is dominated by a pronounced two-fold symmetry, which is completely in contradiction with the crystalline symmetry. Note that the normal state resistance above the upper critical field does not show any variation for the different in-plane orientations of the magnetic field, thus suggesting an isotropic normal state within the trigonal basal plane. The superconductivity thus appears to be nematic, and the in-plane angular dependence of the resistive transition is almost identical to what has been observed for SrxBi2Se3, 30 although the upper critical field is clearly lower in Nb0.25Bi2Se3.
Magnetoresistance of Nb0.25Bi2Se3 as a function of in-plane magnetic field orientation. All data were taken at T = 0.34 K. For clarity, offsets have been added to all data (except at −90°). The orientation of the magnetic field applied strictly parallel to the Bi2Se3 basal plane is marked on the right axis. The additional dots mark the points at which the magnetoresistance reaches 75% of the normal state resistance. Inset: zero-field resistivity showing the superconducting transition with onset at 3.2 K
Upper critical field as a function of the in-plane magnetic field orientation of Nb0.25Bi2Se3. The data was determined from the magnetoresistance data in Fig. 1. The critical fields were estimated according to various criteria when the magnetoresistance reaches 50% (squares), 75% (filled circles) and 90% (triangles) of the normal state value. The continuous line corresponds to a theoretical model of nematic superconductivity with a single domain, while the dashed line considers an additional minority phase of ~ 10% volume fraction rotated by 60°, thus causing the additional bump at ~ 30° (see text for details). θ = 0 is the normal direction to the mirror plane within the trigonal basal plane. The inset shows the same data in form of a polar plot
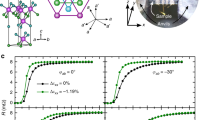
In Fig. 3 we show a selection of magnetization hysteresis loop data of a second sample (Sample 2), which are taken at T = 1.8 K for different directions of the magnetic field applied parallel to the basal plane. The anisotropy of the upper critical field is evident. The data at the 101° angle have a clearly higher critical field, while the data at 0° show the lowest value as seen in the main figure showing an enlargement of the reversible regime of the magnetization above the irreversibility field H irr below which the hysteresis loops open. Data were collected under identical conditions at 0, 48, 101, 138, 180, 228, 281 and 318 degrees. For clarity, we have only included angles from −43° (318°) to 101°, while larger angles follow exactly the same trend. The anisotropy is also reflected in the irreversible part, where the largest hysteresis occurs at 0° and the smallest at ~ 101°, as shown for the two extreme angles (0° and 101°) in the inset.
Magnetization hysteresis loops of Nb0.25Bi2Se3 for a selection of magnetic field directions in the basal plane. The data were recorded at T = 1.8 K. The inset shows complete hysteresis loops for 0° and 101°, while the main graph shows an enlargement of the region in the range near H c2 for −43° (317°), 0°, 48° and 101°. The dotted line marks the normal state limit
In Fig. 4a we show the dependence of the upper critical field H c2 on the orientation of the magnetic field vector in the basal plane over the full 360-degree range, and in Fig. 4b the irreversibility fields H irr below which flux pinning becomes efficient, thus causing an opening of the hysteresis loops. Both data show a similar two-fold anisotropy. Upper critical field data of two different samples (Sample 2 and Sample 3) have been included in Fig. 4a, both of which show a very similar trend. In Fig. 4c, we show the magnetization value for Sample 2 from the initial zero-field-cooled branch of the magnetization loop at 8.5 mT, where the minimum associated with the lower critical field H c1 occurs. The dependence on the in-plane direction of the magnetic field also reflects the two-fold anisotropy of the superconducting phase. The inset shows the corresponding magnetization data at 0° and 101°. The same field angular dependence is observed in the reversible part of the DC magnetization above the irreversibility field (Fig. 4d), which represents the purely thermodynamic contribution to the DC magnetization, and thus provides a bulk thermodynamic proof of nematic superconductivity.
Dependence of Hc2, Hirr and the magnetization value on the in-plane magnetic field direction. a H c2 determined from the magnetization hysteresis loops at 1.8 K for Sample 2 (empty circles) and Sample 3 (empty stars). The two additional datapoints (filled stars) are taken from magnetoresistance data of Sample 3 as a check of consistency between the two methods. b Irreversibility fields H irr of Sample 2 below which the hysteresis loops open. c Dependence of the magnetization in the initial zero-field-cooled branch at 8.5 mT on the in-plane orientation of the magnetic field (Sample 2). The inset shows the corresponding magnetization data for 0° and 101°. c Dependence of the thermodynamic contribution of the magnetization taken in the reversible regime above H irr at 0.32 T on the in-plane orientation of the magnetic field (Sample 2). The lines in all graphs correspond to a theoretical model of nematic superconductivity (see text for details)
In Fig. 5. we show the temperature dependence of the upper critical field transition as obtained from the magnetoresistance for three different characteristic directions: for in-plane fields along −90° (Fig. 5a) and 0° (Fig. 5b), where the maximum and minimum of the critical field is observed, respectively, and for magnetic fields applied perpendicular to the Nb0.25Bi2Se3 basal plane (Fig. 5c). The resulting phase diagram (Fig. 5d), compiled using the field at which the magnetoresistance reaches 90% of the normal state value, shows that the two-fold in-plane anisotropy is present at all temperatures below the superconducting transition temperature, although it becomes weaker with increasing temperature.
Anisotropy of the temperature dependence of Hc2 of Nb0.25Bi2Se3. Magnetic field applied in-plane along −90° a and 0° b within the trigonal basal plane, and applied perpendicular to the Bi2Se3 basal plane c. Panel d shows the corresponding magnetic field phase diagram. Here the criterion where the resistivity reaches 90% of the normal state resistance was chosen
Discussion
Both, the magneto-resistive and the magnetic upper critical field transitions of NbxBi2Se3 show a clear two-fold symmetry instead of the expected three-fold symmetry, which suggests that the superconducting state of NbxBi2Se3 is nematic and spontaneously breaks the three-fold crystalline symmetry, in perfect agreement with what has been observed for CuxBi2Se3 28,29 and SrxBi2Se3.30,31 Since the metal dopants are intercalated in the van der Waals gap between the Bi2Se3 layers, it has been argued that 1D clustering in the form of stripe like ion patters could be responsible for the two-fold anisotropy.30 While we cannot rule this out from our experiments, the fact that the normal state resistance does not show any dependence on the in-plane field direction does make this scenario unlikely, and rather suggests a true nematic superconducting state. The superconducting Nb-doped Bi2Se3 thus appears to be very similar to CuxBi2Se3 28,29 and SrxBi2Se3,30 ,31 despite it has been shown that the Nb ions exhibit finite magnetic moments.25 The latter can be seen in the form of a small paramagnetic contribution in the normal state magnetization in Fig. 6, which follows a Curie Weiss behavior as illustrated by the fit. The paramagnetic behavior is observed down to T c without any sign of magnetic ordering.
The pronounced two-fold symmetry observed in in-plane upper critical fields can be explained consistently within the Ginzburg-Landau theory and could be identified as a signature of the nematic superconducting state. It is known that for a nematic superconductor at zero field, the two-component order parameter \(\left( {\eta _1,\eta _2} \right)\) is pinned to \(\eta _0\left( {1,0} \right)\) or \(\eta _0\left( {0,1} \right)\) by sixth order terms in the Ginzburg-Landau free energy that arise from the crystalline anisotropy. Ref. 41 predicts that the in-plane upper critical field \(H_{c2}\) of a nematic superconductor would have a six-fold symmetry, assuming that the nematic pinning effect on \(\left( {\eta _1,\eta _2} \right)\) is negligible in the field-driven phase transition. This assumption, however, only applies if the superconducting phase is sufficiently close to the normal phase. The experimental data of \(H_{c2}\) show a strong two-fold symmetry up to the 90% criterion, as shown in Fig. 2, indicating that to the precision of the experiment, the pinning effect on the \(\left( {\eta _1,\eta _2} \right)\) maintains. Based on these facts, we assume that \(\left( {\eta _1,\eta _2} \right)\)is pinned to \(\eta _0\left( {1,0} \right)\) or \(\eta _0\left( {0,1} \right)\) and solve the corresponding Ginzburg-Landau equation. In this way one obtains the in-plane upper critical field as
Here \(\Gamma\) indicates the in-plane anisotropy in the superconducting phase and the angle Θ is defined such that Θ = 0 is the normal direction to the mirror plane. The details of the derivation from the Ginzburg-Landau theory can be found in the Methods section. The above formula well describes the two-fold symmetry in the in-plane upper critical fields of nematic superconductors. With this formula, we fit the experimentally measured in-plane upper critical field of Sample 1 as shown by the lines in Fig. 2, with fitting parameters: Γ = 3.32 and H c2(0) = 1.44 T.
Of the three single crystals of different shapes we measured (see Methods section for details), no apparent correlation was observed with the orientation of the macroscopic crystal shape. In fact, the demagnetization factors for our samples with the parallel field orientation are hardly expected to have any significant influence on the in-plane variation of the magnetic properties. Indeed, the initial ZFC branch of the magnetization for the different in-plane field orientations all fall on top of each other (see inset of Fig. 4c). In any case, the upper critical field is not affected by the demagnetization factor and provides a solid proof of the nematic superconducting state. The theoretical model fits out data very well and further supports the existence of nematic superconductivity in NbxBi2Se3. One open question is what determines the direction of the two-fold superconducting gap function within the three-fold symmetry of the basal plane. The gap function appears pinned along one of three identical crystalline directions and remains there during the entire experiment, even if the sample is brought into the normal state in between. Which direction the anisotropic superconducting gap function chooses likely only depends on microscopic details of the single crystal, such as surface roughness, defects, micro-cracks or local stress. However, the in-plane anisotropy for Sample 1 (64% at 1.8 K) is much greater than that for Sample 2 and 3 (18% and 21% at 1.8 K, respectively). This is not an artifact from the different methods used since the upper critical field values for Sample 3 from magnetization and magnetoresistance agree very well (see Fig. 4a). This difference can only be understood if there are different domains in these samples in which the 2-fold gap function is pinned along different crystalline directions and partially cancel the macroscopic anisotropy. Sample 1 is probably almost a mono-domain sample with large anisotropy factor Γ = 11, which causes the particularly sharp maxima in Fig. 2. Otherwise, additional smaller peaks should occur at ±30°. In fact, there is actually a small bump at +30°, which could indicate an ~ 10% volume fraction of a minority domain rotated by 60° with respect to the majority domain. This is illustrated by the dashed line in Fig. 2, which represents a fit that takes into account such an admixture of a minority phase. However, this feature is very weak and at the resolution limit. For samples 2 and 3, the maxima are much broader, which is taken into account in the fitting curve in Fig. 4a by considering a smaller anisotropy factor Γ = 1.44. For a small Γ value, the cosine term dominates the angular in-plane H c2 dependence. In the presence of minority domains, the individual sinusoidal terms would basically merge together without causing any side maxima in the angular H c2 dependence, but reducing the overall variation. What causes the strong variation in Γ is unclear, but Sample 1 is likely to be of higher crystalline quality, as evidenced by its shiny flat surfaces. Sample 2 and 3 have rather rough surfaces, and surface roughness, along with internal crystal irregularities, could lead to a broadening of the 2-fold gap structure, in addition to the occurrence of minority domains.
To summarize, we have carefully determined the field-angular dependence of the magnetoresistive and the magnetic upper critical field transitions of Nb-doped Bi2Se3 with 0.25 Nb atoms per formula unit. The in-plane angular dependence when the field is applied strictly parallel to the Nb0.25Bi2Se3 basal plane shows a pronounced two-fold symmetry very similar to CuxBi2Se3 28,29 and SrxBi2Se3,30,31 and thus provides further experimental evidence from two different experimental methods that nematic superconductivity also exists in NbxBi2Se3. The two-fold symmetry is also reflected in the absolute value of the magnetization (for example in the initial curve of the hysteresis after zero-field cooling, as well as in the thermodynamic reversible regime above the irreversibility field) and in the anisotropic characteristics, such as the width of the hysteresis loop and the irreversibility field. The in-plane anisotropy of the upper critical field can be perfectly fitted with a theoretical model32,33,41 for nematic superconductivity. The existence of magnetic moments without macroscopic magnetic order could provide a way of tuning the superconducting properties, e.g., by varying the Nb concentration or by introducing different magnetic ions with stronger moments to see whether the unconventional pairing symmetry of the superconducting state could be dramatically altered by the internal magnetic fields.
Methods
The detailed growth method and characterization of Nb0.25Bi2Se3 in the single crystalline form can be found in refs. 24,25. Measurements have been done on three different samples of dimensions and geometry as illustrated in Fig. 7. The magnetic field directions of 0 and 90 degrees are marked by arrows.
Electrical transport
We carried out standard four-probe resistance measurements in a 15 T magnet cryostat with 3He variable temperature insert. The single crystal (Sample 1) of approximate dimensions 1.7 × 0.8 × 0.2 mm3 and demagnetization factor of ~ 0.7 was mounted on an Attocube ANR51/RES precise nano rotary stepper with resistive encoder, which provides a millidegree precision with integrated angle measurement. The current was injected along the long direction (Fig. 7) and coincided with the magnetic field direction for an in-plane field orientation of 225°. The Nb0.25Bi2Se3 basal plane was aligned precisely parallel to the magnetic field and the rotator allowed us to rotate the sample so that the magnetic field direction could be varied within the basal plane. In a subsequent separate measurement, we oriented the same device with the basal plane perpendicular to the field to derive the complete temperature dependence of upper critical fields along different crystalline directions. The measurements were performed with both an AC and a DC method to check for consistency. All resistance data shown in this article were measured with the AC technique with an alternating current of 0.1 mA amplitude and a frequency of 17.7 Hz using a Keithley 6221 AC/DC current source. The signal was sent through a bandpass filter and measured by a SRS830 digital lock-in amplifier.
DC magnetization
The DC magnetization was measured on two single-crystalline samples of 847 μg (Sample 2) and 4.5 mg (Sample 3) mass with a Quantum Design Vibrating Sample SQUID magnetometer (VSM-SQUID). The measurement was deliberately performed on samples of different shapes and sizes to eliminate any effects of the sample shape and quality. The shape of Sample 2 can be approximately described as a rectangular prism of 1.5 × 0.8 × 0.1 mm3 with demagnetization factor of ~ 0.8. Sample 3 yields an approximately cylindrical shape of ~ 1 mm diameter and 0.3 mm height with demagnetization factor of ~ 0.6. The samples were first cleaved to obtain a shiny and very flat bottom plane of the crystal, which was then fixed with vacuum grease to the flat surface of a quartz sample holder so that the basal plane of Nb0.25Bi2Se3 was oriented parallel to the applied magnetic field in all experiments. The vacuum grease allowed us to rotate the sample at room temperature by carefully pushing the sample with a toothpick into the desired angular orientation characterized by the in-plane angle θ, carefully avoiding a contact with the grease. The sample holder was then inserted into the magnetometer. The sample was cooled to 1.8 K in zero field and a full hysteresis loop with maximum field of ±1 T was measured. Subsequently, the sample was heated above T c and again cooled in zero field to repeat the measurement, but with reverse field direction to obtain data at an angle of θ + 180°. After this measurement cycle, the sample holder was removed, the sample was rotated by ~ 45°, and the procedure was repeated until the full 360° angle range was obtained. The exact angular orientations were determined with an accuracy of 0.5° from a photograph by measuring the angle between a linear edge of the sample with respect to the sample holder using a protractor. The absolute values of the in-plane field direction θ are chosen so that θ = 0 is the normal direction to the mirror plane within the trigonal basal plane.
Theory
In the Ginzburg-Landau theory for a superconductor, the phenomenological free energy density f tot is the sum of a homogeneous term f hom and a gradient term f D so that f tot = f hom + f D. The superconducting Nb x Bi2Se3 has a crystal structure belonging to the D3d point group. In the Eu representation, the homogeneous part of the free energy density up to the sixth order has the form33
where A, B 1, 2 and C 1, 2, 3 are the Ginzburg-Landau coefficients and \(\eta _ \pm = \eta _1 \pm i\eta _2\). Here A ∝ (T−T c), B 2 > 0 for the nematic phase, and C 1 is responsible for pinning the nematic state from \(\left( {\eta _1,\eta _2} \right)\) to \(\eta _0\left( {1,0} \right)\) or \(\eta _0\left( {0,1} \right)\). Defining the covariant derivative \(D_i = - i\partial _i - qA_i\), where \(A_i\) is the electromagnetic vector potential and q = 2e, the gradient term, f D can be written as41
where we set i = x, y, and a = 1, 2, and J 1, J 2, J 3, J 4, J 5 are the phenomenological Ginzburg-Landau coefficients. Here \(\varepsilon _{\left( {i,j} \right),\left( {a,b} \right)}\)is the anti-symmetric tensor and \(\tau _{\left( {ij} \right),\left( {ab} \right)}^{\left( x \right),\left( z \right)}\) is the Pauli matrix acting on the index (ij) and (ab). In the presence of the in-plane magnetic field \(\vec H = H\left( {\cos \Theta ,\sin \Theta ,0} \right)\) with the gauge \(\vec A = Hz\left( {\sin \Theta , - \cos \Theta ,0} \right)\), the covariant derivative is defined as \(D_x = - i\partial _x + 2eHz\sin \Theta\), \(D_y = - i\partial _y - 2eHz\cos \Theta\) and \(D_z = - i\partial _z\). The linearized Ginzburg-Landau equation can be derived from the functional variation with respect to the pairing field \(\frac{{\delta f_{{\mathrm{tot}}}}}{{\delta \eta _a^ * }} = 0\) so that
where \(\vec \eta = \left( {\eta _1,\eta _2} \right)^T\) and \(D_ \bot = D_x\sin \Theta - D_y\cos \Theta\). The parallel covariant derivative terms\(\left( {D_x\sin \Theta - D_y\cos \Theta } \right)\eta _a\) are dropped. We set \(\left( {\eta _1,\eta _2} \right)\) to be \(\eta _0\left( {0,1} \right)\) (which is a fully gapped state31,32) and the coupled Ginzburg-Landau equations reduce to one equation
The right-hand side of Eq. 5 can be treated as the Hamiltonian for a simple Harmonic oscillator, and the in-plane upper critical field can be obtained from its ground state energy level
Here the dimensionless parameter \(\Gamma ^2 = \frac{{J_1J_3 - J_3J_4}}{{J_1J_3 + J_3J_4 - J_5^2}}\) indicates the in-plane anisotropy and \(H_{c2}\left( 0 \right) = - \frac{A}{{2e\sqrt {J_1J_3 + J_3J_4 - J_5^2} }}\). The in-plane upper critical field has the same form for the nematic phase \(\eta _0\left( {1,0} \right)\) while the definitions of related parameters are different.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Wilczek, F. Majorana returns. Nat. Phys. 5, 614–618 (2009).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Qi, X. L. & Zhang, S. C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Alicea, J. New directions in the pursuit of Majorana fermions in solid state systems. Rep. Prog. Phys. 75, 076501 (2012).
Beenakker, C. W. J. Search for Majorana fermions in superconductors. Annu. Rev. Con. Mat. Phys. 4, 113–136 (2013).
Kitaev, A. Y. Unpaired Majorana fermions in quantum wires. Phys. Usp. 44, 131–136 (2001).
Ivanov, D. A. Non-Abelian statistics of half-quantum vortices in p-wave superconductors. Phys. Rev. Lett. 86, 268–271 (2001).
Alicea, J., Oreg, Y., Refael, G., von Oppen, F. & Fisher, M. P. A. Non-Abelian statistics and topological quantum information processing in 1D wire networks. Nat. Phys. 7, 412–417 (2011).
Fu, L. & Kane, C. L. Superconducting proximity effect and Majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 100, 096407 (2008).
Lutchyn, R. M., Sau, J. D. & Sarma, S. D. Majorana fermions and a topological phase transition in semiconductor–superconductor heterostructures. Phys. Rev. Lett. 105, 077001 (2010).
Alicea, J. Majorana fermions in a tunable semiconductor device. Phys. Rev. B 81, 125318 (2010).
Oreg, Y., Refael, G. & von Oppen, F. Helical liquids and Majorana bound states in quantum wires. Phys. Rev. Lett. 105, 177002 (2010).
Lee P. A. Proposal for creating a spin-polarized p x + ip y state and majorana fermions. Preprint at https://arxiv.org/abs/0907.2681 (2009).
Sato, M. & Fujimoto, S. Topological phases of noncentrosymmetric superconductors: edge states, Majorana fermions, and the non-abelian statistics. Phys. Rev. B 79, 094504 (2009).
Potter, A. C. & Lee, P. A. Multichannel generalization of Kitaev’s Majorana end states and a practical route to realize them in thin films. Phys. Rev. Lett. 105, 227003 (2010).
Mourik, V. et al. Signatures of Majorana fermions in hybrid superconductor–semiconductor nanowire devices. Science 336, 1003–1007 (2012).
Deng, M. T. et al. Anomalous zero-bias conductance peak in a Nb–InSb nanowire–Nb hybrid device. Nano Lett. 12, 6414–6419 (2012).
Das, A. et al. Zero-bias peaks and splitting in an Al–InAs nanowire topological superconductor as a signature of Majorana fermions. Nat. Phys. 8, 887–895 (2012).
Hor, Y. S. et al. Superconductivity in CuxBi2Se3 and its implications for pairing in the undoped topological insulator. Phys. Rev. Lett. 104, 057001 (2010).
Kriener, M., Segawa, K., Ren, Z., Sasaki, S. & Ando, Y. Bulk superconducting phase with a full energy gap in the doped topological insulator CuxBi2Se3. Phys. Rev. Lett. 106, 127004 (2011).
Sasaki, S. et al. Topological superconductivity in CuxBi2Se3. Phys. Rev. Lett. 107, 217001 (2011).
Liu, Z. et al. Superconductivity with topological surface state in SrxBi2Se3. J. Am. Chem. Soc. 137, 10512–10515 (2015).
Shruti, V. K., Maurya, P., Neha, P., Srivastava, P. & Patnaik, S. Superconductivity by Sr intercalation in the layered topological insulator Bi22Se3. Phys. Rev. B 92, 020506(R) (2015).
Asaba, T. et al. Rotational symmetry breaking in a trigonal superconductor Nb-doped Bi2Se3. Phys. Rev. X 7, 011009 (2017).
Qiu, Y. et al. Time reversal symmetry breaking superconductivity in topological materials. Preprint at https://arxiv.org/abs/1512.03519 (2015).
Fu, L. & Berg, E. Odd-parity topological superconductors: theory and application to CuxBi2Se3. Phys. Rev. Lett. 105, 097001 (2010).
Levy, N. et al. Experimental evidence for s-wave pairing symmetry in superconducting CuxBi2Se3 single crystals using a scanning tunneling microscope. Phys. Rev. Lett. 110, 117001 (2013).
Yonezawa, S. et al. Thermodynamic evidence for nematic superconductivity in CuxBi2Se3. Nat. Phys. 13, 123–126 (2017).
Matano, K., Kriener, M., Segawa, K., Ando, Y. & Zheng, G.-Q. Spin-rotation symmetry breaking in the superconducting state of CuxBi2Se3. Nat. Phys. 12, 852–854 (2016).
Pan, Y. et al. Rotational symmetry breaking in the topological superconductor SrxBi2Se3 probed by upper-critical field experiments. Sci. Rep. 6, 28632 (2016).
Du, G., Li, Y.-F., Schneeloch, J., Zhong, R. D., Gu, G.-D., Yang, H., Lin, H. & Wen, H.-H. Superconductivity with two-fold symmetry in topological superconductor SrxBi2Se3. Sci. China Phys. Mech. Astron. 60, 037411 (2017).
Fu, L. Odd-parity topological superconductor with nematic order: application to CuxBi2Se3. Phys. Rev. B 90, 100509(R) (2016).
Venderbos, J. W. F., Kozii, V. & Fu, L. Odd-parity superconductors with two-component order parameters: nematic and chiral, full gap, and majorana node. Phys. Rev. B 94, 180504(R) (2016).
Yuan, N. F. Q., He, W.-Y. & Law, K. T. Superconductivity-induced ferromagnetism and weyl superconductivity in Nb-doped Bi2Se3. Phys. Rev. B. 95, 201109 (2017).
Meng, T. & Balents, L. Weyl superconductors. Phys. Rev. B 86, 054504 (2012).
Yang, S. A., Pan, H. & Zhang, F. Dirac and Weyl superconductors in three dimensions. Phys. Rev. Lett. 113, 046401 (2014).
Lu, B., Yada, K., Sato, M. & Tanaka, Y. Crossed surface flat bands of weyl semimetal superconductors. Phys. Rev. Lett. 114, 096804 (2015).
Smylie, M. P. et al. Evidence of nodes in the order parameter of the superconducting doped topological insulator NbxBi2Se3 via penetration depth measurements. Phys. Rev. B 94, 180510(R) (2016).
Smylie, M. P. et al. Robust odd-parity superconductivity in the doped topological insulator NbxBi2Se3. Phys. Rev. B 96, 115145 (2017).
Kurter, C. et al. Andreev reflection spectroscopy of topological superconductor candidate NbxBi2Se3. Preprint at https://arxiv.org/abs/1707.08516 (2017).
Venderbos, J. W. F., Kozii, V. & Fu, L. Identification of nematic superconductivity from the upper critical field. Phys. Rev. B 94, 094522 (2016).
Acknowledgements
R.L. thanks U. Lampe for technical support. This work was supported by grants from the Research Grants Council of the Hong Kong Special Administrative Region, China (SBI15SC10, HKUST3/CRF/13G and C6026-16W). Y.S.H. acknowledges support from National Science Foundation DMR-1255607. K.T.L. acknowledges the financial support from the Croucher Foundation and the Dr. Tai-Chin Lo Foundation.
Author information
Authors and Affiliations
Contributions
J.S. performed the electrical transport experiments with the help of C.-W.C. R.L. performed the magnetization measurements. S.H.L. and Y.S.H. did the sample preparation and characterization. J.S., R.L., C.-W.C and H.Z. analyzed the data. W.Y.H., N.F.Q.Y. and K.T.L. did the theoretical interpretation and fitting of the data. R.L. and K.T.L. contributed to the original idea and supervised the project. J.S., R.L., K.T.L., W.Y.H. and N.F.Q.Y. wrote the manuscript. All authors contributed to the discussion and data interpretation and have read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Shen, J., He, WY., Yuan, N.F.Q. et al. Nematic topological superconducting phase in Nb-doped Bi2Se3 . npj Quant Mater 2, 59 (2017). https://doi.org/10.1038/s41535-017-0064-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-017-0064-1
This article is cited by
-
Two-component nematic superconductivity in 4Hb-TaS2
Nature Communications (2024)
-
Emerging symmetric strain response and weakening nematic fluctuations in strongly hole-doped iron-based superconductors
Nature Communications (2021)
-
Superconducting properties and topological nodal lines features in centrosymmetric Sn0.5TaSe2
Nano Research (2021)
-
Identify the Nematic Superconductivity of Topological Superconductor Pd\(_x\)Bi\(_2\)Te\(_3\) by Angle-dependent Upper Critical Field Measurement
Journal of Superconductivity and Novel Magnetism (2021)
-
Z3-vestigial nematic order due to superconducting fluctuations in the doped topological insulators NbxBi2Se3 and CuxBi2Se3
Nature Communications (2020)