Abstract
In second-order quantum phase transitions from magnetically ordered to paramagnetic states at T = 0, tuned by pressure or chemical substitution, a quantum critical point is expected to appear with critical behavior manifesting in the slowing down of spin fluctuations in the paramagnetic state and a continuous development of the order parameter in the ordered state. Quantum criticality is discussed widely as a possible driving force for unconventional superconductivity and other exotic phenomena in correlated electron systems. In the real world, however, quantum critical points and quantum criticality are often masked by a preceding first-order transition and/or the development of competing states. Pressure tuning of the itinerant-electron helical magnet MnSi is a well-known example of the suppression of a quantum critical point due to a first-order phase transition and resulting destruction of the ordered state. Utilizing muon spin relaxation experiments, here we report that 15% Fe-substituted (Mn,Fe)Si exhibits completely different behavior with pressure tuning, including the restoration of second-order quantum critical behavior and a quantum critical point at p QPC ~ 21–23 kbar, which coincides with the T = 0 crossing point of the extrapolated phase boundary line of pure MnSi. This result is quantitatively consistent with the recent theory of itinerant-electron ferromagnets by Sang, Belitz, and Kirkpatrick, who argued that disorder would restore a quantum critical point which is otherwise hidden by a first-order transition.
Similar content being viewed by others
Introduction
A first-order phase transition is associated with a discontinuous change of the order parameter (such as staggered magnetization), while a second-order transition involves the slowing down of critical fluctuations at the phase boundary and a continuous development of the order parameter from zero in the disordered phase to non-zero values in the ordered phase. Whereas thermal phase transitions are achieved by changing the temperature T, quantum phase transitions occur when the phase boundary is crossed at T → 0 by tuning nonthermal parameters, such as pressure or chemical composition. Quantum phase transitions have become an important topic in modern condensed matter physics. In addition to unconventional superconductors,1,2,3 heavy-fermion systems,4, 5 and Mott transition systems,6 extensive studies of thermal and quantum phase transitions have been conducted on itinerant-electron magnets, theoretically by Moriya7 and Belitz, Kirkpatrick and others,8, 9 and experimentally in MnSi tuned by temperature10 and pressure11,12,13 and in (Mn,Fe)Si,14 (Sr,Ca)RuO3 13 and (Sc,Lu)3In15 by chemical substitution and/or pressure.
MnSi is a representative metallic magnet which has a small ordered moment (~0.4 Bohr magneton per formula unit at T = 0) and a helical spin structure below a relatively low ordering temperature T C ~ 29 K in ambient pressure. From 1970–1990, the thermal transition in this system was studied by neutron scattering16 and muon spin relaxation (MuSR),17 which observed second-order-like critical behavior and paramagnetic spin fluctuations, consistent with predictions of the self-consistent renormalization theory7 developed for metallic ferromagnets. In 1997, Pfleiderer et al.11 discovered that the magnetic order of MnSi can be suppressed by the application of hydrostatic pressure beyond a critical pressure p c ~ 15 kbar, as shown in the phase diagram of Fig. 1a. MnSi has a hierarchy of energy scales, starting from the strongest ferromagnetic exchange interaction J, followed by the Dzyaloshinskii–Moriya interaction D which leads to helical spin correlations, and finally the crystal anisotropy I, which stabilizes the moment direction. The interplay of these energy scales, combined with the B20 crystal structure that lacks inversion symmetry, results in a variety of novel phenomena, including a Skyrmion lattice state in applied magnetic fields below T C 18, 19 and chiral spin fluctuations/Skyrmion liquid above T C .20,21,22
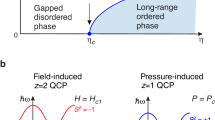
Temperature–pressure phase diagrams of MnSi and (Mn,Fe)Si. a Temperature versus hydrostatic pressure phase diagram in pure MnSi and (Mn,Fe)Si in zero magnetic field. Open triangles represent the magnetic transition temperature determined by resistivity and susceptibility,11 gray-colored triangles from MuSR,13 and closed triangles represent the onset temperature of diffuse scattering “partial order” in quasi-elastic neutron scattering (QNS).12 The yellow-colored region (S) represents the helically ordered phase, the green colored region (P) indicates phase separation between ordered and paramagnetic phases, and the blue colored region (D) indicates slow, dynamic, diffusive helical spin fluctuations.12, 13 The small pink region (HF) above T C has helical spin fluctuations leading to a weakly first-order thermal transition. Red circles indicate the transition temperature for (Mn0.85Fe0.15)Si, determined by the present MuSR measurements. b–d Expected phase diagrams of itinerant-electron magnets according to theories by Belitz, Kirkpatrick and co-workers8, 9, 34,35,36,37 with the effect of disorder. TCP denotes the tri-critical point and QCP denotes the quantum critical point. The blue line indicates a second-order phase transition, while the red line shows a first-order phase transition. The first-order line in b intersects the p axis vertically at T = 0. The MuSR results for pure MnSi13 can be viewed as a manifestation of case c, and the present results for (Mn,Fe)Si as case d. The recent MuSR results on V2O3 40 may correspond to c, while the second-order phase transition in a highly random percolation network may be related to d
At temperatures 1–2 K above T C in ambient pressure, the spin correlation length ξ in MnSi becomes comparable to the pitch length l ~ 18 nm of the helical spiral, transforming the ferromagnetic critical behavior into helical spin fluctuations. The process of stabilizing the helical fluctuations by I leads to weakly first-order behavior at T C , as detected by neutron scattering (chiral fluctuations),10, 20,21,22 transport (sharp peaking in the T-derivative of the resistivity),11, 23 and specific heat23 (a shoulder above T C with a sharp peak at T C ). In MuSR studies, this feature is manifest as a discontinuous change of the order parameter below T C 24 and a modification of the critical exponent above T C .25, 26 The spin correlation time τ, however, keeps increasing with decreasing T even in this narrow temperature region above T C ,22 resulting in a peak of the muon spin relaxation rate 1/T 1 at T C .13, 17, 25, 26 This narrow temperature region above T C is illustrated by the pink region (HF) in Fig. 1a.
As the pressure is increased above p*, the ac susceptibility of a clean specimen (with residual resistivity ratio RRR = 243) was observed to exhibit a clearly discontinuous change at T C ,11 indicating a first-order thermal transition. The ordering temperature, which decreases nearly linearly with p from ambient pressure up to p*, acquires a steeper slope at p* < p < p c ,11 while neutron scattering12 observes a diffuse signal (initially called ‘partial order’) below the extrapolated T C (p) line (broken line in Fig. 1a). MuSR measurements with pressure13 showed that the “partial order”, seen in the blue region “D” in Fig. 1a, is a manifestation of slow dynamic spin fluctuations with the time scale τ ~ 10−10–10−11 s.
Zero-field nuclear magnetic resonance (NMR)27 and MuSR13, 28 measurements in MnSi found that the magnitude of the static internal magnetic field at T → 0, which is proportional to the ordered moment size, exhibits only a slight reduction with increasing p at p* < p < p c , followed by an abrupt reduction to zero above p c . This discontinuous change of the order parameter at p c clearly demonstrates the first-order character of the quantum phase transition in MnSi tuned with pressure p. Signatures of phase separation between ordered and disordered volumes were reported from MuSR13 and NMR27 experiments at p* < p < p c , corresponding to the green region “P” in Fig. 1a. Neutron scattering observed a continuous variation of the helical Bragg peak intensity I B at T = 2 K near p c .29, 30 This, however, cannot be taken as evidence for a second-order quantum transition, since I B ∝ S 2 × V ord is proportional to the product of the square of the ordered moment S and the volume fraction V ord of the ordered region, and neutron studies cannot distinguish between contributions from S and V ord . In the case of MnSi, the continuous variation of I B is due to the discontinuous change of S at p c multiplied by the continuous development of V ord below p = p c .
Results
In this paper, we report MuSR measurements of (Mn,Fe)Si with 15% Fe in ambient and hydrostatic pressure. We find that this Fe-doped sample exhibits drastically different behavior than the above-mentioned results in pure MnSi. Although both (Mn,Fe) substitution14 and the application of pressure suppress the magnetic order in MnSi, these two tuning methods could be different, as the former varies both the carrier density and lattice constant,31 while the latter mainly alters the band width, in a way reminiscent of filling and band-width control in Mott transitions.6 As shown in Fig. 1a, iron substitution suppresses T C in (Mn0.85Fe0.15)Si to T C ~ 4 K at ambient pressure. At the genral purpose decay-channel (GPD) instrument of the Paul Scherrer Institut (PSI), we carried out MuSR measurements in zero field (ZF) and longitudinal field (LF) on a single crystal specimen of (Mn0.85Fe0.15)Si in hydrostatic pressure p using a standard piston pressure cell and a 3He cryostat.32 Details of the MuSR method, crystal preparation, and the pressure cell are described in the “Methods” section. The static magnetic order in (Mn0.85Fe0.15)Si survives up to p c = 21–23 kbar with clear signatures of dynamic critical behavior, a continuous evolution of the ordered moment size, and a full magnetically ordered volume fraction. These behaviors demonstrate the restoration of second-order thermal and quantum phase transitions due presumably to substantial disorder caused by the (Mn,Fe) substitution.
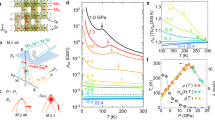
Figure 2a–e displays representative zero-field (ZF) MuSR time spectra from (Mn,Fe)Si in ambient and applied pressure. These spectra include contributions not only from the sample but also from the pressure cell, which corresponds to about 45% of the total signal amplitude. The ZF MuSR spectra under ambient pressure (Fig. 2a) show fast relaxation below T C ~ 4 K and a strongly overdamped oscillation at 0.25 K. This indicates that the static internal magnetic field of (Mn0.85Fe0.15)Si has a broad distribution, in contrast to that of MnSi, which may be attributed to spatially random (Mn,Fe) substitutions. The spectra at p = 11.7 kbar in Fig. 2b, in the vicinity of p* for pure MnSi, are qualitatively the same as at ambient pressure, but without any clear oscillation observed down to T = 0.25 K. As shown in Fig. 2c, d, fast relaxation is observed in (Mn,Fe)Si even at p = 16.4 and 19.3 kbar, i.e., pressures higher than the critical pressure p c for pure MnSi. The fast relaxation in ZF at low temperature finally disappears at p = 23 kbar (Fig. 2e). The ZF relaxation at T = 0.25 K for p = 0–19.3 kbar can be substantially restored (decoupled) by the application of a small LF = 500 G, as shown in Fig. 2f, which confirms that static magnetic order is the origin of the observed ZF relaxation at low temperatures. The absence of fast relaxation in ZF at p = 23 kbar also confirms that muons landing in the pressure cell do not make significant contributions to the observed temperature dependence of the MuSR spectra.
MuSR time spectra observed in a single crystal specimen of (Mn0.85Fe0.15)Si. a–e Results in zero field at hydrostatic pressures p = 0.0, 11.7, 16.4, 19.3 and 23.0 kbar. f Results with a longitudinal field (LF) of 500 G applied parallel to the initial spin direction of the incident positive muons. The lines represent fits to the relaxation functions given by Eqs. (1)–(4) in the main text. More details can be found in the Supplementary Information. Panel e shows that static magnetic order disappears at p = 23 kbar, and that the effect of the pressure cell on the observed spectra is minimal. Panel f demonstrates that the fast relaxation seen at low temperature is due to static random local fields, which can be decoupled by the application of LF
We analyzed the ZF-MuSR spectra P(t) with the formula
where A sp , A cl , and A bg correspond to the initial asymmetries for the signals from the sample, pressure cell, and pressure-independent background, respectively. These parameters are fixed for all temperatures, and fixed for pressures in a given pressure cell (we used two cells), with typical contributions close to 45, 45, and 10% each of the total asymmetry signal. The time evolution of the signal from the sample, G sp (t) was fitted with the form
with f mag representing the volume fraction of the magnetically ordered region, and 1/T 1 the dynamic muon spin relaxation rate. Among a few possible choices of functional forms for representing the effect of static internal fields from the ordered moments, the best fit to the observed data were obtained by the generalized Kubo–Toyabe function G gkt (t)33
where σ denotes the static relaxation rate proportional to the ordered moment size, and β is the stretching power, ranging between 1.1–1.4, which was fixed independent of temperature for a given pressure. More details of the data analysis in ZF, including estimates of the cell and background contributions, are presented in the Supplementary Information (SI) together with the fitted results of each parameter for all the pressure and temperature values.
Figure 3a shows the temperature dependence of the magnetic volume fraction V M = f mag in (Mn,Fe)Si. Although the thermal transition exhibits a small spread/rounding indicated by a gradual increase of V M, magnetic order occupies the full volume at T = 0.25 K for p = 0–19.3 kbar, and the system becomes fully paramagnetic at p = 23 kbar. Figure 3b shows that the width σ of the static internal field, proportional to the order parameter, exhibits a nearly linear increase with decreasing temperature below T C . The values of V M and σ at T = 0.25 K are shown in Fig. 3c as a function of pressure p. These results include clear signatures of second-order quantum critical behavior: an abrupt reduction of V M from 1.0 to zero across p ~ 20 kbar, and a continuous increase of σ (T → 0) from 0 to nonzero values as p is decreased below the critical pressure. The pressure-tuned destruction of the magnetic order with a continuous reduction of the order parameter σ in (Mn,Fe)Si, shown in Fig. 3c, is in clear contrast to the “volume-wise destruction” of magnetic order in pure MnSi, shown in Fig. 3e. The former is expected for second order quantum criticality, and the latter for first-order quantum evolution.
Static local field, ordered volume fraction and dynamic relaxation rate in (Mn,Fe)Si and MnSi. a–d: MuSR results for (Mn0.85Fe0.15)Si in ZF (a–c) and in LF = 500 G (d). a Temperature and pressure dependence of the magnetically ordered volume fraction determined by ZF-MuSR. b Static muon spin relaxation rate σ, which is proportional to the ordered moment size. c Pressure dependence of the magnetic volume fraction and the static spin relaxation rate at T ~ 250 mK (lowest temperature achievable by the 3He cryostat), demonstrating the continuous evolution of the order parameter σ from zero in the paramagnetic phase to finite values in the ordered phase, and the development of static magnetic order in the full volume fraction in the ordered phase at low temperatures. d Dynamic relaxation rate 1/T 1 observed in LF = 500 G. The sharp peak of 1/T 1 is a signature of dynamic critical behavior expected for a second-order thermal phase transition. e, f Results of a previous MuSR study13 in pure MnSi, replotted here to be contrasted to those of (Mn,Fe)Si. Panel e demonstrates that the ordered moment size, proportional to the ZF MuSR frequency, changes discontinuously at the phase boundary, while the magnetic volume fraction changes continuously. Panel f demonstrates that the dynamic critical behavior is suppressed with increasing pressure and completely eliminated at p = 12.7 kbar for MnSi. This behavior in MnSi is characteristic of first-order quantum evolution
To study the effects of dynamic spin fluctuations in (Mn,Fe)Si, we also performed MuSR measurements in LF = 500 G, and analyzed the data with
using the fit time range of 0.1–2 μs, as illustrated in Fig. 2f for low temperatures. For the data analysis in LF, the parameter A sp was allowed to vary as a temperature-dependent parameter representing different degrees of LF decoupling for different magnitudes σ of the static internal field below T C . As shown in Fig. 3d, 1/T 1 exhibits a clear maximum due to critical slowing down of spin fluctuations around T C for all the pressure values between p = 0–19.3 kbar. Qualitatively similar behavior can also be seen in the variation of 1/T 1 in ZF shown in the SI, and the magnitude of 1/T 1 exhibits a dependence on LF similar to the known results for pure MnSi at ambient pressure.26 The prominent peaks in the plot of 1/T 1 vs T for (Mn,Fe)Si over a wide pressure range in Fig. 3d is in a clear contrast to the pressure dependence of 1/T 1 observed in pure MnSi13 re-plotted here in Fig. 3f, where the peaking of the relaxation rate was suppressed with increasing pressure and completely eliminated at p ~ p*. The peaking of 1/T 1 is an additional signature of the restoration of second-order thermal critical behavior in (Mn0.85Fe0.15)Si.
Discussion
The results for pure MnSi and the more disordered (Mn0.85Fe0.15)Si are consistent with the theories of Belitz, Kirkpatrick and co-workers.8, 9, 34,35,36,37 Considering the effect of a negative m 3 ln(m) term of the magnetization m (order parameter) on the free energy in itinerant ferromagnets due to soft modes and particle-hole excitations, they proposed that the second-order thermal transition in ferromagnets is replaced by a first-order transition at a tri-critical point (TCP) when approaching the quantum critical point (QCP), as illustrated in Fig. 1b.8, 9 This behavior matches the results in pure MnSi, except for the effect of helical spin correlations, which adds a weakly first-order character to the thermal transition before the TCP is reached, and phase separation at p* < p, which cannot be expected for ideally thermodynamic behavior in systems without disorder.36, 37 In their recent studies,36, 37 quenched disorder was suggested as a possible origin for the phase separation observed in pure MnSi. This situation is illustrated in Fig. 1b, c. Furthermore, they also recently predicted34, 35 that the effect of disorder weakens the negative m 3 ln(m) term, leading to a reduction of the region between the TCP and QCP, and finally leads to a disappearance of the TCP as illustrated in Fig 1d. The present results showing the restoration of second-order quantum criticality in (Mn0.85Fe0.15)Si are qualitatively consistent with this prediction.
The residual resistivity of the present single-crystal specimen of (Mn0.85Fe0.15)Si is estimated to be 60–100 μΩ cm, from the published results38 for (Mn,Fe)Si made by the same research group with comparable Fe concentration. This puts the present system into the “highly disordered” region in refs. 34, 35, where a restoration of second-order criticality is expected. For this region, the order parameter at T = 0 is predicted to show asymptotic critical behavior as m(Δp) ∝ (Δp)βQCP as a function of pressure Δp = (p QCP − p), with the quantum critical exponent β QCP = 2/(d − 2 + λ) = 1.2 as shown in Table 1 of ref. 35 (third row of the fourth column, “Dirty (pre-asymptotic)”, with dimension d = 3 and the effective exponent λ = 2/3). The present results fit well to the relation σ (T → 0) ∝ (Δp)βQCP with the order-parameter exponent β QCP = 1.10 for p c = 23.0 kbar, and 0.80 for p c = 21.0 kbar. Although the present set of data cannot determine the value of beta more precisely due to uncertainty in the critical pressure p c at the QCP, these values are unquestionably different from the power β QCP = 0.5 (second column of Table 135) expected in calculations without including large disorder. To this extent, the present results are quantitatively consistent with the theoretical prediction. Further theoretical studies, however, may be helpful to discuss the possible effect of the Dzyaloshinskii–Moriya interaction and to elucidate any relationship with different theoretical approaches.39
Strong sensitivity of first-order behavior to disorder in pure MnSi was also found in ac-susceptibility measurements, which showed a discontinuous T dependence of the susceptibility at T C for p* < p < p c for a very pure specimen with RRR = 243, while a continuous gradual change was observed for a less clean specimen with RRR = 40, as demonstrated in Figs. 5 and 7 in ref. 11 A MuSR study28 of a sample of MnSi with RRR = 40 reported first-order quantum evolution but no phase separation at T → 0, in apparent disagreement with ref. 13 which found both first order evolution and phase separation at p* < p < p c in a cleaner crystal with RRR ~ 100. This difference may be related to a general tendency toward second-order behavior in less clean systems.
The red filled circles in the phase diagram of Fig. 1a mark the critical temperature T C of (Mn0.85Fe0.15)Si as determined from the peak position of 1/T 1 . It is quite interesting that the QCP of (Mn0.85Fe0.15)Si at p ~ 21–23 kbar coincides with the extrapolation of the linear T C (p < p*) trend of MnSi to T = 0. Thus, the (Mn,Fe) substitution restored second-order quantum criticality and even revealed the QCP in pure MnSi hidden by the first-order thermal and quantum transitions for p > p*.
We note that phase separation of paramagnetic and magnetically ordered volumes is observed in many systems, including substitution-tuned (Sr,Ca)RuO3 13 and RENiO3 (RE = rare earth), pressure-tuned V2O3,40 and high-T c cuprates with substitution and pressure tuning.41, 42 It may seem counter-intuitive to imagine that greater disorder could help restore sharp features and second-order criticality near a QCP, since disorder often “smears out” sharp features. On the other hand, percolation networks and dilute-alloy spin glasses, which involve large amounts of disorder, exhibit second-order critical behavior, such as that illustrated in Fig. 1d. It would then be highly interesting to determine whether the present observation of the role of disorder for an itinerant-electron system could be extended to the cases of quantum phase transitions in other metallic ferromagnets,43 Mott transitions systems, insulating magnets, and geometrically frustrated and/or low dimensional magnetic system.
Previous studies of quantum criticality in (Mn,Fe)Si have been performed mostly in ambient pressure with Fe composition as the tuning parameter.14, 44, 45 Near the disappearance of magnetic order, which occurs for Fe concentrations of approximately 0.16–0.19, a continuous reduction of the ordered moment size was noticed. This suggests a tendency toward second-order criticality, consistent with the present results via pressure tuning. However, the present MuSR study provides some additional benefits beyond these earlier studies, in particular by involving only a fixed amount of disorder in a single sample, independently distinguishing the effects of pressure on moment size and volume fraction, and providing information on both the static order parameter and the dynamic critical behavior. Furthermore, the unexpected finding that the critical pressure for Fe 15% (Mn,Fe)Si is even larger than that of pure MnSi demonstrates that pressure and substitution tune the electronic structure not in a simple additive manner but in a more complicated way.
In conclusion, we demonstrated that the first-order thermal and quantum phase transitions in pure MnSi near QCP are replaced by second-order thermal and quantum transitions in (Mn0.85Fe0.15)Si. The QCP in MnSi, hidden in the pure compound by a preceding first-order quantum phase transition, is now revealed in (Mn,Fe)Si through the restorative effects of disorder. Up to now, most of the evidence for magnetic second-order quantum criticality have been based on magnetization, transport, or neutron scattering experiments, which reflect volume-integrated properties insensitive to phase separation. Together with the previous work13 in pure MnSi, the present work in (Mn,Fe)Si has demonstrated the importance of using a volume-sensitive probe for elucidating quantum phase transitions. This work also demonstrates that for studying possible roles of disorder, quantum tuning with hydrostatic pressure and a fixed amount of disorder provides unambiguous information, in contrast to the uncertainty arising from varying degrees of disorder inherent in substitution tuning.
Methods
In positive MuSR (μ+SR) measurements, spin-polarized positive muons are implanted in the specimen for condensed matter physics studies. In the case of measurements under applied pressure at PSI, a high-momentum (60–125 MeV/c) muon beam generated from pions decaying in flight must be used so that the muons can penetrate the pressure cell and reach the specimen. After losing its kinetic energy within 1 ns after implantation, the muon stops at an interstitial site in the specimen (or the wall of the pressure cell), and usually rests there with a mean lifetime of 2.2 μs until it decays and emits a positron. The angular distribution of positron emission is maximal along the muon spin direction at the time of decay. For the dc muon beam facilities at PSI and TRIUMF, beam collimation and logic circuits ensure that only one muon exists within the specimen at a given time. The time spectra of positron events F(t) and B(t), where t is the time after muon implantation, are recorded by two sets of counters, labeled forward (F) and backward (B), that are placed in front of and behind the sample with respect to the initial muon spin direction. After normalizing the solid-angle factors between the two counters, the ratio [B(t) − F(t)]/[F(t) + B(t)] represents the time evolution of muon spin polarization AG(t), where A = 0.2–0.3 is the initial decay asymmetry and G(t) denotes the muon spin relaxation function. In the present paper, the time spectra AG(t) are displayed in Fig. 2. A discussion of relaxation functions in various systems can be found in ref. 33, while technical details of the measurements under applied pressure at PSI are described in ref. 32.
In MuSR, muons stopping in different environments contribute additively to the observed asymmetry AG(t). In the present study, out of total initial asymmetry of A ~ 0.27, the contributions from the specimen, pressure cell wall, and other backgrounds were approximately 0.12, 0.12, and 0.03, respectively, as described in the Supplementary Information (SI). This implies that about 40% of the total signal came from the specimen. Similarly, if there are two different phases in the specimen, the signals from different regions (phases) can be observed as different additive responses. In the present analyses, the observed signal from the specimen was decomposed into a signal from the magnetically ordered volumes with the temperature-dependent initial asymmetry A 1 (T) and a signal from the paramagnetic volume with A 2 (T), as shown in the SI. This allows a determination of the ordered volume fraction f mag = A 1 /(A 1 + A 2 ), which is shown in Fig. 3a, c, e in the main text, for various temperatures T and pressures p.
The single crystal of (Mn,Fe)Si used in the present study was grown at Karlsruhe Institute of Technology by the vertical Bridgman technique from a stoichiometric mixture of Mn (4N), Fe (2N5+), and Si (5N) in an Al2O3 crucible. A second crucible filled with pieces of Zr sponge was placed underneath the Bridgman crucible to getter gaseous impurities inside the working tube during crystal growth. Results for single crystals made by the same method as the present specimens were reported in ref. 38. The size of the present single crystal and the ratio of the signals from the specimen and the pressure cell wall are described in the SI.
Data availability
The data of the MuSR measurements discussed in this work were obtained using the GPD instrument at PSI. They can be accessed at the PSI web site http://musruser.psi.ch/cgi-bin/SearchDB.cgi, as Run # 706 – # 1175 of the year 2009.
References
Uchida, S. High Temperature Superconductivity: The Road to Higher Critical Temperature (Springer Verlag, 2015).
Keimer, B., Kivelson, S. A., Norman, M. R., Uchida, S. & Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015).
Uemura, Y. J. Commonalities in phase and mode. Nat. Mater 8, 253–255 (2009).
Mathur, N. D. et al. Magnetically mediated superconductivity in heavy fermion compounds. Nature 394, 39–43 (1994).
Pfleiderer, C. Superconducting phases of f-electron compounds. Rev. Mod. Phys. 81, 1551–1624 (2009).
Imada, M., Fujimori, A. & Tokura, Y. Metal-insulator transitions. Rev. Mod. Phys. 70, 1039–1263 (1998).
Moriya, T. Spin Flucutations in Itinerant Electron Magnetism (Springer-Verlag, 1985).
Belitz, D., Kirkpatrick, T. R. & Vojta, T. First order transitions and multicritical points in weak itinerant ferromagnets. Phys. Rev. Lett. 82, 4707–4710 (1999).
Belitz, D., Kirkpatrick, T. R. & Rollbühler, J. Tricritical behavior in itinerant quantum ferromagnets. Phys. Rev. Lett. 94, 247205 (2005).
Janoschek, M. et al. Fluctuation-induced first-order phase transition in Dzyaloshinskii-Moriya helimagnets. Phys. Rev. B 87, 134407 (2013).
Pfleiderer, C., McMullan, G. J., Julian, S. R. & Lonzarich, G. G. Magnetic quantum phase transition in MnSi under hydrostatic pressure. Phys. Rev. B 55, 8330–8338 (1997).
Pfleiderer, C. et al. Partial order in the non-Fermi-liquid phase of MnSi. Nature 427, 227–231 (2004).
Uemura, Y. J. et al. Phase separation and suppression of critical dynamics at quantum phase transitions of MnSi and (Sr1−xCax)RuO3. Nat. Phys. 3, 29–35 (2007).
Bauer, A. et al. Quantum phase transitions in single-crystal Mn1−xFexSi and Mn1−xCoxSi: Crystal growth, magnetization, ac susceptibility, and specific heat. Phys. Rev. B 82, 064404 (2010).
Svanidze, E. Non-fermi liquid behavior close to a quantum critical point in a ferromagnetic state without local moments. Phys. Rev. X 5, 011026 (2015).
Ishikawa, Y., Noda, Y., Uemura, Y. J., Majkrzak, C. F. & Shirane, G. Paramagnetic Spin Fluctuations in the Weak Itinerant Ferromagnet MnSi. Phys. Rev. B 31, 5884–5893 (1985).
Hayano, R. S. et al. Observation of the T/(T − Tc) divergence of the μ+ spin relaxation rate in MnSi near Tc. Phys. Rev. Lett. 41, 1743–1746 (1978).
Muehlbauer, S. et al. Skyrmion lattice in a chiral magnet. Science 323, 915–919 (2009).
Yu, X. Z. Real-space observation of a two-dimensional skyrmion crystal. Nature 465, 901–904 (2010).
Roessli, B., Böni, P., Fischer, W. E. & Endoh, Y. Chiral fluctuations in MnSi above the curie temperature. Phys. Rev. Lett. 88, 237204 (2002).
Grigoriev, S. V. et al. Critical fluctuations in MnSi near TC: A polarized neutron scattering study. Phys. Rev. B 72, 134420 (2005).
Pappas, C. et al. Magnetic fluctuations and correlations in MnSi: Evidence for a chiral skyrmion spin liquid phase. Phys. Rev. B 83, 224405 (2011).
Stishov, S. M. & Petrova, A. E. Itinerant helimagnet MnSi. Phys. Uspekhi 54, 1117–1130 (2011).
Takigawa, M. et al. Positive muon spin rotation and relaxation in the helically ordered state of MnSi. J. Phys. Soc. Jpn. 49, 1760–1767 (1980).
Yaouanc, A. et al. Testing the self-consistent renormalization theory for the description of the spin-fluctuation modes of MnSi at ambient pressure. J. Phys. Condens. Matter 17, 129–135 (2005).
Gat-Maruleanu, I. M. et al. Field dependence of muon spin relaxation rate in MnSi. Phys. Rev. Lett. 90, 157201 (2003).
Yu, W. et al. Phase inhomogeneity of the itinerant ferromagnet MnSi at high pressures. Phys. Rev. Lett. 92, 086403 (2004).
Andreica, D., Dalmas de Réotier, P., Yaouanc, A., Amato, A. & Lapertot, G. Absence of magnetic phase separation in MnSi under pressure. Phys. Rev. B81 060412(R) (2010).
Fåk, B., Sadykov, R.A., Flouquet, J., Lapertot, G. Pressure dependence of the magnetic structure of the itinerant electron magnet MnSi. J. Phys. Condens. Matter 17, 1635–1644 (2005).
Pfleiderer, C., Reznik, D., Pintschovius, L. & Haug, J. Magnetic Field and Pressure Dependence of Small Angle Neutron Scattering in MnSi. Phys. Rev. Lett. 99, 156406 (2007).
Manyala, N. et al. Large anomalous Hall effect in a silicon-based magnetic semiconductor. Nat. Mater. 3, 255–262 (2004).
Khasanov, R. et al. High pressure research using muons at the Paul Scherrer Institute. High Press Res. 36, 140–166 (2016).
Uemura, Y. J. µSR relaxation functions in magnetic materials. In Muon Science: Muons in Physics, Chemistry and Materials Proceedings of the Fifty First Scottish Universities Summer School in Physics, (eds Lee, S. L., Kilcoyne, S. H. & Cywinski, R.) 85–114 (Inst. of Physics Publishing, 1999).
Sang, Y., Belitz, D. & Kirkpatrick, T. R. Disorder Dependence of the Ferromagnetic Quantum Phase Transition. Phys. Rev. Lett. 113, 207201 (2014).
Kirkpatrick, T. R. & Belitz, D. Exponent relations at quantum phase transitions with applications to metallic quantum ferromagnets. Phys. Rev. B 91, 214407 (2015).
Kirkpatrick, T. R. & Belitz, D. Third law of thermodynamics and the shape of the phase diagram for systems with a first-order quantum phase transition. Phys. Rev. Lett. 115, 020402 (2015).
Kirkpatrick, T. R. & Belitz, D. Stable phase separation and heterogeneity away from coexistence curve. Phys. Rev. B 93, 144203 (2016).
Chapman, B. J., Grossnickle, M. G., Wolf, T. & Lee, M. Large enhancement of emergent magnetic fields in MnSi with impurities and pressure. Phys. Rev. B 88, 214406 (2013).
Krüger, F., Karahasanovic, U. & Green, A. G. Quantum order-by-disorder near criticality and the secret of partial order in MnSi. Phys. Rev. Lett. 108, 067003 (2012).
Frandsen, B. A. et al. Volume-wise destruction of the antiferromagnetic Mott insulating state through quantum tuning. Nat. Commun. 7, 12519 (2016).
Kojima, K. M. et al. Superfluid density and volume fraction of static magnetism in stripe-stabilized La1.85−yEuySr0.15CuO4. Physica B36, 316–320 (2003).
Guguchia, Z. et al. Tuning the static spin-stripe phase and superconductivity in La2−xBaxCuO4 (x = 1/8) by hydrostatic pressure. New J. Phys. 15, 093005 (2013).
Brando, M., Belitz, D., Grosche, F. M. & Kirkpatrick, T. R. Metallic quantum ferromagnets. Rev. Mod. Phys. 88, 025006 (2016).
Franz, C. et al. Real-space and reciprocal-space berry phases in the Hall effect of Mn1−xFexSi. Phys. Rev. Lett. 112, 186601 (2014).
Glushkov, V. V. et al. Scrutinizing Hall effect in Mn1−xFexSi: Fermi surface evolution and hidden quantum criticality. Phys. Rev. Lett. 115, 256601 (2015).
Acknowledgements
The authors would like to thank Dietrich Belitz, Andy Millis and Christian Pfleiderer for useful discussions, and Benjamin Frandsen for editing English of the manuscript. Work at Columbia was supported by the US National Science Foundation grants DMR-1105961, DMR-1436095 (DMREF grant), DMR-1610633, OISE-0968226 (PIRE), the Japan Atomic Energy Agency Reimei project during 2011–17, the Friends of University of Tokyo Inc. D.R. at the University of Colorado Boulder was supported by the US DOE, Office of Basic Energy Sciences, Materials Sciences and Engineering Division under Contract No. DE-SC0006939, and M.L. was supported by the US DOE, Basic Energy Sciences, Materials Sciences and Engineering Division under Award Number DE-SC0006888. The MuSR measurements were performed at the Swiss Muon Source (SμS), PSI, Villigen, Switzerland.
Author information
Authors and Affiliations
Contributions
Y.J.U. and D.R. conceived the experiment, T.W. prepared the single crystal specimen, T.G. designed the pressure cell, T.G., C.J.A., Y.J.U., A.H., D.R., A.M., R.K., and E.M. performed MuSR measurements at PSI, M.L. performed resistivity measurements on relevant crystals, and T.G. and Y.J.U. performed data analysis and drafted the manuscript, which was then revised and agreed upon by all the authors.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Goko, T., Arguello, C.J., Hamann, A. et al. Restoration of quantum critical behavior by disorder in pressure-tuned (Mn,Fe)Si. npj Quant Mater 2, 44 (2017). https://doi.org/10.1038/s41535-017-0049-0
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-017-0049-0
This article is cited by
-
Multiple quantum phase transitions of different nature in the topological kagome magnet Co3Sn2−xInxS2
npj Quantum Materials (2021)
-
Unconventional Hund metal in a weak itinerant ferromagnet
Nature Communications (2020)
-
Magnetic field-temperature phase diagram of multiferroic (NH4)2FeCl5·H2O
npj Quantum Materials (2019)