Abstract
Ferroelectric vortex in multiferroic materials has been considered as a promising alternative to current memory cells for the merit of high storage density. However, the formation of regular natural ferroelectric vortex is difficult, restricting the achievement of vortex memory device. Here, we demonstrated the creation of ferroelectric vortex-antivortex pairs in BiFeO3 thin films by using local electric field. The evolution of the polar vortex structure is studied by piezoresponse force microscopy at nanoscale. The results reveal that the patterns and stability of vortex structures are sensitive to the poling position. Consecutive writing and erasing processes cause no influence on the original domain configuration. The Z4 proper coloring vortex-antivortex network is then analyzed by graph theory, which verifies the rationality of artificial vortex-antivortex pairs. This study paves a foundation for artificial regulation of vortex, which provides a possible pathway for the design and realization of non-volatile vortex memory devices and logical devices.
Similar content being viewed by others
Introduction
Topological vortices are ubiquitous in condensed matter physics and are highly involved in the correlated properties of superconductor, superfluid, ferroelectric material, and ferrimagnet.1,2,3 The structures derived from the interaction among vortices are associated with various fascinating phenomena. It is acknowledged that vortices are insensitive to disturbance, as a result, information bits can store in vortex state with little cross-talk between adjacent bits.4 Besides, the individual magnetic skyrmions can be created and annihilated, which demonstrates the potential for topological charge in future information-storage concepts.5
In condensed matter systems, the study of topological defects is crucial to ferroic materials, such as the conductivity of domain walls,6,7,8 and the electric field manipulating and imprinting of ferroelectric domains into ferromagnets.9, 10 In recent years, a wide spectrum of ferroelectric vortices have been investigated in the forms of nanostructure, epitaxial thin film, oxide superlattice and single crystal, in which the vortices are widespread in ferroelectric systems with perovskite structure.11,12,13,14,15,16,17 Balke et al. explored the physical properties of single vortex and observed the enhanced electrical conductivity at ferroelectric vortex core in BiFeO3(BFO).13 Moreover, the geometric configuration and evolution of domains in hexagonal REMnO3 (RE: rare earth) were studied by Cheong et al., by whom the distribution rule of domains with graph theory was disclosed.18,19,20,21 Tang et al. and Yadav et al. produced the polar vortex arrays in PbTiO3 by making use of tensile strain, as well as charge, orbital and lattice degrees of freedom.17, 22 Based on these studies, fundamental cognition regarding to ferroelectric vortex and the surrounding domain configuration have been formed. However, it is still crucial how to manufacture the polar vortex structures that fit practical requirement, which is the main barrier towards vortex devices. To resolve this problem, we develop a method to create vortex-antivortex pairs in BFO thin films by scanning probe microscopy (SPM) with voltage pulse. With reliable 3D-Piezoresponse Force Microscopy (3D-PFM)23, 24 images of polar vortex network, the correlativity among the vortex cores, domains, and the surrounding domain walls are discussed. The relaxation and erasability of polar vortex structures are also investigated.
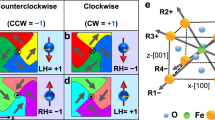
In this paper, we define two kinds of in-plane ferroelectric vortices (shown in Fig. 1a). When the line segment OE, as indicated in the Fig. 1a, rotates clockwise around the vortex core, a series of domains passed by OE are named with 1, 2,…, n. The in-plane polarizations of these domains are marked in rectangular coordinate successively. If the clockwise rotation of the in-plane polarization is required when it varies from “1” to “n”, this structure is termed as vortex (winding number 1). Otherwise, if the counterclockwise rotation is required, it is termed as antivortex (winding number −1).
Ferroelectric domains in BiFeO3 films. a Schematic of vortex and antivortex structures. b Schematic of PFM detection of (001) BFO/SRO/STO. c Possible directions of the polarization vector P (solid lines) and switching paths in a (001)-oriented BFO thin film. d x-Lateral Piezoelectric Force Microscope (x-LPFM) (d1), y-LPFM(d2), Vertical Piezoelectric Force Microscope (VPFM) (d3) images, and 3D domain pattern (d4) of the same region. x and y indicate slow scan axis and fast scan axis, respectively. The dark blue ring represents the poling position. White, light gray, dark gray, and black regions represent for domains with in-plane polarization along [1−1], [−1−1], [11], and [−11] direction, respectively
Epitaxial BFO films with the thickness about 60 nm were grown on (001) single-crystal SrTiO3 (STO) substrates by pulsed laser deposition, as schematically illustrated in Fig. 1b. An epitaxial SrRuO3 (SRO) with a thickness of 50 nm was deposited as the bottom electrode for electrical-contact purpose.25,26,27 The original out-of-plane polarizations point downward, resulting in four possible polarization directions (Fig. 1c) and dominating 71o domain configuration in BFO film. With a given downward polarization state, four switching directions are feasible under an external electric field along the out-of-plane direction. For example, the initial polarization state [1−1−1] can switch to [−111], [1−11] or two equivalent states [111] and [−1−11], through 180, 71, or 109° switching, respectively.
Results
To begin with, a 2 × 2 μm square region was scanned along two orthometric directions (x and y), respectively, in PFM mode under +5 V tip bias at 35 kHz. Fig. d1–d3, VPFM, x-LPFM, and y-LPFM represent out-of-plane (OP), in-plane-x, and in-plane-y PFM signals, respectively. A 3D ferroelectric domain configuration can therefore be depicted in Fig. 1d, in which white, light gray, dark gray, and black regions represent domains with in-plane polarizations along [1−1], [−1−1], [11], and [−11] directions, respectively. There are no dark gray ([11]) domains in Fig. 1d, because this kind of domains is very rare in our sample, which might be determined by the special substrate stress. Moreover, the dark blue arrows indicate the direction of in-plane polarization of original domains.
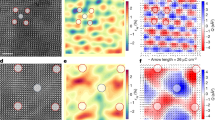
Subsequently, we applied −10 V, 20 s tip electrical pulse near the 71° domain wall marked with blue circle in Fig. 1d4. The domain structure after 1 h is shown in Fig. 2a, where the yellow dashed square box represents the region influenced by tip field. The PFM signals along three orthometric directions are disclosed in Fig. 2 a1–2 a3. The VPFM image (Fig. 2 a3) indicates the OP polarizations around the poling center switch from downward (dark) to upward (light), while the inner part remains the original OP polarization possibly due to the tip-induced back-switching related to the charge injection around the domain wall.28, 29 Figure 2 a4 shows the complex ferroelectric domain structure derived from Fig. 2 a1–2 a3, where the dashed (solid) arrows denote the domains with upward (downward) OP polarizations, the yellow (light blue) arrows denote the in-plane polarization around the vortex (anti-vortex), and the red and green lines represent 71 and 109° domain walls, respectively. It can be seen that the switched region is an annular region (about 1.7 × 104 nm2) surrounded by 109° domain walls. Interestingly, six vortices emerge in polarized area, and each domain is surrounded by 2n (n = 1,2,3) vortices (n pairs of vortex and anti-vortex). Meanwhile, each domain wall links a vortex to an anti-vortex, in other words, the domain wall is a type of special line which originates from a vortex and end at an anti-vortex. Similar vortex feature has also been observed in the natural vortex network,17, 18, 22, 30,31,32 which suggests the artificial vortex network may present as the natural ones.
Evolution of the polar vortex structure. a–c PFM images and 3D domain patterns of the same region at 1, 5, and 22 h after poling, respectively. The yellow squares indicate the polarized regions. The red (blue) lines represent the 71o (109o) domain walls. The yellow (light blue) arrows indicate vortex (antivortex) structure. The dotted (dash) arrows mean the OP polarization of the domain is downward (upward)
To study the evolution of vortex domain, the vortex structures are obtained after 5 and 22 h, as displayed in Fig. 2b and Fig. 2c, respectively. The main characteristic of domain evolution can be described in the following three aspects. (1) The morphology of domains changes. The black domain (marked with “2” in Fig. 2 a4), originally through the polarization area, breaks up into two relatively small domains (“2 m” and “2k”); while the smallest “1” domain ([−1−1]) merges with the original “A” domain ([−1−1]). The neck area below the “2 m” domain gradually shrinks and finally separates from the original “C” domain, becoming a small island domain (“6”). (2) Polarized domain area shrinks. After 5 and 22 h, the switched domain area reduced to 1.26 × 104 nm2 and 7.53 × 104 nm2, respectively, which are smaller than that of 1.7 × 104 nm2 in Fig. 2 a4. It is generally acknowledged that the “back-switching” evolution is driven by local energy (stress and electrostatic energy). (3) Vortex cores are relatively stable. After 22 h, the average displacement of vortex cores is only about 18.5 nm, which is much smaller than the polarized area (about 105 nm). Although the domain morphology, polarized area and the position of vortex cores have changed more or less, the number and the winding number of vortex kept constant, which can be considered as topological invariants. In our experiments, the domain walls in polarized area are either 109o or 71o, where the stress concentrates.22, 33, 34 When four domain walls converge to form a vortex (antivortex), the stress around the vortex core could become a high barrier for any changes in domain structure.
To study the influence of the poling position on the patterns of polar vortex, a series of control experiments was conducted. The vortex structure written near domain wall (termed as P1 in Fig. 1d) has been studied above. Here, we investigate vortex structures at the center (P2 in Fig. 3a) and at the end of strip domain (P3 in Fig. 3 d5). Poling and measuring parameters in Fig. 3 we used are the same as that in Fig. 2. After 2 and 20 h, the vortex structures at P2 are illustrated in Fig. 3b and Fig. 3c, respectively, while a relatively stable vortex structure at P3 is shown in Fig. 3d. The main differences of the vortex structures are as follows. (1) Domain geometry. The geometry of polarized area depends on poling position. At P1, the polarized region is an annulus with a circular abnormal switched area in the center, while at P2 and P3, the polarized region becomes a full-filled circle. (2) Domain number. Five domains are produced at P1, whereas three and two domains are produced at P2 and P3, respectively. (3) Vortex number. The number of vortex is sensitive to the poling position. At P1, P2, and P3, three, two, and one pairs of vortex-antivortex are created, respectively. (4) Stability. At P2 and P3, the average displacement of vortex cores is about 10 nm which is smaller than that at P1 (18.5 nm). It is suggested that the relative instability of the vortex core at P1 is related to the abnormal area in the center of the polarized region.
Influence of poling position on polar vortex structure. a Original domain structure, with dark blue circle indicating the poling point. b, c Images of vortex structure 2 and 20 h after poling, respectively. d Vortex structure 30 h after poling at the end of strip domain, where the insert image shows the original domain structure and the blue circle indicates the poling position
Discussion
The main difference of domain structure and vortex number might be caused by the specific charge accumulation and energy state at different poling positions. The charge tends to accumulate at the domain wall, resulting in abnormal switched area under the external electric field because of the more charge injection. The more complex domain structure, the more domains involved, and more vortices would emerge. Additionally, polar vortex structure shows an obvious relaxation in some cases, which might be related to its complex structure. Although diverse vortex structures can be created in different places, there are some similarities among them. (1) The type and distribution of the domain walls. The 109o domain walls are distributed at the borders of polarized domains and normal domain, while the 71o domain walls concentrate in polarized region. (2) The topological characteristics of polar vortex structure. After relaxation, the area of vortex domain shrunk slightly, while the number of vortex-antivortex pairs and the winding number of vortices remain unchanged. Moreover, although vortex networks have various patterns, they could be described by the same simple mathematical formulas. Generally, the basic elements of a vortex network include domain (face) number F, domain wall (edge) number E, vortex (vertex) number V, connected degree γ, and the cycle number C. These variables can be connected as following: (for details of statistical analysis, see Supplementary Information, Sec. 1–4)
Where all of the variate are positive integers and V is even number.
The stability of the vortex with respect to polarization position is then carefully studied. In this part, the electrical write-rewrite ability and reproducibility are investigated because it is a crucial factor towards application of vortex network in electronic device. Figure 4 a1 depicts the PFM images of initial domain structures with white circle representing the poling position. After −10 V polarizing, a vortex structure is created in strip domain as exhibited in Fig. 4 a2. Then +8 V tip (scan rate 1 Hz) field is applied to depolarize the 200 × 200 nm square region marked by the white rectangle in Fig. 4 a2. After this erase operation, the vortex domain disappears and the strip domain almost completely restores to the original state (Fig. 4 a3). It suggests that the vortex domain can be repeatedly written without any effects on the original domain structure. The large-scale vortex network is indispensable for the memory devices based on vortex. Thus we try to create more vortices by PFM tip. After −10 V, 20 s tip pulse is applied at the two poling positions about 167 nm apart represented by two blue circles as shown in Fig. 4a, two similar vortex structures emerge in the original stripe domain. The domain structure is stable after 25 h (Fig. 4c), suggesting suitable-scale vortex network could be produced for practical applications.
Capacity of vortex structure to be memory device. a1 Original domain structure with white circle indicating the poling point. a2 Domain structure after polarized. a3 The domain structure after erase operation. b Original and c polarized domain pattern, with two-point polarization apart from 167 nm (+10 V DC, 20 s tip electrical pulse) poling condition
Graph theory is a powerful mathematical tool to understand the seemingly irregular pattern of domains in condensed matter physics, such as ferroelectric domains in hexagonal REMnO3 and chiral domain topology in FeXTaS2.18, 30,31,32 The graph theory can be also applied to analyze the artificial vortex network in trigonal BiFeO3. In our experiment, the domains’ IP polarization along [1−1], [−1−1], [11], and [−11] directions can be colored with yellow, blue, green, and red, respectively (Fig. 5a). Moreover, the 109o(71o) domain walls are represented by light yellow (light blue) lines and the vortex (antivortex) cores are represented by white (black) dots. Thus, from the perspective of graph theory, the BFO vortex network can be regarded as Z4 colorable in the sense that all domains can be colored with four (yellow, blue, green, and red) colors in a way that adjacent domains are colored in different colors (proper-colorable), and, for example, a yellow, (blue) domain is never surrounded by red (green) domains. Several proper-colorable 4-valent graphs with even number of vortices (vortices and antivortices) are shown in Fig. 5 b–h. We find the practical vortex structures correspond to these proper-colorable graphs. For example, the schematics of ferroelectric domain configurations of Fig. 2 a4, Fig. 3 b4, and Fig. 3 d4 are displayed in Fig. 5 b–d, respectively. Notably, a complex domain pattern can be composed by some simple “unit blocks”. For instance, Fig. 2 b4 is composed of Fig. 5e and Fig. 5g. Similarly, Fig. 2 c4 consists of Fig. 5f and Fig. 5g, and the vortex arrays produced by the method in Fig. 4c is composed by the unit blocks (Fig. 5c), as shown in Fig. 5h. Moreover, the possible structure of arbitrary pairs vortex in BFO can be studied by using unit blocks (see the Supplementary Information, Sec. 4). This method could also be applied in other kind of materials, which provides a new route to investigate the topological properties of domains.
In summary, this study demonstrates the vortex-antivortex pairs can be created by electric field and further reveals the stability and topological properties of artificial vortex network are similar to the natural vortex network. In addition, the vortex network is rewritable by applying appropriate tip field. Large-scale vortex network can also be created by choosing appropriate polarization distance. Combined with enhanced electric conductivity at ferroelectric vortex cores, the artificial vortex-antivortex arrays are potential in manufacturing memory device. The analysis of graph theory indicates that vortex-antivortex pairs are universal in ferroelectric materials which have finite types of domains. These findings provide a possible pathway towards applications based on artificial vortex domain in ferroelectric materials and might promote the development of ferroelectric random access memories and data storage.
Methods
A slice of the (001) BFO epitaxial thin film with SRO bottom electrode is prepared for the experiment, as illustrated in Fig. 1a. A commercial SPM (icon, Bruker) is used to manipulate the ferroelectric domains, while the conductive tip (Platinum-Iridium coated, Bruker’s SCM-PIT) is contacted to the film surface as the top electrode. For obtaining complete vortex domains information, a 1–3 μm square area of BFO films is firstly scanned in 2D PFM mode (tip voltage ~5 V AC, 35 kHz; scan rate ~1 Hz) to simultaneously obtain the out-of-plane z-component and in-plane x-component of piezoresponse (saved as VPFM and x-PFM images, respectively). Then the sample is rotated by 90o to record the in-plane y-component of piezoresponse (y-LPFM image). The three piezoresponse signal images from three mutually perpendicular directions are then composed together by using “Adobe Fireworks”, “Adobe illustrator”, “ImageJ” and “MATLAB” programs, to get the 3D domain pattern of the BFO films. When the sample is rotated 90o, the observed area could not be perfectly coincident. In this case, “Adobe Fireworks” can be used to move and rotate the images to eliminate the errors. The errors caused by image stretching and compression can also be eliminated by Fireworks. The super-resolution PFM images are achieved by using “MATLAB”, while the noises are eliminated by “ImageJ”. During poling process, the selected point is polarized with +10 V DC, 20 s tip electrical pulse and 0 V at bottom electrode. The direction of in-plane polarization is determined by referring to the contrast of the boundary of a squared scan-polarized area.25, 35 In addition, the IP amplitude and grayscale IP phase images related with Figs. 1–4 are shown in the Supplementary Information, Sec. 5.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Catalan, G., Seidel, J., Ramesh, R. & Scott, J. F. Domain wall nanoelectronics. Rev. Mod. Phys. 84, 119–156 (2012).
Zurek, W. H. Cosmological experiments in condensed matter systems. Phys. Rep.-Rev. Sect. Phys. Lett. 276, 177–221 (1996).
Seidel, J., Vasudevan, R. K. & Valanoor, N. Topological structures in multiferroics-domain walls, skyrmions and vortices. Adv. Electronic Mater. 2, doi:10.1002/aelm.201500292 (2016).
Naumov, I. I., Bellaiche, L. & Fu, H. X. Unusual phase transitions in ferroelectric nanodisks and nanorods. Nature 432, 737–740 (2004).
Romming, N. et al. Writing and Deleting Single Magnetic Skyrmions. Science 341, 636–639 (2013).
Vasudevan, R. K. et al. Domain wall geometry controls conduction in ferroelectrics. Nano Lett. 12, 5524–5531 (2012).
Maksymovych, P. et al. Dynamic Conductivity of Ferroelectric Domain Walls in BiFeO3. Nano. Lett. 11, 1906–1912 (2011).
Rojac, T. et al. Domain-wall conduction in ferroelectric BiFeO3 controlled by accumulation of charged defects. Nat. Mater. 16, 322–327 (2017).
Heron, J. T., Schlom, D. G. & Ramesh, R. Electric field control of magnetism using BiFeO3-based heterostructures. Appli. Phys. Rev. 1, doi:10.1063/1.4870957 (2014).
Trassin, M. Low energy consumption spintronics using multiferroic heterostructures. J. Phys. Condens. Matter 28, doi:10.1088/0953-8984/28/3/033001 (2016).
McQuaid, R. G. P., McGilly, L. J., Sharma, P., Gruverman, A. & Gregg, J. M. Mesoscale flux-closure domain formation in single-crystal BaTiO3. Nat. Commun. 2, doi:10.1038/ncomms1413 (2011).
Vasudevan, R. K. et al. Exploring topological defects in epitaxial bifeo3 thin films. Acs Nano 5, 879–887 (2011).
Balke, N. et al. Enhanced electric conductivity at ferroelectric vortex cores in BiFeO3. Nat. Phys. 8, 81–88 (2012).
Hong, L. & Soh, A. K. Unique vortex and stripe domain structures in PbTiO3 epitaxial nanodots. Mech. Mater. 43, 342–347 (2011).
Nelson, C. T. et al. Spontaneous vortex nanodomain arrays at ferroelectric heterointerfaces. Nano Lett. 11, 828–834 (2011).
Rodriguez, B. J. et al. Vortex polarization states in nanoscale ferroelectric arrays. Nano Lett. 9, 1127–1131 (2009).
Yadav, A. K. et al. Observation of polar vortices in oxide superlattices. Nature 530, 198-+, (2016).
Chae, S. C. et al. Evolution of the domain topology in a ferroelectric. Phys. Rev. Lett. 110, doi:10.1103/PhysRevLett.110.167601 (2013).
Huang, F. T. et al. Duality of topological defects in hexagonal manganites. Phys. Rev. Lett. 113, doi:10.1103/PhysRevLett.113.267602 (2014).
Han, M. G. et al. Ferroelectric switching dynamics of topological vortex domains in a hexagonal manganite. Adv. Mater. 25, 2415–2421 (2013).
Ivry, Y., Chu, D., Scott, J. F., Salje, E. K. H. & Durkan, C. Unexpected controllable pair-structure in ferroelectric nanodomains. Nano Lett. 11, 4619–4625 (2011).
Tang, Y. L. et al. Observation of a periodic array of flux-closure quadrants in strained ferroelectric PbTiO3 films. Science 348, 547–551 (2015).
Kalinin, S. V. et al. Vector piezoresponse force microscopy. Microsc. Microanal. 12, 206–220 (2006).
Rodriguez, B. J., Gruverman, A., Kingon, A. I., Nemanich, R. J. & Cross, J. S. Investigation of the mechanism of polarization switching in ferroelectric capacitors by three- dimensional piezoresponse force microscopy. Appl. Phys. a-Mater. Sci. Process. 80, 99–103 (2005).
Zavaliche, F. et al. Polarization switching in epitaxial BiFeO3 films. Appl. Phys. Lett. 87, doi:10.1063/1.2149180 (2005).
Chu, Y. H. et al. Domain control in mulfiferroic BiFeO3 through substrate vicinality. Adv. Mater. 19, 2662-+, (2007).
Zavaliche, F. et al. Ferroelectric domain structure in epitaxial BiFeO3 films. Appl. Phys. Lett. 87, doi:10.1063/1.2126804 (2005).
Kan, Y. et al. Growth evolution and decay properties of the abnormally switched domains in LiNbO3 crystals. Appl. Phys. Lett. 92, doi:10.1063/1.2919733 (2008).
Ievlev, A. V., Morozovska, A. N., Shur, V. Y. & Kalinin, S. V. Ferroelectric switching by the grounded scanning probe microscopy tip. Phys. Rev. B 91, doi:10.1103/PhysRevB.91.214109 (2015).
Xue, F. et al. Evolution of the statistical distribution in a topological defect network. Sci. Rep. 5, doi:10.1038/srep17057 (2015).
Horibe, Y. et al. Color Theorems, Chiral Domain Topology, and Magnetic Properties of FexTaS2. J. Am. Chem. Soc. 136, 8368–8373 (2014).
Mettout, B., Toledano, P., Lilienblum, M. & Fiebig, M. Combinatorial model for the ferroelectric domain-network formation in hexagonal manganites. Phys. Rev. B 89, doi:10.1103/PhysRevB.89.024103 (2014).
Baek, S. H. et al. Ferroelastic switching for nanoscale non-volatile magnetoelectric devices. Nat. Mater. 9, 309–314 (2010).
Heron, J. T. et al. Deterministic switching of ferromagnetism at room temperature using an electric field. Nature 516, 370–3 (2014).
Balke, N. et al. Deterministic control of ferroelastic switching in multiferroic materials. Nat. Nanotechnol. 4, 868–875 (2009).
Acknowledgements
This work was supported by the National Key Research Program of China (No. 2016YFA0201004), the 973 Project of MOST (No. 2015CB921201), the National Natural Science Foundation of China (Nos. 51225201 and 51672123), the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD) and SWC is supported by the Gordon and Betty Moore Foundation’s EPiQS Initiative through Grant GBMF4413 to the Rutgers Center for Emergent Materials.
Author information
Authors and Affiliations
Contributions
Y.L. and X.M.L. conceived and designed the experiments, and wrote the article. J.C.Y. prepared the samples. Y.L. carried out the experiment. Y.L and Y.M.J. analyzed the PFM data and performed graph theory analyzation. Y.H.C. and S.W.C. provided useful advices for writing. F.Z.H. and J.S.Z provided useful discussions. All authors contributed to the manuscript and the interpretation of the data.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, Y., Jin, Y., Lu, X. et al. Rewritable ferroelectric vortex pairs in BiFeO3 . npj Quant Mater 2, 43 (2017). https://doi.org/10.1038/s41535-017-0047-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-017-0047-2
This article is cited by
-
Ferroelectric solitons crafted in epitaxial bismuth ferrite superlattices
Nature Communications (2023)
-
Phase-field simulations of vortex chirality manipulation in ferroelectric thin films
npj Quantum Materials (2022)
-
Quasi-one-dimensional metallic conduction channels in exotic ferroelectric topological defects
Nature Communications (2021)
-
Highly charged 180 degree head-to-head domain walls in lead titanate
Communications Physics (2020)
-
Artificial creation and separation of a single vortex–antivortex pair in a ferroelectric flatland
npj Quantum Materials (2019)