Abstract
Providing a spin-free host material in the development of quantum information technology has made silicon a very interesting and desirable material for qubit design. Much of the work and experimental progress has focused on isolated phosphorous atoms. In this article, we report on the exploration of Ni–Si clusters that are atomically manufactured via self-assembly from the bottom-up and behave as isolated quantum dots. These small quantum dot structures are probed at the atomic-scale with scanning tunneling microscopy and spectroscopy, revealing robust resonance through discrete quantized energy levels within the Ni–Si clusters. The resonance energy is reproducible and the peak spacing of the quantum dot structures increases as the number of atoms in the cluster decrease. Probing these quantum dot structures on degenerately doped silicon results in the observation of negative differential resistance in both I–V and dI/dV spectra. At higher surface coverage of nickel, a well-known √19 surface modification is observed and is essentially a tightly packed array of the clusters. Spatial conductance maps reveal variations in the local density of states that suggest the clusters are influencing the electronic properties of their neighbors. All of these results are extremely encouraging towards the utilization of metal modified silicon surfaces to advance or complement existing quantum information technology.
Similar content being viewed by others
Introduction
There has been significant progress toward the utilization of an electron’s spin for the development of quantum bits (qubits) poised to revolutionize modern computers, where the orientation of the spin serves as the basis for “0” and “1” logic operations.1, 2 A major challenge is scaling this technology toward meaningful quantum computation requiring the entanglement of multiple qubits with coherence times long enough for calculations to occur and simultaneously be measured.3,4,5,6,7,8,9,10,11,12 Not surprisingly, materials are at the heart of this challenge, from the fabrication of the qubits to how the electron or nuclear spin interacts with the host material.13,14,15,16,17 One of the most advantageous platforms has been developing solid-state qubit architectures using traditional semiconductors, where an entire industrial infrastructure exists and hybridization with conventional technology would be greatly beneficial. A predominant approach has been developing qubit systems with quantum dots using III–V semiconductor heterostructures,18,19,20,21,22 where the lowered dimensionality is utilized for quantum confinement. Significant advances have been made toward addressing the spin in these quantum dot structures that include fast optical control and all-electrical measurements. However, the qubit interaction with the nuclear spins, inherent in the III–V materials, reduces the coherence time and presents a significant challenge. Alternatively, group IV semiconductors are quite attractive for qubit design because they can provide a spin-free environment, where electron spin coherence times have been measured on the order of seconds.23,24,25
The utilization of silicon, a zero nuclear spin material, has been the focus of several proposals as an optimal material for qubit design. Kane et al.26 first described using the nuclear spins of phosphorous dopants arranged as an array within a silicon lattice for the development of a quantum computer.26 Several experimental efforts are underway to fully develop qubit and quantum technologies based on phosphorous dopants.27,28,29 A key to these efforts has been the utilization of scanning tunneling microscopy (STM) to both fabricate and characterize the unique placement of single phosphorous donors on both silicon and germanium surfaces. Most impressive has been the placement of isolated phosphorous dopants within electronic contacts that can be macroscopically addressed.30, 31 Although it is not practical to utilize the STM for large-scale qubit fabrication, it has proven to be a powerful tool for the development of proof-of-principle devices and local characterization of quantum structures and phenomena at the atomic-scale.
Rather than fabricating individual quantum structures with the STM, we are interested in exploring large-scale atomic manufacturing of alternative quantum dot structures that self-assemble, consist of only a handful of atoms, and are integrated with a semiconductor substrate. The goal is to find a suitable “bottom-up” approach that is scalable for qubit design. Complimentary to STM fabrication of individual quantum structures between electrical contacts, we envision scalability by controlling the density of self-assembled quantum dots over an entire surface. This would allow for the patterning of contacts anywhere on the surface and, with optimization, result in the desired density of quantum dots (from one to many) to exist between the contacts. There has been significant research in the area of metal functionalization of silicon surfaces in the context of thin film growth, metal silicides, and the modification of surface reconstructions.32,33,34,35 Guided by these efforts, we investigated the submonolayer deposition of Ni on Si(111). At these low coverages, the surface reconstruction is modified and two distinct Ni–Si clusters emerge that consist of either a “1 × 1” or “√19” quantum dot structure consisting of an ordered grouping of Ni and Si atoms. Here, we report the investigation of quantum dot behavior and electron confinement in these Ni–Si atomic clusters. Utilizing scanning tunneling spectroscopy (STS), we observe resonant tunneling through quantized levels at reproducible energies within the clusters and a largerpeak spacing for the smaller clusters, as anticipated for shrinking dimensions. Furthermore, by degenerately doping (n-type) the host substrate, we can give rise to negative differential resistance (NDR) observed at negative sample bias. Finally, at higher surface coverage, the larger clusters form a uniform metal-silicon reconstruction across the surface with a complex electronic landscape. This research presents a model system for large-scale distribution of atomic quantum dots for potential qubit design that are tunable between two distinct sizes, with reproducible quantized energy levels, and can be designed to exhibit NDR.
Results
A submonolayer of Ni was evaporated onto a Si(111) substrate to observe the initial formation of the atomic Ni–Si clusters, as illustrated in the STM image of Fig. 1a (please see Materials and Methods for further details). In the topographic STM images, obtained at a sample temperature of 55 K, we observe regions of clean Si(111) where the 7 × 7 surface reconstruction is unperturbed, thus verifying that we have submonolayer coverage. The majority of the image shows Ni modification to the surface. At low coverage the smaller seven atom clusters are most prevalent. These clusters topographically appear as small “donut” like features in the topographic image as observed in Fig. 1b and are highlighted by yellow dashed circles within the zoomed inset. We classify these as “1 × 1” clusters adopting the nomenclature from the literature where the Ni modification results in a 1 × 1 ordering of the underlying Si atoms.36 The structural model for the 1 × 1 clusters is schematically drawn in Fig. 1b. Looking closely at these STM images, there are larger clusters that appear darker within the topographic image. The STM is sensitive to the local density of states (LDOS) and the electronic difference in the larger clusters at this particular sample bias results in the clusters looking slightly depressed into the first layer of Si. These clusters are classified as “√19” clusters and are highlighted by blue circles within the zoomed inset of Fig. 1b. Again we have adopted nomenclature from the literature where at higher surface coverage these larger clusters order across the surface and give rise to the reported √19 Ni–Si surface reconstruction.34 The schematic of Fig. 1b shows the spatially larger quantum dot clusters.
Atomic-scale imaging of Ni–Si clusters. a Topographic STM image showing submonolayer Ni coverage, where regions of pristine Si(111)-7 × 7 surface reconstruction are visible (Sample Bias + 2.0 V, Setpoint Current 100 pA). Within the Ni restructured area there are predominately “ring-cluster” structures with the underlying reconstruction going 1 × 1. At the right corner boundary near clean Si(111), there are four unique dark ring structures. b Zoom in STM image of the ring-like structures reveals our two cluster formations (1 × 1 and √19). The ball and stick schematics show the atomic arrangement of the Si atoms relative to the central Ni atoms. The 1 × 1 clusters (circled in yellow) and the √19 clusters (circled in blue) consist of self-assembled atomic clusters of Si and Ni
At this point, we can reproducibly fabricate distributions of these atomic Ni–Si clusters on the Si(111) surface, which are consistent with previous surface science studies.32,33,34,35 The true motivation and foundationally unique aspect of this study involve evaluating these atomic Ni–Si clusters as quantum dot structures for potential qubit design. These clusters must possess discrete energy levels resulting from quantum confinement due to the lowered dimensionality and energetically spaced to be technologically accessible. Because these clusters are comprised of only a handful of atoms, it is easy to think of these clusters as small inorganic molecules on the surface. With that analogy, our other concern is whether or not these clusters are electronically unique entities or if they are strongly coupled to the substrate. Thinking of these clusters as quantum dots with electron confinement, we would expect the peak spacing to increase, as the size of the cluster gets smaller, which is schematically illustrated in Fig. 2a.
Resonance reveals quantum dot behavior in the atomic clusters. a Schematic diagram illustrating that the lowered dimensionality results in electron confinement within the clusters resulting in discrete quantized energy levels. As the size of the quantum dot decreases, the peak spacing should increase and is consistent with what we observe. b I–V measurements made over the Ni–Si atomic cluster quantum dots, where the turn-on energies are greater for the smaller 1 × 1 cluster. NDR is observed in both cluster structures at negative sample bias. c Averaged STS dI/dV spectra measured over the 1 × 1 clusters illustrated in the STM image inset. Clear resonance is observed with discrete energy levels in the cluster at positive and negative bias. Negative conductance is observed and correlated with NDR observed in I–V. d Averaged STS spectra of the larger √19 clusters show similar resonance but with a smaller gap between energy levels as illustrated. e Schematic band diagrams showing (I) Equilibrium where the Fermi level aligns and is within the conduction band due to degenerate doping of the Si, (II) Resonance where the chemical potential shifts the band of electrons in the conduction band into alignment with discrete energy level, and (III) NDR where the chemical potentials shift until the discrete level falls within the forbidden gap and cannot contribute to tunneling
To probe the electronic structure of the 1 × 1 and √19 atomic quantum dots we utilized STS, where the STM probe was positioned over a cluster. With the probe parked, the feedback was turned off and I–V measurements were taken, while simultaneously measuring the dI/dV with lock-in techniques. The dI/dV is proportional to the LDOS. Figure 2b shows averaged I–V measurements taken over the two different clusters. The flat region of zero current between the turn-on at negative or positive sample bias is a reflection of the Si band gap. Qualitatively, we can see that the peak spacing is smaller over the √19 cluster in comparison to the slightly larger peak spacing observed for the smaller 1 × 1 cluster. Both gaps appear larger than the intrinsic gap of the Si(111) substrate, which is 1.1 eV. We also qualitatively observe the consistent onset of NDR at negative sample bias, which will be discussed in greater detail.
Figure 2c shows the dI/dV spectrum taken over the 1 × 1 clusters, illustrated in the topographic STM inset. There is a tunneling resonance with a quantized energy level at positive bias that represents tunneling through the highest occupied energy level. An almost symmetric resonance is observed at negative sample bias, where the electrons are tunneling through the lowest unoccupied quantized level. The almost symmetric position of the energy level around the Fermi energy (zero sample bias) is consistent with reported STM measurements in different quantum dot systems.37, 38 The symmetry may be coincidental because it is dictated by how the quantized levels within the quantum dot align at equilibrium, which can be influenced by interaction with the substrate. The fact that resonance is observed at all through these levels suggests that the electronic structure of these clusters is to some extent decoupled from the host substrate. The negative bias resonance peak is clearly depicted because it immediately drops to the observed NDR negative conductance. It is resonance through this energy level that gives rise to the NDR and will be discussed further. The dI/dV spectrum verifies that we are observing resonant tunneling through discrete energy levels and our clusters are behaving as atomic quantum dots. Measuring the distance between the two resonant peaks allows for a quantitative analysis of the energy level spacing plus twice the charging energy (E c) of the quantum dot structures.37, 38 The 1 × 1 quantum dots have a consistent peak spacing of approximately 2.87 eV.
The √19 structures display a similar resonance within the dI/dV spectrum, with a peak more clearly observed at positive bias illustrated in Fig. 2d. The positive bias peak does not drop to a negative value, which is expected. However, as with the 1 × 1 clusters, the √19 structures also display a drop to negative conductance after resonance with the negative bias peak. The quantum dot peak spacing is 2.36 eV when measured between the resonant peaks and is smaller for the larger cluster as expected. At negative sample bias, NDR is occurring as we sweep from a state of “on-resonance” to “off-resonance” with our atomic quantum dot clusters and the degenerately doped substrate. We intentionally utilized degenerately doped n-type Si(111) to help probe these structures. The degenerate doping results in the Fermi level lying just within the conduction band, as illustrated in Fig. 2e. At equilibrium, the Fermi level is aligned between the tip and substrate and should be mid-gap of the quantum dot we are probing. As we sweep the sample bias to negative values, the energy levels shift to a point in which the narrow band of electrons in the conduction band align with the lowest unoccupied level of the quantum dot structure resulting in “on-resonance”. As we sweep to larger negative values the energy shift “off-resonance”, the NDR only happens in this direction because the level of the quantum dot ends up in the forbidden gap of the semiconductor and can no longer participate in tunneling. At positive bias, “on-resonance” occurs and, although there is a decrease in the dI/dV signal, the energy level can still participate in tunneling. These results are analogous to NDR observed in resonant tunneling of molecular orbitals on degenerately doped silicon.39, 40
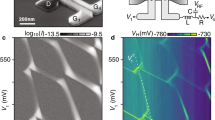
To further confirm our interpretation of the observed NDR behavior resulting from resonance through a discrete level of our quantum dot clusters, we explored the behavior as a function of tip spacing. The further the tip is away from the quantum dot should result in a shift in the resonant energy and observed NDR. The shifting of the relative position of the energy levels is related to the potential drop within the gap, which is modified when moving the position of the STM tip. Figure 3a shows a topographic STM image of a √19 cluster that was probed as a function of tip position. The colored dots represent the tip position to the corresponding dI/dV spectra plotted in Fig. 3b. When the tip is positioned directly over the cluster we observe clear resonance through the discrete energy levels and the onset of NDR. As the tip is moved off of the cluster, the resonance shifts to higher negative values and the NDR is lost. In fact, it is transitioning to resonance through a nearby 1 × 1 cluster. These results help to strengthen our interpretation of the NDR phenomena.
Spatial tip dependence on resonance through quantum dots. a STM image showing a line of spectra measured over a √19 cluster. b As the position of the STM tip moves, it shifts out of resonance and the negative conductance is lost illustrating a dependence on tip-cluster spacing. c The resonant energy for the clusters is extremely reproducible. This histogram shows some statistical analysis of resonant peak energies and minima for the √19 cluster. Although we could benefit from more statistical data to reveal the exact distribution, the peak values lie within 100 meV and there is thermal broadening due to a room temperature tip
One of the most encouraging results, when considering the potential application of these atomic quantum dots for qubit design, is the consistency of the energy level alignment with the substrate. For numerous 1 × 1 and √19 clusters, we observe the resonance phenomena at the same energy values. Figure 3c illustrates statistical distributions analyzed for several measurements made on √19 quantum dots. Although a larger statistical ensemble would be preferred, the data show a clear trend for uniform resonant peak and valley energy positions within our STS spectra. Ultimately, we are illustrating that these clusters can be viewed as atomic-scale quantum dots, but the clusters are randomly distributed on the surface. There are clear advantages of the self-assembly aspect in the formation of these clusters. Further work must be done to see if this route can be applied to the vision of Kane’s quantum computer or provide advantages or complement current experimental efforts with phosphorous atoms.
Discussion
When the Ni coverage is increased on the surface, the √19 clusters become prevalent across the surface until a saturated √19 Ni surface reconstruction is reached, as illustrated in the topographic image of Fig. 4a. This Ni modified surface is stable, robust, and is essentially a tightly packed array of the individual √19 clusters (that were isolated at lower coverage). As the clusters become tightly packed, the electronic structure of the surface is modified and the well-defined resonance observed for the isolated and loosely spaced clusters becomes lost in the STS measurements. The rich electronic structure can be spatially imaged with STS conductance maps that are taken concurrently with the topographic data, as illustrated in Fig. 4. The top image, Fig. 4b, is the topography and the bottom image, Fig. 4c, is the spatial dI/dV conductance map that is proportional to the LDOS for the given imaging sample bias. We also observe very distinct patches of variation within the electronic structure that is visualized by the color scale for high to low values of LDOS.
Saturated surface coverage of √19 cluster self-assembly. a STM image showing domains of saturated Ni–Si √19 cluster formation, where they hexagonally arrange with domain boundaries visible within the image (Sample Bias -2V, Setpoint Current 200 pA). b A zoomed in STM image shows a uniform array of √19 clusters with some defects and vacancies. c A spatial dI/dV map for the same area in b showing a rich electronic ordering within the tightly packed atomic quantum dot array (Sample Bias -2V, Setpoint Current 200 pA). d STS dI/dV spectra measured at different points over the tightly packed √19 clusters. The peak at negative bias has broadened and we do not observe the presence of NDR. e I–V measurements also confirm the loss of NDR and only a slight shoulder is observed. As the clusters pack together tightly, we believe that the levels of the QD structures overlap and broaden the measured spectra
The array of bright circular features corresponds to a network of linking atoms between the clusters. By careful inspection of Fig. 4c, the clusters themselves have a uniform circular LDOS with a slight brighter region directly at the center. However, there are several patches of brighter contrast and some clusters that appear dark, while some of the bright circular regions of linking atoms are missing. We feel that the LDOS variation is in part due to missing atoms in the full √19 reconstruction, defects, and some adsorbates. The intriguing aspect is how uniform the LDOS are for patches of different clusters. A key component to qubit design is achieving entanglement between qubits so information can be transferred. To further explore this possibility, we performed STS measurements of the full √19 reconstruction that are plotted in Figs. 4d, e. The STS measurements no longer display a sharp resonant peak and NDR is not observed at any position on this surface. Instead, a broadened peak is observed at negative bias and no peak is observed at positive bias. The I–V curve in Fig. 4e shows a slight shoulder at negative bias but no NDR. We believe that the loss of resonance in our STS measurements is due to broadening of the levels as the clusters move closer together, which indicates that levels are overlapping and interacting. These aspects are to be explored in further studies that can be performed with instrumentation at lower temperature to increase the energy resolution and spatial stability of the spectroscopy.
In conclusion, we have utilized the STM and STS to investigate atomic-scale Ni-Si clusters on the Si(111) surface. The dI/dV measurements reveal resonant tunneling through discrete energy levels within the clusters. Resonance through these levels suggests that the electronic structure of these clusters is only weakly coupled to the Si(111) substrate. The clusters behave as quantum dots on the Si surface and consist of either (“1 × 1”) or (“√19”) atomic clusters. We have intentionally explored Ni surface modification and cluster formation on degenerately doped n-type Si(111), where the Fermi level lies within the conduction band. The resonance with our highest unoccupied state with the atomic Ni–Si quantum dots results in NDR observed at negative sample bias in both I–V measurements and dI/dV spectra. The peak spacing of the clusters increases as the size of the quantum dot decreases. Further experiments should be run on more sophisticated low temperature instruments to increase the energy resolution. Overall, the self-assembly of Ni–Si clusters on the surface is a promising and intriguing platform for the development qubit and quantum technologies utilizing atomic-scale quantum dots on a Group IV substrate.
Materials and methods
The Si(111) samples were commercially purchased (Virginia Semiconductor Inc.) and degenerately doped n-type with phosphorous (resistivity < 0.01–0.05 Ω-cm). The Si(111) was degassed overnight at 600 °C to remove organic contamination prior to high temperature flashing. To obtain a pristine Si(111)-7 × 7 surface, the samples were repeatedly flashed to 1250 °C for 30 s. Once a pristine surface was achieved and verified with STM, Ni was evaporated onto the surface using an e-beam evaporator (dosing time ~ 15 min). The Ni evaporation occurred while the sample was at elevated temperature (600 °C) to help drive the cluster assembly. The samples were characterized with an Omicron VT-STM at room temperature and 55 K. The Omicron VT grounds the sample and bias control is applied to the tip. All STS measurements were made using a W electrochemically etched tip at room temperature while the sample was cooled to 55 K.
Data availability
All data supporting the findings of this study are available within the paper.
References
Awschalom, D. D., Bassett, L. C., Dzurak, A. S., Hu, E. L. & Petta, J. R. Quantum spintronics: engineering and manipulating atom-like spins in semiconductors. Science 339, 1174–1179 (2013).
Ladd, T. D. et al. Quantum computers. Nature 464, 45–53 (2010).
Bose, S. Quantum communication through spin chain dynamics: an introductory overview. Cont. Phys. 48, 13–30 (2007).
Buckley, B. B., Fuchs, G. D., Bassett, L. C. & Awschalom, D. D. Spin-light coherence for single-spin measurement and control in diamond. Science 330, 1212–1215 (2010).
de Lange, G., Wang, Z. H., Ristè, D., Dobrovitski, V. V. & Hanson, R. Universal dynamical decoupling of a single solid-state spin from a spin bath. Science 330, 60–63 (2010).
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
McNeil, R. P. G. et al. On-demand single-electron transfer between distant quantum dots. Nature 477, 439–442 (2011).
Pfaff, W. et al. Unconditional quantum teleportation between distant solid-state quantum bits. Science 345, 532–535 (2014).
Press, D., Ladd, T. D., Zhang, B. & Yamamoto, Y. Complete quantum control of a single quantum dot spin using ultrafast optical pulses. Nature 456, 218–221 (2008).
Shulman, M. D. et al. Demonstration of entanglement of electrostatically coupled singlet-triplet Qubits. Science 336, 202–205 (2012).
Togan, E. et al. Quantum entanglement between an optical photon and a solid-state spin qubit. Nature 466, 730–734 (2010).
Trifunovic, L. et al. Long-distance spin-spin coupling via floating gates. Phys. Rev. X 2, 011006 (2012).
Fuchs, G. D., Burkard, G., Klimov, P. V. & Awschalom, D. D. A quantum memory intrinsic to single nitrogen-vacancy centres in diamond. Nat. Phys. 7, 789–793 (2011).
Koehl, W. F., Buckley, B. B., Heremans, F. J., Calusine, G. & Awschalom, D. D. Room temperature coherent control of defect spin qubits in silicon carbide. Nature 479, 84–87 (2011).
Kolesov, R. et al. Mapping spin coherence of a single rare-earth ion in a crystal onto a single photon polarization State. Phys. Rev. Lett. 111, 120502 (2013).
Ladd, T. D., Sanaka, K., Yamamoto, Y., Pawlis, A. & Lischka, K. Fluorine-doped ZnSe for applications in quantum information processing. Phys. Stat. Soli. (b) 247, 1543–1546 (2010).
Robledo, L. et al. High-fidelity projective read-out of a solid-state spin quantum register. Nature 477, 574–578 (2011).
Bluhm, H. et al. Dephasing time of GaAs electron-spin qubits coupled to a nuclear bath exceeding 200 μs. Nat. Phys. 7, 109–113 (2011).
Hanson, R., Kouwenhoven, L. P., Petta, J. R., Tarucha, S. & Vandersypen, L. M. K. Spins in few-electron quantum dots. Rev. Mod. Phys. 79, 1217–1265 (2007).
Loss, D. & DiVincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A. 57, 120–126 (1998).
Petta, J. R. et al. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 309, 2180–2184 (2005).
Veldhorst, M. et al. An addressable quantum dot qubit with fault-tolerant control-fidelity. Nat. Nanotechnol. 9, 981–985 (2014).
Morton, J. J. L., McCamey, D. R., Eriksson, M. A. & Lyon, S. A. Embracing the quantum limit in silicon computing. Nature 479, 345–353 (2011).
Steger, M. et al. Quantum information storage for over 180 s using donor spins in a 28Si “Semiconductor Vacuum”. Science 336, 1280–1283 (2012).
Tyryshkin, A. M. et al. Electron spin coherence exceeding seconds in high-purity silicon. Nat. Mater. 11, 143–147 (2012).
Kane, B. E. A silicon-based nuclear spin quantum computer. Nature 393, 133–137 (1998).
Büch, H., Mahapatra, S., Rahman, R., Morello, A. & Simmons, M. Y. Spin readout and addressability of phosphorus-donor clusters in silicon. Nat. Commun. 4, 2017 (2013).
Oberbeck, L. et al. Encapsulation of phosphorus dopants in silicon for the fabrication of a quantum computer. Appl. Phys. Lett. 81, 3197–3199 (2002).
Zwanenburg, F. A. et al. Silicon quantum electronics. Rev. Mod. Phys. 85, 961–1019 (2013).
Fuechsle, M. et al. A single-atom transistor. Nat. Nanotechnol. 7, 242–246 (2012).
Scappucci, G. et al. A complete fabrication route for atomic-scale, donor-based devices in single-crystal germanium. Nano Lett. 11, 2272–2279 (2011).
Bennett, P. A., Copel, M., Cahill, D., Falta, J. & Tromp, R. M. Ring clusters in transition-metal-silicon surface structures. Phys. Rev. Lett. 69, 1224–1227 (1992).
Ichinokawa, T., Tani, T. & Sayama, A. Formation of the Si(111)√19 × √19 structure induced by Ni impurity at low coverage. Surf. Sci. 219, 395–406 (1989).
Tsai, M.-H., Dow, J. D., Bennett, P. A. & Cahill, D. G. Electronic structure and stability of ring clusters in the Si(111)-(√7x√7)Co surface. Phys. Rev. B 48, 2486–2492 (1993).
Wilson, R. J. & Chiang, S. Surface modifications induced by adsorbates at low coverage: A scanning tunneling microscopy study of the Ni/Si(111)√19 surface. Phys. Rev. Lett. 58, 2575–2578 (1987).
Yao, T., Shinabe, S. & Yoshimura, M. Atomistic study of the formation process of Ni silicide on the Si(111)-7 × 7 surface with scanning tunneling microscopy. Appl. Surf. Sci. 104, 213–217 (1996).
Banin, U., Cao, Y., Katz, D. & Millo, O. Identification of atomic-like electronic states in indium arsenide nanocrystal quantum dots. Nature 400, 542–544 (1999).
Millo, O., Katz, D., Cao, Y. & Banin, U. Scanning tunneling spectroscopy of InAs nanocrystal quantum dots. Phys. Rev. B 61, 16773–16777 (2000).
Guisinger, N. P., Greene, M. E., Basu, R., Baluch, A. S. & Hersam, M. C. Room temperature negative differential resistance through individual organic molecules on silicon surfaces. Nano Lett. 4, 55–59 (2004).
Rakshit, T., Liang, G.-C., Ghosh, A. W. & Datta, S. Silicon-based molecular electronics. Nano Lett. 4, 1803–1807 (2004).
Acknowledgements
C. Lilley would like to acknowledge support from the Mechanical and Industrial Engineering Department, the College of Engineering at the University of Illinois, and Argonne National Laboratory during her sabbatical at the Center for Nanoscale Materials. Use of the Center for Nanoscale Materials, an Office of Science user facility, was supported by the U. S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357.
Author information
Authors and Affiliations
Contributions
J.Y.C., N.P.G., and C.M.L. conceived the project; J.Y.C., N.P.G., and C.M.L. carried out the experiment and data analysis. B.L.F. provided engineering support for the experiment. J.Y.C., N.P.G., and C.M.L. wrote and revised the manuscript. All authors contributed to the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing financial interest.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cheng, JY., Fisher, B.L., Guisinger, N.P. et al. Atomically manufactured nickel–silicon quantum dots displaying robust resonant tunneling and negative differential resistance. npj Quant Mater 2, 25 (2017). https://doi.org/10.1038/s41535-017-0029-4
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-017-0029-4
This article is cited by
-
Interface properties of nickel quantum dots on the Si(111) surface
Applied Nanoscience (2023)
-
In2S3 Quantum Dots: Preparation, Properties and Optoelectronic Application
Nanoscale Research Letters (2019)
-
Light-dependent negative differential resistance in MEH-PPV decorated electrospun TiO2 mat
Applied Physics A (2018)