Abstract
When a Dirac fermion system acquires an energy-gap, it is said to have either trivial (positive energy-gap) or non-trivial (negative energy-gap) topology, depending on the parity ordering of its conduction and valence bands. The non-trivial regime is identified by the presence of topological surface or edge-states dispersing in the energy gap of the bulk and is attributed a non-zero topological index. In this work, we show that such topological indices can be determined experimentally via an accurate measurement of the effective velocity of bulk massive Dirac fermions. We demonstrate this approach analytically starting from the Bernevig-Hughes-Zhang Hamiltonian to show how the topological index depends on this velocity. We then experimentally extract the topological index in Pb 1-x Sn x Se and Pb1-x Sn x Te using infrared magnetooptical Landau level spectroscopy. This approach is argued to be universal to all material classes that can be described by a Bernevig-Hughes-Zhang-like model and that host a topological phase transition.
Similar content being viewed by others
Introduction
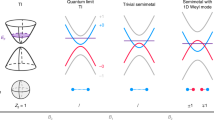
The concept of band topology in condensed matter systems has revolutionized our understanding of quantum phases of matter.1,2,3,4 Fundamentally speaking, it has allowed us to understand how unconventional novel states of matter can emerge in systems where fundamental symmetries are preserved. Typically, the topological character of solids is governed by the orbital and parity ordering of the conduction and valence bands. In a number of materials, band topology is proven to be non-trivial, as the parity of the conduction and valence bands is inverted compared to conventional semiconductors and the sign of the energy gap is said to be negative (Fig. 1a).2, 4,5,6,7 Such energy states of matter are typically attributed a non-zero topological index, that is related to the sign of the energy gap. Under certain symmetry considerations (time reversal symmetry, crystalline symmetries, etc.), systems that have a non-zero topological index host gapless metallic Dirac surface states that disperse in the band gap of the semiconductor.2, 5,6,7,8 These topological surface states (TSS) exhibit striking properties such as a relativistic energy-momentum dispersion, a helical spin texture with electron spin locked to the momentum and a high robustness against disorder.3 The TSS give rise to novel physical effects such as the quantized conductance without magnetic fields,8 the quantum anomalous Hall effect 9, 10 and may provide a basis for the realization of Majorana fermions.11, 12 A considerable number of topological material classes have been thus far identified. Among all, in the Z2 topological insulator (TI) class, the band inversion occurs at an odd number of time-reversal symmetric points13, 14 in the first Brillouin zone (BZ), whereas in topological crystalline insulators (TCI) it occurs at an even number of crystalline mirror symmetric points.5, 15,16,17,18
The topological phase transition and Brillouin zone of Pb1-x Sn x Se and Pb1-x Sn x Te. a Sketch of a topological phase transition that occurs at a critical point x c as a function of composition in a system having a conduction and valence band of opposite parity (different color). The bulk band gap closes at x c. Topological surface states (TSS) emerge in the topological regime x > x c (shaded blue region). In IV–VI TCI, this occurs at a critical Sn concentration x c. b Bulk Brillouin zone of [111] IV–VI semiconductors, showing the longitudinal (black), and oblique (red) valleys. The topological surface band structure above the bulk BZ shows the \(\bar \Gamma \)(blue) and the\(\bar M\)(yellow) Dirac cones
Both the TI8, 19,20,21,22 and TCI15,16,17, 23,24,25,26,27 states have been thoroughly studied experimentally. Moreover, the topological phase transition (Fig. 1a) from trivial to non-trivial5, 28,29,30,31,32,33,34 has also been extensively investigated for both TIs and TCI. However, no direct measurement of a topological index in three-dimensional (3D) condensed matter systems has yet been reported. Typically, the topological index is inferred from angle resolved photoemission spectroscopy measurements that observe helical Dirac surface states in 3D TI, or via the observation of the quantum spin Hall effect in 2D TI. In materials where a topological phase transition from trivial to non-trivial can be induced, the topological index can be also inferred from the observation of a closure and reopening of the energy gap. A direct measurement of the topological index would, however, be interesting to consider fundamentally, as it may allow us to shed light on pending issues concerning the thermodynamics of topological phases. For instance, are topological phase transitions first or second order in nature?28, Does there exist a gapless 3D Dirac state at the critical inversion point?28, 29, 35 What mechanism causes the band-inversion and the gapping of surface-states when the system becomes trivial? Can the gapping of surface-states and their acquisition of mass be described by an analogue of the Higgs mechanism?29, 34
In this work, we show that the topological index can be directly measured in systems exhibiting topological phase transitions using infrared (IR) Landau level spectroscopy. Starting from the Bernevig-Hughes-Zhang (BHZ) Hamiltonian, we show that to order k 2 an energy dispersion that is identical to that of massive Dirac fermions can be obtained, with a modified Dirac velocity that depends on the topological index. Using magnetooptical IR Landau level spectroscopy, we are able to measure this effective velocity with high precision in TCI Pb1-x Sn x Se and Pb1-x Sn x Te and thus experimentally extract the topological index. This is a first proof of concept that topological indices can be experimentally measured, and not just inferred from the observation of edge/surface states. We argue that our result is expected to be valid for other systems that exhibit a topological phase transition such as (Hg, Cd)Te (ref. 36), Cd3As2 (ref. 37), or BiTlS1-δ Se δ (refs. 33, 34)
Results
The topological index in the BHZ Hamiltonian
Let us start by solving the eigenvalue problem for a system described by the general38 BHZ effective Hamiltonian.2 Since we define z to be the direction of the applied magnetic field, cyclotron motion in the plane perpendicular to the field will be considered. We can thus set k z = 0, which gives:
Here, Δ = E g /2 is the half-band gap, v c is a velocity usually related to the k.p matrix element and M 1 (M 1 < 0 in the sign convention of BHZ)38 is a Schrödinger mass term. \(k_\pm = k_x\pm{ik_y}, k^2 = k_x^2 + k_y^2\). The exact eigen-energies for the conduction and valence bands E C/V resulting from this Hamiltonian are given by:
Neglecting k 4 terms, this can be simplified to:
Or,
This is essentially a massive Dirac dispersion having an effective Dirac velocity \(v_D^2 = v_c^2 - \frac{{2{M_1}\Delta }}{{{\hbar ^2}}}\). In this notation v c is the critical velocity of a gapless 3D Dirac state that may exist at the critical point between the trivial and non-trivial phases. Interestingly the term,
is related to the topological index η as previously defined in the literature (−1)η = \(sign\left( { - \frac{{2{M_1}\Delta }}{{{\hbar ^2}}}} \right)\).32, 39, 40 Measuring v D and v c can thus yield a measure of the topological index η (modulo 2).
Note that, even if one cannot neglect k 4, Eq. (4) can still be expressed in terms of a Dirac velocity that yields the topological index. This is discussed later on in the text.
The case of Pb1-x Sn x Se and Pb1-x Sn x Te
In order to experimentally study the topological phase transition, and attempt to measure the topological index, we investigate the case of Pb1-x Sn x Se and Pb1-x Sn x Te IV-VI TCI, where the transition occurs (Fig. 1a) as a function of varying Sn content, at four L-points in the BZ (Fig. 1b).28, 29, 41,42,43 The bulk Fermi surface of Pb1-x Sn x Se and Pb1-x Sn x Te is shown in Fig. 1b. It is degenerate and possesses an ellipsoidal bulk carrier valley oriented parallel to the [111] axis referred to as the longitudinal valley as well as the three tilted valleys referred to as the oblique valleys. The fourfold bulk valley degeneracy combined with the mirror symmetric character of the rock-salt crystal structure of Pb1-x Sn x Se and Pb1-x Sn x Te yields a TCI state that hosts fourfold degenerate TSS.5, 15, 24, 44,45,46,47,48,49
Despite this subtlety, the band structure and Landau levels of IV–VI semiconductors is ideal to study under the proposed scope, due to their relative simplicity23, 50 compared to other materials such as II–VI and V–VI systems that have highly asymmetric conduction and valence bands. It can actually be shown that a description similar to that of BHZ can be applied to describe the band structure of Pb1-x Sn x Se and Pb1-x Sn x Te. Starting from a 2-band k.p Hamiltonian where Δ is defined to be the half-band-gap again, and v c = (P k.p )/(m 0) where P k.p is the k.p matrix element of each respective valley,43 we can then perturbatively introduce contributions from far-bands as \({M_1} = - \frac{{{\hbar ^2}}}{{2\tilde m}}\) where \(\tilde m\) is a far-band correction mass term.41, 43, 50,51,52,53,54 Interestingly, in Pb1-x Sn x Se and Pb1-x Sn x Te, M 1 turns out to be relatively small.55 This theoretical treatment then yields a massive Dirac-like energy dispersion identical to (4) with an effective Dirac velocity given by:
This is equivalent to writing the band-edge mass as:
Δ changes sign through the topological phase transition, as the conduction and valence bands swap, however, \(\tilde m\) does not change sign. Generally, \(\tilde m\) is due to interactions between the valence/conduction band states, and other bands lying far away from the band gap in energy, referred to as far-bands. The ordering of far-bands does not invert when the valence and conduction bands invert, thus the sign of \(\tilde m\) does not change for fundamental reasons.43, 56
The Landau level spectrum in this case can be determined via the standard procedure of performing a Peierls substitution and using a ladder operator formalism, following what is done in ref. 52. This is detailed in supplementary section 1; we get:
Here, N is the Landau level index and \(\tilde \omega = eB/\tilde m\). ± refers to the effective spin. We highlight that this result is analytically equivalent to the result obtained by Mitchell and Wallis in 1966 (ref. 52), and subsequent work on the Landau levels of PbTe and other lead-tin-salts.43, 55 Mitchell and Wallis also neglected terms in B 2 which essentially yields the same result that we have after neglecting k 4 contributions.
For Pb1-x Sn x Se and Pb1-x Sn x Te, we can then evaluate the topological index, as defined by Fu6 and later used by Juricic et al.32 for TCIs, as:
η = 1 corresponds to a non-trivial phase and η = 0 to the trivial phase. Here η is a valley topological index that can be related to the mirror Chern number in TCI via the definition given by Hsieh5 et al. and Fu.6, 57
Growth and characterization
In order to study the topological transition in Pb1-x Sn x Se and Pb1-x Sn x Te, epilayers are grown in the [111]-direction by molecular beam epitaxy (MBE) on freshly cleaved BaF2 (111) substrates.58,59,60 The Sn concentration x is systematically varied over a wide range, 0 ≤ x ≤ 0.3 for Pb1-x Sn x Se and 0 ≤ x ≤ 0.56 for Pb1-x Sn x Te. In-situ reflection high-energy electron diffraction (RHEED) and ex-situ atomic force microscopy are initially used to characterize the films (see supplementary material S2). X-ray diffraction (XRD) (Fig. 2) is used in order to determine the lattice constant and composition with a precision better than 2%. Figures 2a, c shows the (222) XRD Bragg reflection for a series of Pb1-x Sn x Se (Fig. 2a) and Pb1-x Sn x Te (Fig. 2c) films with different Sn content, illustrating the monotonic shift of the (222) diffraction peaks to higher diffraction angles with increasing Sn content. Epilayers having a thickness >0.5 µm are proven to be fully relaxed by studying reciprocal space maps showing the (513) Bragg reflection.23 From the peak positions, the lattice constant a 0 and Sn concentration of the ternary material can be directly obtained from Vegard’s law (Fig. 2b).
X-ray diffraction data and analysis. XRD characterization of a Pb1-x
Sn
x
Se and c Pb1-x
Sn
x
Te epilayers on BaF2 (111) substrates with Sn content x
Sn varying from 0 to 0.3 and 0 to 1, respectively. From the change in lattice constant, the Sn concentration of the layers was derived using the Vegard’s law. The result is shown in b where the composition determined by X-ray diffraction is plotted vs. the measured beam flux ratio Sn/(Sn + Pb) used for growth in the case of Pb1-x
Sn
x
Se ( ) and Pb1-x
Sn
x
Te (
) and Pb1-x
Sn
x
Te ( ). As indicated by the dashed line, the data points agree very well with the nominal values. The boundaries of the Sn solubility limit in single phase cubic Pb1-x
Sn
x
Se of about 0.4 is indicated
). As indicated by the dashed line, the data points agree very well with the nominal values. The boundaries of the Sn solubility limit in single phase cubic Pb1-x
Sn
x
Se of about 0.4 is indicated
Transport measurements are performed to extract the carrier density and mobility. Carrier densities as low as 1017 cm−3 are achieved in Pb1-x Sn x Se. For Pb1-x Sn x Te x > 0.25, moderate Bi doping (<1019 cm−3) (ref. 61) is used to limit the carrier density to no more than p = 2×1018 cm−3. The Hall mobility μ of the samples at 77 K is measured to be around 30,000 to 60,000 cm2/Vs for Pb1-x Sn x Se, and between 5000 and 20,000 cm2/Vs for Pb1-x Sn x Te. These excellent transport properties allow us to observe Landau quantization at low magnetic fields.
Magnetooptical Landau-level spectroscopy of the bulk band structure
Magnetooptical IR Landau level spectroscopy is then performed in transmission mode in the Faraday geometry up to 17 T, at T = 4.5 K in the mid-IR range. The relative transmission at fixed magnetic field T(B)/T(B = 0) is extracted and analyzed. This technique is highly sensitive to the bulk, yet not blind to the TSS, and is thus an ideal tool to study the inversion of bulk energy bands in topological materials to measure the topological index. Additionally, this technique allows a quantitative assessment of the TSS band structure, via cyclotron resonance (CR) measurements.23
Landau level transitions Figs. 3a, b and magnetooptical spectra Figs. 3c, d are shown for two Pb1-x Sn x Se samples that are, respectively, trivial (x = 0.14) and non-trivial (x = 0.19) at T = 4.5 K (refs. 28, 42). Minima observed in Figs. 3c, d correspond to absorptions due to the presence of Landau-level (LL) transitions at high magnetic fields (μB ≫ 1). Transitions from a valence band LL to a conduction band LL are referred to as interband transitions. Transitions between two LL of the same band are referred to as intraband transitions, or more simply as CR. A large number of interband transitions is observed (Figs. 3a, b) down to low energies evidencing a Fermi level position close to the valence band edge in all samples. Sharp absorption lines can be seen in all spectra with a field onset close to 1 T, evidencing a very high mobility. An energy cutoff at 55 meV and down to 22 meV in the far-IR is due to the Reststrahlen band of the BaF2 substrate.
Magnetooptical transition fan-charts and transmission spectra for Pb1-x Sn x Se. a, b Magnetooptical Landau-level transitions for Pb1-x Sn x Se x = 0.14, and x = 0.19 at T = 4.5 K. Interband transitions from the valence to the conduction band are labeled [N v–(N ± 1)c]. Circles denote data points extracted from mid-IR spectra partially shown in c, d. Solid lines are curve fits using the massive Dirac model for bulk states Eq. (10a). Black and red are used for the longitudinal and oblique bulk valleys, respectively. The green frame is the Reststrahlen band of BaF2. c, d Mid-IR magnetooptical transmission spectra measured at different magnetic fields for x = 0.14 and x = 0.19. Curves are shifted for clarity. The double-sided arrow corresponds to T(B)/T(0) = 0.3
Due to the many-valley band structure of [111]-oriented IV–VI semiconductors, two Landau level series, (Figs. 3a, b) pertaining to the longitudinal (black) and oblique (red) valleys (see Fig. 1b) are identified and analyzed for B||[111]. The oblique valleys are tilted by 70.5° with respect to the longitudinal one.62 The oblique velocity is lower than the longitudinal velocity. This anisotropy in v D is small for Pb1-x Sn x Se but rather large for Pb1-x Sn x Te (Supplement (S3)).23 The interband transitions in Figs. 3a, b can be well described using a massive Dirac-like Landau-level spectrum given in Eq. (7). For k z = 0 (k z // B), the selection rules for the Faraday geometry result in the transition energies given by:52
The ground CR energy at k z = 0 is given by:51
The curve fits in Figs. 3a, b allow us to precisely determine the energy gap |E g | = |2Δ| and v D for all compositions. For trivial Pb0.86Sn0.14Se, we find |2Δ| = 25 ± 5 meV, and v D = (5.05 ± 0.10)x105 m/s for the longitudinal and v D = (4.8 ± 0.1)x105 m/s for the oblique valleys, whereas for non-trivial Pb0.81Sn0.19Se we find |2Δ| = 25 ± 10 meV and v D = (4.8 ± 0.1)x105 m/s for the longitudinal and v D = (4.6 ± 0.1)x105 m/s for the oblique valleys. The Fermi level can be extracted from the onset of the 1v-0c transition and the CR. We find 20 meV and 25 meV from the band edge in x = 0.14 and x = 0.19, respectively, in agreement with the bulk carrier density (p≈2x1017 cm−3 and n≈3x1017 cm−3, respectively).
Measurement of the topological index
We systematically study a total of eight Pb1-x Sn x Se samples (0 ≤ x ≤ 0.3) and 20 Pb1-x Sn x Te samples (0 ≤ x ≤ 0.56). Note that in all samples, the magnetooptical transitions can be well interpreted with a massive Dirac model (Eq. 7) in order to extract |2Δ| and v D . The analysis is shown in Fig. 4 for Pb1-x Sn x Se and in the supplement (S3) for Pb1-x Sn x Te. The longitudinal and oblique velocities extracted from the massive Dirac model are, respectively, plotted vs. x in Figs. 4a, b. They show a consistent decrease as x is increased for both materials. The band gap |2Δ| is shown in Fig. 4c. A minimum is observed for x = 0.165 followed by an increase when x is increased beyond this concentration. The smallest measured energy gap is 15 ± 5 meV (ref. 28). We can still estimate the critical velocity v c to be equal to 5.0x105 m/s for the longitudinal valley and 4.7x105 m/s for the oblique valleys (Figs. 4a, b), since the critical composition of Pb1-x Sn x Se is known. In Fig. 4d \(\Delta /\tilde m = v_D^2 - v_c^2\) is depicted. The sign change of \(\Delta /\tilde m\) reflects the emergence of a topological phase in Pb1-x Sn x Se having a non-zero topological index η = 1. A first measurement of the bulk topological index in a material family of 3D topological insulators is thus confirmed in our experiment.
Dependence of the velocity on the energy-gap and its sign inversion in Pb1-x Sn x Se. Longitudinal (a) and oblique (b) velocity and energy-gap (c) measured in Pb1-x Sn x Se at 4.5 K. The blue line in a and b indicates the position of the critical velocity vc. (d) \(\Delta /\tilde m\) plotted as a function of x. Shaded blue area indicates the topological regime
In order to verify the consistency of the approximations used in the theory, we estimate the value of \(\tilde m\) from the measurement of the energy gap and \(\Delta /\tilde m\) and check that its contribution is indeed small. The values are listed in Table 1. We discuss this more thoroughly in the supplement (S4).
Cyclotron resonance of TSSs
Finally, we corroborate our findings by further evidencing the observation of TSSs that appear in the non-trivial regime. Measurements in the far-IR up to 17 T are performed and are shown for x = 0.14 and x = 0.19 in Figs. 5a, b. The Landau level transitions in the far-IR are shown in Figs. 5c, d. The CR of the bulk valleys (CR-LO) and the first interband transition can be seen in Pb0.86Sn0.14Se (Figs. 5a, c). In Pb0.81Sn0.19Se, two transitions can be resolved, the first interband transition, as well as an additional transition marked by a blue arrow in Figs. 5b, d. It occurs at energies higher than 60 meV where the CR of the bulk bands is expected, as seen in Fig. 5d. It is observed in Pb0.81Sn0.19Se (Fig. 5b), but not in Pb0.86Sn0.14Se (Fig. 5a). Its dispersion (blue in Fig. 5d) agrees well with that of Landau-levels of massless Dirac fermions having a velocity v D = (4.7 ± 0.1)x105 m/s—almost equal to that of the bulk valleys:
Far-IR magnetooptical spectra of samples x = 0.14 (a) and x = 0.19 (b). The first interband transition is labeled in both. The bulk CR is labeled in a and the CR-TSS is labeled in blue in b. The double-sided arrow corresponds to T(B)/T(0) = 0.05. c x = 0.14 and d x = 0.19 Landau level dispersions with data points for bulk CR added in black c and for CR-TSS added in blue d. Solid lines are curve fits using massive Dirac model transitions for bulk states in red and black (Eqs. 10a, b) and massless Dirac model for CR-TSS (Eq. 11). The reststrahlen of BaF2 is shown in green
This transition could thus be attributed to the ground-state CR of massless Dirac TSS.
This transition is only visible at 15 T and above in Pb0.81Sn0.19Se. Accordingly, the Fermi level is estimated to be around 60 meV from the Dirac point. We cannot distinguish the \(\bar \Gamma \)-Dirac cone from the \(\bar {\rm M}\)-Dirac cones (see Fig. 1b) in Pb0.81Sn0.19Se since the two have similar Fermi velocities and hence have overlapping CR. This might also explain the large intensity of the transition attributed to the TSS. Further evidence of the observation of massless TSS in Pb1-x Sn x Te (x > 0.40) is presented in the supplement (S2) as well as in a previous work on Pb0.54Sn0.46Te.23 All in all, Fig. 5 shows that a CR resulting from TSS is observed when \(\Delta /\tilde m < 0\).
Discussion
In conclusion, our result is an analytical and experimental proof that the topological index of 3D TIs can be measured by magnetooptical Landau level spectroscopy. Our approach is most suitable for ultra-narrow gap systems, having very light effective masses. It is not as suitable for materials having heavy effective masses such as Bi2Se3.
In [111]-oriented Pb1-x Sn x Se and Pb1-x Sn x Te, we have experimentally shown that a measurement of v D relative to the critical v c allows one to experimentally determine the topological character of a material. This work is thus a proof of concept that the topological index can be measured using a technique that quantifies the bulk band parameters, and not just inferred from the observation of surface states. Our results are further supported by the observation of a CR from massless Dirac topological surface-states in the non-trivial regime. We believe that this approach can be applicable to any system supporting massive or massless Dirac fermions that go through a topological phase transition and that can be described by a BHZ Hamiltonian.19, 33, 34, 36, 38, 63,64,65,66,67,68. Accordingly, we propose to further study under the same scope compound series such as Hg1-x Cd x Te (see supplement 5),36 BiTlS1-δ Se δ ,33, 34 Bi2-x In x Se3 (ref. 66), topological Heusler materials67 as well as Dirac semimetals such as Na3Bi and Cd3As2,37, 68 all expected to have a trivial to non-trivial topological phase transition.
Methods
MBE growth
Epitaxial growth of (111) Pb1-x Sn x Se and Pb1-x Sn x Te58, 59 films on BaF2 (111) substrates is performed using a Riber 1000 and a Varian GEN-II MBE set-up, respectively. Samples are grown under Ultra-high vacuum conditions better than 5 × 10−10 mbar. Effusion cells filled with stoichiometric PbSe, PbTe, SnSe, and SnTe are used as source materials. The chemical composition of the ternary layers is varied over a wide range by control of the SnSe/PbSe (SnTe/PbTe) beam flux ratio that is measured precisely using a quartz microbalance moved into the substrate position. The growth rates are typically 1 µm/hour (~ 1 monolayer/s) and the growth temperature is set to 380 °C as checked by an IRCON IR pyrometer. The thickness of the films is in the range of 1–3 µm. In order to obtain a low free carrier concentration (<1018 cm−3), and compensate the native background hole concentration that increases strongly for higher Sn concentration in Pb1-x Sn x Se and Pb1-x Sn x Te, extrinsic n-type Bi-doping was provided by Bi2Se3 or Bi2Te3 doping cells.61 The growth is monitored in-situ using RHEED.
X-ray diffraction
XRD measurements are performed using Cu-Kα 1 radiation in a Seifert XRD3003 diffractometer, equipped with a parabolic mirror, a Ge(220) primary beam Bartels monochromator and a Meteor 1D linear pixel detector.
Transport characterization
Transport measurements are performed at 77 K using a van der Pauw geometry in order to determine the Hall carrier density and mobility.
Magnetooptical absorption spectroscopy
Magnetooptical absorption experiments are performed in an Oxford Instruments 1.5 K/17 T cryostat at 4.5 K. Spectra are acquired using a Bruker Fourier transform spectrometer. All measurements are made in Faraday geometry. Two different broadband sources are used for different IR ranges: a far-IR source (3–900 cm−1) and a mid-IR source (400–3600 cm−1). Measurements are performed at fixed magnetic fields between 0 and 15 T and occasionally up to 17 T. A He cooled bolometer, is used to detect the transmitted signal. The relative transmission at fixed magnetic field T(B)/T(B = 0) is extracted and analyzed. Baseline signal contributions from the bolometer’s response variations in the magnetic field are negligible in this experiment, due to the large amplitude of the observed transitions.
References
Kane, C. L. & Mele, E. J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 95, 226801 (2005).
Bernevig, B. A., Hughes, T. L. & Zhang, S.-C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757–1761 (2006).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Zhang, H. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438–442 (2009).
Hsieh, T. H. et al. Topological crystalline insulators in the SnTe material class. Nat. Commun. 3, 982 (2012).
Fu, L. Topological crystalline insulators. Phys. Rev. Lett. 106, 106802 (2011).
Fu, L. & Kane, C. Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302 (2007).
Konig, M. et al. Quantum spin Hall insulator state in HgTe quantum wells. Science 318, 766–770 (2007).
Chang, C.-Z. et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 340, 167–170 (2013).
Chang, C.-Z. et al. High-precision realization of robust quantum anomalous Hall state in a hard ferromagnetic topological insulator. Nat. Mater. 14, 473–477 (2015).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Fu, L. & Kane, C. Probing neutral Majorana fermion edge modes with charge transport. Phys. Rev. Lett. 102, 216403 (2009).
Hsieh, D. et al. A topological Dirac insulator in a quantum spin Hall phase. Nature 452, 970–974 (2008).
Hsieh, D. et al. Observation of time-reversal-protected single-Dirac-cone topological-insulator states in Bi2Te3 and Sb2Te3. Phys. Rev. Lett. 103, 146401 (2009).
Dziawa, P. et al. Topological crystalline insulator states in Pb(1-x)Sn(x)Se. Nat. Mater. 11, 1023–1027 (2012).
Tanaka, Y. et al. Experimental realization of a topological crystalline insulator in SnTe. Nat. Phys. 8, 800–803 (2012).
Xu, S.-Y. et al. Observation of a topological crystalline insulator phase and topological phase transition in Pb(1-x)Sn(x)Te. Nat. Commun. 3, 1192 (2012).
Pletikosić, I., Gu, G. D. & Valla, T. Inducing a Lifshitz transition by extrinsic doping of surface bands in the topological crystalline insulator Pb1-xSnxSe. Phys. Rev. Lett. 112, 146403 (2014).
Orlita, M. et al. Magneto-optics of massive Dirac fermions in bulk Bi2Se3. Phys. Rev. Lett. 114, 186401 (2015).
Xia, Y. et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nat. Phys. 5, 398–402 (2009).
Ando, Y. Topological insulator materials. J. Phys. Soc. Japan 82, 102001 (2013).
Sánchez-Barriga, J. et al. Nonmagnetic band gap at the Dirac point of the magnetic topological insulator (Bi1−xMnx)2Se3. Nat. Commun. 7, 10559 (2016).
Assaf, B. A. et al. Massive and massless Dirac fermions in Pb1-xSnxTe topological crystalline insulator probed by magnetooptical absorption. Sci. Rep. 6, 20323 (2016).
Okada, Y. et al. Observation of Dirac node formation and mass acquisition in a topological crystalline insulator. Science 341, 1496–1499 (2013).
Wojek, B. M. et al. Direct observation and temperature control of the surface Dirac gap in a topological crystalline insulator. Nat. Commun. 6, 8463 (2015).
Assaf, B. A. et al. Quantum coherent transport in SnTe topological crystalline insulator thin films. Appl. Phys. Lett. 105, 102108 (2014).
Wang, Y., Luo, G., Liu, J., Sankar, R. & Wang, N. Surface states dominated infrared conductivity in a topological crystalline insulator. arxiv 1611, 04302 (2016). at <http://arxiv.org/abs/1611.04302>.
Wojek, B. M. et al. On the nature of the band inversion and the topological phase transition in (Pb,Sn)Se. Phys. Rev. B 90, 161202 (2014).
Zeljkovic, I. et al. Dirac mass generation from crystal symmetry breaking on the surfaces of topological crystalline insulators. Nat. Mater. 14, 318–324 (2015).
Neupane, M. et al. Topological phase diagram and saddle point singularity in a tunable topological crystalline insulator. Phys. Rev. B 92, 075131 (2015).
Roy, B., Goswami, P. & Sau, J. D. Continuous and discontinuous topological quantum phase transitions. Phys. Rev. B 94, 041101 (2016).
Juricic, V., Abergel, D. S. L. & Balatsky, A. V. First-order quantum phase transition in three-dimensional topological band insulators. Phys. Rev. B 95, 161403 (2017).
Xu, S.-Y. et al. Topological phase transition and texture inversion in a tunable topological insulator. Science 332, 560–564 (2011).
Sato, T. et al. Unexpected mass acquisition of Dirac fermions at the quantum phase transition of a topological insulator. Nat. Phys. 7, 840–844 (2011).
Liu, J., Fang, C. & Fu, L. Tunable Weyl fermions and Fermi arcs in magnetized topological crystalline insulators. arXiv 1604, 03947 (2016). at <http://arxiv.org/abs/1604.03947>.
Guldner, Y., Rigaux, C., Mycielski, a & Couder, Y. Magnetooptical investigation of Hg1-xCdxTe mixed crystals II. Semiconducting configuration and semimetal to semiconductor transition. Phys. Status Solidi 82, 149–158 (1977).
Yuan, X. et al. Direct observation of Landau level resonance and mass generation in Dirac semimetal Cd3As2 thin films. Nanolett 17, 2211–2219 (2017).
Liu, C. X. et al. Model Hamiltonian for topological insulators. Phys. Rev. B 82, 045122 (2010).
Shen, S. -Q. Topological Insulators: Dirac Equation in Condensed Matters, 174, (Springer Science & Business Media, 2013).
Bernevig, B. A. & Hughes, T. L. Topological Insulator and Topological Superconductors, (Princeton University Press, 2013).
Strauss, A. J. Inversion of conduction and valence bands in Pb1-xSnxse alloys. Phys. Rev. 157, 608–611 (1967).
Calawa, A., Dimmock, J., Harman, T. & Melngailis, I. Magnetic field dependence of laser emission in Pb1-XSnXSe diodes. Phys. Rev. Lett. 23, 7–10 (1969).
Bauer, G. In Narrow Gap Semiconductors Physics and Applications: Proceeding of the Internationl Summer School (ed. Zawadzki, W.) 133, 427–446 (Springer Berlin Heidelberg, 1980).
Polley, C. M. et al. Observation of topological crystalline insulator surface states on (111)-oriented Pb 1-x Sn x Se films. Phys. Rev. B 89, 075317 (2014).
Safaei, S., Kacman, P. & Buczko, R. Topological crystalline insulator (Pb,Sn)Te: Surface states and their spin polarization. Phys. Rev. B 88, 045305 (2013).
Wang, Y. J. et al. Nontrivial spin texture of the coaxial Dirac cones on the surface of topological crystalline insulator SnTe. Phys. Rev. B 87, 235317 (2013).
Yan, C. et al. Experimental observation of Dirac-like surface states and topological phase transition in Pb1−xSnxTe(111) films. Phys. Rev. Lett. 112, 186801 (2014).
Liu, J., Duan, W. & Fu, L. Two types of surface states in topological crystalline insulators. Phys. Rev. B 88, 241303 (2013).
Tanaka, Y. et al. Two types of Dirac-cone surface states on the (111) surface of the topological crystalline insulator SnTe. Phys. Rev. B 88, 235216 (2013).
Grisar, R., Burkhard, H., Bauer, G. & Zawadzki, W. Magnetooptical transitions and band parameters of PbTe. In Proceedings of the International Conference on the Physics of Narrow Gap Semiconductors, Warszawa, (ed. Rauluszkiewicz, J.) 115 (PWN-Polish Scientific, 1978).
Burkhard, H., Bauer, G. & Zawadzki, W. Band-population effects and intraband magneto-optical properties of a many-valley semiconductor: PbTe. Phys. Rev. B 19, 5149–5159 (1979).
Mitchell, D. L. & Wallis, R. F. Theoretical energy-band parameters for the lead salts. Phys. Rev. 151, 581–595 (1966).
Martinez, G. Band Inversion of Pb1-xSnxSe alloys under hydrostatic pressure. I. Theoretical band structure analysis. Phys. Rev. B 8, 4678–4685 (1973).
Goerbig, M. O., Montambaux, G. & Piéchon, F. Measure of Diracness in two-dimensional semiconductors. EPL (Europhysics Lett.) 105, 57005 (2014).
Pascher, H., Bauer, G. & Grisar, R. Magnetooptical investigations and four-wave-mixing spectroscopy of PbSe. Phys. Rev. B 38, 3383–3390 (1988).
Nimtz, G. & Schlicht, B. Narrow-Gap Semiconductors. Vol. 98, (Springer, 1983).
Ando, Y. & Fu, L. Topological crystalline insulators and topological superconductors: from concepts to materials. Annu. Rev. Condens. Matter Phys. 6, 361–381 (2015).
Springholz, G. & Bauer, G. In Landolt-Bornstein (ed. Klingsher, C.) 415–561 (Springer, 2013).
Springholz, G. In Molecular Beam Epitaxy (ed. Henini, M.) 263–310 (Elsevier, 2013).
Springholz, G., Ueta, A. Y., Frank, N. & Bauer, G. Spiral growth and threading dislocations for molecular beam epitaxy of PbTe on BaF2 (111) studied by scanning tunneling microscopy. Appl. Phys. Lett. 69, 2822–2824 (1996).
Ueta, A. Y., Springholz, G., Schinagl, F., Marschner, G. & Bauer, G. Doping studies for molecular beam epitaxy of PbTe and Pb1−xEuxTe. Thin Solid Films 306, 320–325 (1997).
Burke, J. R., Houston, B. & Savage, H. T. Anisotropy of the Fermi surface of p-type PbTe. Phys. Rev. B 2, 1977–1988 (1970).
Wang, Z. et al. Dirac semimetal and topological phase transitions in A3Bi (A = Na, K, Rb). Phys. Rev. B 85, 195320 (2012).
Jeon, S. et al. Landau quantization and quasiparticle interference in the three-dimensional Dirac semimetal Cd3As2. Nat. Mater. 13, 851–856 (2014).
Teppe, F. et al. Temperature-driven massless Kane fermions in HgCdTe crystals. Nat. Commun. 7, 12576 (2016).
Wu, L. et al. A sudden collapse in the transport lifetime across the topological phase transition in (Bi1−xInx)2Se3. Nat. Phys. 9, 410–414 (2013).
Chadov, S. et al. Tunable multifunctional topological insulators in ternary Heusler compounds. Nat. Mater. 9, 541–545 (2010).
Pan, H., Wu, M., Liu, Y. & Yang, Sa Electric control of topological phase transitions in Dirac semimetal thin films. Sci. Rep. 5, 14639 (2015).
Acknowledgements
We would like to thank T. Kontos, V. Juricic, S.Q. Shen, and X.R. Wang for useful comments. This work is supported by Agence Nationale de la Recherche LabEx grant ENS-ICFP (ANR-10-LABX-0010/ANR-10-IDEX-0001-02 PSL) and by the Austrian Science Fund, Project SFB F2504-N17 IRON. T.P. acknowledges support from the Mahidol Wittayanusorn Scholarship and the Franco-Thai Scholarship.
Author information
Authors and Affiliations
Contributions
T.P., L.A.V., and Y.G. performed magnetooptical IR measurements. B.A.A., T.P., L.A.V., and Y.G. analyzed the data with the assistance of G.B. B.A.A. and Y.G. developed and tested the theoretical description with the assistance of G.B. V.V.V., and G.S. grew by MBE and characterized the samples using XRD, EDX, RHEED, and transport. B.A.A., L.A.V., and Y.G. conceived the project. All authors collaboratively discussed the results and contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing financial interest.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Assaf, B.A., Phuphachong, T., Volobuev, V.V. et al. Magnetooptical determination of a topological index. npj Quant Mater 2, 26 (2017). https://doi.org/10.1038/s41535-017-0028-5
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-017-0028-5