Abstract
An important challenge in condensed matter physics is understanding iron-based superconductors. Among these systems, the iron selenides hold the record for highest superconducting transition temperature and pose especially striking puzzles regarding the nature of superconductivity. The pairing state of the alkaline iron selenides appears to be of d-wave type based on the observation of a resonance mode in neutron scattering, while it seems to be of s-wave type from the nodeless gaps observed everywhere on the Fermi surface. Here we propose an orbital-selective pairing state, dubbed sτ 3, as a natural explanation of these disparate properties. The pairing function, containing a matrix τ 3 in the basis of 3d-electron orbitals, does not commute with the kinetic part of the Hamiltonian. This dictates the existence of both intraband and interband pairing terms in the band basis. A spin resonance arises from a d-wave-type sign change in the intraband pairing component, whereas the quasiparticle excitation is fully gapped on the FS due to an s-wave-like form factor associated with the addition in quadrature of the intraband and interband pairing terms. We demonstrate that this pairing state is energetically favored when the electron correlation effects are orbitally selective. More generally, our results illustrate how the multiband nature of correlated electrons affords unusual types of superconducting states, thereby shedding new light not only on the iron-based materials but also on a broad range of other unconventional superconductors such as heavy fermion and organic systems.
Similar content being viewed by others
Introduction
Unconventional superconductivity is driven by electron–electron interactions, instead of electron–phonon couplings.1 It occurs in a variety of strongly correlated electron systems, with the iron-based superconductors (FeSCs) representing a prototype case.2,3,4,5,6,7 The field of FeSC started with most of the efforts being directed toward the iron pnictide class. The normal state was found to be a bad metal, with room-temperature resistivity reaching the Mott-Ioffe-Regel limit,3, 8 suggesting the importance of electron correlations.9, 10 More recently, the focus has been shifted to iron selenide systems. The reasons are manifold. They have the highest T c,11, 12 they show even stronger electron correlations, and, as we discuss here, their superconductivity is highly unusual.
The puzzle of the superconducting pairing state is highlighted by the “122” alkaline iron selenides. These systems have a T c of ~31 K at ambient pressure. They have only electron Fermi pockets, lacking the hole pockets that exist in the iron pnictides at the center of the Brillouin zone (BZ).13,14,15 Angle-resolved photoemission spectroscopy (ARPES) experiments show that the quasiparticle dispersion is fully gapped on all the parts of the Fermi surface (FS),13,14,15 including a small electron Fermi pocket at the center of the BZ.16, 17 This is compatible with the usual s-wave A 1g pairing state, but not with the usual d-wave B 1g state (which would produce nodes on the small electron Fermi pocket near the center of the BZ). On the other hand, inelastic neutron scattering experiments18, 19 observe a sharp resonance peak around the wavevector (π, π/2). It is consistent with a pairing function that changes sign20 between the two Fermi pockets at the edge of the BZ, such as would occur in a d-wave B 1g state, but not in the usual s-wave A 1g case.
In this work, we demonstrate how an orbital-selective pairing state, dubbed sτ 3, exhibits properties that are commonly associated with a d-wave B 1g state or a s-wave A 1g state. The key to the emergence of this superconducting state is the multiband nature of the FeSCs. This is associated with the multiplicity of 3d electron orbitals, whose conceptual importance follows the tradition wherein new physics develops out of extra degrees of freedom, similar, for instance, to the way the so-called valley quantum number in the electronic structure introduces new topological properties.21 It is important for the FeSCs that there are multiple orbitals at play in the neighborhood of the Fermi level. Thus, there is reason to expect that correlation effects will be different for different orbitals. In fact, there is evidence for orbitally selective Mott behavior in the iron selenides22,23,24,25,26 and, thus, orbital selectivity is to be expected for pairing as well.
For strongly correlated superconductivity, Cooper pairing is naturally considered in an orbital basis due to the tendency of the electrons to avoid the dominating Coulomb repulsions. Considering a basis formed from all five 3d orbitals, the sτ 3 state has an s-wave form factor, but transforms as a d-wave B 1g state. As such, it represents an energetically favored reconstruction of the conventional s-wave and d-wave pairing states when they are quasi-degenerate, due to frustrated antiferromagnetic interactions.27 The pairing function incorporates a matrix τ 3 in the 3d xz , 3d yz subspace, which does not commute with the kinetic term of the Hamiltonian. Consequently, in the band basis, it must also have a matrix structure, which contains both intraband and interband terms. This allows the intraband pairing component to have a d-wave sign change, while the addition in quadrature of the intraband and interband pairing terms is nonzero everywhere on the FS. Thereby, the spin excitations show a (π, π/2) resonance, while the quasiparticle excitations as measured by ARPES are fully gapped on the FS.
Results
Orbital selectivity in the normal state of iron selenides
In the normal state, ARPES has provided evidence not only for the existence of the orbital degree of freedom but also for the strong orbital-selective correlation effects on the iron selenides. These materials include the alkaline iron selenides, the Te-doped “11” iron selenides FeSe, and the monolayer FeSe on the SrTiO3 substrate.22,23,24,25,26 The effective quasiparticle mass normalized by its non-interacting counterpart, m */m band is on the order of 3–4 for the 3d xz,yz orbitals, but is as large as 20 for the 3d xy orbital.22, 23, 28 Such orbital selectivity has also been the subject of extensive recent theoretical studies.29,30,31 All these aspects make it natural to study orbital-dependent32,33,34 and -related35 superconducting pairing. We are thus motivated to address the hitherto unexplored question, viz. whether there exists an orbital-selective pairing state that can reconcile the seemingly contradictory properties observed in the iron selenide superconductors. We also examine the stability of such a pairing state at the level of an effective Hamiltonian for studying superconductivity, in which we incorporate the orbital selectivity in the short-range exchange interactions (see Supplementary Information).
Orbital-selective sτ3 pairing state—a simplified case
We first discuss the structure and properties of the sτ 3 pairing state in a simplified two-orbital d xz , d yz system. This illustrates how features typically associated with both standard structure-less s- and d-wave states can simultaneously arise. The salient features of the two-orbital model are illustrated in Fig. 1.
Schematic illustration of the two-orbital sτ 3 pairing in a 1-Fe Brillouin zone (BZ), which is obtained by unfolding the 2D crystallographic BZ cell in the conventional manner.55 The solid lines indicate typical Fermi pockets for the Fe-based superconductors. The dotted, red lines indicate the zeroes specific to the intraband pairing (ξ − ), while the dashed, blue lines mark the zeroes specific to the interband pairing (ξ xy ). The intra- and interband components do not vanish at the same subset of k, ensuring that there is always a non-zero pairing given by either of the two components on the entire Fermi surface. For max(ξ − )≈max(ξ xy ) the angle ϕ(k) (Eqs 5–7) can be roughly identified with twice the winding angle shown for fixed |k|. In addition, there is a sign change between the intraband pairing along the two pockets at the edge of the BZ, a condition necessary to the formation of a resonance in the spin-excitation spectrum at the wavevector q = (π, π/2) observed in experiment.50
We consider spin-singlet pairing in the orbital basis, in the case of two orbitals 3d xz , 3d yz .36 The Hamiltonian, incorporating the sτ 3 pairing term, is given by
where \(\psi _{\boldsymbol{k}}^\dag = \left( {c_{{\boldsymbol{k}}i\sigma }^\dag ,{c_{ - {\boldsymbol{k}}j\sigma '}}{{\left( {i{\sigma _2}} \right)}_{\sigma '\sigma }}} \right)\) is equivalent to a Nambu spinor, and i and j are orbital indices (Supplementary Information). The τ i , σ i , and γ i (i = 0,…,4) 2 × 2 Pauli matrices represent orbital iso-spin, spin, and Nambu indices, respectively. The ξ +, ξ −, and ξ xy factors appearing in the kinetic part belong to the A 1g , B 1g , and B 2g irreducible representations of the D 4h point-group. Their exact forms, as well as the resulting electron bands, are given in Supplementary Information.
The even-parity, spin-singlet candidate sτ 3 pairing function with non-trivial orbital structure is included in the \({\hat H_{{\rm{Pair}}}}\) term in Eq. 1. While Δ0 is a (generally) complex number, we choose a real amplitude for convenience. The form factor \({g_{{x^2}{y^2}}}\left( {\boldsymbol{k}} \right)\) is parity-even and belongs to the A 1g representation of the D 4h point-group. In the absence of spin–orbit coupling, the rotational properties of the sτ 3 pairing are of B 1g symmetry. The latter is entirely determined by the tensor product of the \({g_{{x^2}{y^2}}}\left( {\boldsymbol{k}} \right)\) (s-wave) form factor and the τ 3 orbital matrix. To illustrate, under a C 4z rotation, the form-factor is invariant, while the τ 3 matrix transforms as a rank-two B 1g tensor representation of the point-group, i.e., it changes sign. We note that the anti-symmetry under exchange is guaranteed by the spin-singlet nature, together with the even-parity of the form factor. Since the spin-structure is not essential for the following arguments, we shall henceforth omit the explicit σ 0 matrix.
The non-trivial characteristics of this pairing are consequences of the commutator \(\left[ {{{\hat H}_{{\rm{Kinetic}}}},{{\hat H}_{{\rm{Pair}}}}} \right]\ \ne\ 0\) for general momentum k. We use the notation of ref. 34, and rewrite the Hamiltonian Eq. 1 as follows:
where
This is formally similar to a Balian–Werthamer form37,38,39 (see Supplementary Information for more details), with the \(\vec B\left( {\boldsymbol{k}} \right)\) factor being analogous to a k-dependent spin–orbit coupling. To account for the non-commuting \({\hat H_{{\rm{Kinetic}}}}\) and \({\hat H_{{\rm{Pair}}}}\), we write the square of the Hamiltonian matrix as follows:
where the well-known relation \(\left( {\vec a \cdot \vec \tau } \right)\left( {\vec b \cdot \vec \tau } \right) = \vec a \cdot \vec b + i\left( {\vec a \times \vec b} \right) \cdot \vec \tau \) was used. The first two terms, proportional to the γ 0 Nambu matrix, are the squares of the kinetic Hamiltonian and of a pairing contribution with no essential structure in orbital space, given by \({\left| {\vec d\left( {\boldsymbol{k}} \right)} \right|^2}\). The latter is an effective amplitude of the pairing interactions and, as such, is proportional to the square of the s-wave-like \({g_{{x^2}{y^2}}}\) form factor, as can be seen from Eq. 3. Together with the kinetic part, it amounts to the usual (and sole) contribution to the Bogoliubov–de Gennes (BdG) quasiparticle spectrum, whenever \(\left[ {{{\hat H}_{{\rm{Kinetic}}}},{{\hat H}_{{\rm{Pair}}}}} \right] = 0\) for all k. The last term in Eq. 4 reflects the non-commuting \({\hat H_{{\rm{Kinetic}}}}\) and \({\hat H_{{\rm{Pair}}}}\). Since the Nambu matrices γ 0 and iγ 2 commute, \({\hat H^2}\) in Eq. 4 can be easily expressed in block diagonal form (Supplementary Information). The resulting BdG bands are given by
where
The terms proportional to \(\sin \phi \left( {\boldsymbol{k}} \right)\) reflects the non-Abelian aspect of the pairing state. Note that Eq. 5 corresponds to the sum of two positive semi-definite terms. For general \(\vec d\left( {\boldsymbol{k}} \right)\), we see that nodes can appear only when both terms in the square root vanish. The second of these goes to zero when either \({\rm{sin}}\phi \left( {\boldsymbol{k}} \right) = 1\) or, trivially, when \(\left| {\vec d\left( {\boldsymbol{k}} \right)} \right| = 0\). This latter case occurs when the FS intersects the lines of zeros of the \({g_{{x^2}{y^2}}}\) form factor. With the FeSCs in mind, we ignore this simple case in the following. Alternately, when \({\rm{sin}}\phi \left( {\boldsymbol{k}} \right) = 1\), the dispersion reduces to
On the FS, we have \(\xi _ + ^2\left( {\boldsymbol{k}} \right) = {\left| {\vec B\left( {\boldsymbol{k}} \right)} \right|^2}\) (see Supplementary Information). Thus, there are no nodes on the FS.
We note that away from the FS, Eq. 7 does not in general guarantee the absence of nodes. However, because the lifetime of quasiparticles away from the FS will be finite, the corresponding contributions to thermodynamical properties will be much weaker compared to the case of nodes on the FS.
In the band basis, the kinetic part of the Hamiltonian is diagonalized. Given that the kinetic and pairing parts do not commute with each other, the two cannot be simultaneously diagonalized. Thus, the pairing part must contain an interband component. To see this, we apply a canonical transformation that diagonalizes the kinetic part (see Supplementary Information), but which also transforms the pairing into
where α 1 and α 3 are Pauli matrices corresponding to inter- and intraband pairing terms, respectively. The two components are given by
The band-diagonal α 3 and band off-diagonal α 1 pairing components have d(x 2−y 2) and d(xy) form factors, respectively. As illustrated in Fig. 1, these have nodes along the diagonals and axes of the BZ, respectively. Because the two matrices α 1 and α 3 anti-commute, the single-particle excitation energy depends on the addition in quadrature of the two pairing amplitudes Δ1(k) and Δ2(k). This ensures that the excitation gap is nodeless on the entire FS.
As can be seen from Eqs 8 and 9, the band-index diagonal term changes sign about the diagonals (k x = ± k y ) of the BZ, as dictated by the d(x 2−y 2) nature of the intraband component. Thus, the intraband pairing component does indeed change sign between the two-electron Fermi pockets at the BZ boundaries. It ensures that this type of pairing is conducive to the formation of a resonance with a wavevector that connects the two-electron Fermi pockets.
We stress that the two main features of the sτ 3 pairing, i.e., the formation of a gap on the FS and the sign change in the intraband component, cannot be reconciled by the more typical pairing candidates, which lack an orbital structure. In the context of our two-orbital model, the s⊗τ 0 and d⊗τ 0 candidate states, corresponding to the typical orbitally trivial s- and d-wave pairings, commute with \({\hat H_{{\rm{Kinetic}}}}\). Consequently, they are associated with intraband pairing only. As such, neither of the two types can induce a nodeless gap and account for the sign change required for the spin-resonance.
Orbital-selective sτ3 pairing state—the case of iron selenides
Superconductivity in the alkaline iron selenides, like in the related case of the iron pnictides, involves all five Fe 3d-orbitals. Thus, it is important to consider the five-orbital case to address (i) whether the sτ 3 pairing state is energetically favored compared to the more conventional pairing states and (ii) whether it captures the essential properties of this pairing state as they pertain to the iron selenide superconductors.
To study the stability of the sτ 3 pairing state, we start from two previously discussed aspects of the FeSCs. We do so in terms of a strong-coupling approach to superconductivity, in light of the strong correlation effects9, 10, 31, 40,41,42,43,44,45,46,47,48 that are especially clear-cut for the iron selenides.22, 23, 28 This approach is described in Supplementary Information, with superconductivity driven by short-range interactions. The latter include the antiferromagnetic interactions between the nearest-neighbor (\(J_1^\alpha \)) and next-nearest-neighbor (\(J_2^\alpha \)) Fe sites on their square lattice, for the three most relevant orbitals, α = 3d xz , 3d yz , and 3d xy . We reiterate that we will analyze the model in the 1-Fe unit cell and the corresponding BZ.
One of the known aspects of the FeSCs is the large parameter regime where the conventional d-wave B 1g and s-wave A 1g pairing states are quasi-degenerate.27, 49 In terms of a model with short-range antiferromagnetic interactions, this occurs in the regime of magnetic frustration with J 2 being comparable to J 1,27 a condition that is evidenced by both theoretical considerations and experimental measurements.4, 50 To quantify this effect, we introduce the ratio A L ≡ J 2/ J 1 to describe the relative strength of these two interactions. For a proof-of-concept demonstration, we analyze the phase diagram by taking the J 2/ J 1 axis to be a cut in the parameter space along which A L is the same for the different 3d-orbitals. The quasi-degeneracy arises when A L ~ 1.
The second well-known property of the FeSCs is orbital selectivity, as described above. Our effective model incorporates an exchange orbital-anisotropy factor \({A_{\rm{o}}} = J_1^{xy}/J_1^{xz/yz} = J_2^{xy}/J_2^{xz/yz}\), and reflects the orbital selectivity by A o’s deviation from 1. For the iron selenides, A o is expected to be considerably smaller than 1 (see Supplementary Information).
We are now in a position to discuss how the sτ 3 pairing state emerges in a range of parameters where the s- and d-wave pairing channels are quasi-degenerate. Within the five-orbital t−J 1−J 2 model, we focus on the case with a kinetic part appropriate for the alkaline iron selenides K y Fe2−x Se2, although similar behavior emerges in the cases appropriate for the iron pnictides and single-layer FeSe (see Supplementary Information). We present our results for the case of orbital-diagonal exchange interactions. The inter-orbital exchange interactions have only negligible effects on the pairing amplitudes, as demonstrated in Supplementary Information.
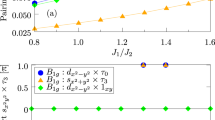
The phase diagram for the alkaline iron selenides is shown in Fig. 2a. In the absence of orbital selectivity, A o = 1, it is known that small and large A L promote the \({s_{{x^2}{y^2}}} \otimes {\tau _0},{A_{1g}}\) and \({d_{{x^2} - {y^2}}} \otimes {\tau _0},{B_{1g}}\), both defined in the d xz , d y subspace.27 Increasing the orbital selectivity, with A o decreasing from 1, these two limiting regimes remain essentially unchanged. However, in the magnetically frustrated regime A L ~ 1, the \({s_{{x^2}{y^2}}} \otimes {\tau _0},{A_{1g}}\) and \({d_{{x^2} - {y^2}}} \otimes {\tau _0},{B_{1g}}\) become quasi-degenerate. When A o is sufficiently smaller than 1, the sτ 3 pairing state becomes the dominant channel in the intermediate regime. Similar phase diagrams are obtained for the iron pnictides and single-layer FeSe shown in Fig. 2b and Fig. S1, respectively. A typical dominant sτ 3 pairing case is shown in Fig. S2 and Fig. S1 for a number of subleading symmetry-allowed channels51 for alkaline iron selenide dispersion with fixed J 2/J 1 = 1.5, A o = 0.3, and varying A L (horizontal axis).
Phase diagrams based on the leading pairing amplitudes given by self-consistent calculations with fixed J 2 = 1 and tight-binding parameters appropriate to a alkaline iron selenides and b iron pnictides. The tight-binding parameters used can be found in ref. 27. The blue shaded areas correspond to dominant pairing channels with an \({s_{{x^2}{y^2}}}\) form factor, while the red shading covers those with a \({d_{{x^2} - {y^2}}}\) form factor. The continuous line separates regions where the pairing belongs to the A 1g and the B 1g representations, respectively. The 1 × 1 matrix in the d xy subspace is represented by 1 xy . The orbital-selective sτ 3 pairing occurs for A O < 1, A L near 1 in all cases
Having established the stability of the sτ 3 pairing state, we now address its salient properties. We first consider the spin-excitation spectrum. In Fig. 3, we show the dynamical spin susceptibility at wavevector q = (π, π/2) for J 2 = 1.5. We note the complicated frequency behavior that can be traced to the anisotropy in the effective gap affecting both the coherence factors and the position of minimum in quasi-particle energy. We show the minimum and maximum particle–hole (p–h) thresholds corresponding to twice the minimum and twice the maximum gaps. As suggested by Fig. 4a and b, states connected by q = (π, π/2) would correspond to a p–h threshold given roughly by the sum of the minimum and maximum gap. A sharp feature appears below this threshold, confirming the existence of the resonance for q = (π, π/2) as found in experiments on the alkaline iron selenides.18, 19, 50 The resonance at this wavevector originates from the sign change of the intraband pairing component across the two Fermi pockets at the edge of the BZ, around (±π, 0) (δ) and (0, ±π), as illustrated in Fig. 4a, and further discussed in Supplementary Information. Without such a sign change, there cannot be a sharp resonance below the p–h threshold energy.
The imaginary part of the dynamical spin susceptibility for the alkaline iron selenides at wavevector q = (π, π/2), for a dominant sτ 3 pairing for parameters J 2 = 1.5, A O = 0.3, and A L = 0.9. The arrows show twice the minimum and maximum gaps (see Fig. 4b). There is a sharp feature ar ω ≈ 0.36 within the bounds of twice the effective gap and below the p–h threshold of roughly 0.41 associated with this wavevector
a The FS (solid line) and the real intraband pairing for the band generating the δ pockets at the edge of the BZ for a dispersion typical of the alkaline iron selenides. Note the clear change in sign between pockets separated by the BZ diagonal. The dashed arrow indicates the q = (π,π/2) wavevector associated with the resonance in the spin spectrum found in experiment.50 b The size of the gap along the δ pocket. Both figures are for J 2 = 1.5, A O = 0.3, and A L = 0.9 with dominant sτ 3 pairing
We next turn to the quasiparticle excitation spectrum. Figure 4b shows the gap at the FS as a function of winding angle θ. It clearly illustrates the node-less dispersion, as the gap is nonzero for all θ.
The electron dispersion considered here does not produce any Fermi pockets close to \(\Gamma \) in the BZ. This is in contrast to ARPES experiments on K y Fe2−x Se2,52, 53 which show a small electron pocket near \(\Gamma \). Because this electron pocket has very small spectral weight, it is to be expected that even if such a pocket were included, the dominant sτ 3 pairing will still arise; moreover, the gap on this Fermi pocket will be node-less as discussed in the two-orbital case. To substantiate this, we consider the results for the iron pnictides class, which do have significant (albeit hole) Fermi pockets at the zone center yet exhibit a full gap. In Fig. 5a, b, we show the FS and the gaps as functions of winding angle θ for A o = 0.5 and A L = 1.3 corresponding to a dominant sτ 3 pairing. The gap along β is finite and exhibits an anisotropy consistent with the two-orbital results in Eq. 5. In the latter case, at winding angle θ = 0, \({\rm{sin}}\phi = 0\), and the spectrum has a minimum/maximum gap for E ±. As θ is increased, the \({\left| {\vec B\left( {\boldsymbol{k}} \right) \times \vec d\left( {\boldsymbol{k}} \right)} \right|^2}\) term increases reaching a maximum at θ = π/4. Here the gap is maximum/minimum for E ±. This is consistent with the anisotropy in the gap shown in Fig. 5.
a The FS for the iron pnictides that includes hole pockets around the \(\Gamma \) point with dominant sτ 3, B 1g for J 2 = 1, A L = 1.3, and A O = 0.5. The tight-binding parameters can be found in ref. 27. b The gaps along the β and δ pockets close to the center and edge of the BZ. A similar gap forms around the α pocket
Discussion
Several remarks are in order. First, the full gap and the sign change of the intraband pairing component discussed above provide evidence that, with strong orbital selectivity, the sτ 3 pairing in a realistic five-orbital model has a behavior very similar to that of the two-orbital case.
Second, with the short-range J 1–J 2 interactions driving superconductivity, pairing involves the electronic states over an extended range of energy about the Fermi energy. The energy window can be determined from the zone-boundary spin-excitation energies, which are on the order of 200 meV for most iron selenides (and pnictides).50 This is important for the consideration of the quasiparticle excitation gap at the small electron pocket of K y Fe2−x Se2 near the origin of the BZ. According to the ARPES experiments,52, 53 this Fermi pocket contains Fe 3d xy and Se 4p z orbitals (α band), while the hole (β) bands containing both 3d xz and 3d yz orbitals are only ~60–80 meV below the Fermi energy. We therefore expect that both the intraband and interband pairing components will be significant for this part of the BZ and the mechanism advanced here will make the quasiparticle excitations to be fully gapped for this small electron pocket.
Third, within our approach, both the iron selenides and pnictides are bad metals in the regime of quasi-degenerate s- and d-wave pairings. However, the iron selenides have stronger correlations, which will lead to a larger ratio of the exchange interaction to renormalized kinetic energy (note that the renormalized bandwidth goes to zero when a bad metal approaches the electron localization transition) and, correspondingly,27 larger pairing amplitudes. We expect that this will contribute to the larger maximum T c observed in the iron selenides than in the iron pnictides. Relatedly, the alkaline iron selenides have a stronger orbital selectivity than the iron pnictides, and we thus expect that the sτ 3 pairing is more likely realized in the former than in the latter.
Fourth, it is instructive to compare the mechanism advanced here with a conventional means of relieving quasi-degenerate s- and d-wave pairing states with the trivial orbital structure, which consists in linearly superposing the two into an s + id state. The latter, breaking the time-reversal symmetry, would be stabilized at temperatures sufficiently below the superconducting transition temperature. By contrast, the sτ 3 pairing state preserves the time-reversal symmetry. It is an irreducible representation of the point group, and is therefore stabilized as the temperature is lowered immediately below the superconducting transition. Thus, the emergence of the intermediate sτ 3 pairing state represents a new means to relieve the quasi-degeneracy through the development of orbital selectivity.
Finally, the nodeless d-wave nature of sτ 3 may shed new light on other strongly correlated multi-band superconductors. For instance, one of the striking puzzles emerging in heavy fermion superconductors is the simultaneous exhibition of a variety of d-wave characteristics and of a gap in the lowest-energy excitation spectrum.54 Whether a multiband pairing state such as sτ 3 provides a systematic understanding of such properties is an intriguing open question for future studies.
To summarize, we have demonstrated that an orbital-selective sτ 3 pairing state exhibits properties that would appear mutually exclusive from the conventional perspective, where the orbital degrees of freedom are ignored. It provides a natural understanding of the enigmatic properties observed in the alkaline iron selenides. These include the single-particle excitations, which are fully gapped on the entire FS, as observed in ARPES experiments, and a pairing function, which changes sign across the electron Fermi pockets at the BZ boundary, as indicated by the resonance peak seen near (π, π/2) in the inelastic neutron scattering experiments. In addition, we have shown that the pairing state is energetically competitive in an orbital-selective model of short-range antiferromagnetic exchange interactions, in the regime where the conventional s- and d-wave pairing channels are quasi-degenerate. As such, our understanding of the properties of the iron selenide superconductors provides evidence that the high-T c superconductivity in the iron-based materials originates from the antiferromagnetic correlations of strongly correlated electrons. More generally, our work highlights how new classes of unconventional superconducting pairing state emerge in the presence of additional internal degrees of freedom, with properties that cannot otherwise be expected. This new insight may well be important for the understanding of a variety of other strongly correlated superconductors, including the heavy fermion and organic systems.
methods
For a detailed account of our methods, please consult Supplementary Information.
References
Anderson, P. W. Is there glue in cuprate superconductors? Science 316, 1705–1707 (2007).
Kamihara, Y., Watanabe, T., Hirano, M. & Hosono, H. Iron-based layered superconductor La[O1−xF x ]FeAs (x=0.05-0.12) with tc=26 K. J. Am. Chem. Soc. 130, 3296–3297 (2008).
Johnston, D. C. The puzzle of high temperature superconductivity in layered iron pnictides and chalcogenides. Adv. Phys. 59, 803–1061 (2010).
Si, Q., Yu, R. & Abrahams, E. High-temperature superconductivity in iron pnictides and chalcogenides. Nat. Rev. Mater. 1, 16017 (2016).
Wang, F. & Lee, D.-H. The electron-pairing mechanism of iron-based superconductors. Science 332, 200–204 (2011).
Hosono, H. & Kuroki, K. Iron-based superconductors: current status of materials and pairing mechanism. Physica C 514, 399–422 (2015).
Hirschfeld, P. J. Using gap symmetry and structure to reveal the pairing mechanism in Fe-based superconductors. C. R. Phys. 17, 197–231 (2016).
Qazilbash, M. M. et al. Electronic correlations in the iron pnictides. Nat. Phys. 5, 647–650 (2009).
Si, Q. & Abrahams, E. Strong correlations and magnetic frustration in the high T c iron pnictides. Phys. Rev. Lett. 101, 076401 (2008).
Yin, Z. P., Haule, K. & Kotliar, G. Magnetism and charge dynamics in iron pnictides. Nat. Phys. 7, 294–297 (2011).
Wang, Q.-Y. et al. Interface-induced high-temperature superconductivity in single unit-cell FeSe films on SrTiO3. Chin. Phys. Lett. 29, 037402 (2012).
Lee, J. J. et al. Interfacial mode coupling as the origin of the enhancement of T c in FeSe films on SrTiO3. Nature. 515, 245–248 (2014).
Mou, D. et al. Distinct fermi surface topology and nodeless superconducting gap in a (Tl0.58Rb0.42)Fe1.72Se2 superconductor. Phys. Rev. Lett. 106, 107001 (2011).
Zhang, C. et al. Measurement of a double neutron-spin resonance and an anisotropic energy gap for underdoped superconducting NaFe0.985Co0.015As using inelastic neutron scattering. Phys. Rev. Lett. 111, 207002 (2013).
Wang, X.-P. et al. Strong nodeless pairing on separate electron Fermi surface sheets in (Tl, K)Fe1.78Se2 probed by ARPES. Europhys. Lett. 93, 57001 (1)–(4). (2011).
Xu, M. et al. Evidence for an s-wave superconducting gap in KxFe2-ySe2 from angle-resolved photoemission. Phys. Rev. B 85, 220504 (2012).
Wang, X.-P. et al. Observation of an isotropic superconducting gap at the Brillouin zone center of Tl0.63K0.37Fe1.78Se2. Europhys. Lett. 99, 67001 (2012).
Park, J. T. et al. Magnetic resonant mode in the low-energy spin-excitation spectrum of superconducting Rb2Fe4Se5 single crystals. Phys. Rev. Lett. 107, 177005 (2011).
Friemel, G. et al. Reciprocal-space structure and dispersion of the magnetic resonant mode in the superconducting phase of Rb x Fe2-y Se2 single crystals. Phys. Rev. B 85, 140511(R) (2012).
Eschrig, M. The effect of collective spin-1 excitations on electronic spectra in high-T c superconductors. Adv. Phys. 55, 47–183 (2006).
Schaibley, J. R. et al. Valleytronics in 2D materials? Nat. Rev. Mater. 1, 16055 (2016).
Yi, M. et al. Observation of universal strong orbital-dependent correlation effects in iron chalcogenides. Nat. Commun. 6, 7777 (2015).
Yi, M. et al. Observation of temperature-induced crossover to an orbital-selective Mott phase in A x Fe2-y Se2 (A=K, Rb) superconductors. Phys. Rev. Lett. 110, 067003 (2013).
Wang, Z. et al. Orbital-selective metalinsulator transition and gap formation above T c in superconducting Rb1-x Fe2-y Se2. Nat. Commun. 5, 3202 (2014).
Ding, X., Pan, Y., Yang, H. & Wen, H.-H. Strong and nonmonotonic temperature dependence of Hall coefficient in superconducting K x Fe2-y Se2. Phys. Rev. B 89, 224515 (2014).
Li, W. et al. Mott behavior in K x Fe2-y Se2 superconductors studied by pump-probe spectroscopy. Phys. Rev. B 89, 134515 (2014).
Yu, R., Goswami, P., Si, Q., Nikolic, P. & Zhu, J.-X. Superconductivity at the border of electron localization and itinerancy. Nat. Commun. 4, 2783 (2013).
Liu, Z. K. et al. Experimental observation of incoherent-coherent crossover and orbital-dependent band renormalization in iron chalcogenide superconductors. Phys. Rev. B 92, 235138 (2015).
Yu, R. & Si, Q. Mott transition in multiorbital models for iron pnictides. Phys. Rev. B 84, 235115 (2011).
Yu, R. & Si, Q. Orbital-selective Mott phase in multiorbital models for alkaline iron selenides K1-x Fe2-y Se2. Phys. Rev. Lett. 110, 146402 (2013).
de Medici, L., Giovannetti, G. & Capone, M. Selective Mott physics as a key to iron superconductors. Phys. Rev. Lett. 112, 177001 (2014).
Yu, R., Zhu, J.-X. & Si, Q. Orbital-selective superconductivity, gap anisotropy, and spin resonance excitations in a multiorbital t−J 1−J 2 model for iron pnictides. Phys. Rev. B 89, 024509 (2014).
Yin, Z. P., Haule, K. & Kotliar, G. Spin dynamics and orbital-antiphase pairing symmetry in iron-based superconductors. Nat. Phys. 10, 845–850 (2014).
Ong, T., Coleman, P. & Schmalian, J. Concealed d-wave pairs in the s ± condensate of iron-based superconductors. Proc. Natl Acad. Sci. USA 113, 5486–5491 (2016).
Hao, N. & Hu, J. Odd parity pairing and nodeless antiphase s ± in iron-based superconductors. Phys. Rev. B 89, 045144 (2014).
Raghu, S., Qi, X.-L., Liu, C.-X., Scalapino, D. J. & Zhang, S.-C. Minimal two-band model of the superconducting iron oxypnictides. Phys. Rev. B 77, 220503(R) (2008).
Balian, R. & Werthamer, N. R. Superconductivity with pairs in a relative p wave. Phys. Rev. 131, 1553–1564 (1963).
Leggett, A. J. A theoretical description of the new phase of 3He. Rev. Mod. Phys. 47, 331–414 (1975).
Sigrist, M. & Ueda, K. Phenomenological theory of unconventional superconductivity. Rev. Mod. Phys. 63, 239–311 (1991).
Fang, C., Yao, H., Tsai, W.-F., Hu, J. P. & Kivelson, S. A. Theory of electron nematic order in LaFeAsO. Phys. Rev. B 77, 224509 (2008).
Xu, C., Müller, M. & Sachdev, S. Ising and spin orders in the iron-based superconductors. Phys. Rev. B 78, 020501(R) (2008).
Seo, K., Bernevig, B. A. & Hu, J. Pairing symmetry in a two-orbital exchange coupling model of oxypnictides. Phys. Rev. Lett. 101, 206404 (2008).
Moreo, A., Daghofer, M., Riera, J. A. & Dagotto, E. Properties of a two-orbital model for oxypnictide superconductors: magnetic order, B 2g spin-singlet pairing channel, and its nodal structure. Phys. Rev. B 79, 134502 (2009).
Chen, W.-Q., Yang, K.-Y., Zhou, Y. & Zhang, F.-C. Strong coupling theory for superconducting iron pnictides. Phys. Rev. Lett. 102, 047006 (2009).
Yang, F., Wang, F. & Lee, D.-H. Fermiology, orbital order, orbital fluctuations, and Cooper pairing in iron-based superconductors. Phys. Rev. B 88, 100504(R) (2013).
Berg, E., Kivelson, S. A. & Scalapino, D. J. A twisted ladder: relating the Fe superconductors to the high-T c cuprates. New J. Phys. 11, 085007 (2009).
Lv, W., Krüger, F. & Phillips, P. Orbital ordering and unfrustrated (π,0) magnetism from degenerate double exchange in the iron pnictides. Phys. Rev. B 82, 045125 (2010).
Bascones, E., Valenzuela, B. & Calderón, M. J. Orbital differentiation and the role of orbital ordering in the magnetic state of fe superconductors. Phys. Rev. B 86, 174508 (2012).
Graser, S., Maier, T. A., Hirschfeld, P. J. & Scalapino, D. J. Near-degeneracy of several pairing channels in multiorbital models for the Fe pnictides. New J. Phys. 11, 025016 (2009).
Dai, P. Antiferromagnetic order and spin dynamics in iron-based superconductors. Rev. Mod. Phys. 87, 855–896 (2015).
Goswami, P., Nikolic, P. & Si, Q. Superconductivity in multi-orbital t-J 1-J 2 model and its implications for iron pnictides. Europhys. Lett. 91, 37006 (2010).
Zhang, Y. et al. Nodeless superconducting gap in A x Fe2Se2(A=K, Cs) revealed by angle-resolved photoemission spectroscopy. Nat. Mater. 10, 273–277 (2011).
Liu, Z.-H. et al. Three dimensionality and orbital characters of the Fermi surface in (Tl, Rb) y Fe2-x Se2. Phys. Rev. Lett. 109, 037003 (2012).
Kittaka, S. et al. Multiband superconductivity in unexpected deficiency of nodal quasiparticles in CeCu2Si2. Phys. Rev. Lett. 112, 067002 (2014).
Nica, E. M., Yu, R. & Si, Q. Glide reflection symmetry, Brillouin zone folding and superconducting pairing for P4/nmm space group. Phys. Rev. B 92, 174520 (2015).
Acknowledgements
We acknowledge useful discussions with E. Abrahams, A. V. Chubukov, G. Kotliar, and P. J. Hirschfeld. The work has been supported in part by the NSF Grant number DMR-1611392 and the Robert A. Welch Foundation Grant number C-1411 (E.M.N. and Q.S.). R.Y. was partially supported by the National Science Foundation of China Grant number 11374361, and the Fundamental Research Funds for the Central Universities and the Research Funds of Renmin University of China. We acknowledge the support provided in part by the NSF Grant number NSF PHY11-25915 at KITP, UCSB.
Author information
Authors and Affiliations
Contributions
All authors contributed to the research of the work and the writing of the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare that they have no competing financial interests.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nica, E.M., Yu, R. & Si, Q. Orbital-selective pairing and superconductivity in iron selenides. npj Quant Mater 2, 24 (2017). https://doi.org/10.1038/s41535-017-0027-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-017-0027-6
This article is cited by
-
Covalent and Non-covalent Functionalized Nanomaterials for Environmental Restoration
Topics in Current Chemistry (2022)
-
Study on the Field-Dependent Activation Energy, U(H,T), Upper Critical Field, Hc2(0), and Irreversibility Field, µ0Hirr, Properties of Superconducting Single-Crystal Ag-Added Fe(Se, Te) Alloys
Journal of Superconductivity and Novel Magnetism (2022)
-
Resonance from antiferromagnetic spin fluctuations for superconductivity in UTe2
Nature (2021)
-
Nematic fluctuations in iron-oxychalcogenide Mott insulators
npj Quantum Materials (2021)
-
Multiorbital singlet pairing and d + d superconductivity
npj Quantum Materials (2021)