Abstract
Entanglement-based quantum networks require quantum photonic interfaces between stationary quantum memories and photons, enabling entanglement distribution. Here we present such a photonic interface, designed for connecting a 40Ca+ single-ion quantum memory to the telecom C-band. The interface combines a memory-resonant, cavity-enhanced spontaneous parametric down-conversion photon pair source with bi-directional polarization-conserving quantum frequency conversion. We demonstrate preservation of high-fidelity entanglement during conversion, fiber transmission over up to 40 km and back-conversion to the memory wavelength. Even for the longest distance and bi-directional conversion the entanglement fidelity remains larger than 95% (98%) without (with) background correction.
Similar content being viewed by others
Introduction
Entanglement-based quantum networks are the backbone for many quantum technology applications connecting remote partners, such as distributed quantum computing1, quantum repeaters2, quantum key distribution (QKD) with entangled photons3 or networks of quantum sensors4. Here we consider networks involving matter-based quantum memories communicating via optical photons. To realize such networks, several requirements have to be fulfilled simultaneously: (i) a source of high-rate and high-fidelity entanglement is essential5,6; (ii) the spectral characteristics of photonic information carriers and matter-based quantum memories have to match; and (iii) the communication wavelength has to be in a low-loss band of optical fibers.
Requirement (i) may be addressed by photon pair sources based on spontaneous parametric down-conversion (SPDC) that have shown immense potential as high-fidelity sources of entanglement since their introduction7. For their interfacing with atom-based quantum memories, requirement (ii)8,9,10, a narrow spectrum of the photon pairs is required. This can be attained by spectral filtering11 or by placing the nonlinear crystal inside a cavity that is tuned to be resonant with the desired atomic transition12,13. The latter scheme also enables very high pair rates, but it may suffer from reduced state purity due to distinguishability induced by the birefringence of both crystal and resonator. An alternative approach with higher-quality entanglement but with a much lower pair rate is to use single-pass conversion in an interferometric configuration, which eliminates all distinguishability and eliminates the 50% background of unsplit photon pairs14,15,16. Ideally, resonator-enhanced generation and interferometric configuration would be combined.
For the distribution of entangled photon pairs over long distances in fiber networks, requirement (iii), transmission loss is a crucial issue, limiting the entanglement rate and thereby the secret key rate of QKD. Thus it is advantageous to use wavelengths in the telecom bands (1260–1625 nm), where fiber absorption is minimal. Most of the relevant transitions in atomic or ionic quantum memories, however, are in the visible or near IR regime17,18,19,20. One possible approach to address quantum memory transitions and at the same time minimize fiber loss is to use non-degenerate SPDC entangled-pair sources. In this case one photon is resonant to the memory transition while the other has a wavelength in the telecom regime8,21,22,23,24. Alternatively, non-degenerate photon pairs may be generated from degenerate pairs by quantum frequency conversion (QFC) of one of the photons25 which shifts the photon wavelength while preserving all other properties. Here, an efficient conversion process is three-wave mixing in χ(2)-nonlinear media26, but its strong polarization dependence is adverse to the conversion of polarization qubits. To overcome this limitation, several schemes for polarization-preserving conversion have been developed27,28,29,30,31,32,33 and employed to demonstrate photon-photon28,32 and light-matter entanglement over short distances30,31 as well as over km-long fibers33,34,35,36.
In this paper we present a photonic interface designed to connect a single-ion quantum memory with the telecom C-band. Our interface combines a 40Ca+-resonant, cavity-enhanced SPDC photon-pair source at 854 nm in interferometric configuration37 with highly efficient polarization-preserving QFC to 1550 nm and back-conversion to the atomic wavelength. It thereby facilitates bi-directional sender and receiver operations between atomic and photonic quantum bits17,38, as needed for a quantum network environment involving atom-based memories. We present four different setups and verify entanglement for each case by quantum state tomography: first, we characterize the source operation, then the combined system with QFC to generate polarization entanglement between a 40Ca+-resonant photon and a telecom photon. In the third step we show entanglement distribution over 20 km of fiber. Finally, we demonstrate the preservation of high-quality entanglement after conversion, transmission over 40 km of fiber, and consecutive back-conversion of the telecom photon to the 40Ca+-wavelength, employing a single bi-directional frequency converter. Even for the longest distance and bi-directional conversion the entanglement fidelity remains larger than 95% (98%) without (with) background correction.
Results
SPDC photon pair source
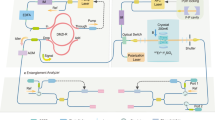
Our SPDC photon pair source combines the interferometric configuration of14,39 with cavity enhancement, enabling the generation of photons with very high pair rate, narrow linewidth and high-fidelity, offset-free entanglement simultaneously. Compared to an earlier version of the source40,41, we also optimized the locking stability and the output mode structure. The experimental setup is shown in Fig. 1 and will be discussed in the following.
In order to address the D5/2-P3/2 transition in 40Ca+ at 854 nm, we use a frequency-stable laser at 427 nm to pump the SPDC process in a periodically poled KTP crystal with type-II phase-matching. The polarized pump light is split on a non-polarizing 50:50 beam splitter (BS), and the two beams are coupled into the nonlinear crystal in opposite directions. The crystal is placed inside a signal- and idler-resonant 3-mirror ring resonator (FSRH = 2π ⋅ 1.85 GHz, FSRV = 2π ⋅ 1.83 GHz). Down-converted photons from both pump directions leave the resonator at the same outcoupling mirror, Mout, under different angles. The polarizations of the signal and idler photons in one of the output arms are interchanged by a half-wave plate. Then, the photons of both output arms are overlapped on a polarizing beam splitter (PBS). This arrangement erases all distinguishability between the two photons of a pair. Moreover, it avoids the background of unsplit pairs that is inherent in single-direction SPDC generation. The photonic 2-qubit state at 854 nm produced by the source is a polarization Bell state42:
where A and B refer to the output ports of the PBS.
SPDC source in interferometric configuration with PDH locking beams. Stabilization of the resonator and the interferometer is achieved by piezo-driven mirrors (PM). During the stabilization runs, the photons are switched off by an optical chopper in order to protect the APDs. HWP/QWP half-/quarter-wave plate, PBS polarizing beamsplitter, BS non-polarizing beamsplitter, DM dichroic mirror, Pol polarizer, WP Wollaston prism, GP glass plate, PM piezo-driven mirror, FPI frequency filter.
As shown in Fig. 1 we use a chopped locking beam, injected via a glass plate, to stabilize one mode of the resonator (the H-polarized mode) to the ion transition by the Pound-Drever-Hall (PDH) technique. The frequency of the corresponding V-polarized mode is shifted by ~480 MHz because of the birefringence of the crystal. Due to the conversion bandwidth of the crystal (200 GHz) and the small polarization dispersion of the resonator, several pairs of modes at different frequencies exhibit cavity-enhanced SPDC (see Supplementary Fig. 1). Filtering out the ion-resonant mode and its partner mode is effected by two monolithic Fabry-Pérot filters (FPI), one in each output. The filters are described in more detail in the Methods section. The SHG light that is produced by the locking beam is detected at the BS that splits the pump beam and is used for the stabilization of the Mach-Zehnder-type interferometer formed between this BS and the PBS that combines the SPDC output arms. By tuning the phase of this interferometer, we tailor the phase φ of the photonic 2-qubit state, Eq. (1). For the experiments described below, we set this phase to φ = 270∘. A more detailed account of the relation between φ and the interferometer phase is given in Supplementary Methods 1.
With the described setup we reach a generated photon pair rate of \({R}_{{{{\rm{pair}}}}}=4.7\cdot 1{0}^{4}\frac{{{{\rm{pairs}}}}}{{\rm{s}}\,{\rm{mW}}}\times {P}_{{{{\rm{pump}}}}}\). In the experiments below, we used a maximum pump power of Ppump = 20 mW. The SPDC photons are available, after spectral filtering and fiber coupling, with 31% (21.4%) efficiency in port A (B). The two efficiencies differ for technical reasons such as coupling efficiencies, filter transmissions, etc. For analysis of the photonic polarization state, we use a projection setup consisting of half-wave plate, quarter-wave plate, and polarizer (film polarizer or Wollaston prism) in each output arm. As single-photon detectors we use two APDs (Excelitas Technologies) with ~10 s−1 dark counts. Detected photons are time-tagged, and time-resolved coincidence functions between the two arms are evaluated for various combinations of polarization settings.
For the characterization of the temporal shape of the photon wavepacket, we measure the polarization-indiscriminate coincidence function between the photons of the two output arms43. Figure 2 shows the result, measured by summing the coincidences for the four settings HV, VH, HH, and VV. The decay times (or wave packet widths) of the two photons differ slightly because of different loss of the two polarization modes in the cavity: we get values of τA = 15.78 ns for photons in output A and τB = 12.94 ns for photons in output B. Hence the photon spectrum matches well the 23 MHz linewidth of the 854-nm D5/2 to P3/2 transition in Ca+.
An important figure of merit is the signal-to-background ratio (SBR) of the coincidence functions. The gray-shaded area in Fig. 2, representing the coincidences in the time-window Δt around zero, is taken as the signal (S). The background (B) is determined using the same time window size but at a delay τ > 150 ns (red shaded area). For our setup the background is dominated by accidental coincidences, originating from the temporal overlap of the generated photons.
Theoretically, the number of polarization-indiscriminate coincidence counts in a time interval T and for a given pair rate Rpair is given by:
where η1 and η2 are the detection efficiencies for the two outputs, and \({\tau }_{{{{\rm{mean}}}}}=\frac{1}{2}({\tau }_{H}+{\tau }_{V})\) is the mean wavepacket width of the photons. The theoretical value for the background is:
Hence the SBR of the source is expected to be given by41:
Figure 3 shows a comparison between this theoretical expression and our measurement, for fixed pump power of 20 mW and variable coincidence window Δt. When Δt is similar to the 1/e width of the photon wavepacket, we reach an SBR of ~30, whereas for a coincidence window that covers 99.97% of the photon, we find an SBR of ~10.
The SBR and the coincidence rate are plotted in dependence of the coincidence time window Δt, for a pump power of 20 mW. The error bars are calculated from the Poissonian noise of the measured coincidences. The dashed lines show the theoretical calculations according to Eq. (4) for the SBR and Eq. (2) for the coincidence rate, with \({R}_{{{{\rm{pair}}}}}=4.7\cdot 1{0}^{4}\frac{{\rm{pairs}}}{{\rm{s}}\,{\rm{mW}}}\) the only fit parameter for both curves.
Figure 3 also shows how the coincidence rate varies with Δt. From fitting Eq. (2) to the data, with η1,2 independently measured, we derive the pair rate Rpair as mentioned before. The SBR enters into the maximally reachable fidelity of the photon pair state to the ideal Bell state of Eq. (1). The fidelity of a measured (i.e., reconstructed) density matrix ρ to a given state \(\left\vert {{\Psi }}\right\rangle\) is calculated as:
where Fw/oBG corresponds to the fidelity of the photonic state when the entire background is subtracted41. This formula is used below for the theoretical curves in Fig. 6.
Polarization preserving frequency conversion
The setup for the polarization-preserving frequency conversion (Fig. 4a) is located in a second lab and is connected to the photon-pair source via 90 m of fiber. We use difference frequency generation (DFG) in a nonlinear PPLN waveguide to convert the 854 nm photons to the telecom C-band at 1550 nm29. As the DFG efficiency in the waveguide is strongly polarization dependent, the setup is realized in a Sagnac configuration31,33. First, the 854 nm signal is filtered by an input bandpass filter to prevent background photons being coupled back into the source setup and overlapped with the strong, diagonally polarized pump field at 1904 nm on a dichroic mirror. Both fields are then split into their H- and V-polarization component on a PBS. To achieve polarization preserving operation, the H-components are rotated to V by an achromatic waveplate inside the Sagnac loop (HWP). All beams are now V-polarized for optimum conversion and are coupled in a counterpropagating way into the waveguide. After exiting the waveguide, the converted 1550-nm light from the original V-component also passes the achromatic waveplate and is thereby rotated to H. Finally, the two converted polarization components are coherently overlapped on the PBS, which closes the Sagnac loop. The light then passes the dichroic mirror a second time where unconverted (or back-converted) light at 854 nm is split off. The same happens to SHG light from the pump that is parasitically generated in the waveguide; it is then blocked by the input bandpass filter. The converted light that is transmitted through the first DM together with the pump light is separated with a second DM and coupled into a telecom fiber, directing it to the detection setup.
a Schematic quantum frequency conversion setup. Details are found in the main text. TDFL thulium-doped fiber laser, LPF low-pass filter, BPF band-pass filter, VBG volume-Bragg grating, DM dichroic mirror, HWP half-wave plate, SNSPD superconducting nanowire single-photon detector; b Device efficiency of the converter for different pump powers and input polarizations. The maximum efficiencies of the H- and V-polarizations are slightly different.
Apart from enabling polarization-independent conversion, an additional advantage of the Sagnac configuration is that all fields have the same optical path, such that no phase difference between the split polarization components occurs, and hence no active phase stabilization is needed. At the same time, the configuration facilitates bi-directional conversion without compromising the conversion efficiency. An experimental demonstration of bi-directional operation will be presented below.
The conversion-induced background in this process mainly originates from anti-Stokes Raman scattering of the pump field29,44,45. As this is spectrally very broad compared to the converted signal, we can significantly reduce the background count rate with a narrowband filtering stage. By combination of a bandpass filter (transmission bandwidth ΔνBPF = 1500 GHz), a volume Bragg grating (VBG, ΔνVBG = 25 GHz) and a Fabry-Pérot etalon (FSR = 12.5 GHz, ΔνFPE = 250 MHz) we achieve broadband suppression outside a 250 MHz transmission bandwidth. To ensure high transmission through VBG and Etalon, a clean gaussian spatial mode is needed. That is why these filters are included in the detection setup, which is separated from the conversion setup by 10 m of fiber (or by the fiber link) acting as spatial filter. With this filtering stage, the total conversion-induced background is reduced from 1.5 μW to 24 s−1; further details are found in Supplementary Methods 2.
The device efficiency including all losses in optical components and spectral filtering for H and V input polarizations and different pump powers in the corresponding converter arm is shown in Fig. 4b. The measurement agrees well with the theoretical curve given by \({\eta }_{{{{\rm{ext}}}}}(P)={\eta }_{{{{\rm{ext,max}}}}}{\sin }^{2}(\sqrt{{\eta }_{{{{\rm{nor}}}}}P}L)\) with the normalized power efficiency ηnor and waveguide length L46. We achieve a maximum external conversion efficiency of \({\eta }_{{{{\rm{ext,max}}}}}=\,60.1 \% \,(57.2 \% )\) for H(V)-polarized input at 660 mW (630 mW) pump power. The difference is explained by slightly different mode overlaps between signal and pump field in the two arms. Since for polarization-preserving operation both efficiencies need to be equal, the pump power in the H-arm is reduced via the two HWPs in the pump laser arm to 485 mW to match 57.2% conversion efficiency. To verify equal conversion efficiency for arbitrary polarized input, the process matrix47 was measured with attenuated laser light, resulting in a value for the process fidelity of 99.947(2)%. Thus the preservation of the input polarization state is confirmed with very high fidelity. Note that in fact the converter rotates the input state by a constant factor π/2 due to the achromatic waveplate. This could be compensated by an additional waveplate at the output, however the polarization also gets arbitrarily rotated in the input and output fibers, so we compensate for all rotations together by rotating the projection bases in all measurements as described in the “Methods” section.
Further details on the conversion setup as well as the background and process fidelity measurements are found in Supplementary Methods 2.
Experimental results
To assess the performance of our quantum photonic interface we analyze the photon pair states via quantum state tomography48 for four different configurations, as sketched in Fig. 5a–d.
a The output state is measured directly at the source. b One of the photons is frequency-converted before its detection. c 20 km of fiber is inserted between conversion and detection. d The 20 km fiber gets terminated with a retro-reflector. The back reflected photons get back-converted after 40 km of fiber and are extracted with a 50:50 fiber beamsplitter before their detection. The background colors correspond to the colors of the data points in Fig. 6.
In the first configuration (Fig. 5a) and for calibration purposes, we measure the output state of the photon pair source itself, i.e., without conversion. In the next configuration (Fig. 5b), we include the frequency converter in the detuned output arm of the photon pair source (arm A in Fig. 1). Tomography is then performed on the pairs of converted and unconverted photons.
In the third configuration (Fig. 5c), we extend the fiber link between converter and detection setup to 20 km in order to evaluate the influence of fiber transmission. We emphasize that the transmission of photons at a wavelength of 854 nm via a suitable single mode fiber would suffer about −70 dB fiber attenuation49 whereas conversion to 1550 nm and using a low-loss telecom fiber results in a total fiber attenuation of −3.4 dB50.
Finally, in the fourth configuration (Fig. 5d) bi-directional conversion is implemented by terminating the 20 km fiber with a retroreflector. Thus, the telecom photons are converted back to 854 nm at the second passage of the converter, after 40 km of fiber transmission. To separate the returning back-converted photons from the outgoing ones in the source lab, we use a 50:50 fiber beamsplitter that reflects 50% of the back-converted photons to the second tomography setup. Note that in this configuration the converter filter stage is not used, but the FPI filter in the 854 nm tomography setup, as explained in Supplementary Notes 1.
In all four configurations, we use source pump powers of 5, 10, 15 and 20 mW. The detected coincidence rates at 20 mW pump power are: 4168 s−1 for setup (a), 974 s−1 for setup (b), 428 s−1 for setup (c) and 40 s−1 for setup (d) (also see Supplementary Fig. 6). From the time-resolved coincidences in the different detection bases, the density matrix is reconstructed by applying an iterative maximum likelihood estimation (MLE) algorithm51. From the density matrix, we then calculate all measures that characterize the quantum state, such as fidelity and purity. For each configuration we show a representative density matrix in Supplementary Fig. 7. Before performing the tomography, the polarization rotations in both arms, including the converter and the fiber link, were calibrated; details on the procedure are found in the methods part.
The results of the four configurations are summarized in Fig. 6. For all configurations and source pump powers, the fidelities with respect to the maximally entangled state (1) are above 95% with and without background correction, for a detection window of Δt = 1.5 τmean (subfigure a). Thus, the entanglement is well-preserved for every scenario of Fig. 5. The uncertainties of the individual data points are smaller than 0.4 %, thus negligible on the scale of the diagram. The values and errors for the fidelities of the two depicted detection windows are shown in Supplementary Tables 3 and 4. For fixed source pump power, the fidelities of the individual configurations differ only slightly outside the error bars, which confirms the high process fidelity of the converter and the low detrimental effect of the fiber link. With increasing source pump power, the fidelity decreases, which is expected according to Eq. (5). The black dashed line shows the theoretically achievable fidelity for the given SBR, considering only accidental coincidences. This line is expected to be an upper bound to the measured values, as additional effects lead to further reductions: (1) errors in the calibration of the polarization rotation compensation; (2) drifts in the polarization rotation of the setup away from the calibration point during the measurements; (3) fluctuations of the photonic state phase resulting from power fluctuations of the locking signal.
a, b Show the measurement results for a detection time window of 1.5τmean which corresponds to 78% of the photon temporal shape. In (a) the non background corrected MLE results are represented by the data points, the dot-dashed line shows the mean background corrected fidelity, while the dashed line shows the theoretical expectation according to Eq. (5). The uncertainties are derived from a simulation; see “Method” section for further details. b Shows the comparison of the SBR for the four different measurement settings. The dashed line is calculated for the given pair rate according to Eq. (4). The error bars are calculated by including the \(\sqrt{N}\)-noise of the measured coincidences59. c, d Show the results when choosing a larger detection window of 5τmean for the evaluation.
The SBR for each individual measurement is shown in Fig. 6b. Here the error bars are calculated by taking Poissonian noise into account. As expected from Eq. (4), the SBR decreases for increasing pump power of the pair source. Again we only see minor differences between the four configurations, as the conversion-induced background rate is negligible compared to the pair rate and source background rate in the relevant time window. For the back-conversion part, the SBR is consistently lower, which is explained by the use of the FPI filter instead of the converter filtering stage.
When choosing a larger detection window, fidelities and SBR decrease due to the temporal overlap of the photons. The results for a detection window of Δt = 5 τmean, corresponding to 91% of the photon, are shown in Fig. 6c, d. Due to the lower SBR, here the fidelities are lower by a few percent, while the detected pair rate is increased by a factor of 1.7.
Discussion
In summary, we have presented and characterized a combined system of entangled photon pair source and bi-directional quantum frequency converter and use it for entanglement distribution over a fiber link. Pair rate and entanglement fidelity of the source are near the theoretical optimum, while efficiency, polarization fidelity and noise performance of the converter are among the best reported values29,31,32. The system is tailored as interface to the 40Ca+ single-ion quantum memory. An application is reported in ref. 37.
The presented measurements demonstrate the preservation of photon entanglement with high fidelity through up to 2 conversion steps and distribution over up to 40 km of fiber. The high-efficiency bi-directional quantum frequency conversion adds low background to the photon pair source and thus enables a proof-of-principle demonstration of a quantum photonic interface suitable to connect remote quantum network nodes based on 40Ca+ single-ion memories.
Several future improvements are readily identified. The coincidence rates can be enhanced by replacing lossy fiber-fiber couplings by direct splices and by replacing the fiber beam splitter by an optical circulator. Given the low unconditional background rate of the QFC process, we can further increase photon count rates by lowering the finesse of the monolithic Fabry-Pérot filters, which results in higher transmission. The conversion fidelity can be improved near the theoretical maximum by repeating the polarization calibration more frequently in a fully automated procedure. Further optimization may be attained by modifying the length of the photon wave packet through the design of the source cavity. Shortening the wave packet would produce less temporal overlap between two subsequent photons and hence improve the SBR, but reduce the spectral overlap with the ion and thereby the absorption probability. Longer photons with a narrower spectrum optimize the signal but increase the background of accidental coincidences. The optimum parameters will depend on the application and on the technical limitations of the cavity setup.
Recent developments in quantum networking operations with single ions52,53,54, together with progress in ion-trap quantum processors55,56 confirm the importance and the potential of quantum photonic interfaces for quantum information technologies. The interface we demonstrate here enables extension toward further fundamental operations in trapped-ion-based quantum networks. In particular, bi-directional QFC allows for teleportation between remote quantum memories, or for their entanglement via direct exchange of a photon (see e.g.,57), employing heralded absorption17,41 of a back-converted telecom photon.
Methods
State characterization
We perform full state tomography to reconstruct the photonic two-qubit state. We project each photon to one of the six polarization basis states (horizontal, vertical, diagonal, anti diagonal, left circular, or right circular), which results in 36 possible measurement combinations. In order to reconstruct the 2-qubit density matrix, 16 combinations are sufficient. We therefore measure two-photon correlations in 16 independent polarization settings58 and reconstruct the density matrix by applying a maximum likelihood algorithm to the count rates inside the detection window51. We infer from the density matrix all characteristic measures such as purity and fidelity. For calculating the error bars, we use a Monte Carlo simulation59 where we run the algorithm repeatedly on randomly generated, Poisson-distributed coincidence rates based on the measured rates. From the distribution of the resulting fidelities, we estimate the error bars.
Polarization bases calibration
Polarization rotation due to the birefringence of optical components in the setup, in particular the fibers, has to be accounted for to ensure projection onto the correct basis states. We model the rotation in each arm by a unitary rotation matrix M that transforms the input polarization λin to an output polarization λout = Mλin. Non-unitary effects such as polarization-dependent loss play only a negligible role on the final state fidelity.
By blocking one pump direction of the source, we deterministically generate photons with linear (H) polarization. Additionally, we can insert a quarter-wave plate directly behind the source to rotate the polarization to R. We then perform single-qubit tomography with the detection setups to measure the rotated polarization states. From this we calculate the rotation matrix M, and the projection bases are rotated accordingly.
Depending on the experimental configuration (Fig. 5), we measure the rotation matrix less or more frequently during the experiments: for the first two configurations, short fibers are used, thus the polarization is very stable over time and is measured only at the beginning of the experiment. In the last two configurations, although the fiber spool is actively temperature stabilized to minimize polarization drifts, the rotation matrix is measured every 60 min.
Fabry–Pérot filter
The Fabry–Pérot filters which we use for filtering the 854 nm photons to a single frequency mode are built from single 2 mm thick NBK-7 lenses. Both sides have a high-reflectivity coating (R = 0.9935). This results in a finesse of 481, a FSR of ~50 GHz and a FWHM of Δν ≈ 104 MHz, which is sufficient for filtering a single mode of the SPDC cavity (FSR ~ 1.84 GHz). Frequency tuning over a whole FSR is possible by changing the temperature in the range between 20 and 70 °C. The stabilization of the temperature with a precision of 1 mK (corresponding to 3 MHz) is sufficient for stable operation; no further active stabilization is needed.
Data availability
The underlying data for this manuscript are openly available in Zenodo at https://doi.org/10.5281/zenodo.7313581. The evaluation algorithms are available from the corresponding author upon reasonable request.
References
Jiang, L., Taylor, J. M., Sørensen, A. S. & Lukin, M. D. Distributed quantum computation based on small quantum registers. Phys. Rev. A 76, 062323 (2007).
Briegel, H.-J., Dür, W., Cirac, J. I. & Zoller, P. Quantum repeaters: the role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81, 5932–5935 (1998).
Ekert, A. K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67, 661–663 (1991).
Proctor, T. J., Knott, P. A. & Dunningham, J. A. Multiparameter estimation in networked quantum sensors. Phys. Rev. Lett. 120, 080501 (2018).
Simon, C. et al. Quantum repeaters with photon pair sources and multimode memories. Phys. Rev. Lett. 98, 190503 (2007).
Wehner, S., Elkouss, D. & Hanson, R. Quantum internet: a vision for the road ahead. Science 362, eaam9288 (2018).
Kwiat, P. G. et al. New high-intensity source of polarization-entangled photon pairs. Phys. Rev. Lett. 75, 4337–4341 (1995).
Lenhard, A. et al. Telecom-heralded single-photon absorption by a single atom. Phys. Rev. A 92, 063827 (2015).
Specht, H. P. et al. A single-atom quantum memory. Nature 473, 190–193 (2011).
Rosenfeld, W., Volz, J., Weber, M. & Weinfurter, H. Coherence of a qubit stored in zeeman levels of a single optically trapped atom. Phys. Rev. A 84, 022343 (2011).
Brito, J., Kucera, S., Eich, P., Müller, P. & Eschner, J. Doubly heralded single-photon absorption by a single atom. Appl. Phys. B 122, 36 (2016).
Luo, K.-H. et al. Direct generation of genuine single-longitudinal-mode narrowband photon pairs. New J. Phys. 17, 073039 (2015).
Tsai, P.-J. & Chen, Y.-C. Ultrabright, narrow-band photon-pair source for atomic quantum memories. Quantum Sci. Technol. 3, 034005 (2018).
Fiorentino, M., Messin, G., Kuklewicz, C. E., Wong, F. N. C. & Shapiro, J. H. Generation of ultrabright tunable polarization entanglement without spatial, spectral, or temporal constraints. Phys. Rev. A 69, 041801 (2004).
Kuzucu, O. & Wong, F. N. C. Pulsed sagnac source of narrow-band polarization-entangled photons. Phys. Rev. A 77, 032314 (2008).
Kim, T., Fiorentino, M. & Wong, F. N. C. Phase-stable source of polarization-entangled photons using a polarization sagnac interferometer. Phys. Rev. A 73, 012316 (2006).
Kurz, C., Eich, P., Schug, M., Müller, P. & Eschner, J. Programmable atom-photon quantum interface. Phys. Rev. A 93, 062348 (2016).
Meyer, H. M. et al. Direct photonic coupling of a semiconductor quantum dot and a trapped ion. Phys. Rev. Lett. 114, 123001 (2015).
Schupp, J. et al. Interface between trapped-ion qubits and traveling photons with close-to-optimal efficiency. PRX Quantum 2, 020331 (2021).
Mount, E. et al. Single qubit manipulation in a microfabricated surface electrode ion trap. New J. Phys. 15, 093018 (2013).
Saglamyurek, E. et al. Broadband waveguide quantum memory for entangled photons. Nature 469, 512–515 (2011).
Fekete, J., Rieländer, D., Cristiani, M. & de Riedmatten, H. Ultranarrow-band photon-pair source compatible with solid state quantum memories and telecommunication networks. Phys. Rev. Lett. 110, 220502 (2013).
Bussières, F. et al. Quantum teleportation from a telecom-wavelength photon to a solid-state quantum memory. Nat. Photonics 8, 775–778 (2014).
Lago-Rivera, D., Grandi, S., Rakonjac, J. V., Seri, A. & de Riedmatten, H. Telecom-heralded entanglement between multimode solid-state quantum memories. Nature 594, 37–40 (2021).
Kumar, P. Quantum frequency conversion. Opt. Lett. 15, 1476–1478 (1990).
Huang, J. & Kumar, P. Observation of quantum frequency conversion. Phys. Rev. Lett. 68, 2153–2156 (1992).
Albota, M. A., Wong, F. N. C. & Shapiro, J. H. Polarization-independent frequency conversion for quantum optical communication. JOSA B 23, 918–924 (2006).
Ramelow, S., Fedrizzi, A., Poppe, A., Langford, N. K. & Zeilinger, A. Polarization-entanglement-conserving frequency conversion of photons. Phys. Rev. A 85, 013845 (2012).
Krutyanskiy, V., Meraner, M., Schupp, J. & Lanyon, B. P. Polarisation-preserving photon frequency conversion from a trapped-ion-compatible wavelength to the telecom c-band. Appl. Phys. B 123, 228 (2017).
Bock, M. et al. High-fidelity entanglement between a trapped ion and a telecom photon via quantum frequency conversion. Nat. Commun. 9, 1998 (2018).
Ikuta, R. et al. Polarization insensitive frequency conversion for an atom-photon entanglement distribution via a telecom network. Nat. Commun. 9, 1997 (2018).
Kaiser, F. et al. Quantum optical frequency up-conversion for polarisation entangled qubits: towards interconnected quantum information devices. Opt. Express 27, 25603–25610 (2019).
van Leent, T. et al. Long-distance distribution of atom-photon entanglement at telecom wavelength. Phys. Rev. Lett. 124, 010510 (2020).
Krutyanskiy, V. et al. Light-matter entanglement over 50 km of optical fibre. NPJ Quantum Inf. 5, 72 (2019).
van Leent, T. et al. Entangling single atoms over 33 km telecom fibre. Nature 607, 69–73 (2022).
Luo, X.-Y. et al. Postselected entanglement between two atomic ensembles separated by 12.5 km. Phys. Rev. Lett. 129, 050503 (2022).
Arenskötter, E. et al. Quantum teleportation with full Bell-basis detection between a 40Ca+ ion and a single photon. Preprint at https://arxiv.org/abs/2301.06091 (2023).
Brekenfeld, M., Niemietz, D., Christesen, J. D. & Rempe, G. A quantum network node with crossed optical fibre cavities. Nat. Phys. 16, 647–651 (2020).
Fedrizzi, A., Herbst, T., Poppe, A., Jennewein, T. & Zeilinger, A. A wavelength-tunable fiber-coupled source of narrowband entangled photons. Opt. Express 15, 15377–15386 (2007).
Arenskoetter, J., Kucera, S. & Eschner, J. Polarization-entangled photon pairs from a cavity-enhanced down-conversion source in sagnac configuration. In 2017 Conference on Lasers and Electro-Optics Europe & European Quantum Electronics Conference (CLEO/Europe-EQEC), 1–1 (2017).
Kucera, S. Experimental distribution of entanglement in ion-photon quantum networks: photon-pairs as resource. Ph.D. thesis, Saarland University (2019).
Braunstein, S. L., Mann, A. & Revzen, M. Maximal violation of bell inequalities for mixed states. Phys. Rev. Lett. 68, 3259–3261 (1992).
Glauber, R. J. Coherent and incoherent states of the radiation field. Phys. Rev. 131, 2766–2788 (1963).
Zaske, S., Lenhard, A. & Becher, C. Efficient frequency downconversion at the single photon level from the red spectral range to the telecommunications c-band. Opt. Express 19, 12825–12836 (2011).
Kuo, P. S., Pelc, J. S., Langrock, C. & Fejer, M. M. Using temperature to reduce noise in quantum frequency conversion. Opt. Lett. 43, 2034–2037 (2018).
Roussev, R. V., Langrock, C., Kurz, J. R. & Fejer, M. M. Periodically poled lithium niobate waveguide sum-frequency generator for efficient single-photon detection at communication wavelengths. Opt. Lett. 29, 1518–1520 (2004).
Chuang, I. L. & Nielsen, M. A. Prescription for experimental determination of the dynamics of a quantum black box. J. Mod. Opt. 44, 2455–2467 (1997).
James, D. F. V., Kwiat, P. G., Munro, W. J. & White, A. G. On the measurement of qubits. In Asymptotic Theory of Quantum Statistical Inference: Selected Papers, 509–538 (World Scientific, 2005).
Nufern. Nufern 780 nm Select Cut-Off Single-Mode Fiber (2006).
Corning. Corning® SMF-28® ULL Optical Fiber (2014).
Hradil, Z. Quantum-state estimation. Phys. Rev. A 55, R1561–R1564 (1997).
Krutyanskiy, V. et al. Entanglement of trapped-ion qubits separated by 230 meters. Phys. Rev. Lett. 130, 050803 (2023).
Krutyanskiy, V. et al. A telecom-wavelength quantum repeater node based on a trapped-ion processor. Preprint at https://arxiv.org/abs/2210.05418 (2022).
Drmota, P. et al. Robust quantum memory in a trapped-ion quantum network node. Phys. Rev. Lett. 130, 090803 (2023).
Pogorelov, I. et al. Compact ion-trap quantum computing demonstrator. PRX Quantum 2, 020343 (2021).
Noel, C. et al. Measurement-induced quantum phases realized in a trapped-ion quantum computer. Nat. Phys. 18, 760–764 (2022).
Luo, X.-Y. et al. Postselected Entanglement between Two Atomic Ensembles Separated by 12.5 km. Phys. Rev. Lett. 129, 050503 (2022).
James, D. F. V., Kwiat, P. G., Munro, W. J. & White, A. G. Measurement of qubits. Phys. Rev. A 64, 052312 (2001).
Altepeter, J. B., Jeffrey, E. R. & Kwiat, P. G. Photonic state tomography. Adv. At. Mol. Opt. Phys. 52, 105–159 (2005).
Acknowledgements
We acknowledge support by the German Federal Ministry of Education and Research (BMBF) through projects Q.Link.X (16KIS0864) and QR.X (16KISQ001K). We acknowledge support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) and Saarland University within the “Open Access Publication Funding” program.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
E.A., T.B., S.K. and M.B. prepared the experimental setup. E.A. and T.B. performed the experiments and analyzed the data. E.A. and T.B. wrote the paper with input from all authors. J.E. and C.B. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Arenskötter, E., Bauer, T., Kucera, S. et al. Telecom quantum photonic interface for a 40Ca+ single-ion quantum memory. npj Quantum Inf 9, 34 (2023). https://doi.org/10.1038/s41534-023-00701-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-023-00701-z