Abstract
In the endeavor to make quantum computers a reality, integrated superconducting circuits have become a promising architecture. A major challenge of this approach is decoherence originating from spurious atomic tunneling defects at the interfaces of qubit electrodes, which may resonantly absorb energy from the qubit’s oscillating electric field and reduce the qubit’s energy relaxation time T1. Here, we show that qubit coherence can be improved by tuning dominating defects away from the qubit resonance using an applied DC-electric field. We demonstrate a method that optimizes the applied field bias and enhances the average qubit T1 time by 23%. We also discuss how local gate electrodes can be implemented in superconducting quantum processors to enable simultaneous in situ coherence optimization of individual qubits.
Similar content being viewed by others
Introduction
Superconducting integrated circuits have evolved into a powerful architecture for creating artificial quantum systems. In state-of-the-art experiments, tens of qubits are coherently operated as quantum simulators and universal processors1,2,3,4 while access to prototype devices is being offered via the cloud to accelerate the development of practical quantum algorithms5. On the way forward, mitigating decoherence is one of the central challenges, because it hinders further up-scaling and implementation of quantum error correction6,7.
Today’s processors typically employ transmon qubits that are based on discrete energy levels in non-linear lumped-element (LC-) resonators formed by a capacitively shunted Josephson junction8. A large part of decoherence in such qubits is due to dielectric loss in the native surface oxides of the capacitor electrodes9,10. This loss shows a remarkably structured frequency dependence11,12 which originates in the individual resonances of spurious atomic tunneling defects13. These defects form a sparse bath of parasitic two-level quantum systems, so-called TLS, which have been evoked long ago to explain the anomalous low-temperature properties of amorphous materials14,15. When a TLS has an electric dipole moment, it may resonantly absorb energy from the oscillating electric field of the qubit mode, and efficiently dissipate it into the phonon-16 or BCS quasiparticle-bath17. Moreover, TLS resonance frequencies may fluctuate in time due to interactions with thermally activated, randomly switching low-energy TLS18,19,20,21,22. This mechanism efficiently transforms thermal noise into the qubit’s environmental spectrum, and causes fluctuations of the qubit’s resonance frequency and energy relaxation rate T123,24,25. For quantum processors, this implies fluctuations of their quantum volume (i.e., computational power)26.
Recently, we have shown that the resonance frequencies of TLS located on thin-film electrodes and the substrate of a qubit circuit can be tuned by an applied DC-electric field10,27. Accordingly, it becomes possible to tune defects that dominate qubit energy relaxation away from the qubit resonance, and this results in longer relaxation times T1. Here, we demonstrate this concept using a simple routine which maximizes the T1 time of a qubit by searching for an optimal electric field bias. The method was tested at various qubit resonance frequencies and increased the 30-minute averaged qubit T1 time by 23%. The ability to control the decohering TLS bath independently from the qubit will be particularly useful for quantum processors using fixed-frequency qubits, where spoilage of individual qubits due to resonance collision with a strongly coupled defect can be alleviated in situ.
Results
Electric field tuning of TLS
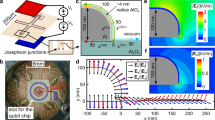
For our experiments, we fabricated a transmon qubit sample in the so-called ’X-Mon’ design following Barends et al.12 as shown in Fig. 1b. The flux-tunable qubit uses a submicron-sized Al/AlOx/Al tunnel junction made by shadow evaporation as described in detail in ref. 28. The electric field for TLS tuning is generated by a DC-electrode installed on the lid of the sample housing ≈0.9mm above the qubit chip’s surface as illustrated in Fig. 1a. The electrode is made from a conventional copper foil that is insulated by Kapton foil from the housing. To improve E-field homogeneity in vicinity of the qubits, the electrode has a comparable size to the qubit chip. More details on this setup are described in ref. 10.
a Cross-section through the sample housing. The electrode to generate the E-field consists of a Copper-foil/Kapton foil stack glued to the lid of the sample holder above the qubit chip, and voltage-biased against ground. b Photograph of the XMon qubit samples used in this work. c Illustration of defects which appear in the amorphous oxides of qubit electrodes. d Exemplary measurements of the decaying qubit population after a long exciting microwave pulse (see inset) to determine the T1 time. Red (blue) points were acquired at zero (the optimized) applied E-field. e Resonances of individual TLS (dark traces), observed as accelerated decay of the qubitʼs excited state population (color scale) using the swap-spectroscopy protocol shown in the inset. The circle marks coupling of a TLS to a metastable fluctuator which may cause hysteresis in E-field sweeps. Rectangle and ellipse indicate the fluctuating resonance frequencies of TLS coupled to slowly and quickly fluctuating thermal TLSs, respectively.
The response of TLS to the applied electric field is observed by measuring the qubit energy relaxation time T1 as a function of qubit frequency, which shows Lorentzian minima whenever sufficiently strongly interacting TLS are tuned into resonance. A detailed view on the rich TLS spectrum as shown in Fig. 1e is obtained using swap-spectroscopy29. With this protocol, TLS are detected by the resonant reduction of the qubit’s excited state population after it was tuned for a fixed time interval to various probing frequencies. In the studied sample, only a single TLS was observed that did not couple to the applied E-field, indicating that it was likely residing in a tunnel barrier of the submicron-sized qubit junctions where no DC-electric field exists8. This confirms that only a few resonant TLS are typically found in small area Josephson junctions6,28,30, and dielectric loss is dominated by defects on the interfaces of the qubit electrodes9,10,27. This is true as long as qubits are fabricated with methods31,32,33 that avoid the formation of large-area stray Josephson junctions which are known to contribute many additional defects10,28.
In Fig. 1e, some TLS are observed whose resonance frequencies show strong fluctuations or telegraphic switching due to their interaction with low-energy TLS that are thermally activated. We note that TLS may also interact with classical bistable charge fluctuators that have a very small switching rate between their states. Since these fluctuators may also be tuned by the applied electric field, hysteresis effects may appear in electric field sweeps since the state of a fluctuator, and hereby the resonance frequency of a high-energy TLS, may depend on the history of applied E-fields34. An example of such an interacting TLS-fluctuator system is marked by the blue circle in Fig. 1e, where the resonance frequency of a TLS abruptly changed.
Method for optimizing the qubit T 1 time
As it is evident from Fig. 1e, at each qubit operation frequency there is a preferable electric field bias where most of the dominating TLS are tuned out of qubit resonance and the T1 time is maximized. In the following, we describe a simple routine by which an optimal E-field bias can be automatically determined.
First, the qubit T1-time is measured for a range of applied electric fields. Hereby, the T1-time is obtained from exponential fits to the decaying qubit population probability after it was excited by a microwave pulse, measured using the common protocol shown in the inset of Fig. 1d. Figure 2a shows the resulting electric field dependence of T1 (black data points), measured at various qubit resonance frequencies (rows I to III). These data are then smoothed by a nearest-neighbor average (gray curve) to average out individual dips and peaks in order to amplify broader maxima that promise a more stable improvement.
Rows I–III were taken at the indicated qubit operation frequencies. a Qubit T1-time vs. applied electric field. Black data points are obtained from fits to exponential decay curves as shown in Fig. 1d. Dips in T1 indicate the resonance with strongly coupled TLS. The gray curve is a 3-point nearest neighbor average, whose maximum (blue circle) is close to the determined optimum bias field. The green line indicates T1 obtained in the second pass, sweeping the field in finer steps in a small range around the E-field of previously determined T1 maximum. b Comparison of qubit T1 times between an optimized E-field bias (blue data) vs. zero applied E-field (red data), measured as a function of time during 30 min.
Next, the E-field is set to the value where the maximum T1-time occurred (blue circle in Fig. 2a). Hereby, it is recommended to approach the detected optimal E-field from the same value where the previous E-field sweep was started. This helps to avoid the mentioned possible hysteresis effects in the TLS resonance frequencies that may occur when they are coupled to meta-stable field-tunable TLS whose state depends on the history of applied E-fields. Finally, a second pass is performed, sweeping the E-field in finer steps around its previously determined optimum value until the obtained T1 time is close to the maximum value that was observed in the previous sweep. This ensures that hysteresis effects are better compensated and the finer step helps to avoid sharp dips that were not resolved in the first pass. Data obtained in the second pass are plotted in green in Fig. 2a).
Benchmarking the method
To test the efficiency of the optimization routine, first the qubit T1 is repeatedly observed during 30 min at zero applied electric field as a reference (red data in Fig. 2b). Afterwards, the optimization routine searches for the electric field which maximizes the qubit’s coherence time by taking data as shown in Fig. 2a. The result is then checked by monitoring the T1-time at the found optimal E-field during another 30 min (blue data in Fig. 2b). Evidently, during most of this time, acquired T1 times after optimization are higher than the reference values that were obtained at zero applied electric field.
To measure the average improvement of the optimization routine, the benchmarking protocol was repeated at various (in total 59) qubit resonance frequencies, see the Supplementary Section IV for the full data set. Figures 3a, b summarize the absolute and relative improvement of the qubit T1-time at all investigated qubit resonance frequencies. In most cases (85%), the routine improved the 30-minute average qubit T1-time. The improvement was larger than 10% T1 in 67% of cases, and enhanced T1 by more than 20% in 46% of all tries.
a Qubit T1 times after E-field optimization (blue data) and at zero applied E-field (red data), tested at various qubit frequencies and averaged over 30 min. The error bars indicate the spread (standard deviation) of T1 over 30 min. b Relative improvement of qubit T1 after optimization. In a few cases, the routine results in a smaller T1 time (red bars). Best and average T1-time improvements are 108 and 23.2%, respectively. c Fluctuations of T1-times (standard deviation over 30 min). On average, the fluctuations were 17% higher for the optimized E-field.
The few cases where the averaged T1-time was smaller after optimization were caused by TLS resonance frequency fluctuations occurring during the 30 min averaging interval. In quantum processors, such deterioration can be detected on the basis of qubit error rates and trigger a renewed E-field optimization.
Averaged over all tested qubit resonance frequencies and a 30 min time interval past optimization, the T1 time improvement was ≈23%. We expect that similar improvements are possible also in state-of-the-art transmon qubits, as all of them show time-dependent and sample specific T1 time variations which indicate their limitation by randomly occuring TLS13,19,20,21,24.
As a consequence of the defects’ resonance frequency fluctuations, the enhancement (gain) of the T1 time tends to diminish with time that has passed after the E-field optimization. A further analysis (see Supplementary Material III) indicates that the average T1 gain drops from an initial value of about 30% immediately after optimization to slightly above 20% after 30 min past optimization.
To check how much the optimization routine affects the temporal fluctuation strength of the qubit’s T1 time, the standard deviation of observed T1 times during the 30 min intervals before and after optimization were compared. The result is shown in Fig. 3c. In slightly more than half cases (59%), the T1 time fluctuations increased after optimization. This might be mitigated by enhancing the optimization algorithm such that it prefers broader T1-time peaks which are less sensitive to TLS frequency fluctuations, and by including the T1 fluctuation strength at detected peaks as a criterion.
Proposed integration with quantum processors
When each qubit in a processor is coupled to a dedicated local gate electrode, the optimization routine can be applied simultaneously on all qubits. This tuneup-process is facilitated when no cross-talk of a gate electrode to neighboring qubits occurs. Moreover, the generated electric field should be sufficiently strong all along the edges of the qubit island and the opposing ground plane (where surface defects are most strongly coupled to the qubit10), so that all relevant TLS can be tuned by δε ≳ 100 MHz to decouple them from the qubit. Assuming a relatively small coupling TLS dipole moment component of p = 0.1 eÅ10,11,35, this corresponds to required field strengths E = δε/p ≈ 40 kV/m. Given a typical distance between the DC-electrode and the qubit electrodes of below 1 mm, such E-fields are unproblematically obtained with a bias voltage of a few Volt on the DC-electrode.
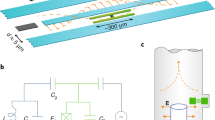
Figure 4 shows a possible implementation of a gate electrode array, which is located on a separate wiring chip that is bumb-bonded to the chip carrying the qubits in a flip-chip configuration36,37. In Fig. 4a, a top view of two Xmon-type12 qubits is shown, where the gate electrode above the left qubit is indicated in orange. The electrode extends slightly over the edges of the qubit island’s opposing ground plane to ensure the tunability of TLS in this region.
a Top view sketch of two Xmon-qubits. The orange region indicates the gate electrode above the left qubit. b Cross-section of the flip-chip stack, sketched along the red line shown in (a). The DC gate electrodes are separated by thin-film insulators from the wiring chipʼs ground plane. c Simulated electric field strength when 1 V is applied to the left gate electrode. The field decays horizontally on a scale of about the distance between the qubit and the wiring chips (here, 15 μm), resulting in small cross-talk below 10−4.
The cross section of the chip stack is sketched in Fig. 4b, showing that the gate electrodes are separated from the ground plane of the wiring chip by a thin film insulator.
The simulated electric field strength in this region is drawn to-scale in Fig. 4c, for the case when the left electrode is biased at 1 V while all other metallic parts (including the qubit island10) are kept at zero potential. As expected, the induced field strength decays on a length scale of roughly the distance between the two chips, given that qubits are surrounded by a ground plane and also the wiring chip has a ground plane. For a qubit-to-qubit separation of d > 100 μm as used in the presented simulation, we accordingly find the cross-talk to be below 10−4.
Alternatively, the local electrodes could also be placed on the backside of the qubit chip. In this case, the substrate thickness will determine the horizontal field screening length, and stronger cross-talk can be expected. However, FEM simulations of the induced E-fields in a given processor layout should allow one to sufficiently compensate for this cross-talk.
The capacitive coupling of the qubit to the gate electrode introduces extra decoherence channels: dielectric loss occurs in the insulation separating the electrode from ground, and by radiative loss, the qubit dissipates energy into the electrode wiring. These losses depend strongly on the dimensions of the electrode. We find a qubit T1 limitation of 5 ms for the setup used in this work, and estimate similar values for the proposed integration into flip-chip quantum processors. For a detailed discussion, see Supplementary Sections I and II.
Discussion
We present an experimental setup and an automatic routine that extends the energy relaxation time T1 of superconducting transmon qubits. The idea is to expose the qubit electrodes to a DC-electric field at which the most detrimental TLS-defects are tuned out of qubit resonance. Averaging over qubit working frequencies and a 30 min time interval (that was limited by time constraints), the T1-time was improved by 23% compared to zero applied electric field.
In our experiments, the optimization routine took less than 10 min (to acquire about 60 values of qubit T1 at several E-fields). However, the data shown in Fig. 2a suggests that the range of applied E-fields may be reduced, which together with further optimizations such as less averaging in individual T1-time measurements, may reduce the optimization time below one minute.
Analysis of the raw data such as shown in Fig. 2 and in the Supplementary Material suggests that more stable improvements might be achieved by improving the algorithm, e.g., by including the width of a peak in T1 vs. E-field as a criterion next to the height of the peak. Moreover, we expect that deterioration of the 30 min average qubit T1 time by the optimization routine, as it occurred in a few (≈15%) cases in these tests, can be avoided by averaging over several E-field sweeps to better account for TLS showing strong resonance frequency fluctuations. Also, one may devise a linear or machine-learning feedback mechanism that regularly readjusts the E-field bias on the basis of the steady stream of qubit error rates obtained during quantum algorithms to ensure continuous coherence enhancement.
Since the dephasing time T2 of contemporary transmon qubits is mostly limited by their energy relaxation rate when they are operated at flux sweet spots or when spin refocussing techniques are used, we expect that our technique also enhances qubit T2 times following the trend in T120,21. We are currently pursuing further experiments to quantify the method’s benefits on qubit dephasing.
The ability to tune TLS out of resonance with a qubit is especially beneficial for processors implementing fixed-frequency qubits, which can be tuned only in a limited range by exploiting the AC-stark shift22. This may still allow one to improve qubit coherence by evading strongly coupled TLS as it was recently demonstrated by Zhao et al.38. However, even when tunable qubits are used, it is still necessary to mutually balance their individual resonance frequencies to avoid crosstalk and to maximize gate fidelities, and this will be greatly simplified if qubit coherence can be optimized at all frequencies by having independent control of the TLS bath. Also, to improve two-qubit gates that require qubit frequency excursions, one could adjust our optimization procedure to minimize the number of TLS that have resonances in the traversed frequency interval.
Our simulations indicated that it is straight-forward to equip each qubit in a processor with local gate electrodes, which will allow one to simultaneously improve T1 of all qubits. We thus see good opportunities for this technique to become a standard in superconducting quantum processors.
Methods
Sample
The qubit sample is a stray-junction free transmon qubit that was fabricated by A. Bilmes as described in detail in ref. 28.
Electric field tuning
For details about the experimental setup, the implementation of the DC-electrode for defect tuning, and simulations of the electric field, we refer to ref. 10.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).
Jurcevic, P. et al. Demonstration of quantum volume 64 on a superconducting quantum computing system. Quantum Sci. Technol. 6, 025020 (2021).
Otterbach, J. et al. Unsupervised machine learning on a hybrid quantum computer. Preprint at https://arxiv.org/abs/1712.05771 (2017).
Wu, Y. et al. Strong quantum computational advantage using a superconducting quantum processor. Phys. Rev. Lett. 127, 180501 (2021).
Blinov, S., Wu, B. & Monroe, C. Comparison of cloud-based ion trap and superconducting quantum computer architectures. AVS Quantum Sci. 3, 033801 (2021).
Murray, C. E. Material matters in superconducting qubits. Mater. Sci. Eng., R. 146, 100646 (2021).
Kjaergaard, M. et al. Superconducting qubits: current state of play. Annu. Rev. Condens. Matter Phys. 11, 369–395 (2020).
Koch, J. et al. Charge-insensitive qubit design derived from the cooper pair box. Phys. Rev. A 76, 042319 (2007).
Wang, C. et al. Surface participation and dielectric loss in superconducting qubits. Appl. Phys. Lett. 107, 162601 (2015).
Lisenfeld, J. et al. Electric field spectroscopy of material defects in transmon qubits. npj Quantum Inf. 5, 1–6 (2019).
Martinis, J. M. et al. Decoherence in Josephson qubits from dielectric loss. Phys. Rev. Lett. 95, 210503 (2005).
Barends, R. et al. Coherent Josephson qubit suitable for scalable quantum integrated circuits. Phys. Rev. Lett. 111, 080502 (2013).
Müller, C., Cole, J. H. & Lisenfeld, J. Towards understanding two-level-systems in amorphous solids: insights from quantum circuits. Rep. Prog. Phys. 82, 124501 (2019).
Phillips, W. A. Two-level states in glasses. Rep. Prog. Phys. 50, 1657 (1987).
Anderson, P. W., Halperin, B. I. & Varma, C. M. Anomalous low-temperature thermal properties of glasses and spin glasses. Philos. Mag. 25, 1–9 (1972).
Jäckle, J. On the ultrasonic attenuation in glasses at low temperatures. Z. Phys. A: Hadrons Nucl. 257, 212–223 (1972).
Bilmes, A. et al. Electronic decoherence of two-level systems in a Josephson junction. Phys. Rev. B 96, 064504 (2017).
Black, J. L. & Halperin, B. I. Spectral diffusion, phonon echoes, and saturation recovery in glasses at low temperatures. Phys. Rev. B 16, 2879 (1977).
Klimov, P. V. et al. Fluctuations of energy-relaxation times in superconducting qubits. Phys. Rev. Lett. 121, 090502 (2018).
Schlör, S. et al. Correlating decoherence in transmon qubits: low frequency noise by single fluctuators. Phys. Rev. Lett. 123, 190502 (2019).
Burnett, J. J. et al. Decoherence benchmarking of superconducting qubits. npj Quantum Inf. 5, 54 (2019).
Carroll, M., Rosenblatt, S., Jurcevic, P., Lauer, I. & Kandala, A. Dynamics of superconducting qubit relaxation times. npj Quantum Inf. 8, 1–7 (2022).
Faoro, L. & Ioffe, L. B. Internal loss of superconducting resonators induced by interacting two-level systems. Phys. Rev. Lett. 109, 157005 (2012).
Müller, C., Lisenfeld, J., Shnirman, A. & Poletto, S. Interacting two-level defects as sources of fluctuating high-frequency noise in superconducting circuits. Phys. Rev. B 92, 035442 (2015).
Burnett, J. et al. Evidence for interacting two-level systems from the 1/f noise of a superconducting resonator. Nat. Commun. 5, 4119 (2014).
Pelofske, E., Bärtschi, A. & Eidenbenz, S. Quantum volume in practice: what users can expect from nisq devices. IEEE Trans. Quantum Eng. 3, 1–19 (2022).
Bilmes, A. et al. Resolving the positions of defects in superconducting quantum bits. Sci. Rep. 10, 1–6 (2020).
Bilmes, A., Volosheniuk, S., Ustinov, A. V. & Lisenfeld, J. Probing defect densities at the edges and inside Josephson junctions of superconducting qubits. npj Quantum Inf. 8, 1–6 (2022).
Lisenfeld, J. et al. Observation of directly interacting coherent two-level systems in an amorphous material. Nat. Commun. 6, 6182 (2015).
Kim, Z. et al. Anomalous avoided level crossings in a cooper-pair box spectrum. Phys. Rev. B 78, 144506 (2008).
Dunsworth, A. et al. Characterization and reduction of capacitive loss induced by sub-micron Josephson junction fabrication in superconducting qubits. Appl. Phys. Lett. 111, 022601 (2017).
Osman, A. et al. Simplified Josephson-junction fabrication process for reproducibly high-performance superconducting qubits. Appl. Phys. Lett. 118, 064002 (2021).
Bilmes, A., Händel, A. K., Volosheniuk, S., Ustinov, A. V. & Lisenfeld, J. In-situ bandaged Josephson junctions for superconducting quantum processors. Supercond. Sci. Technol. 34, 125011 (2021).
Meißner, S. M., Seiler, A., Lisenfeld, J., Ustinov, A. V. & Weiss, G. Probing individual tunneling fluctuators with coherently controlled tunneling systems. Phys. Rev. B 97, 180505 (2018).
Hung, C.-C. et al. Probing hundreds of individual quantum defects in polycrystalline and amorphous alumina. Phys. Rev. Appl. 17, 034025 (2022).
Foxen, B. et al. Qubit compatible superconducting interconnects. Quantum Sci. Technol. 3, 014005 (2017).
Kosen, S. et al. Building blocks of a flip-chip integrated superconducting quantum processor. Quantum Sci. Technol. 7, 035018 (2022).
Zhao, P., Ma, T., Jin, Y. & Yu, H. Combating fluctuations in relaxation times of fixed-frequency transmon qubits with microwave-dressed states. Phys. Rev. A 105, 062605 (2022).
Acknowledgements
This work was funded by Google LLC, which is gratefully acknowledged. We thank for funding from the Baden-Württemberg-Stiftung (Project QuMaS), and for funding from the Bundesministerium für Forschung und Bildung in the frame of the projects QSolid and GeQCoS. We acknowledge support by the KIT-Publication Fund of the Karlsruhe Institute of Technology.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
J.L. devised and implemented idea and method, performed the experiments, and analyzed the data. A.B. built the qubit setup for E-field tuning, designed and fabricated the investigated qubits, and performed FEM simulations. The manuscript was written by J.L. with assistance from A.B.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lisenfeld, J., Bilmes, A. & Ustinov, A.V. Enhancing the coherence of superconducting quantum bits with electric fields. npj Quantum Inf 9, 8 (2023). https://doi.org/10.1038/s41534-023-00678-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-023-00678-9
This article is cited by
-
Blurred interface induced control of electrical transport properties in Josephson junctions
Scientific Reports (2024)
-
Readout error mitigated quantum state tomography tested on superconducting qubits
Communications Physics (2024)