Abstract
Nitrogen-vacancy (NV) center in diamond is a promising quantum sensor with remarkably versatile sensing capabilities. While scanning NV magnetometry is well-established, NV electrometry has been so far limited to bulk diamonds. Here we demonstrate imaging external alternating (AC) and direct (DC) electric fields with a single NV at the apex of a diamond scanning tip under ambient conditions. A strong electric field screening effect is observed at low frequencies. We quantitatively measure its frequency dependence and overcome this screening by mechanically oscillating the tip for imaging DC fields. Our scanning NV electrometry achieved an AC E-field sensitivity of 26 mV μm−1 Hz−1/2, a DC E-field gradient sensitivity of 2 V μm−2 Hz−1/2, and sub-100 nm resolution limited by the NV-sample distance. Our work represents an important step toward building a scanning-probe-based multimodal quantum sensing platform.
Similar content being viewed by others
Introduction
The recent decade has witnessed exciting developments in quantum science and technology, where controlled quantum systems are employed to carry out tasks that are challenging for existing classical techniques. Quantum sensing is a rapidly-growing branch1, which exploits the fragility of quantum states to detect small external signals with high sensitivity. It has many potential applications in the real world, such as geophysical navigation2,3, disease diagnostics4,5, and discovery of new materials6,7,8. The nitrogen-vacancy (NV) center in diamonds is one of the most promising quantum sensors9. Its electron spin has a long coherence time even under ambient conditions. It is sensitive to a variety of signals, such as magnetic fields10,11,12,13, electric fields14,15,16,17,18,19,20, temperature21,22,23,24, and pressure25,26,27. Integrating this atomic-sized versatile quantum sensor into a scanning-probe microscope further allows mapping external signals with nanoscale resolution28,29,30. This holds great potential for probing condensed matter physics. More specifically, NV acts as either a magnetometer or electrometer, depending on the direction of the biased magnetic field. The ability of imaging both magnetic and electric fields can provide a unique insight into strongly correlated matter31 and multiferroic materials32. It also has interdisciplinary applications, such as imaging charge and spin phenomena in chemistry and biology9,33,34,35,36.
Scanning NV magnetometry, as a well-established technique28, has been utilized to image magnetic materials6,37,38,39, hydrodynamic current flows7,8, skyrmion structures40, and vortices in superconductors41. Recently, scanning NV electrometry has also been achieved, where fixed NVs in bulk diamonds are used to image electric fields from a conductive scanning tip19,20. However, NV electrometry has not yet been demonstrated in a diamond scanning tip, which is desired for imaging an arbitrary sample. Major challenges arise from the qubit’s weak coupling strength to electric fields, a relatively short coherence time in nanostructures compared to bulk diamonds, and electric field screening by charge noise on the diamond surface and in the bulk42,43,44. In this work, we demonstrate utilizing a shallow NV at the apex of a diamond nanopillar to image external AC and DC electric fields under ambient conditions. Dynamical-decoupling sequences are used to extend the NV coherence times45. We achieve an AC electric field sensitivity of 26 mV μm−1 Hz−1/2 and sub-100 nm spatial resolution limited by the NV-sample distance. This AC sensitivity presents an improvement by two orders of magnitude as compared to the prior work by Barson et al.19, who demonstrated an AC voltage sensitivity of 310 mV Hz−1/2 over a distance of 50 nm. A strong electric field screening effect is observed at low frequencies, likely caused by mobile charges on the surface under ambient conditions42 and in the bulk diamond46. We quantitatively characterize its frequency dependence, which reveals a resistive-capacitive (RC) time constant of our diamond tip surface ~30 μs. To overcome this screening effect for imaging DC electric fields, we oscillate the diamond probe at a frequency of ~190 kHz, and synchronize the quantum sensing pulse sequences with the mechanical motion. Hence, a local spatial gradient is upconverted to an AC signal, allowing for T2-limited DC sense. This motion-enabled imaging technique has been explored in various scanning measurements47,48,49,50,51,52, and here we apply it to scanning NV electrometry. We achieve a DC electric field gradient sensitivity of 2 V μm−2 Hz−1/2. This is two orders of magnitude better than the previous result by Bian et al.20 who demonstrated a \({T}_{2}^{* }\)-limited DC field sensitivity of 35.2 kV cm−1 Hz−1/2 using a 10 nm-in-diameter conductive tip scanning over a diamond. Our results pave the way for building a scanning-probe-based multimodal quantum sensing platform.
Results
Experimental apparatus and NV electrometry
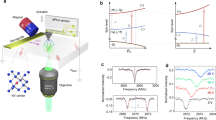
Our home-built diamond-NV scanning setup combines a confocal microscope and an atomic force microscope (AFM) operating in ambient conditions, as sketched in Fig. 1a. The diamond probe and the sample can be independently scanned by piezoelectric nanopositioners. The probe is attached to a quartz crystal tuning fork, allowing for frequency modulation AFM (FM-AFM). The probe oscillates in a motion parallel to the sample surface, so the AFM operates in shear force mode. To improve the scanning robustness, we make multiple nanopillars on a single diamond probe and use different pillars for AFM contact and quantum sensing separately. The NV, at the apex of the sensing pillar, is kept at a fixed distance from the sample. The distance is controlled by the tilting angle of the probe. More details on AFM scanning control can be found in Supplementary Note 2F. To test the electrometry capabilities of our system, we fabricate a U-shaped gold structure on a quartz substrate and use the NV to map out its electric field distribution. An on-chip microwave (MW) stripline delivers MW fields to manipulate the NV spin states. A permanent magnet from beneath exerts a bias magnetic field at the NV.
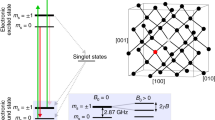
a Schematic of the experimental apparatus showing the confocal objective lens, a diamond probe, a U-shaped gold structure and microwave stripline fabricated on a quartz substrate, and an external magnet. The NV center is located at the apex of the diamond tip at a depth of ~40 nm. The tip has a diameter of 300 nm and hovers above the sample. The NV-sample distance is typically ≲100 nm. The gap between the two electrodes is 500 nm, and Au is (150 ± 5) nm thick. b NV center in the presence of a perpendicular magnetic field, denoted by B⊥ in the XY plane in yellow. The \(\hat{x}\) direction is defined by the projection of one of the carbon atoms. E⊥ is the electric field component in the XY plane, which causes Stark shifts of the NV spin states. ϕB and ϕE denote the azimuth angle of B⊥ and E⊥ relative to the \(\hat{x}\)-axis. c Zoom-in of the XY plane. Gray lines represent the projections of carbon atoms. d NV electron spin energy level under B⊥. The \(\left|\pm \right\rangle\) states are superpositions of \(\left|{m}_{{{{\rm{S}}}}}=\pm\! 1\right\rangle\) (see main text) and sensitive to E⊥. d⊥ = (0.17 ± 0.03) MHz/V/μm is the transverse electric field coupling constant and γ = 2.8 MHz G−1 is the electron spin gyromagnetic ratio. e Top panel: optical and microwave sequence for pulsed optically detected magnetic resonance (ODMR) measurements. Bottom panel: Pulsed ODMR spectrum showing transitions between \(\left|0\right\rangle\) and \(\left|\pm \right\rangle\) under B⊥ ≈ 73 G. The driving efficiencies depend on the MW field polarization. The \(\left|0\right\rangle\)-to-\(\left|+\right\rangle\) transition is used throughout this work for electric field sensing.
Our electrometry measurements were performed under a magnetic field oriented perpendicular to the NV axis, denoted by B⊥. The coordinate system is depicted in Fig. 1b, where \(\hat{z}\) is along the NV axis and the projection of one carbon atom in the perpendicular plane defines the \(\hat{x}\) axis. Under B⊥, the NV electron spin eigenstates are \(\left|0\right\rangle \approx \left|{m}_{{{{\rm{S}}}}}=0\right\rangle\), \(\left|\pm \right\rangle \approx \frac{1}{\sqrt{2}}(\left|{m}_{{{{\rm{S}}}}}=1\right\rangle \pm {e}^{2i{\phi }_{{{{\rm{B}}}}}}\left|{m}_{{{{\rm{S}}}}}=-1\right\rangle )\)14,53, where ϕB is the angle between B⊥ and the \(\hat{x}\) axis (see Fig. 1c). Electric fields induce Stark shifts of the \(\left|\pm \right\rangle\) energy levels. The splitting between the \(\left|\pm \right\rangle\) states is approximately \({{\Delta }}\approx \frac{{\gamma }^{2}{B}_{\perp }^{2}}{D}-2{d}_{\perp }{E}_{\perp }\cos (2{\phi }_{{{{\rm{B}}}}}+{\phi }_{{{{\rm{E}}}}})\), where ϕB and ϕE are the angles of magnetic and electric fields in the transverse plane as shown in Fig. 1c, Dgs ≈ 2.87 GHz is the zero-field splitting (ZFS), γB = 2.8 MHz G−1 is the electron spin gyromagnetic ratio and d⊥ = (0.17 ± 0.03) MHz μm V−1 is the transverse electric field coupling strength54. We ignore the coupling to Ez since the longitudinal coupling strength d∥ = (3.5 ± 0.2) × 10−3 MHz μm V−1 54 is much smaller. Strain is measured to be negligible in our diamond probe for the scope of this work.
We choose to work with 15NV under B⊥ > 70 G53. The splitting between the \(\left|\pm \right\rangle\) states is therefore much larger than the hyperfine coupling ≈ 3 MHz55, and both nuclear spin sublevels (mI = ± 1/2) are sensitive to electric fields. Consequently, the full NV optical contrast contributes to the signal without the need of resolving hyperfine states. We use NVs with moderate \({T}_{2}^{* }\) dephasing times (\({T}_{2}^{* } \sim 1.5\) μs, see Supplementary Note 2A) and apply relatively strong MW power to drive transitions between spin states (π pulse duration ~100 ns). These are in contrast to NV electrometry performed under a weak magnetic field where typically B⊥ < 20 G14,15. A detailed comparison between 15NV and 14NV electrometry under different magnetic field regimes can be found in Supplementary Note 1B.
Figure 1 d shows a pulsed optically detected magnetic resonance (ODMR) spectrum under B⊥ ≈ 73 G. The transition efficiencies between \(\left|0\right\rangle\) and \(\left|\pm \right\rangle\) depend on the linear polarization of the MW fields (see Supplementary Note 1B). We use the \(\left|0\right\rangle\)-to-\(\left|+\right\rangle\) transition throughout this work for electric field sensing.
Frequency dependence of the electric field screening
A strong electric field screening effect is observed at DC and low frequencies (see Supplementary Fig. 10), likely caused by mobile charges on the diamond surface and in the bulk42. Possible sources include adsorbed water layer under ambient conditions, electronic trapping states due to near-surface band-bending43,56, and internal charge defects such as vacancy complexes and substitutional nitrogen generated during diamond growth or NV creation46,57. We characterize this screening effect by measuring its frequency dependence. NV is positioned within a metal gap. An AC reference voltage is applied across the gap, generating an electric field at the NV. Lock-in detection is employed in order to extract both the amplitude and phase of the NV signal relative to the reference signal.
At low frequencies, we use a Ramsey-based lock-in sequence, where a train of equally spaced Ramsey measurements is synchronized with the reference signal, as shown in Fig. 2a. In each Ramsey measurement, the NV spin is prepared in a superposition of \(\left|0\right\rangle\) and \(\left|+\right\rangle\), and then accumulates phase induced by the DC electric field within the free evolution time τ = 800 ns. The accumulated phase ϕNV can be extracted from the NV fluorescence signal measured after the final π/2 pulse (see Supplementary Note 2D). This phase is proportional to the local electric field, \({\phi }_{{{{\rm{NV}}}}}={d}_{\perp }{E}_{\perp }\cos (2{\phi }_{{{{\rm{B}}}}}+{\phi }_{{{{\rm{E}}}}})\tau\), hence each Ramey measurement samples the electric field strength at the corresponding time step. The first Ramsey starts at 4 μs after the reference trigger, and the spacing between neighboring Ramsey measurements is also 4 μs. To have a sufficient number of sampling points, we performed measurements at reference signal frequencies below 50 kHz. As shown in Fig. 2b, the NV Ramsey phase ϕNV oscillates in time, with the amplitude increasing with the reference frequency. Sinusoidal curve fitting extracts the amplitude and phase relative to the reference, which is represented by blue dots in Fig. 2e.
a Top panel: Ramsey-based lock-in detection sequence used at low frequencies. A train of Ramsey measurements is synchronized with the external reference signal, and samples the local electric field every 4 μs. Bottom panel: Zoom-in of two Ramsey sequences. b Top three panels: Time traces of the Ramsey phase signal ϕNV at reference frequencies of 4, 12, and 30 kHz, respectively. Bottom panel: The reference input with the aforementioned frequencies). Dynamical-decoupling-based lock-in detection at high frequencies. XY-4 sequence is shown as an example. The NV phase signal ϕNV is maximized when the detected field is in-phase with XY-4 (lower left plot), and minimized when out-of-phase by π/2 (lower right plot). d NV phase signals ϕNV at 200, 800, and 1200 kHz. No discernible frequency dependence is observed. Pulse sequences see Supplementary Fig. 6. e Frequency dependence of signal attenuation (top panel) and phase delay (bottom panel), extracted from the lock-in measurements in b and d). Signal is normalized with respect to the expected phase induced by the applied electric field in the absence of screening. The red solid traces represent an ideal high-pass filter with a cut-off frequency of 35.4 kHz. PDD stands for periodic dynamical decoupling58, which refers to XY pulse sequences used at high frequencies. Error bars represent standard deviations estimated from sinusoidal curve fitting. f A high-pass filter circuit model. NV is positioned within a metal gap. g A phenomenological circuit model showing capacitive coupling between the diamond surface and a sample.
At high frequencies, the lock-in detection is based on a dynamical-decoupling pulse sequence58, such as XY-4 shown in Fig. 2c. The spacing between neighboring π pulses is set to be half of the period of the reference signal. More π pulses are inserted to match high frequencies. Due to the finite coherence time T2, these measurements were performed above 200 kHz (see Supplementary Note 2A for NV T2 characterizations using various dynamical-decoupling sequences). The NV spin, prepared in a superposition of \(\left|0\right\rangle\) and \(\left|+\right\rangle\), accumulates a phase induced by the AC electric field within the evolution time τ. The coherent phase signal ϕNV is maximized when the detected local field is ‘in-phase’ (φ = 0) with the XY-4 sequence and minimized when ‘90° out-of-phase’ (φ = π/2). To measure the amplitude and phase of the detected signal relative to the reference, we vary the initial phase offset by sweeping the delay between the reference trigger and the first π/2 pulse. As shown in Fig. 2d, ϕNV is maximized at zero initial phase offset, and minimized near π/2, which indicates very little relative phase between the detected and reference signal. In contrast to the low-frequency regime, here, the oscillation amplitude shows no obvious dependence on the frequency. The extracted amplitude and phase by sinusoidal curve fitting are represented by orange dots in Fig. 2e.
Figure 2e summarizes the results in both low and high-frequency regimes. The trend resembles the frequency response of a high-pass filter. The red solid curves represent an ideal high-pass filter with a cut-off frequency fc at 35.4 kHz, corresponding to an RC time constant ~30 μs. A simplified circuit model in Fig. 2f illustrates a possible high-pass filter consisting of the resistive diamond surface and capacitance between the tip and electrodes. For a general sample, Fig. 2g shows the capacitive coupling between the diamond surface and the sample. Screening is significantly reduced at high frequencies due to the finite mobility of charge carriers. The specific frequency cut-off can vary between different probes since the NV location, the geometry of the tip surface, and diamond purity all affect the screening effect. We emphasize that this circuit model is only phenomenological. Figure 2e mainly allows us to identify the frequency at which the screening effect significantly diminishes, which is essential information for implementing motion-enabled DC sensing, as will be discussed in the next section.
Spatial mapping of AC and DC electric field distribution
We now demonstrate imaging of the AC electric field distribution. A single NV at the apex of a diamond nanopillar (300 nm in diameter) scans over a U-shaped gold structure (Fig. 3a). Our spatial resolution is limited by the NV-sample distance, which can be ≲100 nm. The diamond is attached to a piezoelectric tuning fork, which oscillates on resonance (~32 kHz) and provides frequency feedback to regulate the distance to the sample. In our AC electric field imaging, the oscillation amplitude is kept small (estimated to be <1 nm), and no reduction of the NV coherence time is observed. The probe motion is therefore represented by a flat line in Fig. 3a. An AC signal Vpp = 0.96 V at 250 kHz is applied to the middle electrode and synchronized in-phase with the XY-4 pulse sequence with a free evolution time τ = 8 μs. The accumulated phase is \({\phi }_{{{{\rm{NV}}}}}={d}_{\perp }\cdot {E}_{\perp }\cos (2{\phi }_{{{{\rm{B}}}}}+{\phi }_{{{{\rm{E}}}}})\cdot \tau ={d}_{\perp }{E}_{\zeta }\tau\), where \(\hat{\zeta }\) denotes the maximum electric coupling direction, and Eζ is the \(\hat{\zeta }\) component of E⊥. Figure 3b plots ϕNV as a function of the AC input amplitude, measured by the NV at a fixed point within the gap. ϕNV grows proportionally as expected. The cosine and sine values are measured by rotating the phase of the final π/2 pulse (see Supplementary Note 2D). Dashed traces in Fig. 3c show 1D line scans of ϕNV and the corresponding e-field Eζ at different NV-sample distances (controlled by the probe tilting angle). They are in good agreement with the simulated Eζ distribution shown by the solid traces. The azimuth and zenith angles of \(\hat{\zeta }\) in the simulation are at ϕ = 20° and θ = 45°, respectively (Supplementary Fig. 14a). Based on a NV fluorescence rate >100 kcps, an optical contrast >20%, and a phase accumulation time τ = 8 μs in our experiment, we have achieved an AC electric field sensitivity of 26 mV μm−1 Hz−1/2 under ambient conditions (see Supplementary Note 2E). A 2D map of the AC electric field is shown in Fig. 3d, and a simulated field distribution at a distance of d = 90 nm is shown in Fig. 3e.
a Schematic of scanning NV microscopy and the pulse sequence for AC electrometry. The probe oscillates with an amplitude <1 nm, hence represented by a black flat curve. The AC reference input is in-phase with the XY-4 detection sequence. b NV measurements performed at a fixed point within the gap. Top panel: the cosine and sine values measured by rotating the phase of the final π/2 pulse. Bottom panel: Extracted phase ϕNV proportional to the AC input amplitude. c Top panel: 1D line scans of the NV phase signal ϕNV at different NV-sample distances controlled by the tilting angle of the diamond probe. The AC input has a peak-to-peak amplitude of 0.96 V. Dashed traces are the experimental data, and solid traces show the COMSOL simulation. Bottom panel: the height profile of the metal. d 2D mapping of the AC electric field distribution in the U-shaped Au structure. e Simulated electric field distribution along the maximum coupling axis \(\hat{\zeta }\) at a distance of 90 nm. The azimuth angle of \(\hat{\zeta }\) with respect to the coordinate system shown in (a) is ϕ = 20°, and the zenith angle θ = 45°. The white dashed lines outline the edge of the Au structure used in the simulation.
To map DC electric fields, we employ a motion-enabled imaging technique12 that converts the DC signal to AC in order to overcome the screening effect. More concretely, the probe oscillates with a relatively large amplitude (>10 nm) such that the NV experiences an AC local field proportional to the local spatial gradient \(E^{\prime}_\zeta (x)\) (Fig. 4a). In addition, the bending of the tuning fork induces a rotational motion of the NV axis, giving rise to an AC modulation proportional to the local static field Eζ. This latter effect cannot be ignored as shown by the data below. The amplitude of the total motion-enabled AC signal has a form of \({E}_{{{{\rm{amp}}}}}=E^{\prime}_\zeta (x)A+\beta {E}_{\zeta }\), where A is the probe oscillation amplitude, and β is an empirical constant capturing the NV axis rotation. To operate at a sufficiently high frequency at which the screening diminishes, we drive the clang mode of the tuning fork at ~190 kHz59 (Supplementary Fig. 11). The sensing pulse sequence is synchronized with the mechanical motion, so the NV accumulates a coherent phase ϕNV = d⊥Eampτ. Figure 4b shows the NV measurement at a fixed point within the gap, where ϕNV is proportional to the applied DC voltage Vdc. Based on our experimental parameters, we achieved a DC field gradient sensitivity of 2 V μm−2 Hz−1/2 (Supplementary Note 2E). Figure 4c compares a 1D line scan of ϕNV along the \(\hat{x}\)-axis at Vdc = 16 V with the expected signal deduced from the measurements in Fig. 3c and simulated signal by COMSOL. The top panel shows a clear discrepancy between data and expected signal or simulation, when only the gradient term \(E^{\prime}_\zeta (x)A\) in Eamp is considered. The sign of the discrepancy coincides with the sign of Eζ shown in Fig. 3c. Including the term βEζ in Eamp leads to an improved agreement between data and model (using A = 13 nm and β = −0.03 in the model), as shown in the middle panel. Since the probe oscillates at a large amplitude while performing contact-mode AFM scanning, the actual motion highly depends on the details of the probe-sample engagement. This is challenging to simulate accurately and could account for the remaining discrepancy. A 2D map of ϕNV is shown in Fig. 4d, showing a reasonable agreement with the simulation result in Fig. 4e.
a Schematic of scanning NV microscopy and the pulse sequence for DC electrometry. The input signal is DC, represented by a blue flat line. The probe motion at ~190 kHz is synchronized with the XY-4 sensing pulse sequences. b NV measurements performed at a fixed point within the gap. Top panel: the cosine and sine values measured by rotating the phase of the final π/2 pulse. Bottom panel: Extracted phase ϕNV proportional to the DC input amplitude. c 1D line scans of ϕNV. The center electrode is at Vdc = 16 V. Top panel: Discrepancy between the model \({\phi }_{{{{\rm{NV}}}}}={d}_{\perp }E^{\prime}_\zeta (x)A\tau\) and data. The green trace shows the expected gradient field signal calculated from tilt 4 in Fig. 3c. The blue trace shows the COMSOL simulation. The red (blue) background corresponds to the region of Eζ > 0 (Eζ < 0) as shown in Fig. 3c. Middle panel: The model \({\phi }_{{{{\rm{NV}}}}}={d}_{\perp }(E^{\prime}_\zeta (x)A+\beta {E}_{\zeta })\tau\) showing an improved agreement with data, where A = 13 nm is the oscillation amplitude and β = −0.03 is the proportionality constant that captures the NV axis rotation. Bottom panel: the height profile of the metal. d 2D mapping of ϕNV measured at Vdc = 16 V. e Simulated signal ϕNV at a distance of 140 nm from the sample. The maximum coupling axis \(\hat{\zeta }\) is set to be same as in Fig. 3e, and the oscillation amplitude is 13 nm. The white dashed lines outline the edge of the Au structure used in the simulation.
Discussion
In conclusion, we demonstrated electric field imaging with a single NV at the apex of a diamond scanning tip under ambient conditions. External electric fields are significantly screened at low frequencies. We quantitatively measured its frequency dependence using lock-in detection sequences and therefore revealed the RC time constant of the tip surface (~30 μs). To overcome screening, we introduced a motion-enabled technique and demonstrated spatial mapping of the DC electric field gradients.
Potential improvements to these demonstrations can be achieved as follows. First, AFM operating in tapping or non-contact mode would avoid direct contact between the probe and sample and allow the probe to oscillate with a larger amplitude more stably (see more in Supplementary Note 2G). This will give a higher field gradient sensitivity in motion-enabled imaging. Second, given an unknown sample, the DC field distribution along the maximum coupling axis ζ can be reconstructed by carefully pre-calibrating the probe oscillation direction and amplitude using a well-defined sample as described in this paper. Third, using multiple NVs of different orientations or multiple pillars with NVs of different orientations, one can extract both the magnitude and the direction of external electric fields, i.e. vector electrometry16. Finally, a higher spatial resolution is achievable by using even shallower NVs and motorized goniometers for better control of the probe tilting angle.
NV electrometry possesses a unique combination of properties as compared to other existing techniques. In this work, we achieved an AC electric field sensitivity of 26 mV μm−1 Hz−1/2, DC electric field gradient sensitivity of 2 V μm−2 Hz−1/2, and sub-100 nm spatial resolution limited by the NV-sample distance, all under ambient conditions. Most other electrometry techniques are based on measuring potentials, and many require cryogenic conditions. For example, scanning single-electron-transistor (SET)60,61,62,63 is capable of measuring microvolt local potential; however, this remarkable sensitivity requires low-temperature operation and its spatial resolution is limited by the tip size (>100 nm). Kelvin probe force microscopy (KPFM)64,65 and electrostatic force microscopy (EFM)66 can achieve sub-10 nm spatial resolution and operate under ambient conditions; however, they are not optimal for quantitative electric field measurements. NV center is therefore a valuable addition as a unique electric field sensor with complementary advantages. We also highlight that NVs have unparalleled sensing versatility with a broad operating frequency range. Integrating electrometry and magnetometry into a single scanning probe will open up exciting opportunities in imaging nanoscale phenomena.
Methods
Diamond scanning probe and AFM control
The diamond probe was made from an electronic-grade CVD diamond purchased from Element Six, with a natural abundance (1.1%) of 13C impurity spins. The probe is of ~50 × 55 × 125 μm in dimension. Each probe has seven tips in a row with a spacing of 7 μm. Details of the multiple-pillar probe design and fabrication process are described in8,67,68.
The probe is attached to one prong of a quartz tuning fork using optical adhesive (Thorlabs NOA63). Two manual goniometers (Edmund) control its tilting angle and the NV-sample distance. The AFM contact between probe and sample is controlled by an attocube SPM controller (ASC500). Piezoelectric nanopositioners (attocube ANPxyz101 and ANPxyz100) were used for sample scanning. More details can be found in Supplementary Note 2F.
Optical setup
NV experiments were performed on a home-built confocal laser scanning microscope. A 532 nm green laser (Cobolt Samba 100), focused by a ×100, NA = 0.7 objective (Mitutoyo M Plan NIR HR), was used to initialize the NV spin to the \(\left|{m}_{{{{\rm{S}}}}}=0\right\rangle\) state and generate spin-dependent photoluminescence for optical readout. An avalanche photodiode (APD, Excelitas Technologies Photon Counting Module SPCM-AQRH-13) was used to measure the NV fluorescence rate.
Quantum control setup
The microwaves were generated from a signal generator (Rohde & Schwarz SGS100A 6GHz SGMA RF Source) and amplified by a MW amplifier (Amplifier Research 30S1G6). All quantum measurements were performed on the Quantum Orchestration Platform (Quantum Machines). An Operator-X (OPX) generated control pulse sequences, output AC input voltages (Vpp = 0.96 V), and measured the photon counts. DC input (Vdc = 16 V) is provided by a voltage source (Yokogawa GS200).
Electrostatics simulation
The finite-element calculation package COMSOL performs the electrostatic simulations. To model the geometry, we use real device dimensions by importing the lithography design into the software. 2D simulation produces plots in Figs. 3c and 4c. 3D simulation produces the plots in Figs. 3e and 4e.
Data availability
The data generated and analyzed during this study are available from the authors upon reasonable request.
References
Degen, C. L., Reinhard, F. & Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 89, 035002 (2017).
Little, B. J. et al. A passively pumped vacuum package sustaining cold atoms for more than 200 days. AVS Quantum Sci. 3, 035001 (2021).
Soshenko, V. V. et al. Nuclear spin gyroscope based on the nitrogen vacancy center in diamond. Phys. Rev. Lett. 126, 197702 (2021).
Miller, B. S. et al. Spin-enhanced nanodiamond biosensing for ultrasensitive diagnostics. Nature 587, 588–593 (2020).
Li, C., Soleyman, R., Kohandel, M. & Cappellaro, P. Sars-cov-2 quantum sensor based on nitrogen-vacancy centers in diamond. Nano Lett. 22, 43–49 (2021).
Thiel, L. et al. Probing magnetism in 2d materials at the nanoscale with single-spin microscopy. Science 364, 973–976 (2019).
Ku, M. J. et al. Imaging viscous flow of the dirac fluid in graphene. Nature 583, 537–541 (2020).
Vool, U. et al. Imaging phonon-mediated hydrodynamic flow in wte2. Nat. Phys. 17, 1216–1220 (2021).
Schirhagl, R., Chang, K., Loretz, M. & Degen, C. L. Nitrogen-vacancy centers in diamond: nanoscale sensors for physics and biology. Annu. Rev. Phys. Chem. 65, 83–105 (2014).
Maze, J. R. et al. Nanoscale magnetic sensing with an individual electronic spin in diamond. Nature 455, 644–647 (2008).
Mamin, H. et al. Nanoscale nuclear magnetic resonance with a nitrogen-vacancy spin sensor. Science 339, 557–560 (2013).
Hong, S. et al. Nanoscale magnetometry with nv centers in diamond. MRS Bull. 38, 155–161 (2013).
Casola, F., Van Der Sar, T. & Yacoby, A. Probing condensed matter physics with magnetometry based on nitrogen-vacancy centres in diamond. Nat. Rev. Mater. 3, 1–13 (2018).
Dolde, F. et al. Electric-field sensing using single diamond spins. Nat. Phys. 7, 459–463 (2011).
Michl, J. et al. Robust and accurate electric field sensing with solid state spin ensembles. Nano Lett. 19, 4904–4910 (2019).
Yang, B. et al. Vector electrometry in a wide-gap-semiconductor device using a spin-ensemble quantum sensor. Phys. Rev. Appl. 14, 044049 (2020).
Li, R. et al. Nanoscale electrometry based on a magnetic-field-resistant spin sensor. Phys. Rev. Lett. 124, 247701 (2020).
Block, M. et al. Optically enhanced electric field sensing using nitrogen-vacancy ensembles. Phys. Rev. Appl. 16, 024024 (2021).
Barson, M. S. et al. Nanoscale vector electric field imaging using a single electron spin. Nano Lett. 21, 2962–2967 (2021).
Bian, K. et al. Nanoscale electric-field imaging based on a quantum sensor and its charge-state control under ambient condition. Nat. Commun. 12, 1–9 (2021).
Kucsko, G. et al. Nanometre-scale thermometry in a living cell. Nature 500, 54–58 (2013).
Neumann, P. et al. High-precision nanoscale temperature sensing using single defects in diamond. Nano Lett. 13, 2738–2742 (2013).
Toyli, D. M., Charles, F., Christle, D. J., Dobrovitski, V. V. & Awschalom, D. D. Fluorescence thermometry enhanced by the quantum coherence of single spins in diamond. Proc. Natl Acad. Sci. USA 110, 8417–8421 (2013).
Choi, J. et al. Probing and manipulating embryogenesis via nanoscale thermometry and temperature control. Proc. Natl Acad. Sci. USA 117, 14636–14641 (2020).
Doherty, M. W. et al. Electronic properties and metrology applications of the diamond nv- center under pressure. Phys. Rev. Lett. 112, 047601 (2014).
Ivády, V., Simon, T., Maze, J. R., Abrikosov, I. & Gali, A. Pressure and temperature dependence of the zero-field splitting in the ground state of nv centers in diamond: a first-principles study. Phys. Rev. B. 90, 235205 (2014).
Kehayias, P. et al. Imaging crystal stress in diamond using ensembles of nitrogen-vacancy centers. Phys. Rev. B. 100, 174103 (2019).
Maletinsky, P. et al. A robust scanning diamond sensor for nanoscale imaging with single nitrogen-vacancy centres. Nat. Nanotechnol. 7, 320–324 (2012).
Rondin, L. et al. Nanoscale magnetic field mapping with a single spin scanning probe magnetometer. Appl. Phys. Lett. 100, 153118 (2012).
Pelliccione, M. et al. Scanned probe imaging of nanoscale magnetism at cryogenic temperatures with a single-spin quantum sensor. Nat. Nanotechnol. 11, 700–705 (2016).
Wu, F., Lovorn, T., Tutuc, E. & MacDonald, A. H. Hubbard model physics in transition metal dichalcogenide moiré bands. Phys. Rev. Lett. 121, 026402 (2018).
Mundy, J. A. et al. Atomically engineered ferroic layers yield a room-temperature magnetoelectric multiferroic. Nature 537, 523–527 (2016).
Barry, J. F. et al. Optical magnetic detection of single-neuron action potentials using quantum defects in diamond. Proc. Natl Acad. Sci. USA 113, 14133–14138 (2016).
Liu, H., Plenio, M. B. & Cai, J. Scheme for detection of single-molecule radical pair reaction using spin in diamond. Phys. Rev. Lett. 118, 200402 (2017).
Petrini, G. et al. Is a quantum biosensing revolution approaching? perspectives in nv-assisted current and thermal biosensing in living cells. Adv. Quantum Technol. 3, 2000066 (2020).
Webb, J. L. et al. Detection of biological signals from a live mammalian muscle using an early stage diamond quantum sensor. Sci. Rep. 11, 1–11 (2021).
Tetienne, J.-P. et al. Nanoscale imaging and control of domain-wall hopping with a nitrogen-vacancy center microscope. Science 344, 1366–1369 (2014).
Tetienne, J.-P. et al. The nature of domain walls in ultrathin ferromagnets revealed by scanning nanomagnetometry. Nat. Commun. 6, 1–6 (2015).
Gross, I. et al. Real-space imaging of non-collinear antiferromagnetic order with a single-spin magnetometer. Nature 549, 252–256 (2017).
Dovzhenko, Y. et al. Magnetostatic twists in room-temperature skyrmions explored by nitrogen-vacancy center spin texture reconstruction. Nat. Commun. 9, 1–7 (2018).
Thiel, L. et al. Quantitative nanoscale vortex imaging using a cryogenic quantum magnetometer. Nat. Nanotechnol. 11, 677–681 (2016).
Oberg, L. M. et al. Solution to electric field screening in diamond quantum electrometers. Phys. Rev. Appl. 14, 014085 (2020).
Stacey, A. et al. Evidence for primal sp2 defects at the diamond surface: candidates for electron trapping and noise sources. Adv. Mater. Interfaces 6, 1801449 (2019).
Mertens, M. et al. Patterned hydrophobic and hydrophilic surfaces of ultra-smooth nanocrystalline diamond layers. Appl. Surf. Sci. 390, 526–530 (2016).
De Lange, G., Wang, Z., Riste, D., Dobrovitski, V. & Hanson, R. Universal dynamical decoupling of a single solid-state spin from a spin bath. Science 330, 60–63 (2010).
Bassett, L., Heremans, F., Yale, C., Buckley, B. & Awschalom, D. Electrical tuning of single nitrogen-vacancy center optical transitions enhanced by photoinduced fields. Phys. Rev. Lett. 107, 266403 (2011).
Hong, S. et al. Coherent, mechanical control of a single electronic spin. Nano Lett. 12, 3920–3924 (2012).
Kolkowitz, S. et al. Coherent sensing of a mechanical resonator with a single-spin qubit. Science 335, 1603–1606 (2012).
Teissier, J., Barfuss, A., Appel, P., Neu, E. & Maletinsky, P. Strain coupling of a nitrogen-vacancy center spin to a diamond mechanical oscillator. Phys. Rev. Lett. 113, 020503 (2014).
Halbertal, D. et al. Imaging resonant dissipation from individual atomic defects in graphene. Science 358, 1303–1306 (2017).
Wood, A. et al. T2-limited sensing of static magnetic fields via fast rotation of quantum spins. Phys. Rev. B. 98, 174114 (2018).
Huxter, W. S. et al. Scanning gradiometry with a single spin quantum magnetometer. Nat. Commun. 13, 3761 (2022).
Qiu, Z., Vool, U., Hamo, A. & Yacoby, A. Nuclear spin assisted magnetic field angle sensing. npj Quantum Inf. 7, 1–7 (2021).
Van Oort, E. & Glasbeek, M. Electric-field-induced modulation of spin echoes of nv centers in diamond. Chem. Phys. Lett. 168, 529–532 (1990).
Ohno, K. et al. Engineering shallow spins in diamond with nitrogen delta-doping. Appl. Phys. Lett. 101, 082413 (2012).
Shirafuji, J. & Sugino, T. Electrical properties of diamond surfaces. Diam. Relat. Mater. 5, 706–713 (1996).
Collins, A. Spectroscopy of defects and transition metals in diamond. Diam. Relat. Mater. 9, 417–423 (2000).
Souza, A. M., Álvarez, G. A. & Suter, D. Robust dynamical decoupling. Philos. Trans. A Math. Phys. Eng. Sci. 370, 4748–4769 (2012).
Rossing, T. D., Russell, D. A. & Brown, D. E. On the acoustics of tuning forks. Am. J. Phys. 60, 620–626 (1992).
Yoo, M. et al. Scanning single-electron transistor microscopy: Imaging individual charges. Science 276, 579–582 (1997).
Yacoby, A., Hess, H., Fulton, T., Pfeiffer, L. & West, K. Electrical imaging of the quantum hall state. Solid State Commun. 111, 1–13 (1999).
Martin, J. et al. Observation of electron–hole puddles in graphene using a scanning single-electron transistor. Nat. Phys. 4, 144–148 (2008).
Sulpizio, J. A. et al. Visualizing poiseuille flow of hydrodynamic electrons. Nature 576, 75–79 (2019).
Nonnenmacher, M., o’Boyle, M. & Wickramasinghe, H. K. Kelvin probe force microscopy. Appl. Phys. Lett. 58, 2921–2923 (1991).
Melitz, W., Shen, J., Kummel, A. C. & Lee, S. Kelvin probe force microscopy and its application. Surf. Sci. Rep. 66, 1–27 (2011).
Girard, P. Electrostatic force microscopy: principles and some applications to semiconductors. Nanotechnology 12, 485 (2001).
Zhou, T. X., Stöhr, R. J. & Yacoby, A. Scanning diamond nv center probes compatible with conventional afm technology. Appl. Phys. Lett. 111, 163106 (2017).
Xie, L., Zhou, T. X., Stöhr, R. J. & Yacoby, A. Crystallographic orientation dependent reactive ion etching in single crystal diamond. Adv. Mater. 30, 1705501 (2018).
Acknowledgements
We thank Yonatan Cohen and Niv Drucker for their support on the Quantum Orchestration Platform, Shaowen Chen, and Elizabeth Park for their assistance in the sample fabrication and diamond probe gluing processes. This work was primarily supported by the Quantum Science Center (QSC), a National Quantum Information Science Research Center of the U.S. Department of Energy (DOE).
Author information
Authors and Affiliations
Contributions
Z.Q. and A.Y. conceived the project. Z.Q. fabricated the sample, performed the measurements, simulation, and analyzed the data. Z.Q., A.H., U.V., and A.Y. discussed the results. T.X.Z. fabricated the diamond scanning probes. Z.Q. and T.X.Z. built the scanning-probe setup. A.Y. supervised the project. All the authors contributed to the writing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Qiu, Z., Hamo, A., Vool, U. et al. Nanoscale electric field imaging with an ambient scanning quantum sensor microscope. npj Quantum Inf 8, 107 (2022). https://doi.org/10.1038/s41534-022-00622-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-022-00622-3
This article is cited by
-
Quantum double lock-in amplifier
Communications Physics (2024)
-
Imaging ferroelectric domains with a single-spin scanning quantum sensor
Nature Physics (2023)
-
Perspective: nanoscale electric sensing and imaging based on quantum sensors
Quantum Frontiers (2023)