Abstract
We propose a scheme to implement general quantum measurements, also known as Positive Operator Valued Measures (POVMs) in dimension d using only classical resources and a single ancillary qubit. Our method is based on probabilistic implementation of d-outcome measurements which is followed by postselection of some of the received outcomes. We conjecture that success probability of our scheme is larger than a constant independent of d for all POVMs in dimension d. Crucially, this conjecture implies the possibility of realizing arbitrary nonadaptive quantum measurement protocol on d-dimensional system using a single auxiliary qubit with only a constant overhead in sampling complexity. We show that the conjecture holds for typical rank-one Haar-random POVMs in arbitrary dimensions. Furthermore, we carry out extensive numerical computations showing success probability above a constant for a variety of extremal POVMs, including SIC-POVMs in dimension up to 1299. Finally, we argue that our scheme can be favorable for experimental realization of POVMs, as noise compounding in circuits required by our scheme is typically substantially lower than in the standard scheme that directly uses Naimark’s dilation theorem.
Similar content being viewed by others
Introduction
Quantum measurements recover classical information stored in quantum systems and, as such, constitute an essential part of virtually any quantum information protocol. Every physical platform has its native measurements that can be realized with relative ease. In many cases, the class of easily implementable measurements contains projective (von Neumann) measurements. However, there are numerous applications1,2,3,4,5,6,7,8,9 in which more general quantum measurements, so called Positive-Operator-Valued Measures (POVMs), need to be implemented. Implementation of these measurements requires additional resources. A recent generalization10 of Naimark’s dilation theorem11 showed that the most general measurement on N qubits requires N auxiliary qubits, when projective measurements can be implemented on the combined system in a randomized manner.
From the perspective of implementation in near-term quantum devices12, it is desirable to implement arbitrary POVMs with fewer resources. Particularly, one would like to reduce the number of auxiliary qubits needed to implement a complex quantum measurement. A related problem is to quantify the relative power that generalized measurements in d-dimensional quantum systems have with respect to projective measurements in the same dimension. While POVMs appear as natural measurements for a variety of quantum information tasks: quantum state discrimination13, quantum tomography14,15,16, multi-parameter metrology17,18, randomness generation19, entanglement20 and nonlocality detection21, hidden subgroup problem22,23, port-based-teleportation24,25,26, to name just a few. It is, however, not clear in general what quantitative advantage the more complex measurements offer over their simpler projective counterparts. This is because of the possibility to realize non-projective quantum measurements via randomization and post-processing of simpler measurements10,27,28,29,30,31,32. Specifically, taking convex combinations of projective measurements can result in implementation of a priori quite complicated nonprojective POVMs10,32.
In this work we advance understanding of the relative power between projective and generalized measurements by focusing on a simpler problem, namely the relation between d-outcome POVMs and general (with arbitrary number of outcomes) POVMs acting on a d-dimensional Hilbert space \({{{\mathcal{H}}}}\approx {{\mathbb{C}}}^{d}\). We find a strong evidence that general quantum measurements do not offer an asymptotically increasing advantage over d-outcome POVMs for general quantum state discrimination problems13, as d tends to infinity. Specifically, we generalize the method of POVM simulation from32 based on randomized implementation of restricted-class POVMs, followed by post-processing and postselection (defined later, see also Fig. 1). Here by postselection we mean disregarding certain measurement outcomes and accepting only the selected ones. In32 it was shown that postselection allows to implement arbitrary POVM on \({{\mathbb{C}}}^{d}\) using only projective measurements and classical resources. This, however, comes with a cost - the method outputs a sample from a target quantum measurement with success probability \({{{{\rm{q}}}}}_{{{{\rm{succ}}}}}=\frac{1}{d}\). In this work we find that, surprisingly, there exists a protocol that allows to simulate a very broad class of POVMs on \({{\mathbb{C}}}^{d}\) via d-outcome POVMs and postselection with success probability qsucc above a constant which is independent on the dimension d. Importantly, our construction ensures d-outcome POVMs used in the simulation can be implemented using projective measurements in Hilbert space of dimension 2d. Therefore, our method gives a way to implement quantum measurements on \({{\mathbb{C}}}^{d}\) using only a single auxiliary qubit and projective measurements with constant success probability. We note that there exist schemes implementing arbitrary POVMs on \({{\mathbb{C}}}^{d}\) using a sequence of von Neumann instruments (i.e., a description of quantum measurements which includes post-measurement state of the system) on a system extended by a single auxiliary qubit33,34. Our method is potentially simpler to implement as, in a given round of the experiment, only a single projective measurement has to be realized on the extended system and post-measurement states need not to be considered.
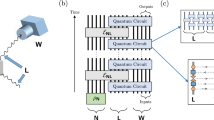
Left figure illustrates a general idea of the scheme, while in the right figure the method is illustrated in more detail–in b, the m-outcome POVMs \({{{{\bf{N}}}}}_{{X}_{j}}\) are constructed using effects of M that correspond to different subsets Xγ forming a partition of [n] into subsets of cardinality m − 1 (figure shows the standard partition and effects of [n]: \({X}_{1}=\left\{1,2,\cdots \,,m-1\right\}\), \({X}_{2}=\left\{m,\cdots \,,2m-2\right\}\), etc.) In c, POVMs \({{{{\bf{N}}}}}^{{X}_{\gamma }}\) are implemented probabilistically and the resulting outcomes ai undergo suitable post-processing and post-selection steps which simulate M.
While we do not prove that the success probability qsucc of our scheme is lower bounded by a dimension-independent constant for any POVMs on \({{\mathbb{C}}}^{d}\), we give strong evidence that this is indeed the case. First, we prove that for generic d-outcome Haar-random rank-one POVMs in \({{\mathbb{C}}}^{d}\)35 the success probability is above 6.5% (numerically we observe ≈ 25%). We also support our conjecture by numerically studying specific examples of symmetric informationally complete POVMs (SIC-POVMs)36,37,38 and for a class of nonsymmetric informationally complete POVMs39 (IC-POVMs), both for dimensions up to 1299. As the dimension increases, we observe that the success probability qsucc both for SIC-POVMs and IC-POVMs is ≈ 1/5. Importantly, if true, our conjecture implies that any non-adaptive measurement protocol can be realized using only single ancillary qubit with a sampling overhead that does not depend on the system size.
Finally, our scheme gives a possibility of more reliable implementation of complicated POVMs in noisy quantum devices. To support this claim, we employ the noise model used in Google’s recent demonstration of quantum computational advantage40. We make the following comparison between our method and the standard Naimark’s scheme of POVM implementation: for implementing typical random POVMs on N qubits, the fidelity of circuits which implement our scheme is exponentially higher than for Naimark’s implementation. This is due to the lower number of ancillary qubits required.
Results
Preliminaries
We start by introducing notation and the concepts necessary to explain our POVM implementation scheme. We will be studying generalized quantum measurements on d-dimensional Hilbert space \({{{\mathcal{H}}}}\approx {{\mathbb{C}}}^{d}\). An n-outcome POVM, is an n-tuple of linear operators on \({{\mathbb{C}}}^{d}\) (usually called effects), i.e., \({{{\bf{M}}}}=\left({M}_{1},{M}_{2},\cdots \,,{M}_{n}\right)\), satisfying Mi ≥ 0 and \(\mathop{\sum }\nolimits_{i = 1}^{n}{M}_{i}={\mathbb{1}}\), where \({\mathbb{1}}\) is identity on \({{\mathbb{C}}}^{d}\). A POVM \({{{\bf{P}}}}=\left({P}_{1},{P}_{2},\cdots \,,{P}_{n}\right)\) is called projective if all its effects satisfy the following relations: PiPj = δijPi. Measurement of M on a quantum state ρ results in a random outcome i, distributed according to the Born rule \({{{\rm{p}}}}(i| \rho,{{{\bf{M}}}})={{{\rm{tr}}}}\left(\rho {M}_{i}\right)\). We will denote the set of all all n-outcome POVMs by \({{{\mathcal{P}}}}(d,n)\). The set \({{{\mathcal{P}}}}(d,n)\) is convex30: for \({{{\bf{M}}}},{{{\bf{N}}}}\in {{{\mathcal{P}}}}(d,n)\), and p ∈ [0, 1] we define pM + (1 − p)N to be an n-outcome POVM with the i-th effect given by \({\left[p{{{\bf{M}}}}+(1-p){{{\bf{N}}}}\right]}_{i}=p{M}_{i}+(1-p){N}_{i}\). A convex mixture pM + (1 − p)N can be operationally interpreted as a POVM realized by applying, in a given experimental run, measurements M, N with probabilities p and 1 − p respectively. A POVM \({{{\bf{M}}}}\in {{{\mathcal{P}}}}(d,n)\) is called extremal if it cannot be decomposed as a nontrivial convex combination of other POVMs.
Another classical operation that can be applied to POVMs is classical post-processing29,41: given a POVM M, we obtain another POVM \({{{\mathcal{Q}}}}\left({{{\bf{M}}}}\right)\) by probabilistically relabeling the outcomes of the measurement M. Effects of \({{{\mathcal{Q}}}}\left({{{\bf{M}}}}\right)\) are given by \({{{\mathcal{Q}}}}{({{{\bf{M}}}})}_{i}={\sum }_{j}{q}_{i| j}{M}_{j}\), where qi∣j are conditional probabilities, i.e., qi∣j ≥ 0 and ∑iqi∣j = 1. Lastly, postselection, i.e., the process of disregarding certain outcomes can be used to implement otherwise inaccessible POVMs. We say that a POVM L = (L1, …, Ln, Ln+1) simulates a POVM M = (M1, …, Mn) with postselection probability q if Li = qMi for i = 1, …, n. This nomenclature is motivated by realizing that when we implement L, then, conditioned on getting the first n outcomes, we obtain samples from M. Thus, we can simulate M by implementing L, and post-selecting on non-observing outcome n + 1. The probability of successfully doing so is q which means that a single sample of M is obtained by implementing L on average 1/q number of times. The reader is referred to32 for a more detailed discussion of simulation via post-selection.
We will use ∥A∥ to denote the operator norm of a linear operator A, and [n] to denote n-element set {1, …n}. Moreover, we will use μn to refer to Haar measure on n-dimensional unitary group U(n), and by \({{\mathbb{P}}}_{U \sim {\mu }_{n}}({{{\mathcal{A}}}})\) we will denote probability of occurrence of an event \({{{\mathcal{A}}}}\) according to this probability measure. Finally, for two positive-valued functions f(x), g(x) we will write f = Θ(g) if there exist positive constants c, C > 0 such that cf(x) < g(x) < Cf(x), for sufficiently large x.
General POVM simulation protocol
The following theorem gives a general lower bound on the success probability of simulation of n-outcome POVMs via measurements with bounded number of outcomes and postselection.
Theorem 1
Let M = (M1, M2, …, Mn) be an n-outcome POVM on \({{\mathbb{C}}}^{d}\). Let m ≤ d be a natural number and let \({\{{X}_{\gamma }\}}_{\gamma = 1}^{\alpha }\) be a partition of [n] into disjoint subsets Xγ satisfying ∣Xγ∣ ≤ m − 1. Then, there exists a simulation scheme that uses measurements having at most m outcomes, classical randomness and post-selection that implements M with success probability
Furthermore, if rank Mi ≤ 1, and m ≤ d, then measurements realizing the scheme can be implemented by projective measurements in dimension 2d, i.e., using a single auxiliary qubit.
Proof
In what follows we give an explicit simulation protocol that generalizes earlier result from32,42 that concerned the case of simulation via dichotomic measurements (m = 2). The idea of the scheme is given in Fig. 1. We start by defining, for every element Xγ of the partition, auxiliary measurements \({{{{\bf{N}}}}}^{{X}_{\gamma }}\), each having m + 1 outcomes, whose purpose is to “mimick” measurement M for outputs belonging to Xγ and collect other (i.e., not belonging to Xγ) results in the “trash” output labelled by n + 1. Effects of \({{{{\bf{N}}}}}^{{X}_{\gamma }}\) are defined by \({N}_{i}^{{X}_{\gamma }}={\lambda }_{\gamma }{M}_{i}\) for i ∈ Xγ, \({N}_{i}^{{X}_{\gamma }}=0\) for i ∈ [n]⧹Xγ, and \({N}_{n+1}^{{X}_{\gamma }}={\mathbb{1}}-{\lambda }_{\gamma }{\sum }_{i\in {X}_{\gamma }}{M}_{i}\), where \({\lambda }_{\gamma }=\parallel {\sum }_{i\in {X}_{\gamma }}{M}_{i}{\parallel }^{-1}\).
We then define a probability distribution \({\{\frac{{{{{\rm{q}}}}}_{{{{\rm{succ}}}}}}{{\lambda }_{\gamma }}\}}_{\gamma = 1}^{\alpha }\). The simulation of M is realized by considering a convex combination of \({{{{\bf{N}}}}}^{{X}_{\gamma }}\) according to this distribution: \({{{\bf{L}}}}=\mathop{\sum }\nolimits_{\gamma = 1}^{\alpha }\frac{{{{{\rm{q}}}}}_{{{{\rm{succ}}}}}}{{\lambda }_{\gamma }}{{{{\bf{N}}}}}^{{X}_{\gamma }}\). An explicit computation shows that we have Li = qsuccMi, for i ∈ [n] and therefore L simulates the target measurement M with success probability qsucc.
Finally, each of the measurements \({{{{\bf{N}}}}}^{{X}_{\gamma }}\) comprising L has at most ∣Xγ∣ + 1 nonzero effects and therefore they can be implemented with POVMs with at most m outcomes. From the standard Naimark scheme of implementation of POVMs (c.f.11) we see that the dimension needed to implement a POVM \({{{{\bf{N}}}}}^{{X}_{\gamma }}\) via projective measurements equals at most the sum of ranks of effects of \({{{{\bf{N}}}}}^{{X}_{\gamma }}\). In the case of rank-one M and ∣Xγ∣ ≤ m − 1 this sum for each \({{{{\bf{N}}}}}^{{X}_{\gamma }}\) is at most d + m − 1 ≤ 2d, which completes the proof.
Crucially, we recall that an arbitrary quantum measurement on \({{\mathbb{C}}}^{d}\) can be implemented by a convex combination of rank-one POVMs having at most d2 outcomes followed by suitable post-processing27,30. This implies that our protocol facilitates the simulation of any POVM on \({{\mathbb{C}}}^{d}\) using only a single ancillary qubit – first by decomposing the target POVM into a convex combination of rank-one ≤ d2-outcome measurements, and subsequently applying Theorem 1 to each of them.
Importantly, the standard Naimark’s implementation of a general POVM would require appending an extra system of dimension d (which can be realised by \({\log }_{2}d\) ancillary qubits) and carrying out a global projective measurement. Our simulation protocol greatly reduces this requirement on the dimension cost of implementing M with the possible downside being the probabilistic nature of the scheme. The success probability qsucc depends on the choice of the partition \({\{{X}_{\gamma }\}}_{\gamma = 1}^{\alpha }\), and finding the optimal one (for a given bound on the size of Xγ) is in general a difficult combinatorial problem. In what follows we collect analytical and numerical results suggesting the following
Conjecture
For arbitrary extremal rank-one POVM M = (M1, …, Mn) on \({{\mathbb{C}}}^{d}\), there exists a partition \({\{{X}_{\gamma }\}}_{\gamma = 1}^{\alpha }\) of [n] satisfying ∣Xγ∣ ≤ d − 1 such that the corresponding value of success probability qsucc from Eq. (1) is larger than a positive constant independent of d.
Let us explore the intriguing conceptual consequences of the validity of this conjecture. First, consider a general nonadaptive measurement protocol that utilizes some quantum measurement M on \({{\mathbb{C}}}^{d}\). Such a protocol consists of S independent measurement rounds of a quantum state ρ resulting in outcomes i1, i2, …, iS distributed according to the probability distribution \(p(i| {{{\bf{M}}}},\rho)={{{\rm{tr}}}}({M}_{i}\rho)\). This experimental data is then processed to solve a specific problem at hand. If we can simulate any arbitrary M (see comment below proof of Theorem 1) via POVMs that can be implemented using only a single auxiliary qubit with probability q, which is independent of the dimension d, then this means that we can, on average, exactly reproduce the implementation of the above protocol for qS of the total S rounds. Importantly, we also know in which rounds the simulated protocol was successful, so we know which part of the output data generated by our simulation comes from the target distribution. Crucially, the above considerations are completely oblivious to the figure of merit and the structure of the problem that measurements of M aim to solve.
For many quantum information tasks, losing only a constant fraction of the measurement rounds is not prohibitive and hence, assuming the validity of the conjecture, our POVM simulation scheme offers a way to significantly reduce quantum resources needed for said POVM’s implementation. Such exemplary tasks include quantum state tomography16, quantum state discrimination13, multi-parameter quantum metrology17,18 or port-based teleportation24, and will be explored by us in future works.
Our simulation protocol and the above conjecture are also relevant from the perspective of POVM simulability10,32,43 that attracted a lot of attention recently in the context of resource theories44,45,46,47,48,49,50. Namely, the maximal post-selection probability, q(m)(M), with which a target POVM M on \({{\mathbb{C}}}^{d}\) can be simulated using strategies utilizing randomized POVMs with at most m outcomes, quantifies how far M is from the set of m-outcome simulable POVMs in \({{\mathbb{C}}}^{d}\), denoted by \({{\mathbb{S}}}_{m}\). Moreover, q(m)(M) imposes bounds on the so-called white noise critical visibility t(m)(M)10 and the robustness R(m)(M)44 against simulation via POVMs from \({{\mathbb{S}}}_{m}\). Here by critical visibility we mean a parameter \({t}^{(m)}\left({{{\bf{M}}}}\right)\) associated with a minimal amount of white noise that ensures that noisy version of M belongs to subset \({{\mathbb{S}}}_{m}\), namely
where \({{{\Phi }}}_{t}\left({{{\bf{M}}}}\right)\) is a POVM with effects \({{{\Phi }}}_{t}({M}_{i}):= t{M}_{i}+(1-t)\frac{{{{\rm{tr}}}}{M}_{i}}{d}{\mathbb{1}}\). By robustness R(m)(M) with respect to \({{\mathbb{S}}}_{m}\), we mean the minimal amount of mixing of M with a POVM from \({{\mathbb{S}}}_{m}\) so that the resulting POVM belongs to \({{\mathbb{S}}}_{m}\), i.e.,
Now, the above quantities are bounded with the success probability of our scheme via (see Section A of Supplementary Material):
Importantly, we note that the robustness R(m)(M) has an appealing operational interpretation: it is also expressible as the maximal relative advantage that M offers over any POVM in \({{\mathbb{S}}}_{m}\) for a state discrimination task44:
where \({{{\mathcal{E}}}}={\left\{({q}_{i},{\sigma }_{i})\right\}}_{i = 1}^{n}\) is an ensemble of quantum states, and \({{{{\rm{P}}}}}_{{{{\rm{succ}}}}}\left({{{\mathcal{E}}}},{{{\bf{M}}}}\right)\) is the probability for the minimum error discrimination of the states from \({{{\mathcal{E}}}}\) with M. Now, from the second inequality in (4) and the (conjectured) constant lower bound on q(d) we get a surprising conclusion: general POVMs on \({{\mathbb{C}}}^{d}\)do not offer asymptotically increasing (with d) advantage over d-outcome simulable measurements for general quantum state discrimination problems.
Haar random POVMs
We want to qualitatively understand how qsucc depends on the total number of outcomes n, the number of POVM outcomes used in the simulation m, and the dimension d. To make the problem feasible we turn to study Haar-random POVMs on \({{\mathbb{C}}}^{d}\). Quantum measurements comprising this ensemble can be realized by a construction motivated by Naimark’s extension theorem: (i) attach to \({{\mathbb{C}}}^{d}\) an ancillary system \({{\mathbb{C}}}^{a}\) so that the composite system is n-dimensional: \({{\mathbb{C}}}^{d}\otimes {{\mathbb{C}}}^{a}\approx {{\mathbb{C}}}^{n}\), (ii) apply on this composite system a random unitary U chosen from the Haar measure μn in \({{{\rm{U}}}}({{\mathbb{C}}}^{n})\), and (iii) measure the composite system in the computational basis. Effects of this measurement MU are given by \({M}_{i}^{U}={{{{\rm{tr}}}}}_{{{\mathbb{C}}}^{a}}\left({\mathbb{1}}\otimes \left|0\right\rangle \left\langle 0\right|\,{U}^{{\dagger} }\left|i\right\rangle \left\langle i\right|U\right)\), where \(\left|0\right\rangle \left\langle 0\right|\) is a fixed state on \({{\mathbb{C}}}^{a}\). Haar-random POVMs were introduced first in23 in the context of the hidden subgroup problem and are a special case of a more general family of random POVMs studied recently in35. Measurements MU are extremal for almost all U ∈ U(n). Furthermore, all extremal rank-one POVMs in \({{\mathbb{C}}}^{d}\) are of the form MU for some U ∈ U(n), and n ∈ {d, d + 1, …, d2}. Hence, Haar-random POVMs form an ensemble consisting of extremal non-projective measurements, making them a natural test-bed for studying the performance of our simulation algorithm.
Theorem 2
(Success probability of the implementation of Haar-random POVMs) Let \(n\in \left\{d,\ldots,{d}^{2}\right\}\), m ≤ d. Let MU denote a rank-one n-outcome Haar-random POVM on \({{\mathbb{C}}}^{d}\). Let \({{{{\rm{q}}}}}_{{{{\rm{succ}}}}}^{(m)}({{{{\bf{M}}}}}^{U})\) denote the success probability of implementing MU via m-outcome measurements as in Eq. (1) for the standard partition of \(\left[n\right]\), i.e., \({X}_{1}=\left\{1,\ldots m-1\right\},\,{X}_{2}=\left\{m,m+1,\ldots,2m-2\right\}\), etc. We then have
Moreover, let q(m)(MU) be the maximal success probability of implementing MU with postselection via convex combination of m-outcome measurements using any simulation protocol. We then have
The above result shows that when simulating Haar-random POVMs on \({{\mathbb{C}}}^{d}\) with m-outcome measurements in our scheme, the success probability scales as \(\frac{m}{d}\). Furthermore, Eq. (7) shows the optimality of our method up to a factor logarithmic in d. Specifically, we obtain the following crucial result: when m = d, with overwhelming probability over the choice of random U ∈ U(d2), \({{{{\rm{q}}}}}_{{{{\rm{succ}}}}}^{(d)}({{{{\bf{M}}}}}^{U})\) is above 6.74%. Below we sketch the proof for Theorem 2. We provide a complete proof in Section C of the Supplementary material, with expressions for finite d, for bounds in Eqs. (6) and (7). A sketch of this proof is provided in the Methods section.
Numerical investigation
We tested the performance of our POVM simulation scheme by computing qsucc for SIC-POVMs36,37,38, IC-POVMs39 and for Haar-random d2-outcome POVMs. We focused on simulation strategies via POVMs that can be implemented with a single auxiliary qubit (this corresponds to setting m = d in Theorem 1). Results of our numerical investigation are given in Fig. 2. For every considered measurement, the success probability was obtained via direct maximization over only ≤24 random partitions of [d2]. The graph shows that with increasing dimension, qsucc approaches ≈ 25% for SIC POVMs and random POVMs, while for IC it is above ≈ 20% even up to d = 1299. For details on the construction of these POVMs we refer the reader to the Methods section.
Results are shown for Weyl-Heisenberg SIC-POVMs (green stars), non-symmetric IC-POVMs (blue dots), and random POVMs (magenta triangles) for dimensions upto 1299. For each dimension, we plot the maximum of qsucc (computed according to the Eq. (1)), which was obtained from random ≤ 24 partitions. For random POVMs, in each dimension, we generate 10 to 500 random POVMs (lower number for higher dimensions) and plot the minimum qsucc across them. For IC-POVMs, the measurement operators are specified by a single parameter α which we keep at a fixed value across all dimensions (see Section E of the Supplementary material for details).
Noise analysis
Let us now discuss the effects of experimental imperfections on practical implementation of our scheme for generic POVMs. The quantum circuits implementing Haar-random POVMs can be considered generic random circuits. The simplest noise model often adopted for such circuits (see ref. 51) is a global completely depolarizing channel described by a “visibility” parameter η. In what follows we assume that this noise is going to affect implementation of circuits used to realize a target POVM M (either via Naimark’s construction or via our method). This noise acts in the following way on effects of n-outcome POVM: \({M}_{i}\to {M}_{i}^{\eta }:=\eta {M}_{i}+\left(1-\eta \right)\frac{{\mathbb{1}}}{n}\) (see Section D of the Supplementary material for details).
To quantitatively compare noisy and ideal implementation of a POVM we use Total-Variation Distance \({{{{\rm{d}}}}}_{{{{\rm{TV}}}}}\left({{{\bf{p}}}}\left({{{\bf{M}}}}| \rho \right),{{{\bf{p}}}}\left({{{\bf{N}}}}| \rho \right)\right):=\frac{1}{2}\mathop{\sum }\nolimits_{i = 1}^{n}| p\left(i| \rho,{{{\bf{M}}}}\right)-p\left(i| \rho,{{{\bf{N}}}}\right)|\) between probability distributions \({{{\bf{p}}}}\left({{{\bf{M}}}}| \rho \right)\) (\({{{\bf{p}}}}\left({{{\bf{N}}}}| \rho \right)\)) obtained when ρ is measured by M (N). In particular, we will be interested in the worst-case distance, i.e., TVD maximized over quantum states ρ, which can be interpreted as measure of statistical distinguishability of M and N (without using entanglement52). This notion of distance is used to benchmark quality of quantum measurements on near-term devices53,54,55.
The following result, proven in Section D of the Supplementary material, gives a lower bound for the average worst-case distance between ideal and noisy implementation of Haar-random POVMs.
Proposition 1
Let MU be a Haar-random n-outcome rank-one POVM on \({{\mathbb{C}}}^{d}\) and let MU,η be its noisy implementation with effects \({\left({{{{\bf{M}}}}}^{U,\eta }\right)}_{i}=\eta {M}_{i}^{U}+\left(1-\eta \right)\frac{{\mathbb{1}}}{n}\). We then have
where \({c}_{n}={\left(1-\frac{1}{n}\right)}^{n}\approx \frac{1}{{{{\rm{e}}}}}\).
To make qualitative comparison between our and standard (i.e., based on Naimark’s dilation theorem) implementation of POVMs, we use noise model used in Google’s recent demonstration of quantum advantage40. Assuming that main source of errors are multiple two-qubit gates, we get that dominating term in visibility is exponentially decaying function: \(\eta =\eta \left({r}_{2},{g}_{2}\right)\approx \exp \left(-{r}_{2}{g}_{2}\right)\), where r2 is two-qubit error rate and g2 is the number of two-qubit gates needed to construct a given circuit. Now recall that for implementation of d2-outcome POVM using Naimark’s dilation, one needs to implement circuits on the Hilbert space with doubled number of qubits 2N (we assume d = 2N), while our post-selection scheme requires only a single additional qubit, hence the target space has only N + 1 qubits. We note that for implementation of generic circuits on 2N qubits, the theoretical lower bound56 for needed number of CNOT gates is \({g}_{2}^{{{{\rm{Naimark}}}}}={{\Theta }}\left({4}^{2N}\right)={{\Theta }}\left(1{6}^{N}\right)\), while our scheme gives the scaling \({g}_{2}^{{{{\rm{post}}}}}={{\Theta }}\left({4}^{N}\right)\).
Finally, combining the above considerations with Proposition 1, we get expected worst-case distance between ideal and noisy Naimark implementation of generic d2-outcome measurement is lower bounded by \(\approx \left(1-\exp \left(-{{\Theta }}\left(1{6}^{N}\right)\right)\right){e}^{-1}\), which corresponds to \({\eta }^{{{\mathrm{Naimark}}}}=\exp \left(-{{\Theta }}\left(1{6}^{N}\right)\right)\). We compare this to the quality of probability distribution \({{{{\bf{p}}}}}_{{{{\rm{post}}}}}^{{{{\rm{noise}}}}}({{{\bf{M}}}}| \rho)\) generated by the noisy version of our simulation scheme which is based on implementation of projective measurements on N + 1 (not 2N) qubits and hence incurring noise with \({\eta }^{{{\rm{post}}}}\approx \exp \left(-{{\Theta }}\left({4}^{N}\right)\right)\). In Section D of the Supplementary material we show that postselection step in our scheme does not significantly affect the quality of produced samples by proving that for typical Haar random MU
where C is an absolute constant. Therefore, for generic measurements, implementation via our scheme will be affected by much lower noise than in the case of Naimark’s. We expect that similar behaviour (i.e., amount of noise in our scheme compared to Naimark’s dilation) should be exhibited also for more realistic noise models – the high reduction of the dimension of the Hilbert space is, reasonably, expected to highly reduce the noise.
Discussion
Aside from their practical relevance, our results shred light onto the question whether POVMs are more powerful (in quantum information tasks requiring sampling) than projective measurements. Indeed, since typical POVMs in \({{\mathbb{C}}}^{d}\) can be implemented using d-outcome measurements, it suggests (and if our conjecture is true, then it implies) that, if there exists a gap in the relative usefulness (quantified for example via robustness), then it is between projective measurements and d-outcome POVMs. Moreover, the surprisingly high value of \({{{{\rm{q}}}}}_{{{{\rm{succ}}}}}^{(d)}\) will likely have potential applications to nonlocality. First, it significantly limits (due to inequality (4)) the amount of local depolarizing noise that can be tolerated in schemes for generation secure quantum randomness using extremal d2-outcome measurements19,57. We also anticipate that our results can be used to construct new local models for entangled quantum states that undergo general POVM measurement (by using techniques similar to those of refs. 10,58).
We conclude with giving directions for future research. First, naturally, is to verify whether our conjecture is true. The difficulty in proving it comes from the combinatorial nature of the optimization problem in Eq. (1)—it is difficult to analytically find the optimal partition of [n] that maximizes qsucc for a target POVM M. Effects of Haar random POVMs have similar properties - in particular, they have (on average) equal operator norms—this symmetry allowed us to study them analytically. However, general POVMs can be highly unbalanced (in the sense of having effects whose operator norms can vary significantly) and suitable strategies need to be devised to tackle such situations. Second, it is desirable to devise an algorithmic method which, when given the circuit description of some POVM, returns the circuits needed to implement it with postselection. Another direction is to identify and quantify the real-time implementation costs of randomisation and post-processing, and how these schemes could be suitably modified to offset these cost considerations. Finally, it would be interesting to see if the success probability is connected to other properties of POVMs – for instance, their entanglement cost59.
Methods
Sketch of Proof of Theorem 2
An explicit computation shows that for any subset X ⊂ [n], we have \(\parallel {\sum }_{i\in X}{M}_{i}^{U}\parallel =\parallel {U}_{X}{\parallel }^{2}\), where UX is a d × ∣X∣ matrix, obtained by choosing the first d rows of U, and then taking from the resulting matrix those columns with indices in X. With this we analyze the statistical behaviour of qsucc(MU) in the regime d → ∞ using tools from random matrix theory. Specifically, the proof relies on the phenomenon of concentration of measure60 on the unitary group U(n) equipped with the Haar measure and distance induced by the Hilbert-Schmidt norm. It shows that as n ⟶ ∞, Lipschitz-continuous random variables on U(n) are with high probability close to their Haar-averages - this is captured by large deviation bounds (also known as concentration inequalities), that upper bound the probability that a random variable take values drastically different form its Haar-average.
In order to prove Eq. (6), we choose ∥UX∥ as the random variable to which we apply the machinery of concentration of measure. An upper bound to its Haar-average is obtained by performing a discrete optimization over an ϵ-net of an m − 1-dimensional complex sphere. Since the concentration inequality is true for all subsets X in the partition of [n], the union bound shows that \({\sum }_{X}\parallel {\sum }_{i\in X}{M}_{i}^{U}\parallel\) also exhibits concentration of measure, which gives Eq. (6).
In order to prove Eq. (7), we invoke the inequality in Eq. (4), and use it to upper bound q(m) with the robustness R(m)(MU) of a random POVM MU with respect to m-outcome simulable POVMs in \({{\mathbb{C}}}^{d}\). Using the interpretation of robustness in the context of state-discrimination (see Eq. (5)), we lower bound it by constructing a specific ensemble of quantum states obtained by rescaling the effects of MU. In this way, a lower bound on the robustness (hence an upper bound on the success probability) becomes a function of the matrix elements ∣Uij∣2 of the Haar-random unitary U. Finally, we prove a concentration of measures inequality for this resulting function, by again invoking the union bound and the cumulative distribution function of ∣Uij∣2, which was obtained in61.
Description of POVMs in the numerics
For every dimension, we generated effects of symmetric POVMs numerically from a single fiducial pure state via transformations \({X}_{d}^{i}{Z}_{d}^{j}\), where i, j ∈ [0, d − 1] and Xd, Zd are d − dimensional analogues of Pauli X and Z operators. For IC-POVMs we used a one-parameter family of fiducial states \(\left|{\psi }_{\alpha }\right\rangle\) described in ref. 39 for the specific value \(\alpha =\frac{1}{2}\left(1+i\right)\) (we remark that POVMs originating from other values of α exhibited a similar behaviour). For SIC-POVMs we used fiducial states from a catalogue in ref. 62 for d < 100 and states in higher dimension (up to d = 1299), which were provided to us by Markus Grassl in a private correspondence. The construction of random POVMs is described in Section E of the Supplementary material.
Data availability
The data obtained in numerical simulations is available from FBM upon request.
Code availability
The code used to obtain numerical simulations is available from FBM upon request.
References
Knill, E. & Laflamme, R. Theory of quantum error-correcting codes. Phys. Rev. A 55, 900–911 (1997).
Briegel, H. J., Browne, D. E., Dür, W., Raussendorf, R. & Van den Nest, M. Measurement-based quantum computation. Nat. Phys. 5, 19–26 (2009).
Gisin, N. & Thew, R. Quantum communication. Nat. Photonics 1, 165–171 (2007).
Bergou, J. A. Discrimination of quantum states. J. Mod. Optic. 57, 160–180 (2010).
Braunstein, S. L. & Caves, C. M. Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 72, 3439–3443 (1994).
Braunstein, S. L., Caves, C. M. & Milburn, G. Generalized uncertainty relations: theory, examples, and lorentz invariance. Ann. Phys. 247, 135–173 (1996).
Tóth, G. & Apellaniz, I. Quantum metrology from a quantum information science perspective. J. Phys. A. Math. Theor. 47, 424006 (2014).
Pirandola, S., Bardhan, B. R., Gehring, T., Weedbrook, C. & Lloyd, S. Advances in photonic quantum sensing. Nat. Photonics 12, 724–733 (2018).
Degen, C. L., Reinhard, F. & Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 89, 035002 (2017).
Oszmaniec, M., Guerini, L., Wittek, P. & Acín, A. Simulating positive-operator-valued measures with projective measurements. Phys. Rev. Lett. 119, 190501 (2017).
Peres, A. Quantum Theory: Concepts and Methods (Springer Netherlands, 2002).
Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2, 79 (2018).
Bae, J. & Kwek, L.-C. Quantum state discrimination and its applications. J. Phys. A. Math. Theor. 48, 083001 (2015).
Derka, R., Bužek, V. & Ekert, A. K. Universal algorithm for optimal estimation of quantum states from finite ensembles via realizable generalized measurement. Phys. Rev. Lett. 80, 1571–1575 (1998).
Renes, J. M., Blume-Kohout, R., Scott, A. J. & Caves, C. M. Symmetric informationally complete quantum measurements. J. Math. Phys. 45, 2171–2180 (2004).
Haah, J., Harrow, A. W., Ji, Z., Wu, X. & Yu, N. Sample-optimal tomography of quantum states. IEEE Trans. Inf. Theory 63, 5628–5641 (2017).
Ragy, S., Jarzyna, M. & Demkowicz-Dobrzański, R. Compatibility in multiparameter quantum metrology. Phys. Rev. A 94, 052108 (2016).
Szczykulska, M., Baumgratz, T. & Datta, A. Multi-parameter quantum metrology. Adv. Phys.-X. 1, 621–639 (2016).
Acín, A., Pironio, S., Vértesi, T. & Wittek, P. Optimal randomness certification from one entangled bit. Phys. Rev. A 93, 040102 (2016).
Shang, J., Asadian, A., Zhu, H. & Gühne, O. Enhanced entanglement criterion via symmetric informationally complete measurements. Phys. Rev. A 98, 022309 (2018).
Vértesi, T. & Bene, E. Two-qubit bell inequality for which positive operator-valued measurements are relevant. Phys. Rev. A 82, 062115 (2010).
Bacon, D., Childs, A. M. & Dam, W. V. Optimal measurements for the dihedral hidden subgroup problem. Chic. J. Theor. Comput. 2006 (2006).
Sen, P. Random measurement bases, quantum state distinction and applications to the hidden subgroup problem. In 21st Annual IEEE Conference on Computational Complexity (CCC’06), 14 pp. 287 (IEEE, 2006).
Ishizaka, S. & Hiroshima, T. Asymptotic teleportation scheme as a universal programmable quantum processor. Phys. Rev. Lett. 101, 240501 (2008).
Studziński, M., Strelchuk, S., Mozrzymas, M. & Horodecki, M. Port-based teleportation in arbitrary dimension. Sci. Rep. 7, 10871 (2017).
Mozrzymas, M., Studziński, M., Strelchuk, S. & Horodecki, M. Optimal port-based teleportation. New J. Phys. 20, 053006 (2018).
Davies, E. B. Quantum Theory of Open Systems (Academic Press, 1976).
Chiribella, G. & D’Ariano, G. M. Extremal covariant positive operator valued measures. J. Math. Phys. 45, 4435–4447 (2004).
Buscemi, F., Keyl, M., D’Ariano, G. M., Perinotti, P. & Werner, R. F. Clean positive operator valued measures. J. Math. Phys. 46, 082109 (2005).
D’Ariano, G. M., Presti, P. L. & Perinotti, P. Classical randomness in quantum measurements. J. Phys. A: Math. Gen. 38, 5979–5991 (2005).
Ali, S. T., Carmeli, C., Heinosaari, T. & Toigo, A. Commutative povms and fuzzy observables. Found. Phys. 39, 593–612 (2009).
Oszmaniec, M., Maciejewski, F. B. & Puchała, Z. Simulating all quantum measurements using only projective measurements and postselection. Phys. Rev. A 100, 012351 (2019).
Andersson, E. & Oi, D. K. L. Binary search trees for generalized measurements. Phys. Rev. A 77, 052104 (2008).
Bouda, J. & Reitzner, D. General measurements with limited resources and their application to quantum unambiguous state discrimination. Preprint at https://arxiv.org/abs/2009.05276 (2020).
Heinosaari, T., Jivulescu, M. A. & Nechita, I. Random positive operator valued measures. J. Math. Phys. 61, 042202 (2020).
Scott, A. J. & Grassl, M. Symmetric informationally complete positive-operator-valued measures: A new computer study. J. Math. Phys. 51, 042203 (2010).
Appleby, D. M. Symmetric informationally complete-positive operator valued measures and the extended clifford group. J. Math. Phys. 46, 052107 (2005).
Fuchs, C., Hoang, M. & Stacey, B. The sic question: History and state of play. Axioms 6, 21 (2017).
Ariano, G. M. D., Perinotti, P. & Sacchi, M. F. Informationally complete measurements and group representation. J. Opt. B Quantum Semiclass. Opt. 6, S487–S491 (2004).
Arute, F. et al. Quantum supremacy using a programmable super-conducting processor. Nature 574, 505–510 (2019).
Haapasalo, E., Heinosaari, T. & Pellonpää, J.-P. Quantum measurements on finite dimensional systems: relabeling and mixing. Quantum Inf. Process. 11, 1751–1763 (2012).
Hirsch, F., Quintino, M. T., Bowles, J. & Brunner, N. Genuine hidden quantum nonlocality. Phys. Rev. Lett. 111, 160402 (2013).
Guerini, L., Bavaresco, J., Terra Cunha, M. & Acín, A. Operational framework for quantum measurement simulability. J. Math. Phys. 58, 092102 (2017).
Oszmaniec, M. & Biswas, T. Operational relevance of resource theories of quantum measurements. Quantum 3, 133 (2019).
Uola, R., Kraft, T., Shang, J., Yu, X.-D. & Gühne, O. Quantifying quantum resources with conic programming. Phys. Rev. Lett. 122, 130404 (2019).
Carmeli, C., Heinosaari, T. & Toigo, A. Quantum incompatibility witnesses. Phys. Rev. Lett. 122, 130402 (2019).
Takagi, R. & Regula, B. General resource theories in quantum mechanics and beyond: Operational characterization via discrimination tasks. Phys. Rev. X 9, 031053 (2019).
Skrzypczyk, P., Šupić, I. & Cavalcanti, D. All sets of incompatible measurements give an advantage in quantum state discrimination. Phys. Rev. Lett. 122, 130403 (2019).
Kuramochi, Y. Compact convex structure of measurements and its applications to simulability, incompatibility, and convex resource theory of continuous-outcome measurements (2020). Preprint at https://arxiv.org/abs/2002.03504 (2020).
Guff, T., McMahon, N. A., Sanders, Y. R. & Gilchrist, A. A resource theory of quantum measurements. J. Phys. A. Math. Theor. 54, 225301 (2021).
Boixo, S. et al. Characterizing quantum supremacy in near-term devices. Nat. Phys. 14, 595–600 (2018).
Puchała, Z., Pawela, L., Krawiec, A. & Kukulski, R. Strategies for optimal single-shot discrimination of quantum measurements. Phys. Rev. A 98, 042103 (2018).
Maciejewski, F. B., Zimborás, Z. & Oszmaniec, M. Mitigation of readout noise in near-term quantum devices by classical post-processing based on detector tomography. Quantum 4, 257 (2020).
Bravyi, S., Sheldon, S., Kandala, A., Mckay, D. C. & Gambetta, J. M. Mitigating measurement errors in multiqubit experiments. Phys. Rev. A 103, 042605 (2021).
Maciejewski, F. B., Baccari, F., Zimborás, Z. & Oszmaniec, M. Modeling and mitigation of cross-talk effects in readout noise with applications to the quantum approximate optimization algorithm. Quantum 5, 464 (2021).
Shende, V. V., Markov, I. L. & Bullock, S. S. Minimal universal two-qubit controlled-not-based circuits. Phys. Rev. A 69, 062321 (2004).
Woodhead, E. et al. Maximal randomness from partially entangled states. Phys. Rev. Res. 2, 042028 (2020).
Hirsch, F., Quintino, M. T., Vértesi, T., Navascués, M. & Brunner, N. Better local hidden variable models for two-qubit Werner states and an upper bound on the Grothendieck constant KG(3). Quantum 1, 3 (2017).
Jozsa, R. et al. Entanglement cost of generalised measurements. Quantum Info. Comput. 3, 405–422 (2003).
Aubrun, G. & Szarek, S. J. Alice and Bob meet Banach (American Mathematical Society, 2017).
Zyczkowski, K. & Sommers, H.-J. Truncations of random unitary matrices. J. Phys. A: Math. Gen. 33, 2045–2057 (2000).
Fuchs, C., Stacey, B., Stacey, B. & DeBrota, J. Sic povm solutions (qbism: Quantum theory as a hero’s handbook). http://www.physics.umb.edu/Research/QBism/solutions.html.
Acknowledgements
We are sincerely grateful to Markus Grassl for fruitful discussions and for sharing with us the numerical form of fiducial kets of SIC POVMs for high dimensions. We thank Zbigniew Puchała for the discussions at the initial stage of this project and Michał Horodecki for suggesting potential application of our scheme in PBT. We thank Susane Calegari for creating a part of Fig. 1. We acknowledge the financial support by TEAM-NET project co-financed by EU within the Smart Growth Operational Programme (contract no. POIR.04.04.00-00-17C1/18-00). A portion of this work was done while T.S. was in Fudan University, and T.S. acknowledges support from the National Natural Science Foundation of China (Grant No. 11875110) and Shanghai Municipal Science and Technology Major Project (Grant No. 2019SHZDZX01).
Author information
Authors and Affiliations
Contributions
T.S. had a leading role in proving Theorem 2, Proposition 1 and many auxiliary technical results. F.B.M. carried out numerical simulations and proved results concerning noise robustness of POVM implementation methods. M.O. contributed with the main idea of the project, proved Theorem 1 and supervised the other parts project. All authors equally contributed to writing the manuscript equally.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Singal, T., Maciejewski, F.B. & Oszmaniec, M. Implementation of quantum measurements using classical resources and only a single ancillary qubit. npj Quantum Inf 8, 82 (2022). https://doi.org/10.1038/s41534-022-00589-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-022-00589-1
This article is cited by
-
General measurements with limited resources and their application to quantum unambiguous state discrimination
Quantum Information Processing (2024)