Abstract
The major task of detecting axions or axion-like particles has two challenges. On the one hand, the ultimate sensitivity is required, down to the energy of a single microwave photon of the yoctojoule range. On the other hand, since the detected events are supposed to be rare, the dark count rate of the detector must be extremely low. We show that this trade-off can be approached due to the peculiar switching dynamics of an underdamped Josephson junction in the phase diffusion regime. The detection of a few photons’ energy at 10 GHz with dark count time above 10 s and the efficiency close to unity was demonstrated. Further enhancements require a detailed investigation of the junction switching dynamics.
Similar content being viewed by others
Introduction
A long-standing puzzle in quantum chromodynamics — why charge conjugation parity symmetry seems to be preserved1,2 — belongs to the list of unsolved problems in physics. A proposed solution to the problem is novel pseudoscalar particles called axions. Being the imprint of dark matter, axions can also resolve the problem of missing mass in the Universe as well as the anisotropy of the cosmic microwave background3,4,5. The theory predicts that in a magnetic field, galactic axions are converted into microwave photons2,6, attracting the renewed interest to the axions search6,7,8,9,10,11.
The development of quantum technology requires efficient detection of electromagnetic waves at a single-photon level. A practical solution for the microwave frequency range is still challenging. Indeed, the sensitivity of conventional detectors such as transition-edge sensors12 or superconducting nanowire13,14 is not sufficient since the microwave photon energy is very low, just 6.6 yoctojoule (6.6 × 10−24 J) at 10 GHz. Moreover, the sensitivity of the most widespread devices, such as Superconducting Quantum Interference Devices (SQUIDs) or Josephson parametric amplifiers, is inevitably restricted by quantum fluctuations15, making them unfavourable for the registration of weak photon fluxes and almost useless for detecting individual photons.
The circuit quantum electrodynamics platform, based on superconducting qubits with microwave-ranged transition frequency, can potentially provide all necessary elements16,17,18,19,20,21,22,23,24,25,26 to realise a procedure for single microwave photon measurements. Indeed, several protocols, differing in specific purpose, have been demonstrated. However, their detection efficiency and the dark count time are restricted by low coherence times of qubits, which is unacceptable for searching axions.
Specific features of the axions dynamics dictate an optimised choice of the mentioned above detector. The events of the axion-photon conversion are expected to be rare. This means that the low dark count rate of such a detector is required. On the other hand, the destructive nature of the measurements, as well as relatively long initialisation time, is not of practical importance. Consequently, the implementation of the next generation of threshold single-photon counters is needed for the progress in axions search27,28.
To realise a microwave Single-Photon Counter (SPC), we use a conventional Al-based tunnel Josephson junction in a current-biased regime. This junction, coupled to a photon field, caused its switching to the resistive state by the absorbed photons, giving an output voltage of the order of 0.4 mV. While some attempts to exploit Josephson tunnel junctions for SPC applications have been performed earlier29,30,31,32,33,34, the following trade-off limits its potential ability. On the one hand, to obtain maximal sensitivity, a junction should be biased close to the photon-assistant switch to the resistive state. On the other hand, to minimise the dark count rate, the bias current should not be close to the transition point.
In this work, we have demonstrated 5-photon detection at 10 GHz frequency with efficiency close to unity with the dark count time of about 10 s. At the same time, the single-photon sensitivity is achieved with an efficiency of 0.02 and with the dark count time above 0.01 s. The dark count times, much larger than predicted from the existing theories, have been reached due to the phase diffusion regime34,35,36,37,38,39,40,41. This shows intriguing perspectives for the implementation of a Single-Photon Counter for axion search.
Results
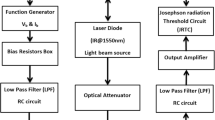
The aluminium superconductor-insulator-superconductor (SIS) tunnel junction with the area of 0.8 μm2 has been measured at the temperatures of 10–300 mK in a low noise environment42,43. The scheme of the experimental setup is shown in Fig. 1. The experiment was performed in three steps. The first one was the lifetime measurements without an itinerant microwave field to get the SPC dark count time. The second step was the procedure of calibration to find out the actual power absorbed by the SIS junction. And the third step was to test the SPC performance as a function of a microwave power P0 and bias current I.
The sample was mounted in an RF-tight box with superconducting shielding on the 10 mK cryostat plate. The DC bias wires were filtered with feed-through capacitors at room temperature and RC filters at the 10 mK plate, minimising the effect of low-frequency noise. A pulse of 10 GHz signal after a two-stage attenuation at room temperature was further attenuated by 30 dB by the twisted pair and sent to the loop antenna, weakly coupled to the sample. The coupling efficiency and the power received by the SPC was measured in situ. In such a setup, a classical pulse (violet rectangle) was attenuated until it was absorbed by the SPC as separate photons during the response time δt, see the text.
For SIS junctions with critical currents of the order of 1 μA and above, it has been shown theoretically in44,45 that it is possible to tune the parameters to get the single-photon sensitivity along with a sufficiently long lifetime. In this work, we choose for the experimental study a SIS junction with a small critical current of only 23 nA, expecting high single-photon sensitivity due to the lower threshold, with a trade-off of decreasing the dark count time.
The conventional theory of escape, both in the thermal46,47,48,49, and the quantum47,48 limits, predicts a lifetime for such junctions of the order of nanoseconds. However, the dark count time can be seriously increased due to the phase diffusion regime34,35,36,37,38,39,40,41 at the millikelvin temperatures. The supercurrent across the SIS junction is defined by the phase difference φ(t) between its superconducting electrodes. The dynamics of this phase difference can be modelled by an effective particle, moving in the washboard potential50. Basically, the escape of the particle from the potential well leads to its continuous motion down the potential profile, i.e., to switch into the resistive state with a finite voltage. However, if the dissipation is high enough, the escape of the particle from the well does not always lead to the appearance of a constant voltage because it stops in the adjacent well, which corresponds to a return into the superconducting state. Such SIS junction dynamics with phase slips is called the phase diffusion regime34,35,36,37,38,39,40,41, and the corresponding parameter space plots, where this regime is realised, are given in38,41.
To confirm the findings above, we have calculated the junction lifetime through numerical simulations of the junction switching in the frame of the resistively-capacitively shunted junction (RCSJ) model with thermal noise50, as well as by the Kramers’ formula for the thermal escape of a particle from a well51:
Here k is the Boltzmann constant and Φ0 = h/(2e) is the flux quantum, with the Planck constant h and the electron charge e. The numerical simulations are performed with the following parameters: critical current Ic = 23 nA, capacitance C = 46 fF, normal state resistance RN = 4200 Ω, temperature T = 300 mK. The calculations with the Kramers’ theory (1) are straightforward, while by the numerical simulations we reconstruct two dependencies, φ(t) and dφ(t)/dt. The latter, due to the second Josephson law, is the voltage V(t) across the junction. The phase dynamics is computed by numerical solution of the second-order differential Langevin equation with noise in the frame of the RCSJ (a mechanical pendulum) model using the Heun scheme52,53. Here, we can compute the lifetime either as the escape time of the potential barrier by the phase variable, or by the first passage time of the value 0.2 mV by the voltage variable. In the latter case, we automatically consider multiple phase slips before the switching to the finite voltage state.
The obtained results are presented in Fig. 2a. Considering the approximate nature of the formula (1) in the considered parameter range of moderate damping50, the obtained agreement between the Kramers’ theory (green diamonds) and the first phase-slip event in the RCSJ model (violet dashed line) is rather good. Moreover, the experimental data (blue dots with error bars) are perfectly fitted by the voltage simulations (red dots), considering multiple phase slips before approaching a finite voltage, see the upper curves in Fig. 2a. Since we are restricted by switching times above 0.01 s due to experimental constraints and simulation times grow exponentially, it is impossible to cover the full experimental parameter range; that is why we show only partial overlap between curves. Interestingly, the voltage simulation was performed with the only slight fitting of capacitance due to possible variation of oxidation barrier thickness, but with other fixed parameters defined independently above. Thus, the phase diffusion regime is fully confirmed and indeed, the junction lifetime is drastically increased; see the voltage traces in the inset of Fig. 2a.
a The temperature is 300 mK. Experiment (blue dots with error bars computed as standard errors) is compared with numerical results (red dots) of the voltage escape with account of multiple phase slips. The dashed violet curve is the numerical results of the phase escape across the barrier, the diamonds represent the corresponding Kramers' theory (1). The parameters are: Ic = 23 nA, C = 46 fF, RN = 4200 Ω, T = 300 mK. Inset: Examples of voltage traces at I = 5 nA, when the SPC switches into the resistive state, showing the lifetime in the range from 1000 to 2200 s from trial to trial. b The temperature is 50 mK. Experiment is given by blue dots with error bars computed as standard errors. The green stars represent the quantum tunnelling theory from32. Inset: Examples of voltage traces at I = 11 nA, when the SPC switches into the resistive state, showing the lifetime in the range from 3000 to 5500 s from trial to trial.
At low temperatures, the SIS junction represents the phase qubit with discrete energy levels in a potential well. The main escape mechanism here is the tunnelling under the potential barrier. It is intuitively clear that the change of the escape origin (tunnelling through the barrier instead of thermal escape) would not seriously modify the phase dynamics38, expecting the quantum phase diffusion regime. Since in the case of tunnelling under the barrier, the potential energy will be smaller than in the case of thermal escape above the barrier, the quantum phase diffusion will develop in a more broad parameter range than the classical one. In this case, we cannot any more recourse to the numerical modelling of the classical Langevin equation, since it only works for higher temperatures well above the quantum crossover. However, the comparison between the experiment and the quantum tunnelling theory32, indeed demonstrates our expectations: the calculated lifetime is again much smaller than the experimental data, see Fig. 2b.
The advantage of the presented setup for single-photon counting is the ability to calibrate the absorbed power in situ, using the photon-assisted tunnelling (PAT) steps at the current-voltage characteristics of the SIS junction54,55, see Methods. The 70 fW power level is easily seen with the help of PAT steps and further attenuation from this power level by 10–20 dB can be done by a remotely controlled room temperature attenuator without any other change in the route of the microwave signal, see Fig. 1.
To characterise the performance of the photon counter, a photon source is needed. However, there are no available microwave single photon sources on demand. Therefore, in the microwave range, one can only use classical sources with subsequent strong signal attenuation. Since the monochromatic beam can be presented as a flux of photons obeying Poissonian statistics56, the probability of appearing of single photons, photon pairs, triples and so on, in the source output scales with the beam power. For an incident photon flux with the power P0 at the frequency ν, the average number of photons N within the SPC response time δt can be expressed as N = P0 × δt/(hν). If N is small, the Poisson distribution (see Eq. (6) in Methods) dictates that the switching probability scales as \(\log {p}_{{{{\rm{sw}}}}}\approx j\log N\). The latter sets the slope of the switching probability psw curve in logarithmic axes by the number of photons j. The same methodology has been used before for infrared single-photon detectors57.
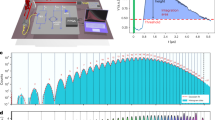
In the experiment, we used the pulses of the duration tpulse = 50 ms, which greatly exceeds the SPC response time δt. The SPC was first initialised in the zero-voltage state and after that was biased to a working point by quasi-adiabatic ramping up current58 during 50 ms. If, by incoming pulse, the SPC switched into the resistive state, the run was counted as 1, otherwise, as 0. The obtained results are presented in Fig. 3. Each experimental curve here is the average of 103−104 runs.
The fitting red curves are plotted against the middle x-axis “mean photon number”. The lower x-axis is the power in Watts, obtained from the PAT steps (the correspondence between the normalised power and the power in Watts is given in Methods). A green dashed line is given to guide eyes, indicating the beginning of the dark count floors.
The obtained experimental data were fitted by making use of Eqs. 6–8 (see Methods), which can be reduced to
where q[0] is the probability of the false detection without a photon, and q[1], q[2], q[3], etc., are the detection efficiencies of 1, 2, 3, etc., photons.
All the fitting curves (see Fig. 3) are obtained using the same values of δt = 0.2 ns and the number of attempts M = 150, and only differ by the number of the detected photons j and the detection efficiency q. These curves are plotted along the “mean photon number N” axis, which is determined by the value of the controlled attenuator voltage. We also give for reference the power axis in Watts under the N axis, which is obtained by calculating the absorbed power at PAT steps on the resistive branch of the IV curve, see Methods. Even though the PAT calibration method is a bit rough in terms of absolute input power, we don’t need this to be exactly correct, since the number of photons, initiating the switching, come from fitting to the slopes of the switching curves. Thus, the relative power along the x-axis of Fig. 3 is more important than small offset in the absolute power.
The obtained results are summarised in Table 1. Here the detection efficiencies q[i] versus bias currents, corresponding to the detection of 1, 2, 3, etc. photons, are shown (see the red curves in Fig. 3).
Discussion
We have developed a photon counter prototype, which can detect an energy equivalent of 5 photons at frequency of 10 GHz with a dark count time above 10 s and the efficiency close to unity (see the curve for 12 nA in Fig. 3 and compare with the lifetime in Fig. 2b). While smaller number of photons is also detected, the efficiency and dark count time have to be improved. Such a threshold detector exploits a current biased Al SIS junction coupled to an incident photon flux. Due to the phase diffusion regime, the achieved dark count times are much higher than previously thought, enhancing the prospects for using an SIS junction as a single-photon counter. Looking forward, the counter performance can be further improved by altering junction parameters, aiming to an optimisation of a relationship between the counter sensitivity and its dark count rate.
Methods
Sample fabrication
The samples studied in this work were fabricated at Chalmers University of Technology. All layers, except for the SIS junctions themselves, were formed by the method of lift-off lithography, performed using a laser-writer, and the subsequent deposition of thin films by an electron beam. For the fabrication of aluminium tunnel junction, an electronic lithograph and a shadow evaporation technique at three different angles were used, which made it possible to deposit tunnel junctions without breaking the vacuum.
Methodology of single-photon detection
A photon absorption in an SPC is a complex process involving both active and reactive part of the junction impedance44. If the Josephson plasma frequency matches the incoming signal frequency, the signal causes the oscillations in the reactive branches with the highest amplitude. The active part of the impedance equals to Rqp50, while the parallel resonant RLC circuit increases the current through the Josephson inductance LJ by a factor of
The photon energy hν is divided between the energy Es stored in the tank circuit, and the energy Ed dissipated in the resistor Rqp, so that Es + Ed = hν. The amplitude IJ of current oscillations induced in a Josephson inductance is related to Es by
Since Es/Ed = Q/(2π), we find an expression for IJ by combining (3) and (4):
If the current reaches a value close to the critical current, the probability of the switching into the resistive state increases significantly.
We analyse the switching statistics under the assumption that several photons can participate in an SPC switching, but only if they hit the SPC synchronously and simultaneously. If the photons are absorbed sequentially one after another, the energy of the first photons is dissipated over the times set by the Q-factor of the resonant circuit of the SPC, which is about 10 in our case.
Consider the photon flow with the power P0 and the frequency ν, accepted by the SPC. The average number of photons within a time interval δt is N = P0 × δt/(hν). Then the probability p[j] to find j photons during δt is given by Poisson distribution56:
The power P0 can be measured in situ by PAT steps, see below, that links the experimental probabilities with Eq. (6).
For the counter, the Poissonian statistics of the incoming signal means that the switching may happen within δt due to the arrival of one photon, and also of 2, 3, 4 and so on, photons at a given bias current. The probability of the SPC switching during δt at a given bias current can be fully described by an array of the detection efficiencies q[j], where q[0] is the probability of false switching if no photons are absorbed (dark count), q[1] is the probability to switch if one photon is absorbed, and so on. For an ideal single-photon detector, the array q[j] will look like [0, 1, 1, . . . , 1], which means absence of dark counts and 100% probability of switching due to one and consequently more than one photon.
The expression for the total switching probability pδt during δt in an experiment, where we do not know the exact number of the absorbed photons, has the form of a sum over the products of the probability p[j] to absorb j photons and the probability q[j] to switch due to j photons:
Here the probability q[j] is the detection efficiency.
Let us discuss the meaning of the SPC switching time δt. We assume that δt is determined as the time needed to dissipate the energy of absorbed photons. For a threshold detector, such as an SPC, it is determined from the non-switching event (the photon is absorbed, but the jump to the resistive state does not happen) using the dynamics of the Josephson phase. If the next photon or a group of photons comes later than δt, the SPC already forgets that there has been a previous photon (or several photons). In this case, we can say that the experiment starts from the beginning, and this will be the second attempt to switch. Now, if we open the shutter of the photon source for a longer time, there will be more attempts for the SPC to switch unless it happened, for example, during the previous steps. Thus, the switching probability psw will be given by the following expression:
where M is the number of “elementary” experiments (attempts). This expression is used to fit the experimental switching probabilities (the simplified expression (2) is given in the main text) with three fitting parameters: the time interval δt, the number of attempts M, and the detection efficiency q. It should be noted that all psw curves can be fitted by the same values of δt and M, while their difference is described by the only detection efficiency q.
Experimental setup
The radio frequency (RF) signal from an external microwave synthesiser was attenuated using constant attenuators from 1 dB to 30 dB and voltage controlled room-temperature attenuator, calibrated with a commercial spectrum analyser. The measurements of the power passed through the variable attenuator versus voltage on the attenuator are shown in Fig. 4a, where the decrease in the power by >3 orders of magnitude is seen.
a The output power through the variable attenuator versus the attenuator voltage. b An example of obtaining a PAT step from the IVC using Eq. (9) and fitting an experimental I–V characteristics. c The power absorbed in the SIS junction for the attenuator voltages from 1.66 V to 3 V.
To study the dynamics of an Al/AlOx/Al SIS tunnel junction, we thermally anchored the sample to the mixing chamber of a He3/He4 Oxford dilution refrigerator Triton 200. The reverse branch of the current-voltage characteristic of the investigated SIS junction with parameters Ic = 23 nA, RN = 4.2 kΩ, C = 46 fF is presented in Fig. 4b.
For a high-frequency experiment, a microwave signal was fed into the cryostat via a phosphor bronze twisted-pair with attenuation of −15 dB per meter at 10 GHz and with a loop antenna at the end near the Josephson junction. The level of the RF signal passing through two metres of a twisted pair inside the cryostat was also measured as a function of the control voltage on the attenuator by a spectrum analyser. In total, the initial signal with a power of the order of mW was attenuated to a level of several nW passing through several constant attenuators and two metres of the twisted pair. In turn, the absorbed signal (described further) appears to be smaller by several orders of magnitude (~pW) due to poor coupling between the loop antenna and the SIS junction. For switching statistics measurements, this signal was reduced even further to a few femtowatts using a controlled attenuator.
The absorbed power was measured using the well-pronounced photon assisted tunnelling (PAT) steps at the IV curve, see Fig. 4b. Its dependence on the attenuator voltage follows the same curve as the calibration curve, see Fig. 4a. That’s how we find the correspondence between relative attenuated power and power in Watts. The lower power, for which the PAT steps are not visible yet, can be probed only with the help of the switching histograms and by the decrease of the superconducting state lifetime.
For the switching probability measurements, to bias the junction at the initial state, the bias current of the junction was ramped up quasi-adiabatically, with slow start and stop parts to decrease the disturbance of the quantum system58. The voltage was measured using a low noise room-temperature differential amplifier AD745 and further digitised by a high-speed NI-DAQmx card.
Absorbed power
Even if we know the losses in each element of the microwave path including the antenna pattern, antenna—receiver matching, etc., it is still useful to establish an independent way to measure the power, absorbed by the SIS junction. The PAT steps55 give us such an opportunity because the height of the steps is unambiguously related to the power absorbed by the quasiparticles of the superconducting electrodes of the SIS junction.
In the presence of a high-frequency signal with a frequency exceeding the scale of the gap smearing, the I–V characteristic (IVC) of the SIS junction takes on a characteristic stepped shape, see Fig. 4b. In this case, the IVC can be represented as the sum of the IVCs without a signal I0(V), shifted relative to each other along the voltage axis by an integer hν/e:
Here Jn(x) is the Bessel function whose argument x = eVrf/(hν) is proportional to the voltage Vrf through the junction at the frequency of the external signal ν. Approximation of the experimental IVC by (9) with the adjustable parameter x makes it possible to determine Vrf. Further, the absorbed power is expressed as follows:
where σ is the conductivity of the SIS junction at the frequency ν. In Ref. 55, it is proposed to determine σ through the difference of the shifted IVCs since the IVC changes so sharply with the signal that the usual expression dI/dV is not applicable:
Let us find the absorbed power using the described method for the junction with the critical current of 23 nA. Figure 4b shows the reverse branch of the IVC without the external signal, with a fitted analytical function (red). A good agreement with the reverse branch is observed both below and above the gap. The only difference from the experiment is the absence of the heating effect with an increasing current. To estimate the power of the RF signal, we will analyse the IVCs with only the first PAT step. In this case, Eq. (9) can be restricted to the first three terms.
To find Vrf, we use Eq. (9), where we substitute I0(V) with the found analytical function. The argument x of the Bessel function is the only fitting parameter. Figure 4b shows the terms from the sum of Eq. (9) without coefficients (dashed red) and the result of the sum in the form of an IVC with a PAT step (dashed blue). Furthermore, Fig. 4b shows real IVCs without (black dots) and with a PAT step (grey dots). As it can be seen, the experimental data and the fitting results are in a good agreement.
The absorbed power is obtained from Eq. (10). Figure 4c shows the power dependence versus the junction voltage. The maximal power is absorbed at the step. When the attenuator voltage is 3 V, the maximum absorbed power is 6.8 × 10−14 W. This means that at least this power always comes to the junction, but whether it is absorbed or not depends on the voltage at the junction.
To estimate the power absorbed when SIS is biased at supercurrent, we use the power level at voltages above the gap, since it is believed that at zero-voltage across the SIS junction, its quasiparticle resistance is equal to RN59.
Data availability
The data that support the findings of this study are available from A.V. Gordeeva upon reasonable request.
References
Peccei, R. D. & Quinn, H. R. CP conservation in the presence of pseudoparticles. Phys. Rev. Lett. 38, 1440–1443 (1977).
Wilczek, F. Problem of strong P and T invariance in the presence of instantons. Phys. Rev. Lett. 40, 279–282 (1978).
Editorial. Light in darkness. Nat. Astron. 1, 0082 (2017).
Peebles, P. J. E. Growth of the nonbaryonic dark matter theory. Nat. Astron. 1, 0057 (2017).
de Swart, J. G., Bertone, G. & van Dongen, J. How dark matter came to matter. Nat. Astron. 1, 0059 (2017).
Sikivie, P. Invisible axion search methods. Rev. Mod. Phys. 90, 015004 (2021).
McAllister, B. T. et al. The ORGAN experiment: an axion haloscope above 15 GHz. Phys. Dark Universe 18, 67–72 (2017).
Caldwell, A. et al. Dielectric haloscopes: a new way to detect axion dark matter. Phys. Rev. Lett. 118, 091801 (2017).
Lawson, M., Millar, A. J., Pancaldi, M., Vitagliano, E. & Wilczek, F. Tunable axion plasma haloscopes. Phys. Rev. Lett. 123, 141802 (2019).
Alesini, D. et al. Status of the SIMP project: toward the single microwave photon detection. J. Low. Temp. Phys. 199, 348–354 (2020).
Crescini, N. et al. Axion search with a quantum-limited ferromagnetic haloscope. Phys. Rev. Lett. 124, 171801 (2020).
Förtsch, M. et al. Near-infrared single-photon spectroscopy of a whispering gallery mode resonator using energy-resolving transition edge sensors. J. Opt. 17, 065501 (2015).
Natarajan, C. M., Tanner, M. G. & Hadfield, R. H. Superconducting nanowire single-photon detectors: physics and applications. Superconductor Sci. Technol. 25, 063001 (2012).
Kahl, O. et al. Waveguide integrated superconducting single-photon detectors with high internal quantum efficiency at telecom wavelengths. Sci. Rep. 5, 10941 (2015).
Lamoreaux, S. K., van Bibber, K. A., Lehnert, K. W. & Carosi, G. Analysis of single-photon and linear amplifier detectors for microwave cavity dark matter axion searches. Phys. Rev. D. 88, 035020 (2013).
Schuster, D. I. et al. Resolving photon number states in a superconducting circuit. Nature 445, 515–518 (2007).
Inomata, K. et al. Single microwave-photon detector using an artificial Λ-type three-level system. Nat. Commun. 7, 12303 (2016).
Peng, Z. H., de Graaf, S. E., Tsai, J. S. & Astafiev, O. V. Tuneable on-demand single-photon source in the microwave range. Nat. Commun. 7, 12588 (2016).
Walter, T. et al. Rapid high-fidelity single-shot dispersive readout of superconducting qubits. Phys. Rev. Appl. 7, 054020 (2017).
Besse, J.-C. et al. Single-shot quantum nondemolition detection of individual itinerant microwave photons. Phys. Rev. X 8, 021003 (2018).
Royer, B., Grimsmo, A. L., Choquette-Poitevin, A. & Blais, A. Itinerant microwave photon detector. Phys. Rev. Lett. 120, 203602 (2018).
Kono, S., Koshino, K., Tabuchi, Y., Noguchi, A. & Nakamura, Y. Quantum non-demolition detection of an itinerant microwave photon. Nat. Phys. 14, 546–549 (2018).
Opremcak, A. et al. Measurement of a superconducting qubit with a microwave photon counter. Science 361, 1239–1242 (2018).
Ilves, J. et al. On-demand generation and characterization of a microwave time-bin qubit. npj Quantum Inf. 6, 1–7 (2020).
Kristen, M. et al. Amplitude and frequency sensing of microwave fields with a superconducting transmon qudit. npj Quantum Inf. 6, 1–5 (2020).
Lu, Y. et al. Quantum efficiency, purity and stability of a tunable, narrowband microwave single-photon source. npj Quantum Inf. 7, 1–8 (2021).
Kokkoniemi, R. et al. Bolometer operating at the threshold for circuit quantum electrodynamics. Nature 586, 47–51 (2020).
Lee, G.-H. et al. Graphene-based Josephson junction microwave bolometer. Nature 586, 42–46 (2020).
Wallraff, A., Duty, T., Lukashenko, A. & Ustinov, A. V. Multiphoton transitions between energy levels in a current-biased Josephson tunnel junction. Phys. Rev. Lett. 90, 037003 (2003).
Chen, Y.-F. et al. Microwave photon counter based on Josephson junctions. Phys. Rev. Lett. 107, 217401 (2011).
Poudel, A., McDermott, R. & Vavilov, M. G. Quantum efficiency of a microwave photon detector based on a current-biased Josephson junction. Phys. Rev. B 86, 174506 (2012).
Oelsner, G. et al. Underdamped Josephson junction as a switching current detector. Appl. Phys. Lett. 103, 142605 (2013).
Oelsner, G. et al. Detection of weak microwave fields with an underdamped Josephson junction. Phys. Rev. Appl. 7, 014012 (2017).
Revin, L. S. et al. Microwave photon detection by an Al Josephson junction. Beilstein J. Nanotechnol. 11, 960–965 (2020).
Martinis, J. M. & Kautz, R. L. Classical phase diffusion in small hysteretic Josephson junctions. Phys. Rev. Lett. 63, 1507–1510 (1989).
Vion, D., Götz, M., Joyez, P., Esteve, D. & Devoret, M. H. Thermal activation above a dissipation barrier: switching of a small Josephson junction. Phys. Rev. Lett. 77, 3435–3438 (1996).
Koval, Y., Fistul, M. V. & Ustinov, A. V. Enhancement of Josephson phase diffusion by microwaves. Phys. Rev. Lett. 93, 087004 (2004).
Kivioja, J. M. et al. Observation of transition from escape dynamics tounderdamped phase diffusion in a Josephson junction. Phys. Rev. Lett. 94, 247002 (2005).
Yu, H. F. et al. Quantum phase diffusion in a small underdamped Josephson junction. Phys. Rev. Lett. 107, 067004 (2011).
Longobardi, L. et al. Thermal hopping and retrapping of a Brownian particle in the tilted periodic potential of a NbN/MgO/NbN Josephson junction. Phys. Rev. B 84, 184504 (2011).
Longobardi, L. et al. Direct transition from quantum escape to a phase diffusion regime in YBaCuO biepitaxial Josephson junctions. Phys. Rev. Lett. 109, 050601 (2012).
Kuzmin, L. S. et al. Photon-noise-limited cold-electron bolometer based on strong electron self-cooling for high-performance cosmology missions. Commun. Phys. 2, 104 (2019).
Gordeeva, A. V. et al. Record electron self-cooling in cold-electron bolometers with a hybrid superconductor-ferromagnetic nanoabsorber and traps. Sci. Rep. 10, 21961 (2020).
Kuzmin, L. S. et al. Single photon counter based on a Josephson junction at 14 GHz for searching galactic axions. IEEE Trans. Appl. Supercond. 28, 1–5 (2018).
Golubev, D. S., Il’ichev, E. V. & Kuzmin, L. S. Single-photon detection with a Josephson junction coupled to a resonator. Phys. Rev. Appl. 16, 014025 (2021).
Fulton, T. A. & Dunkleberger, L. N. Lifetime of the zero-voltage state in Josephson tunnel junctions. Phys. Rev. B 9, 4760–4768 (1974).
Voss, R. F. & Webb, R. A. Macroscopic quantum tunneling in 1-μm Nb Josephson junctions. Phys. Rev. Lett. 47, 265–268 (1981).
Washburn, S., Webb, R. A., Voss, R. F. & Faris, S. M. Effects of dissipation and temperature on macroscopic quantum tunneling. Phys. Rev. Lett. 54, 2712–2715 (1985).
Wallraff, A. et al. Switching current measurements of large area Josephson tunnel junctions. Rev. Sci. Instrum. 74, 3740–3748 (2003).
Likharev, K. K. Dynamics of Josephson Junctions and Circuits (Gordon and Breach Science Publishers, 1986).
Martinis, J. M., Devoret, M. H. & Clarke, J. Experimental tests for the quantum behavior of a macroscopic degree of freedom: the phase difference across a Josephson junction. Phys. Rev. B 35, 4682–4698 (1987).
Yablokov, A. A., Mylnikov, V. M., Pankratov, A. L., Pankratova, E. V. & Gordeeva, A. V. Suppression of switching errors in weakly damped Josephson junctions. Chaos, Solitons Fractals 136, 109817 (2020).
Yablokov, A. A. et al. Resonant response drives sensitivity of Josephson escape detector. Chaos, Solitons Fractals 148, 111058 (2021).
Tien, P. K. & Gordon, J. P. Multiphoton process observed in the interaction of microwave fields with the tunneling between superconductor films. Phys. Rev. 129, 647–651 (1963).
Tucker, J. R. & Feldman, M. J. Quantum detection at millimeter wavelengths. Rev. Mod. Phys. 57, 1055–1113 (1985).
Fox, M. Quantum Optics: An Introduction Vol. 15 (Oxford University Press, 2006).
Gol’tsman, G. N. et al. Picosecond superconducting single-photon optical detector. Appl. Phys. Lett. 79, 705–707 (2001).
Revin, L. S. & Pankratov, A. L. Fine tuning of phase qubit parameters for optimization of fast single-pulse readout. Appl. Phys. Lett. 98, 162501 (2011).
Kautz, R. L. & Martinis, J. M. Noise-affected I–V curves in small hysteretic Josephson junctions. Phys. Rev. B 42, 9903–9937 (1990).
Acknowledgements
The work is supported by the Russian Science Foundation (Project No. 19-79-10170, experimental results and comparison with theory in classical limit). E. I. acknowledges the support by the European Union’s Horizon 2020 research and innovation programme under Grant Agreement No. 863313 (SUPERGALAX, conceptualisation and comparison with theory in quantum limit). We thank D. Golubev for fruitful discussions. The samples were fabricated in the Chalmers Nanotechnology Centre. The measurements were performed using the facilities of the Laboratory of Superconducting Nanoelectronics of NNSTU. The SEM image of the sample was obtained using the Common Research Centre “Physics and technology of micro- and nanostructures” of IPM RAS.
Funding
Open access funding provided by Chalmers University of Technology.
Author information
Authors and Affiliations
Contributions
L.S.K., E.I., A.V.G., L.S.R., and A.L.P. conceived the experiments. A.L.P., L.S.R., A.A.Y., and A.V.G. conducted the experiments. A.V.G. and L.S.R. analysed the results. All authors discussed the results and reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pankratov, A.L., Revin, L.S., Gordeeva, A.V. et al. Towards a microwave single-photon counter for searching axions. npj Quantum Inf 8, 61 (2022). https://doi.org/10.1038/s41534-022-00569-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-022-00569-5
This article is cited by
-
Josephson radiation threshold detector
Scientific Reports (2024)
-
Continuous wideband microwave-to-optical converter based on room-temperature Rydberg atoms
Nature Photonics (2024)