Abstract
Developing quantum key distribution (QKD) has been recently directed toward distance extension and network expansion for real-world secure communications. Considering a recent report on a quantum communication network over 4,600 km, it seems that QKD networks using conventional protocols have been sufficiently studied. However, although the twin-field QKD (TF-QKD) proposed for long-distance QKD has been studied deeply enough to succeed the demonstrations over 428- and 511-km deployed fibers, TF-QKD networks have been verified only for a ring network. In this work, we propose a star topological 2 × N TF-QKD network scheme, where the coherence maintenance issue, being the primary obstacle to implementing TF-QKD, can be minimized by the automatic mode-matching feature of the Sagnac-based plug-and-play architecture. A lower number of active controllers is required for our scheme in comparison with one-way TF-QKD networks. Moreover, our scheme adopts a cost-effective configuration that requires only a single pair of single-photon detectors for the entire network system. We conducted a proof-of-concept experiment over a 50-km fiber successfully, achieving an average secret key rate of 1.31 × 10−4 bit per pulse (1.52 bit per second) with the finite-size effect.
Similar content being viewed by others
Introduction
Recent advances in quantum computing1,2,3,4,5,6 have highlighted security concerns associated with it, and efforts to commercialize quantum key distribution (QKD) are being actively conducted7,8,9,10,11,12,13,14,15. Although QKD has been developed significantly, issues such as distance extension and network expansion limit its commercializaion16,17,18.
Since conventional QKD systems generally employ extremely weak laser pulses, there are fundamental limitations on the communication distance and secret key rate (SKR) due to the inevitable fiber optic and system induced losses. The Takeoka–Guha–Wilde and Pirandola–Laurenza–Ottaviani–Banchi bounds are repeater-less upper bounds of the SKR19,20 that scale linearly with the channel transmittance η. Significant efforts have been made for resolving the aforementioned issue, including the quantum repeater and measurement-device-independent QKD together with either quantum memories21,22 or quantum non-demolition measurement23. However, since these methods are not currently practical, their experimental feasibility in surpassing the repeater-less bounds has not been verified despite recent remarkable reports24,25.
In this regard, twin-field QKD (TF-QKD)26 is an innovative protocol that can overcome the repeater-less bound with current technologies by employing an intermediate node, Charlie, which measures the first-order interference of two optical fields (twin fields) from Alice and Bob. Since only single-photon detection events are valid in TF-QKD, i.e., photons from both Alice and Bob do not have to arrive at Charlie simultaneously, only half of the attenuation applies to the SKR. Therefore, the SKR of TF-QKD scales with \(\sqrt \eta\), equivalent to the scale of the single-repeater QKD. Inspired by the first proposal, many variants of TF-QKD have been theoretically studied27,28,29,30. As a result, strict security proofs27,31, practical structures and protocols such as plug-and-play (PnP) architecture32,33,34, no phase post-selection TF-QKD28 (NPP-TF-QKD), and sending or not-sending TF-QKD29 (SNS TF-QKD) were developed. Moreover, these have been experimentally demonstrated9,10,11,33,35,36,37,38,39,40,41,42, including lab tests on 600- and 658-km fiber reels10,40 and field tests on 428- and 511-km fibers9,41. Thus, TF-QKD is considered as a realistic solution for long-distance QKD.
However, QKD network expansion remains a major challenge as following points. QKD networks do not guarantee perfect conversion between electrical and quantum signals, thereby limiting network structure configurability. Moreover, most QKD networks connected via deployed fibers comprise simple relays of point-to-point systems43,44,45,46,47,48, and it was only after the remarkable quantum access network architecture proposed in 201349 that a true 1 × N QKD network system was implemented50,51,52,53,54. Finally, an integrated space-to-ground quantum communication network spanning over 4600 km was demonstrated in 202152, comprising various QKD architectures and network topologies, such as point-to-point, one-to-many, ring, tree, and star. However, TF-QKD networks have been proposed and verified only for the ring topology11,42.
In this paper, we propose a 2 × N plug-and-play (PnP) TF-QKD network scheme, where coherence maintenance can be efficiently achieved using a Sagnac-based PnP architecture. Moreover, we present a proof-of-principle experimental demonstration. Although our scheme adopts the Sagnac configuration, such as that in the established TF-QKD networks11,42, the scheme forms a 2 × N star network rather than an N × N ring network, implying a difference in applicability. For our applications, the structure can be used for networks where server–client communication is more significant than communications between clients, such as networks for banks, data centers, electronic voting, and the military. In particular, it is suitable for secure electronic voting systems requiring only server–client communications. Moreover, it can be employed in secure military communications between upper and lower units for confidential tactical strategies and in data centers requiring secure communications between a server and multiple clients. Although our setup cannot be extended to an N × N structure, it is useful at least for the applications described above. Furthermore, there are other features similar to those in the established PnP TF-QKD networks11,42 as follows. Our scheme requires only a single pair of single-photon detectors (SPDs) for the entire system due to the common feature of QKD networks adopting SPDs based on time division multiplexing (TDM)42,49,50,51,52,53,54. In addition, our scheme can reduce the efforts for realizing active control systems in TF-QKD systems, because the PnP architecture has advantages for optical mode-matchings11,33,50,51,55,56,57,58,59. Since conventional TF-QKD systems require many active control systems9,10,35,36,37,38,39,40,41, this feature provides a practical method for TF-QKD implementation. Moreover, most of the expensive and difficult-to-control devices such as lasers and SPDs are installed in Charlie (measurement setup), whereas Alice (server) and Bob (client) comprise simple optical components only for timing synchronization and quantum state preparation11,33,49,50,51,52,55,56,57,58,59. Thus, it is relatively easy to add and remove a new client, because key exchange can start immediately by plugging the client device to the end of the fiber and synchronizing the signal without wavelength and polarization controls, which are required in one-way TF-QKD.
To show the feasibility of our architecture, we experimentally implemented our network scheme and performed a proof-of-principle demonstration using the SNS TF-QKD protocol29,35,60,61; then, we obtained reasonable SKRs for 16 network connections with the complete finite-size effect35,60,61. Furthermore, we applied efficient control systems to achieve long-term stability and reduce performance degradation from environmental changes.
Results
Architecture
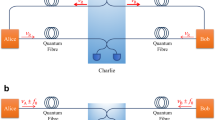
The proposed 2 × N PnP TF-QKD network scheme is shown in Fig. 1. We use three multiplexing methods, namely, polarization, wavelength, and time division multiplexing (PDM-WDM-TDM), to realize a 2 × N network. PDM doubles the channel capacity of the server and client compared with using only WDM. Connections between two servers (AliceH and AliceV, where H and V denote the horizontal and vertical polarization states, respectively) and client groups (BobHi and BobVi with i={1,…,N}, where i indicates the wavelength channel in the arrayed waveguide grating (AWG) device) are switched by the modulation of two electrical polarization controllers (EPCs) in Charlie. As shown in Fig. 2, AliceH connects to BobHi (BobVi) and AliceV connects to BobVi (BobHi) when EPCs are modulated to 0° (90°). The red and blue lines represent the optical paths for the AliceH and AliceV connections, respectively. Optical pulses with wavelength and polarization corresponding to each connection are provided by a polarization beam splitter (PBS) and wavelength-tunable lasers (TLDs), which generate optical pulses with N different wavelengths. Then, the pulses are sent to each device via the AWG devices. TLDH and TLDV are allocated to the AliceH and AliceV connections, respectively. To apply TDM, TLDs are driven independently in the time slots for each connection. According to network connections, Charlie should consider the appropriate pulse generation timings to prevent overlaps of pulses from different connections, because the round trip time of the twin fields changes based on the network connections. Moreover, Charlie needs to compensate for a timing mismatch between photon arrivals and detection gates caused by environmental changes. As all the TLDs and SPDs are installed in Charlie, the timing alignments can be efficiently performed50,51. For Alice’s and Bob’s synchronizations with Charlie, a method frequently used in PnP QKD systems34,50,51,57,59,62,63 is adopted. In this method, Alice and Bob use a beam splitter (BS) and a photodiode (PD) to split and measure the incoming optical pulse train from Charlie. Then, they can generate trigger signals and synchronize their clocks with the signals.
Three multiplexing methods of polarization, wavelength, and time division multiplexing (PDM-WDM-TDM) are used to configure a 2 × N network. Alice and Bob identically consist of simple devices for synchronization and state preparation, while expensive and complicated devices such as lasers and SPDs are placed in Charlie. The abbreviation definitions are as follows. TLD wavelength-tunable laser driver, PBS polarization beamsplitter, CIR circulator, BS beamsplitter, SNSPD superconducting nano-wire single-photon detector, EPC electrical polarization controller, AWG arrayed waveguide grating, PD photodiode, VOA variable optical attenuator, IM intensity modulator, PM phase modulator, FM Faraday rotator mirror.
As shown in the table, by modulating EPCs to 0° (90°), AliceH and AliceV are connected to BobHi (BobVi) and BobVi (BobHi), respectively. The paths for the AliceH and AliceV connections are represented by red and blue solid lines, respectively. The definitions of the abbreviations are as follows. TLD wavelength-tunable laser driver, EPC electrical polarization controller.
Owing to the PnP (two-way) architecture55, our network scheme has three advantages in experimental implementation, compared to one-way TF-QKD. Firstly, polarization drift due to the birefringence effect in the optical fiber can be naturally compensated by the round trip of the optical signals using a Faraday rotator mirror (FM). Hence, a polarization control system is not required for the proposed architecture. Secondly, since the server and client share a common laser in Charlie, the twin fields have fundamentally the same wavelength. Such a structure using an untrusted source may open a potential backdoor for Eve to launch source attacks, such as Trojan-horse and phase remapping attacks64,65,66. However, these vulnerabilities can be circumvented by applying countermeasures developed for a general PnP QKD62,67,68,69. Moreover, the countermeasures can be applied to our architecture without additional optical devices because both Alice and Bob have a BS and a PD each, which are the key devices for the countermeasures. Note that the main goal of this work is to show the feasibility of the proposed TF-QKD network configuration (See Discussion for further details of security). Thirdly, arrival times of the twin fields are naturally identical because the twin fields pass through the same route in opposite directions, clockwise or counterclockwise. This is significant for networks where users are placed at arbitrary distances from the central relay. Due to the second and third advantages, matching the photon arrival times is not required, and we can eliminate the wavelength control system, which is the primary obstacle in implementing TF-QKD. Thus, only a phase controller is required to maintain coherence between the twin fields. Note that timing controls for other active devices such as the laser, modulators, detectors, and switches are still necessary for system operation. In fact, it has been reported previously11,33 that the common path nature of the Sagnac interferometer guarantees automatic phase stability until an overall path length of ~300 km. However, the phase stability was not observed in our experiment despite using a much shorter optical path of 160 km (overall path). As shown in Fig. 3a and b, the relative phase between clockwise and counterclockwise trains of the AliceV–BobH33 connection is arbitrarily changed with 1.43 rad per train and has uniformly distributed probabilities in the histogram. The averaged phase drift rate for all connections is 1.36 rad per train. Since the optical pulse train had a period of approximately 8 ms, the phase drift rates were indicated in units of rad per train rather than rad per millisecond, unlike in Refs. 9,10,35,38,39,41. These results may be attributed to thermal and vibration noises, and thus, we expect that the stability can be achieved by employing shorter fiber spools or by sealing the setup carefully.
a Relative phase drift between clockwise and counterclockwise trains of AliceV and BobH33. The relative phase between clockwise and counterclockwise trains of the AliceV–BobH33 connection is arbitrarily changed with 1.43 rad per train. Since the optical pulse train had a period time of ~8 ms, it was indicated in units of rad per train rather than rad per millisecond. b Probability distribution of the relative phase between the clockwise and counterclockwise trains of AliceV and BobH33. The randomly distributed probabilities indicate that the phase stability from the common path nature is not sufficient in our experimental setup. The bin width of the relative phase is 2°.
As shown in Fig. 4, the signal flow, for example, in the AliceH–BobH3 connection, is described in six steps. Each connection has slightly different steps based on the polarization and wavelength, but it is straightforward to infer appropriate steps from the ones below. While Step 1 is indicated by black arrows with a black number, the clockwise and counterclockwise signal flows are represented by red solid lines with red numbers and violet dashed lines with violet numbers, respectively.
The clockwise and counterclockwise signal flows are represented by red solid lines with red numbers and violet dashed lines with violet numbers, respectively. The abbreviation definitions are as follows. TLD wavelength-tunable laser driver, PD photodiode, VOA variable optical attenuator, IM intensity modulator, PM phase modulator, FM Faraday rotator mirror.
Step 1: To connect AliceH with BobH, both EPCs are modulated to 0°.
Step 2: TLDH generates a horizontally polarized strong pulse with λ3. The pulse passes through a PBS and a circulator (CIR). Then, it is divided into clockwise and counterclockwise pulses by a 50:50 BS. Pulses are transmitted to AliceH and BobH by a PBS in each path. The transmitted pulse to BobH is sent to BobH3 via an AWG device since its wavelength is λ3.
Step 3: AliceH and BobH3 generate trigger signals for active devices by measuring the approaching pulses using a BS and a PD. Then, they reflect the approaching pulses as vertically polarized pulses using the FMs, allowing the pulses to just pass through the phase modulators (PMs) and intensity modulators (IMs) without encoding. As they do not encode information at this time, the information leakage due to the bright pulse can be ignored (See Discussion for further details of security).
Step 4: The vertically polarized pulse returned from AliceH (BobH) is sent to its counterpart, BobH (AliceH), by two PBSs. The polarization state does not change because the EPCs are transparent, as mentioned in Step 1. Moreover, the transmitted pulse to BobH is sent to BobH3 by the AWG device.
Step 5: AliceH and BobH3 apply the TF-QKD protocol to the approaching pulses using the IMs and PMs, and reflect the pulses as horizontally polarized pulses using the FMs. At this time, the pulses are attenuated to the single-photon level by IMs and variable optical attenuators (VOAs) set to a constant attenuation. Synchronization can be achieved using the same method as in Step 3.
Step 6: The attenuated pulses, namely, the weak coherent pulses (WCPs) of AliceH and BobH3 return to Charlie and interfere with each other at the BS. Then, Charlie measures the interference result using two superconducting nano-wire SPDs (SNSPDs). Since WCPs are generated by a common laser and pass through the same route, the wavelength, and arrival time are naturally identical. Moreover, polarization drift from the quantum channel (QC) is automatically compensated by the round trip of the pulses55,59. The automatic phase stability verified previously11,33,42 is expected to be achieved if quantum channels are sufficiently short.
These six steps occur in every time slot allocated to the AliceH–BobH3 connection and are repeated until Charlie accumulates sufficient detection events. After accumulation, Charlie announces the interference results. Then, AliceH and BobH3 perform post-processing to distribute secure keys.
Protocol
The protocol implemented in this study is the four-intensity decoy-state SNS protocol29,35,60,61. It is described as follows. Alice and Bob randomly choose either X or Z bases with probabilities pX and 1-pX, respectively. On the X basis, they randomly select and send one of three sources \(\rho _{\alpha _i}\) with a probability \(p_{x_i}\) for i=0,1,2, where \(\rho _{\alpha _0} = \left| 0 \rangle \langle 0 \right|\) is the vacuum source, and \(\rho _{\alpha _1}\) and \(\rho _{\alpha _2}\) are two phase-randomized coherent sources with intensities μ1 and μ2 (\(\mu _1 < \mu _2\)), respectively. On the Z basis, they send the phase-randomized coherent state \(\rho _{\alpha _z}\) and the vacuum state with probabilities \(p_{z_1}\) and \(1 - p_{z_1}\), respectively. Meanwhile, random phase values are applied to the pulses, regardless of the selected bases. The random phase values, θA and θB, where A and B denote Alice and Bob, respectively, are selected in the semi-open interval [0,2π), which is split into M equal slices Δm=2πm/M, with m={0,…,M-1}, and M set to 16 in this work. Then, Charlie measures the incoming pulses and records which detector clicks. After measurement, he publicly announces all the information about the effective events caused by single clicks, and discards coincidence clicks. Alice and Bob reveal their bases for the effective events. In addition, they disclose the intensities and phase values corresponding to the effective events when Alice or Bob choose the X basis, whereas the phase information of the Z basis should not be revealed. With this information, Alice and Bob obtain the observable \(N_{jk}\) (j,k=0,1,2,z), which are the number of instances when Alice and Bob send \(\rho _{\alpha _j}\) and \(\rho _{\alpha _k}\), respectively. Accordingly, the yields can be defined as \(S_{jk} = n_{jk}/N_{jk}\), where \(n_{jk}\) are the number of effective events caused by \(N_{jk}\). Furthermore, to improve the results, we consider the instances for the effective events with unmatched bases as below. Even though the effective events of these instances cannot be used for the key distillation, they can be used in the decoy-state analysis.
where \(p_{x_0} = 1 - p_{x_1} - p_{x_2}\) is the probability of sending a vacuum state in the X basis, \(N_X = p_X^2N_{total}\) is the number of instances when both Alice and Bob choose the X basis, and \(N_{XZ} = p_X\left( {1 - p_X} \right)N_{total}\) is the number of instances when Alice (Bob) chooses the X basis and Bob (Alice) chooses the Z basis.
Subsequently, we define two sets \(C_{\Delta ^ + }\) and \(C_{\Delta ^ - }\) containing the instances when both Alice and Bob send \(\rho _{\alpha _1}\) with the phase information θA and θB satisfying the phase slice condition of Eq. (2) or Eq. (3). The number of the instances in \(C_{\Delta ^ \pm }\) are \(N_{11}^{\Delta ^ \pm } = \frac{\Delta }{{2\pi }}N_{11}\). Correspondingly, \(n_{11}^{\Delta _0^ \pm }\) and \(n_{11}^{\Delta _1^ \pm }\) are used to denote the number of the effective events for detector 0 and detector 1, respectively.
where Δ is the phase slice size, θA (θB) is the random phase value of Alice (Bob), and θD is the phase difference between the optical paths of Alice and Bob. Conventionally35,60,61, ∣x∣ means the degree of the minor angle enclosed by the two rays that enclose the rotational angle of degree x, e.g., \(\left| {\left. { - 15\pi /8} \right|} \right. = \left| {\left. {15\pi /8} \right|} \right. = \pi /8\) and \(\left| {\left. { - \pi /10} \right|} \right. = \pi /10\).
In the protocol, phase- and bit-flip errors can be classified as follows. In the X window, i.e., when both Alice and Bob choose the X basis, effective events inconsistent with the expected results from the first-order interference of Alice and Bob are defined as phase-flip errors. For example, a phase-flip error occurs if detector 0 (detector 1) clicks even though detector 1 (detector 0) has to click according to the phase combination. Furthermore, in the Z window, effective events when Alice (Bob) has decided to send and Bob (Alice) has decided not to send are distilled as raw key bits, 1 (0), while effective events when Alice and Bob decide to send the same states cause bit-flip errors.
With these observables, Alice and Bob can estimate the lower bound of s1 and upper bound of \(e_1^{ph}\), to calculate the SKR with a finite-size effect by using the following formula35,60,61 (See Methods for further details of the decoy-state method and finite-size effect analyses).
where R is the secret key rate, s1 is the yield of the single-photon state in the Z basis, \(e_1^{ph}\) is the phase-flip error rate for the instances of s1, SZ and EZ are the yield and bit-flip error rate in the Z basis, respectively, \(a_1 = \mu _ze^{ - \mu _z}\) is the probability when the emitted state collapses to the single-photon state, pX is the probability of the X basis, \(p_{z_1}\) (\(p_{z_0} = 1 - p_{z_1}\)) is the probability of sending μz (vacuum) in the Z basis, and \(H\left( x \right) = - x\log _2x - \left( {1 - x} \right)\log _2\left( {1 - x} \right)\) represents the binary Shannon entropy function. Ntotal is the total number of signal pulses, \({\it{\epsilon }} = 10^{ - 10}\) is a failure probability of the Chernoff bound, and the error correction efficiency of f is assumed as 1.1.
Experimental setup
Our full experimental setup is shown in Fig. 5a. Despite drawing all pairs of Alice and Bob, only one pair was realized, and manually swapped according to the network connection. A distributed feedback (DFB) laser and polarization controller (PC) were used as substitutes for TLDH and TLDV. The temperature of the DFB laser and the PC were modulated appropriately to provide each connection with optical pulses of the corresponding wavelength and polarization. The quantum efficiencies (QEs) of SNSPDs for the BS and CIR sides were 46.5% and 51.3%, respectively. They include the PC and optical switch (OSW) efficiencies. A higher QE is applied to the CIR-side SNSPD to compensate for the CIR insertion loss. The overall detection efficiencies of Charlie are 12.8% (BS side) and 12.6% (CIR side). Two default-off OSWs, which are triggered only when optical pulse trains return after the round trip time, are used to avoid the latching effect of the detectors caused by strong light leaked from the BS and CIR. The pulse width of the OSW trigger signals is sufficiently set to 0.2 ms by considering the train’s activated duration, and the round trip time can be estimated based on the path lengths of the devices. In our setup, the round trip time is approximately 0.8 ms, since pulses make a round trip of two 25-km QCs and two 15-km storage lines (SLs). Note that any OSW with a moderate on/off rate corresponding to the train period can be used for this purpose. Alice and Bob are connected to Charlie using 25-km QCs. In addition, 15-km SLs are used to reduce the backscattering noise count by dividing forward signal pulses and backward scattering noises in the time domain70. For the same purpose, SLs have been frequently used in PnP QKD systems50,51,58,59,63,71. 100-GHz AWG devices with four channels ranging from ITU DWDM-31 (1552.52 nm) to 34 (1550.12 nm) are placed in the Bob sides. The channel isolations of the AWG devices are greater than 30 dB. We use two IMs to improve the overall extinction ratio (ER), which mainly affects the quantum bit error rate on the Z basis (QBERZ).
a Full experimental setup. Although all pairs of Alice and Bob were presented in the figure, only a single pair was implemented and swapped according to the network connection in the experiment. b Network connections based on the modulations of two polarization controllers (PCs). The abbreviation definitions are as follows. DFB distributed feedback laser driver, VOA variable optical attenuator, AWG arrayed waveguide grating, OSW optical switch, BS beamsplitter, PBS polarization beamsplitter, IM intensity modulator, PM phase modulator, SL storage line, QC quantum channel, PC polarization controller, CIR circulator, SNSPD superconducting nano-wire single-photon detector, FM Faraday rotator mirror.
Moreover, a field-programmable gate array (FPGA) board equipped with multiple digital-to-analog converters was used for synchronizing active devices and random encoding. In this study, as a proof-of-concept experiment, we realized timing synchronization of Alice, Bob, and Charlie by connecting the FPGA board and active devices using electrical cables. The timing diagram of active devices is shown in Fig. 6. However, in a practical system, the synchronization method using the BS and PD described in the architecture needs to be considered50,51. It is noteworthy that such a method can be applied easily to our current setup.
(1) At 0 s, Charlie generates an optical pulse train using the DFB laser and divides the pulse train into clockwise and counterclockwise trains. Then, he sends them to Alice and Bob. (2) After 200 µs, Alice (Bob) receives the clockwise (counterclockwise) train from Charlie and just sends it back using IMs operating at the peak bias point. (3) After 400 µs, Alice (Bob) receives the counterclockwise (clockwise) train from Bob (Alice) and sends it back with random encoding using the IMs and PM. (4) After 200 µs, Charlie measures the incoming trains from Alice and Bob using OSWs and SNSPDs. (5) Lastly, data communication between FPGA and PC is performed for approximately 7 ms. The transmission distances (delays) for sections (1)-(2), (2)-(3), and (3)-(4) are 40 km (200 µs), 80 km (400 µs), and 40 km (200 µs), respectively. The inset shows the sequence of the pulse train. It consists of 924 reference pulses followed by 100 signal pulses. Each pulse is sent at 10 MHz with a pulse width of 2 ns (FWHM). Thus, the activated duration of the train is 102.4 µs. The abbreviation definitions are as follows. DFB distributed feedback, OSW optical switch, SL 15-km storage line, QC 25-km quantum channel, IM intensity modulator, PM phase modulator, SNSPD superconducting nano-wire single-photon detector.
As described in the architecture, the phase stability by the common path nature11,33,42 was not observed in our experiment, so we employed a phase post-compensation method35,38 to compensate for the phase drift. We selected this method because it can be implemented more practically than a real-time compensation system. In this method, Alice and Bob compensate for the phase difference (θD) during post-processing, as shown in Eqs. (2), (3). To estimate θD, the optical pulse train is composed of 924 reference and 100 signal pulses, as shown in the inset of Fig. 6. Since our FPGA does not have enough memory to store the data for a number of trains, the vacuum time is set to more than 7 ms to perform data communication with a PC immediately after each train ends, despite the round trip time of 0.8 ms. We remark that it can be easily reduced using larger storage in a practical system. The reference pulses are divided into four equal parts. Moreover, Alice modulates the phase of each part to 0, π/2, π, and 3π/2 while Bob modulates all to 0. Then, θD can be estimated from the interference results of the reference pulses using the least square method35,38. We use more reference pulses than the signal pulses to improve the accuracy of the phase difference estimation. In this work, the intensity contrast between the signal and reference pulses is negligible, as summarized in Table 1. However, if a much longer quantum channel is used, the intensity of the reference pulse has to increase for precise phase estimation. Then, mitigating the backscattering noise induced by the strong reference becomes challenging, since the reference and signal wavelengths are equal. Furthermore, if the phase drift rate is too high, there may be a significant phase drift between the signal and reference parts, making it difficult to estimate the phase difference accurately. Thus, the space between the first reference pulse and the last signal pulse needs to be shorter with increasing phase drift rate. This should be considered in any TF-QKD using the post-compensation method.
Moreover, we added three features to achieve long-term stable system performance. Firstly, we implemented an interferometer in Alice and Bob to reduce the performance degradation due to the polarization dependency of the lithium niobate-based IM50,51,58. Particularly, as the degradation of the insertion loss and ER directly affects the SKR in the QKD system, it needs to be resolved. Although using an active polarization controller is feasible, it is not practical, owing to the requirement of an additional EPC, PBS, and detector. Thus, we solved this issue passively by placing the IMs between two PBSs with connector keys aligned to slow axes. Owing to the FM and PBSs, the pulses passing through the IMs are always vertically polarized, even if the polarization state of the input pulses into the PBS is not exactly defined. Two pulses divided and combined by PBSs are always orthogonally polarized, so there is no interference between them. Consequently, the IMs can always work properly, regardless of the input polarization state. To apply our method to the IMs working with horizontally polarized input states, the connector keys of the PBSs need to be aligned to fast axes. Besides, we adopted the double phase modulation (DPM) method72 enabling phase modulation of an arbitrary polarized input. In the DPM method, the different phase modulations due to polarization dependency are automatically compensated since the phase modulation is performed twice, before and after reflection by the FM. Thus, the input polarization state into the PM is not considered. These methods can be implemented without any active components, thus reducing system complexity.
Secondly, we implemented an IM bias control system to maintain the ER. Since the operating bias point of the IM easily drifts away from the optimal point owing to the ambient temperature change as well as the inherent photorefractive effect, the initially optimized ER is not ensured for a long time. Our bias control system compensates for the voltage drift from the null point (bias point for minimal transmission) whenever the estimated QBERZ is higher than a threshold value.
Thirdly, we applied a timing calibration system. Since the effective channel length of any fiber-based QKD varies with the temperature change, it is necessary to compensate for the variation. Although the arrival times of the twin fields are naturally identical in our scheme, there exists a timing mismatch between the photon arrivals and detection gates. Our calibration system adjusts each detection gate timing until the count rate is the highest when the single-photon count rate is lower than the threshold value.
To check the long-term stability of our system, we recorded the sifted key rate and QBERs of the AliceH–BobH33 connection for a week. The experimental results are presented in Fig. 7a. The stabilities of the sifted key rate (average 1.41 × 10−3 bit per pulse) and QBERs (average 3.52% and 3.73% on the Z and X bases, respectively) indicate that our system can compensate for environmental changes for a long time. In addition, we measured the single-photon count rate and optimal gate timing while heating and cooling the QC and SL of BobH33 between 22 °C and 60 °C. As shown in Fig. 7b, the single-photon count rate is maintained above the threshold value (blue dashed line) by optimizing the detection gate timing according to heating and cooling. From this result, we can conclude that our timing calibration system can cope with rapid temperature changes.
a Sifted key rate and quantum bit error rates (QBERs) for a week. The stable sifted key rate and QBERs verify our system’s ability to compensate for the environmental change. b Single-photon count rate (count per second) and optimal gate delay when heating and cooling the quantum channel (QC) and storage line (SL) between 22 °C and 60 °C. It shows that the timing calibration system can cope with the rapid temperature change.
Experimental results
We implemented our experimental setup over a 50-km fiber and demonstrated the feasibility using the SNS protocol29,35,60,61. We sequentially measured the QKD performances for 16 network connections determined by two different modulations of PCs and four different wavelengths. AliceV and AliceH can be connected to eight Bobs each. In the experiment, only one pair of Alice and Bob was implemented and swapped manually according to the network connection, which requires an hour. The experiment on each network connection was performed for a day to accumulate sufficient data for calculating the SKR. The number of signal pulses sent to each connection, Ntotal is 109 on average. Figure 8a–c, and d show the sifted key rate and QBERs for channels ITU DWDM-31, 32, 33, and 34, respectively. Each subfigure consists of the results for AliceV–BobV, AliceV–BobH, AliceH–BobV, and AliceH–BobH connections. As an overall average, we obtained the sifted key rate of 2.03 × 10−3 bit per pulse and QBERs of 3.24% (Z basis) and 4.31% (X basis). Since we performed this experiment with higher QEs, the sifted key rates increased compared to those in Fig. 7a. Finally, we achieved an average SKR of 1.31 × 10−4 bit per pulse (1.52 bit per second) for all connections using Eq. (4) with the finite-size effect. This result is comparable to that of Ref. 35. Detailed experimental conditions and results are presented in Table 1.
a Result of ITU channel 31. b Result of ITU channel 32. c Result of ITU channel 33. d Result of ITU channel 34. The results are drawn in different colors depending on the network connections of AliceV–BobV, AliceV–BobH, AliceH–BobV, and AliceH–BobH. Sifted key rate is indicated by a solid line and QBERs are represented by dot lines with upward- or downward-pointing triangles, respectively.
Discussion
In summary, we proposed a 2 × N Sagnac-based PnP TF-QKD network scheme. Although there exist reports11,42 on the Sagnac-based TF-QKD network, our scheme is evidently different from it. Firstly, our architecture forms a star network rather than a ring network, and it is possible to add and remove a Bob without changing the channel losses and distances of the existing users. Moreover, channels between Charlie and Bobs are independent of each other. For example, operation failure of BobV3 channel does not affect operation of BobH1. On the contrary, there are some features similar to those in the established TF-QKD networks11,42 as follows. Given that SPDs are the most expensive devices for realizing QKD, our network scheme is cost-effective because it requires only a single pair of SPDs regardless of the number of network users, similar to other QKD networks42,49,50,51,52,53,54 adopting TDM-based SPDs. Moreover, the optical modes of polarization, wavelength, and arrival time are naturally identical by the common path and laser properties of the Sagnac-based PnP architecture, and therefore, our setup can be implemented using fewer active controllers than in one-way TF-QKD networks, where the users have their own light sources. Lastly, as Alice and Bob comprise components only for timing synchronization and quantum state preparation, it would be relatively easy to add or remove them in comparison with the one-way TF-QKD networks.
We performed a proof-of-principle experimental demonstration over a 50-km fiber successfully, measuring the QKD performances for 16 network connections using the SNS protocol35,60,61. Although our experiment uses the SNS protocol, our architecture is also suitable for other variants of the TF-QKD protocol27,28,30, including asymmetric TF-QKD protocols73,74,75,76. From the experimental observables, we finally estimated the SKRs with a complete finite-size effect and obtained 1.31 × 10−4 bit per pulse (1.52 bit per second) as an average SKR of 16 network connections. Considering different conditions such as the QE, overall loss, and system specifications, our results are comparable with those of Ref. 35 using the same protocol. This shows the feasibility of our TF-QKD network configuration.
We focused on establishing the feasibility of our proposal in this work; however, several points should be considered for future practical systems. Firstly, as a proof-of-concept demonstration, we implemented our setup without careful packaging, such as using insulation and dedicated hardware cases for each user. However, when implementing a practical system, it should be sealed more carefully and located in an operating room to reduce errors induced by environmental factors such as thermal and vibration noises. Secondly, although we allocated more than 7 ms for the vacuum time due to our FPGA with insufficient memory, this should be reduced to increase the train repetition rate and lead to the SKR improvement. For example, with half the current train period time, the SKR in bit per second is expected to double. Using an FPGA with larger memory or external memory can be considered as a simple solution. Thirdly, we did not take account of reducing the round trip time between IM and FM, even though this primarily determines the pulse repetition rate. Thus, we set the repetition rate as 10 MHz considering a 60-ns round trip time. However, in a practical system, the round trip time should be reduced for increasing the pulse repetition rate. This also leads to improvement of the SKR due to the same principle as the second point. It is expected that this can be solved naturally to some extent by using chip-based devices. Fourthly, since the overall loss increases significantly owing to the length extension (twice that of original length) for the round trip, either a higher-power laser or an optical amplifier is required to overcome such a significant loss. For instance, with a quantum channel extended by 5 km (10-km round trip), the overall loss increases by 2 dB (10 km × 0.2 dB). Thus, the initial optical power should become higher to compensate for the increased loss. Furthermore, for using either a higher-power laser or an optical amplifier, careful management for the backscattering noise proportional to the laser power should be employed. Using longer SLs can mitigate the issue since they divide the signals and noises more strictly in the time domain. However, it should be taken into account that this can increase the round trip time. Other available methods are presented in Refs. 11,42. Fifthly, there is no theoretical limit on the number of users. However, since the SKR for each user scales linearly with the number of network users, an efficient time arrangement is required. As a solution, dividing the users into several groups and allocating time to each group in sequence can be implemented. Using more detectors is another simple solution, but not an efficient method. Sixthly, Alice must distinguish wavelengths because she is connected to several Bobs with different wavelengths. There are two manners for this condition to be realized. The first is for Alice to measure the different wavelengths using N PDs and an AWG with N channels. This is the simplest method, but additional optical devices are required. Another method is for Alice to acquire timing information of different Bobs through classical communication with Charlie. Since Alice also knows the channel lengths between Charlie and Bobs, she can estimate Bob’s timing easily. In fact, by assuming Alice’s seamless communication with Charlie, the latter method is equivalent to that of Refs. 50,51. Seventhly, an error rejection method38,77,78 and optimization of operation parameters, such as the mean photon number, phase slice size, and signal proportion should be performed to improve the SKR. Finally, since the initial proposal of the PnP architecture, there have been concerns that using an untrusted light source may weaken the security against source attacks64,65,66. However, since deep verifications of security have been realized34,62,67,68,69, and most attacks using light injection can be prevented by power and timing monitoring11,33,42, it has been widely used as a secure and practical structure in many studies11,33,34,42,48,50,51,56,57,58,62,63,79 to date. Nevertheless, at least the following attacks and countermeasures34 should be considered.
In the PnP architecture, as the worst case, Eve could substitute a stronger pulse and check the reflected signal to estimate the phase value sent by Alice and Bob. However, like usual PnP QKDs, our scheme can detect this attack by monitoring the pulse power. Furthermore, since the reflected signal involving phase information is strongly attenuated, Eve has to prepare significantly higher energy pulses in order to eavesdrop on sufficient information from the reflected weak signals. However, an alarm is triggered by power monitoring when the pulse energy exceeds the threshold. Besides, phase randomization can separate Alice and Bob from any possible reference system that Eve prepares in advance.
If Eve can change the arrival time of the pulses, the pulses pass through the phase modulator at different times, resulting in different phase modulations. This phase remapping process allows Eve to launch an intercept-and-resend attack. However, users can detect this attack by monitoring the time-shifted pulses. Moreover, this attack commonly induces a large QBER, such as 15.5% in the theoretical limit. However, as shown in our experimental result, QBERs were maintained at <5%, enabling easy detection.
-
(3)
Photon number splitting (PNS) attack34
In our scheme, Alice (Bob) reflects the pulses with or without modulations twice. For the reflection case without modulations, Eve cannot eavesdrop on any information since no information is encoded on the pulses. Furthermore, the case with modulations does not allow Eve’s PNS attack as the attack is detected easily by using the decoy-state method.
Although several improvements and considerations need to be accounted for, we believe that our current results provide a foundation for QKD commercialization.
Methods
Decoy-state method analysis
The same method as in Ref. 61 is used to calculate \(s_1^Z\) and \(e_1^{ph}\) in this work. In the protocol, Alice and Bob prepare and send the phase-randomized coherent pulses, regarded as a mixture of photon number states
where \(\mu _j = \left| {\left. {\alpha _j} \right|} \right.^2\) is the intensity of the coherent state \(\left| {\alpha _j}\rangle \right.\).
Then, the state when Alice decides to send the vacuum state and Bob decides to send \(\rho _{\alpha _k}\) is \(\rho _{\alpha _0\alpha _k} = e^{ - \mu _k}\mathop {\sum }\limits_{n = 0}^\infty \mu _k^n/n!\left| {0n}\rangle \langle {0n} \right|\). With these convex forms, the lower bounds of the yields of the state \(\rho _{\alpha _{z_{01}}} = \left| {01}\rangle \langle {01} \right|\) and \(\rho _{\alpha _{z_{10}}} = \left| {10}\rangle \langle {10} \right|\) can be written as the following formulas80.
where S0k are the yields of the sources \(\rho _{\alpha _0\alpha _k}\) for k = 1,2, Sj0 are the yields of the sources \(\rho _{\alpha _j\alpha _0}\) for j = 1,2, and S00 is the yield when both Alice and Bob send the vacuum state.
With these formulas, the lower bound of the yield of single-photon state in the Z basis, i.e., the state \(\rho _1^Z = \frac{1}{2}( {\rho _{\alpha _{z_{01}}} + \rho _{\alpha _{z_{10}}}})\), can be described as
From Ref. 61, we know that the phase-flip error rate \(e_1^{ph}\) is asymptotically equal to the bit-flip error rate of the single-photon state in set C∆. The bit-flip error yield for all instances in set C∆ is
where Tk (\(k = \Delta ,\Delta ^ + ,\Delta ^ -\)) is the proportion of wrong effective events in Ck.
Then, attributing all the errors to the single-photon state and vacuum state, the upper bound of the phase-flip error rate \(e_1^{ph}\) can be estimated by
where \(\underline s _1^Z\) is the lower bound of \(s_1^Z\).
Finite-size effect analysis
The analysis used in this work is the same as that in Refs. 35,60,61. To extract the secure final key from finite-size data, we have to consider the effectiveness of statistical fluctuations and the security coefficient of the protocol. To obtain the lower bound of s1 and the upper bound of \(e_1^{ph}\) in the real protocol with finite Ntotal, one can employ the average yield. Thus, we define 〈S〉 as the mean value of yield S. Although Sjk (j,k = 0,1,2,z) can be directly observed in the experiment, the mean value 〈Sjk〉 cannot be observed. However, given Sjk and Njk, the confidence lower and upper limits of 〈Sjk〉 can be calculated. For strict estimation of the lower bound of \(\langle s_1^Z\rangle\), we introduce the following two yields.
Replacing the observed yields with their mean values in Eqs. (8) and (10), we can derive the mean values of the lower bound of \(\langle s_1^Z\rangle\) and the upper bound of \(\langle e_1^{ph} \rangle\) as follows.
and
with
for \({{{\mathcal{B}}}} = S,T\,{{{\mathrm{and}}}}\,k = 00,1,2,\Delta\).
By using the multiplicative form of the Chernoff bound with a fixed failure probability ϵ and the observable Sk, we can obtain an interval of 〈Sk〉, i.e., \(\left[ {\underline S _k,\bar S_k} \right]\), which can bound the value of 〈Sk〉 with a probability of at least 1-ϵ. Explicitly, with a function \(f_\delta \left( {x,y} \right) = \left[ { - \ln \left( {y/2} \right) + \sqrt {\left( {\ln \left( {y/2} \right)} \right)^2 - 8\ln \left( {y/2} \right)x} } \right]/\left( {2x} \right)\), we have \(\delta _{00} = f_\delta \left( {N_{00}S_{00},{\it{\epsilon }}} \right)\), \(\delta _j = f_\delta \left( {\left( {N_{0j} + N_{j0}} \right)S_j,{\it{\epsilon }}} \right)\) with j = 1,2 and \(\delta _{{\Delta }} = f_\delta \left( {\left( {N_{11}^{{{\Delta }}^ + } + N_{11}^{{{\Delta }}^ - }} \right)T_{{\Delta }},{\it{\epsilon }}} \right)\).
With \(\langle\underline s _1^Z\rangle\) and \(\langle\bar e_1^{ph}\rangle\) defined in Eqs. (12) and (13), respectively, the lower bound of the yield \(\underline s _1\) and the upper bound of the phase-flip error rate \(\bar e_1^{ph}\) corresponding to Eq. (4) can be estimated by
and
where \(\delta _1^c = f_\delta \left( {a_1N_{zz}^c\langle \underline s _1^Z \rangle,{\it{\epsilon }}} \right)\) and \(\delta _1^{\prime c} = f_\delta \left( {a_1N_{zz}^c\underline s _1\langle\bar e_1^{ph}\rangle,{\it{\epsilon }}} \right)\) with \(N_{zz}^c = 2p_{z_1}\left( {1 - p_{z_1}} \right)N_{zz}\) and \(a_1 = \mu _ze^{ - \mu _z}\) being the probabilities of emitting a single-photon state from source \(\rho _{\alpha _z}\).
With the strict bounds in Eqs. (15) and (16), the SKR with the finite-size effect can be calculated by
Where R is the secret key rate, SZ and EZ are the yield and bit-flip error rate in the Z basis, respectively, pX is the probability of the X basis, \(p_{z_1}\) \(\left( {p_{z_0} = 1 - p_{z_1}} \right)\) is the probability of sending μz (vacuum) in the Z basis, and \(H\left( x \right) = - x\log _2x - \left( {1 - x} \right)\log _2\left( {1 - x} \right)\) represents the binary Shannon entropy function. Ntotal is the total number of signal pulses and f is the error correction efficiency.
With this key rate, the protocol is denoted as εsec-secret and εcor-correct. The entire security coefficient of the protocol is εtot = εcor + εsec, where \(\varepsilon _{sec} = 2\hat \varepsilon + 4\bar \varepsilon + \varepsilon _{PA} + \varepsilon _{s_1}\). Here, εcor is the failure probability of error correction, εsec is the probability that the secret key is not secure, \(\hat \varepsilon\) is the coefficient while using the chain rules of smooth min- and max-entropies, \(\bar \varepsilon\) is the failure probability for the estimation of \(e_1^{ph}\), \(\varepsilon _{PA}\) is the failure probability of privacy amplification, and \(\varepsilon _{s_1}\) is the failure probability for the estimation of s1. Here, we set \(\varepsilon _{cor} = \hat \varepsilon = \varepsilon _{PA} = {\it{\epsilon }} = 10^{ - 10}\), \(\bar \varepsilon = 3{\it{\epsilon }}\), and \(\varepsilon _{s_1} = 4{\it{\epsilon }}\), and thus, the security coefficient of the whole protocol is \(\varepsilon _{tot} = 20{\it{\epsilon }} = 2 \times 10^{ - 9}\). Equation (4) is derived from Eq. (17) with these values. We set \(\bar \varepsilon = 3{\it{\epsilon }}\) and \(\varepsilon _{s_1} = 4{\it{\epsilon }}\), because we use the Chernoff bound with a failure probability ϵ three times to estimate \(e_1^{ph}\) and four times to estimate s1, respectively.
Data availability
The datasets generated and analyzed in this study are available from the corresponding author on reasonable request.
Code availability
The code used in this paper is available from the corresponding author on reasonable request.
References
Wright, K. et al. Benchmarking an 11-qubit quantum computer. Nat. Commun. 10, 5464 (2019).
Bruzewicz, C. D., Chiaverini, J., McConnell, R. & Sage, J. M. Trapped-ion quantum computing: Progress and challenges. Appl. Phys. Rev. 6, 021314 (2019).
Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).
Kjaergaard, M. et al. Superconducting qubits: current state of play. Annu. Rev. Condens. Matter Phys. 11, 369–395 (2020).
Wu, Y. et al. Strong quantum computational advantage using a superconducting quantum processor. Phys. Rev. Lett. 127, 180501 (2021).
Pezzagna, S. & Meijer, J. Quantum computer based on color centers in diamond. Appl. Phys. Rev. 8, 011308 (2021).
Bennett, C. H. & Brassard, G. Quantum Cryptography: Public Key Distribution and Coin Tossing. In Proc. IEEE International conference on Computers, Systems and Signal Processing, 175–179 (1984).
Bennett, C. H. & Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theor. Comput. Sci. 560, 7–11 (2014).
Chen, J.-P. et al. Twin-field quantum key distribution over a 511 km optical fibre linking two distant metropolitan areas. Nat. Photonics 15, 570–575 (2021).
Pittaluga, M. et al. 600-km repeater-like quantum communications with dual-band stabilization. Nat. Photonics 15, 530–535 (2021).
Zhong, X., Wang, W., Qian, L. & Lo, H.-K. Proof-of-principle experimental demonstration of twin-field quantum key distribution over optical channels with asymmetric losses. npj Quantum Inf. 7, 8 (2021).
Cao, Y. et al. Long-distance free-space measurement-device-independent quantum key distribution. Phys. Rev. Lett. 125, 260503 (2020).
Wei, K. et al. High-speed measurement-device-independent quantum key distribution with integrated silicon photonics. Phys. Rev. X 10, 031030 (2020).
Liao, S. K. et al. Satellite-to-ground quantum key distribution. Nature 549, 43–47 (2017).
Liao, S. K. et al. Satellite-relayed intercontinental quantum network. Phys. Rev. Lett. 120, 030501 (2018).
Diamanti, E., Lo, H.-K., Qi, B. & Yuan, Z. Practical challenges in quantum key distribution. npj Quantum Inf. 2, 16025 (2016).
Pirandola, S. et al. Advances in quantum cryptography. Adv. Opt. Photonics 12, 1012–1236 (2020).
Xu, F., Ma, X., Zhang, Q., Lo, H.-K. & Pan, J.-W. Secure quantum key distribution with realistic devices. Rev. Mod. Phys. 92, 025002 (2020).
Takeoka, M., Guha, S. & Wilde, M. M. Fundamental rate-loss tradeoff for optical quantum key distribution. Nat. Commun. 5, 5235 (2014).
Pirandola, S., Laurenza, R., Ottaviani, C. & Banchi, L. Fundamental limits of repeaterless quantum communications. Nat. Commun. 8, 15043 (2017).
Panayi, C., Razavi, M., Ma, X. & Lütkenhaus, N. Memory-assisted measurement-device-independent quantum key distribution. N. J. Phys. 16, 043005 (2014).
Abruzzo, S., Kampermann, H. & Bruß, D. Measurement-device-independent quantum key distribution with quantum memories. Phy. Rev. A 89, 012301 (2014).
Azuma, K., Tamaki, K. & Munro, W. J. All-photonic intercity quantum key distribution. Nat. Commun. 6, 10171 (2015).
Bhaskar, M. K. et al. Experimental demonstration of memory-enhanced quantum communication. Nature 580, 60–64 (2020).
Langenfeld, S., Thomas, P., Morin, O. & Rempe, G. Quantum repeater node demonstrating unconditionally secure key distribution. Phys. Rev. Lett. 126, 230506 (2021).
Lucamarini, M., Yuan, Z. L., Dynes, J. F. & Shields, A. J. Overcoming the rate-distance limit of quantum key distribution without quantum repeaters. Nature 557, 400–403 (2018).
Ma, X., Zeng, P. & Zhou, H. Phase-matching quantum key distribution. Phys. Rev. X 8, 031043 (2018).
Cui, C. et al. Twin-field quantum key distribution without phase postselection. Phys. Rev. Appl. 11, 034053 (2019).
Wang, X.-B., Yu, Z.-W. & Hu, X.-L. Twin-field quantum key distribution with large misalignment error. Phy. Rev. A 98, 062323 (2018).
Curty, M., Azuma, K. & Lo, H.-K. Simple security proof of twin-field type quantum key distribution protocol. npj Quantum Inf. 5, 64 (2019).
Tamaki, K., Lo, H.-K., Wang, W. & Lucamarini, M. Information theoretic security of quantum key distribution overcoming the repeaterless secret key capacity bound. Preprint at https://arxiv.org/abs/1805.05511 (2018).
Yin, H. L. & Fu, Y. Measurement-device-independent twin-field quantum key distribution. Sci. Rep. 9, 3045 (2019).
Zhong, X., Hu, J., Curty, M., Qian, L. & Lo, H. K. Proof-of-principle experimental demonstration of twin-field type quantum key distribution. Phys. Rev. Lett. 123, 100506 (2019).
Xue, K., Zhao, S., Mao, Q. & Xu, R. Plug-and-play sending-or-not-sending twin-field quantum key distribution. Quantum Inf. Process. 20, 320 (2021).
Liu, Y. et al. Experimental twin-field quantum key distribution through sending or not sending. Phys. Rev. Lett. 123, 100505 (2019).
Minder, M. et al. Experimental quantum key distribution beyond the repeaterless secret key capacity. Nat. Photonics 13, 334–338 (2019).
Wang, S. et al. Beating the fundamental rate-distance limit in a proof-of-principle quantum key distribution system. Phys. Rev. X 9, 021046 (2019).
Chen, J. P. et al. Sending-or-not-sending with independent lasers: secure twin-field quantum key distribution over 509 km. Phys. Rev. Lett. 124, 070501 (2020).
Fang, X.-T. et al. Implementation of quantum key distribution surpassing the linear rate-transmittance bound. Nat. Photonics 14, 422–425 (2020).
Chen, J.-P. et al. Quantum key distribution over 658 km fiber with distributed vibration sensing. Preprint at https://arxiv.org/abs/2110.11671 (2021).
Liu, H. et al. Field test of twin-field quantum key distribution through sending-or-not-sending over 428 km. Phys. Rev. Lett. 126, 250502 (2021).
Zhong, X., Wang, W., Mandil, R., Lo, H.-K. & Qian, L. Simple multiuser twin-field quantum key distribution network. Phys. Rev. Appl. 17, 014025 (2022).
Elliott, C. Building the quantum network*. N. J. Phys. 4, 46 (2002).
Elliott, C. et al. Current status of the DARPA quantum network. Proc. SPIE 5815, 138–149 (2005).
Peev, M. et al. The SECOQC quantum key distribution network in Vienna. N. J. Phys. 11, 075001 (2009).
Xu, F. et al. Field experiment on a robust hierarchical metropolitan quantum cryptography network. Chin. Sci. Bull. 54, 2991–2997 (2009).
Sasaki, M. et al. Field test of quantum key distribution in the Tokyo QKD Network. Opt. Express 19, 10387–10409 (2011).
Stucki, D. et al. Long-term performance of the SwissQuantum quantum key distribution network in a field environment. N. J. Phys. 13, 123001 (2011).
Frohlich, B. et al. A quantum access network. Nature 501, 69–72 (2013).
Park, B. K. et al. User-independent optical path length compensation scheme with sub-nanosecond timing resolution for a 1 × N quantum key distribution network system. Photonics Res. 8, 296–302 (2020).
Woo, M. K. et al. One to many QKD network system using polarization-wavelength division multiplexing. IEEE Access 8, 194007–194014 (2020).
Chen, Y. A. et al. An integrated space-to-ground quantum communication network over 4,600 kilometres. Nature 589, 214–219 (2021).
Wang, S. et al. Field and long-term demonstration of a wide area quantum key distribution network. Opt. Express 22, 21739–21756 (2014).
Tang, Y.-L. et al. Measurement-device-independent quantum key distribution over untrustful metropolitan network. Phys. Rev. X 6, 011024 (2016).
Muller, A. et al. “Plug and play” systems for quantum cryptography. Appl. Phys. Lett. 70, 793–795 (1997).
Tang, G.-Z. et al. Experimental asymmetric plug-and-play measurement-device-independent quantum key distribution. Phy. Rev. A 94, 032326 (2016).
Choi, Y. et al. Plug-and-play measurement-device-independent quantum key distribution. Phy. Rev. A 93, 032319 (2016).
Park, C. H. et al. Practical plug-and-play measurement-device-independent quantum key distribution with polarization division multiplexing. IEEE Access 6, 58587–58593 (2018).
Stucki, D., Gisin, N., Guinnard, O., Ribordy, G. & Zbinden, H. Quantum key distribution over 67 km with a plug&play system. N. J. Phys. 4, 41 (2002).
Jiang, C., Yu, Z.-W., Hu, X.-L. & Wang, X.-B. Unconditional security of sending or not sending twin-field quantum key distribution with finite pulses. Phys. Rev. Appl. 12, 024061 (2019).
Yu, Z. W., Hu, X. L., Jiang, C., Xu, H. & Wang, X. B. Sending-or-not-sending twin-field quantum key distribution in practice. Sci. Rep. 9, 3080 (2019).
Mao, Q. P., Wang, L. & Zhao, S. M. Plug-and-play round-robin differential phase-shift quantum key distribution. Sci. Rep. 7, 15435 (2017).
Park, B. K. et al. QKD system with fast active optical path length compensation. Sci. China Phys. Mech. Astron. 60, 060311 (2017).
Gisin, N., Fasel, S., Kraus, B., Zbinden, H. & Ribordy, G. Trojan-horse attacks on quantum-key-distribution systems. Phy. Rev. A 73, 022320 (2006).
Fung, C.-H. F., Qi, B., Tamaki, K. & Lo, H.-K. Phase-remapping attack in practical quantum-key-distribution systems. Phy. Rev. A 75, 032314 (2007).
Xu, F., Qi, B. & Lo, H.-K. Experimental demonstration of phase-remapping attack in a practical quantum key distribution system. N. J. Phys. 12, 113026 (2010).
Zhao, Y., Qi, B. & Lo, H.-K. Quantum key distribution with an unknown and untrusted source. Phy. Rev. A 77, 052327 (2008).
Zhao, Y., Qi, B., Lo, H.-K. & Qian, L. Security analysis of an untrusted source for quantum key distribution: passive approach. N. J. Phys. 12, 023024 (2010).
Xu, F. Measurement-device-independent quantum communication with an untrusted source. Phy. Rev. A 92, 012333 (2015).
Ribordy, G., Gautier, J.-D., Gisin, N., Guinnard, O. & Zbinden, H. Fast and user-friendly quantum key distribution. J. Mod. Opt. 47, 517–531 (2000).
Peng, X., Jiang, H., Xu, B., Ma, X. & Guo, H. Experimental quantum-key distribution with an untrusted source. Opt. Lett. 33, 2077–2079 (2008).
Kwon, O. et al. Characterization of polarization-independent phase modulation method for practical plug and play quantum cryptography. Laser Phys. 25, 125201 (2015).
Zhou, X.-Y., Zhang, C.-H., Zhang, C.-M. & Wang, Q. Asymmetric sending or not sending twin-field quantum key distribution in practice. Phy. Rev. A 99, 062316 (2019).
Hu, X.-L., Jiang, C., Yu, Z.-W. & Wang, X.-B. Sending-or-not-sending twin-field protocol for quantum key distribution with asymmetric source parameters. Phy. Rev. A 100, 062337 (2019).
Grasselli, F., Navarrete, Á. & Curty, M. Asymmetric twin-field quantum key distribution. N. J. Phys. 21, 113032 (2019).
Wang, W. & Lo, H.-K. Simple method for asymmetric twin-field quantum key distribution. N. J. Phys. 22, 013020 (2020).
Chau, H. F. Practical scheme to share a secret key through a quantum channel with a 27.6% bit error rate. Phy. Rev. A 66, 060302 (2002).
Xu, H., Yu, Z.-W., Jiang, C., Hu, X.-L. & Wang, X.-B. Sending-or-not-sending twin-field quantum key distribution: Breaking the direct transmission key rate. Phy. Rev. A 101, 042330 (2020).
Hu, M., Zhang, L., Guo, B. & Li, J. Polarization-based plug-and-play measurement-device-independent quantum key distribution. Opt. Quantum Electron. 51, 22 (2019).
Yu, Z.-W., Zhou, Y.-H. & Wang, X.-B. Three-intensity decoy-state method for measurement-device-independent quantum key distribution. Phy. Rev. A 88, 062339 (2013).
Acknowledgements
National Research Foundation of Korea (2019M3E4A1079777, 2019R1A2C2006381, 2019M3E4A107866011, 2021M1A2A2043892), MSIT/IITP (2020-0-00972 and 2020-0-00947), and the KIST research program (2E31021).
Author information
Authors and Affiliations
Contributions
S.-W.H. and S.K. planned and supervised the research. C.H.P., M.K.W., and B.K.P. performed the experiment and analyzed the data; all authors contributed to analysis and discussion of the results. C.H.P., S.-W.H., and S.K. wrote the manuscript with input from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Park, C.H., Woo, M.K., Park, B.K. et al. 2×N twin-field quantum key distribution network configuration based on polarization, wavelength, and time division multiplexing. npj Quantum Inf 8, 48 (2022). https://doi.org/10.1038/s41534-022-00558-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-022-00558-8
This article is cited by
-
A cost-efficient quantum access network with qubit-based synchronization
Science China Physics, Mechanics & Astronomy (2024)
-
Symmetric private information retrieval supported by quantum-secure key-exchange network
Light: Science & Applications (2022)