Abstract
Quantum information processing (QIP) with solid state spin qubits strongly depends on the efficient initialisation of the qubit’s desired charge state. While the negatively charged tin-vacancy (SnV−) centre in diamond has emerged as an excellent platform for realising QIP protocols due to long spin coherence times at liquid helium temperature and lifetime limited optical transitions, its usefulness is severely limited by termination of the fluorescence under resonant excitation. Here, we unveil the underlying charge cycle, potentially applicable to all group IV-vacancy (G4V) centres, and exploit it to demonstrate highly efficient and rapid initialisation of the desired negative charge state of single SnV centres while preserving long term stable optical resonances. In addition to investigating the optical coherence, we all-optically probe the coherence of the ground state spins by means of coherent population trapping and find a spin dephasing time of 5(1) μs. Furthermore, we demonstrate proof-of-principle single shot spin state readout without the necessity of a magnetic field aligned to the symmetry axis of the defect.
Similar content being viewed by others
Introduction
Colour centres in diamond have recently emerged as competitive platforms in the field of QIP1,2,3. In particular the G4V centres combine long spin coherence times4,5 with favourable optical properties such as large Debye-Waller factors6,7 and transform limited resonance linewidths6,8,9,10. While the large spectral diffusion for the nitrogen vacancy centre in diamond11 is to be expected, G4V centres should be protected by their inversion symmetry from large first order Stark shifts. Nevertheless, spectral diffusion due to second order effects is still common to impose a strong limit on the usefulness in quantum information and simulation applications8,12,13,14,15,16, which makes overcoming these spectral instabilities a crucial task. The origin of the unstable resonance lines is oftentimes introduced by fluctuating charges resulting from impurities or lattice defects in the vicinity of the colour centre. Furthermore, these environmental impurities and defects can act as charge traps or electron donors leading to an ill-defined charge state of the emitter. Among the G4V centres, the SnV− centre6,17,18,19 shows great promise in terms of spin coherence at easily accessible liquid helium temperatures4 and lifetime limited optical transitions6,8. Unfortunately, its potential for application in QIP is suffering strongly from the termination of fluorescence under resonant excitation4,6,8. In this work, we investigate the mechanism leading to the charge instability of a single SnV− centre in diamond and find it to be a single photon process. We furthermore fully explore the charge cycle of the SnV centre and use it to implement a straightforward, highly efficient and rapid initialisation of the negative charge state while preserving long-term stablility of dipole allowed optical transitions. We find that the principle of this charge cycle can also directly be applied to other G4V centres for efficient control of their charge state. Subsequently, we probe the coherence of the charge stabilised SnV− centre by an all-optical coherent population trapping (CPT) scheme, yielding a spin dephasing time of the ground state of \({T}_{2}^{* }=5(1)\,\mu {{{\rm{s}}}}\). By employing a proof-of-principle single shot readout protocol, we demonstrate the presence of highly cycling optical transitions even in the case of large angles between the magnetic field and the symmetry axis of the defect.
Results
Charge cycle of the SnV− centre
We investigate single SnV− centres in diamond created upon ion implantation and subsequent high-pressure-high-temperature (HPHT) annealing (sample NI58, see method section for details on the sample and the experimental setup) at temperatures of 2 K, for which termination of fluorescence is reliably observed under resonant excitation of the defect4,6,8. Without additional measures, we find this termination to be permanent, even after hour long waiting times in the dark. Furthermore, by performing resonant excitation scans over a large spectral range of several GHz, we can exclude that the resonance line is simply shifted due to spectral diffusion, the range of which is typically limited to ≪ 1 GHz for the SnV− centre. Applying an additional 532 nm laser pulse, as often used in experiments with G4V centres, suffices to recover the fluorescence, but usually leads to a resonance line shifted by up to several hundred MHz6, much larger than the typical lifetime-limited linewidths of 20–30 MHz. A similar effect was also found for germanium vacancy centres in diamond20. These spectral shifts impose a strong limitation on the usefulness of the SnV− centre in QIP. The origin of the instability of the resonance line is most likely caused by an altered charge environment after the application of the 532 nm laser. Understanding these charge dynamics is crucial in order to fully exploit the superior spin coherence of single SnV− centres at liquid helium temperatures compared to other G4V centres4,5,17,21,22.
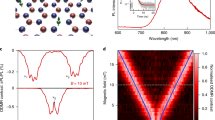
In order to stabilise the desired negative charge state of the SnV centre without inducing spectral shifts, we systematically vary the wavelength of an additionally applied light field. To this end we perform a measurement in which we use a continuous wave dye laser to resonantly excite an ensemble of SnV− centres on the C-transition (see Fig. 1c), add a second light field provided by a pulsed supercontinuum laser source at a repetition rate of 80 MHz and monitor the count rate on the phonon sideband (Bandpass filter: 655(47) nm). We scan the wavelength of the second laser from 420 nm up to 580 nm with a spectral bandwidth of 10 nm while keeping the power fixed and compare the count rate of the purely resonant excitation to the count rate of the two-colour excitation while substracting the counts caused by the second light field alone (Fig. 1b). For wavelengths of the second light field ≳ 520 nm the ensemble fluorescence remains at a low level due to the fluorescence termination discussed above. However, we observe a fluorescence enhancement starting at wavelengths (energies) shorter (larger) than 520 nm (2.4 eV), for which we define the enhancement factor \(\beta =\frac{{I}_{{{{\rm{w}}}}}}{{I}_{{{{\rm{wo}}}}}}\) as the ratio between emitted fluorescence intensity with (Iw) and without (Iwo) the second laser being applied. This is depicted by the green triangles in (Fig. 1b). The observed fluorescence enhancement indicates a stabilisation of the desired negative charge state for photon energies above 2.4 eV, hinting at a charge transfer process occuring at a certain threshold. This result is confirmed by a similar measurement on a second HPHT annealed sample labelled BOJO_001, see method section and Supplementary Note 3 for further information.
a Proposed scheme for the charge cycle of the SnV centre. In (I) the SnV− centre gets excited by a resonant 2 eV photon. In (II) a second 2 eV photon promotes an electron from the valence band to the SnV− centre, transforming it into its optically inactive charge state SnV2−. In (III) a photon with an energy above 2.4 eV drives the charge transition of a defect in the diamond lattice, most likely the neutral divacancy. In this process a hole is created in the valence band which diffuses in (IV) towards the SnV2− centre, where a recombination takes place. All absolute energy positions related to the charge states of the SnV− centre are extracted from ref. 19. b Enhancement of fluorescence factor of an ensemble of SnV− centres, excited resonantly on the C-transition and under addition of a second laser with tunable wavelength. The enhancement factor is defined as the ratio between counts with and without the second laser. For comparison, the normalised excitation probability measured via excitation by the second laser only is plotted. The excitation probability peaks at 2.4 eV due to excitation to a higher excited state of the SnV−6 and an indication of an even higher lying excited state is seen at photon energies larger 2.8 eV most likely resulting from a deeper lying electron state in the valence band19. y-errors (s.d.): Poisson distributed count rate errors. c Fine structure and Zeeman splitting of the SnV− centre. The relevant optical transitions and splittings at B=0 T and B=0.2 T for this work are labelled.
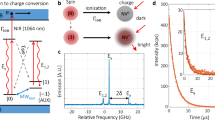
Before devising a model for the SnV charge cycle, we further investigate the charge dynamics. To this end, we select 445 nm as the optimised wavelength for recovery of the negative charge state of the SnV centre, because it lies at the optimum of fluorescence enhancement while minimising the direct excitation of the SnV− centre. The latter can be seen by the normalised excitation probability, which is depicted as blue dots in (Fig. 1b), as function of the excitation wavelength. We derive it from the count rate emitted upon excitation with the second wavelength laser only and normalise it by the maximum count rate measured for all excitation wavelengths. The minimised direct excitation is important, since the termination of the fluorescence is only occuring from the excited state of the SnV− centre as we will show below. Thus direct excitation with the charge initialisation laser can lead to a subsequent termination of the fluorescence stimulated by a second photon from the initialisation laser and therefore to a reduced initialisation efficiency. We now evaluate the number of photons that are taking part in the charge transfer process under resonant excitation. To this end, we employ a 10 ms laser pulse at 445 nm to initialise the negative charge state of a single SnV− centre (Emitter 1, characterisation of the single photon emission can be found in the Supplementary Note 1). Subsequently, we apply a 1 s long laser pulse resonant with the C-transition of the defect and collect photons emitted into the phonon sideband. The duration of the resonant laser pulse is chosen sufficiently long such that charge transfer will occur during this time even for the lowest power used. An exemplary excerpt of such a time trace is depicted in (Fig. 2a). We repeat this measurement about 500 times for each laser power and extract the charge state lifetime, which we define as the duration until charge transfer occurs under resonant excitation, by evaluating the duration of emission of the SnV− centre until the fluorescence is terminated. A histogram of such a measurement together with a mono-exponential fit is shown in Fig. 2b. The charge lifetime is extracted as the time constant of the exponential decay. The inverse of the lifetime yields the charge transfer rate, which increases linearly with the resonant excitation power (see Fig. 2c). The linear fit in red, with the y-intercept being set to zero, yields a slope of \(1.28(5)\frac{{{{\rm{Hz}}}}}{{{{\rm{nW}}}}}.\) We therefore conclude that charge transfer occurs as a single photon process. It takes place when the SnV− centre is in the excited state, since termination of fluorescence does not occur when the excitation laser is far detuned from resonance. In such a case one would intuitively expect a two photon process where the first photon excites the emitter and the second photon causes the charge transfer, therefore leading to a quadratic power dependence of the charge transfer rate. However, the charge transfer happens at time scales much longer (6 orders of magnitude) than the lifetime of the excited state. We thus expect that the charge transfer starts from a steady state population of the excited state created by the resonant excitation and consequently involves only a single photon.
a Exemplary part of a measurement sequence of the charge initialisation and electron capture experiments on a single SnV− centre (Emitter 1). After the 10 ms laser pulse at 445 nm initialises the charge state, a fluorescence response by the 1 s long resonant laser pulse on the C-transition is visible. The fluorescence response lasts until electron capture occurs. b Histogram of the lengths of the fluorescence responses for a given resonant laser power of 20.7 nW. An exponential fit yields the charge state lifetime until charge transfer occurs. This lifetime translates directly to a charge transfer rate for every given laser power. y-errors (s.d.): Poisson distributed count rate errors. c Charge transfer rate plotted against the resonant excitation laser power. The linear dependence of the charge capture rate on the power indicates a single photon process from the excited state, since termination of fluorescence does not occur, if the laser is not resonant with the C-transition. The blue data point corresponds to the laser power chosen for the charge state initialisation measurement in (d), while the greyed out data point results from a measurement aborted earlier than the others. y-errors (s.d.): Fitting error from measurements in (b). d Measurement of the charge state initialisation efficiency. The 445 nm laser pulse of variable pulse length is followed by a 0.5 s long resonant laser pulse with a power chosen such, that electron capture occurs with a probability close to unity for each pulse. The initialisation efficiency is extracted by counting the number of fluorescence response pulses that occur and dividing them by the total number of pulses. For increasing pulse length of the blue laser, the initialisation efficiency follows an exponential law with a time constant of τCI = 780(27) μs and saturates at 91(1) %. y-errors (s.d.): Poisson distributed count rate errors.
To explain the charge transfer processes ocurring under resonant excitation and illumination with a second light field we start with the position of the energy levels of the SnV− centre in the diamond bandgap (Fig. 1a). All absolute energy values of SnV states are taken from theoretical calculations conducted in ref. 19. Under resonant excitation with the ZPL energy of about 2.0 eV, the absolute energy position of the SnV− levels shift about 0.6 eV upwards in the diamond bandgap, which is 5.47 eV wide. The highest occupied levels of the SnV− excited state thus lie 0.6 eV + 2.0 eV above the valence band and consequently 5.47 eV − 2.6 eV = 2.87 eV below the conduction band. We exclude a charge transfer process under resonant illumination by photo-ionisation of an electron from the excited state to the conduction band based on the following facts and observations: (i) the photon energy of 2.0 eV is not sufficient for a one-photon excitation from the excited state to the conduction band; (ii) a two-photon process from the excited state (2 ⋅ 2.0 eV > 2.87 eV) is excluded as we observe a one-photon charge transfer process (see discussion above); (iii) electron ionisation would leave the SnV centre in its neutral state. Although it is very challenging to unambiguously observe emission from different charge states (due to potential charge transfer happening upon excitation) we gather evidence against transfer into the neutral charge state: When exciting an ensemble of SnV− centres resonantly without any charge stabilising laser being applied and measuring spectra integrated longer than 10 min in the spectral region from 620-900 nm, these measurements do not show the slightest hint of SnV0 centre emission, which is theoretically predicted to lie at 680(40) nm23. In this case, the 620 nm excitation should not only transfer the SnV centres to their neutral charge state but also have significant overlap with its excited state vibrational ladder. For comparison, the vibrational ladder spans about 100 nm for the SnV−6. Thus, the 620 nm radiation should also excite the SnV0, which we do not observe. Transfer of a single charge then only leaves the alternative of transfer to the doubly negative charge state SnV2− which is an optically inactive state and cannot be observed spectroscopically. However, our combined observations as discussed above lead to the conclusion that the dark state of the SnV centre is indeed the SnV2−. This claim furthermore is in agreement with recent experimental findings on the SiV− centre where a doubly negative charge state was identified as the dark state24.
We here go a step further and propose a model which not only explains the SnV centre charge dynamics but should be generally valid for all G4V centres. Our model is based on the charge state conversion process identified in ref. 24, i.e. capture of an electron from the valence band (hole generation) for the SnV− → SnV2− process and release of an electron to a hole in the valence band (hole capture) for going from SnV2− → SnV−. The latter process requires the presence of a valence band hole in the vicinity of the SnV centre which might be created by another close-by defect upon photo-excitation. We identify this defect by the measurement of fluorescence enhancement presented in (Fig. 1b): The onset and also the shape of the fluorescence enhancement curve agree very well with the theoretically proposed25 and experimentally confirmed26 charge transition of the neutral divacancy in diamond to its negative charge state. This charge transition occurs due to promotion of an electron from the valence band to the divacancy25,26. It was also reported, that the efficiency of this ionisation reaches unity charge conversion at photon energies >3 eV. The diamond sample investigated in this study is very likely to contain many divacancies even after the HPHT annealing (27, p.32-34), since the implantation of one tin ion with an energy of 700 keV creates about 3000 vacancies (Monte Carlo Simulation, SRIM) which tend to form divacancies in an exothermic reaction during annealing due to single vacancies becoming mobile28. Hence, monovacancies will no longer be present as was also found in ref. 26. Regarding other common impurities in diamond such as boron and nitrogen, they are present in low concentrations as specified in the methods section. However, their typical absorption energies29 do not match the observed fluorescence enhancement threshold. While we cannot exclude that the charge transition originates from a different vacancy or impurity complex in diamond, we find the divacancy to be the most likely candidate. Based on these considerations we propose the following charge cycle for the SnV− centre: A resonant 620 nm (2 eV) photon first excites the SnV− centre to a fully occupied eg state (see Fig. 1a). A subsequent 620 nm photon promotes an electron from the valence band to the SnV− centre’s empty eu orbital and transforms it into its optically inactive charge state SnV2−. The created hole left in the valence band diffuses to a defect in the vicinity where it is caught, the SnV2− cannot recombine with it and the SnV−fluorescence is terminated. A photon with a wavelength (energy) of 420-520 nm (2.4-3 eV) excites an electron from the valence band to a defect in the diamond lattice, the most likely candidate being the neutral divacancy. This process creates a hole in the valence band which diffuses towards the SnV2− centre where a recombination leads to the return to SnV−, which closes the cycle. In the second run of the charge cycle the divacancy is in its negative charge state and will act as the trap for the hole created in step II in (Fig. 1a). For our considerations above, we restricted the charge repump energy to the range of 2.4–3 eV, since we were limited to energies below 3 eV by the utilised supercontinuum laser in the measurement of the enhancement factor. It might well be possible that higher photon energies are also suitable for charge stabilisation of the SnV−. The developed charge cycle scheme is also able to explain the large spectral shifts that occur when applying 532 nm laser light as a charge repump. The energy of the green light is not sufficient to efficiently convert all the surrounding divacancies to their negative charge state and therefore leaves a fluctuating charge environment. The 445 nm light, in contrast, will also be sufficient to ionise most common impurities that might occur in low densities (B,N,..) and therefore create a charge environment that is the same after each application of the charge stabilisation laser. A direct comparison of the effect of blue and green laser light charge stabilisation can be found in the Supplementary Note 6.
Building on these results, we evaluate the efficiency with which we can initialise the negative charge state of the investigated SnV centre. For this we apply a 445 nm initialisation pulse with variable pulse length and a cw power of 50 μW which is followed by a 0.5 s resonant laser pulse creating a fluorescence response if the SnV− charge state is properly initialised. A timegap of a few microseconds ensures that the effects of charge stabilisation and electron capture do not overlap. The power of the resonant laser pulse is chosen corresponding to an electron capture rate of 46(2) Hz (blue dot in Fig. 2c) ensuring electron capture with a probability close to unity. The theoretical value can be calculated to \(1-\exp (-0.5{{{\rm{s}}}}\cdot 46\frac{1}{{{{\rm{s}}}}})\), with the error to unity being below 10−10 under consideration of the error bar of the electron capture rate. For each blue pulse length, we repeat the measurement about 250 times and count the number of initialisation pulses after which a fluorescence response is observable. The ratio of observed pulses to the total number of pulses used yields the initialisation efficiency, which is depicted in (Fig. 2d). We reach a saturation value of 91(1) % charge initialisation, which we fit by a mono-exponential growth law, \(1-\exp (-\frac{t}{{\tau }_{{{{\rm{CI}}}}}})\), with τCI being the time constant of the charge repumping. The time dependence of the pumping results from transferring the electron from the valence band to the neutral divacancy and the subsequent hole capture of the SnV2−. Its dependence on the blue laser power is discussed in the Supplementary Note 6. We find that the rate of charge state initialisation increases linearly (190(8)\(\frac{{{{\rm{Hz}}}}}{\mu {{{\rm{W}}}}}\)) with blue laser power, again confirming the model of a single-photon charge transfer process. At the largest laser power used ( ~ 600 μW), we demonstrate rapid charge initialisation in about 10 μs. 4(1) % of the missing initialisation efficiency are due to the number of pulses where electron capture occurs too fast to create a sufficiently strong fluorescence response to be distinguished from the dark counts and background in our system. The missing 5 % to unity might be caused either by the restrictive threshold on fluorescence counts that we set for a positive pulse count after initialisation or by spurious electron capture by the blue laser itself due to the small but measurable direct excitation probability and the possibility of a second blue laser photon transferring an electron from deep within the valence band to the SnV−, thus turning it dark. It is worth noting, that we found this concept of initialisation to work on every emitter that we investigated in this sample and a similar HPHT annealed second sample (see Supplementary Note 3). Detailed results of a second emitter under investigation reaching 97 % of charge state initialisation efficiency can be found in the Supplementary Note 6.
Another noteworthy finding is that under resonant pulsed excitation well below saturation with a low duty cycle (about 0.2 ‰) in order to prevent electron capture, the charge state set by a one-time application of the initialisation laser was found to persist over more than an hour of measurement time. In the dark it was maintained over several hours and thus we conclude that its lifetime is only limited by laser induced electron capture. While we utilise pulsed and continuous wave stabilisation schemes within this work, generally it would be fully sufficient to employ pulsed charge stabilisation with high efficiency and repeat initialisation with a rate larger than the electron capture rate imposed by the resonant excitation. Further results on the photophysics of SnV− centres in low-pressure-low-temperature annealed diamond samples which are induced by the charge cycle described above will be published elsewhere.
We would furthermore like to emphasise that the proposed charge cycle model and and the method for stabilising the negative charge state are most probably universal to the G4V centres in diamond. The reason is that their general electronic level structure is identical and the lower eu orbitals generally lie close to the valence band edge such that the charge transfer as discussed here for SnV centres works in an analogous fashion. Small differences might evolve due to different concentrations of divacancies introduced in the implantation process and absolute energy positions within the band gap of diamond. This claim is strongly supported by an experiment on a resonantly excited ensemble of SiV−centres in which a very similar fluorescence enhancement under illumination with a second tunable laser is observed (see Supplementary Note 4) and furthermore by the findings reported in24.
Long term stability of the resonances of a charge stabilised SnV− centre
The ability to reliably initialise the negative charge state of the SnV− centre enables us to investigate the influence of spectral diffusion on the long term stability of the electronic transitions. There are two cases to distinguish: Firstly, light-induced fluctuations of the charge environment that introduce Stark shifts13,14 as a result of the charge stabilisation laser being applied. These disturbances occur without the SnV− centre undergoing a full charge cycle (e.g. the negative charge state is preserved), resulting in a dynamic equilibrium of the charge environment. In the second case, this equilibrium is disturbed when the SnV− centre captures an electron under resonant excitation and the charge cycle is initalised. It is not guarantueed that the hole necessary for the recombination will result from the same divacancy for each charge cycle. It is thus possible that the near scale charge environment will not end up in its original state. Therefore, we expect stronger influence on the spectral diffusion in the latter case. In order to separate the two effects, we perform photoluminescence excitation (PLE) spectroscopy and use very low excitation powers below 0.5 nW in order to avoid power broadening and electron capture. The power is chosen such that it is about a factor of four below the saturation power ( ~ 2 nW). In this way, one can resolve very small spectral shifts on the order of the natural linewidth of about 25 MHz that are only caused by environmental fluctuations. During the measurement, the SnV− centre is permanently charge stabilised by continuous wave 445 nm radiation. The resonance line peak position shift exhibits a standard deviation of less than 4(2) MHz and a total width of the summed PLE spectra of 33(2) MHz for the whole duration of the measurement, as displayed in (Fig. 3a). This value has an uncertainty of 2 MHz caused by the uncertainty of our wavemeter which was measured independently. Due to a technical problem of our positioning system within the cryostat, after this measurement, emitter 1 could no longer be accessed. The following measurements were therefore performed on a different emitter (Emitter 2, see Supplementary Note 1) on which all concepts, that were shown before, work in the same manner. On this SnV− centre, we investigate the effect of the emitter undergoing the charge cycle by choosing a laser power of 10 nW as a trade-off to ensure continuous electron capture in every single resonance scan while introducing as little as possible power broadening. Even in this case we observe only small shifts in the central resonance position with a standard deviation of 10(2) MHz and a total width of the summed PLE spectra of 103(2) MHz compared to 88 MHz purely power broadened linewidth, see (Fig. 3b). The small but visible oscillations with a period of about 10 min in the central resonance position are related to the air conditioning cycle in our laboratory. We consequently claim that the shift is caused by tiny alterations of the position of the blue laser on the sample with respect to the emitter, since slightly misaligning the blue laser spot on the sample has similar effects. This is in agreement with a spatially asymetric charge distribution caused by the ionised divacancies. This effect has the potential of a tuning mechanism of < 100 MHz in resonance frequency, limited by imperfect charge initialisation for strongly misaligned blue laser light. It is remarkable that contrary to the observations reported in ref. 16, the charge stabilisation enables us to limit spectral fluctuations to less than 16 % (11 %) of the homogeneous (power broadened) linewidth of 25 MHz (88 MHz) over the course of one hour. For the shifts observed in the low power measurement, even for photons separated by an arbitrary time distance within the one hour measurement, a Hong-Ou-Mandel visibility close to 90 % would be achievable for photons emitted from this SnV− centre (calculated using the simulation tool implemented in ref. 30 (“remote HOM testbed”), available from the website of the journal). The same holds true when interfering photons retrieved from two independent emitters with the same properties, which is an important prerequisite for effectively entangling two SnV− centres. As the experiments on the additional emitters presented in Supplementary Notes 3 and 6 demonstrate, finding two emitters similarly marginally impacted by spectral diffusion is straightforward in the investigated samples. Thus, the photons emitted by a charge stabilised SnV− centre should be highly indistinguishable, which is a key factor in many QIP protocols and quantum communication. Since the measurements for low and high power excitation had to be conducted on two different emitters, an additional measurement on a further emitter accessing both power limits is presented in the Supplementary Note 6, emphasising frequency stability of SnV− centres obtained by the charge stabilisation scheme presented in this work.
a Low excitation power of 0.5 nW long-term PLE in order to resolve spectral shifts caused by the charge environment or the 445 nm laser without initiating the charge cycle of the centre. The constantly charge stabilised emitter’s line position exhibits a standard deviation of less than 4(2) MHz over one hour of measurement. On the right, the integrated spectrum over all scans (black) with a width of 33(2) MHz is compared with the Fourier limited Lorentzian line (red, 25 MHz). b Long-term PLE on Emitter 2 with a power of 10 nW ensuring electron capture in every resonance scan while minimising power broadening. In the duration of one hour, the central resonance position exhibits a standard deviation of 10(2) MHz. The oscillations with a period of about 10 min in the central resonance position are related to the air conditioning cycle in our laboratory. On the right, the integrated spectrum over all scans (black) with a width of 103(2) MHz is compared to a Lorentzian that is only subject to power broadening (red) and exhibits a width of 88(2) MHz.
Coherent population trapping
With the means of a stable SnV− centre resonance line at hand, we explore the possibility of all-optical coherent manipulation of its spin degree of freedom. To this end, we perform CPT between the states \(\left|1\downarrow \right\rangle\), \(\left|2\uparrow \right\rangle\) via the excited state \(\left|{{{\rm{A}}}}\downarrow \right\rangle\). In order to lift the degeneracy of the spin states, we apply a magnetic field B=0.2 T at an angle of 54. 7 ∘ relative to the axis of the defect. When applying a magnetic field to the SnV− centre, the splitting of the spin states and the long ground state spin T1 time, which we measure to be larger than 20 ms at 200 mT and 1.7 K (see Supplementary Note 5) lead to a vanishing PLE signal due to optical pumping. Introduction of a weak population repump laser at 532 nm leads to the recovery of the PLE signal of the spin conserving (SC) transitions, while the spin flipping (SF) transitions are so weak, that they can be found only via CPT measurements. This is following directly from the isolated atom like selection rules that are a result of the low strain environment and the strong spin-orbit coupling in comparison with the Jahn-Teller effect present for the SnV− centre8. To generate the light fields for CPT we set the carrier laser frequency resonant to the SF transition A2 and generate the second laser field with the first harmonic of an electro optical phase modulator (EOM). An exemplary characteristic single scan CPT signal is shown in (Fig. 4a), which is fitted using a three level density matrix formalism (see Supplementary Note 7). We relate count rate to populations of the excited state in the following way: In PLE scans with an excitation power P ≫ Psat and without a magnetic field being applied, we measure a fluorescence rate of ~45 kcts/s into the phonon sideband, which corresponds to the limit of incoherent excitation and therefore relates to 50 % of the population residing in the excited state. This gives us an estimate for the relation of measured count rate to population. A more exact value under the given experimental setting is derived by conducting a high power CPT measurement, shown in (Fig. 4a) and fitting it with our model. The mismatch of the simulation and the data on the high frequency side of the measurement is caused by approaching the edge of the amplification range of the microwave amplifier used, therefore effectively changing the power in the sideband during the scan. We subsequently decrease the laser power stepwise and change the ratio between control and signal field via the applied microwave power to the EOM. These sets of measurements are used to step by step eliminate free parameters in the fit such as the ratios between Rabi frequencies and laser power, the branching ratio between SC and SF transitions and the exact number of dark counts resulting from background fluorescence of the sample induced by the blue laser light and the dark counts of the avalanche photo diodes (APD) which can be found in the Supplementary Note 7. Finally the most interesting parameter, the spin ground state decoherence rate is fitted and yields a value of 64(10) kHz, see (Fig. 4b). This relates to a spin dephasing time of \({T}_{2}^{* }=5(1)\,\mu {{{\rm{s}}}}\) which is slightly larger than found in refs. 4,8. In comparison to ref. 4, the branching ratio η between SC and SF transitions amounts to ~650(100), which is about a factor 8 larger. This is due to working with an emitter in a nearly unstrained diamond environment.
a CPT measurement on Emitter 2 with 300 nW of total laser power. This measurement is used to relate measured count rate to excited spin state populations of the SnV− centre. The mismatch of the simulation and the data on the high frequency side of the measurement is caused by approaching the edge of the amplification range of the microwave amplifier used, thereby effectively decreasing the sideband laser power. b Measurement of the CPT dip width with lowest possible total laser power, while preserving a reasonable signal to noise ratio. The data is fitted with a ground state decoherence rate of 64(10) kHz relating to a spin dephasing time of \({{{{\rm{T}}}}}_{2}^{* }=5(1)\,\mu {{{\rm{s}}}}\).
We wish to emphasise that coherent optical spin control via CPT on an unstrained emitter in a clean diamond environment is only possible using the charge stabilisation method, enabling remarkable long-term stability of the resonance frequency and thus the CPT resonance. In a material where strain is sufficiently large to lower the branching ratio by almost an order or magnitude compared to our findings, CPT with less effective charge stabilisation is possible on selected emitters4. We would like to point out that the principles presented in this paper worked straightforwardly on several emitters within our samples, where no preselection of the emitters was applied.
Single shot readout
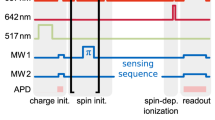
As an outlook to further applications, we investigate whether the strong selection rules, that are described in the previous section, lead to sufficiently strong cycling transitions even when the magnetic field is applied at a large angle with respect to the symmetry axis of the SnV− centre. To this end, we probe the cyclicity by investigating the possibility of a single shot readout. The experiment consists of a 200 μs long initialisation pulse resonant with the SC transition B2 and a 200 μs read pulse on the SC transition A1, separated by 300 μs waiting time. In the subsequent waiting time of about 50 ms following the two pulses, thermal equilibrium spin population of about 50 % in each state is approached (spin lifetime of 22 ms, see Supplementary Note 5). Therefore, the initialisation peak in (Fig. 5a) amounts to roughly half the height of the read out peak. As it can be seen in (Fig. 5a), we achieve an initialisation efficiency of 98.9(4) % in state \(\left|2\uparrow \right\rangle\) while detecting an average of 1.21 (1.13) photons per pulse without (with) dark count substraction. This number is derived from comparing the photons collected in the 200 μs read out interval to the 11139 readout pulses send on to the emitter. We furthermore extract a histogram of photon counts in the readout time interval and compare it to a time interval of the same length where no laser pulse was applied (see Fig. 5b). We extract the readout fidelity following the definition in ref. 31 and set a threshold of one detected photon for a state readout to be detected as bright, while no detected photon corresponds to the state to be dark. The readout error for a bright state to be detected as dark is ϵB = 0.45, while the readout error for a dark state to be detected as bright can be extracted from the dark pulse measurement with additionally taking into account the 1.1 % of residual population resulting from imperfect state initialisation, which yields ϵD = 0.08. The latter is limited by the dark counts of the APD of about 150 cts/s. From the averaged state readout error \(\epsilon =\frac{1}{2}({\epsilon }_{{{{\rm{B}}}}}+{\epsilon }_{{{{\rm{D}}}}})\) we calculate the total readout fidelity as \({{{\mathcal{F}}}}=1-\epsilon =0.74\). This readout fidelity of 74 % surpasses the threshold of 50 % above which a meaningful readout can be implemented, thus demonstrating the potential of the SnV− centre’s strong cycling transitions. The readout fidelity can be further improved by using superconducting nanowire single photon detectors which have an improved dark count rate of below 1 Hz compared to 100-200 Hz of the APDs used in our experiments. Furthermore, since our total collection efficiency from bulk diamond is below 1% there are straightforward measures to improve the number of collected photons and thereby enabling high fidelity single shot readout without the necessity of an aligned magnetic field.
a Histogram of the single shot readout measurement on Emitter 2. The 200 μs long initialisation pulse resonant with the A1 transition initialises the spin with an efficiency of 98.9(4) % in the state \(\left|2\uparrow \right\rangle\). For each 200 μs long read pulse we detect an average of 1.21 (1.13) photons without (with) dark count substraction. b Histogram of photon counts in the readout time interval compared to a time interval of the same length where no laser pulse was applied. The overlap of the two measurements, while taking the imperfect state initialisation into account, yields a total readout fidelity of 74 % when setting 1 photon count as threshold for a state to be detected as bright.
Discussion
In this work, we thoroughly investigated the charge processes taking place for SnV− centres in diamond. We find a dominant single photon electron capture process of single SnV− centres while being in the excited state as the reason for termination of fluorescence under resonant excitation. We propose a charge cycle model, potentially universal to all G4V centres, which explains the charging and de-charging in the presence of an additional divacancy defect. Based on this model we demonstrate a highly efficient and rapid charge initialisation exceeding 90 % utilising a laser with a wavelength of 445 nm as a charge repump. The charge stabilised single SnV− centres are investigated in terms of the long term stability of the resonance line with and without undergoing a full charge cycle. We find that the charge stabilisation preserves very stable optical transitions with deviations of the line centres well below the lifetime-limited linewidth over the duration of one hour in both cases. Furthermore, we probe the spin coherence of a charge stabilised SnV− centre and find a spin lifetime T1 > 20 ms and a spin dephasing time of \({T}_{2}^{* }=5(1)\,\mu {{{\rm{s}}}}\) at a temperature of 1.7 K. As an outlook for further applications, we implement a single shot readout scheme which yields a readout fidelity of 74 %, demonstrating the highly cycling spin conserving transitions even in the case of a large angle of 54.7∘ between magnetic field and the symmetry axis of the defect. It is straightforward to increase the readout fidelity by implementing means to improve the total collection efficiency of our optical setup such as utilising optical antennas32, micropillars8, solid immersion lenses, or photonic crystal structures33,34. In summary, we have shown that the charge stabilisation protocol developed in this work renders the SnV− centre suitable for reliable application in QIP, in which well defined charge states, long-term stable optical resonances for the emission of highly indistinguishable photons, long spin coherence times and efficient state readout are absolutely crucial.
Methods
Sample preparation
The predominantly investigated sample NI58 is an (001) electronic grade bulk diamond, with the sample substrate being obtained by Element Six. It is specified to contain less than 5 ppb (typically 0.1-1 ppb) of substitutional nitrogen, while the boron concentration is below 1 ppb. The sample is homogeneously implanted with tin ions at an implantation energy of 700 keV and a fluence of 8x\(1{0}^{13}\frac{{{{\rm{Ions}}}}}{{{{{\rm{cm}}}}}^{2}}\). A subsequent annealing at 2100 ∘C and 7.7 GPa is employed to reduce implantation damage. A detailed characterisation of the sample can be found in ref. 6. The second sample BOJO_001 is produced starting with a diamond substrate of the same type as used for NI58 and is investigated in the Supplementary Note 3. It is produced by tin ion implantation at an implantation energy of 700 keV and 4 different fluences ranging from \(1{0}^{9}\frac{{{{\rm{Ions}}}}}{{{{{\rm{cm}}}}}^{2}}\) to \(1{0}^{12}\frac{{{{\rm{Ions}}}}}{{{{{\rm{cm}}}}}^{2}}\). A subsequent annealing 2100 ∘C and 8 GPa for 2 h strongly reduces implantation damage.
Experimental setup
The measurements were conducted in a home built confocal microscope with the sample being situated inside a closed cycle helium cryostat (attodry2100, attocube systems AG) which operates at a base temperature of ~1.7 K. The sample is moved via a combination of stepper (2x ANPx51, ANPz51, attocube systems AG) and scanner positioners (ANSxy50, attocube systems AG). We use an NA 0.9 objective (MPLN100x, Olympus) for photon collection.
The second wavelength for the fluorescence enhancement measurement is retrieved from a supercontinuum laser source (SuperK FIANIUM FIU-15, NKT Photonics) with ~100 ps long pulses and with a bandwidth of 10 nm. The resonant laser fields are generated from a side of fringe stabilised Dye cw laser (Matisse 2DS, Sirah Lasertechnik GmbH) which can be locked to a wavemeter (WS6-200, HighFinesse GmbH), while the laser light at 445 nm is emitted by a diode laser (Cobolt 06-MLD, Hübner Photonics). Pulses are carved from the cw lasers using acousto optical amplitude modulators (AOM, AOMO 3200-146, Crystal Technology).
The timing of the pulse sequences for the electron capture, charge initialisation and single shot readout experiments is controlled via a digital delay generator (DG645, Stanford Research Systems).
The optical sidebands for the CPT experiments are introduced by an electro-optical phase modulator (EOM, WPM-K0620, AdvR). The microwave signals used to drive this modulator are emitted from a microwave generator (mg3692c, Anritsu) and sent through a microwave amplifier (ZHL-42+, Mini-Circuits).
For the single shot readout, a second microwave generator (SG384, Stanford Research Systems) is employed in order to implement two sidebands with frequencies resonant with both SC transitions. The sidebands are switched using two microwave switches (ZASW-2-50DRA+, Mini-Circuits).
Data availability
The underlying data for this manuscript is openly available in Zenodo at https://doi.org/10.5281/zenodo.5561219.
Code availability
The evaluation algorithms are available from the corresponding author upon reasonable request.
References
Pompili, M. et al. Realization of a multinode quantum network of remote solid-state qubits. Science 372, 259–264 (2021).
Nguyen, C. T. et al. Quantum network nodes based on diamond qubits with an efficient nanophotonic interface. Phys. Rev. Lett. 123, 183602 (2019).
Bhaskar, M. K. et al. Experimental demonstration of memory-enhanced quantum communication. Nature 580, 60–64 (2020).
Debroux, R. et al. Quantum control of the tin-vacancy spin qubit in diamond. Phys. Rev. X 11, 041041 (2021).
Sukachev, D. D. et al. Silicon-vacancy spin qubit in diamond: A quantum memory exceeding 10 ms with single-shot state readout. Phys. Rev. Lett. 119, 223602 (2017).
Görlitz, J. et al. Spectroscopic investigations of negatively charged tin-vacancy centres in diamond. N. J. Phys. 22, 013048 (2020).
Neu, E. et al. Single photon emission from silicon-vacancy colour centres in chemical vapour deposition nano-diamonds on iridium. N. J. of Phys. 13, 025012 (2011).
Trusheim, M. E. et al. Transform-limited photons from a coherent tin-vacancy spin in diamond. Phys. Rev. Lett. 124, 023602 (2020).
Rogers, L. J. et al. Multiple intrinsically identical single-photon emitters in the solid state. Nat. Commun. 5, 4739 (2014).
Bhaskar, M. K. et al. Quantum nonlinear optics with a germanium-vacancy color center in a nanoscale diamond waveguide. Phys. Rev. Lett. 118, 223603 (2017).
van Dam, S. B. et al. Optical coherence of diamond nitrogen-vacancy centers formed by ion implantation and annealing. Phys. Rev. B 99, 161203 (2019).
Fu, K.-M. C., Santori, C., Barclay, P. E. & Beausoleil, R. G. Conversion of neutral nitrogen-vacancy centers to negatively charged nitrogen-vacancy centers through selective oxidation. Appl. Phys. Lett. 96, 121907 (2010).
De Santis, L., Trusheim, M. E., Chen, K. C. & Englund, D. R. Investigation of the stark effect on a centrosymmetric quantum emitter in diamond. Phys. Rev. Lett. 127, 147402 (2021).
Aghaeimeibodi, S., Riedel, D., Rugar, A. E., Dory, C. & Vučković, J. Electrical tuning of tin-vacancy centers in diamond. Phys. Rev. Appl. 15, 064010 (2021).
Nguyen, C. T. et al. An integrated nanophotonic quantum register based on silicon-vacancy spins in diamond. Phys. Rev. B 100, 165428 (2019).
Rugar, A. E. et al. Narrow-linewidth tin-vacancy centers in a diamond waveguide. ACS Photonics 7, 2356–2361 (2020).
Iwasaki, T. et al. Tin-vacancy quantum emitters in diamond. Phys. Rev. Lett. 119, 253601 (2017).
Tchernij, S. D. et al. Single-photon-emitting optical centers in diamond fabricated upon Sn implantation. ACS Photonics 4, 2580–2586 (2017).
Thiering, G. & Gali, A. Ab initio magneto-optical spectrum of group-IV vacancy color centers in diamond. Phys. Rev. X 8, 021063 (2018).
Chen, D. et al. Optical gating of resonance fluorescence from a single germanium vacancy color center in diamond. Phys. Rev. Lett. 123, 033602 (2019).
Becker, J. N. et al. All-optical control of the silicon-vacancy spin in diamond at millikelvin temperatures. Phys. Rev. Lett. 120, 053603 (2018).
Siyushev, P. et al. Optical and microwave control of germanium-vacancy center spins in diamond. Phys. Rev. B 96, 081201 (2017).
Thiering, G. & Gali, A. The (eg ⊗ eu) ⊗ eg product jahn–teller effect in the neutral group-iv vacancy quantum bits in diamond. npj Computational Materials 5, 18 (2019).
Gardill, A. et al. Probing charge dynamics in diamond with an individual color center. Nano Lett. 21, 6960–6966 (2021).
Deák, P., Aradi, B., Kaviani, M., Frauenheim, T. & Gali, A. Formation of NV centers in diamond: A theoretical study based on calculated transitions and migration of nitrogen and vacancy related defects. Phys. Rev. B 89, 075203 (2014).
Pu, A., Avalos, V. & Dannefaer, S. Negative charging of mono-and divacancies in IIa diamonds by monochromatic illumination. Diamond and Related Materials 10, 585–587 (2001). 11th European Conference on Diamond, Diamond-like Materials, Carbon Nanotubes, Nitrides and Silicon Carbide.
Dobrinets, I. A., Vins, V. G. & Zaitsev, A. M.HPHT-treated diamonds, vol. 181 (Springer-Verlag Berlin Heidelberg, 2013). https://www.springer.com/gp/book/9783642374890.
Slepetz, B. & Kertesz, M. Divacancies in diamond: a stepwise formation mechanism. Phys. Chem. Chem. Phys. 16, 1515–1521 (2014).
Zaitsev, M. Optical Properties of Diamond (Springer, 2001).
Kambs, B. & Becher, C. Limitations on the indistinguishability of photons from remote solid state sources. N. J. of Phys. 20, 115003 (2018).
Myerson, A. H. et al. High-fidelity readout of trapped-ion qubits. Phys. Rev. Lett. 100, 200502 (2008).
Fuchs, P., Jung, T., Kieschnick, M., Meijer, J. & Becher, C. A cavity-based optical antenna for color centers in diamond. APL Photonics 6, 086102 (2021).
Kuruma, K. et al. Coupling of a single tin-vacancy center to a photonic crystal cavity in diamond. Appl. Phys. Lett. 118, 230601 (2021).
Rugar, A. E. et al. Quantum photonic interface for tin-vacancy centers in diamond. Phys. Rev. X 11, 031021 (2021).
Acknowledgements
We thank Anna Maria Fuchs for significant contribution to reducing the computational overhead of the matrix density formalism and the enhancement measurement on the SiV ensemble. We thank Elke Neu and Richard Nelz for providing the additional microwave source and for fruitful discussions. We thank Adam Gali and Jero Maze for helpful theoretical insight and discussions on the charge cycle of colour centres in diamond. This research received funding from the European Union’s Horizon 2020 research and innovation programme under Grant Agreement No. 820394 (ASTERIQS), the EMPIR programme co-financed by the Participating States and from the European Union’s Horizon 2020 research and innovation programme (Project No. 17FUN06 SIQUST and 20FUN05 SEQUME), the German Federal Ministry of Education and Research (Bundesministerium für Bildung und Forschung, BMBF) within the projects Q.Link.X (Contract No. 16KIS0864) and QR.X (Contract No. 16KISQ001K) and the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project-ID 429529648 – TRR 306 QuCoLiMa (“Quantum Cooperativity of Light and Matter”). T.I. and M.H. acknowledge the Toray Science Foundation and the MEXT Quantum Leap Flagship Program (MEXT Q-LEAP) (Grant No. JPMXS0118067395). T.T. acknowledges support from MEXT Q-LEAP (Grant No. JPMXS0118068379) and JSPS KAKENHI (Grant No. JP20K21096).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
J.G. and D.He. designed and J.G. conceived the experiment. J.G., D.He., P.F. and C.B. discussed and designed the charge cycle model. T.I. and T.T. prepared the main sample, D.R., J.G., D.He., D.Ha. and P.-O. C. prepared the additional HPHT sample. M.H. and M.M. supervised the HPHT sample preparation for the two samples. C.B. supervised the whole project. The paper was written with input from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Görlitz, J., Herrmann, D., Fuchs, P. et al. Coherence of a charge stabilised tin-vacancy spin in diamond. npj Quantum Inf 8, 45 (2022). https://doi.org/10.1038/s41534-022-00552-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-022-00552-0