Abstract
Quantum walks represent paradigmatic quantum evolutions, enabling powerful applications in the context of topological physics and quantum computation. They have been implemented in diverse photonic architectures, but the realization of two-particle dynamics on a multidimensional lattice has hitherto been limited to continuous-time evolutions. To fully exploit the computational capabilities of quantum interference it is crucial to develop platforms handling multiple photons that propagate across multidimensional lattices. Here, we report a discrete-time quantum walk of two correlated photons in a two-dimensional lattice, synthetically engineered by manipulating a set of optical modes carrying quantized amounts of transverse momentum. Mode-couplings are introduced via the polarization-controlled diffractive action of thin geometric-phase optical elements. The entire platform is compact, efficient, scalable, and represents a versatile tool to simulate quantum evolutions on complex lattices. We expect that it will have a strong impact on diverse fields such as quantum state engineering, topological quantum photonics, and Boson Sampling.
Similar content being viewed by others
Introduction
A quantum walk1 (QW) is the quantum-mechanical analog of the classical random walk, describing the evolution of a quantum particle that moves on a discrete lattice, hopping between adjacent sites. These quantum dynamics can be either continuous or discrete in time, depending on whether the couplings between neighboring lattice positions are continuously active or can be described as sudden kicks, occurring at discrete time-steps. In the latter case, at each step the walker moves in a direction that reflects the state of a spin-like internal degree of freedom, playing the role of “quantum coin”. The growing interest in QWs is due to their potential use in diverse quantum applications, such as for instance quantum search algorithms2, quantum gates for universal quantum computation3,4,5,6, quantum state engineering7,8,9,10, and quantum simulations of topological and physical phenomena11,12,13,14,15,16,17,18,19,20,21,22,23.
Quantum walk dynamics exhibit a richer variety of phenomena when the evolution involves more than one particle. These walks indeed are characterized by multiparticle interferences24,25,26,27,28, having no classical analog and incorporating an inherent source of complexity, as highlighted by their central role in computational models such as Boson Sampling29,30. The dimensionality of the lattice where the QW takes place is also a crucial ingredient. As an example, quantum search algorithms based on QWs overcome their classical counterparts solely when the spatial dimension of the lattice is equal or greater than two31. Furthermore, two-dimensional (2D) QWs display a richer landscape of topological features when compared to the 1D case11,32.
Photonic platforms developed to implement QWs differ in terms of the methods to encode both walker and coin systems into optical degrees of freedom. Starting from the first experiments in linear optical interferometers composed of beamsplitters and phase shifters33, integrated photonic technology has enabled significantly larger instances both in their continuous-time21,26,34,35,36,37,38 and discrete-time version8,25,39,40. Other schemes rely on light polarization and orbital angular momentum degrees of freedom9,41, multimode fibers36, or fiber network loops14,15,42,43,44, where the walker position is simulated by the temporal separation between the laser pulses. Other remarkable experiments have been conducted by controlling confined waves in arrays of micro-resonators45,46. Multiparticle regimes have been already implemented in continuous-time QWs47,48,49, even in 2D lattices38. However, the demonstration of multiphoton discrete-time QWs in more than one spatial dimension has remained elusive thus far. Here we devise and experimentally validate a compact, flexible and scalable photonic platform that achieves this goal. Specifically, we realize a three-step quantum walk dynamics with coherent light, one-photon, and two-photon inputs, spanning 2, 6, and 12 modes for the first, second, and third step, respectively.
Results
Model and encoding
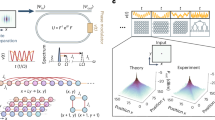
The essential elements of a discrete-time QW are captured by the single-step evolution operator U, as after t time-steps the system is described by a quantum state \(\left|{\psi }_{t}\right\rangle ={U}^{t}\left|{\psi }_{0}\right\rangle\), where \(\left|{\psi }_{0}\right\rangle\) is the input state. The operator U typically includes a spin rotation C, acting only on the coin Hilbert space, and a spin-dependent shift. When the walker moves on a 2D square lattice [see Fig. 1], the conditional shift embeds translation operators Tx and Ty along x and y directions, respectively (more details can be found in Supplementary Note 1).
Our platform builds on a recent approach to the simulation of single-particle 2D QWs using coherent laser light22. Here, the walker positions are provided by optical modes \(\left|m,n\right\rangle\) with the following spatial profile:
where A(x, y, z) is a Gaussian envelope with a large beam radius w0 in the transverse xy plane, Δk⊥ represents a quantum of transverse momentum, and the z axis is regarded as the main propagation direction. Δk⊥ fulfills the condition Δk⊥ ≪ 2π/λ, λ being the optical wavelength. Modes in Eq. (1) are essentially Gaussian beams propagating along a direction that is slightly tilted with respect to the main propagation axis [see Fig. 1a]. Photons associated with mode \(\left|m,n\right\rangle\) carry an average transverse momentum 〈(kx, ky)〉 = (mΔk⊥, nΔk⊥). Basis states of the coin space (\(\left|\downarrow \right\rangle\), \(\left|\uparrow \right\rangle\)) are encoded in right-handed (\(\left|R\right\rangle\)) and left-handed (\(\left|L\right\rangle\)) circularly polarized states, respectively. The conditional shift is realized via a liquid-crystal polarization grating, that is a g-plate22. These plates are made of a thin layer of liquid crystal, whose molecular orientation is arranged in a periodic pattern along one of the directions that are transverse to the propagation direction. Considering for instance a g-plate with modulation along the x direction, with a period Λ = 2π/Δk⊥, its action on spatial modes defined in Eq. (1), combined with circularly polarized states, has the following expression:
A similar expression holds in case the modulation is along the y axis. The parameter δ is the birefringent optical retardation of the plate, that can be adjusted by applying an external voltage across the liquid-crystal cell50. Thus, in our encoding the g-plates implement the generalized shift operators Tx(δ) and Ty(δ), with the value of δ determining the fraction of the wavefunction that is shifted to neighboring sites [see Fig. 1a]. We use optical waveplates with tunable retardation ω (based on uniformly patterned liquid-crystals) to implement adjustable coin rotations C(ω) [see Fig. 2b]. Therefore, the single-step operator is an ordered sequence of g-plates and waveplates. A large variety of QWs can be implemented with this platform, by tuning the parameters δ and ω, as already shown in ref. 22. In this work, we will focus on a fully-balanced 2D-QW protocol described by the following one-step operator U = Ty(π)C(π/4)Tx(π)C(π/4) [see Fig. 2c].
a Translation operator: g-plate. The action of a g-plate oriented along y for different values of δ. For δ = 0 the g-plate acts as the identity operator and the light beam is unchanged, while for δ = π the g-plate performs a full conversion. Finally, for all the other values of δ, the g-plates convert only partially the input beam. b Coin toss: tunable waveplate. A waveplate with tunable retardation performs the coin rotation. In the balanced case (shown in the figure), the coin toss is performed by setting ω = π/4 (quarter waveplate), implementing for instance the transformations \(\left|R\right\rangle \to \left|A\right\rangle =(\left|H\right\rangle -\left|V\right\rangle )/\sqrt{2}\) and \(\left|L\right\rangle \to \left|D\right\rangle =(\left|H\right\rangle +\left|V\right\rangle )/\sqrt{2}\). c 2D lattice encoding. The walker position on the 2D lattice is encoded in the transverse momentum of the beam. We consider a linearly polarized input beam, without a transverse momentum component. The corresponding position on the lattice is (0,0). A g-plate, oriented along y (x) with δ = π, divides a horizontally-polarized input beam in two parts, which acquire two opposite transverse momentum components along y (x), ky(x) = ± Δk⊥ or θy(x) = ± θ0. Then, after coin tossing, a second g-plate is oriented along the orthogonal direction. Four different beams with different angular deviations (±θ0, ±θ0) are obtained at the output, mapping the lattice positions (m, n) = (±1, ±1), respectively. The red lines on the images indicate the propagation direction of the Gaussian beams. The beam deviations have been overemphasized for the sake of visualization. The deflected beams remain spatially overlapping while they travel along the setup, except in the final imaging stage.
Experimental setup
The complete setup is shown in Fig. 3 (more details can be found in Supplementary Notes 2–4 and Supplementary Figs. 1–3). A photon-pair source is employed to generate and then inject single- and two-photon inputs into the quantum walk platform. In particular, in the two-photon case, an appropriate optical system is implemented to inject the two particles in different sites of the lattice, corresponding to different optical modes (see Methods). The same apparatus can be used to inject classical laser light. The quantum walk itself is implemented via a cascade of the single-step building blocks described above. Note that, by turning on and off individual g-plates in sequence, that is by setting δ to π or 0, respectively, it is possible to measure the spatial distribution of the walker after each step of the protocol. Finally, the output of the quantum walk is sent to the detection stage. In the focal plane of a lens, our modes can be spatially resolved as they form a grid of small spots. A suitable 2D fiber array and a micro-lens system are placed at this position so that each spot matches the core of the corresponding fiber in the array (see Methods). With a classical light input, the output can be measured via a charge-coupled device (CCD) camera.
Photon preparation. Two photons are generated by a spontaneous parametric down-conversion source and independently injected into single-mode fibers. Polarization controllers are employed to change their polarization state, while delay lines enable controlling their degree of indistinguishability. For two-photon inputs, both photons are injected in the QW implementation and they propagate along two parallel paths. A lens system enlarges their waist radius and introduces a relative angle between the optical modes. The relative inclinations of the optical modes represent different lattice positions. In this way, the photons start the walk at positions (−1, 0) and (1, 0) of the lattice. In the single-particle case, one of the two photons is directly measured to act as a trigger. QW implementations. The quantum walk is performed by using waveplates and g-plates arranged in a cascade configuration. Each g-plate is controlled independently by tuning its phase retardation via a voltage controller. Measurement stage. A lens system at the output stage converts the different momentum values into a spatial grid. Then, for single-photon acquisition, an array of micro-lenses is used to efficiently inject the output modes in a 2D square-lattice fiber array. Finally, each output fiber is plugged into an avalanche photodiode detector connected to a coincidence electronic system. For the coherent light data acquisition, we inserted a beamsplitter between the last lens and the micro-lense array, and we positioned the CCD on the reflected path to perform image acquisition.
We have employed our platform to implement a balanced quantum walk U with single- and two-photon inputs, up to three time-steps.
Single-photon quantum walk
We performed a single-particle experiment by injecting a single photon in position (1, 0) with polarization \(\left|D\right\rangle =(\left|H\right\rangle +\left|V\right\rangle )/\sqrt{2}\), and then measuring the output distributions after each step (obtained by sequentially switching on the g-plates). The single-photon experimental distributions are shown in Fig. 4 (related analysis for coherent light input is reported in Supplementary Note 5). The slight differences between theoretical and experimental output distributions are due to experimental imperfections such as inaccuracies of g-plates tuning values and of their relative horizontal alignment. The agreement between experimental data and the expected distributions is quantified by the similarity, defined as:
where P(t)(r) and \({\tilde{P}}^{(t)}({{{\bf{r}}}})\) are the theoretical and experimental distributions of the quantum walk at the t-th step, respectively, while r is the particle position on the lattice. The similarity value of the last step \({{{{\mathcal{S}}}}}_{1{{{\rm{p}}}}}^{(3)}=0.9773\pm 0.0002\) shows a high agreement with the expected distribution. Similar results were observed when injecting classical light to the quantum walk platform (see Table 1).
a Experimental distribution of one-particle quantum walk performed with single-photon input, in comparison with theoretical predictions after each step. Data were collected using single-photon detectors. The initial position of the walker is (1, 0) and the initial polarization is \(\left|D\right\rangle\). Shaded regions on top of each bar correspond to the experimental error at 1 standard deviation. The error bars were obtained through a bootstrapping approach. b Images reconstructed with a CCD camera with classical light inputs on the same site and with the same polarization.
Two-photon quantum walk
Next, we realized a two-photon, 2D quantum walk by injecting two photons with polarizations \(\left|A\right\rangle =(\left|H\right\rangle -\left|V\right\rangle )/\sqrt{2}\) and \(\left|D\right\rangle\) in (−1, 0) and (1, 0) lattice positions, respectively. It is worth noticing that at the input of the quantum walk the two-photon state is separable. Temporal synchronization between the particles is ensured in advance by performing a direct Hong-Ou-Mandel (HOM) measurement at the output of the quantum walk, which provides a measured visibility \(v\) = 0.95 ± 0.02. Further details on the HOM measurement are reported in Supplementary Note 6 and Supplementary Fig. 4. For the multiphoton case, the obtained theoretical and experimental distributions depicted in Fig. 5 show a high quantitative agreement. This is confirmed by their similarities defined as:
where P(t)(r1, r2) and \({\tilde{P}}^{(t)}({{{{\bf{r}}}}}_{1},{{{{\bf{r}}}}}_{2})\) are the theoretical and experimental distributions of the quantum walk at the t-th step, respectively, while r1 and r2 are the positions on the lattice of the two particles. The theoretical distribution was computed by considering an initial state described by the density matrix ρ0 = c0ρind + (1 − c0)ρdis, where ρind indicates the density matrix of two completely indistinguishable photons and ρdis is the density matrix describing two distinguishable particles. c0, that corresponds to the measured visibility of the HOM test, is equal to 0.95. For the experimental distribution at the third step, we obtain a similarity value \({{{{\mathcal{S}}}}}_{2{{{\rm{p}}}}}^{(3)}=0.914\pm 0.002\) (related results with a distinguishable two-photon input are reported in Supplementary Note 7 and Supplementary Fig. 5).
a In order to obtain a three-dimensional representation of the distributions, the two-dimensional lattice was linearized in the following way: (m, n) = m + 7n, with m, n ∈ [−3, 3]. The figure graphically shows the linearization map. b Comparison between the theoretical predictions and the measured experimental distributions with two-photon inputs. Shaded regions on top of each bar correspond to the experimental errors. The error bars were obtained through a bootstrapping approach. The bunching probabilities are highlighted by the yellow line.
Nonclassical correlation witness
The presence of nonclassical correlations in the output distributions is witnessed by applying the non-classicality test of refs. 48,51, given by:
where \({{{\Gamma }}}_{{{{{\bf{m}}}}}_{1},{{{{\bf{m}}}}}_{2}}^{({{{\rm{cl}}}})}\) is the classical probability that light exits from the m1 and m2 output ports of an interferometer. How this formula adapts to our specific case is shown in detail in Supplementary Note 7. The obtained maximum violation of the inequality are of 96, 14, and 11 standard deviations, respectively for 1, 2, and 3 QW steps, thus unambiguously proving the quantum behavior of the reported two-photon 2D quantum walk. The indistinguishability between injected photons gives rise to quantum interferences, yielding in turn probability distributions that cannot be reproduced by classical states of light. In Fig. 6, we report the complete plots of \({{{\mathcal{V}}}}\) over the standard deviation for the second and third steps, respectively. All the results of one-particle and two-particle QWs are summarized in Table 1. In the last column, we also reported the maximum value of the violation \({{{\mathcal{V}}}}\) and its error, for each step. These results highlight that the proposed platform has the potential to be employed for significantly larger instances, with a high degree of control on the implemented protocol.
a Plots of \({{{\mathcal{V}}}}({{{{\bf{r}}}}}_{1},{{{{\bf{r}}}}}_{2})\) with their error \({\sigma }_{{{{\mathcal{V}}}}}({{{{\bf{r}}}}}_{1},{{{{\bf{r}}}}}_{2})\) for the second and third step, for the lattice sites that satisfy the conditions explained in Supplementary Note 7. b Plots of \({{{\mathcal{V}}}}({{{{\bf{r}}}}}_{1},{{{{\bf{r}}}}}_{2})/{\sigma }_{{{{\mathcal{V}}}}}({{{{\bf{r}}}}}_{1},{{{{\bf{r}}}}}_{2})\), for those lattice sites where such quantity is positive, thus violating Eq. (5) for the second and the third step.
Discussion
We have presented and realized a platform for the implementation of two-dimensional, multiphoton discrete-time quantum walks, demonstrating experimentally single- and two-photon operations on a 2D squared lattice. The presented platform is compact, flexible, and enables the implementation of a large variety of different topological quantum walks22. Hence, it can represent a powerful tool for the investigation of rich dynamics that are experimentally unexplored. Recent works reported 2D continuous-time quantum walks of correlated photons, relying on arrays of coupled waveguides21,38,52, and important results have been also achieved by means of superconductive quantum processors6. We stress that our system is based on a very different approach, exploiting a synthetic 2D lattice made of internal modes of a single optical beam, as opposed to real-space neighboring lattice sites and implementing discrete-time evolutions that can be actively controlled and easily reconfigured. We believe that these different approaches may have complementary advantages. In our platform, several quantum walk protocols can be dynamically realized. This can be achieved by tuning the retardation of each plate in the range [0, π], by changing their orientation and their position in the plane transverse to the photon’s main propagation direction. By controlling these parameters, diverse single-particle QWs mimicking periodically driven Chern insulators have been reported22. Here we implement a different split-step quantum walk, that is proved to realize the Grover search algorithm in the high step-number limit53. The number of steps that can be currently realized is essentially limited by the optical losses, which are mainly due to photon reflections at each plate. However, these can be significantly reduced (from ~15% to at least ~5%) by adding a standard anti-reflection coating on the plate outer surfaces. Several applications can be foreseen, including quantum state engineering7,8,9 or quantum algorithms based on the quantum walk paradigm2,3. Furthermore, given the possibility to exploit multiphoton inputs and to control the performed transformation, this approach can also represent a promising platform for the implementation of Boson Sampling and Gaussian Boson Sampling experiments in large optical lattices30.
Methods
Photons preparation
The photon pairs used in our experiment are generated by a parametric down-conversion source, composed of a nonlinear beta barium borate crystal (BBO) pumped by a pulsed laser with λ = 392.5 nm. The generated photons, λ = 785 nm, are then injected into two identical single-mode fibers for spatial mode selection. On each fiber, an independent polarization controller allows choosing the polarization of each input photon. Then, delay lines are used to temporally synchronize the optical paths through a Hong–Ou–Mandel interference measurement.
Once the photons are temporally indistinguishable, they are injected into the QW platform. In order to precisely control the distance between the injected photons and match the coupling conditions of the fiber array, a half-mirror on one of the two paths is used. By translating this mirror, the distance between the paths can be modified from 3 to 8 mm, while its tilting can change the relative orientation between the two photons. Finally, an appropriate lens system superposes the two paths and introduces a small prescribed angle between them (see Supplementary Note 4). This relative angle corresponds to a difference in the photon transverse momentum.
Measurement stage
At the output of the quantum walk structure, a three-lens system is used to decrease the relative distance between adjacent beams and reduce the corresponding beam waists. Then, a micro-lens array, composed of a hundred micro-lenses with a short effective focal distance (~5 mm), separated by 250 μm, is used to inject the photons into a square-lattice multimode fiber array, reaching an individual waist of 15 μm without changing the corresponding distances. The adoption of the micro-lens array enables an improvement in the coupling efficiency from 0.1 to 0.75. Overall, the fiber array sets an 8 × 8 spatial grid, where the output fibers are separated by a 250 μm pitch. Each of these multimode fibers is connected to a single-photon avalanche photodiode. The output signal of each detector is directed to a coincidence apparatus, able to record single-photon counts and twofold coincidences.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
Code availability
The codes for data processing are available from the corresponding authors upon reasonable request.
References
Venegas-Andraca, S. E. Quantum walks: a comprehensive review. Quantum Inf. Process 11, 1015–1106 (2012).
Ambainis, A. Quantum search algorithms. ACM SIGACT News 35, 22–35 (2004).
Childs, A. M. Universal computation by quantum walk. Phys. Rev. Lett. 102, 180501 (2009).
Childs, A. M., Gosset, D. & Webb, Z. Universal computation by multiparticle quantum walk. Science 339, 791–794 (2013).
Yan, Z. et al. Strongly correlated quantum walks with a 12-qubit superconducting processor. Science 364, 753–756 (2019).
Gong, M. et al. Quantum walks on a programmable two-dimensional 62-qubit superconducting processor. Science 372, 948–952 (2021).
Gräfe, M. et al. On-chip generation of high-order single-photon w-states. Nat. Photonics 8, 791 (2014).
Pitsios, I. et al. Photonic simulation of entanglement growth and engineering after a spin chain quench. Nat. Commun. 8, 1569 (2017).
Giordani, T. et al. Experimental engineering of arbitrary qudit states with discrete-time quantum walks. Phys. Rev. Lett. 122, 020503 (2019).
Giordani, T. et al. Entanglement transfer, accumulation and retrieval via quantum-walk-based qubit–qudit dynamics. New J. Phys. 23, 023012 (2021).
Kitagawa, T. Topological phenomena in quantum walks: elementary introduction to the physics of topological phases. Quantum Inf. Process 11, 1107–1148 (2012).
Kitagawa, T. et al. Observation of topologically protected bound states in photonic quantum walks. Nat. Commun. 3, 882 (2012).
Cardano, F. et al. Detection of zak phases and topological invariants in a chiral quantum walk of twisted photons. Nat. Commun. 8, 15516 (2017).
Barkhofen, S. et al. Measuring topological invariants in disordered discrete-time quantum walks. Phys. Rev. A 96, 033846 (2017).
Chen, C. et al. Observation of topologically protected edge states in a photonic two-dimensional quantum walk. Phys. Rev. Lett. 121, 100502 (2018).
Xu, X. et al. Measuring a dynamical topological order parameter in quantum walks. Light Sci. Appl. 9, 1–11 (2020).
Nitsche, T. et al. Eigenvalue measurement of topologically protected edge states in split-step quantum walks. New J. Phys. 21, 043031 (2019).
Geraldi, A. et al. Experimental investigation of superdiffusion via coherent disordered quantum walks. Phys. Rev. Lett. 123, 140501 (2019).
Wang, K. et al. Simulating dynamic quantum phase transitions in photonic quantum walks. Phys. Rev. Lett. 122, 020501 (2019).
Zhan, X. et al. Detecting topological invariants in nonunitary discrete-time quantum walks. Phys. Rev. Lett. 119, 130501 (2017).
Ehrhardt, M. et al. Exploring complex graphs using three-dimensional quantum walks of correlated photons. Sci. Adv. 7, eabc5266 (2021).
D’Errico, A. et al. Two-dimensional topological quantum walks in the momentum space of structured light. Optica 7, 108 (2020).
Geraldi, A. et al. Transient subdiffusion via disordered quantum walks. Phys. Rev. Res. 3, 023052 (2021).
Sansoni, L. et al. Two-particle bosonic-fermionic quantum walk via integrated photonics. Phys. Rev. Lett. 108, 010502 (2012).
Crespi, A. et al. Anderson localization of entangled photons in an integrated quantum walk. Nat. Photonics 7, 322 (2013).
Carolan, J. et al. On the experimental verification of quantum complexity in linear optics. Nat. Photonics 8, 621–626 (2014).
Preiss, P. M. et al. Strongly correlated quantum walks in optical lattices. Science 347, 1229–1233 (2015).
Laneve, A. et al. Enhancing nonclassical bosonic correlations in a quantum walk network through experimental control of disorder. Phys. Rev. Res. 3, 033235 (2021).
Aaronson, S. & Arkhipov, A. The computational complexity of linear optics. In Proc. 43rd Annual ACM Symposium on Theory of Computing 333–342 (ACM, 2011).
Brod, D. J. et al. Photonic implementation of boson sampling: a review. Adv. Photonics 1, 034001 (2019).
Tulsi, A. Faster quantum-walk algorithm for the two-dimensional spatial search. Phys. Rev. A 78, 012310 (2008).
Asboth, J. K. & Edge, J. M. Edge-state-enhanced transport in a two-dimensional quantum walk. Phys. Rev. A 91, 022324 (2015).
Broome, M. A. et al. Discrete single-photon quantum walks with tunable decoherence. Phys. Rev. Lett. 104, 153602 (2010).
Carolan, J. et al. Universal linear optics. Science 349, 711–716 (2015).
Qiang, X. et al. Efficient quantum walk on a quantum processor. Nat. Commun. 7, 11511 (2016).
Defienne, H., Barbieri, M., Walmsley, I. A., Smith, B. J. & Gigan, S. Two-photon quantum walk in a multimode fiber. Sci. Adv. 2, e1501054 (2016).
Tang, H. et al. Experimental two-dimensional quantum walk on a photonic chip. Sci. Adv. 4, eaat3174 (2018).
Jiao, Z.-Q. et al. Two-dimensional quantum walks of correlated photons. Optica 8, 1129–1135 (2021).
Harris, N. C. et al. Quantum transport simulations in a programmable nanophotonic processor. Nat. Photonics 11, 447 (2017).
Imany, P., Lingaraju, N. B., Alshaykh, M. S., Leaird, D. E. & Weiner, A. M. Probing quantum walks through coherent control of high-dimensionally entangled photons. Sci. Adv. 6, eaba8066 (2020).
Cardano, F. et al. Quantum walks and wavepacket dynamics on a lattice with twisted photons. Sci. Adv. 1, e1500087 (2015).
Schreiber, A. et al. Photons walking the line: a quantum walk with adjustable coin operations. Phys. Rev. Lett. 104, 050502 (2010).
Schreiber, A. et al. A 2d quantum walk simulation of two-particle dynamics. Science 336, 55–58 (2012).
Weidemann, S. et al. Topological funneling of light. Science 368, 311–314 (2020).
Mittal, S., Ganeshan, S., Fan, J., Vaezi, A. & Hafezi, M. Measurement of topological invariants in a 2D photonic system. Nat. Photonics 10, 180–183 (2016).
Zhao, H. et al. Non-Hermitian topological light steering. Science 365, 1163–1166 (2019).
Szameit, A. & Nolte, S. Discrete optics in femtosecond-laser-written photonic structures. J. Phys. B 43, 163001 (2010).
Peruzzo, A. et al. Quantum walks of correlated photons. Science 329, 1500–1503 (2010).
Poulios, K. et al. Quantum walks of correlated photon pairs in two-dimensional waveguide arrays. Phys. Rev. Lett. 112, 143604 (2014).
Piccirillo, B., D’Ambrosio, V., Slussarenko, S., Marrucci, L. & Santamato, E. Photon spin-to-orbital angular momentum conversion via an electrically tunable q-plate. Appl. Phys. Lett. 97, 4085–4090 (2010).
Bromberg, Y., Lahini, Y., Morandotti, R. & Silberberg, Y. Quantum and classical correlations in waveguide lattices. Phys. Rev. Lett. 102, 253904 (2009).
Qiang, X. et al. Implementing graph-theoretic quantum algorithms on a silicon photonic quantum walk processor. Sci. Adv. 7, eabb8375 (2021).
Di Franco, C., Mc Gettrick, M. & Busch, T. Mimicking the probability distribution of a two-dimensional grover walk with a single-qubit coin. Phys. Rev. Lett. 106, 080502 (2011).
Acknowledgements
The authors acknowledge D. Poderini for software assistance and G. Amico for valuable technical support. This work was supported by the European Union Horizon 2020 program, within the European Research Council (ERC) Grant No. 694683, PHOSPhOR; by project PRIN 2017 “Taming complexity via QUantum Strategies: a Hybrid Integrated Photonic approach” (QUSHIP) Id. 2017SRNBRK.
Author information
Authors and Affiliations
Contributions
C.E., G.C., N.S., F.C., L.M. and F.S. conceived the project. C.E., M.R.B., A.D.H., G.C. and N.S. performed the experiment. C.E., M.R.B., G.C., F.C., N.S., L.M. and F.S. performed the data analysis. F.D.C., R.B., F.C. and L.M. developed the g-plate devices. All authors discussed the results and participated in preparing the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Esposito, C., Barros, M.R., Durán Hernández, A. et al. Quantum walks of two correlated photons in a 2D synthetic lattice. npj Quantum Inf 8, 34 (2022). https://doi.org/10.1038/s41534-022-00544-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-022-00544-0
This article is cited by
-
Manifestation of the quantum metric in chiral lattice systems
Communications Physics (2024)
-
Exponentially Decaying Velocity Bounds of Quantum Walks in Periodic Fields
Communications in Mathematical Physics (2023)
-
Single-photon source with sub-MHz linewidth for cesium-based quantum information processing
Frontiers of Physics (2023)