Abstract
Anonymity in networked communication is vital for many privacy-preserving tasks. Secure key distribution alone is insufficient for high-security communications. Often, knowing who transmits a message to whom and when must also be kept hidden from an adversary. Here, we experimentally demonstrate five information-theoretically secure anonymity protocols on an eight user city-wide quantum network using polarisation entangled photon pairs. At the heart of these protocols is anonymous broadcasting, which is a cryptographic primitive that allows one user to reveal one bit of information while keeping their identity anonymous. For a network of n users, the protocols retain anonymity for the sender, given that no more than n − 2 users are colluding. This is an implementation of genuine multi-user cryptographic protocols beyond standard QKD. Our anonymous protocols enhance the functionality of any fully-connected Quantum Key Distribution network without trusted nodes.
Similar content being viewed by others
Introduction
Quantum cryptography is one of the fastest-growing quantum technologies. Quantum Key Distribution (QKD) has been demonstrated across a huge spectrum of platforms1,2, and proof-of-principle demonstrations are quickly being adapted into commercial prototypes. Recent experimental progress and the development of potentially large-scale networks3,4,5,6,7 open up the possibility of a full-scale quantum internet8,9,10. Many protocols have been developed for multi-user quantum networks, such as secret voting11,12, secret sharing13,14, clock synchronisation15, and distributed blind quantum computation16; these all use multipartite states. However, multipartite states are very complex to create and the performance of protocols based on such states can degrade rapidly with losses (i.e., distance). Protocols based on bipartite states, such as the ones presented here, are often the simplest and best choice given any realistic amount of loss. Further, they are compatible with today’s state-of-the-art quantum networks, which distribute bipartite entanglement and use this to perform quantum communication.
As QKD matures as a technology, researchers turn their attention towards networked tasks beyond QKD, see, e.g., Refs. 17,18,19,20,21,22,23,24. As we build the world’s most secure networks, it is important to ensure that traffic on these networks is anonymous in addition to being impossible to decrypt. Thus, anonymity as a cryptographic primitive is becoming increasingly important for networked applications due to concerns for privacy and censorship. Applications include anonymous communication, secret auctions25 and anonymous cryptocurrency transactions26.
The first anonymous broadcating protocol was named the ‘cryptographer’s dining problem’27. There, n users establish shared secret keys with all the other users, allowing one (and only one) user to send a single bit of classical information whilst keeping their identity secret; we refer to this protocol as ‘anonymous broadcasting’. Anonymous broadcasting is a particular case of a ‘parity’ protocol that allows n users to compute the parity of their local bit strings without revealing them. Later, Broadbent et al. derived a class of information-theoretically secure protocols based on the parity protocol that allows for practical anonymous communication to take place28.
A traceless and efficient quantum anonymous broadcasting protocol was reported in Ref. 29. There, a trusted resource distributes ahead of time an n-partite entangled GHZ (Greenberger-Horne-Zeilinger) state \({\left|\psi \right\rangle }_{{{{\rm{GHZ}}}}}=\frac{1}{\sqrt{2}}\left({\left|0\right\rangle }^{\otimes n}+{\left|1\right\rangle }^{\otimes n}\right)\). While GHZ state-based networks are difficult to scale-up to many users, our approach exploits a scalable, fully connected, metropolitan-sized quantum network test bed7.
The key enabler for the anonymity protocols in Ref. 28 is anonymous broadcasting, which requires pairwise shared secret keys between the users. In our setup, we use our quantum network to distribute pairwise secret keys between all the users, then perform secure anonymous protocols. While anonymous protocols can be achieved using classical cryptography primitives, the security of such protocols remains vulnerable to every form of attack that can compromise the classical keys used. By using quantum keys, we have upgraded the classical protocols to the general security assumptions of the underlying QKD protocol. Thus the QKD keys allow us to guarantee anonymity based on the fundamental laws of physics rather than computational complexity.
After obtaining keys from QKD, we solve the classical ‘cryptographer’s dining problem’ and implement a number of practical communication protocols:
-
1.
Anonymous broadcasting (parity) allows a single user to anonymously broadcast one bit of information.
-
2.
Veto allows a single user to unilaterally stop or pass a binary decision-making task whilst remaining anonymous.
-
3.
Notification: here, a user notifies a list of others but revealing neither the number of users nor their identity.
-
4.
Collision detection is a protocol to verify whether there is a single sender or multiple senders.
-
5.
Anonymous private message transmission allows a sender to anonymously transmit an encrypted message to a receiver, despite possible malicious interference from other users. The identities of both sender and receiver remain unknown to other users in the network.
The parity protocol (1) is derived in Ref. 27, and protocols 2–5 are proposed in Ref. 28. Parity serves as a fundamental building block for the other protocols. Protocols 1–4 are combined to yield anonymous private message transmission (5).
The structure of the paper follows. In Section The Quantum Network, we introduce the quantum network we used to distribute unconditionally secure secret keys, and the experimental details are given in Section Methods. In Section Anonymous broadcasting (parity) to Anonymous private message transmission, we describe in detail the anonymous multi-user network protocols we executed using the quantum network. We present the communication rates in Section Communication rates.
Results
The quantum network
The experiment was implemented using an eight-node city-scale quantum network based on bipartite entanglement distribution described in detail in Ref. 7. Each of the eight users shares a different bipartite entangled state with every other user, forming the fully connected graph our protocols require. Furthermore, since every node directly shares entanglement with every other node, we do not make use of trusted nodes.
The network architecture can be understood as arising from the superposition of different layers, as shown in Fig. 1: (a) the physical layer consists of the hardware; (b) in the entanglement distribution layer, bipartite entanglement states are distributed and measured; (c) within the communication layer, users use authenticated classical communication channels to perform all the steps needed to generate QKD keys. The physical layer is shown in more detail in Fig. 2. It consists of the entanglement source, the multiplexers and demultiplexers needed to distribute the entanglement, a single transmission fibre for each user, and each user’s detection module with the single photon detectors.
The physical layer consists of a broadband source of bipartite polarisation entanglement that is multiplexed and distributed to several users via one fibre each. In the entanglement distribution layer, polarisation entangled states are distributed to, and measured by each user. In the communication layer, they perform classical communication to generate the QKD keys, and execute the anonymous protocols described in this paper.
The entangled photon pair source is based on a type-0 MgO:ppLN crystal pumped bidirectionally by a 775.1 nm laser. A flip-mirror and motorised half wave plate (HWP) are used to couple a tunable telecom laser into the output fibre for polarisation control. The multiplexers/demultiplexers combine the shown combination of wavelength channels and distribute them to all eight users. The channel numbers are shown here plus 34 correspond to the standard ITU 100 GHz DWDM grid. Due to energy conservation photons in channels {1,−1}, {2,−2}, and so on are the only ones entangled. Each user is connected to the central hub by one fibre. The figure also shows the setup of each user’s polarisation analysis and detection module. (PBS Polarisation beam splitter, DM Dichroic mirror, SNSPD Superconducting nanowire single photon detector, TT Time tagger, BS non-polarising Beam Splitter.
Each user measures all the photons they receive in either the horizontal/vertical (HV) or the diagonal/anti-diagonal (DA) polarisation basis. The modules to perform this measurement are shown in Fig. 2. Note that each user performs a passive basis choice using a 50:50 beam splitter and utilises just two detectors (rather than the typical four) by introducing a delay of 3.7 ns for detection events in the DA basis. Due to the distribution of photons and the measurements performed, every user now shares bipartite entanglement with every other user. This is depicted by the entanglement distribution layer (see Fig. 1).
In the communication layer, the above measurement outcomes are compared to generate a secret key following the BBM92 protocol30 of QKD. To generate the secret keys, the users exchanged arrival time information. Since our network uses a unique two-detector measurement scheme (see Ref. 7 for implementation and security proof), the basis choice reconciliation information can be extracted from the temporal cross-correlation of the arrival time of photon detection events at any two users. For every user pair, these sifted keys are error corrected using a Low-Density Parity Check (LDPC) error correction code. Every user runs multiple instances of the key generation routine to generate keys from the sifted data. We used a security parameter of 10−5 for this implementation users maintain a separate key store for every other user. The security and communication model assumptions follow from those of standard BBM9230 protocol, taking into account the details of our particular implementation7.
In summary, we use the quantum network for establishing secret keys between all users. To perform any of our anonymous protocols, users consume the desired number of bits from the appropriate key stores. Keys from the key stores are used only once.
Having established secure keys, the users can now perform multiple-party network protocols. As anticipated above, we perform five protocols: (1) anonymous broadcasting (parity), (2) veto, (3) notification, (4) collision detection, and (5) anonymous private message transmission. The relationship between the protocols is summarized in Fig. 3. The parity protocol (1) is the basic building block. All other protocols are based on it, adding more complexity and resilience against attacks. The veto protocol is instrumental for collision detection. The anonymous private message transmission is obtained by combining protocols 1–4 and represents our ultimate goal in this paper.
A schematic that shows the dependence relationship between the protocols: anonymous broadcasting (parity) is the building block for all other protocols. The anonymous private message transmission requires collision detection, veto, and notification; collision detection is also made up of two veto protocols.
Anonymous broadcasting (parity)
The prerequisite of the anonymous broadcasting protocol is that each user holds a string of n − 1 bits, in such a way that each pair of users shares a unique secret bit.
The goal of the protocol is for one of the user (called the speaker) to broadcast one bit of information to all other users anonymously. The assumption of the protocol is that there is only one speaker, and that at least two users are not colluding to guess the identity of the speaker. The classical communication protocol that achieves this goal is from Ref. 27 and is as follows:
-
1.
If the speaker wishes to broadcast the bit value c = 0, they do nothing. If, instead, they wish to broadcast the bit value c = 1, then they flip one and only one of the n − 1 bits in their local bit string.
-
2.
Each user announces the modulo-two sum (i.e., the parity) of their local bit string.
Since every secret bit enters the addition modulo-two exactly twice, if no one transmits or if the transmitted bit is c = 0, the parity of the outputs is also 0, otherwise it is equal to 1. In conclusion, the overall parity of the local strings, which is public, reveals the bit value c broadcast by the anonymous speaker.
Note that the purpose of the quantum network is to provide the unconditionally secure secret keys between each of the users, and the rest is classical. Each round of the anonymous broadcasting protocol consumes in total n(n − 1)/2 secret bits. Ref. 27 provides an information-theoretic proof of the security of the anonymous broadcasting protocol, given that each user shares a private communication channel, i.e., a secure key with one another.
Anonymity: Intuitively, the protocol is anonymous for the following reasons: since a bit-flip is applied locally, no information transmission is necessary to change the overall parity. At the same time, the parity is a global feature and does not reveal the identity of the speaker.
Security: Some of the users may cooperate to uncover the identity of the speaker. If all n − 1 users cooperate, then no protocol can keep the sender’s identity secret. However, if there are t colluding users, then all other n − t users are equally likely to be the sender.
What happens if there is more than one speaker? If more than one user flip their bit, this will lead to a collision error. Given that one speaker has sent the bit value c = 1, let p be the probability that another speaker also wants to communicate the same bit value. An error in the overall parity value depends on having an odd or even number of additional speakers. The probability that i users want to communicate and n − i − 1 do not is pi(1−p)n−i−1. Summing over odd values of i and overall permutations of the users, we obtain
Collision errors become more problematic as the number of users becomes large. The collision detection protocol discussed in Subsection Collision detection addresses this issue.
Veto
The goal of this protocol is to allow the users to agree on a resolution unanimously, in such a way that if one or more users veto it, their identities remain undisclosed. Note that the parity protocol is unsuitable to achieve this goal. In fact, in the event of a collision with an even number of users transmitting the bit 1, the parity of the overall output will be 0.
Here, the aims of dishonest users would be to (1) uncover who has vetoed, (2) over turn the veto by attempting to set the overall parity to 0. Furthermore, (3) if the parity announcements are not simultaneous, the last user to announce their parity can always choose their input such that the overall parity is 0. The parity protocol ensures that (1) is not possible, (2) is addressed by introducing the auxiliary random variable ci, and (3) is solved by changing the ordering of the users, as explained below.
To overcome these limitations, the users repeat the parity protocol βn times, for some integer β > 1, that plays the role of a success probability parameter. For each implementation of the parity protocol, the order in which the users announce their local parity is changed, in such a way that each user has the opportunity to have the last word β times. Therefore, the prerequisite of the veto protocol is that each users pair shares βn secret random bits. This time it is allowed to have more than one speaker.
We assign to each user a binary variable. If the ith user chooses to veto, then xi = 1, otherwise xi = 0. The final output is 1 if at least one user submits the bit 1: therefore, the output of the veto protocol, when successful, is effectively the logical OR function of all of the xi’s, allowing all users to cast a vote.
The protocol is as follows28:
-
1.
The n users agree on n orderings such that each ordering has a different last user. This step ensures that every user has a chance to be the last to broadcast. By changing the last user each round, the protocols ensure the last user cannot manipulate the result.
-
2.
For each ordering, the following is repeated β times:
-
(a)
Depending on xi, each user sets the value of another binary variable, ci, in the following way: if xi = 0, then ci = 0; otherwise if xi = 1, then ci is chosen randomly.
-
(b)
The users execute the anonymous broadcasting protocol with inputs {ci}. That is, if ci = 0, they do nothing, and if ci = 1, they flip the bit value of one of their modulo-two sum.
-
(c)
If the parity at any round is 1, or if any user refuses to broadcast, then the result is set to 1 (implying a veto).
-
(a)
If for any of the β rounds the output is 1, then we know someone has vetoed. The value of ci is randomly chosen to be either 0 or 1, so that if an even number of people want to veto, they do not end up with an even number of collisions all the time.
A single round of the veto protocol consumes βn2(n − 1)/2 secret bits and succeeds with probability at least 1 − 2−β. If all users in the protocol have xi = 0, then the inputs to the anonymous broadcasting protocols are ci = 0, then the output of the protocol is 0 with probability 1.
The protocol is designed such that a potential adversary is helpless to over turn the veto: suppose they want to set the output to be 0, then it is unfruitful for them to perform any action preemptively, since they do not know the value of the speaker’s bit ci.
Notification
The notification protocol allows any user to notify any other users, in such a way that the identities of both the notifier and the recipients remain secret, as well as the number of recipients. The notification protocol is essentially the veto protocol, except the potential recipient does not broadcast. It will be used as an intermediate step to achieve anonymous private message transmission.
For n users, each user has a n-bit string \(({x}_{j}^{1},\ldots ,{x}_{j}^{n})\), where the index j = 1, …, n label the users. If user j wants to notify user i, he/she sets \({x}_{j}^{i}=1\), and 0 otherwise. For each user i waiting to be notified, the following is repeated β times
-
1.
Each user j ≠ i sets the value of another bit, \({c}_{j}^{i}\), in the following way: if \({x}_{j}^{i}=0\), then \({c}_{j}^{i}\) = 0; if \({x}_{j}^{i}=1\), then \({c}_{j}^{i}\) is chosen randomly.
-
2.
The parity protocol is executed with inputs \({c}_{1}^{i},{c}_{2}^{i},\ldots ,{c}_{n}^{i}\), with the exception that user i does not broadcast.
-
3.
user i computes the overall parity in secret; he/she is notified if the parity is 1 for any run of the protocol.
Each round of the notification protocol consumes βn2(n − 1)/2 secret bits, and succeeds with probability at least 1 − 2−β.
Collision detection
As we have seen above, the parity protocol assumes that only one user wants to speak. Here we modify it in such a way that the protocol detects if more there is more than one speaker. Collision detection will be implemented as a part of anonymous private message transmission. The protocol is divided into two steps, A and B.
Step A is an application of the veto protocol. Each user who wants to speak inputs a bit value xi = 1, or xi = 0 otherwise. Note that if a user is a speaker, at the end of the veto protocol, they know (with high confidence if β is chosen large enough) if they are the only speaker. However, this information needs to remain private in order to protect the identity of the speaker.
Step B is a second run of the veto protocol. If during step A a speaker has detected the presence of another speaker, i.e., there was a collision, then they input the bit value bi = 1. In this way, all the users will be notified of the collision.
The three outcomes for the collision detection protocol are:
These correspond to no speaker, single speaker, and multiple speakers respectively. The collision detection protocol consumes at most βn2(n − 1) secret bits, and succeeds with probability at least \({(1-{2}^{-\beta })}^{2}\).
Anonymous private message transmission
The anonymous private message transmission allows a sender to anonymously transmit an encrypted message to a receiver. To send an m-bit message, each user pair needs to share \((m+2(\log [m+1]+\beta ))+4\beta n\) secret random bits with one another. The protocol first deals with potential collisions, verifying whether there is a single sender. Then the sender anonymously notifies the receiver (and only the receiver) that they are about to receive a message, followed by the message transmission. The message is encoded with an error detection code, which maps a m-bit string onto a \(m^{\prime} =m+2\gamma\)-bit string, where \(\gamma\, < \,\beta +\log (m+1)\). The decoding process reveals whether the message has been tampered with, with success probability 1 − 2−β31. See Supplementary Material for details of the encoding and decoding. The protocol follows.
-
1.
The users execute the collision detection protocol, and continue if there is a single sender.
-
2.
Denote the unique sender as S and the receiver as R. The users perform the notification protocol, where S notifies that R is to receive a message.
-
3.
The following message transmission protocol is executed:
-
(a)
The sender encodes the message using an algebraic manipulation and detection code (see Supplementary Material), which maps the message M (of length m bits) into \(M^{\prime}\), which has length \(m^{\prime} \approx m+2(\log m+\beta )\) bits.
-
(b)
The users perform \(m^{\prime}\) rounds of the parity, where S uses \(M^{\prime}\) as the input, R uses a random \(m^{\prime}\)-bit string r as the input (a one-time pad), and all other users input 0 at every round.
-
(c)
Let d be the output of the \(m^{\prime}\) anonymous broadcasting protocol. The receiver computes M″ = d ⊕ r.
-
(d)
A veto protocol is performed. Everyone inputs 0 except for the receiver, who inputs 1 if an error is detected in the message, otherwise she inputs 0. If the output of veto is 1, this broadcasts to the sender that the message has been corrupted.
-
(a)
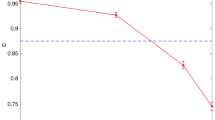
For anonymous private message transmission, we define the efficiency of the encoding as m/(m + 2γ), which is the ratio of the message length to the required encoding. We plot m/(m + 2γ) for β = 16 in Fig. 4. Evidently, the longer the input message, the more efficient the encoding becomes. For the experiment, we used two encodings. We map a 512 and 1024-bit message to a 554 and 1068-bit encoding, respectively, with γ = 21 (for the 512-bit message) and 22 (for the 1 kb message).
Ideally, we would like all protocols to be jamming-proof. However, the ideal functionality cannot always be achieved, since a single party can make the message transmission protocol abort. This is the price to pay to tolerate an arbitrary number of corrupt users and still provide information-theoretic privacy of the inputs28.
Communication rates
We successfully implemented the five anonymous protocols on our quantum network testbed consisting of eight simultaneously connected users without trusted nodes. Our fully connected network, where every user exchanges secure keys with every other, is crucial to the implementation of these protocols. The superconducting detectors used provide roughly 18.4 h of continuous operation before the cryostats need to be thermally cycled. During this ~ 18 h run of the network, we chose to implement the basic anonymous broadcasting protocol throughout, then use this to implement the other four protocols one by one.
To demonstrate the stability of our network, we show the rate at which the protocols can be performed over the 18.4 h in Fig. 5. To be able to account for finite key effects with a security parameter of 10−5, we generated the private keys once every 20 min. For each protocol, we use keys generated over a total time of 280 min. Due to the nature of the anonymous broadcasting protocol, the rate at which the protocol can be implemented is limited by the slowest link. This can be seen in the disparity between the average key rate and the anonymous broadcasting rate.
We show: the data the average key generation rate across all the links (green dotted line), anonymous broadcasting (parity) (blue solid line) and rate at which veto (purple crosses), notification (yellow diamonds), collision detection (black triangles) and message transmission (red stars) were performed. To ensure a minimum success probability of >99.99% (1 for veto) we used β = 16. Here the keys are generated every 20 min while including finite key effects.
We implemented the veto protocol, for a random mixture of input 0 and 1’s, likewise for the collision detection protocol. The veto protocol consumes the equivalent of only a few rounds of the anonymous broadcasting protocol if the input is 1, and βn rounds if the input is 0. The notification protocol consumes βn rounds regardless of the input. We believe that these protocols will prove to be useful for voting-based applications and truly private social media. Collision detection must become an important part of any anonymous network application. We believe that this could form the basis of a completely anonymous network control plane, which could optimally allocate resources and communication bandwidth without collecting individual users’ network usage information.
For anonymous private message transmission, the protocol requires running an anonymous collision detection, veto and notification step. Thus the total number of bits consumed is larger. We executed the anonymous private message protocol using a mixture of 1 kb and 0.5 kb message lengths. The communication efficiency, which is the number of bits transmitted per parity protocol, is at least \(m/(m+2\log m+2\beta +4\beta n)\). The term of 4βn is due to the overheads associated with the sub-routines of collision detection, notification and veto protocols. This rate can be made arbitrarily close to 1 by choosing m large enough.
A summary of the number of secret bits consumed by each protocol is given in Table 1. We note that our protocols are tolerant to errors in the secure keys, and we discuss how in the Supplementary Material.
Discussions
Quantum communication networks have largely focused on key distribution. Here, we have shown how these networks can be used to protect user privacy, a task often just as important as ensuring that a transmitted message is secure. In this work, we have implemented a set of five information-theoretically secure anonymous protocols – broadcasting, veto, notification, collision detection, and anonymous private message transmission on an eight-user quantum network. Since every user in the network shares a perfectly random, private and secure key with every other user, it becomes possible to implement these protocols. All the above protocols can be used as primitives for a wide range of applications.
We anticipate that the most useful protocol would be anonymous private message transmission, which allows one user to send an arbitrary-sized message to another user in secret. This has important implications for privacy-preserving applications, such as tipping off the police anonymously26, secret voting, secure electronic auctions25, and anonymous cryptocurrency transactions32, multi-party computation33 etc. Here we provide an explicit construction for the encoding and decoding of the message.
The above protocols only preserve anonymity within a single quantum network and their usefulness will grow as the size of the network increases. Maintaining anonymity in networks where active switching is used to choose which users can communicate at any given point in time or in scenarios where independent quantum networks are interconnected remains an open challenge.
We have used secret keys generated via QKD to perform protocols that allow for complete anonymity in a communication network. Our experiment represents quantum communications protocols beyond point-to-point QKD. It thus demonstrates the capabilities of a quantum network to realise non-trivial security tasks even when quantum memories are not available.
Methods
Experimental setup
The entangled states are all produced by a single broadband source of polarisation entangled photon pairs. Polarisation entanglement is used to simplify each user’s measurement module and is also compatible with long distance passively stable distribution over deployed fibres34,35. The output is de-multiplexed into 16 wavelength channels using International Telecommunications Union (ITU) 100 GHz top hat Dense Wavelength Division Multiplexing (DWDM) channels. The source itself is based on spontaneous parametric down-conversion of a 775.1 nm pump beam in a Magnesium oxide doped Periodically Poled Lithium Niobate (MgO:ppLN) crystal within a Sagnac interferometer, producing degenerate entangled photons centred at 1550.2 nm (which coincides with the 100 GHz (i.e.,0,8 nm) wide ITU channel Ch34 at 1550.12 nm) with a Full Width at Half Maximum bandwidth of ≈ 60 nm. Due to energy conservation during down-conversion, pairs are only found in channels at equal spectral distance from the central frequency. A 50-50 fibre beam splitter, attached to each DWDM channel, sends photons randomly to one of two output ports, which is equivalent to passive time division multiplexing. A multiplexing stage combines the channels together such that every user receives four frequency channels containing photons whose entangled partner photons were routed to four other users. The additional passive time division multiplexing due to the beam splitters expands the number of users in the network to eight, and ensures that every user shares entangled states with all seven other users.
Data availability
All data from this publication is stored for at least 10 years on the University of Bristol’s Research Data Storage Facility (RDSF). The processed data for the findings in this paper and programs to execute all protocols are available publicly from the RDSF, the raw data consisting of timetag files is too large to host publicly and available from the corresponding author (S.K.J.) on request.
Change history
01 June 2022
A Correction to this paper has been published: https://doi.org/10.1038/s41534-022-00575-7
References
Scarani, V. et al. The security of practical quantum key distribution. Rev. Mod. Phys 81, 1301 (2009).
Pirandola, S. et al. Advances in quantum cryptography. Adv. Opt 12, 1012 (2020).
Bradley, C. et al. A ten-qubit solid-state spin register with quantum memory up to one minute. Phys. Rev. X 9, 031045 (2019).
Yin, J. et al. Satellite-based entanglement distribution over 1200 kilometers. Science 356, 1140–1144 (2017).
Sun, Q.-C. et al. Quantum teleportation with independent sources and prior entanglement distribution over a network. Nat. Photon 10, 671–675 (2016).
Wengerowsky, S., Joshi, S. K., Steinlechner, F., Hübel, H. & Ursin, R. An entanglement-based wavelength-multiplexed quantum communication network. Nature 564, 225 (2018).
Joshi, S. K. et al. A trusted node–free eight-user metropolitan quantum communication network. Sci. Adv. 6, eaba0959 (2020).
Wehner, S., Elkouss, D. & Hanson, R. Quantum internet: A vision for the road ahead. Science 362, eaam9288 (2018).
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Li, G. Information Science & Technology in China: A Roadmap to 2050 (Springer, 2011).
Vaccaro, J. A., Spring, J. & Chefles, A. Quantum protocols for anonymous voting and surveying. Phys. Rev. A 75, 012333 (2007).
Hillery, M., Ziman, M., Bužek, V. & Bieliková, M. Towards quantum-based privacy and voting. Phys. Lett. A 349, 75–81 (2006).
Xiao, L., Long, G. L., Deng, F.-G. & Pan, J.-W. Efficient multiparty quantum-secret-sharing schemes. Phys. Rev. A 69, 052307 (2004).
Hillery, M., Bužek, V. & Berthiaume, A. Quantum secret sharing. Phys. Rev. A 59, 1829 (1999).
Komar, P. et al. A quantum network of clocks. Nat. Phys 10, 582–587 (2014).
Beals, R. et al. Efficient distributed quantum computing. Proc. Math. Phys. Eng. Sci. 469, 20120686 (2013).
Zhao, Z. et al. Experimental demonstration of five-photon entanglement and open-destination teleportation. Nature 430, 54–58 (2004).
Yao, X.-C. et al. Observation of eight-photon entanglement. Nat. Photon 6, 225–228 (2012).
Hahn, F., de Jong, J. & Pappa, A. Anonymous quantum conference key agreement. PRX Quantum 1, 020325 (2020).
Hahn, F. et al. Anonymous conference key agreement in quantum networks. Preprint at https://arxiv.org/abs/2007.07995v1 (2020).
Pappa, A. et al. Experimental plug and play quantum coin flipping. Nat. Commun 5, 1–8 (2014).
Solomons, N. R. et al. Scalable authentication and optimal flooding in a quantum network. Preprint at https://arxiv.org/abs/2101.12225v1 (2021).
Ng, N. H. Y., Joshi, S. K., Ming, C. C., Kurtsiefer, C. & Wehner, S. Experimental implementation of bit commitment in the noisy-storage model. Nat. Commun 3, 1–7 (2012).
Zhou, H., Lv, K., Huang, L. & Ma, X. Security assessment and key management in a quantum network. arXiv:1907.08963 (2019).
Stajano, F. & Anderson, R. The cocaine auction protocol: On the power of anonymous broadcast. In International Workshop on Information Hiding, 434–447 (Springer, 1999).
Menicucci, N. C., Baragiola, B. Q., Demarie, T. F. & Brennen, G. K. Anonymous broadcasting of classical information with a continuous-variable topological quantum code. Phys. Rev. A 97, 032345 (2018).
Chaum, D. The dining cryptographers problem: Unconditional sender and recipient untraceability. J. Cryptol. 1, 65–75 (1988).
Broadbent, A. & Tapp, A. Information-theoretic security without an honest majority. In International Conference on the Theory and Application of Cryptology and Information Security, 410–426 (Springer, 2007).
Christandl, M. & Wehner, S. Advances in Cryptology–ASIACRYPT 2005, Proceedings 3788, 217–235 (2005).
Bennett, C. H., Brassard, G. & Mermin, N. D. Quantum cryptography without bell’s theorem. Phys. Rev. Lett. 68, 557 (1992).
Cramer, R., Dodis, Y., Fehr, S., Padró, C. & Wichs, D. Detection of algebraic manipulation with applications to robust secret sharing and fuzzy extractors. In Annual International Conference on the Theory and Applications of Cryptographic Techniques, 471–488 (Springer, 2008).
Ruffing, T., Moreno-Sanchez, P. & Kate, A. P2p mixing and unlinkable bitcoin transactions. In NDSS, 1–15 (2017).
Movahedi, M., Saia, J. & Zamani, M. Secure anonymous broadcast. Preprint at http://arXiv:1405.5326 (2014).
Wengerowsky, S. et al. Entanglement distribution over a 96-km-long submarine optical fiber. PNAS 116, 6684–6688 (2019).
Wengerowsky, S. et al. Passively stable distribution of polarisation entanglement over 192 km of deployed optical fibre. Npj Quantum Inf. 6, 1–5 (2020).
Acknowledgements
The research leading to this work has received funding from the Engineering and Physical Science Research Council (EPSRC) Quantum Communications Hubs EP/M013472/1 & EP/T001011/1 and equipment procured by the QuPIC project EP/N015126/1. Z.H. is supported by a Sydney Quantum Academy Fellowship. We acknowledge the Ministry of Science and Education (MSE) of Croatia, contract No. KK.01.1.1.01.0001. We acknowledge financial support from the Austrian Research Promotion Agency (FFG) project ASAP12-85 and project SatNetQ 854022. This work was partially supported by the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement number 675662 (QCALL). The authors would also like to thank Peter P. Rohde for insightful discussions.
Author information
Authors and Affiliations
Contributions
The theoretical aspects of this work was led by Z.H. with help from C.L. and A.O.Q. The experimental team was led by S.K.J. with D.A., S.W., M.L., S.P.N., Z.S., L.K., M.S., R.U. and J.G.R. Z.H. and S.K.J. contributed equally to this work. The software for processing the keys and implementing the algorithms was written by N.V., Z.H. and B.L. with help from S.K.J. The user modules were built by M.L., Z.S. and M.S., the source by S.W., S.P.N., S.K.J. and R.U. The multiplexing and distribution scheme was built by D.A. Funding for this work was obtained by J.G.R. with help from S.K.J. and D.A. S.K.J. coordinated the project. The paper was written by Z.H., S.K.J., D.A., C.L. and A.O.Q., the other authors proofread. All authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Huang, Z., Joshi, S.K., Aktas, D. et al. Experimental implementation of secure anonymous protocols on an eight-user quantum key distribution network. npj Quantum Inf 8, 25 (2022). https://doi.org/10.1038/s41534-022-00535-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-022-00535-1
This article is cited by
-
Advancements in Quantum Optics: Harnessing the Power of Photons for Next-Generation Technologies
Journal of Optics (2023)
-
A fully-connected three-user quantum hyperentangled network
Quantum Frontiers (2023)